Riemannian Manifolds for Biological Imaging Applications Based on Unsupervised Learning
Abstract
:1. Introduction
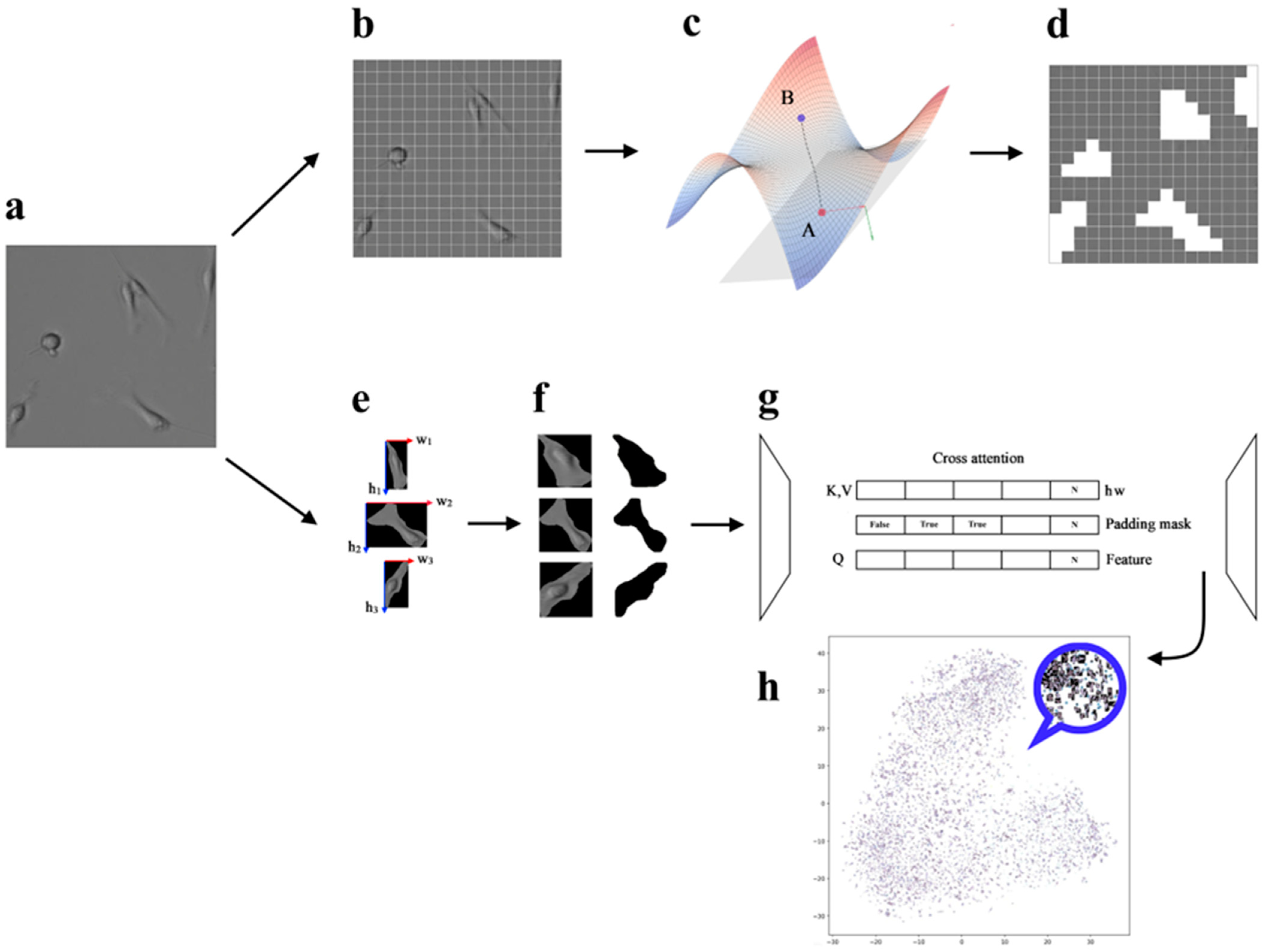
2. Materials and Methods
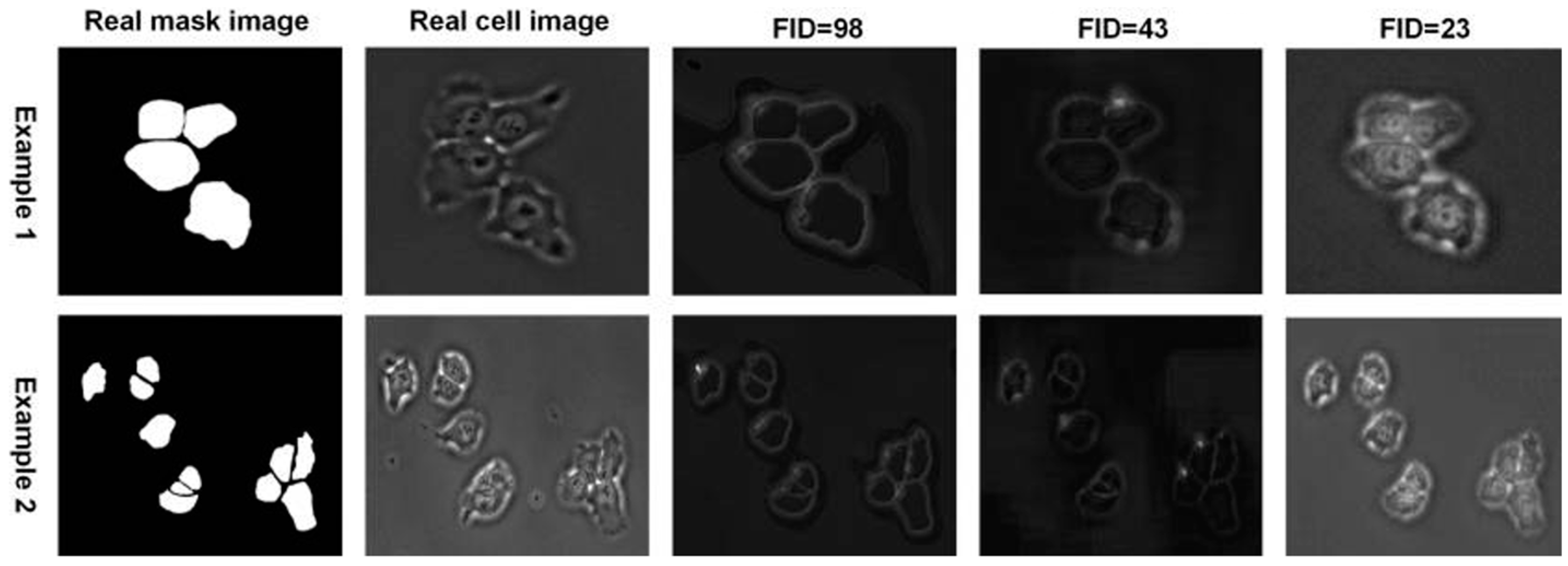
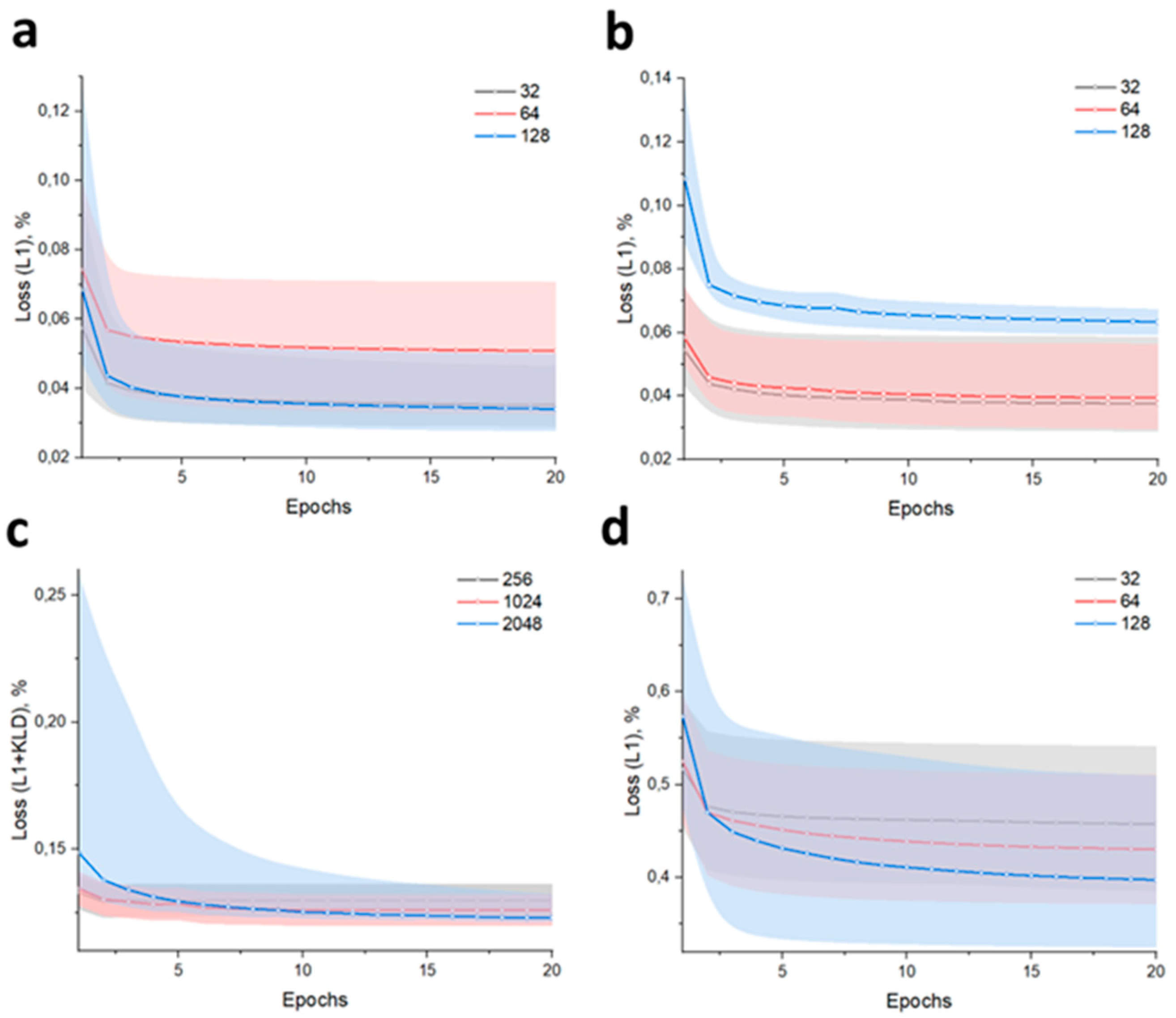
3. Results and Discussion
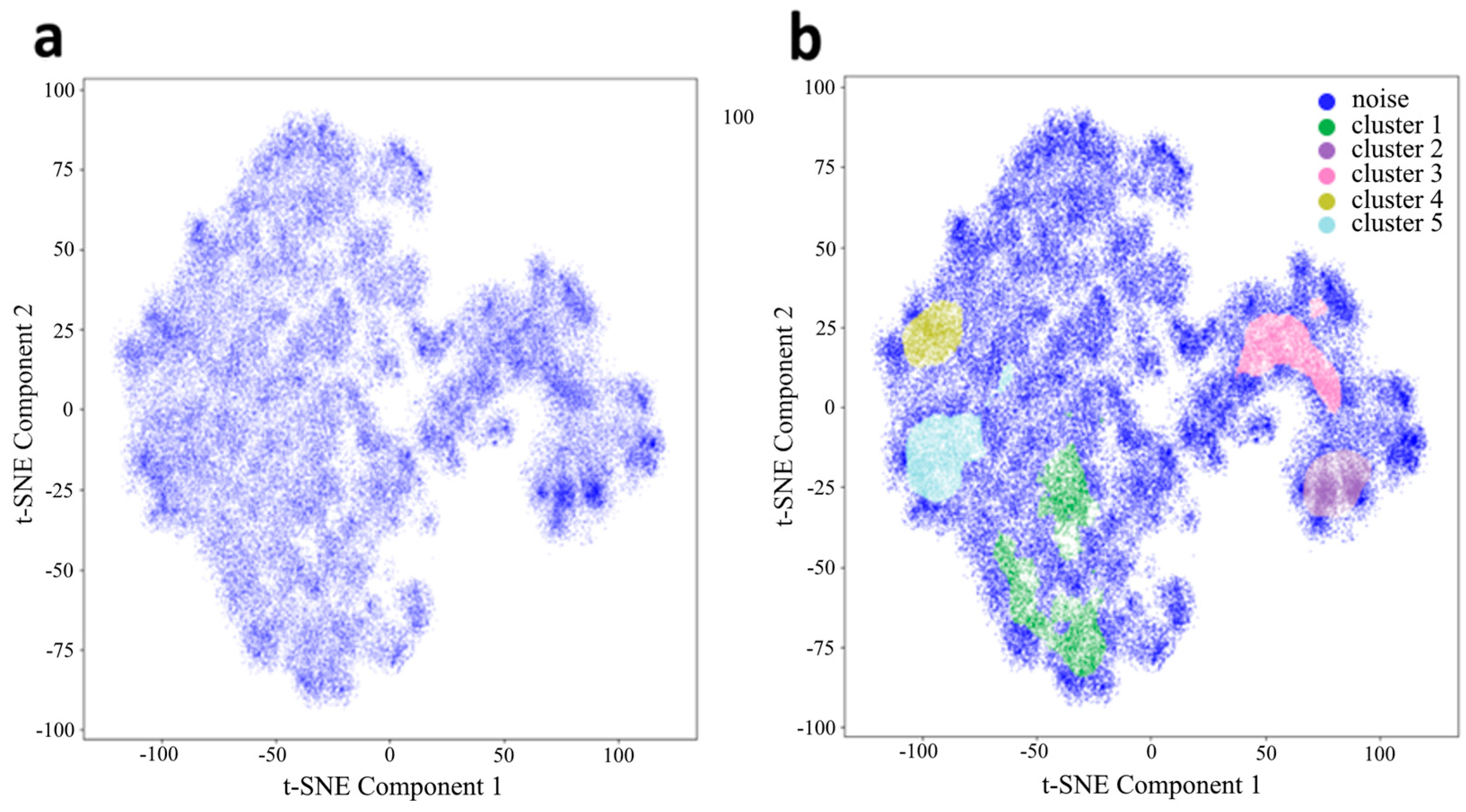
3.1. Low-Dimension Representation
3.2. Riemannian Manifold
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maška, M.; Ulman, V.; Delgado-Rodriguez, P.; Gómez-De-Mariscal, E.; Nečasová, T.; Peña, F.A.G.; Ren, T.I.; Meyerowitz, E.M.; Scherr, T.; Löffler, K.; et al. The cell tracking challenge: 10 years of objective benchmarking. Nat. Methods 2023, 20, 1010–1020. [Google Scholar] [CrossRef] [PubMed]
- Stringer, C.; Pachitariu, M. Cellpose3: One-click image restoration for improved cellular segmentation. bioRxiv 2024. preprint. [Google Scholar] [CrossRef] [PubMed]
- López, C.; Lejeune, M.; Bosch, R.; Korzyńska, A.; García-Rojo, M.; Salvadó, M.-T.; Alvaro, T.; Callau, C.; Roso, A.; Jaén, J. Digital image analysis in breast cancer: An example of an automated methodology and the effects of image compression. In Perspectives on Digital Pathology; IOS Press: Amsterdam, The Netherland, 2012; pp. 155–171. [Google Scholar]
- Xing, F.; Yang, L. Robust nucleus/cell detection and segmentation in digital pathology and microscopy images: A comprehensive review. IEEE Rev. Biomed. Eng. 2016, 9, 234–263. [Google Scholar] [CrossRef]
- Kromp, F.; Fischer, L.; Bozsaky, E.; Ambros, I.M.; Dörr, W.; Beiske, K.; Ambros, P.F.; Hanbury, A.; Taschner-Mandl, S. Evaluation of deep learning architectures for complex immunofluorescence nuclear image segmentation. IEEE Trans. Med. Imaging 2021, 40, 1934–1949. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Cheung, A.M.; Yaffe, M.J.; Martel, A.L. Cell segmentation for immunofluorescence multiplexed images using two-stage domain adaptation and weakly labeled data for pre-training. Sci. Rep. 2022, 12, 4399. [Google Scholar] [CrossRef]
- Caicedo, J.C.; Roth, J.; Goodman, A.; Becker, T.; Karhohs, K.W.; Broisin, M.; Molnar, C.; McQuin, C.; Singh, S.; Theis, F.J.; et al. Evaluation of deep learning strategies for nucleus segmentation in fluorescence images. Cytom. Part A 2019, 95, 952–965. [Google Scholar] [CrossRef]
- Larin, I.I.; Shatalova, R.O.; Laktyushkin, V.S.; Rybtsov, S.A.; Lapshin, E.V.; Shevyrev, D.V.; Karabelsky, A.V.; Moskalets, A.P.; Klinov, D.V.; Ivanov, D.A. Deep Learning for Cell Migration in Nonwoven Materials and Evaluating Gene Transfer Effects following AAV6-ND4 Transduction. Polymers 2024, 16, 1187. [Google Scholar] [CrossRef]
- Niioka, H.; Asatani, S.; Yoshimura, A.; Ohigashi, H.; Tagawa, S.; Miyake, J. Classification of C2C12 cells at differentiation by convolutional neural network of deep learning using phase contrast images. Hum. Cell 2018, 31, 87–93. [Google Scholar] [CrossRef]
- Yao, K.; Rochman, N.D.; Sun, S.X. Cell type classification and unsupervised morphological phenotyping from low-resolution images using deep learning. Sci. Rep. 2019, 9, 13467. [Google Scholar] [CrossRef]
- Khwaja, E.; Song, Y.S.; Agarunov, A.; Huang, B. CELLE-2: Translating Proteins to Pictures and Back with a Bidirectional Text-to-Image Transformer. Adv. Neural Inf. Process. Syst. 2024, 36, 4899–4914. [Google Scholar]
- Carnevali, D.; Zhong, L.; González-Almela, E.; Viana, C.; Rotkevich, M.; Wang, A.; Franco-Barranco, D.; Gonzalez-Marfil, A.; Neguembor, M.V.; Castells-Garcia, A.; et al. A deep learning method that identifies cellular heterogeneity using nanoscale nuclear features. Nat. Mach. Intell. 2024, 6, 1021–1033. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Yang, F.; Huang, L.; Li, W.; Song, J.; Gasser, R.B.; Aebersold, R.; Wang, G.; Yao, J. Deep domain adversarial neural network for the deconvolution of cell type mixtures in tissue proteome profiling. Nat. Mach. Intell. 2023, 5, 1236–1249. [Google Scholar] [CrossRef]
- Ma, J.; Xie, R.; Ayyadhury, S.; Ge, C.; Gupta, A.; Gupta, R.; Gu, S.; Zhang, Y.; Lee, G.; Kim, J.; et al. The multimodality cell segmentation challenge: Toward universal solutions. Nat. Methods 2024, 21, 1103–1113. [Google Scholar] [CrossRef]
- Jing, Y.; Wang, X.; Tao, D. Segment anything in non-euclidean domains: Challenges and opportunities. arXiv 2023, arXiv:2304.11595. [Google Scholar]
- Liu, X.; Huang, W.; Zhang, Y.; Xiong, Z. Biological Instance Segmentation with a Superpixel-Guided Graph. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence (IJCAI-22), Vienna, Austria, 23–29 July 2022; pp. 1209–1215. [Google Scholar]
- Lin, S.; Sabyrbayev, T.; Jin, Z.; Li, G.; Cao, H.; Zou, D. TopoUT: Enhancing Cell Segmentation Through Efficient Topological Regularization. In Proceedings of the 2024 IEEE International Symposium on Biomedical Imaging (ISBI), Athens, Greece, 27–30 May 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Lin, Y.; Zhang, D.; Fang, X.; Chen, Y.; Cheng, K.T.; Chen, H. Rethinking boundary detection in deep learning models for medical image segmentation. In International Conference on Information Processing in Medical Imaging; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Yao, K.; Huang, K.; Sun, J.; Jude, C. Ad-gan: End-to-end unsupervised nuclei segmentation with aligned disentangling training. arXiv 2021, arXiv:2107.11022. [Google Scholar]
- Zargari, A.; Topacio, B.R.; Mashhadi, N.; Shariati, S.A. Enhanced cell segmentation with limited training datasets using cycle generative adversarial networks. Iscience 2024, 27, 109740. [Google Scholar] [CrossRef]
- Stringer, C.; Wang, T.; Michaelos, M.; Pachitariu, M. Cellpose: A generalist algorithm for cellular segmentation. Nat. Methods 2020, 18, 100–106. [Google Scholar] [CrossRef]
- Serna-Aguilera, M.; Luu, K.; Harris, N.; Zou, M. Neural Cell Video Synthesis via Optical-Flow Diffusion. arXiv 2022, arXiv:2212.03250. [Google Scholar]
- Lu, H.; Yang, G.; Fei, N.; Huo, Y.; Lu, Z.; Luo, P.; Ding, M. sVdt: General-purpose video diffusion transformers via mask modeling. arXiv 2023, arXiv:2305.13311. [Google Scholar]
- Liu, C.; Liao, D.; Parada-Mayorga, A.; Ribeiro, A.; DiStasio, M.; Krishnaswamy, S. Diffkillr: Killing and recreating diffeomorphisms for cell annotation in dense microscopy images. arXiv 2024, arXiv:2410.03058. [Google Scholar]
- Cherian, A.; Sra, S. Riemannian dictionary learning and sparse coding for positive definite matrices. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2859–2871. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larin, I.; Karabelsky, A. Riemannian Manifolds for Biological Imaging Applications Based on Unsupervised Learning. J. Imaging 2025, 11, 103. https://doi.org/10.3390/jimaging11040103
Larin I, Karabelsky A. Riemannian Manifolds for Biological Imaging Applications Based on Unsupervised Learning. Journal of Imaging. 2025; 11(4):103. https://doi.org/10.3390/jimaging11040103
Chicago/Turabian StyleLarin, Ilya, and Alexander Karabelsky. 2025. "Riemannian Manifolds for Biological Imaging Applications Based on Unsupervised Learning" Journal of Imaging 11, no. 4: 103. https://doi.org/10.3390/jimaging11040103
APA StyleLarin, I., & Karabelsky, A. (2025). Riemannian Manifolds for Biological Imaging Applications Based on Unsupervised Learning. Journal of Imaging, 11(4), 103. https://doi.org/10.3390/jimaging11040103





