Assessing Cancer Presence in Prostate MRI Using Multi-Encoder Cross-Attention Networks
Abstract
:1. Introduction
- Establishing a new performance benchmark adopting and processing the largest and most diverse multi-centric PCa MR image database worldwide (6458 retrospective cases and 436 prospective cases)
- Design and implementation of a classification scheme to distinguish pathologically confirmed PCa patients from conditions with no suspicious PCa findings from whole MRI volumes
- Introducing a novel multi-encoder-cross-sequence attention neural network architecture for bpMRI data, enhanced by the integration of clinical variables
- The proposed architecture shows better generalisation performance, AUC of 0.87, in an out-of-distribution setting compared to radiologists (AUC of 0.76) and other architectures frequently used in the literature (AUC of 0.80 and 0.84), respectively.
- Thorough fairness analysis to identify potential biases in the modelling process
2. Materials and Methods
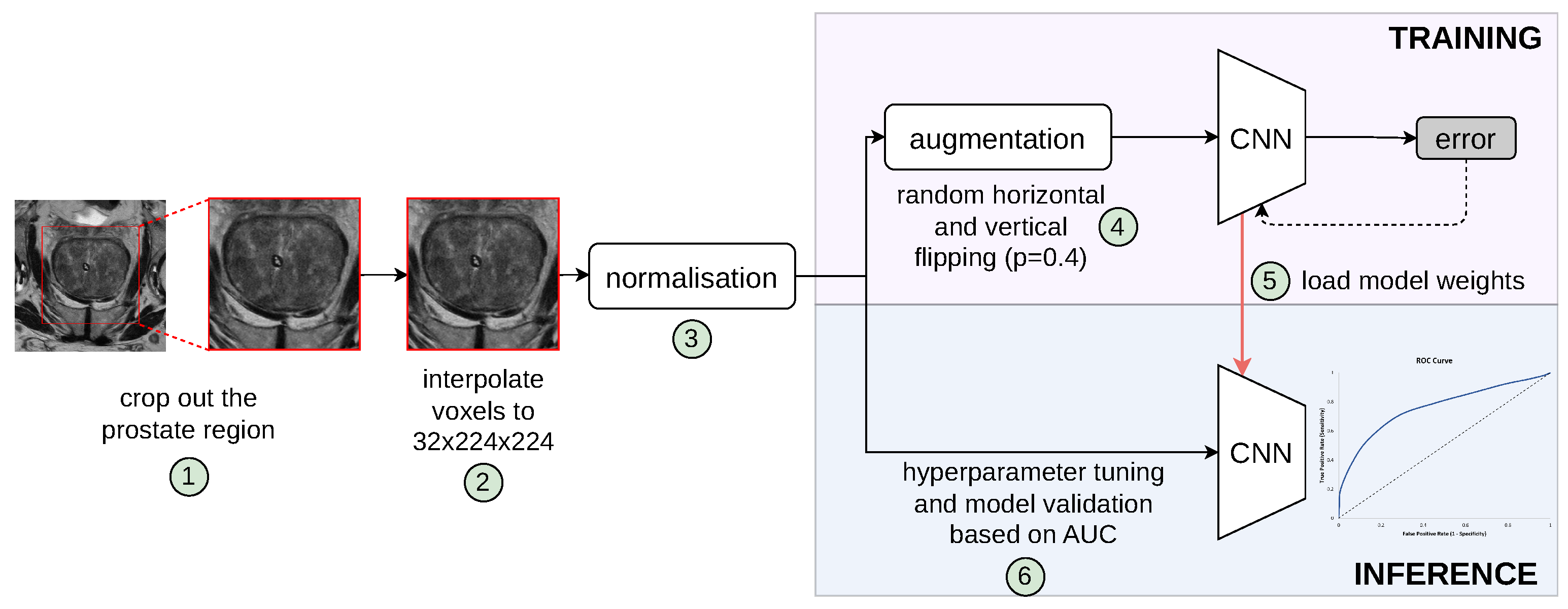
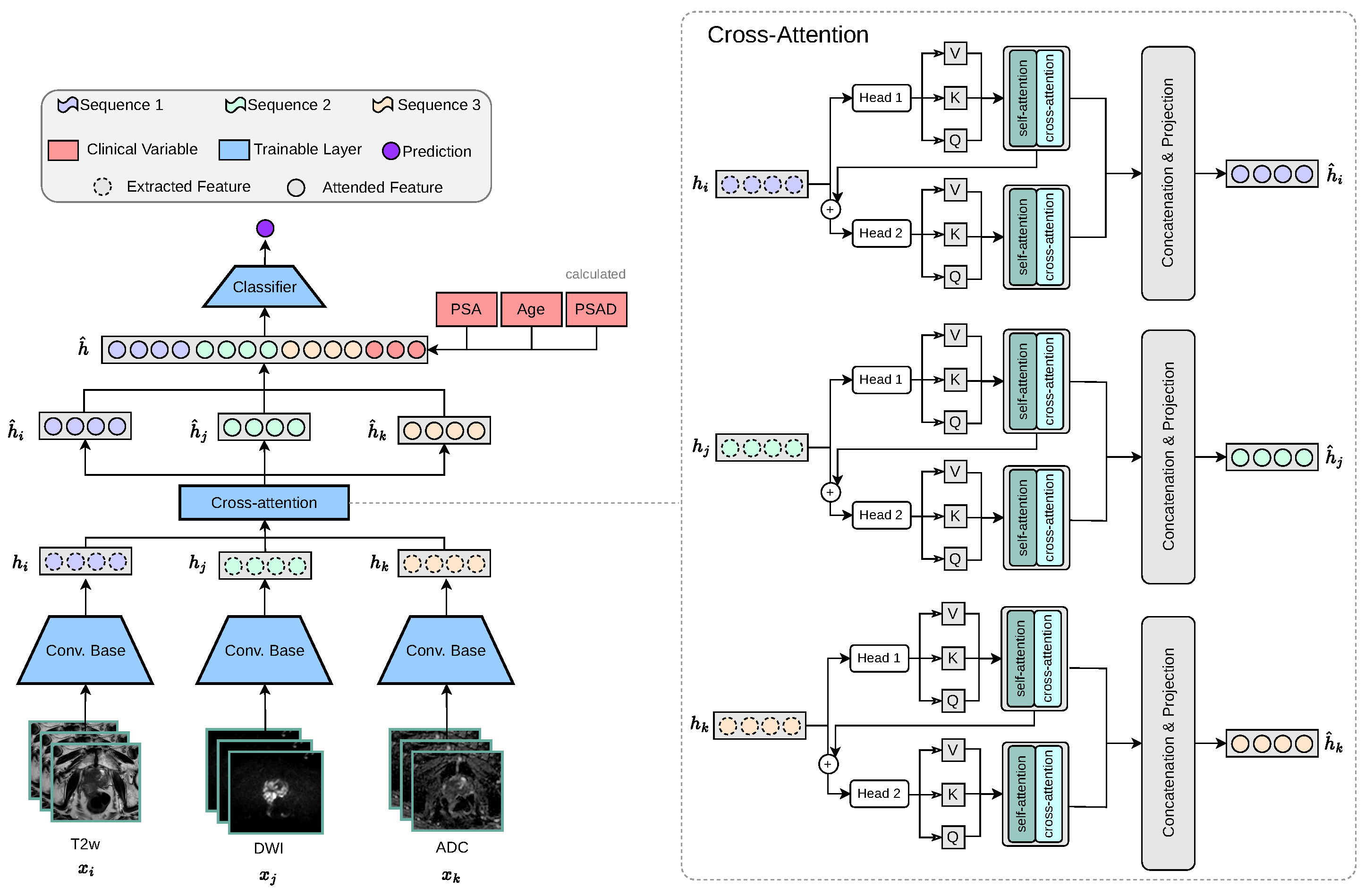
2.1. Patient-Level PCa Classification Workflow
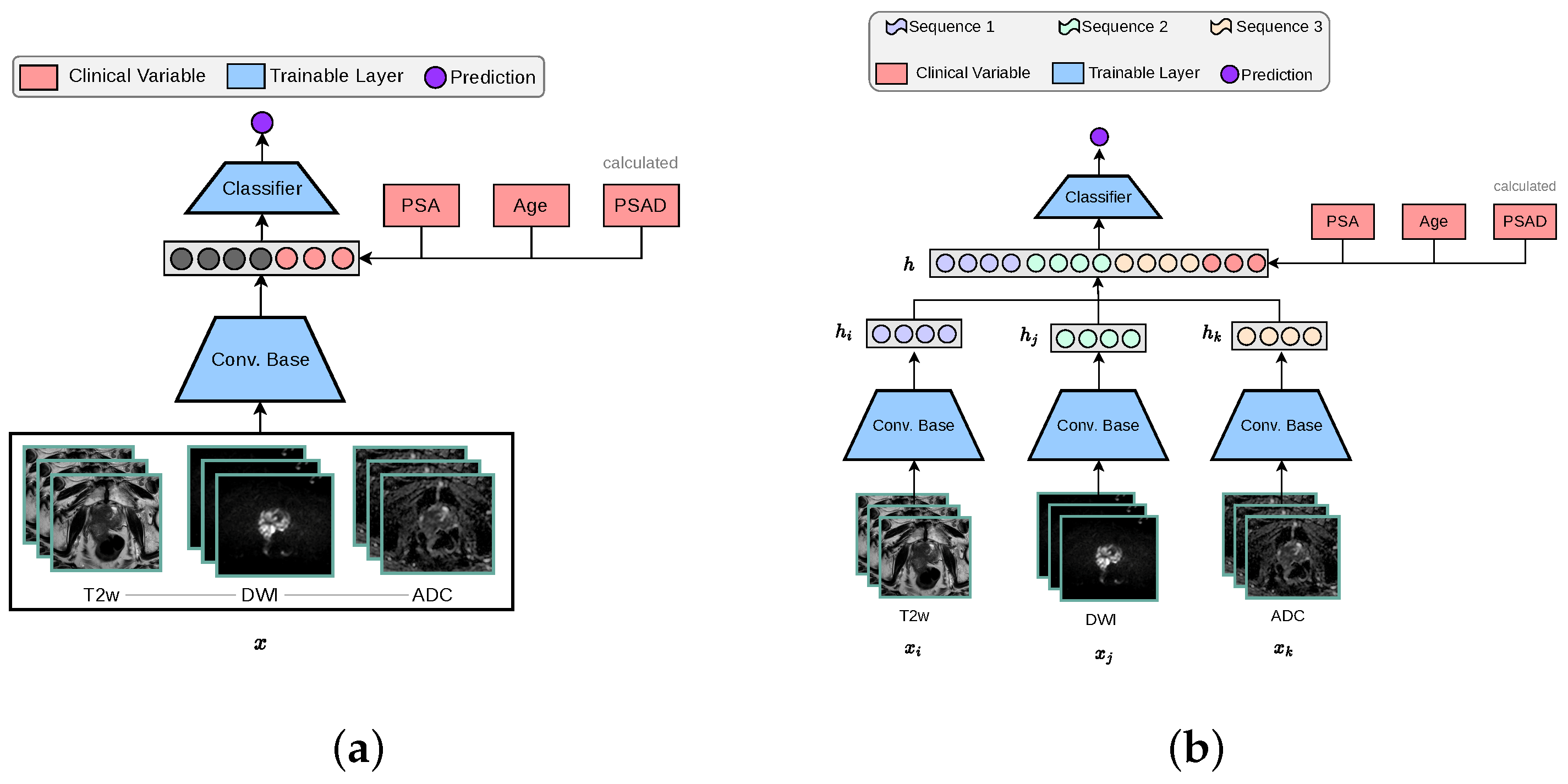
2.2. Clinical Variables
2.3. Deep Convolutional Networks
2.3.1. 3-Channel Architecture
2.3.2. Multi-Encoder-Fusion Architecture
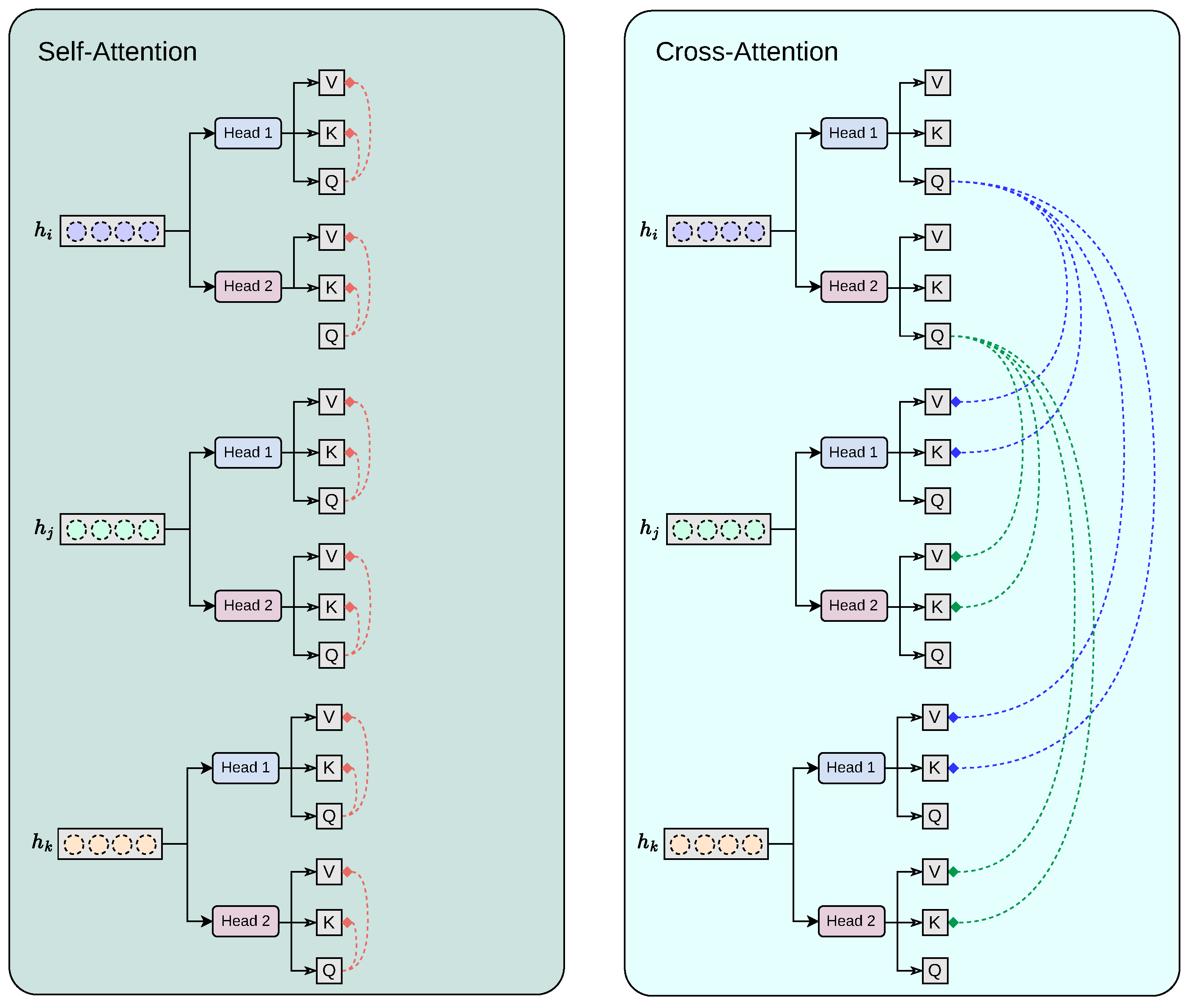
2.3.3. Multi-Encoder-Cross-Attention-Fusion Architecture
2.4. Experimental Setting
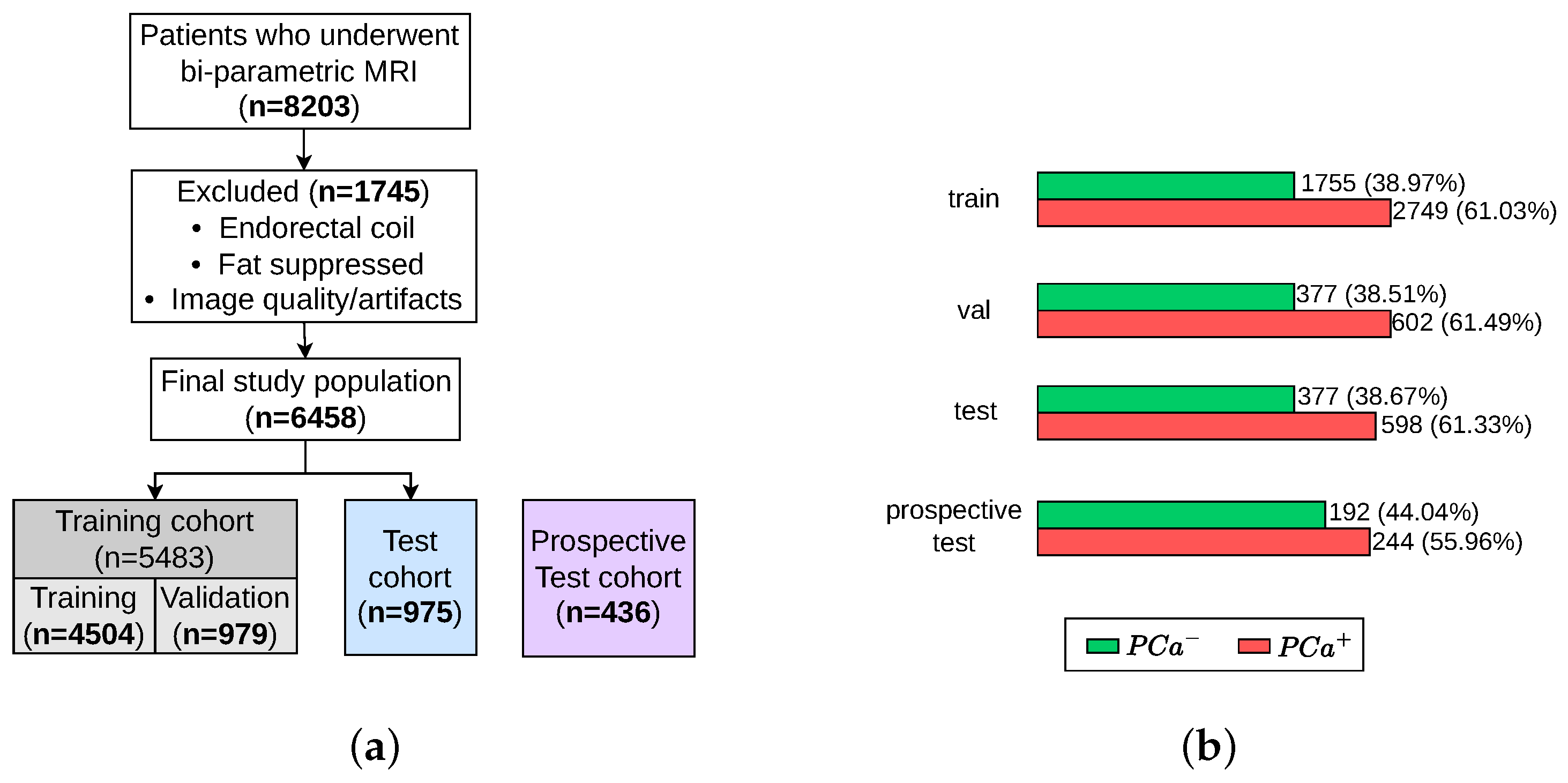
2.5. Prostate MRI Dataset
3. Experimental Results
3.1. Evaluation Metrics
3.2. Results
3.3. Statistical Analysis
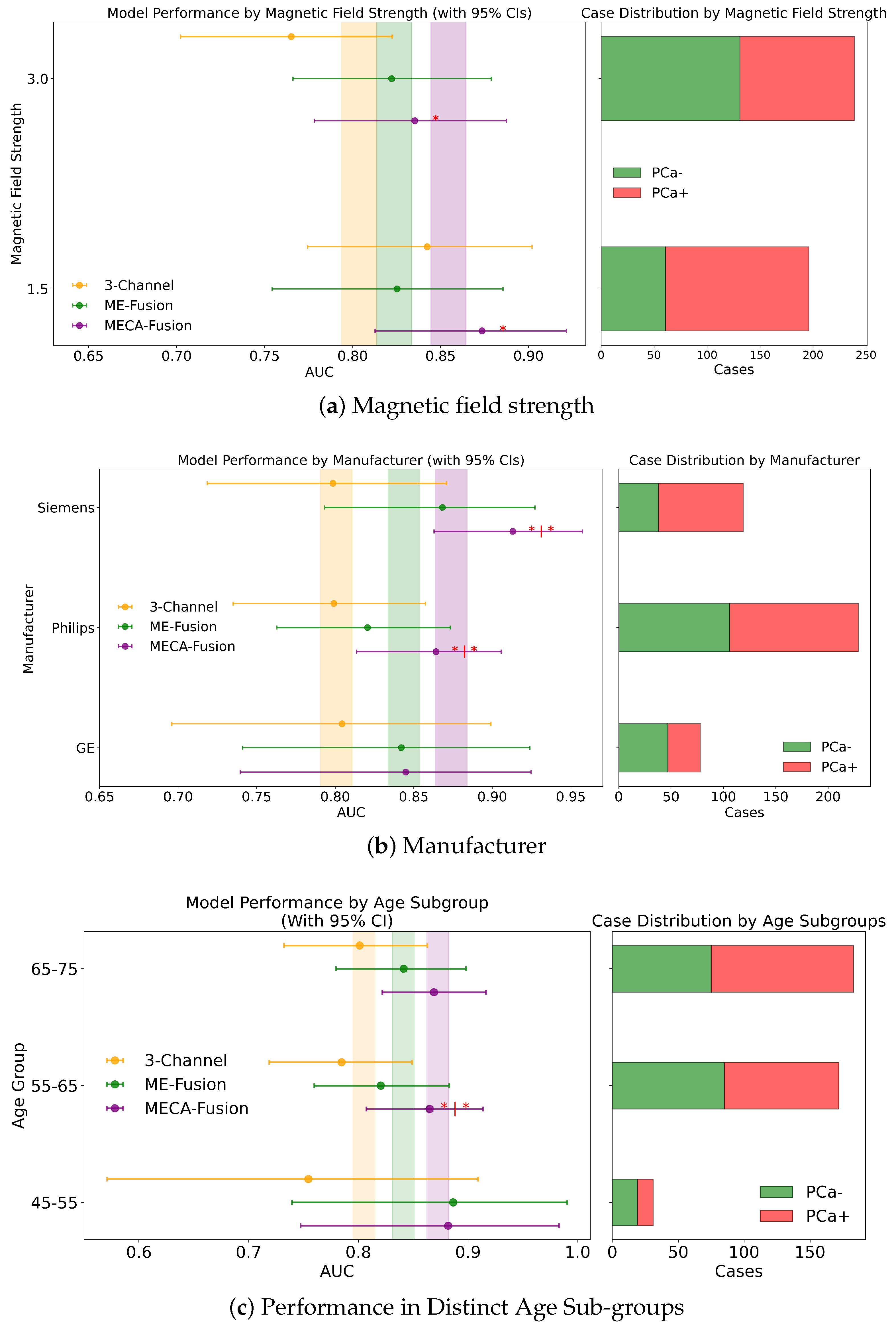
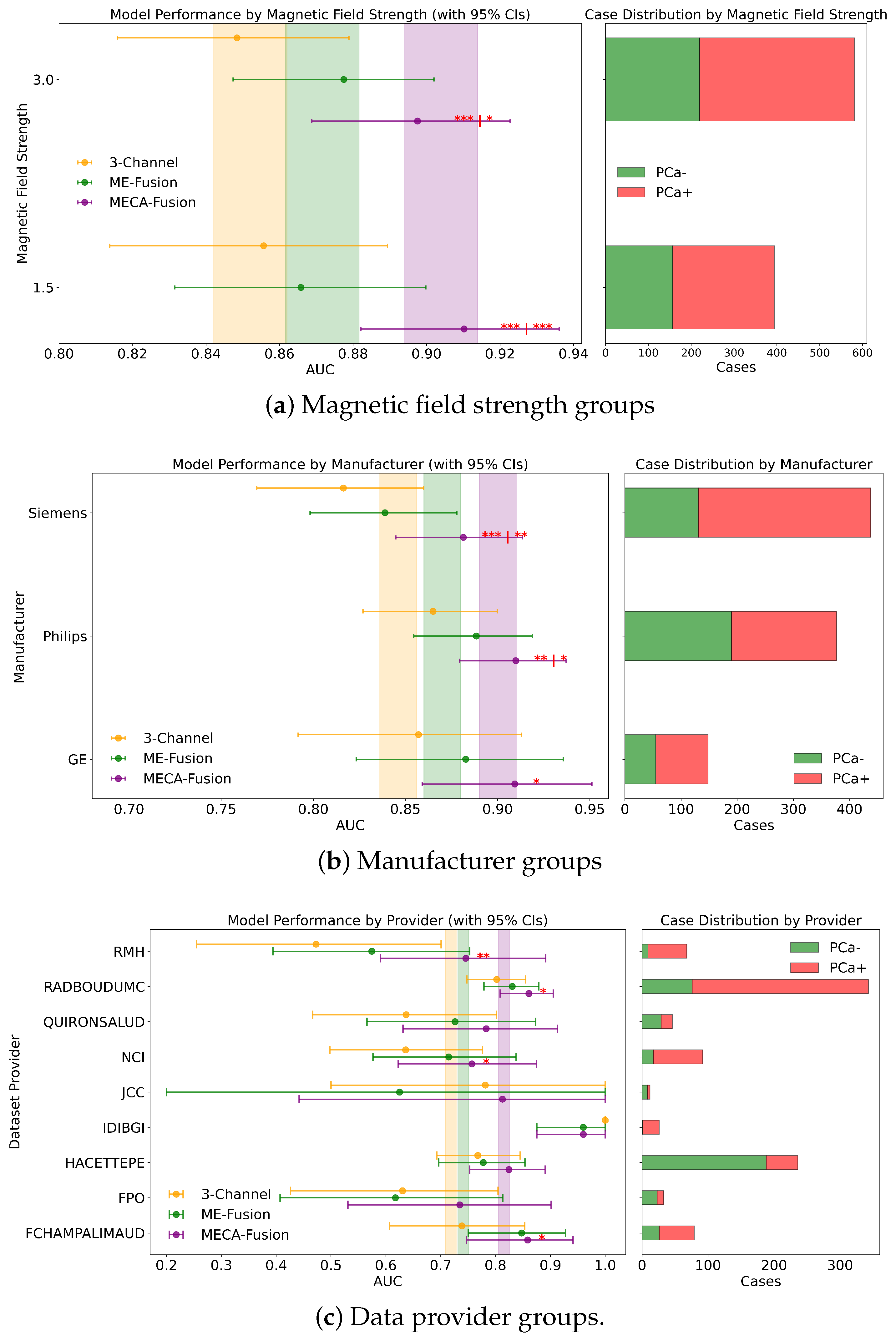
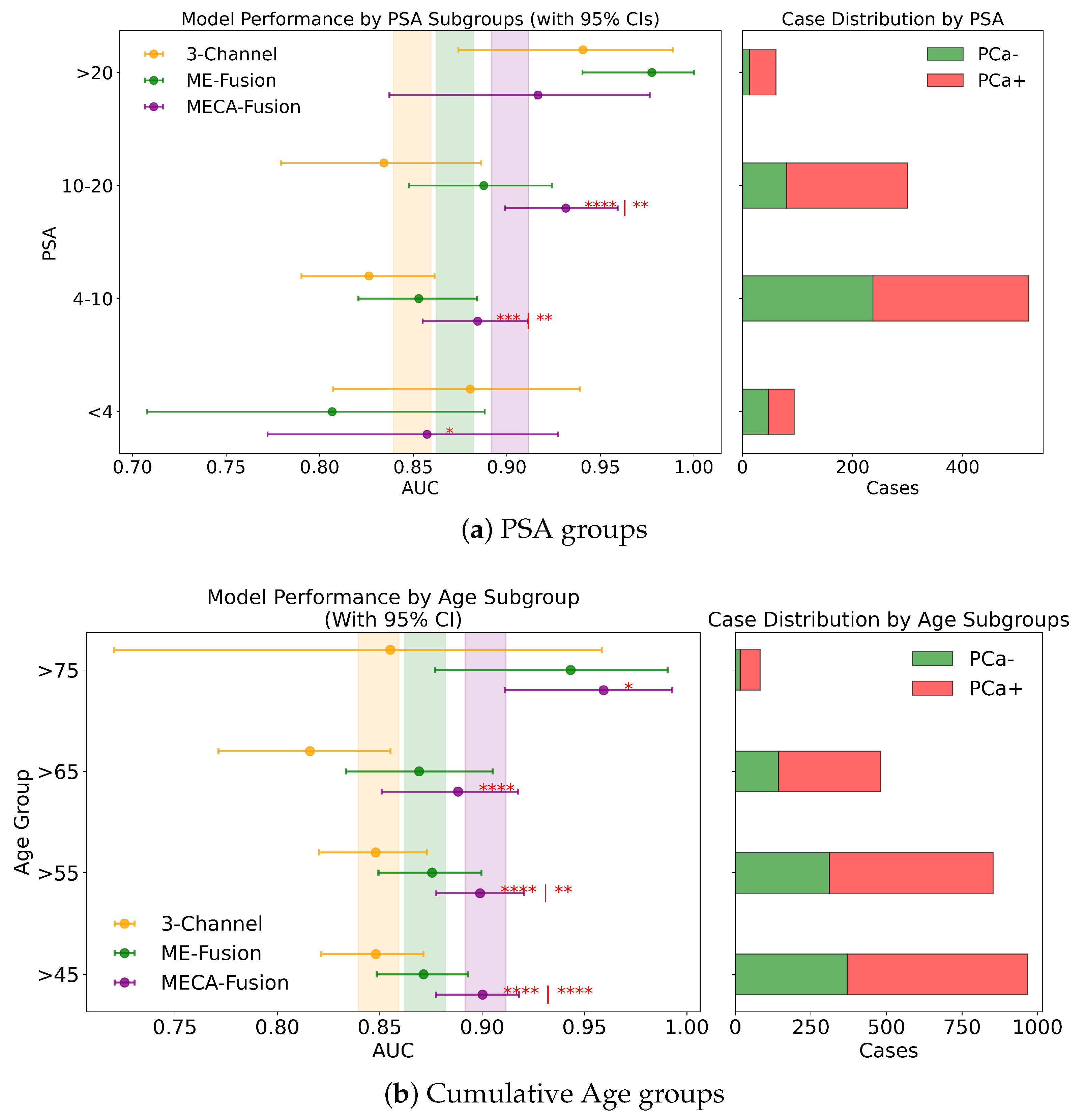
3.4. Fairness and Sub-Cohort Analysis
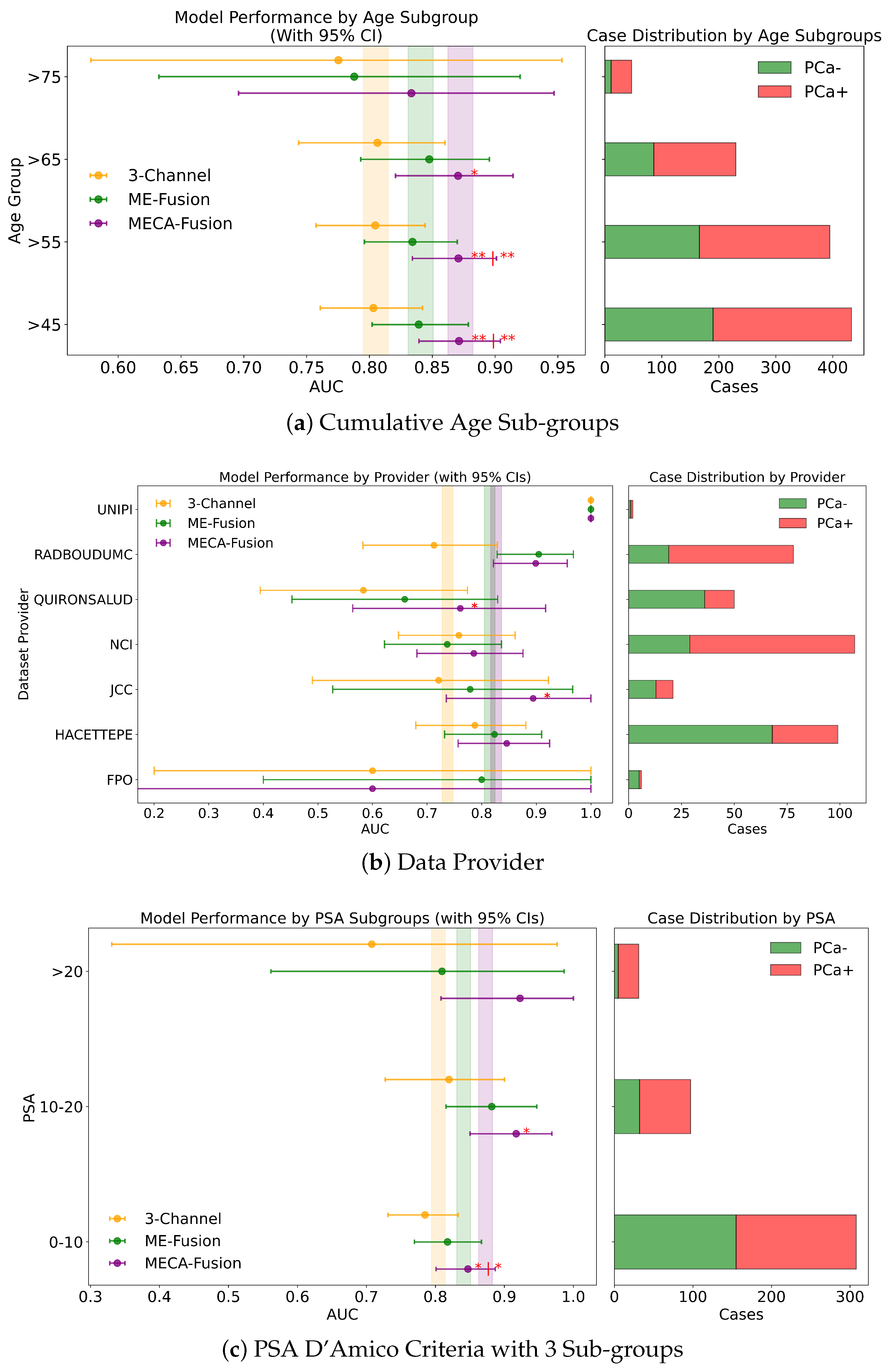
3.4.1. PSA
3.4.2. Age
- Patients who are less likely to undergo surgery (age group > 75), due to their health status and life expectancy, compared to men with ⩽75 years
- Men candidates for prostate cancer screening programs, according to urology guidelines, i.e., aged 55–65 years, compared to the other age groups, i.e., <55 or >65 years
- Increasing age groups (i.e., >45 vs. >55 vs. >65 vs. >75) to identify possible trends of the models performance on specific dichotomised patients groups
- Increasing age groups, classified as young (45–55), middle age (55–65), and older (65–75) patients
3.4.3. Dataset Provider
3.4.4. Magnetic Field
3.4.5. Manufacturer
4. Discussion
4.1. Value of Clinical Data
4.2. Critical Cases
4.3. Design Choices and the Role of the Cross-Modality Fusion Mechanism
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Code Availability
Appendix B. List of ProCAncer-I Consortium Members
- FORTH Institute of Computer Science-Computational BioMedicine Lab, Greece: Stelios Sfakianakis, Varvara Kalokyri, Eleftherios Trivizakis
- FORTH-Institute of Molecular Biology and Biotechnology (FORTH-IMBB/BR), Greece: Nikolaos Tachos, Eugenia Mylona, Dimitris Zaridis, Charalampos Kalantzopoulos
- Champalimaud Foundation, Portugal: José Guilherme de Almeida, Ana Castro Verde, Ana Carolina Rodrigues, Nuno Rodrigues, Miguel Chambel
- Radboud, Netherlands: Henkjan Huisman, Maarten de Rooij, Anindo Saha, Jasper J. Twilt, Jurgen Futterer
- HULAFE-Biomedical Imaging Research Group, Instituto de Investigación Sanitaria La Fe, Spain: Luis Martí-Bonmatí, Leonor Cerdá-Alberich, Gloria Ribas, Silvia Navarro, Manuel Marfil
- University of Pisa, Italy: Emanuele Neri, Giacomo Aringhieri, Lorenzo Tumminello, Vincenzo Mendola
- Hacettepe-Department of Radiology, Turkey: Deniz Akata, Mustafa Özmen, Ali Devrim Karaosmanoglu, Firat Atak, Musturay Karcaaltincaba
- Institute of Biomedical Research of Girona Dr. Josep Trueta (IDIBGI), Spain: Joan C. Vilanova
- National Cancer Institute, Vilnius, Lithuania: Jurgita Usinskiene, Ruta Briediene, Audrius Untanas, Kristina Slidevska
- General Anti-Cancer and Oncological Hospital of Athens, Greece: Katsaros Vasilis, Georgiou Georgios
- Radiology & AI Research Hub, The Royal Marsden NHS Foundation Trust, London, UK: Dow-Mu Koh, Robby Emsley, Sharon Vit, Ana Ribeiro, Simon Doran, Tiaan Jacobs
- Quirónsalud Hospital/CIBERSAM, Valencia, Spain: Gracián García-Martí
- Candiolo Cancer Institute, FPO-IRCCS, Turin, Italy: Valentina Giannini, Giovanni Cappello, Giovanni Maimone, Valentina Napolitano
- Institute of Information Science and Technologies, National Research Council of Italy, Italy: Sara Colantonio, Maria Antonietta Pascali, Eva Pachetti, Giulio del Corso, Danila Germanese, Andrea Berti, Gianluca Carloni
- Mass General Hospital, Boston, MA, USA: Jayashree Kalpathy-Cramer, Christopher Bridge
- B3D, UK: Joao Correia, Walter Hernandez
- Advantis, Greece: Zoi Giavri, Christos Pollalis, Dimitrios Agraniotis
- Quibim, S.L., Valencia, Spain: Ana Jiménez Pastor, Jose Munuera Mora
- Univie, Austria: Clara Saillant, Theresa Henne, Rodessa Marquez
Appendix C. Fairness Analysis

References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2018. CA Cancer J. Clin. 2018, 68, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Torre, L.A.; Bray, F.; Siegel, R.L.; Ferlay, J.; Lortet-Tieulent, J.; Jemal, A. Global cancer statistics, 2012. CA Cancer J. Clin. 2015, 65, 87–108. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Zhao, J.; Liu, Y.; Liu, S.; Liu, Y.; Zhao, J. Computer auxiliary diagnosis technique of detecting cholangiocarcinoma based on medical imaging: A review. Comput. Methods Prog. Biomed. 2021, 208, 106265. [Google Scholar] [CrossRef]
- Sandhu, G.S.; Andriole, G.L. Overdiagnosis of prostate cancer. J. Natl. Cancer Inst. Monogr. 2012, 2012, 146–151. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Glazer, D.I.; Dunne, R.M.; Fennessy, F.M.; Harisinghani, M.G.; Tempany, C.M. Prostate imaging reporting and data system version 2 (PI-RADS v2): A pictorial review. Abdom. Radiol. 2017, 42, 278–289. [Google Scholar] [CrossRef]
- Rosenkrantz, A.B.; Ginocchio, L.A.; Cornfeld, D.; Froemming, A.T.; Gupta, R.T.; Turkbey, B.; Westphalen, A.C.; Babb, J.S.; Margolis, D.J. Interobserver reproducibility of the PI-RADS version 2 lexicon: A multicenter study of six experienced prostate radiologists. Radiology 2016, 280, 793–804. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Twilt, J.J.; van Leeuwen, K.G.; Huisman, H.J.; Fütterer, J.J.; de Rooij, M. Artificial intelligence based algorithms for prostate cancer classification and detection on magnetic resonance imaging: A narrative review. Diagnostics 2021, 11, 959. [Google Scholar] [CrossRef]
- Mehta, P.; Antonelli, M.; Ahmed, H.U.; Emberton, M.; Punwani, S.; Ourselin, S. Computer-aided diagnosis of prostate cancer using multiparametric MRI and clinical features: A patient-level classification framework. Med. Image Anal. 2021, 73, 102153. [Google Scholar] [CrossRef]
- Wang, X.; Yang, W.; Weinreb, J.; Han, J.; Li, Q.; Kong, X.; Yan, Y.; Ke, Z.; Luo, B.; Liu, T.; et al. Searching for prostate cancer by fully automated magnetic resonance imaging classification: Deep learning versus non-deep learning. Sci. Rep. 2017, 7, 15415. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S.; Gujrathi, I.; Haider, M.A.; Khalvati, F. Prostate cancer detection using deep convolutional neural networks. Sci. Rep. 2019, 9, 19518. [Google Scholar]
- Aldoj, N.; Lukas, S.; Dewey, M.; Penzkofer, T. Semi-automatic classification of prostate cancer on multi-parametric MR imaging using a multi-channel 3D convolutional neural network. Eur. Radiol. 2020, 30, 1243–1253. [Google Scholar] [CrossRef]
- Armato III, S.G.; Huisman, H.; Drukker, K.; Hadjiiski, L.; Kirby, J.S.; Petrick, N.; Redmond, G.; Giger, M.L.; Cha, K.; Mamonov, A.; et al. PROSTATEx Challenges for computerized classification of prostate lesions from multiparametric magnetic resonance images. J. Med. Imaging 2018, 5, 044501. [Google Scholar] [CrossRef]
- Karagoz, A.; Alis, D.; Seker, M.E.; Zeybel, G.; Yergin, M.; Oksuz, I.; Karaarslan, E. Anatomically guided self-adapting deep neural network for clinically significant prostate cancer detection on bi-parametric MRI: A multi-center study. Insights Imaging 2023, 14, 110. [Google Scholar] [CrossRef]
- Pachetti, E.; Colantonio, S.; Pascali, M.A. On the effectiveness of 3D vision transformers for the prediction of prostate cancer aggressiveness. In Proceedings of the International Conference on Image Analysis and Processing, Lecce, Italy, 23 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 317–328. [Google Scholar]
- Gavade, A.B.; Nerli, R.; Kanwal, N.; Gavade, P.A.; Pol, S.S.; Rizvi, S.T.H. Automated diagnosis of prostate cancer using mpmri images: A deep learning approach for clinical decision support. Computers 2023, 12, 152. [Google Scholar] [CrossRef]
- Jue, J.S.; Barboza, M.P.; Prakash, N.S.; Venkatramani, V.; Sinha, V.R.; Pavan, N.; Nahar, B.; Kanabur, P.; Ahdoot, M.; Dong, Y.; et al. Re-examining prostate-specific antigen (PSA) density: Defining the optimal PSA range and patients for using PSA density to predict prostate cancer using extended template biopsy. Urology 2017, 105, 123–128. [Google Scholar] [CrossRef]
- Kundu, S.D.; Roehl, K.A.; Yu, X.; Antenor, J.A.V.; Suarez, B.K.; Catalona, W.J. Prostate specific antigen density correlates with features of prostate cancer aggressiveness. J. Urol. 2007, 177, 505–509. [Google Scholar] [CrossRef]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]
- Cardoso, M.J.; Li, W.; Brown, R.; Ma, N.; Kerfoot, E.; Wang, Y.; Murrey, B.; Myronenko, A.; Zhao, C.; Yang, D.; et al. Monai: An open-source framework for deep learning in healthcare. arXiv 2022, arXiv:2211.02701. [Google Scholar]
- ProstateNET Imaging Archive. Available online: https://prostatenet.eu/ (accessed on 31 January 2024).
- Fassia, M.K.; Balasubramanian, A.; Woo, S.; Vargas, H.A.; Hricak, H.; Konukoglu, E.; Becker, A.S. Deep learning prostate MRI segmentation accuracy and robustness: A systematic review. Radiol. Artif. Intell. 2024, 6, e230138. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Akobeng, A.K. Understanding diagnostic tests 2: Likelihood ratios, pre-and post-test probabilities and their use in clinical practice. Acta Paediatr. 2007, 96, 487–491. [Google Scholar]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [PubMed]

| Model | AUC (95% CI) | Sensitivity | Specificity | PPV | NPV |
|---|---|---|---|---|---|
| radiologists | 0.82 | 0.83 | 0.71 | 81.95% | 72.48% |
| 3-Channel | 0.82 (0.78–0.84) | 0.85 | 0.62 | 78.01% | 72.27% |
| 3-Channel+clinical | 0.85 (0.82–0.87) | 0.89 | 0.62 | 78.79% | 78.04% |
| ME-Fusion | 0.85 (0.83–0.87) | 0.81 | 0.74 | 83.17% | 71.06% |
| ME-Fusion+clinical | 0.87 (0.84–0.89) | 0.86 | 0.69 | 81.48% | 75.65% |
| MECA-Fusion | 0.86 (0.84–0.89) | 0.86 | 0.7 | 81.97% | 75.92% |
| MECA-Fusion+clinical | 0.90 (0.88–0.91) | 0.91 | 0.72 | 83.75% | 83.46% |
| Model | AUC (95% CI) | Sensitivity | Specificity | PPV | NPV |
|---|---|---|---|---|---|
| radiologists | 0.76 | 0.87 | 0.65 | 73.15% | 82.02% |
| 3-Channel | 0.71 (0.66–0.75) | 0.71 | 0.53 | 62.34% | 62.51% |
| 3-Channel+clinical | 0.80 (0.76–0.84) | 0.78 | 0.67 | 72.15% | 73.54% |
| ME-Fusion | 0.80 (0.75–0.84) | 0.75 | 0.71 | 73.92% | 72.15% |
| ME-Fusion+clinical | 0.84 (0.80–0.87) | 0.78 | 0.77 | 78.80% | 76.15% |
| MECA-Fusion | 0.83 (0.78–0.86) | 0.80 | 0.73 | 76.46% | 76.91% |
| MECA-Fusion+clinical | 0.87 (0.83–0.90) | 0.86 | 0.75 | 79.04% | 83.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitriadis, A.; Kalliatakis, G.; Osuala, R.; Kessler, D.; Mazzetti, S.; Regge, D.; Diaz, O.; Lekadir, K.; Fotiadis, D.; Tsiknakis, M.; et al. Assessing Cancer Presence in Prostate MRI Using Multi-Encoder Cross-Attention Networks. J. Imaging 2025, 11, 98. https://doi.org/10.3390/jimaging11040098
Dimitriadis A, Kalliatakis G, Osuala R, Kessler D, Mazzetti S, Regge D, Diaz O, Lekadir K, Fotiadis D, Tsiknakis M, et al. Assessing Cancer Presence in Prostate MRI Using Multi-Encoder Cross-Attention Networks. Journal of Imaging. 2025; 11(4):98. https://doi.org/10.3390/jimaging11040098
Chicago/Turabian StyleDimitriadis, Avtantil, Grigorios Kalliatakis, Richard Osuala, Dimitri Kessler, Simone Mazzetti, Daniele Regge, Oliver Diaz, Karim Lekadir, Dimitrios Fotiadis, Manolis Tsiknakis, and et al. 2025. "Assessing Cancer Presence in Prostate MRI Using Multi-Encoder Cross-Attention Networks" Journal of Imaging 11, no. 4: 98. https://doi.org/10.3390/jimaging11040098
APA StyleDimitriadis, A., Kalliatakis, G., Osuala, R., Kessler, D., Mazzetti, S., Regge, D., Diaz, O., Lekadir, K., Fotiadis, D., Tsiknakis, M., Papanikolaou, N., ProCAncer-I Consortium, & Marias, K. (2025). Assessing Cancer Presence in Prostate MRI Using Multi-Encoder Cross-Attention Networks. Journal of Imaging, 11(4), 98. https://doi.org/10.3390/jimaging11040098













