Deep Learning for Breast Cancer Diagnosis from Mammograms—A Comparative Study
Abstract
:1. Introduction
2. Methodology
2.1. Convolutional Neural Networks
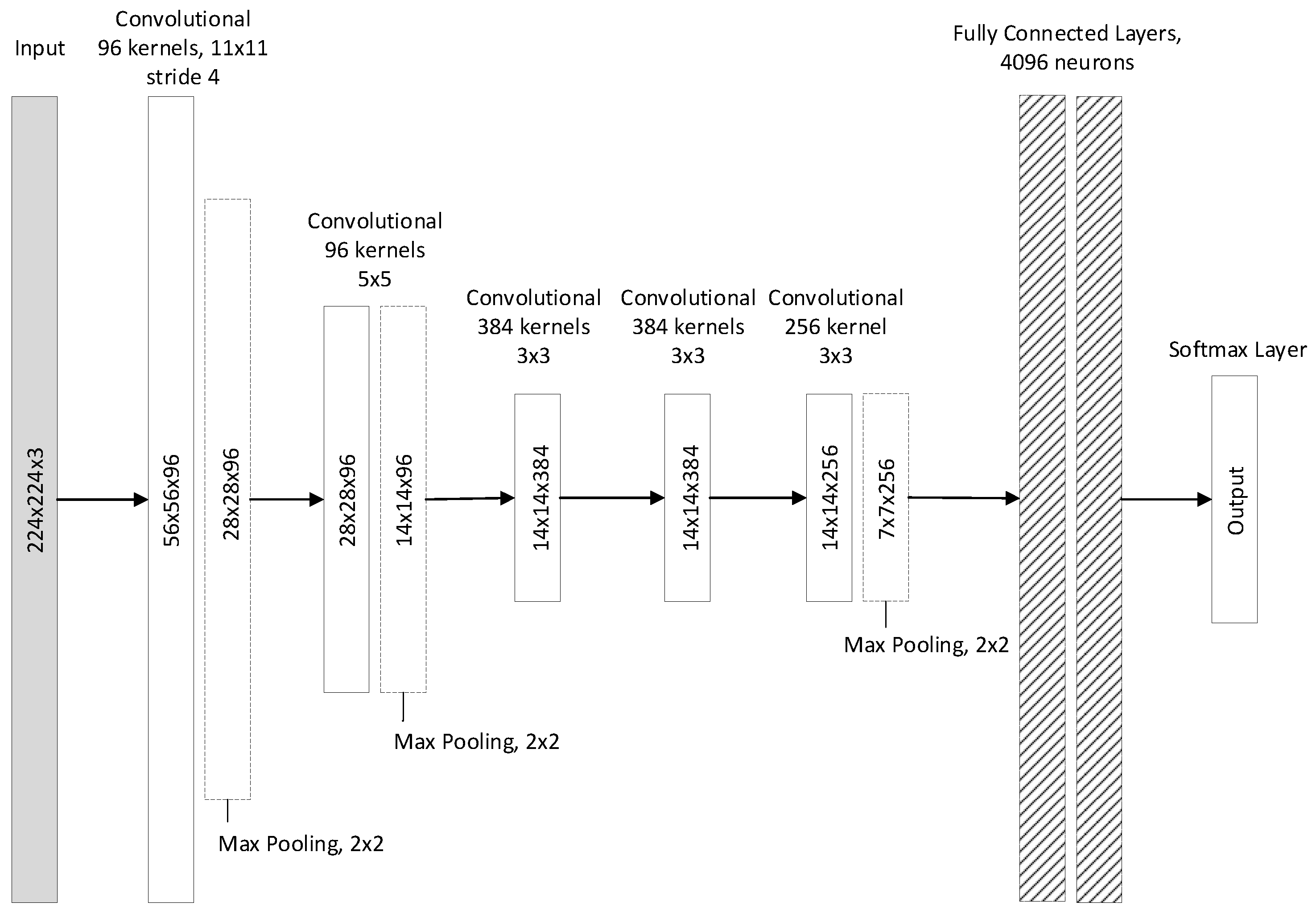
2.1.1. AlexNet
2.1.2. VGG
2.1.3. GoogLeNet/Inception
2.1.4. Residual Networks
3. Experimental Results
4. Discussion and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2015. CA Cancer J. Clin. 2015, 65, 5–29. [Google Scholar] [CrossRef] [PubMed]
- American Cancer Society. Breast Cancer Facts & Figures; American Cancer Society, Inc.: Atlanta, GA, USA, 2015. [Google Scholar]
- Eurostat. Health Statistics: Atlas on Mortality in the European Union; Office for Official Publications of the European Union: Luxembourg, 2009. [Google Scholar]
- Hubbard, R.A.; Kerlikowske, K.; Flowers, C.I.; Yankaskas, B.C.; Zhu, W.; Miglioretti, D.L. Cumulative probability of false-positive recall or biopsy recommendation after 10 years of screening mammography: A cohort study. Ann. Intern. Med. 2011, 155, 481–492. [Google Scholar] [CrossRef] [PubMed]
- Hamidinekoo, A.; Denton, E.; Rampun, A.; Honnor, K.; Zwiggelaar, R. Deep learning in mammography and breast histology, an overview and future trends. Med. Image Anal. 2018, 47, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Arevalo, J.; González, F.A.; Ramos-Pollán, R.; Oliveira, J.L.; Lopez, M.A.G. Representation learning for mammography mass lesion classification with convolutional neural networks. Comput. Methods Programs Biomed. 2016, 127, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Carneiro, G.; Nascimento, J.; Bradley, A.P. Unregistered multiview mammogram analysis with pre-trained deep learning models. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 652–660. [Google Scholar]
- Huynh, B.Q.; Li, H.; Giger, M.L. Digital mammographic tumor classification using transfer learning from deep convolutional neural networks. J. Med. Imaging 2016, 3, 034501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Jiao, Z.; Gao, X.; Wang, Y.; Li, J. A deep feature based framework for breast masses classification. Neurocomputing 2016, 197, 221–231. [Google Scholar] [CrossRef]
- Lévy, D.; Jain, A. Breast mass classification from mammograms using deep convolutional neural networks. arXiv, 2016; arXiv:1612.00542. [Google Scholar]
- Ting, F.F.; Tan, Y.J.; Sim, K.S. Convolutional neural network improvement for breast cancer classification. Expert Syst. Appl. 2019, 120, 103–115. [Google Scholar] [CrossRef]
- Rampun, A.; Scotney, B.W.; Morrow, P.J.; Wang, H. Breast Mass Classification in Mammograms using Ensemble Convolutional Neural Networks. In Proceedings of the 20th International Conference on e-Health Networking, Applications and Services (Healthcom), Ostrava, Czech Republic, 17–20 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Krizhevsky, A. One weird trick for parallelizing convolutional neural networks. arXiv, 2014; arXiv:1404.5997. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv, 2012; arXiv:1207.0580. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Heath, M.; Bowyer, K.; Kopans, D.; Kegelmeyer, P., Jr.; Moore, R.; Chang, K.; Munishkumaran, S. Current status of the digital database for screening mammography. In Digital Mammography; Springer: Berlin/Heidelberg, Germany, 1998; pp. 457–460. [Google Scholar]
- Tsochatzidis, L.; Zagoris, K.; Arikidis, N.; Karahaliou, A.; Costaridou, L.; Pratikakis, I. Computer-aided diagnosis of mammographic masses based on a supervised content-based image retrieval approach. Pattern Recognit. 2017, 71, 106–117. [Google Scholar] [CrossRef]
- Arikidis, N.; Vassiou, K.; Kazantzi, A.; Skiadopoulos, S.; Karahaliou, A.; Costaridoua, L. A two-stage method for microcalcification cluster segmentation in mammography by deformable models. Med. Phys. 2015, 42, 5848–5861. [Google Scholar]
- Lee, R.S.; Gimenez, F.; Hoogi, A.; Miyake, K.K.; Gorovoy, M.; Rubin, D. A curated mammography data set for use in computer-aided detection and diagnosis research. Sci. Data 2017, 4, 170–177. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Rouhi, R.; Jafari, M.; Kasaei, S.; Keshavarzian, P. Benign and malignant breast tumors classification based on region growing and CNN segmentation. Expert Syst. Appl. 2015, 42, 990–1002. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y.; Ma, Y. Breast mass classification in digital mammography based on extreme learning machine. Neurocomputing 2016, 173, 930–941. [Google Scholar] [CrossRef]
- Oeffinger, K.C.; Fontham, E.T.; Etzioni, R.; Herzig, A.; Michaelson, J.S.; Shih, Y.C.T.; Walter, L.C.; Church, T.R.; Flowers, C.R.; LaMonte, S.J.; et al. Breast cancer screening for women at average risk: 2015 guideline update from the American Cancer Society. JAMA 2015, 314, 1599–1614. [Google Scholar] [CrossRef] [PubMed]





| CNN | Number of Weights | Batch Size | Learning Rate | Best Model Iter. | |||
|---|---|---|---|---|---|---|---|
| FT | SC | FT | SC | ||||
| AlexNet | 32 | 6 | 65 | ||||
| VGG-16 | 32 | 9 | 58 | ||||
| VGG-19 | 32 | 14 | 64 | ||||
| ResNet-50 | 32 | 4 | 104 | ||||
| ResNet-101 | 16 | 13 | 92 | ||||
| ResNet-152 | 10 | 31 | 38 | ||||
| GoogLeNet | 32 | 12 | 12 | ||||
| Inception-BN (v2) | 32 | 43 | 108 | ||||
| CNN | DDSM-400 | CBIS-DDSM | |||
|---|---|---|---|---|---|
| AUC | ACC | AUC | ACC | ||
| AlexNet | |||||
| VGG-16 | |||||
| VGG-19 | |||||
| ResNet-50 | |||||
| ResNet-101 | |||||
| ResNet-152 | |||||
| GoogLeNet | |||||
| Inception-BN (v2) | |||||
| CNN | DDSM-400 | CBIS-DDSM | |||
|---|---|---|---|---|---|
| AUC | ACC | AUC | ACC | ||
| AlexNet | |||||
| VGG-16 | |||||
| VGG-19 | |||||
| ResNet-50 | |||||
| ResNet-101 | |||||
| ResNet-152 | |||||
| GoogLeNet | |||||
| Inception-BN (v2) | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsochatzidis, L.; Costaridou, L.; Pratikakis, I. Deep Learning for Breast Cancer Diagnosis from Mammograms—A Comparative Study. J. Imaging 2019, 5, 37. https://doi.org/10.3390/jimaging5030037
Tsochatzidis L, Costaridou L, Pratikakis I. Deep Learning for Breast Cancer Diagnosis from Mammograms—A Comparative Study. Journal of Imaging. 2019; 5(3):37. https://doi.org/10.3390/jimaging5030037
Chicago/Turabian StyleTsochatzidis, Lazaros, Lena Costaridou, and Ioannis Pratikakis. 2019. "Deep Learning for Breast Cancer Diagnosis from Mammograms—A Comparative Study" Journal of Imaging 5, no. 3: 37. https://doi.org/10.3390/jimaging5030037
APA StyleTsochatzidis, L., Costaridou, L., & Pratikakis, I. (2019). Deep Learning for Breast Cancer Diagnosis from Mammograms—A Comparative Study. Journal of Imaging, 5(3), 37. https://doi.org/10.3390/jimaging5030037






