Two-Stage Alignment of FIB-SEM Images of Rock Samples
Abstract
:1. Introduction
2. Existing Approaches
3. Datasets
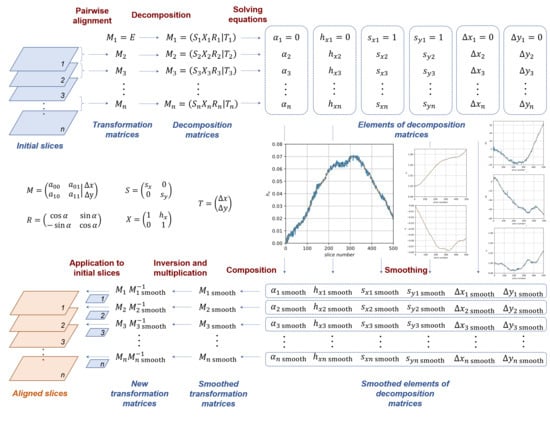
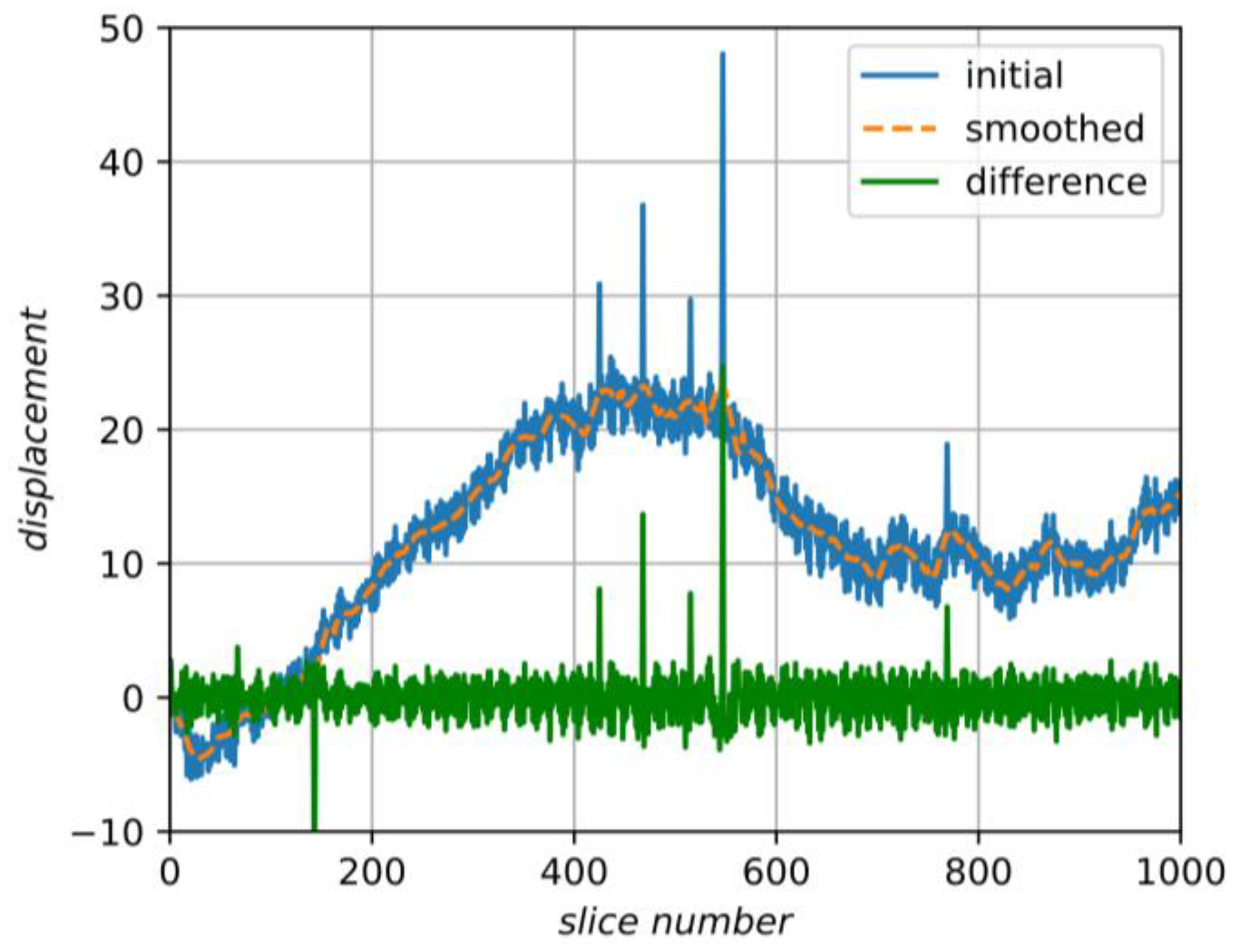
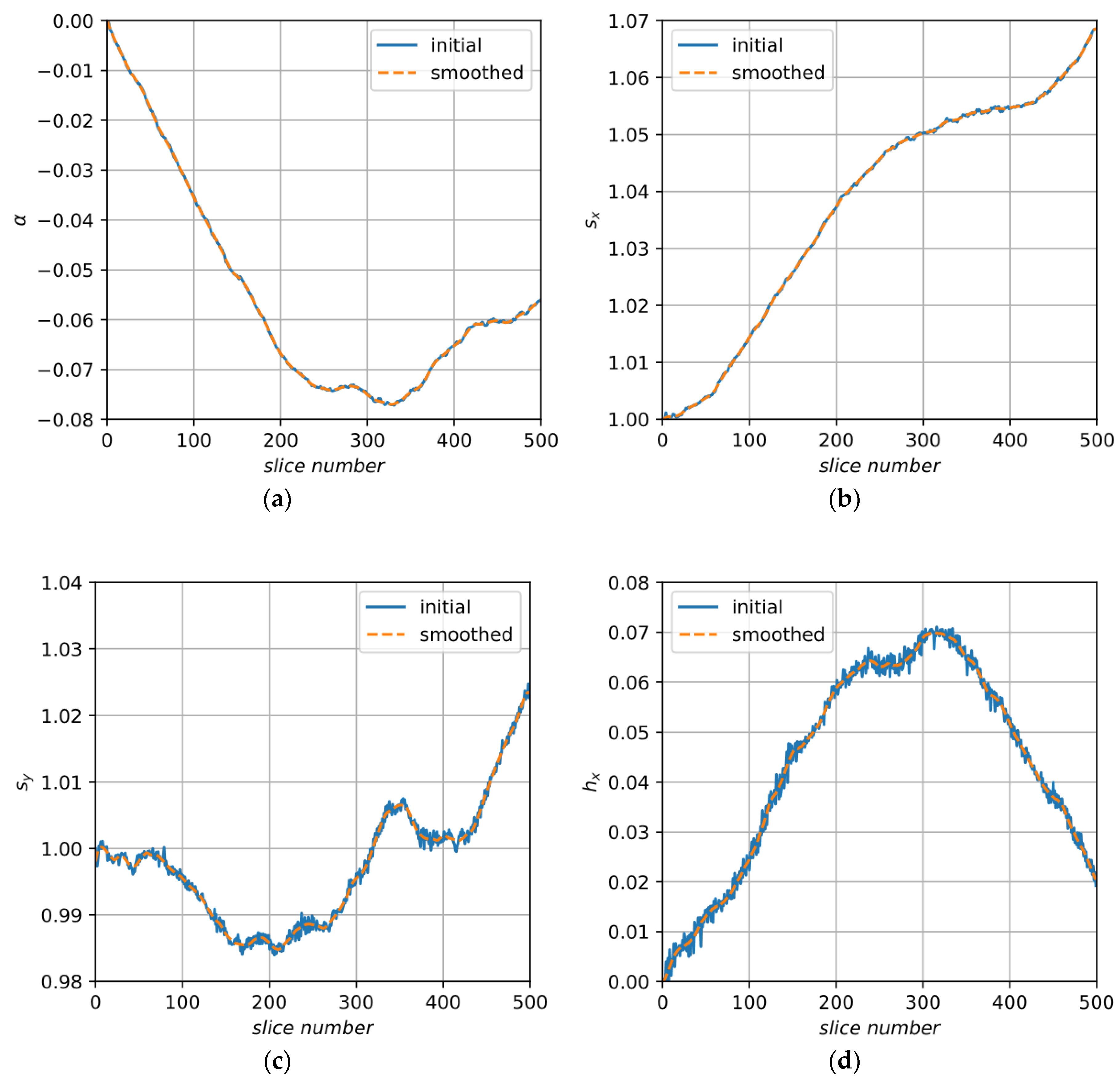
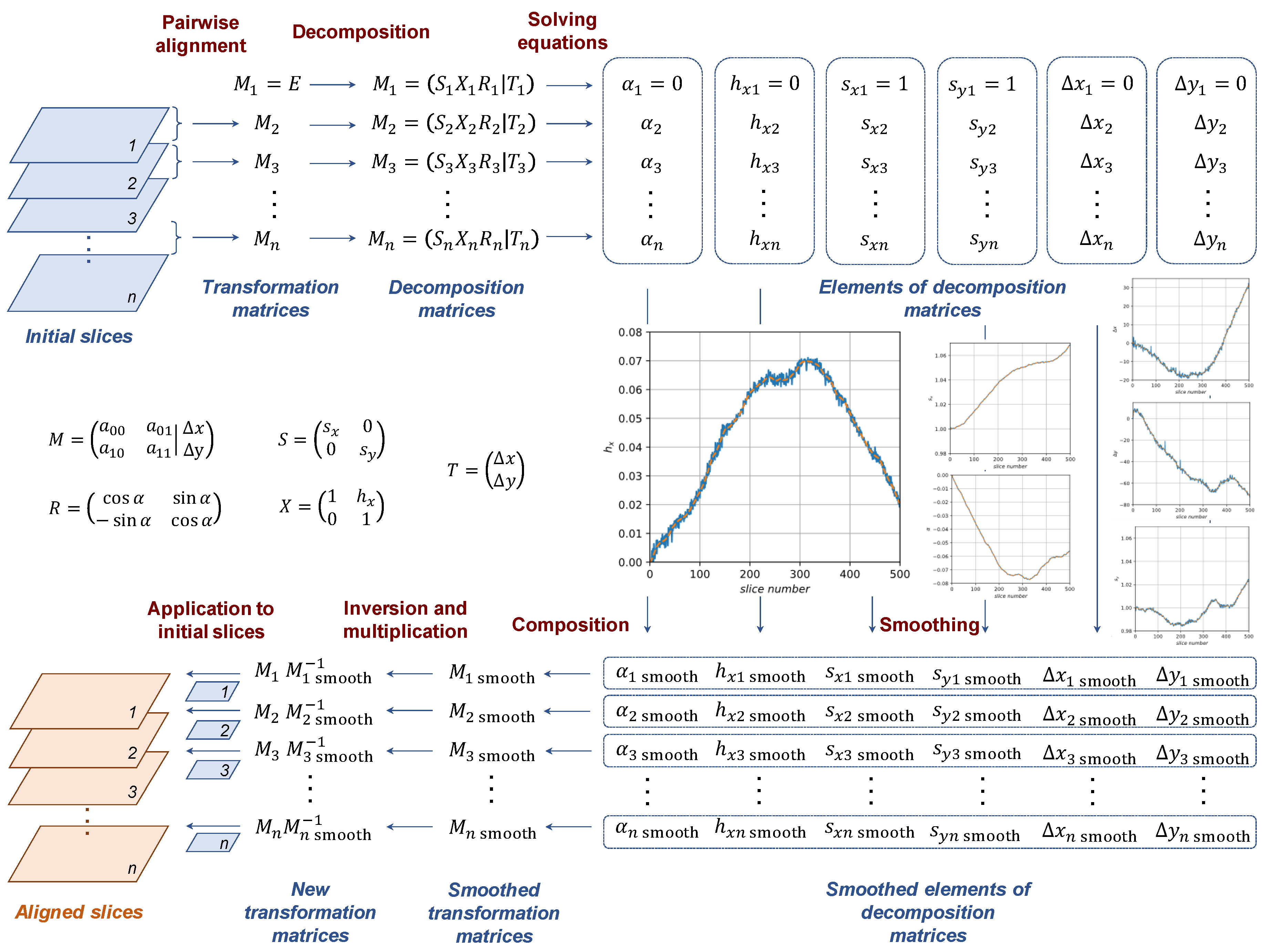
4. Proposed Method
5. Results and Discussion
5.1. Quality Metrics for Alignment
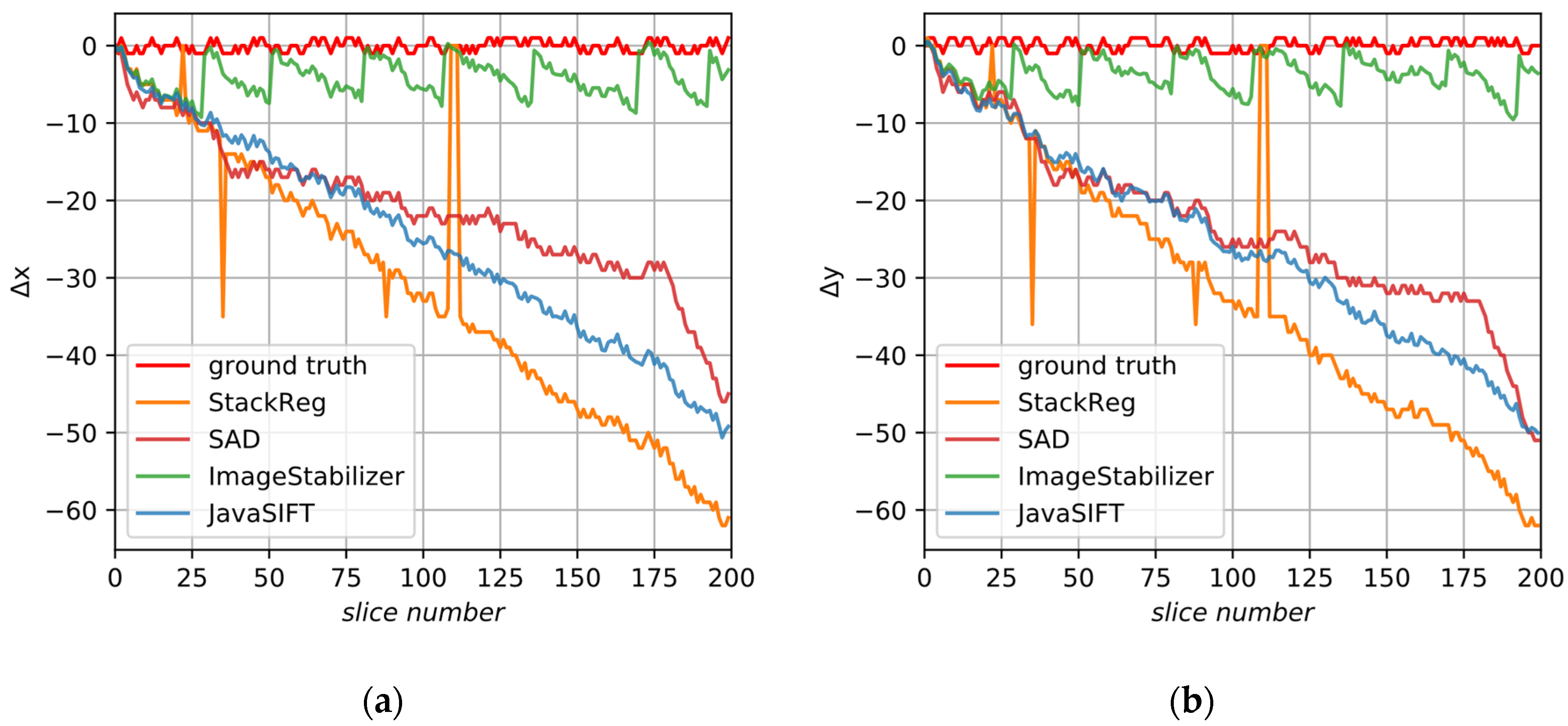
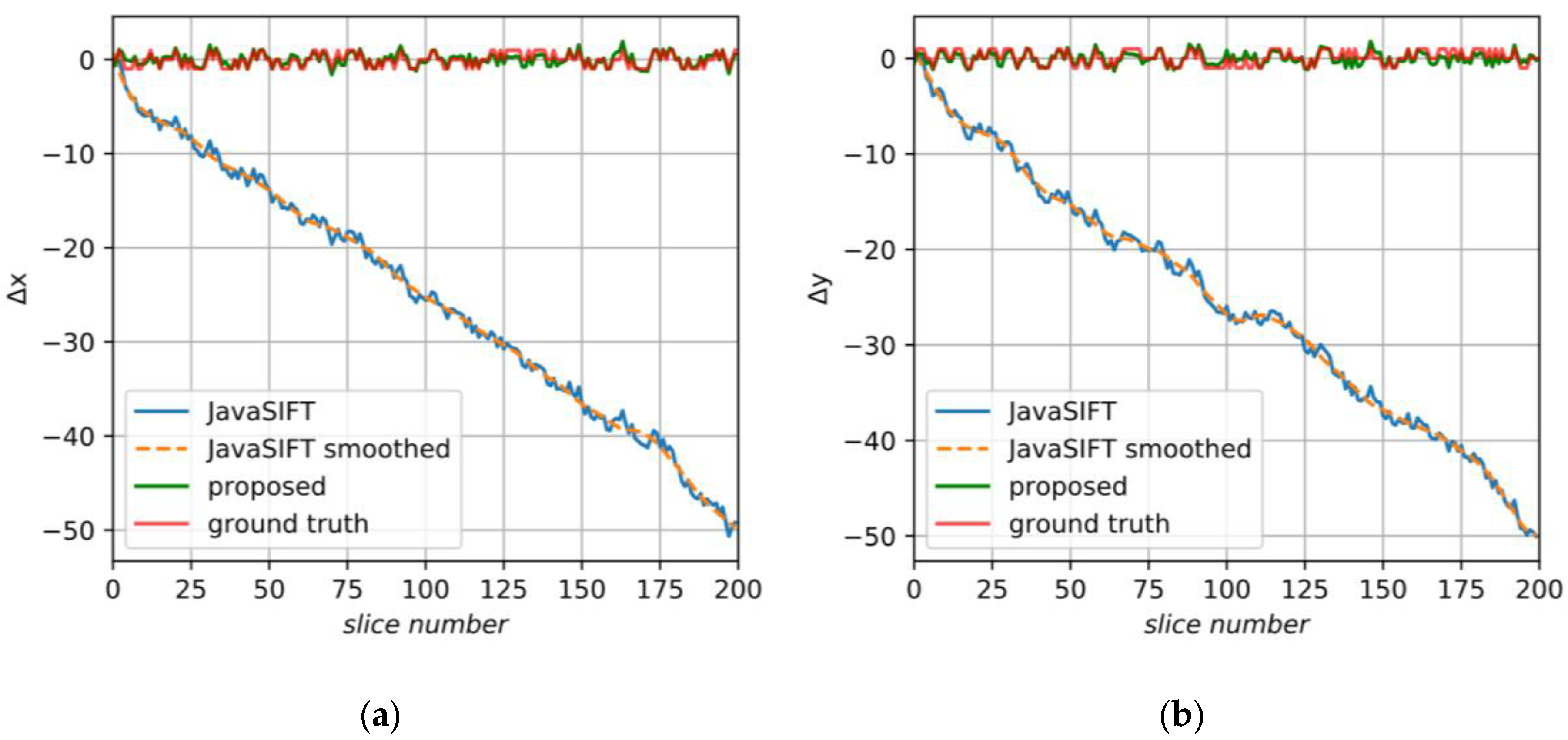
5.2. Alignment of the Synthetic Image
5.3. Alignment of Image A
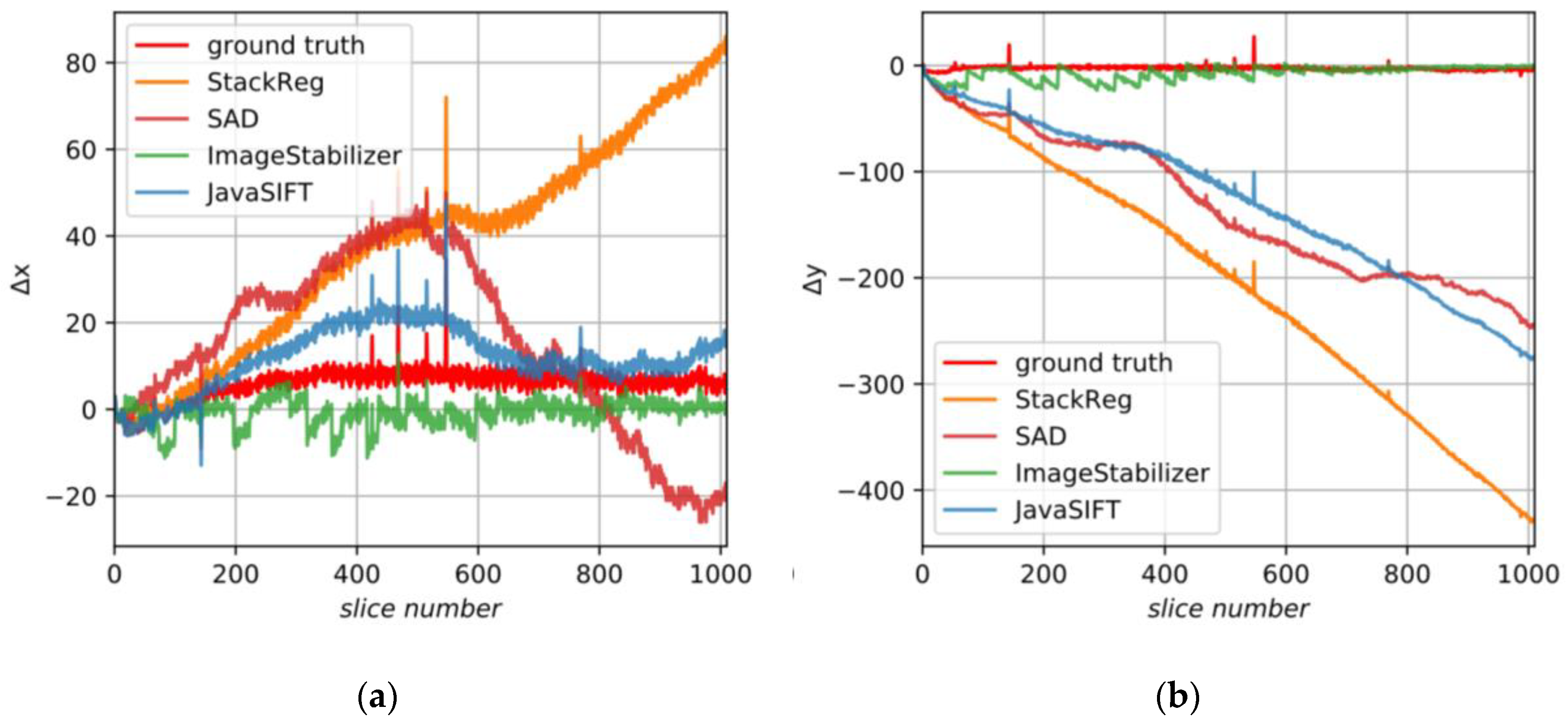
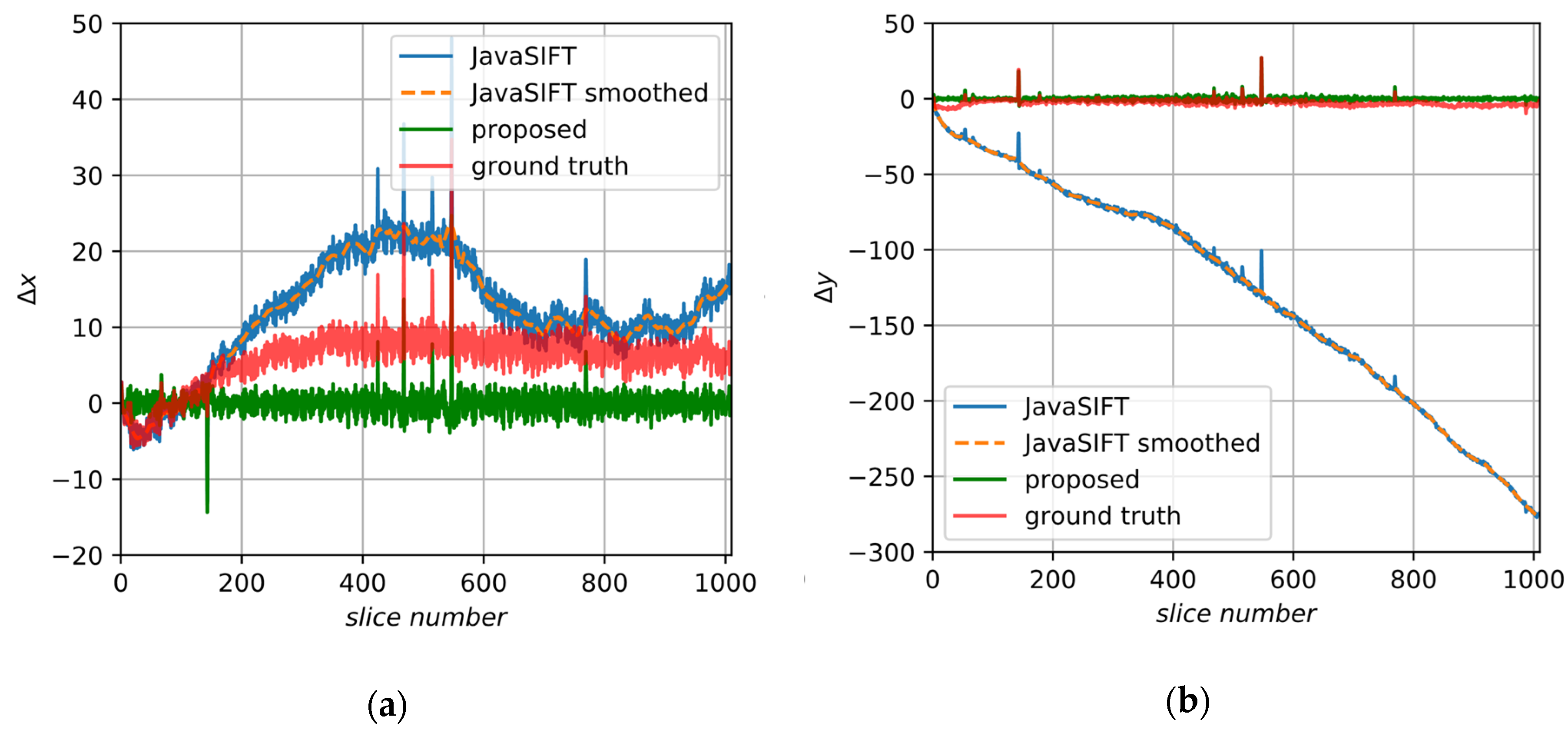
5.4. Alignment of Image B
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holzer, L.; Cantoni, M. Review of FIB-tomography. In Nanofabrication Using Focused Ion and Electron Beams: Principles and Applications; Oxford University Press: Oxford, UK, 2012; pp. 410–435. [Google Scholar]
- Liu, Y.; King, H.; van Huis, M.; Drury, M.; Plümper, O. Nano-Tomography of Porous Geological Materials Using Focused Ion Beam-Scanning Electron Microscopy. Minerals 2016, 6, 104. [Google Scholar] [CrossRef] [Green Version]
- Joos, J.; Carraro, T.; Weber, A.; Ivers-Tiffée, E. Reconstruction of porous electrodes by FIB/SEM for detailed microstructure modeling. J. Power Sources 2011, 196, 7302–7307. [Google Scholar] [CrossRef]
- Bosch, C.; Martínez, A.; Masachs, N.; Teixeira, C.M.; Fernaud, I.; Ulloa, F.; Pérez-Martínez, E.; Lois, C.; Comella, J.X.; DeFelipe, J. FIB/SEM technology and high-throughput 3D reconstruction of dendritic spines and synapses in GFP-labeled adult-generated neurons. Front. Neuroanat. 2015, 9, 60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lepinay, K.; Lorut, F. Three-Dimensional Semiconductor Device Investigation Using Focused Ion Beam and Scanning Electron Microscopy Imaging (FIB/SEM Tomography). Microsc. Microanal. 2013, 19, 85–92. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhandari, Y.; Groeber, M. CAD-based reconstruction of 3D polycrystalline alloy microstructures from FIB generated serial sections. Comput. Aided Des. 2008, 40, 293–310. [Google Scholar] [CrossRef]
- Röding, M.; Fager, C.; Olsson, A.; Corswant, C.V.; Olsson, E.; Lorén, N. Three-dimensional reconstruction of porous polymer films from FIB-SEM nanotomography data using random forests. J. Microsc. 2020. [Google Scholar] [CrossRef]
- Berg, C.F.; Lopez, O.; Berland, H. Industrial applications of digital rock technology. J. Pet. Sci. Eng. 2017, 157, 131–147. [Google Scholar] [CrossRef]
- Koroteev, D.; Dinariev, O.; Evseev, N.; Klemin, D.; Nadeev, A.; Safonov, S.; Gurpinar, O.; Berg, S.; van Kruijsdijk, C.; Armstrong, R.; et al. Direct Hydrodynamic Simulation of Multiphase Flow in Porous Rock. Petrophysics 2014, 55, 294–303. [Google Scholar]
- Klemin, D.; Serebryanskaya, A.; Savelev, O.; Melnikov, S. Digital Rock Technology Accelerates Carbonate Rock Laboratory Analysis. In Proceedings of the SPE Gas & Oil Technology Showcase and Conference, Dubai, UAE, 21–23 October 2019. [Google Scholar]
- Dinariev, O.Y.; Evseev, N.V. Modeling of nanoscale liquid mixture transport by density functional hydrodynamics. Phys. Rev. E 2017, 95, 063307. [Google Scholar] [CrossRef]
- Goshtasby, A.A. 2-D and 3-D Image Registration: For Medical, Remote Sensing, and Industrial Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 0-471-72426-2. [Google Scholar]
- Modersitzki, J. Numerical Methods for Image Registration; Oxford University Press on Demand: Oxford, UK, 2004; ISBN 0-19-852841-8. [Google Scholar]
- Brown, L.G. A survey of image registration techniques. ACM Comput. Surv. 1992, 24, 325–376. [Google Scholar] [CrossRef]
- Zitová, B.; Flusser, J. Image registration methods a survey. Image Vision Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef] [Green Version]
- Salzer, M.; Thiele, S.; Zengerle, R.; Schmidt, V. On the importance of FIB-SEM specific segmentation algorithms for porous media. Mater. Charact. 2014, 95, 36–43. [Google Scholar] [CrossRef]
- Prill, T.; Schladitz, K.; Jeulin, D.; Faessel, M.; Wieser, C. Morphological segmentation of FIB-SEM data of highly porous media. J. Microsc. 2013, 250, 77–87. [Google Scholar] [CrossRef]
- Moroni, R.; Thiele, S. FIB/SEM tomography segmentation by optical flow estimation. Ultramicroscopy 2020, 219, 113090. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [Green Version]
- ImageJ Website. Available online: http://imagej.net (accessed on 24 June 2020).
- Avizo Website. Available online: https://www.thermofisher.com/uk/en/home/industrial/electron-microscopy/electron-microscopy-instruments-workflow-solutions/3d-visualization-analysis-software.html (accessed on 24 June 2020).
- Viola, P.; Wells III, W.M. Alignment by maximization of mutual information. Int. J. Comput. Vis. 1997, 24, 137–154. [Google Scholar] [CrossRef]
- Maes, F.; Vandermeulen, D.; Suetens, P. Medical image registration using mutual information. Proc. IEEE 2003, 91, 1699–1722. [Google Scholar] [CrossRef] [Green Version]
- IMOD Website. Available online: http://bio3d.colorado.edu/imod (accessed on 26 June 2020).
- Elastix Website. Available online: https://elastix.lumc.nl/index.php (accessed on 26 June 2020).
- Klein, S.; Staring, M.; Murphy, K.; Viergever, M.A.; Pluim, J. elastix: A Toolbox for Intensity-Based Medical Image Registration. IEEE Trans. Med. Imaging 2010, 29, 196–205. [Google Scholar] [CrossRef]
- Dewers, T.A.; Heath, J.; Ewy, R.; Duranti, L. Three-dimensional pore networks and transport properties of a shale gas formation determined from focused ion beam serial imaging. Int. J. Oil Gas Coal Technol. 2012, 5, 229–248. [Google Scholar] [CrossRef]
- Gaboreau, S.; Robinet, J.-C.; Prêt, D. Optimization of pore-network characterization of a compacted clay material by TEM and FIB/SEM imaging. Microporous Mesoporous Mater. 2016, 224, 116–128. [Google Scholar] [CrossRef]
- Saalfeld, S. ImageJ Plugin—Linear Stack Alignment with SIFT. Available online: https://imagej.net/Linear_Stack_Alignment_with_SIFT (accessed on 24 June 2020).
- Thévenaz, P. ImageJ Plugin—StackReg. Available online: http://bigwww.epfl.ch/thevenaz/stackreg (accessed on 24 June 2020).
- Thevenaz, P.; Ruttimann, U.E.; Unser, M. A pyramid approach to subpixel registration based on intensity. IEEE Trans. Image Process. 1998, 7, 27–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Li, K. ImageJ Plugin—Image Stabilizer. Available online: http://www.cs.cmu.edu/~kangli/code/Image_Stabilizer.html (accessed on 24 June 2020).
- Lucas, B.; Kanade, T. An iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the Imaging Understanding Workshop, Vancouver, BC, Canada, 24–28 August 1981; pp. 121–130. [Google Scholar]
- Saalfeld, S. ImageJ Plugin—Elastic Alignment and Montage. Available online: https://imagej.net/Elastic_Alignment_and_Montage (accessed on 26 June 2020).
- Saalfeld, S.; Fetter, R.; Cardona, A.; Tomancak, P. Elastic volume reconstruction from series of ultra-thin microscopy sections. Nat. Methods 2012, 9, 717–720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hennies, J.; Lleti, J.M.S.; Schieber, N.L.; Templin, R.M.; Steyer, A.M.; Schwab, Y. AMST—Alignment to Median Smoothed Template for Focused Ion Beam Scanning Electron Microscopy Image Stacks. Sci Rep. 2020, 10, 2004. [Google Scholar] [CrossRef]
- Stephensen, H.J.T.; Darkner, S.; Sporring, J. A Highly Accurate Model Based Registration Method for FIB-SEM Images of Neurons. arXiv 2018, arXiv:1810.01159. [Google Scholar] [CrossRef] [Green Version]
- Putyatin, E.P.; Yakovleva, E.V.; Lubchenko, V.A. Decomposition of the centro-affine transformation matrix for normalization of images. Radioelektron. Inform. 1998, 4, 91–94. (In Russian) [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Reimers, I.; Safonov, I.; Yakimchuk, I. Construction of 3D Digital Model of a Rock Sample Based on FIB-SEM Data. In Proceedings of the 2019 24th Conference of Open Innovations Association (FRUCT), Moscow, Russia, 9–10 April 2019; pp. 351–359. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Vogel, H.-J.; Weller, U.; Schlüter, S. Quantification of soil structure based on Minkowski functions. Comput. Geosci. 2010, 36, 1236–1245. [Google Scholar] [CrossRef]
- Blasquez, I.; Poiraudeau, J.-F. Efficient processing of Minkowski functionals on a 3D binary image using binary decision diagrams. J. WSCG 2003, 11, 1–8. [Google Scholar]














| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| No alignment | 1 | 0.51 | 0.55 | 0.53 | 0.60 | 0.51 | 0.56 | 0.43 |
| SAD | 0.19 | 21.1 | 23.3 | 22.2 | 0.23 | 0.26 | 0.24 | 0.28 |
| StackReg | 0.79 | 31.1 | 30.1 | 31.0 | 1.05 | 1.08 | 1.06 | 0.32 |
| ImageStabilizer | 0.30 | 4.08 | 3.82 | 3.95 | 0.53 | 0.51 | 0.52 | 0.53 |
| JavaSIFT | 0.08 | 25.0 | 25.4 | 25.2 | 0.28 | 0.28 | 0.28 | 0.43 |
| Elastic | 0.25 | 0.29 | ||||||
| Proposed algorithm (SAD) | 0.13 | 0.38 | 0.43 | 0.41 | 0.22 | 0.24 | 0.23 | 0.62 |
| Proposed algorithm (subpixel JavaSIFT) | 0.10 | 0.33 | 0.39 | 0.36 | 0.17 | 0.17 | 0.17 | 0.63 |
| Image | ||||
|---|---|---|---|---|
| GT | 3,104,667 | 949,114 | 8933 | −11 |
| With displaced slices | 3,104,667 | 1,077,930 | 10,159 | −176 |
| Aligned by JavaSIFT | 3,104,667 | 986,102 | 9074 | −62 |
| Aligned by the proposed method | 3,104,667 | 974,658 | 9368 | −52 |
| Method | |
|---|---|
| No alignment | 1.00 |
| SAD | 0.18 |
| StackReg | 0.05 |
| ImageStabilizer | 0.26 |
| JavaSIFT | 0.02 |
| Elastic | 0.10 |
| Proposed algorithm | 0.02 |
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| No alignment | 1.00 | 6.30 | 2.87 | 4.59 | 2.69 | 1.57 | 2.13 | 0.31 |
| SAD | 0.77 | 17.9 | 130.4 | 74.2 | 0.42 | 0.65 | 0.54 | 0.27 |
| StackReg | 0.73 | 32.1 | 204.2 | 118.2 | 0.42 | 0.64 | 0.53 | 0.28 |
| ImageStabilizer | 0.62 | 6.88 | 5.83 | 6.35 | 0.45 | 0.78 | 0.62 | 0.34 |
| JavaSIFT | 0.64 | 7.98 | 59.4 | 33.7 | 0.51 | 0.74 | 0.62 | 0.31 |
| Elastic | 0.78 | 0.27 | ||||||
| Proposed algorithm | 0.64 | 6.27 | 2.74 | 4.51 | 0.38 | 0.48 | 0.43 | 0.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reimers, I.; Safonov, I.; Kornilov, A.; Yakimchuk, I. Two-Stage Alignment of FIB-SEM Images of Rock Samples. J. Imaging 2020, 6, 107. https://doi.org/10.3390/jimaging6100107
Reimers I, Safonov I, Kornilov A, Yakimchuk I. Two-Stage Alignment of FIB-SEM Images of Rock Samples. Journal of Imaging. 2020; 6(10):107. https://doi.org/10.3390/jimaging6100107
Chicago/Turabian StyleReimers, Iryna, Ilia Safonov, Anton Kornilov, and Ivan Yakimchuk. 2020. "Two-Stage Alignment of FIB-SEM Images of Rock Samples" Journal of Imaging 6, no. 10: 107. https://doi.org/10.3390/jimaging6100107
APA StyleReimers, I., Safonov, I., Kornilov, A., & Yakimchuk, I. (2020). Two-Stage Alignment of FIB-SEM Images of Rock Samples. Journal of Imaging, 6(10), 107. https://doi.org/10.3390/jimaging6100107