Mitral Valve Segmentation Using Robust Nonnegative Matrix Factorization
Abstract
1. Introduction
- We use Bregman iteration to avoid the inherent bias of regularization in the RNMF model within the context of mitral valve segmentation.
- As an additional variational segmentation technique, we use the Chan–Vese segmentation algorithm [12] to which we add a new regularization term so that it matches the problem of mitral valve segmentation.
- We proposed a new segmentation refinement algorithm that takes into account the opening and closing motion of the heart valve and, in combination with the unbiased RNMF model and the regularized variational segmentation technique, allows us to perform fully automatic segmentation without any further knowledge about the heart valve.
2. Related Work
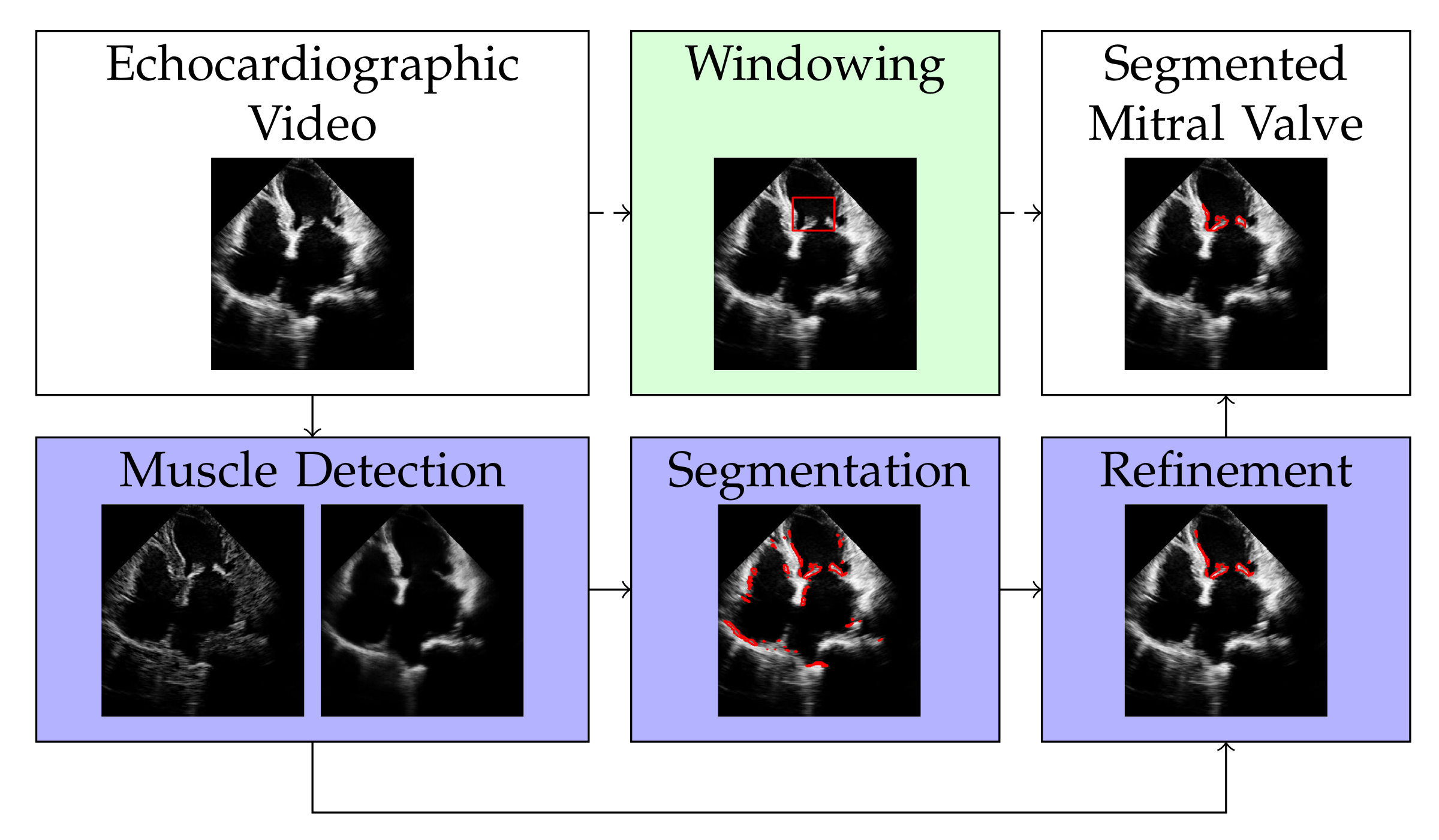
3. Method
3.1. Muscle Detection
| Algorithm 1: Update step of W, H, S and p for muscle detection. |
|
3.2. Valve Segmentation
| Algorithm 2: Update step of B for segmentation. |
|
3.3. Refinement
3.3.1. Calculation of the Centroid
| Algorithm 3: Iterative calculation of the mitral valve position. |
|
3.3.2. Clustering
3.4. Windowing
| Algorithm 4: Update step of W, H, S and p for windowing. |
|
4. Dataset
5. Results
5.1. On Bregman Iteration and RNMF
5.2. Automatic Segmentation
5.3. Windowing
5.4. Segmentation with Windowing
5.5. Results on the EchoNet-Dynamic Dataset
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pocock, G.; Richards, C.D.; Richards, D.A. Human Physiology; Oxford University Press: Oxford, UK, 2018; pp. 419–420. [Google Scholar]
- Mohty, D.; Pislaru, S. Valvular Heart Disease in Older Adults. 2019. Available online: https://www.uptodate.com/contents/valvular-heart-disease-in-older-adults (accessed on 5 December 2019).
- Nkomo, V.T.; Gardin, J.M.; Skelton, T.N.; Gottdiener, J.S.; Scott, C.G.; Enriquez-Sarano, M. Burden of valvular heart diseases: A population-based study. Lancet 2006, 368, 1005–1011. [Google Scholar] [CrossRef]
- Leech, G.J.; McCulloch, M.L.; Adams, D. Physical principles of ultrasound. In Echocardiography; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–31. [Google Scholar] [CrossRef]
- Abraham, T. Case Based Echocardiography: Fundamentals and Clinical Practice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; p. V. [Google Scholar]
- Hauff, P.; Reinhardt, M.; Foster, S. Ultrasound basics. In Molecular Imaging I; Springer: Berlin/Heidelberg, Germany, 2008; pp. 91–107. [Google Scholar] [CrossRef]
- Liu, X.; Cheung, Y.M.; Peng, S.J.; Peng, Q. Automatic mitral valve leaflet tracking in Echocardiography via constrained outlier pursuit and region-scalable active contours. Neurocomputing 2014, 144, 47–57. [Google Scholar] [CrossRef]
- Mikic, I.; Krucinski, S.; Thomas, J.D. Segmentation and tracking in echocardiographic sequences: Active contours guided by optical flow estimates. IEEE Trans. Med. Imaging 1998, 17, 274–284. [Google Scholar] [CrossRef]
- Dukler, Y.; Ge, Y.; Qian, Y.; Yamamoto, S.; Yuan, B.; Zhao, L.; Bertozzi, A.L.; Hunter, B.; Llerena, R.; Yen, J.T. Automatic valve segmentation in cardiac ultrasound time series data. In Proceedings of the Medical Imaging 2018: Image Processing, Houston, TX, USA, 11–13 February 2018; Volume 10574, p. 105741Y. [Google Scholar]
- Zhou, X.; Yang, C.; Yu, W. Automatic mitral leaflet tracking in echocardiography by outlier detection in the low-rank representation. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 972–979. [Google Scholar]
- Burlina, P.; Sprouse, C.; DeMenthon, D.; Jorstad, A.; Juang, R.; Contijoch, F.; Abraham, T.; Yuh, D.; McVeigh, E. Patient-specific modeling and analysis of the mitral valve using 3D-TEE. In Proceedings of the International Conference on Information Processing in Computer-Assisted Interventions, Geneva, Switzerland, 23 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 135–146. [Google Scholar]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Costa, E.; Martins, N.; Sultan, M.S.; Veiga, D.; Ferreira, M.; Mattos, S.; Coimbra, M. Mitral Valve Leaflets Segmentation in Echocardiography using Convolutional Neural Networks. In Proceedings of the 2019 IEEE 6th Portuguese Meeting on Bioengineering (ENBENG), Lisbon, Portugal, 22–23 February 2019; pp. 1–4. [Google Scholar]
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Fu, K.S.; Mui, J. A survey on image segmentation. Pattern Recognit. 1981, 13, 3–16. [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Boykov, Y.Y.; Jolly, M.P. Interactive graph cuts for optimal boundary region segmentation of objects in N-D images. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; Volume 1, pp. 105–112. [Google Scholar]
- Rother, C.; Kolmogorov, V.; Blake, A. Grabcut: Interactive Foreground Extraction Using Iterated Graph Cuts. ACM Trans. Graph. 2004, 23, 309–314. [Google Scholar]
- Boykov, Y.; Funka-Lea, G. Graph cuts and efficient ND image segmentation. Int. J. Comput. Vis. 2006, 70, 109–131. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Arifi, A.A.; Omran, A. The basics of echocardiography. J. Saudi Heart Assoc. 2010, 22, 71–76. [Google Scholar] [CrossRef][Green Version]
- Martin, S.; Daanen, V.; Chavanon, O.; Troccaz, J. Fast segmentation of the mitral valve leaflet in echocardiography. In International Workshop on Computer Vision Approaches to Medical Image Analysis; Springer: Berlin, Germany, 2006; pp. 225–235. [Google Scholar]
- Sultan, M.S.; Martins, N.; Veiga, D.; Ferreira, M.J.; Coimbra, M.T. Tracking of the anterior mitral leaflet in echocardiographic sequences using active contours. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 1074–1077. [Google Scholar]
- Sultan, M.S.; Martins, N.; Costa, E.; Veiga, D.; Ferreira, M.J.; Mattos, S.; Coimbra, M.T. Tracking large anterior mitral leaflet displacements by incorporating optical flow in an active contours framework. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 3244–3247. [Google Scholar]
- Shang, Y.; Yang, X.; Zhu, L.; Deklerck, R.; Nyssen, E. Region competition based active contour for medical object extraction. Comput. Med. Imaging Graph. 2008, 32, 109–117. [Google Scholar] [CrossRef]
- Yuan, B.; Chitturi, S.R.; Iyer, G.; Li, N.; Xu, X.; Zhan, R.; Llerena, R.; Yen, J.T.; Bertozzi, A.L. Machine learning for cardiac ultrasound time series data. In Medical Imaging 2017: Biomedical Applications in Molecular, Structural, and Functional Imaging; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10137, p. 101372D. [Google Scholar]
- Zhang, L.; Chen, Z.; Zheng, M.; He, X. Robust non-negative matrix factorization. Front. Electr. Electron. Eng. China 2011, 6, 192–200. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Guillamet, D.; Vitria, J. Non-negative matrix factorization for face recognition. In Catalonian Conference on Artificial Intelligence; Springer: Berlin, Germany, 2002; pp. 336–344. [Google Scholar]
- Lee, J.S.; Lee, D.D.; Choi, S.; Lee, D.S. Application of nonnegative matrix factorization to dynamic positron emission tomography. In Proceedings of the 3rd International Conference on Independent Component Analysis and Blind Signal Separation, San Diego, CA, USA, 9–13 December 2001; pp. 556–562. [Google Scholar]
- Ji, Z.; Meng, G.; Huang, D.; Yue, X.; Wang, B. NMFBFS: A NMF-based feature selection method in identifying pivotal clinical symptoms of hepatocellular carcinoma. Comput. Math. Methods Med. 2015, 2015, 846942. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Ding, C.C. Nonnegative matrix factorizations for clustering: A survey. In Data Clustering; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 149–176. [Google Scholar]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 556–562. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Amari, S.I. Hierarchical ALS algorithms for nonnegative matrix and 3D tensor factorization. In Proceedings of the International Conference on Independent Component Analysis and Signal Separation, London, UK, 9–12 September 2007; Springer: Berlin, Germany, 2007; pp. 169–176. [Google Scholar]
- Gillis, N. The why and how of nonnegative matrix factorization. Connections 2014, 12, 2. [Google Scholar]
- Berry, M.W.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Ding, C.; Li, T.; Peng, W.; Park, H. Orthogonal nonnegative matrix t-factorizations for clustering. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 20–23 August 2006; pp. 126–135. [Google Scholar]
- Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Pascual-Montano, A.; Carazo, J.M.; Kochi, K.; Lehmann, D.; Pascual-Marqui, R.D. Nonsmooth nonnegative matrix factorization (nsNMF). IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 403–415. [Google Scholar] [CrossRef]
- Corinzia, L.; Provost, J.; Candreva, A.; Tamarasso, M.; Maisano, F.; Buhmann, J.M. Unsupervised Mitral Valve Segmentation in Echocardiography with Neural Network Matrix Factorization. In Proceedings of the Conference on Artificial Intelligence in Medicine in Europe, Poznan, Poland, 26–29 June 2019; Springer: Berlin, Germany, 2019; pp. 410–419. [Google Scholar]
- Corinzia, L.; Laumer, F.; Candreva, A.; Taramasso, M.; Maisano, F.; Buhmann, J.M. Neural collaborative filtering for unsupervised mitral valve segmentation in echocardiography. Artif. Intell. Med. 2020, 110, 101975. Available online: https://github.com/lucori/NN-MitralSeg (accessed on 2 March 2021). [CrossRef] [PubMed]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Pedrosa, J.; Queirós, S.; Bernard, O.; Engvall, J.; Edvardsen, T.; Nagel, E.; D’hooge, J. Fast and fully automatic left ventricular segmentation and tracking in echocardiography using shape-based b-spline explicit active surfaces. IEEE Trans. Med. Imaging 2017, 36, 2287–2296. [Google Scholar] [CrossRef]
- Ciecholewski, M. An edge-based active contour model using an inflation/deflation force with a damping coefficient. Expert Syst. Appl. 2016, 44, 22–36. [Google Scholar] [CrossRef]
- Carneiro, G.; Nascimento, J.C.; Freitas, A. The segmentation of the left ventricle of the heart from ultrasound data using deep learning architectures and derivative-based search methods. IEEE Trans. Image Process. 2011, 21, 968–982. [Google Scholar] [CrossRef] [PubMed]
- Ali, Y.; Janabi-Sharifi, F.; Beheshti, S. Echocardiographic image segmentation using deep Res-U network. Biomed. Signal Process. Control 2021, 64, 102248. [Google Scholar] [CrossRef]
- Bernard, O.; Bosch, J.G.; Heyde, B.; Alessandrini, M.; Barbosa, D.; Camarasu-Pop, S.; Cervenansky, F.; Valette, S.; Mirea, O.; Bernier, M.; et al. Standardized evaluation system for left ventricular segmentation algorithms in 3D echocardiography. IEEE Trans. Med. Imaging 2015, 35, 967–977. [Google Scholar] [CrossRef]
- Osher, S.; Ruan, F.; Xiong, J.; Yao, Y.; Yin, W. Sparse recovery via differential inclusions. Appl. Comput. Harmon. Anal. 2016, 41, 436–469. [Google Scholar] [CrossRef]
- Bachmayr, M.; Burger, M. Iterative total variation schemes for nonlinear inverse problems. Inverse Probl. 2009, 25, 105004. [Google Scholar] [CrossRef][Green Version]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Condat, L. Discrete total variation: New definition and minimization. SIAM J. Imaging Sci. 2017, 10, 1258–1290. [Google Scholar] [CrossRef]
- Chambolle, A.; Pock, T. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 2011, 40, 120–145. [Google Scholar] [CrossRef]
- Ouyang, D.; He, B.; Ghorbani, A.; Lungren, M.P.; Ashley, E.A.; Liang, D.H.; Zou, J.Y. EchoNet-Dynamic: A Large New Cardiac Motion Video Data Resource for Medical Machine Learning; NeurIPS ML4H Workshop: Vancouver, BC, Canada, 2019. [Google Scholar]


















| Method | Category | Prior Knowledge | Pros and Cons | Paper |
|---|---|---|---|---|
| Energy Minimization Method | Active Contours | Initial Contour | Reduces the effort of the manual segmentation of each frame to the segmentation of only one frame. However, the disadvantage is that there has to be prior knowledge of the position of the mitral valve and it has to be drawn in by an expert. In addition, a tuning of parameters is necessary. | [8,21,22,23,24] |
| While this method has the advantage that no prior knowledge of mitral valve position is required, it has the disadvantage of requiring an extensive parameter adjustment. | [7] | |||
| Matrix Factorization | Mitral Valve Size | These methods do not require a prior drawn contour of the mitral valve in the first frame, but the size of the mitral valve for a windowing method must be known in advance. In addition, an adjustment of parameters is also necessary here. | [9,10] | |
| Matrix Factorization with Bias Avoiding | Optional: Mitral Valve Size | An advantage of this method is that the size of the mitral valve does not need to be known (optional), but the disadvantage is the required adjustment of parameters. | ours | |
| Machine Learning Method | Unsupervised, Videowise Training | Mitral Valve Size | These methods do not require a prior drawn contour of the mitral valve in the first frame, but the size of the mitral valve for a windowing method must be known in advance. In addition, an adjustment of parameters is also necessary here. | [39,40] |
| Supervised | Training Data | An automatic segmentation method without parameter adjustment for each video. However, a drawback is that training data and annotations must be available, which is especially difficult for medical data. In addition, there is an unknown bias shift of segmentation toward the training data. | [13] |
| Rank | |||||
|---|---|---|---|---|---|
| (a) | 0.1 | 0.04 | 0.075 | 1.0 | 2 |
| (b) | 0.1 | 0.04 | 0.05 | 1.0 | 2 |
| Rank | ||
|---|---|---|
| 1 | 0.4 | 5 |
| Recall | Precision | f1-Score | |
|---|---|---|---|
| (a) | 0.494 | 0.692 | 0.565 |
| (b) | 0.44 | 0.558 | 0.45 |
| (c) | 0.165 | 0.551 | 0.244 |
| (d) | 0.378 | 0.43 | 0.377 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dröge, H.; Yuan, B.; Llerena, R.; Yen, J.T.; Moeller, M.; Bertozzi, A.L. Mitral Valve Segmentation Using Robust Nonnegative Matrix Factorization. J. Imaging 2021, 7, 213. https://doi.org/10.3390/jimaging7100213
Dröge H, Yuan B, Llerena R, Yen JT, Moeller M, Bertozzi AL. Mitral Valve Segmentation Using Robust Nonnegative Matrix Factorization. Journal of Imaging. 2021; 7(10):213. https://doi.org/10.3390/jimaging7100213
Chicago/Turabian StyleDröge, Hannah, Baichuan Yuan, Rafael Llerena, Jesse T. Yen, Michael Moeller, and Andrea L. Bertozzi. 2021. "Mitral Valve Segmentation Using Robust Nonnegative Matrix Factorization" Journal of Imaging 7, no. 10: 213. https://doi.org/10.3390/jimaging7100213
APA StyleDröge, H., Yuan, B., Llerena, R., Yen, J. T., Moeller, M., & Bertozzi, A. L. (2021). Mitral Valve Segmentation Using Robust Nonnegative Matrix Factorization. Journal of Imaging, 7(10), 213. https://doi.org/10.3390/jimaging7100213






