On the Relationship between Corneal Biomechanics, Macrostructure, and Optical Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Measurements
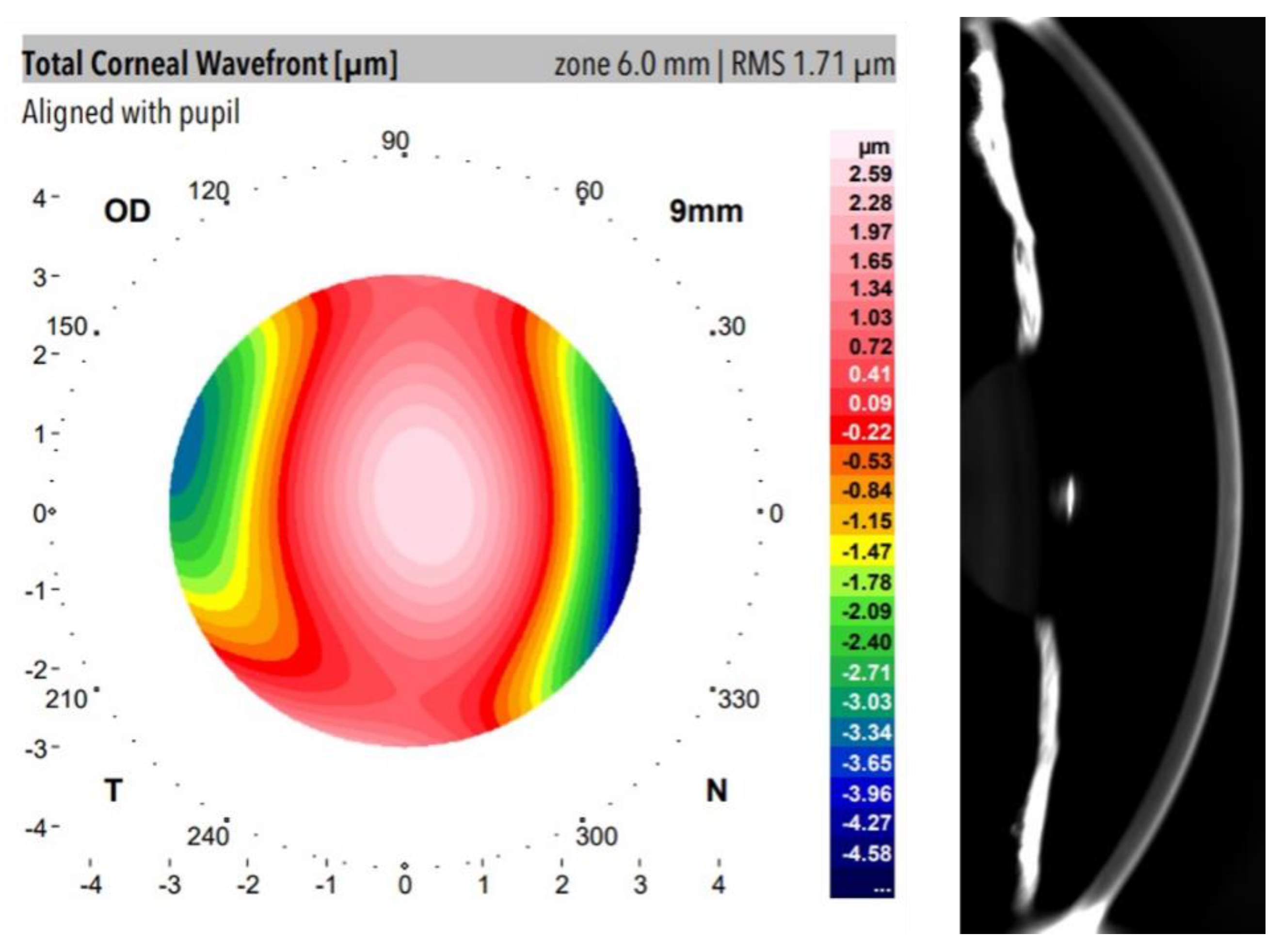
2.2.1. Dual Placido–Scheimpflug Imaging: Structural and Optical Parameters
Optical Transparency Index Calculation
2.2.2. Corneal Biomechanics Assessment
2.2.3. Data Analysis
Dataset Clustering
3. Results
3.1. Optical Density and Corneal Aberrations
3.2. Optical Density and Corneal Macro-Structure
3.3. Optical Density and Corneal Biomechanics
3.4. Experimental Expression to Predict the Human Corneal Transparency through Macroscopic Parameters
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Piñero, D.P.; Alcón, N. Corneal biomechanics: A review. Clin. Exp. Optom. 2015, 98, 107–116. [Google Scholar] [CrossRef]
- King, S.; Hafezi, F. Corneal biomechanics—A review. Opthalmic. Physiol. Opt. 2017, 37, 240–252. [Google Scholar] [CrossRef] [Green Version]
- Del Buey, M.A.; Casas, P.; Caramello, C.; López, N.; de la Rica, M.; Subirón, A.B.; Lanchares, E.; Huerva, V.; Grzybowski, A.; Ascaso, F.J. An update on corneal biomechanical cornal differences between type-2 diabetic and nondiabetic patients. J. Ophthalmol. 2019, 2019, 7645352. [Google Scholar] [PubMed]
- Beato, J.N.; Esteves-Leandro, J.; Reis, D.; Falcão, M.; Rosas, V.; Ângela, C.; Falcao-Reis, F. Structural and Biomechanical Corneal Differences between Type 2 Diabetic and Nondiabetic Patients. J. Ophthalmol. 2019, 2019, 3764878. [Google Scholar] [CrossRef]
- Ayhan, Z.; Kaya, M.; Ozturk, T.; Arikan, G.; Birlik, M. Association between Skin Thickness Measurements with Corneal Biomechanical Properties and Dry Eye Tests in Systemic Sclerosis. Ocul. Immunol. Inflamm. 2019, 27, 1138–1143. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, N.; Brandt, S.; Brünner, J.; Erb, C. Evaluation changes in corneal biomechanics in patients with systemic sclerosis. Klin. Monbl. Augenheilkd. 2019, 236, 806–815. [Google Scholar]
- Parker, J.S.; van Dijk, K.; Melles, G.R. Treatment options for advanced keratoconus: A review. Surv. Ophthalmol. 2018, 60, 459–480. [Google Scholar] [CrossRef]
- Roy, A.S.; Shetty, R.; Kummelil, M.K. Keratoconus: A biomechanical perspective on loss of corneal stiffness. Indian J. Ophthalmol. 2013, 61, 392–393. [Google Scholar] [CrossRef] [PubMed]
- Binder, P.S.; May, C.H.; Grant, S.C. An Evaluation of Orthokeratology. Ophthalmology 1980, 87, 729–744. [Google Scholar] [CrossRef]
- Ambrósio, R.; Correira, F.F.; Lopes, B.; Salomão, M.Q.; Luz, A.; Dawson, D.G.; Elsheikh, A.; Vinciguerra, R.; Vinciguerra, P.; Roberts, C.J. Corneal biomechanics in ectatic diseases: Refractive surgery implications. Open Ophthalmol. J. 2017, 11, 176–193. [Google Scholar] [CrossRef] [Green Version]
- Aksoy, S.; Akkaya, S.; Özkurt, Y.; Kurna, S.; Açıkalın, B.; Şengör, T. Topography and higher order corneal aberrations of the fellow eye in unilateral kerato-conus. Turk J. Ophthalmol. 2017, 47, 249–254. [Google Scholar] [CrossRef]
- Naderan, M.; Jahanrad, A.; Farjadnia, M. Ocular, corneal, and internal aberrations in eyes with keratoconus, forme fruste keratoconus, and healthy eyes. Int. Ophthalmol. 2018, 38, 1565–1573. [Google Scholar] [CrossRef]
- Wilkinson, J.M.; Cozine, E.W.; Kahn, A.R. Refractive Eye Surgery: Helping Patients Make Informed Decisions About LASIK. Am. Fam. Physician 2017, 95, 637–644. [Google Scholar] [PubMed]
- Zhang, Y.; Shen, Q.; Jia, Y.; Zhou, D.; Zhou, J. Clinical outcomes of SMILE and FS-LASIK used to treat myopia: A meta análisis. J. Refract. Surg. 2016, 32, 256–265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sultan, M.B.; Mansberger, S.L.; Lee, P.P. Understanding the Importance of IOP Variables in Glaucoma: A Systematic Review. Surv. Ophthalmol. 2009, 54, 643–662. [Google Scholar] [CrossRef]
- Meek, K.M.; Knupp, C. Corneal structure and transparency. Prog. Retin. Eye Res. 2015, 49, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ávila, F.J.; Gambín, A.; Artal, P.; Bueno, J.M. In vivo two-photon microscopy of the human eye. Sci. Rep. 2019, 9, 10121. [Google Scholar] [CrossRef] [Green Version]
- Petroll, W.M.; Robertson, D.M. In Vivo Confocal Microscopy of the Cornea: New Developments in Image Acquisition, Reconstruction, and Analysis Using the HRT-Rostock Corneal Module. Ocul. Surf. 2015, 13, 187–203. [Google Scholar] [CrossRef] [Green Version]
- Otri, A.M.; Fares, U.; Al-Aqaba, M.A.; Dua, H.S. Corneal Densitometry as an Indicator of Corneal Health. Ophthalmology 2012, 119, 501–508. [Google Scholar] [CrossRef] [PubMed]
- Belin, M.W.; Ambrósio, R. Scheimpflug imaging for keratoconus and ectatic disease. Indian J. Ophthalmol. 2013, 61, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Boulze-Pankert, M.; Dariel, R.; Hoffart, L. Corneal Scheimpflug Densitometry Following Photorefractive Keratectomy in Myopic Eyes. J. Refract. Surg. 2016, 32, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Tian, L.; Zhang, H.; Chen, X.; Li, L. Evaluation of corneal elastic modulus based on Corneal Visualization Scheimpflug Technology. Biomed. Eng. Online 2019, 18, 42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luce, D.A. Determining in vivo biomechanical properties of the cornea with an ocular response analyzer. J. Cataract. Refract. Surg. 2005, 31, 156–162. [Google Scholar] [CrossRef] [PubMed]
- Motevasseli, T.; Baradaran-Rafii, A.; Yazdizadeh, F.; Karimian, F.; Fekri, S.; Baradaran-Rafii, A. Comparison between two scheimpflug anterior segment analyzers. J. Ophthalmic Vis. Res. 2017, 12, 23–29. [Google Scholar] [CrossRef] [Green Version]
- Piñero, D.; Alcón, N. In vivo characterization of corneal biomechanics. J. Cataract. Refract. Surg. 2014, 40, 870–877. [Google Scholar] [CrossRef]
- Kaushik, S.; Pandav, S.S. Ocular Response Analyzer. J. Curr. Glaucoma Pract. 2012, 6, 17–19. [Google Scholar] [CrossRef]
- Lau, W.; Pye, D. A Clinical Description of Ocular Response Analyzer Measurements. Investig. Opthalmology Vis. Sci. 2011, 52, 2911–2916. [Google Scholar] [CrossRef] [Green Version]
- Roberts, C.J.; Mahmoud, A.M.; Bons, J.P.; Hossain, A.; Elsheikh, A.; Vinciguerra, R.; Vinciguerra, P.; Ambrósio, R., Jr. Introduction of two novel stiffness parameters and interpretation of air puff bio-mechanical deformation parameters with a Dynamic Scheimpflug analyzer. J. Refract. Surg. 2017, 33, 266–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Llorente, L.; Barbero, S.; Merayo, J.; Marcos, S. Total and corneal optical aberrations induced by laser in situ keratomileusis for hypero-pia. J. Refract. Surg. 2004, 20, 203–216. [Google Scholar] [CrossRef]
- Pérez, G.M.; Manzanera, S.; Artal, P. Impact of scattering and spherical aberration in contrast sensitivity. J. Vis. 2009, 9, 19. [Google Scholar] [CrossRef]
- Ávila, F.J.; Ares, J.; Collados, M.V.; Marcellán, M.C.; Remón, L. An Update on Corneal Imaging Techniques: From Macroscale to Nanostructure. SN Compr. Clin. Med. 2019, 2, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, E.; Yamaguchi, T.; Tsubota, K.; Shimazaki, J. Corneal high-order aberrations in eyes with corneal scar after traumatic perfora-tion. Eye Contact Lens 2019, 45, 124–131. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, M.; Rosati, M.; Pileri, M.; Schiano-Lomoriello, D.; Serrao, S. evaluation of corneal optical properties in subjects wearing hydrogel etafilcon A contact lenses and the effect of administering mannitol-enriched sodium hyaluronate ophthalmic solution. Clin. Ophthalmol. 2014, 8, 2347–2354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wegener, A.R.; Meyer, L.; Hauch, C.; Sacchetti, M.; Plateroti, R.; Lambiase, A. Changes of Corneal Transparency and Thickness in Dry–Eye Syndrome Single and in Combination With Other Ocular Diseases. Investig. Opthalmol. Vis. Sci. 2005, 46, 4473. [Google Scholar]
- Spadea, L.; Maraone, G.; Verboschi, F.; Vingolo, E.M.; Tognetto, D. Effect of corneal light scatter on vision: A review of the literature. Int. J. Ophthalmol. 2016, 9, 459–464. [Google Scholar] [CrossRef]
- Mohammadi, S.-F.; Khorrami-Nejad, M.; Hamidirad, M. Posterior corneal astigmatism: A review article. Clin. Optom. 2019, 11, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Whitford, C.; Studer, H.; Boote, C.; Meek, K.M.; Elsheikh, A. Biomechanical model of the human cornea: Considering shear stiffness and regional variation of collagen anisotropy and density. J. Mech. Behav. Biomed. Mater. 2015, 42, 76–87. [Google Scholar] [CrossRef]
- Blackburn, B.J.; Jenkins, M.W.; Rollins, A.M.; Dupps, W.J. A Review of Structural and Biomechanical Changes in the Cornea in Aging, Disease, and Photochemical Crosslinking. Front. Bioeng. Biotechnol. 2019, 7, 66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ariza-Gracia, M.A.; Zurita, J.F.; Piñero, D.P.; Rodriguez-Matas, J.F.; Calvo, B. Coupled biomechanical response of the cornea assessed by non-contact tonom-etry. A simulation study. PLoS ONE 2015, 10, e0121486. [Google Scholar] [CrossRef] [Green Version]
- Piñero, D.P.; Alio, J.L.; Barraquer, R.I.; Michael, R.; Jiménez, R. Corneal biomechanics, refraction and corneal aberrometry in Keratoconus: An inte-grated study. Investig. Opthalmol. Vis. Sci. 2010, 51, 1948–1955. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Wang, Y.; Dou, R. Aberration compensation between anterior and posterior corneal surfaces after Small incision lenticule extraction and Femtosecond laser-assisted laser in-situ keratomileusis. Ophthalmic Physiol. Opt. 2015, 35, 540–551. [Google Scholar] [CrossRef]
- Garzón, N.; Poyales, F.; Illarramendi, I.; Mendicute, J.; Jáñez, Óscar; Caro, P.; López-Muñoz, A.; Argüeso, F. Corneal densitometry and its correlation with age, pachymetry, corneal curvature, and refraction. Int. Ophthalmol. 2017, 37, 1263–1268. [Google Scholar] [CrossRef]







| Structural Parameters | Optical Parameters |
|---|---|
| Central Thickness | Total Aberration RMS |
| Middle Thickness | Spherical Aberration RMS |
| Peripheral Thickness | |
| Anterior Eccentricity | |
| Posterior Eccentricity | Optical Density |
| Total Corneal Astigmatism |
| OTI | N | Cluster |
|---|---|---|
| 78.5 | 14 | 1 |
| 79.0 | 9 | 2 |
| 79.5 | 22 | 3 |
| 80.0 | 16 | 4 |
| 80.5 | 15 | 5 |
| 81.0 | 12 | 6 |
| 81.5 | 8 | 7 |
| OTI | TA RMS * (µm) | SA RMS ** (µm) | Spearman’s * | Spearman’s ** |
|---|---|---|---|---|
| 80.0 ± 0.9 | 1.45 ± 0.28 | −0.15 ± 0.05 | Failed, p = 0.38. | Failed, p = 0.26. |
| Structural Parameter | Location | Mean Value | Spearman’s |
|---|---|---|---|
| Corneal Thickness | Central | 554 ± 30 µm | Failed, p = 0.58. |
| Middle | 601 ± 30 µm | Failed, p = 0.42. | |
| Peripheral | 674 ± 69 µm | Failed, p = 0.29. | |
| Corneal Astigmatism | Global | 0.87 ± 0.34 Dpt. | R2 = 0.87 |
| Anterior Eccentricity | Global | 0.24 ± 0.16 | Failed, p = 0.39 |
| Posterior Eccentricity | Global | 0.42 ± 0.12 | R2 = 0.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ávila, F.J.; Marcellán, M.C.; Remón, L. On the Relationship between Corneal Biomechanics, Macrostructure, and Optical Properties. J. Imaging 2021, 7, 280. https://doi.org/10.3390/jimaging7120280
Ávila FJ, Marcellán MC, Remón L. On the Relationship between Corneal Biomechanics, Macrostructure, and Optical Properties. Journal of Imaging. 2021; 7(12):280. https://doi.org/10.3390/jimaging7120280
Chicago/Turabian StyleÁvila, Francisco J., Maria Concepción Marcellán, and Laura Remón. 2021. "On the Relationship between Corneal Biomechanics, Macrostructure, and Optical Properties" Journal of Imaging 7, no. 12: 280. https://doi.org/10.3390/jimaging7120280
APA StyleÁvila, F. J., Marcellán, M. C., & Remón, L. (2021). On the Relationship between Corneal Biomechanics, Macrostructure, and Optical Properties. Journal of Imaging, 7(12), 280. https://doi.org/10.3390/jimaging7120280







