Critical Aspects of Person Counting and Density Estimation
Abstract
1. Introduction
2. Related Work
2.1. Concepts of Counting
2.1.1. Counting by Detection
2.1.2. Counting by Regression
2.1.3. Counting by Density Estimation
2.2. CNN-Based Methods for Counting
2.2.1. Multi Column Method
2.2.2. Contextual Pyramid Method
2.2.3. Context-Aware Method
3. Baseline Method–Congested Scene Recognition Network
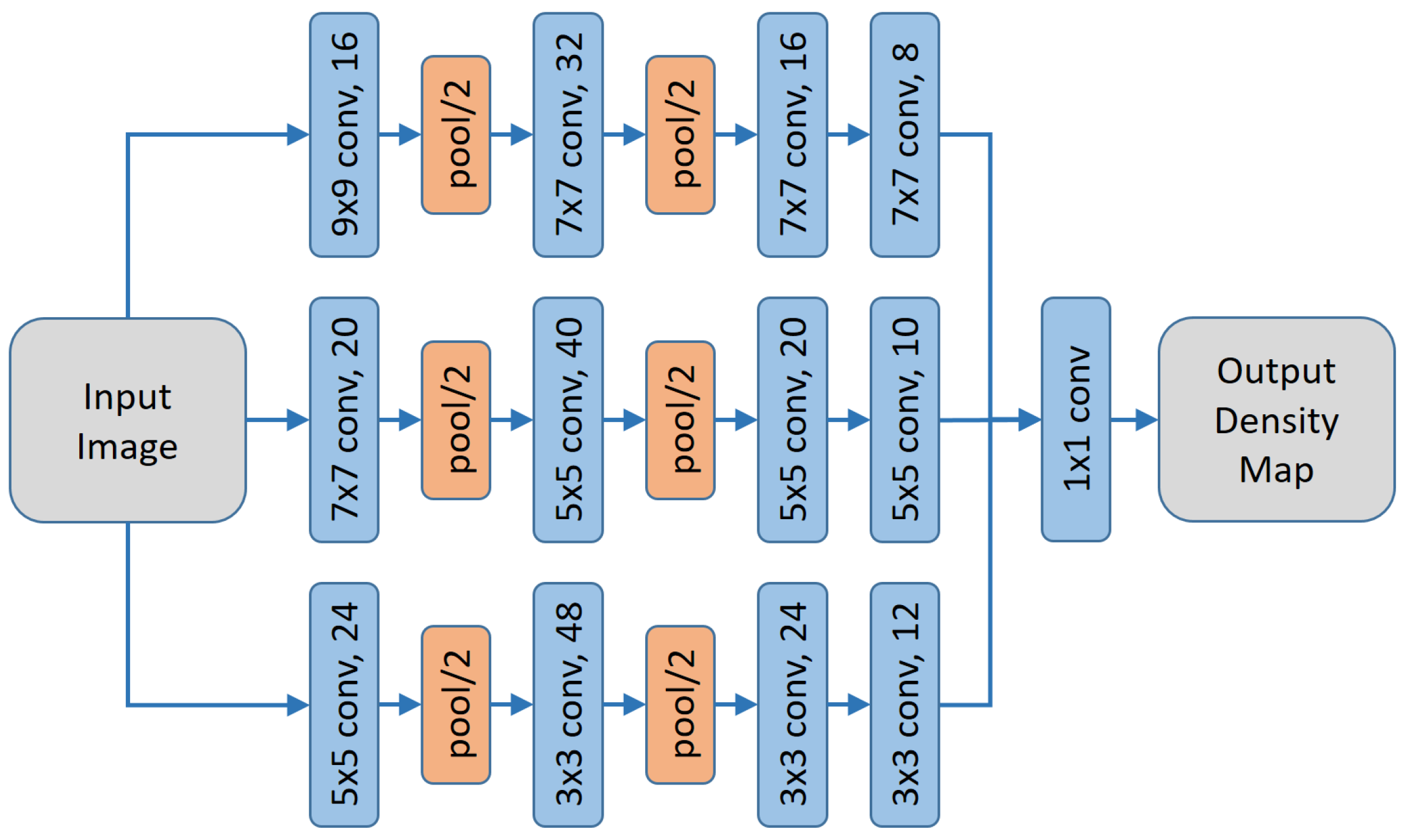
3.1. Architecture
3.2. Training
3.3. Evaluation
4. Discussion of Critical Aspects
4.1. Datasets
4.2. Ground Truth Generation
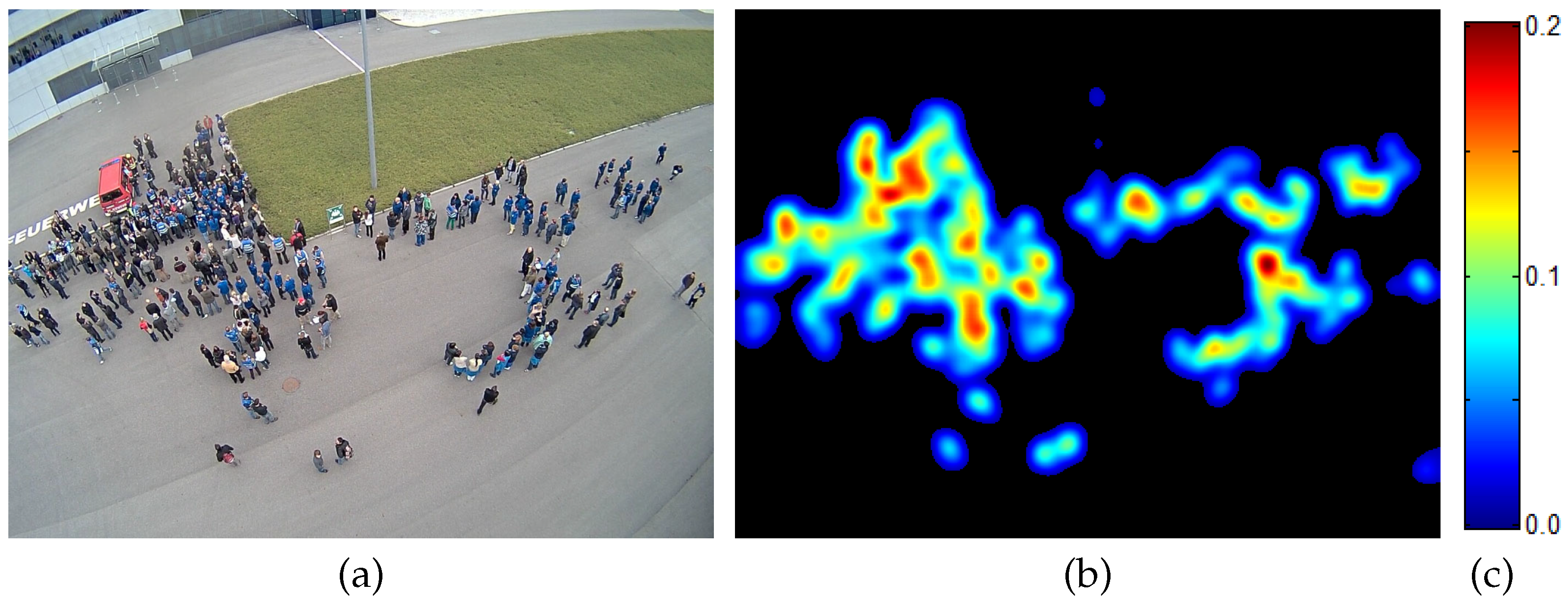
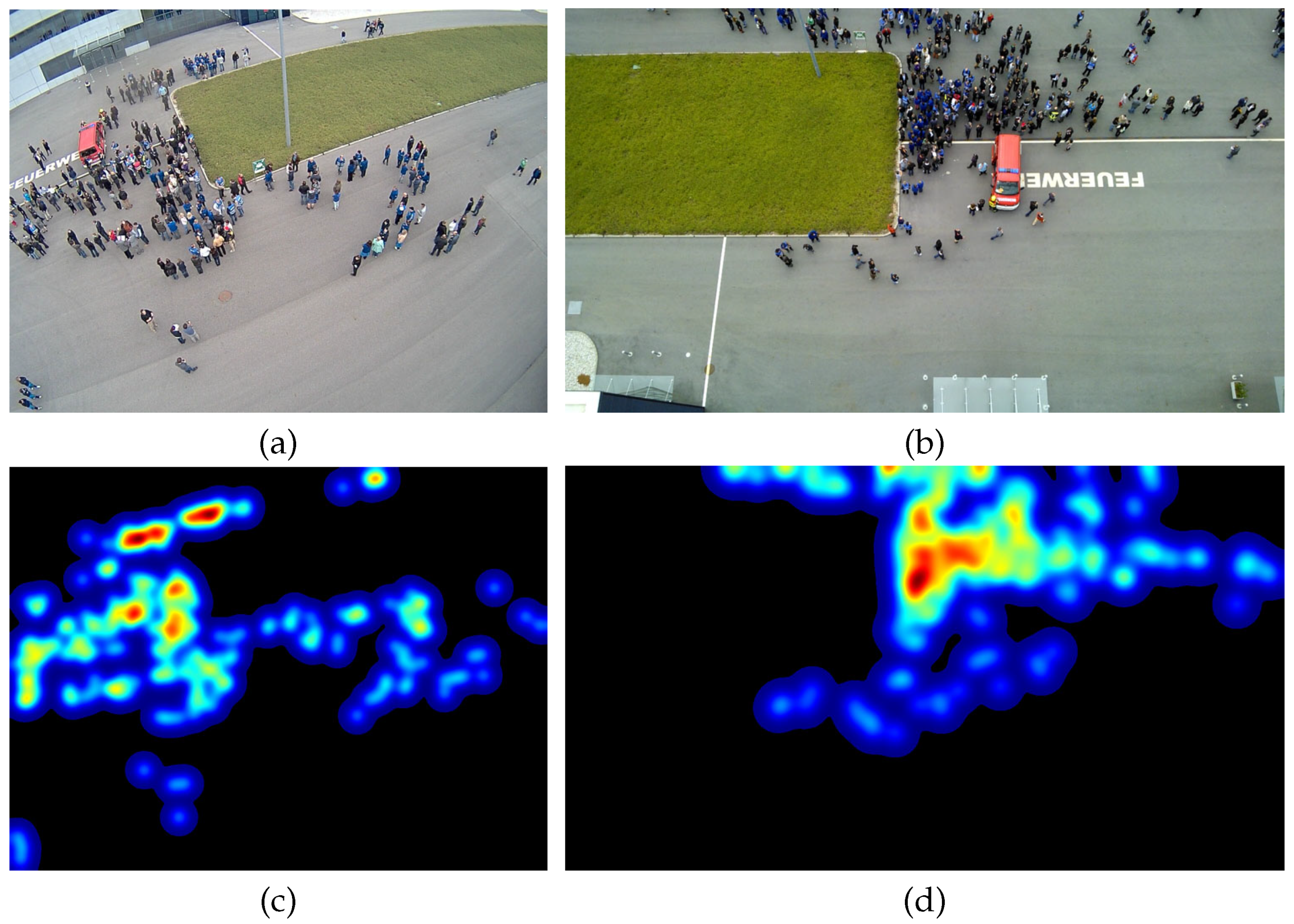
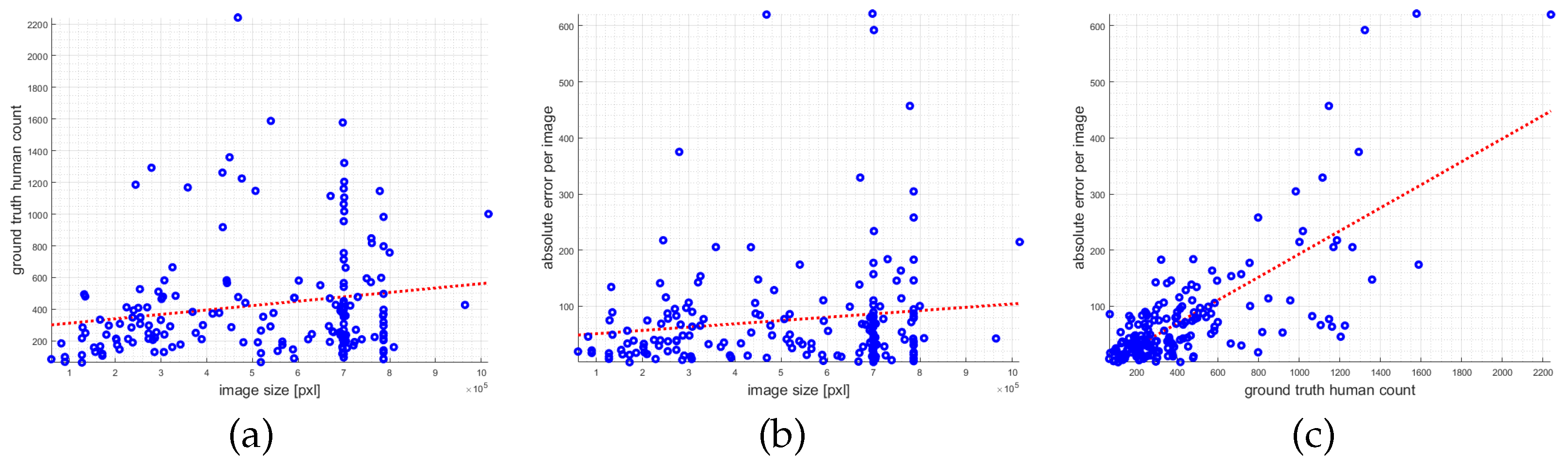
4.3. Evaluation
4.4. Data Augmentation
- Rotations up to 10 degrees.
- Shifts in width and height of 2% of image dimensions.
- Zoom range of 1%.
- Horizontal flipping.
- Radiometric offset and gain of 1% for each image channel.
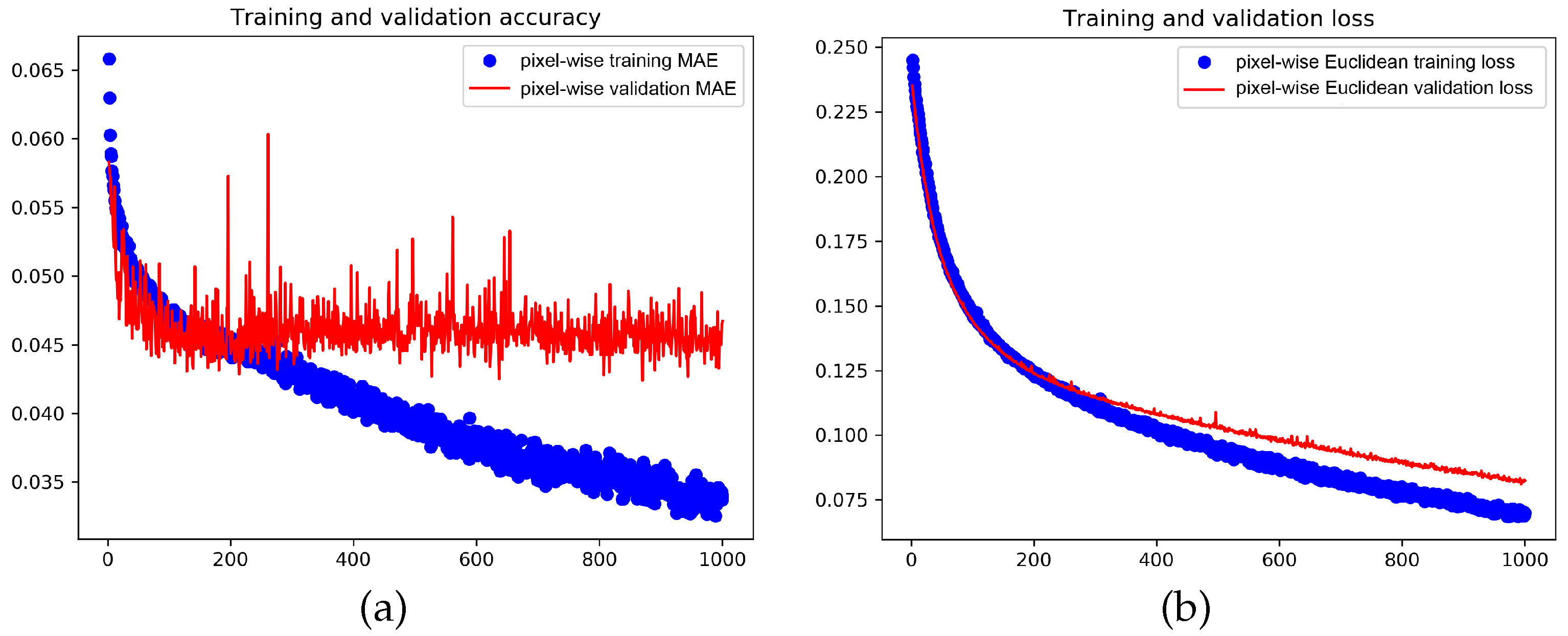
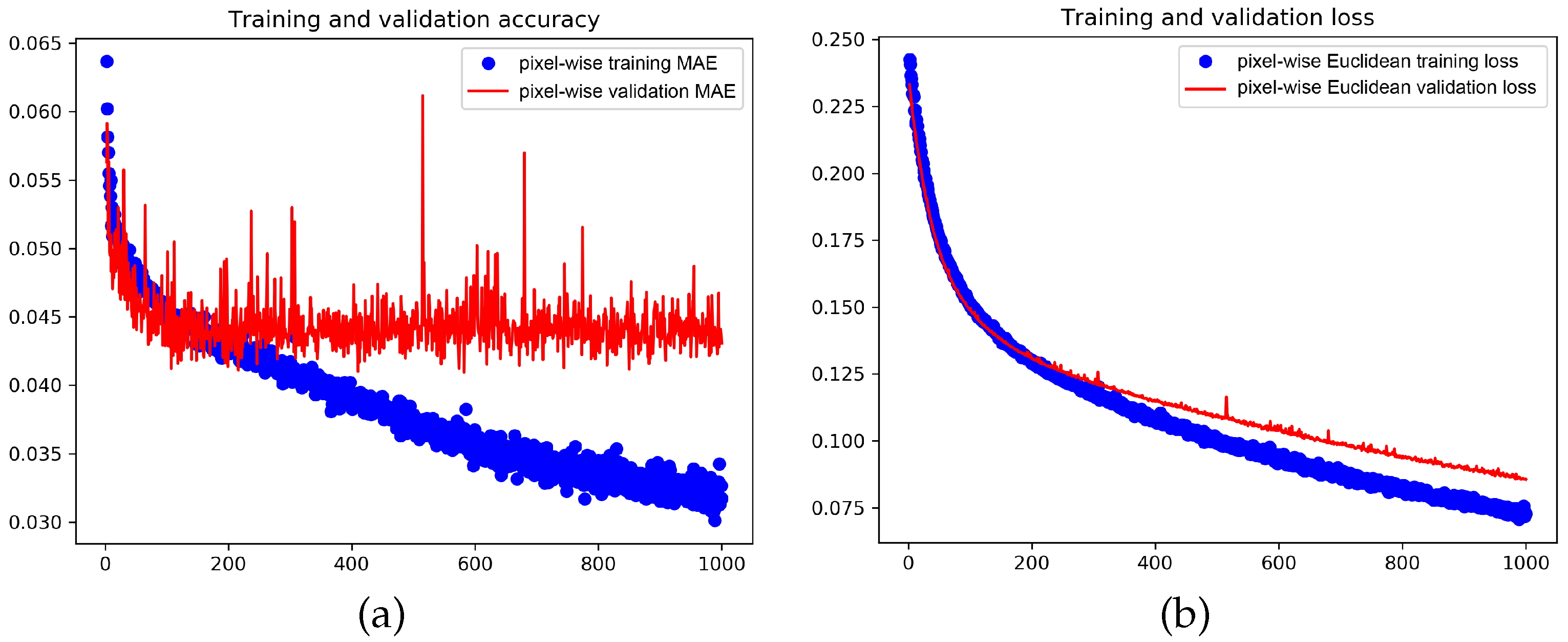
4.5. Hyperparameters and Training
4.6. Physical Plausibility
5. Implementation Details
6. Results
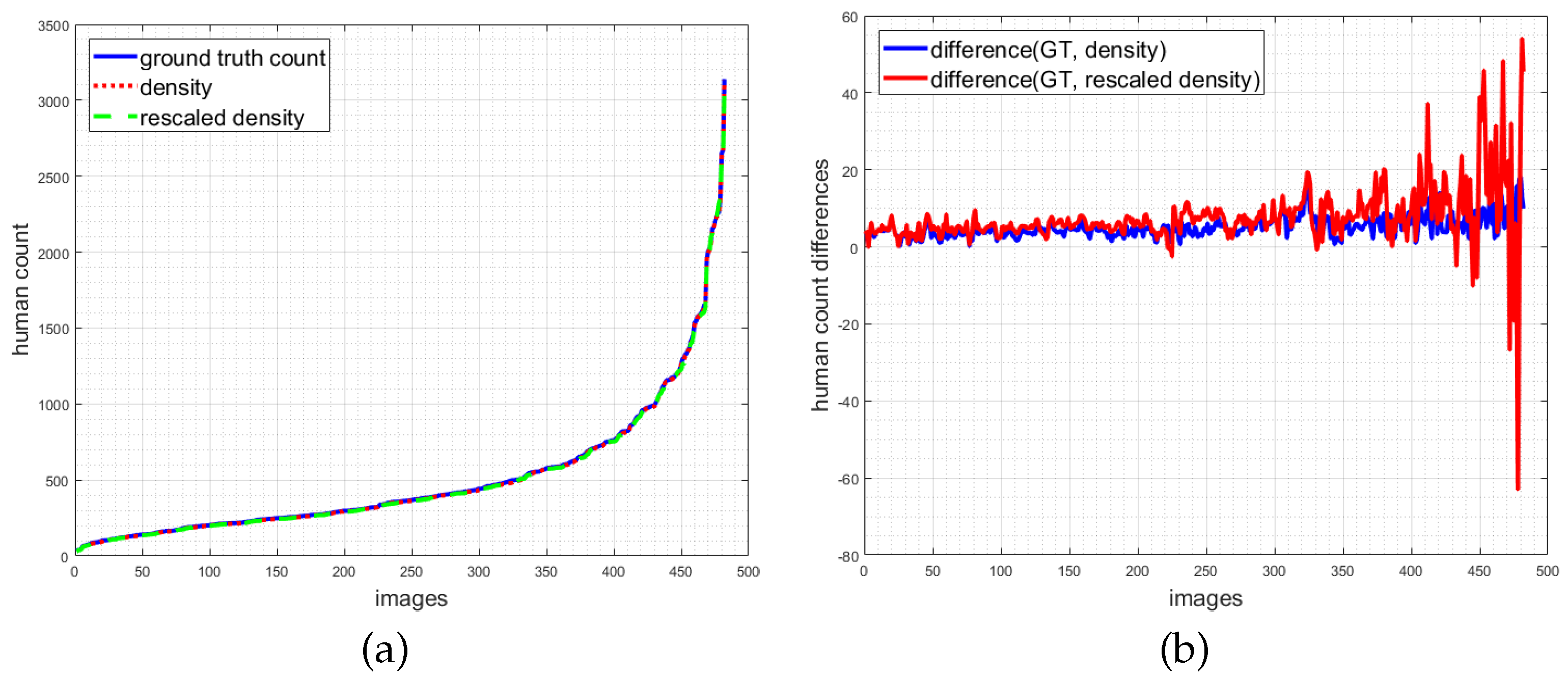
6.1. ShanghaiTech Part A Dataset
6.2. Real-World Videos
7. Recommendations
7.1. Ground Truth Density Generation
7.2. Evaluation Metrics
7.3. Fair and Unbiased Dataset
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CAN | context-aware network |
| CNN | convolutional neural network |
| CP-CNN | contextual pyramid convolutional neural network |
| CSRNet | congested scene recognition network |
| GPU | graphical processing unit |
| HoG | histograms of oriented gradients |
| MAE | mean absolute error |
| MCNN | multi column neural network |
| MESA | maximum excess over subarrays |
| MNAE | mean normalized absolute error |
| RMSE | root mean squared error |
| MRCNet | multi-resolution crowd network |
| NWPU-Crowd | crowd dataset from Northwestern Polytechnical University |
| ReLU | rectified linear unit |
| RMSE | root mean squared error |
| SANet | scale aggregation network |
| SGD | stochastic gradient descent |
| SIFT | scale-invariant feature transform |
| SSIM | structural similarity index measure |
| UCF-QNRF | large crowd counting data set from University of Central Florida |
| UCF-CC-50 | crowd counting data set from University of Central Florida |
| UCSD | crowd counting data set from University of California San Diego |
| VGG | very deep convolutional network from University of Oxford |
References
- Hopkins, I.H.G.; Pountney, S.J.; Hayes, P.; Sheppard, M.A. Crowd pressure monitoring. Eng. Crowd Saf. 1993, 389–398. [Google Scholar]
- Lee, R.S.C.; Hughes, R.L. Prediction of human crowd pressures. Accid. Anal. Prev. 2006, 38, 712–722. [Google Scholar] [CrossRef] [PubMed]
- Perko, R.; Schnabel, T.; Fritz, G.; Almer, A.; Paletta, L. Counting people from above: Airborne video based crowd analysis. Workshop of the Austrian Association for Pattern Recognition. arXiv 2013, arXiv:1304.6213. [Google Scholar]
- Helbing, D.; Johansson, A. Pedestrian, crowd and evacuation dynamics. In Encyclopedia of Complexity and Systems Science; Springer: New York, NY, USA, 2009; pp. 6476–6495. [Google Scholar]
- Helbing, D.; Johansson, A.; Al-Abideen, H.Z. Dynamics of crowd disasters: An empirical study. Phys. Rev. E 2007, 75, 046109. [Google Scholar] [CrossRef] [PubMed]
- Almer, A.; Perko, R.; Schrom-Feiertag, H.; Schnabel, T.; Paletta, L. Critical Situation Monitoring at Large Scale Events from Airborne Video based Crowd Dynamics Analysis. In Geospatial Data in a Changing World—Selected papers of the AGILE Conference on Geographic Information Science; Springer: Cham, Switzerland, 2016; pp. 351–368. [Google Scholar]
- Perko, R.; Schnabel, T.; Fritz, G.; Almer, A.; Paletta, L. Airborne based High Performance Crowd Monitoring for Security Applications. In Scandinavian Conference on Image Analysis; Springer: Berlin/Heidelberg, Germany, 2013; pp. 664–674. [Google Scholar]
- Perko, R.; Schnabel, T.; Almer, A.; Paletta, L. Towards View Invariant Person Counting and Crowd Density Estimation for Remote Vision-Based Services. In Proceedings of the IEEE Electrotechnical and Computer Science Conference, Bhopal, India, 1–2 March 2014; Volume B, pp. 80–83. [Google Scholar]
- Li, Y.; Zhang, X.; Chen, D. CSRNet: Dilated convolutional neural networks for understanding the highly congested scenes. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1091–1100. [Google Scholar]
- Lempitsky, V.; Zisserman, A. Learning to Count Objects in Images. Advances in Neural Information Processing Systems. 2010, pp. 1324–1332. Available online: https://proceedings.neurips.cc/paper/2010 (accessed on 31 January 2021).
- Everingham, M.; Eslami, S.M.A.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The PASCAL visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Lin, Z.; Davis, L.S. Shape-based human detection and segmentation via hierarchical part-template matching. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 604–618. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Nevatia, R. Detection of multiple, partially occluded humans in a single image by bayesian combination of edgelet part detectors. In Proceedings of the International Conference on Computer Vision, Beijing, China, 17–21 October 2005; pp. 90–97. [Google Scholar]
- Kong, D.; Gray, D.; Tao, H. A viewpoint invariant approach for crowd counting. In Proceedings of the International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; Volume 3, pp. 1187–1190. [Google Scholar]
- Marana, A.N.; Velastin, S.; Costa, L.; Lotufo, R. Estimation of crowd density using image processing. In Proceedings of the IEE Colloquium on Image Processing for Security Applications, London, UK, 10 March 1997; pp. 1–8. [Google Scholar]
- Cho, S.Y.; Chow, T.W.; Leung, C.T. A neural-based crowd estimation by hybrid global learning algorithm. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 535–541. [Google Scholar]
- Arteta, C.; Lempitsky, V.; Noble, J.A.; Zisserman, A. Interactive object counting. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 504–518. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Fiaschi, L.; Köthe, U.; Nair, R.; Hamprecht, F.A. Learning to count with regression forest and structured labels. In Proceedings of the International Conference on Pattern Recognition, Tsukuba, Japan, 11–15 November 2012; pp. 2685–2688. [Google Scholar]
- Sam, D.B.; Surya, S.; Babu, R.V. Switching convolutional neural network for crowd counting. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Volume 1, pp. 5744–5752. [Google Scholar]
- Cao, X.; Wang, Z.; Zhao, Y.; Su, F. Scale aggregation network for accurate and efficient crowd counting. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 757–773. [Google Scholar]
- Zhang, Y.; Zhou, D.; Chen, S.; Gao, S.; Ma, Y. Single-image crowd counting via multi-column convolutional neural network. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 589–597. [Google Scholar]
- Idrees, H.; Tayyab, M.; Athrey, K.; Zhang, D.; Al-Maadeed, S.; Rajpoot, N.; Shah, M. Composition loss for counting, density map estimation and localization in dense crowds. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 532–546. [Google Scholar]
- Bahmanyar, R.; Vig, E.; Reinartz, P. MRCNet: Crowd counting and density map estimation in aerial and ground imagery. In Proceedings of the British Machine Vision Conference Workshop on Object Detection and Recognition for Security Screening, Cardiff, UK, 9–12 September 2019; pp. 1–12. [Google Scholar]
- Sindagi, V.A.; Patel, V.M. Generating high-quality crowd density maps using contextual pyramid CNNs. In Proceedings of the International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1879–1888. [Google Scholar]
- Liu, W.; Salzmann, M.; Fua, P. Context-aware Crowd Counting. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5099–5108. [Google Scholar]
- Gao, Z.; Li, Y.; Yang, Y.; Wang, X.; Dong, N.; Chiang, H.D. A GPSO-optimized convolutional neural networks for EEG-based emotion recognition. Neurocomputing 2020, 380, 225–235. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Monarch Butterfly Optimization Based Convolutional Neural Network Design. Mathematics 2020, 8, 936. [Google Scholar] [CrossRef]
- Johnson, F.; Valderrama, A.; Valle, C.; Crawford, B.; Soto, R.; Ñanculef, R. Automating configuration of convolutional neural network hyperparameters using genetic algorithm. IEEE Access 2020, 8, 156139–156152. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. The role of context in object recognition. Trends Cogn. Sci. 2007, 11, 520–527. [Google Scholar] [CrossRef] [PubMed]
- Perko, R.; Leonardis, A. A framework for visual-context-aware object detection in still images. Comput. Vis. Image Underst. 2010, 114, 700–711. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Zhang, C.; Li, H.; Wang, X.; Yang, X. Cross-scene crowd counting via deep convolutional neural networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 833–841. [Google Scholar]
- Wang, Q.; Gao, J.; Lin, W.; Li, X. NWPU-Crowd: A large-scale benchmark for crowd counting. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Torralba, A.; Efros, A.A. Unbiased look at dataset bias. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1521–1528. [Google Scholar]
- Dijk, T.v.; Croon, G.d. How do neural networks see depth in single images? In Proceedings of the International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2183–2191. [Google Scholar]
- Idrees, H.; Saleemi, I.; Seibert, C.; Shah, M. Multi-source multi-scale counting in extremely dense crowd images. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2547–2554. [Google Scholar]
- Chan, A.B.; Liang, Z.S.J.; Vasconcelos, N. Privacy preserving crowd monitoring: Counting people without people models or tracking. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–7. [Google Scholar]
- Liu, J.; Gao, C.; Meng, D.; Hauptmann, A.G. DecideNet: Counting varying density crowds through attention guided detection and density estimation. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5197–5206. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]









| Dataset | Number of Images | Number of Annotations | Average Count | Average Resolution | Publication |
|---|---|---|---|---|---|
| ShanghaiTech Part A | 482 | ∼240 k | 501 | 868 × 589 (*) | [24] |
| ShanghaiTech Part B | 716 | ∼90 k | 124 | 1024 × 768 | [24] |
| UCF-CC-50 | 50 | ∼64 k | 1280 | 2888 × 2101 (*) | [41] |
| WorldExpo10 | 3980 | ∼200 k | 56 | 720 × 576 | [37] |
| UCSD | 2000 | ∼50 k | 25 | 238 × 158 | [42] |
| UCF-QNRF | 1535 | ∼1250 k | 815 | 2902 × 2013 (*) | [25] |
| NWPU-Crowd | 5109 | ∼2130 k | 418 | 3209 × 2191 (*) | [38] |
| Architecture | MAE |
|---|---|
| dilation 1 | 69.7 |
| dilation 2 | 68.2 |
| dilation 2 and 4 | 71.9 |
| dilation 4 | 75.8 |
| Method | MAE | Size Factor |
|---|---|---|
| MCNN [24] | 110.2 | 1/4 |
| Switching CNN [22] | 90.4 | 1/4 |
| CP-CNN [27] | 73.6 | 1/4 |
| CSRNet [9] | 68.2 | 1/8 |
| SANet [23] | 67.0 | 1/1 |
| MRCNet [26] | 66.2 | 1/1 |
| this work | 64.8 | 1/8 |
| CAN [28] | 62.3 | 1/1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perko, R.; Klopschitz, M.; Almer, A.; Roth, P.M. Critical Aspects of Person Counting and Density Estimation. J. Imaging 2021, 7, 21. https://doi.org/10.3390/jimaging7020021
Perko R, Klopschitz M, Almer A, Roth PM. Critical Aspects of Person Counting and Density Estimation. Journal of Imaging. 2021; 7(2):21. https://doi.org/10.3390/jimaging7020021
Chicago/Turabian StylePerko, Roland, Manfred Klopschitz, Alexander Almer, and Peter M. Roth. 2021. "Critical Aspects of Person Counting and Density Estimation" Journal of Imaging 7, no. 2: 21. https://doi.org/10.3390/jimaging7020021
APA StylePerko, R., Klopschitz, M., Almer, A., & Roth, P. M. (2021). Critical Aspects of Person Counting and Density Estimation. Journal of Imaging, 7(2), 21. https://doi.org/10.3390/jimaging7020021








