Force Estimation during Cell Migration Using Mathematical Modelling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model for Membrane Force Estimation
2.2. Formulation and Approximation of the Optimal Control Problem and Biological Interpretation
2.3. Model Parameters for the Different Biological Datasets
3. Results
Geometric Quantities That Are of Biological Interest
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- File link for “keratocyte.avi”, accessed on 11 July 2022:Caption for media file with file name “keratocyte.avi”:Top-left: the original image from experimental observation; top-right, our segmentation of the keratocyte from the image; bottom-left: we define the interfacial region of the cell and its centroid position, within this sub-figure, we continually overlay the cell shapes and positions as it migrates; bottom-right: we use colour coding to identify red as protrusion and blue as retraction forces and the locations where they are exerted on the cellular interfacial region, the bar on the right-hand side shows the maximum and minimum amount of forcing that the colour coding is illustrating. Bars indicate 20 m.
- File link for “T24.avi”, accessed on 11 July 2022:Caption for media file with file name “T24.avi”: Top-left: the original image from experimental observation; top-right, our segmentation of the T24 cancer cell from the image; bottom-left: we define the interfacial region of the cell and its centroid position, within this sub-figure, we continually overlay the cell shapes and positions as it migrates; bottom-right: we use colour coding to identify red as protrusion, and blue as retraction forces and the locations where they are exerted on the cellular interfacial region, the dark shadows in the background illustrate the targeted shapes that our model is trying to replicate, the bar on the right-hand side shows the maximum and minimum amount of forcing that the colour coding is illustrating. Bars indicate 20 m.
- File link for “MDCK.avi”, accessed on 11 July 2022:Caption for media file with file name “MDCK.avi”: The first image on the first row: the original image from experimental observation and our choice of three cells which are used in our simulation; the second image on the first row: our segmentation of the cells from the image on the left; the first image on the second row: we define the interfacial region of the cell and its centroid position, within this sub-figure, we continually overlay the cell shapes and positions as it migrates; the second image on the second row: we use colour coding to identify red as protrusion, and blue as retraction forces and the locations they are exerted on the cellular interfacial region, the dark shadows in the background illustrate the targeted shapes that our model is trying to replicate, the bar on the right-hand side shows the maximum and minimum amount of forcing that the colour coding is illustrating.; the only image on the third row: we show our Euler number from Equation (5) computed at each and red circles indicate the events of cell division. Bars indicate 20 m.
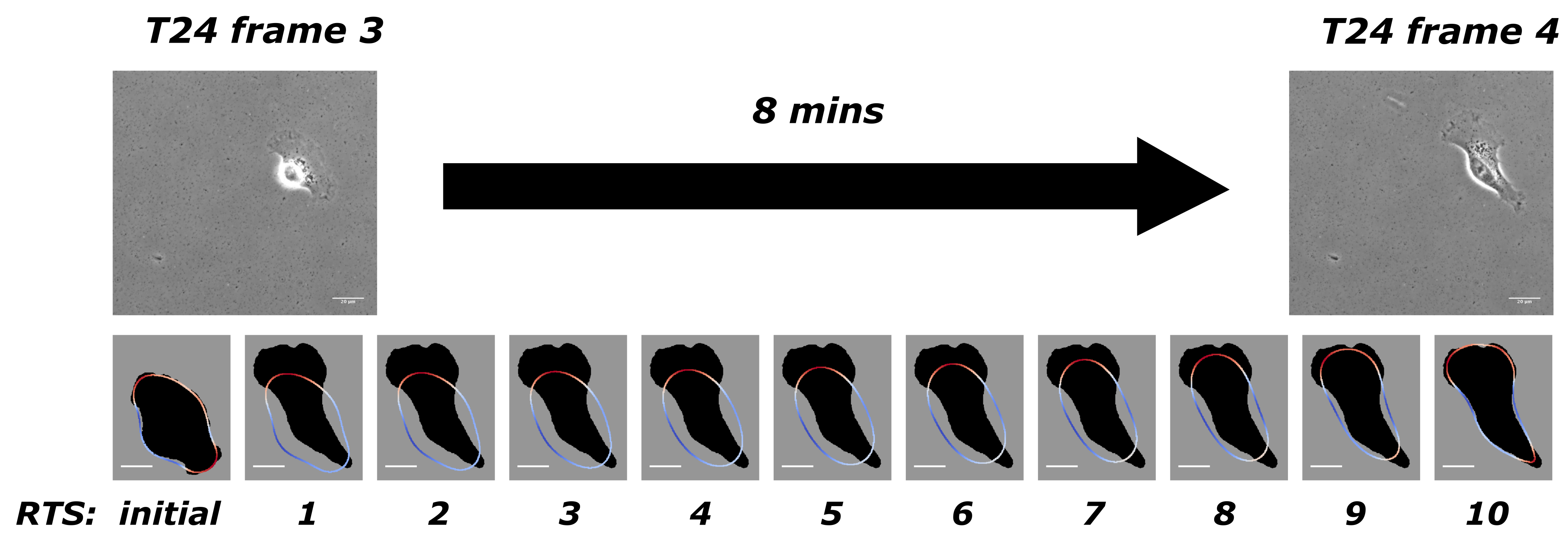
- Our approach to present simulation results The mathematical model in Equation (1) and its dimensionless form (i.e., Equation (4)) exist continuously in both space and time in the closed domain . We apply discretisation schemes to obtain a discrete system at each reconstructed time step (). For example, the situation presented in Figure 1 has been discretised into 10 time steps. Solving such a system yields its simulation result at its corresponding reconstructed time step. We use and to represent the discrete solutions on a grid point i where there are N grid points, and is the number of grid points on one axis of the square domain . describes the evolution of the cell shape and takes values either or 1 in- or outside of the cell. When is between and 1, it illustrates the phase-field interfacial region and the cell shape. The phase-field variable undergoes a smooth transition between the values of 1 and −1. The membrane corresponds to the zero level set of the phase field variable. In order to evaluate quantities on the membrane in our simulations results we need to specify the interfacial region from our simulation by considering a small interval around zero to be the interfacial region since our method does not explicitly track the interface itself. We define grid points i that has values of between and as the cell membrane. We evaluate the average length of the cell membrane on the interval I, where using the formula, . is the forcing, and we are interested in these exerted closely around the cell membrane. The total protrusion force on the interval I is evaluated using the formula, . The total retraction force on interval I is evaluated using the formula, . The choice of affects the stability of the solution methods, and we refer the reader to [34,35,36] for the computational details.
References
- Ridley, A.; Schwartz, M.; Burridge, K.; Firtel, R.; Ginsberg, M.; Borisy, G.; Parsons, J.; Horwitz, A. Cell migration: Integrating signals from front to back. Science 2003, 302, 1704–1709. [Google Scholar] [CrossRef] [Green Version]
- Friedl, P.; Wolf, K. Plasticity of cell migration: A multiscale tuning model. J. Cell Biol. 2010, 188, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olson, M.; Sahai, E. The actin cytoskeleton in cancer cell motility. Clin. Exp. Metastasis 2009, 26, 273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stephens, L.; Milne, L.; Hawkins, P. Moving towards a better understanding of chemotaxis. Curr. Biol. 2008, 18, R485–R494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scarpa, E.; Mayor, R. Collective cell migration in development. J. Cell Biol. 2016, 212, 143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pollard, T.; Borisy, G. Cellular motility driven by assembly and disassembly of actin filaments. Cell 2003, 112, 453–465. [Google Scholar] [CrossRef] [Green Version]
- Pollard, T.; Cooper, J. Actin, A central player in cell shape and movement. Science 2009, 326, 1208–1212. [Google Scholar] [CrossRef] [Green Version]
- Barbieri, L.; Colin-York, H.; Korobchevskaya, K.; Li, D.; Wolfson, D.; Karedla, N.; Schneider, F.; Ahluwalia, B.; Seternes, T.; Dalmo, R.; et al. Two-dimensional TIRF-SIM–traction force microscopy (2D TIRF-SIM-TFM). Nat. Commun. 2021, 12, 2169. [Google Scholar] [CrossRef]
- Simson, R.; Wallraff, E.; Faix, J.; Niewohner, J.; Gerisch, G.; Sackmann, E. Membrane bending modulus and adhesion energy of wild-type and mutant cells of dictyostelium lacing talin or cortexillins. Biophys. J. 1998, 74, 514–522. [Google Scholar] [CrossRef] [Green Version]
- Lieber, A.; Yehudai-Resheff, S.; Barnhart, E.; Theriot, J.; Keren, K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Curr. Biol. 2013, 23, 1409–1417. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Zhang, X. Microsystems for cellular force measurement: A review. J. Micromechanics Microeng. 2011, 21, 054003. [Google Scholar] [CrossRef]
- Charras, G.; Coughlin, M.; Mitchison, T.; Mahadevan, L. Life and times of a cellular bleb. Biophys. J. 2008, 94, 1836–1853. [Google Scholar] [CrossRef] [Green Version]
- Samora, C.; Mogessie, B.; Conway, L.; Ross, J.; Straube, A.; McAinsh, A. MAP4 and CLASP1 operate as a safety mechanism to maintain a stable spindle position in mitosis. Nat. Cell Biol. 2011, 13, 1040–1050. [Google Scholar] [CrossRef]
- Pietuch, A.; Bruckner, B.; Janshoff, A. Membrane tension homeostasis of epithelial cells through surface area regulation in response to osmotic stress. Biochim. Biophys. Acta 2013, 1833, 712–722. [Google Scholar] [CrossRef] [Green Version]
- Kemper, B.; Langehanenberg, P.; von Bally, G. Digital Holographic Microscopy A New Method for Surface Analysis and Marker-Free Dynamic Life Cell Imaging. Opt. Photonik 2007, 2, 41–44. [Google Scholar] [CrossRef] [Green Version]
- Barty, A.; Nugent, K.; Paganin, D.; Roberts, A. Quantitative optical phase microscopy. Opt. Lett. 1998, 23, 817–819. [Google Scholar] [CrossRef]
- Alexopoulos, L.; Erickson, G.; Guilak, F. A method for quantifying cell size from differential interference contrast images: Validation and application to osmotically stressed chondrocytes. J. Microsc. 2001, 205, 125–135. [Google Scholar] [CrossRef] [Green Version]
- Popescu, G.; Deflores, L.; Vaughan, J.; Badizadegan, K.; Iwai, H.; Dasari, R.; Feld, M.S. Fourier phase microscopy for investigation of biological structures and dynamics. Opt. Lett. 2004, 29, 2503–2505. [Google Scholar] [CrossRef]
- Ikeda, T.; Popescu, G.; Dasari, R.; Feld, M.S. Hilbert phase microscopy for investigating fast dynamics in transparent systems. Opt. Lett. 2005, 30, 1165–1167. [Google Scholar] [CrossRef]
- Aguirre, A.; Hsiung, P.; Ko, T.; Hartl, I.; Fujimoto, J.G. High-resolution optical coherence microscopy for high-speed, in vivo cellular imaging. Opt. Lett. 2003, 28, 2064–2066. [Google Scholar] [CrossRef]
- Marquet, P.; Rappaz, B.; Magistretti, P.; Cuche, E.; Emery, Y.; Colomb, T.; Depeursinge, C. Digital holographic microscopy: A noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt. Lett. 2005, 30, 468–470. [Google Scholar] [CrossRef] [Green Version]
- Tu, Y.; Wang, X. Tracking cell migration by cellular force footprint recorded with a mechano-optical biosensor. Biosens. Bioelectron. 2021, 193, 113533. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, K. Soft Polymer-Based Technique for Cellular Force Sensing. Polymers 2021, 13, 2672. [Google Scholar] [CrossRef]
- Shao, D.; Rappel, W.; Levine, H. Computational model for cell morphodynamics. Phys. Rev. Lett. 2010, 105, 108104. [Google Scholar] [CrossRef]
- Bischofs, I.; Schmidt, S.; Schwarz, U. Effect of Adhesion Geometry and Rigidity on Cellular Force Distributions. Phys. Rev. Lett. 2009, 103, 048101. [Google Scholar] [CrossRef] [Green Version]
- Blazakis, K.; Madzvamuse, A.; Reyes-Aldasoro, C.; Styles, V.; Venkataraman, C. Whole cell tracking through the optimal control of geometric evolution laws. J. Comput. Phys. 2015, 297, 495–514. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Venkataraman, C.; Styles, V.; Madzvamuse, A. A robust and efficient adaptive multigrid solver for the optimal control of phase field formulations of geometric evolution laws. Commun. Comput. Phys. 2017, 21, 65–92. [Google Scholar] [CrossRef] [Green Version]
- Haußer, F.; Janssen, S.; Voigt, A. Control of nanostructures through electric fields and related free boundary problems. In Constrained Optimization and Optimal Control for Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2012; pp. 561–572. [Google Scholar]
- Tsugiyama, H.; Okimura, C.; Mizuno, T.; Iwadate, Y. Electroporation of adherent cells with low sample volumes on a microscope stage. J. Exp. Biol. 2013, 216, 3591–3596. [Google Scholar] [CrossRef] [Green Version]
- Peschetola, V.; Laurent, V.; Duperray, A.; Michel, R.; Ambrosi, D.; Preziosi, L.; Verdier, C. Time-dependent traction force microscopy for cancer cells as a measure of invasiveness. Cytoskeleton 2013, 70, 201–214. [Google Scholar] [CrossRef] [Green Version]
- De Rooij, J.; Kerstens, A.; Danuser, G.; Schwartz, M.; Waterman-Storer, C. Integrin-dependent actomyosin contraction regulates epithelial cell scattering. J. Cell Biol. 2005, 171, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Blowey, J.; Elliott, C. Curvature dependent phase boundary motion and parabolic double obstacle problems. In Degenerate Diffusions; Springer: New York, NY, USA, 1993; pp. 19–60. [Google Scholar]
- Fischer-Friedrich, E.; Hyman, A.; Julicher, F.; Muller, D.; Helenius, J. Quantification of surface tension and internal pressure generated by single mitotic cells. Sci. Rep. 2014, 4, 6213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bollada, P.; Goodyer, C.; Jimack, P.; Mullis, A.; Yang, F. Thermalsolute phase field three dimensional simulation of binary alloy solidification. J. Comput. Phys. 2015, 287, 130–150. [Google Scholar] [CrossRef] [Green Version]
- Caginalp, G. Stefan and Hele-Shaw type models as asymptotic limits of the phase-field equations. Phys. Rev. A 1989, 39, 5887–5896. [Google Scholar] [CrossRef]
- Rosam, J.; Jimack, P.; Mullis, G. A fully implicit, fully adaptive time and space discretisation method for phase-field simulation of binary alloy solidification. J. Comput. Phys. 2007, 225, 1271–1287. [Google Scholar] [CrossRef] [Green Version]
- Otsu, N. A threshold selection method from gray level histograms. IEEE Trans. Systems Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Prass, M.; Jacobson, K.; Mogilner, A.; Radmacher, M. Direct measurement of the lamellipodial protrusive force in a migrating cell. J. Cell Biol. 2006, 174, 767–772. [Google Scholar] [CrossRef]
- Du, Q.; Liu, C.; Wang, X. Retrieving topological information for phase field models. Siam J. Appl. Math. 2005, 65, 1913–1932. [Google Scholar] [CrossRef]
- Camley, B.A.; Rappel, W.J. Physical models of collective cell motility: From cell to tissue. J. Phys. Appl. Phys. 2017, 50, 113002. [Google Scholar] [CrossRef]
- Hobson, C.M.; Stephens, A.D. Modeling of cell nuclear mechanics: Classes, components, and applications. Cells 2020, 9, 1623. [Google Scholar] [CrossRef]
- Yamada, K.M.; Sixt, M. Mechanisms of 3D cell migration. Nat. Rev. Mol. Cell Biol. 2019, 20, 738–752. [Google Scholar] [CrossRef]
- Kraning-Rush, C.; Carey, S.; Califano, J.; Smith, B.; Reinhart-King, C. The role of the cytoskeleton in cellular force generation in 2D and 3D environments. Phys. Biol. 2011, 8, 015009. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Description |
|---|---|
| Membrane thickness | |
| Friction | |
| Volume fraction | |
| Spatial coordinate | |
| t | Time variable |
| L | Domain length |
| T | Time of entire experiment |
| Surface tension | |
| Forcing exerted on cell membrane |
| Parameter | Description | Value |
|---|---|---|
| Surface tension | 1–10 [14,24,33] | |
| Friction force | ≈2.62 s/µm [24] | |
| Membrane thickness | ≈1.0 m [24] | |
| Forcing exerted on cell membrane | Fitting variable to be computed | |
| in the remainder of this paper |
| Parameter | Description | Value |
|---|---|---|
| keratocyte | ||
| x | Domain length in x axis | m |
| y | Domain length in y axis | m |
| t | Length of time | 360 s |
| Time interval between frames in the video | 20 s | |
| L | Characteristic length | m |
| Characteristic time | 360 s | |
| F | Characteristic force for surface tension | 10 |
| (Dimensionless) friction force | 4.85 | |
| Numerical interfacial width | 0.01 | |
| No. Reconstructed Time Steps between frames | 10 | |
| T24 | ||
| x | Domain length in x axis | 170 m |
| y | Domain length in y axis | 170 m |
| t | Length of time | 1920 s |
| Time interval between frames in the video | 480 s | |
| L | Characteristic length | 170 m |
| Characteristic time | 1920 s | |
| F | Characteristic force for surface tension | 10 |
| (Dimensionless) friction force | 3.16 | |
| Numerical interfacial width | 0.005 | |
| No. Reconstructed Time Steps between frames | 10 | |
| MDCK | ||
| x | Domain length in x axis | 220 m |
| y | Domain length in y axis | 220 m |
| t | Length of time | 1800 s |
| Time interval between frames in the video | 300 s | |
| L | Characteristic length | 220 m |
| Characteristic time | 1800 s | |
| F | Characteristic force for surface tension | 10 |
| (Dimensionless) friction force | 7.04 | |
| Numerical interfacial width | 0.05 | |
| No. Reconstructed Time Steps between frames | 5 | |
| Time Duration. | Avg. C. M. | Total Protrusion | Over % of | Total Retraction | Over % of |
|---|---|---|---|---|---|
| between Frames | Len. (µm) | Force () | C. M. | Force () | C. M. |
| 1–2 (20 s) | 94 | 33,480 | 75.3 | 5637 | 24.7 |
| 2–3 (20 s) | 97 | 34,457 | 70.0 | 8253 | 30.0 |
| 3–4 (20 s) | 97 | 37,047 | 73.8 | 7999 | 26.2 |
| 4–5 (20 s) | 98 | 36,450 | 70.0 | 9301 | 30.0 |
| 5–6 (20 s) | 98 | 37,076 | 70.3 | 10,334 | 29.7 |
| 6–7 (20 s) | 99 | 36,338 | 70.2 | 10,688 | 29.8 |
| 7–8 (20 s) | 100 | 36,076 | 70.5 | 10,722 | 29.5 |
| 8–9 (20 s) | 101 | 38,377 | 71.6 | 9625 | 28.4 |
| 9–10 (20 s) | 101 | 38,553 | 68.9 | 10,630 | 31.1 |
| 10–11 (20 s) | 102 | 38,768 | 72.2 | 9723 | 27.8 |
| 11–12 (20 s) | 88 | 37,751 | 68.2 | 10,788 | 31.8 |
| 12–13 (20 s) | 90 | 36,796 | 70.4 | 10,001 | 29.6 |
| 13–14 (20 s) | 89 | 40,149 | 72.4 | 9289 | 27.6 |
| 14–15 (20 s) | 90 | 38,893 | 68.6 | 10,743 | 31.4 |
| 15–16 (20 s) | 91 | 39,012 | 69.0 | 11,296 | 31.0 |
| 16–17 (20 s) | 92 | 42,167 | 71.1 | 11,013 | 28.9 |
| 17–18 (20 s) | 92 | 39,910 | 69.7 | 10,920 | 30.3 |
| 18–19 (20 s) | 93 | 39,074 | 67.8 | 11,753 | 32.2 |
| Time Duration. | Avg. C. M. | Total Protrusion | Over % of | Total Retraction | Over % of |
|---|---|---|---|---|---|
| between Frames | Len. (µm) | Force () | C. M. | Force () | C. M. |
| 1–2 (8 min) | 224 | 165,361 | 43.8 | 134,424 | 56.2 |
| 2–3 (8 min) | 178 | 212,371 | 55.6 | 48,428 | 44.4 |
| 3–4 (8 min) | 191 | 161,132 | 57.6 | 37,831 | 42.4 |
| 4–5 (8 min) | 175 | 173,554 | 51.0 | 45,541 | 49.0 |
| Time Duration. | Avg. C. M. | Total Protrusion | Over % of | Total Retraction | Over % of |
|---|---|---|---|---|---|
| between Frames | Len. (µm) | Force () | C. M. | Force () | C. M. |
| 1–2 (5 min) | 427 | 256,865 | 48.7 | 186,380 | 51.3 |
| 2–3 (5 min) | 730 | 617,225 | 69.0 | 183,354 | 31.0 |
| 3–4 (5 min) | 1063 | 692,221 | 61.9 | 466,208 | 38.1 |
| 4–5 (5 min) | 1066 | 566,266 | 54.8 | 465,805 | 45.2 |
| 5–6 (5 min) | 1022 | 537,507 | 56.7 | 310,618 | 43.3 |
| 6–7 (5 min) | 1077 | 655,875 | 60.0 | 340,670 | 40.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Venkataraman, C.; Gu, S.; Styles, V.; Madzvamuse, A. Force Estimation during Cell Migration Using Mathematical Modelling. J. Imaging 2022, 8, 199. https://doi.org/10.3390/jimaging8070199
Yang F, Venkataraman C, Gu S, Styles V, Madzvamuse A. Force Estimation during Cell Migration Using Mathematical Modelling. Journal of Imaging. 2022; 8(7):199. https://doi.org/10.3390/jimaging8070199
Chicago/Turabian StyleYang, Fengwei, Chandrasekhar Venkataraman, Sai Gu, Vanessa Styles, and Anotida Madzvamuse. 2022. "Force Estimation during Cell Migration Using Mathematical Modelling" Journal of Imaging 8, no. 7: 199. https://doi.org/10.3390/jimaging8070199
APA StyleYang, F., Venkataraman, C., Gu, S., Styles, V., & Madzvamuse, A. (2022). Force Estimation during Cell Migration Using Mathematical Modelling. Journal of Imaging, 8(7), 199. https://doi.org/10.3390/jimaging8070199







