Varroa Destructor Classification Using Legendre–Fourier Moments with Different Color Spaces
Abstract
:1. Introduction
2. Materials and Methods
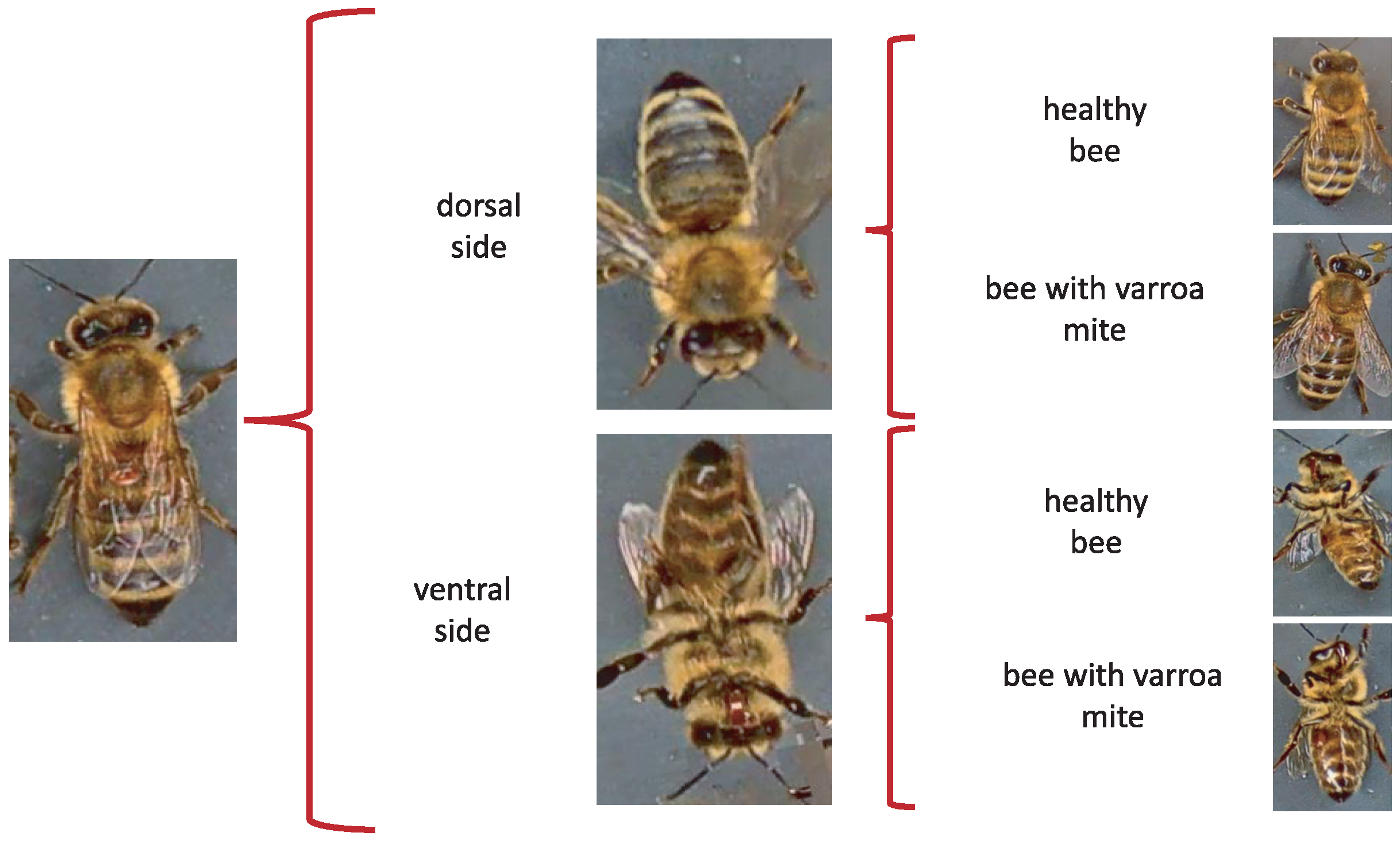
2.1. Database of Honey Bees with Varroa
2.2. Implementation and Comparison of DeepLabV3 and YOLOv5 Models
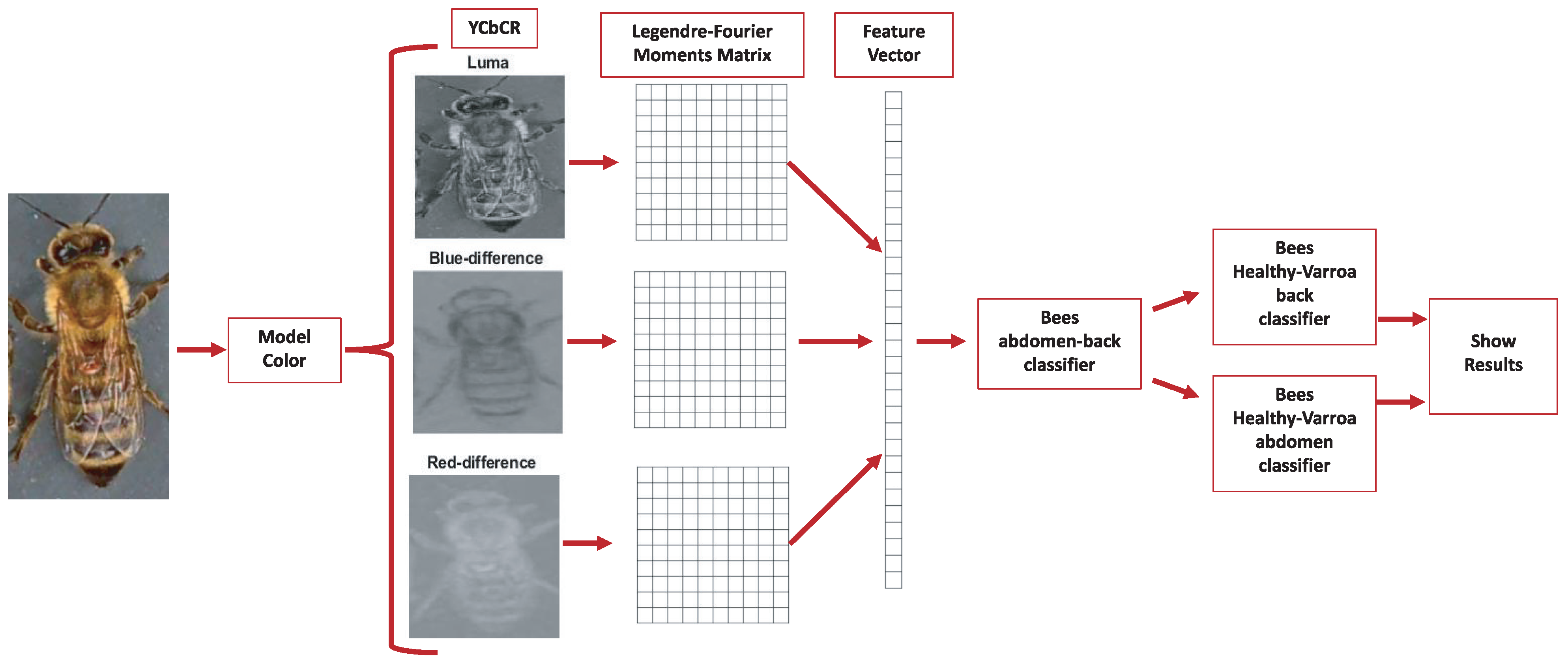
2.3. Color Space
2.4. Multichannel Legendre–Fourier Moments
3. Multichannel Legendre–Fourier Moments for the Varroa Detection
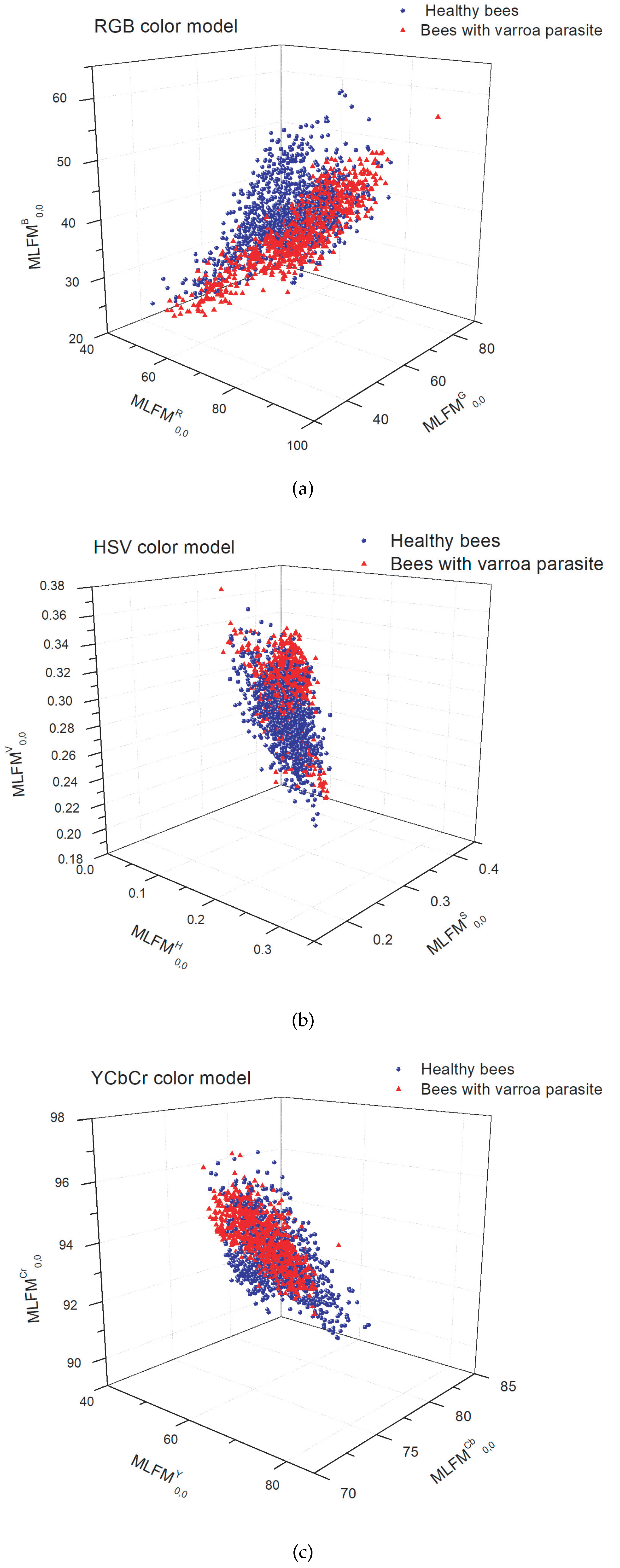
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| R | Red |
| G | Green |
| B | Blue |
| H | Hue |
| S | Saturation |
| V | Brightness |
| Y | Luminance |
| Cb | Chrominance |
| Cr | Red chrominance component |
| SVM | Support vector machine |
| TPR | True positive rate |
| FPR | False positive rate |
| TNR | True negative rate |
| FNR | False negative rate |
References
- Hung, K.L.J.; Kingston, J.M.; Albrecht, M.; Holway, D.A.; Kohn, J.R. The worldwide importance of honey bees as pollinators in natural habitats. Proc. R. Soc. B Biol. Sci. 2018, 285, 20172140. [Google Scholar] [CrossRef] [Green Version]
- Potts, S.G.; Imperatriz-Fonseca, V.; Ngo, H.T.; Aizen, M.A.; Biesmeijer, J.C.; Breeze, T.D.; Dicks, L.V.; Garibaldi, L.A.; Hill, R.; Settele, J.; et al. Safeguarding pollinators and their values to human well-being. Nature 2016, 540, 220–229. [Google Scholar] [CrossRef] [Green Version]
- Magaña Magaña, M.Á.; Moguel Ordóñez, Y.B.; Sanginés García, J.R.; Leyva Morales, C.E. Estructura e importancia de la cadena productiva y comercial de la miel en México. Rev. Mex. Cienc. Pecu. 2012, 3, 49–64. [Google Scholar]
- Requier, F.; Garnery, L.; Kohl, P.L.; Njovu, H.K.; Pirk, C.W.; Crewe, R.M.; Steffan-Dewenter, I. The conservation of native honey bees is crucial. Trends Ecol. Evol. 2019, 34, 789–798. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.J.; Paxton, R.J. The conservation of bees: A global perspective. Apidologie 2009, 40, 410–416. [Google Scholar] [CrossRef] [Green Version]
- Rosenkranz, P.; Aumeier, P.; Ziegelmann, B. Biology and control of Varroa destructor. J. Invertebr. Pathol. 2010, 103, S96–S119. [Google Scholar] [CrossRef] [PubMed]
- Noël, A.; Le Conte, Y.; Mondet, F. Varroa destructor: How does it harm Apis mellifera honey bees and what can be done about it? Emerg. Top. Life Sci. 2020, 4, 45–57. [Google Scholar]
- Rodriguez, I.F.; Megret, R.; Acuna, E.; Agosto-Rivera, J.L.; Giray, T. Recognition of pollen-bearing bees from video using convolutional neural network. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 314–322. [Google Scholar]
- Sledevič, T. The application of convolutional neural network for pollen bearing bee classification. In Proceedings of the 2018 IEEE 6th Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Vilnius, Lithuania, 8–10 November 2018; pp. 1–4. [Google Scholar]
- Marstaller, J.; Tausch, F.; Stock, S. Deepbees-building and scaling convolutional neuronal nets for fast and large-scale visual monitoring of bee hives. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Tiwari, A. A Deep Learning Approach to Recognizing Bees in Video Analysis of Bee Traffic. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2018. [Google Scholar]
- Rodríguez, I.; Branson, K.; Acuña, E.; Agosto-Rivera, J.; Giray, T.; Mégret, R. Honeybee detection and pose estimation using convolutional neural networks. In Congrès Reconnaissance des Formes, Image, Apprentissage et Perception (RFIAP); National Science Foundation: Alexandria, VA, USA, 2018. [Google Scholar]
- Tashakkori, R.; Hamza, A.S.; Crawford, M.B. Beemon: An IoT-based beehive monitoring system. Comput. Electron. Agric. 2021, 190, 106427. [Google Scholar] [CrossRef]
- Bjerge, K.; Frigaard, C.E.; Mikkelsen, P.H.; Nielsen, T.H.; Misbih, M.; Kryger, P. A computer vision system to monitor the infestation level of Varroa destructor in a honeybee colony. Comput. Electron. Agric. 2019, 164, 104898. [Google Scholar] [CrossRef]
- Sevin, S.; Tutun, H.; Mutlu, S. Detection of Varroa mites from honey bee hives by smart technology Var-Gor: A hive monitoring and image processing device. Turk. J. Vet. Anim. Sci. 2021, 45, 487–491. [Google Scholar] [CrossRef]
- Bilik, S.; Kratochvila, L.; Ligocki, A.; Bostik, O.; Zemcik, T.; Hybl, M.; Horak, K.; Zalud, L. Visual diagnosis of the Varroa destructor parasitic mite in honeybees using object detector techniques. Sensors 2021, 21, 2764. [Google Scholar] [CrossRef]
- Schurischuster, S.; Kampel, M. Image-based Classification of Honeybees. In Proceedings of the 2020 Tenth International Conference on Image Processing Theory, Tools and Applications (IPTA), Paris, France, 9–12 November 2020; pp. 1–6. [Google Scholar]
- Teague, M.R. Image analysis via the general theory of moments. Josa 1980, 70, 920–930. [Google Scholar] [CrossRef]
- Singh, C.; Singh, J. Multi-channel versus quaternion orthogonal rotation invariant moments for color image representation. Digit. Signal Process. 2018, 78, 376–392. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M. New set of multi-channel orthogonal moments for color image representation and recognition. Pattern Recognit. 2019, 88, 153–173. [Google Scholar] [CrossRef]
- Hosny, K.M.; Elaziz, M.; Selim, I.; Darwish, M.M. Classification of galaxy color images using quaternion polar complex exponential transform and binary Stochastic Fractal Search. Astron. Comput. 2020, 31, 100383. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M.; Eltoukhy, M.M. New fractional-order shifted Gegenbauer moments for image analysis and recognition. J. Adv. Res. 2020, 25, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Hosny, K.M.; Darwish, M.M.; Aboelenen, T. Novel fractional-order generic Jacobi-Fourier moments for image analysis. Signal Process. 2020, 172, 107545. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M.; Aboelenen, T. Novel fractional-order polar harmonic transforms for gray-scale and color image analysis. J. Frankl. Inst. 2020, 357, 2533–2560. [Google Scholar] [CrossRef]
- Singh, J.; Singh, C. Multi-channel generalized pseudo-Jacobi-Fourier moments for color image reconstruction and object recognition. In Proceedings of the 2017 Ninth International Conference on Advances in Pattern Recognition (ICAPR), Bangalore, India, 27–30 December 2017; pp. 1–6. [Google Scholar]
- Camacho-Bello, C.; Báez-Rojas, J.; Toxqui-Quitl, C.; Padilla-Vivanco, A. Color image reconstruction using quaternion Legendre-Fourier moments in polar pixels. In Proceedings of the 2014 International Conference on Mechatronics, Electronics and Automotive Engineering, Cuernavaca, Mexico, 18–21 November 2014; pp. 3–8. [Google Scholar]
- Hosny, K.M.; Darwish, M.M. Robust color image watermarking using invariant quaternion Legendre-Fourier moments. Multimed. Tools Appl. 2018, 77, 24727–24750. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M.; Fouda, M.M. New color image zero-watermarking using orthogonal Multi-Channel fractional-order legendre-fourier moments. IEEE Access 2021, 9, 91209–91219. [Google Scholar] [CrossRef]
- Hosny, K.M.; Magdy, T.; Lashin, N.A. Improved color texture recognition using multi-channel orthogonal moments and local binary pattern. Multimed. Tools Appl. 2021, 80, 13179–13194. [Google Scholar] [CrossRef]
- Madhavi, B.G.K.; Basak, J.K.; Paudel, B.; Kim, N.E.; Choi, G.M.; Kim, H.T. Prediction of Strawberry Leaf Color Using RGB Mean Values Based on Soil Physicochemical Parameters Using Machine Learning Models. Agronomy 2022, 12, 981. [Google Scholar] [CrossRef]
- Domino, M.; Borowska, M.; Kozłowska, N.; Trojakowska, A.; Zdrojkowski, Ł..; Jasiński, T.; Smyth, G.; Maśko, M. Selection of image texture analysis and color model in the advanced image processing of thermal images of horses following exercise. Animals 2022, 12, 444. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Dang, L.; Ren, J. Forest fire image recognition based on convolutional neural network. J. Algorithms Comput. Technol. 2019, 13, 1748302619887689. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, V.; Gil, S.; Flores, J.M.; Quiles, F.J.; Ortiz, M.A.; Luna, J.J. Implementation of an electronic system to monitor the thermoregulatory capacity of honeybee colonies in hives with open-screened bottom boards. Comput. Electron. Agric. 2015, 119, 209–216. [Google Scholar] [CrossRef]
- Li, Y.; Mao, H.; Girshick, R.; He, K. Exploring plain vision transformer backbones for object detection. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 280–296. [Google Scholar]
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 7464–7475. [Google Scholar]
- Liu, H.; Jin, F.; Zeng, H.; Pu, H.; Fan, B. Image Enhancement Guided Object Detection in Visually Degraded Scenes. IEEE Trans. Neural Netw. Learn. Syst. 2023. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; He, Y.; Jiang, R.; Zhang, J.; Zou, W.; Fan, B. DSLA: Dynamic smooth label assignment for efficient anchor-free object detection. Pattern Recognit. 2022, 131, 108868. [Google Scholar] [CrossRef]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 7262–7272. [Google Scholar]
- Zhang, W.; Huang, Z.; Luo, G.; Chen, T.; Wang, X.; Liu, W.; Yu, G.; Shen, C. TopFormer: Token pyramid transformer for mobile semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12083–12093. [Google Scholar]
- Yan, L.; Fan, B.; Liu, H.; Huo, C.; Xiang, S.; Pan, C. Triplet adversarial domain adaptation for pixel-level classification of VHR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3558–3573. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.; Markovskyi, P. YOLOv5: Ultralytics/YOLOv5 GitHub Repository. 2020. Available online: https://github.com/ultralytics/yolov5 (accessed on 9 July 2023).
- Gonzalez, R.C.; Woods, R.E. Image processing. Digit. Image Process. 2007, 402. [Google Scholar]
- Alejo, D.A.C.; Funes, F.J.G. Comparación de dos técnicas propuestas HS-CbCr y HS-ab para el modelado de color de piel en imágenes. Res. Comput. Sci. 2016, 114, 33–44. [Google Scholar] [CrossRef]
- Camacho-Bello, C.; Toxqui-Quitl, C.; Padilla-Vivanco, A.; Báez-Rojas, J. High-precision and fast computation of Jacobi–Fourier moments for image description. JOSA A 2014, 31, 124–134. [Google Scholar] [CrossRef] [PubMed]
- Khotanzad, A.; Hong, Y.H. Invariant image recognition by Zernike moments. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 489–497. [Google Scholar] [CrossRef] [Green Version]
- Singh, C.; Singh, J. A survey on rotation invariance of orthogonal moments and transforms. Signal Process. 2021, 185, 108086. [Google Scholar] [CrossRef]


| Total | Train | Test | Val | |
|---|---|---|---|---|
| Infested | 3947 | 2554 | 942 | 451 |
| Healthy | 9562 | 5671 | 2466 | 1425 |
 |  |  |  |  | |
| Original | k = 0.5 | k = 1.5 | |||
| MLFMs | |||||
| 53.023 | 53.023 | 53.023 | 53.023 | 53.023 | |
| 0.628 | 0.628 | 0.628 | 0.628 | 0.628 | |
| 2.080 | 2.080 | 2.080 | 2.080 | 2.080 |
| Healthy | With Varroa Mite | |
|---|---|---|
| Bee dorsal side | ||
 |  | |
| Bee ventral side | ||
 |  |
| Measure | Formula |
|---|---|
| True positive rate (TPR) | TPR = TP/(FN + TP) |
| False positive rate (FPR) | FPR = FP/(TN + FP) |
| True negative rate (TNR) | TNR = TN/(TN + FP) |
| False negative rate (FNR) | FNR = FN/(FN + TP) |
| Accuracy | Accuracy = (TP + TN)/(TP + FP + FN + TN) |
| F1 score | F1 = (2 * TP)/(2 * TP + FP * FN) |
| TPR | TNR | FPR | FNR | Accuracy | F1 Score | |
|---|---|---|---|---|---|---|
| Healthy bees and bees | ||||||
| with Varroa parasite | ||||||
| RGB | 89.5 | 87.6 | 12.4 | 10.6 | 88.5 | 88.4 |
| HSV | 92.4 | 89.4 | 10.6 | 7.7 | 90.9 | 90.8 |
| YCbCr | 91.7 | 92.0 | 8.0 | 8.3 | 91.9 | 91.9 |
| VarroaDataset with subdivision | ||||||
| Bees dorsal side and ventral side | ||||||
| RGB | 97.6 | 98.8 | 1.2 | 2.4 | 98.2 | 98.2 |
| HSV | 97.4 | 98.6 | 1.4 | 2.6 | 98.0 | 98.0 |
| YCbCr | 99.4 | 98.8 | 1.2 | 0.6 | 99.1 | 99.1 |
| Healthy bees and Varroa- | ||||||
| infested bee on dorsal side | ||||||
| RGB | 96.0 | 92.3 | 7.7 | 4.0 | 94.1 | 94.0 |
| HSV | 97.9 | 95.5 | 4.5 | 2.1 | 96.7 | 96.7 |
| YCbCr | 97.6 | 97.8 | 2.2 | 2.4 | 97.7 | 97.7 |
| Healthy bees and Varroa- | ||||||
| infested bee on ventral side | ||||||
| RGB | 95.7 | 94.7 | 5.3 | 4.3 | 95.2 | 95.2 |
| HSV | 97.4 | 96.2 | 3.8 | 2.6 | 96.8 | 96.8 |
| YCbCr | 99.6 | 95.4 | 4.6 | 41.8 | 97.4 | 97.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noriega-Escamilla, A.; Camacho-Bello, C.J.; Ortega-Mendoza, R.M.; Arroyo-Núñez, J.H.; Gutiérrez-Lazcano, L. Varroa Destructor Classification Using Legendre–Fourier Moments with Different Color Spaces. J. Imaging 2023, 9, 144. https://doi.org/10.3390/jimaging9070144
Noriega-Escamilla A, Camacho-Bello CJ, Ortega-Mendoza RM, Arroyo-Núñez JH, Gutiérrez-Lazcano L. Varroa Destructor Classification Using Legendre–Fourier Moments with Different Color Spaces. Journal of Imaging. 2023; 9(7):144. https://doi.org/10.3390/jimaging9070144
Chicago/Turabian StyleNoriega-Escamilla, Alicia, César J. Camacho-Bello, Rosa M. Ortega-Mendoza, José H. Arroyo-Núñez, and Lucia Gutiérrez-Lazcano. 2023. "Varroa Destructor Classification Using Legendre–Fourier Moments with Different Color Spaces" Journal of Imaging 9, no. 7: 144. https://doi.org/10.3390/jimaging9070144
APA StyleNoriega-Escamilla, A., Camacho-Bello, C. J., Ortega-Mendoza, R. M., Arroyo-Núñez, J. H., & Gutiérrez-Lazcano, L. (2023). Varroa Destructor Classification Using Legendre–Fourier Moments with Different Color Spaces. Journal of Imaging, 9(7), 144. https://doi.org/10.3390/jimaging9070144







