Aerodynamic Characteristics of a Tandem Flapping Wing in Inclined Stroke Plane Hovering with Ground Effect
Abstract
:1. Introduction
2. Numerical Method and Validation
- The flapping wing trajectory is assumed to be linear, whereas real dragonflies exhibit a complex figure-eight motion, with the upstroke and downstroke motions following different figure-eight trajectory.
- The downstroke and upstroke durations are assumed equal, while in reality, the downstroke is significantly longer than the upstroke.
- The pitch motion is modeled as a continuous sinusoidal function. However, in real dragonflies, the pronation and supination phases are relatively shorter than the translation phase, which is not considered in the wing kinematics.
- The wings are treated as rigid, without considering flexibility or twisting.
3. Results and Discussion
3.1. Comparison of Aerodynamic Force Generation at Various Flapping Frequencies f
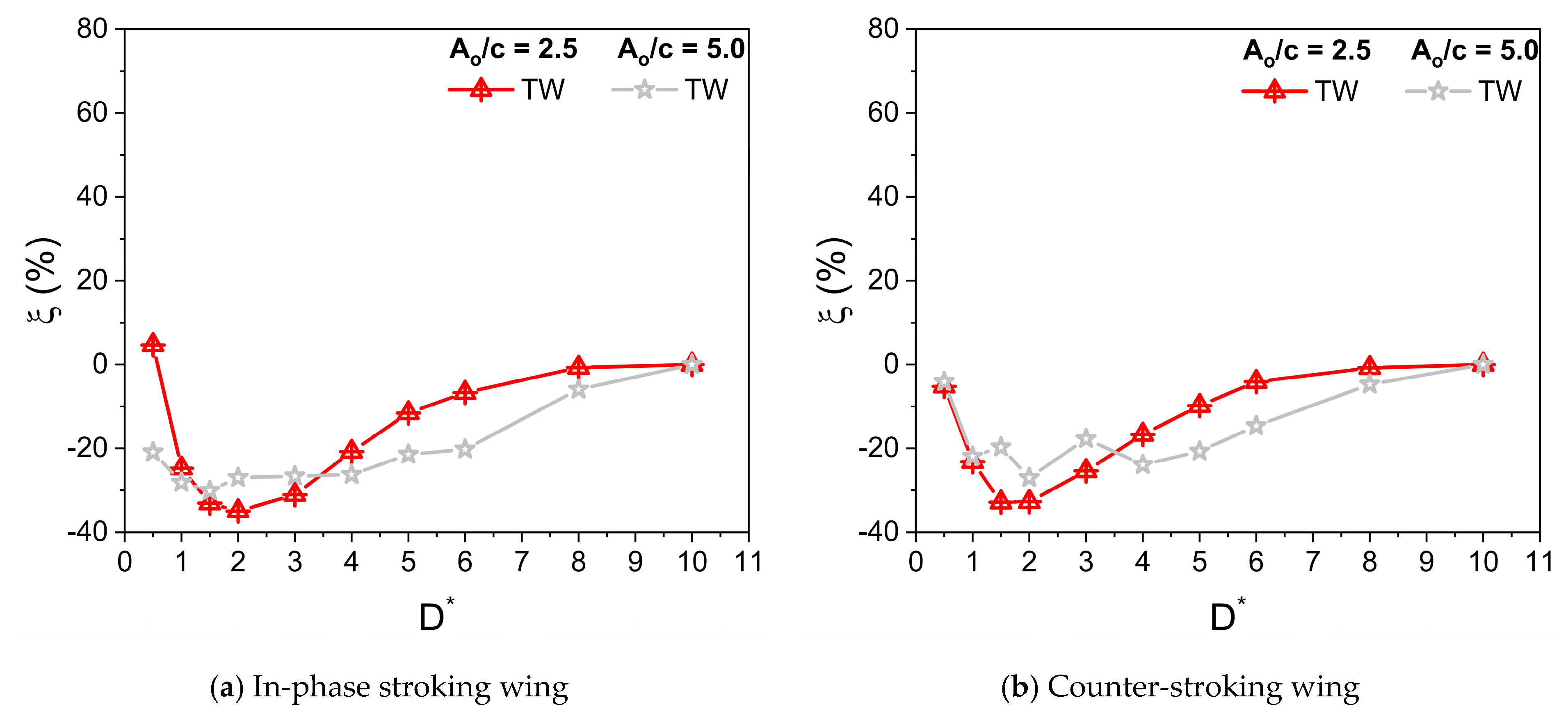
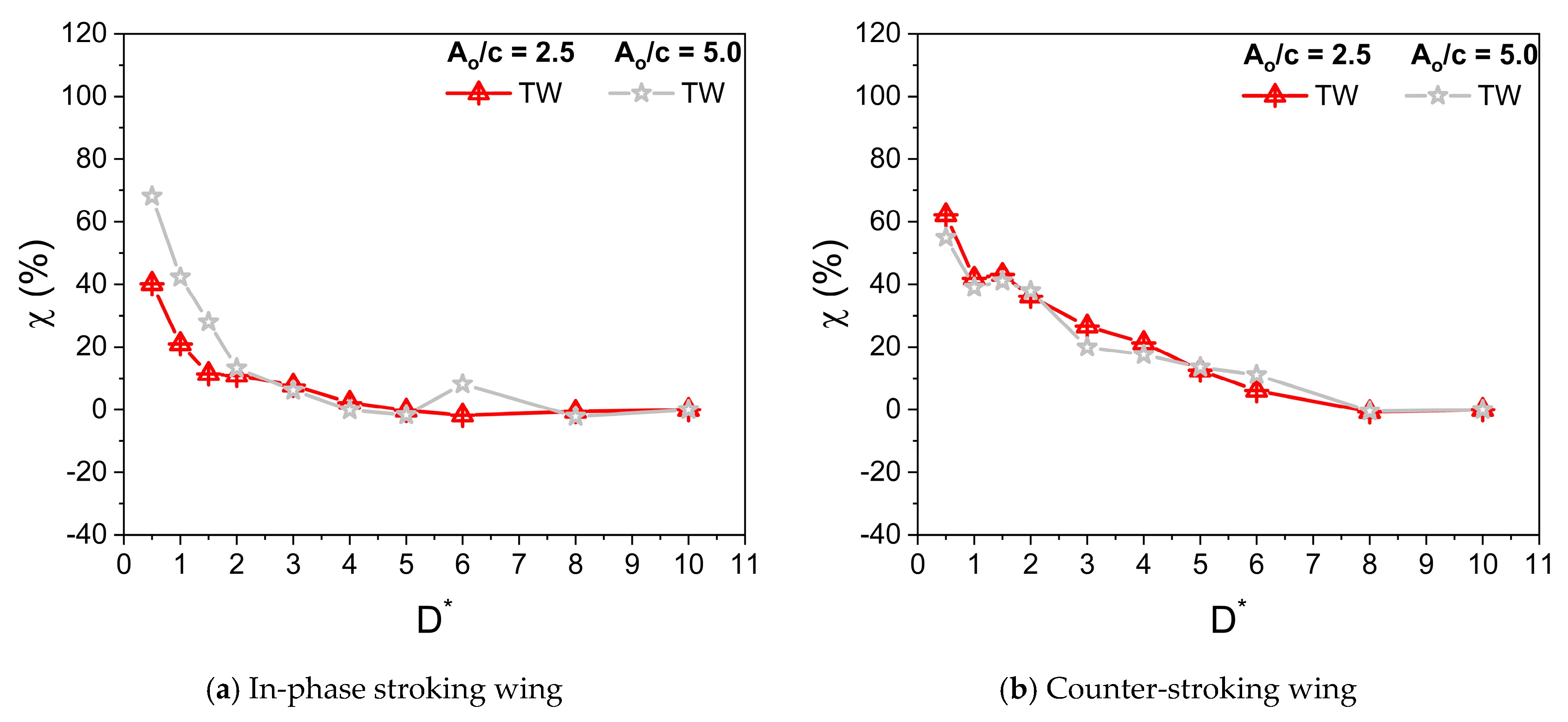
3.2. Comparison of Aerodynamic Force Generation at Various Stroke Amplitude Ao/c
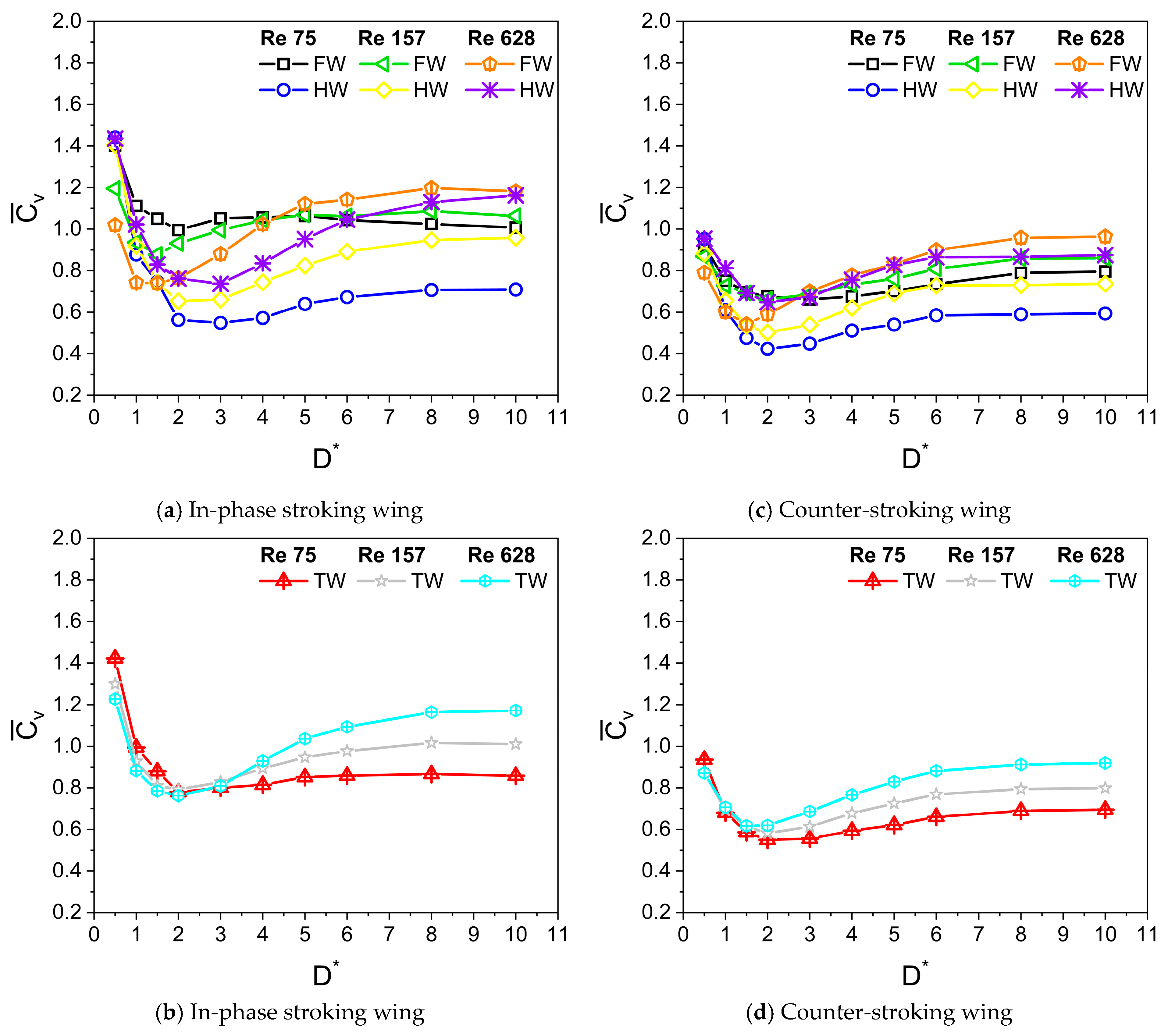
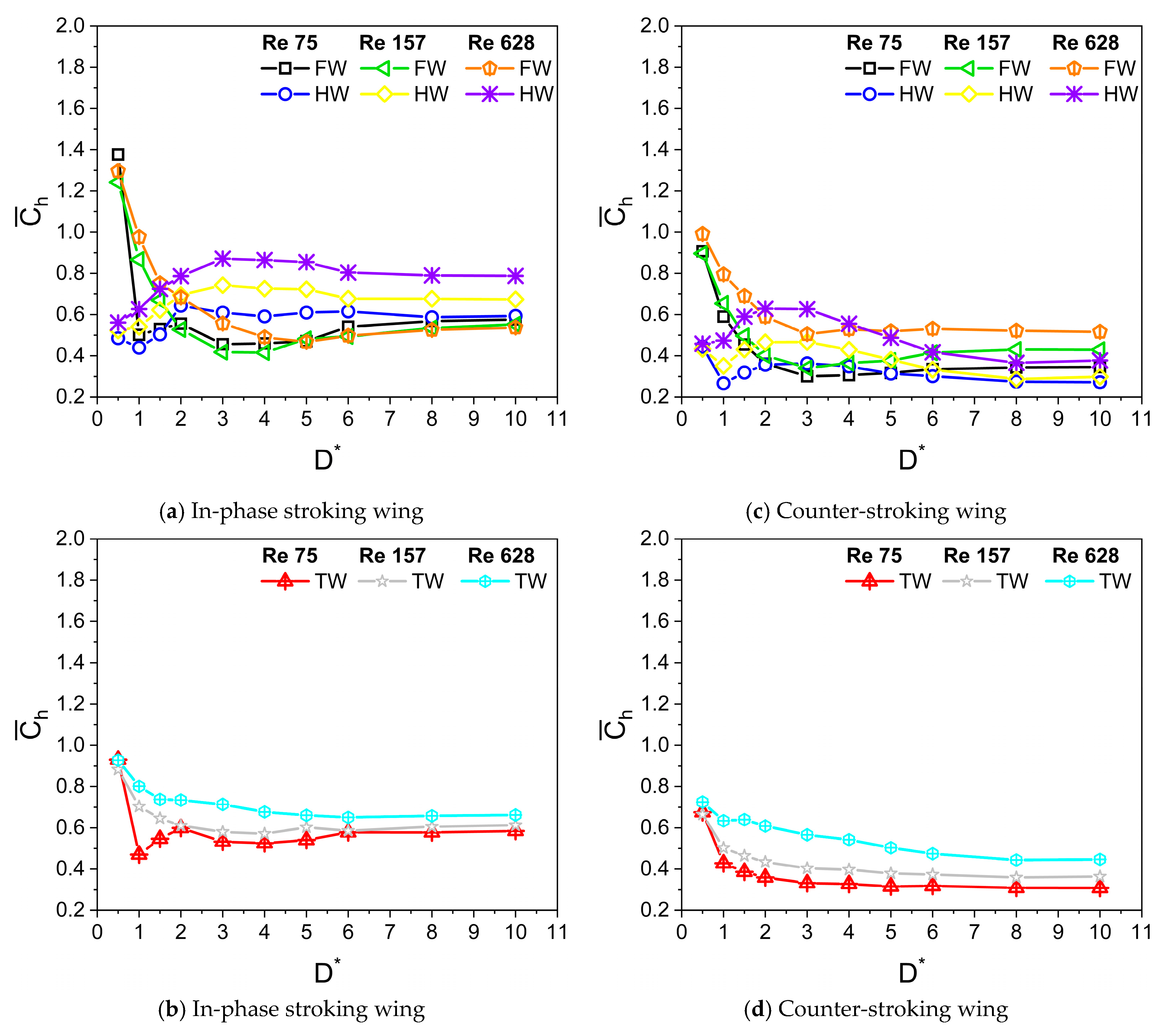
3.3. Comparison of Aerodynamic Force Generation at Various Reynolds Numbers Re
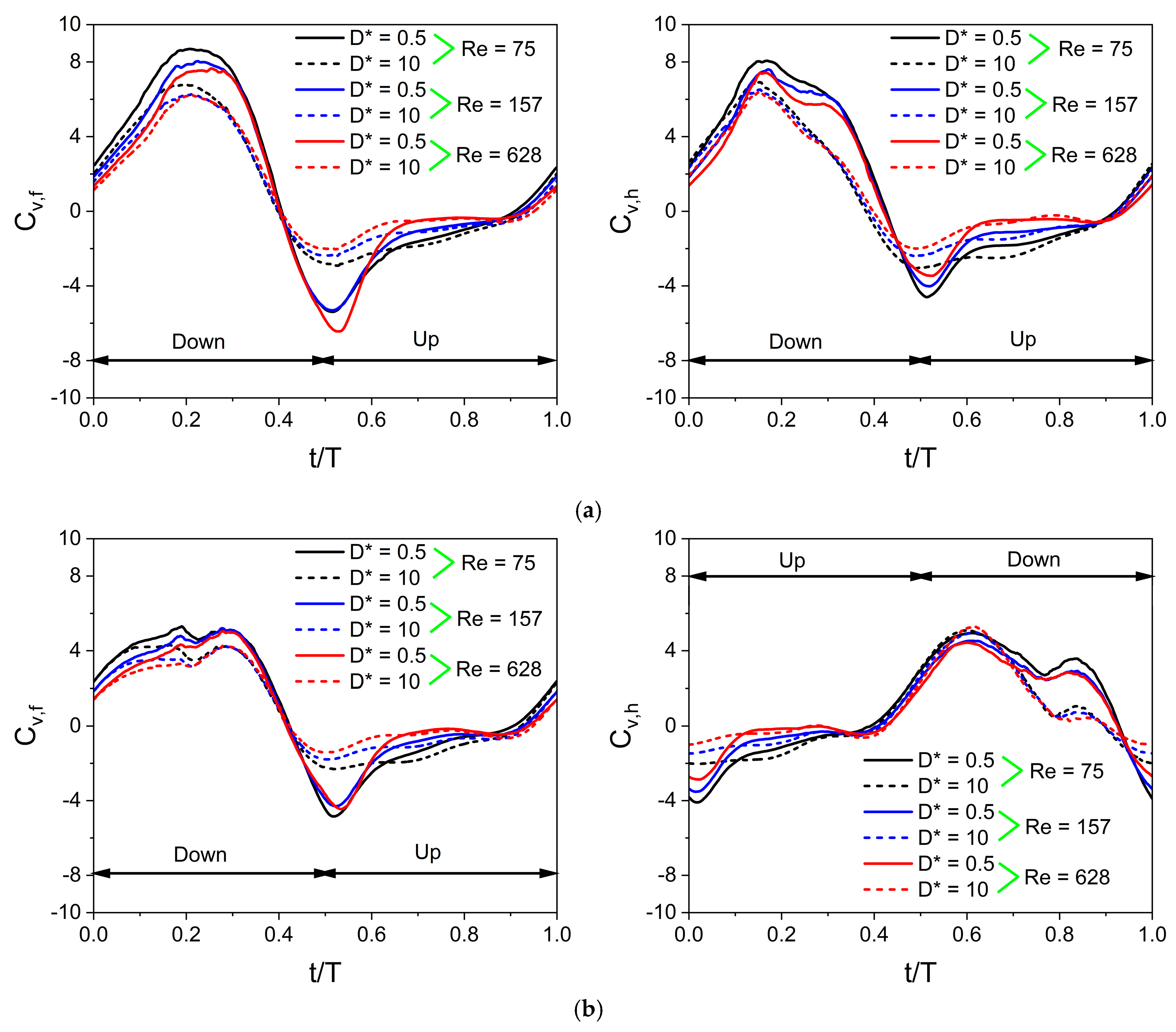
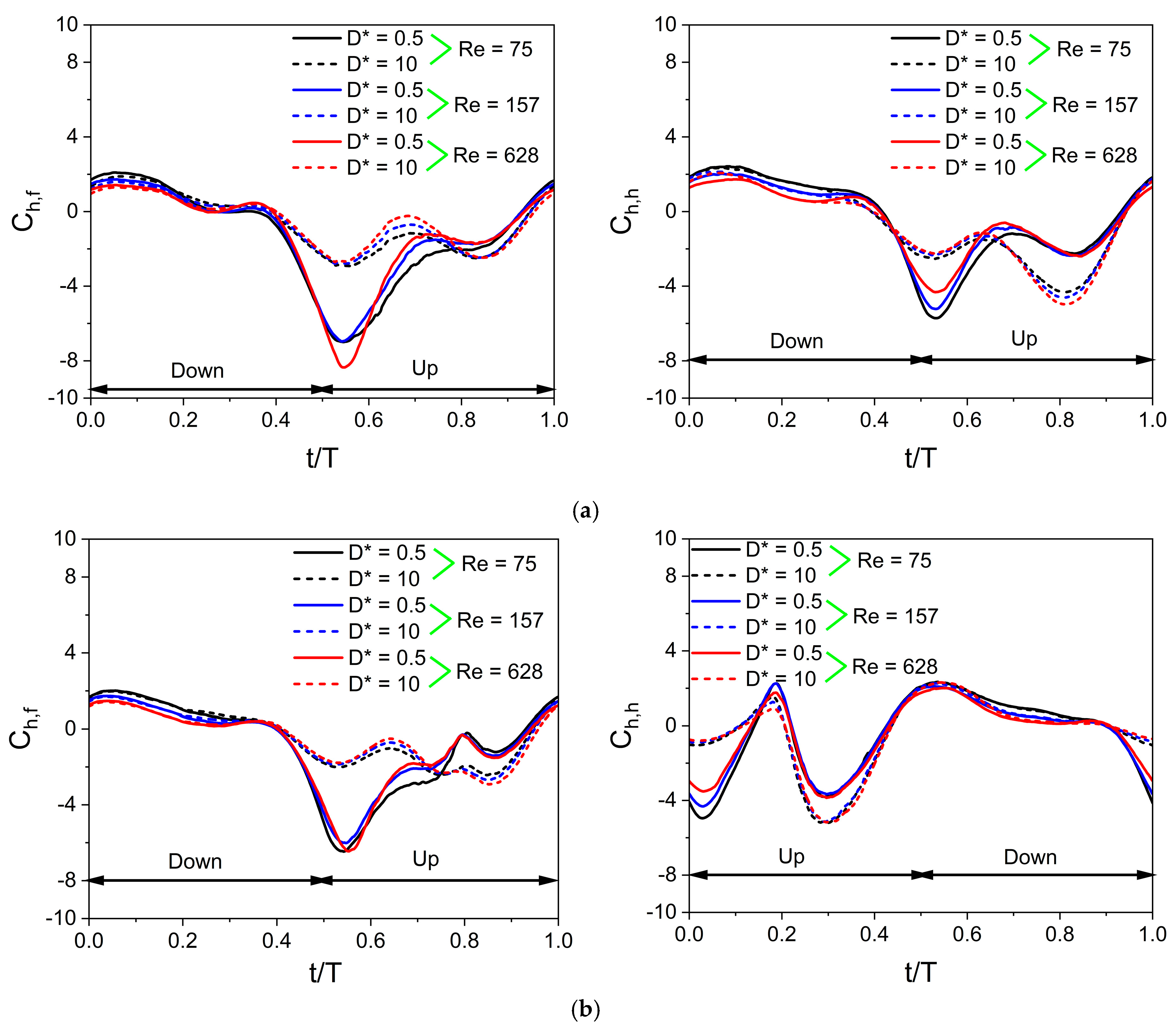
3.4. Time Histories of Vertical and Horizontal Force Coefficients at Various Re
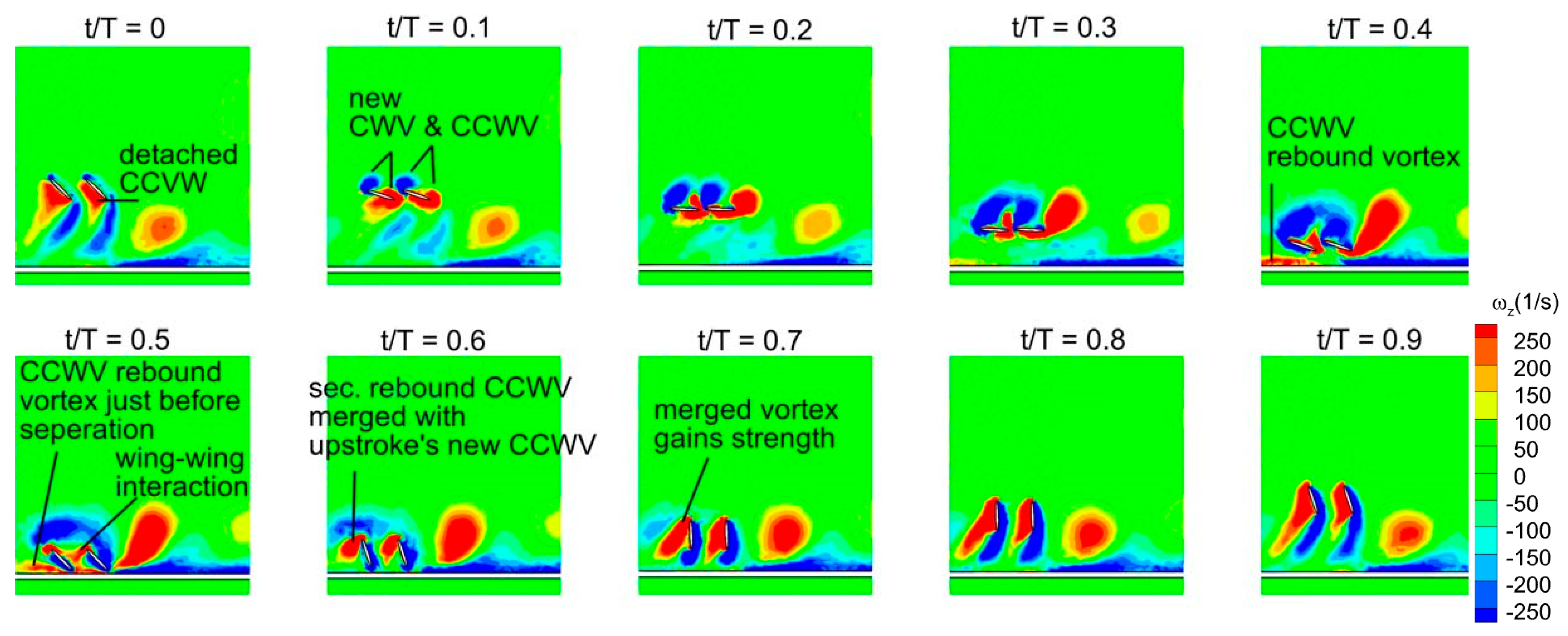
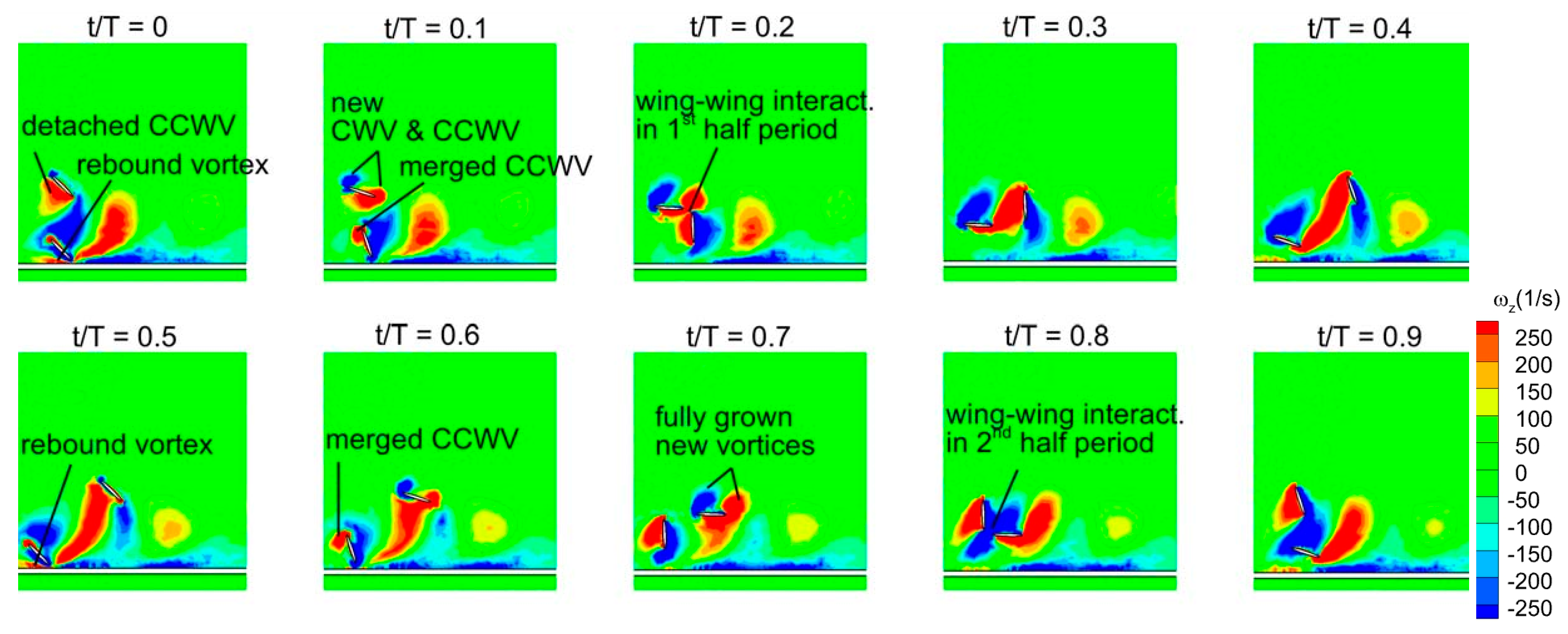
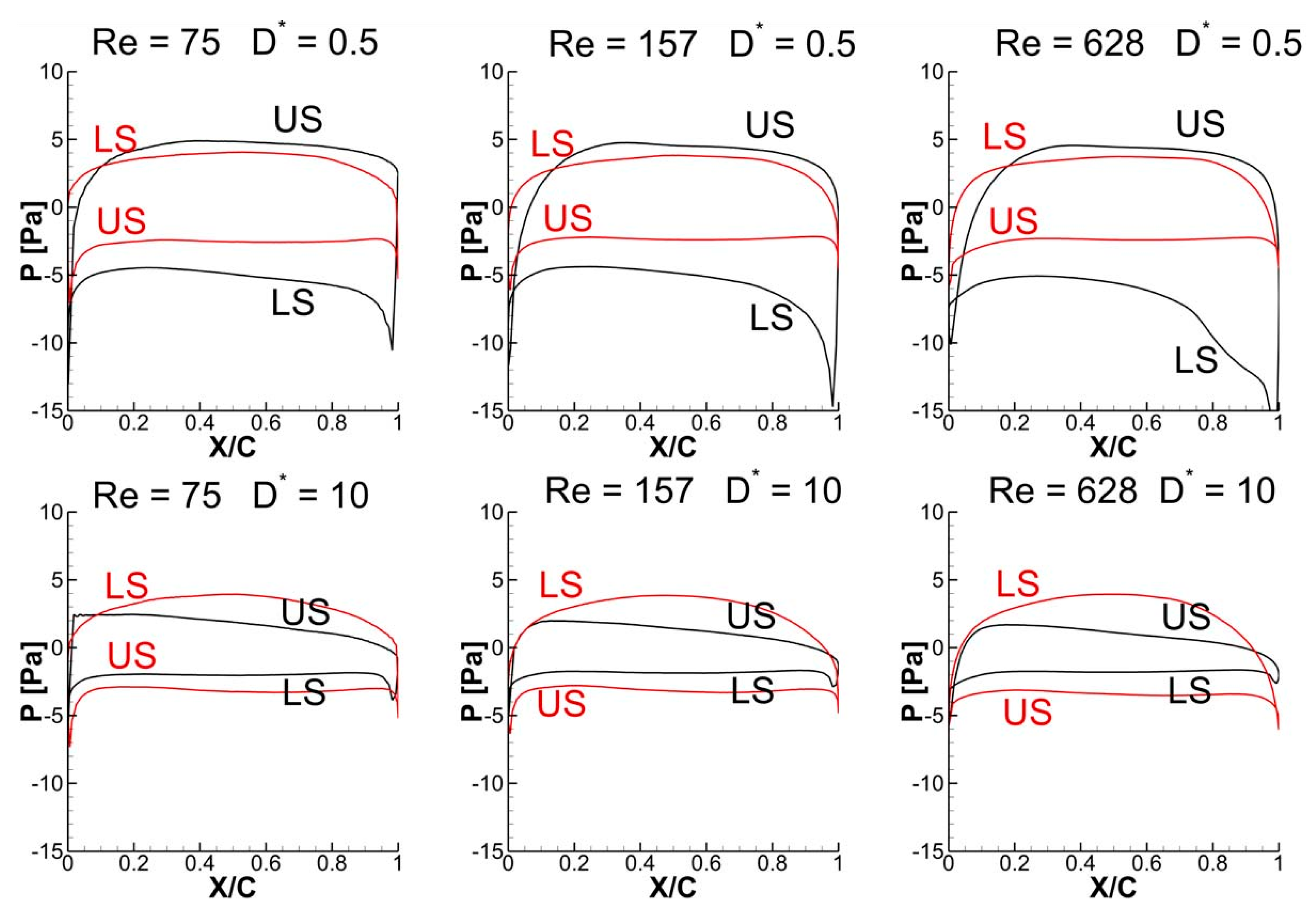
3.5. Vortex Structures and Surface Pressure Distribution
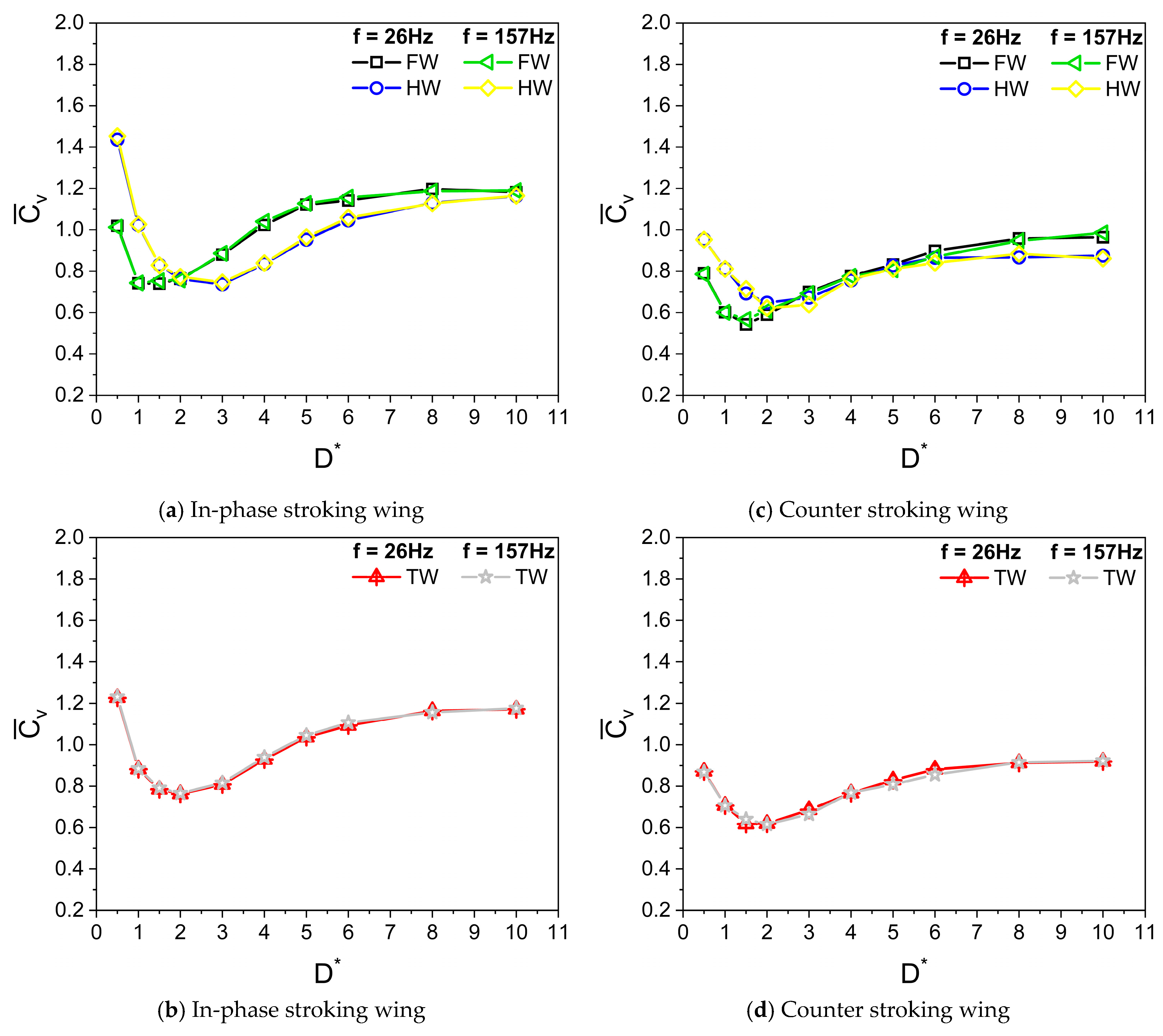
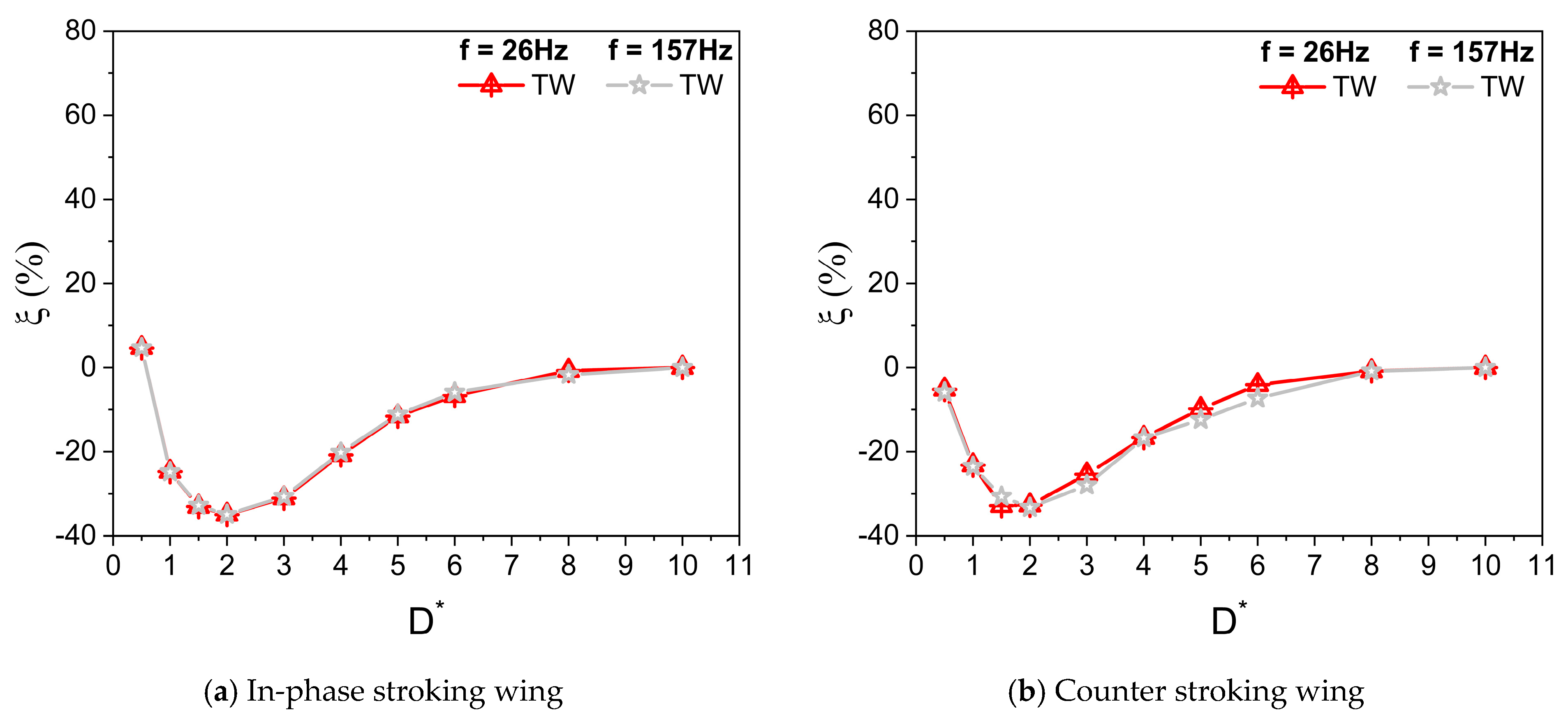
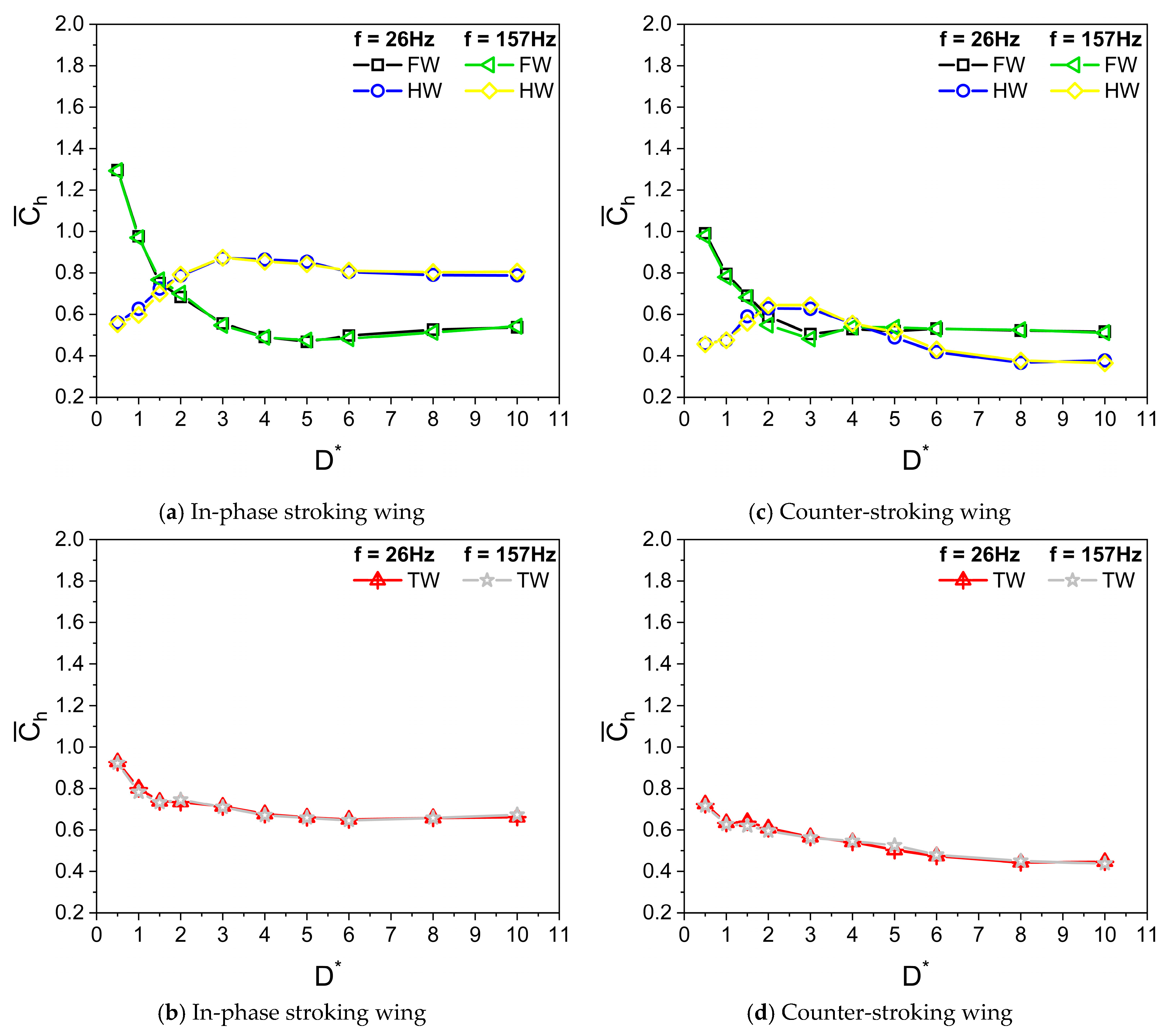
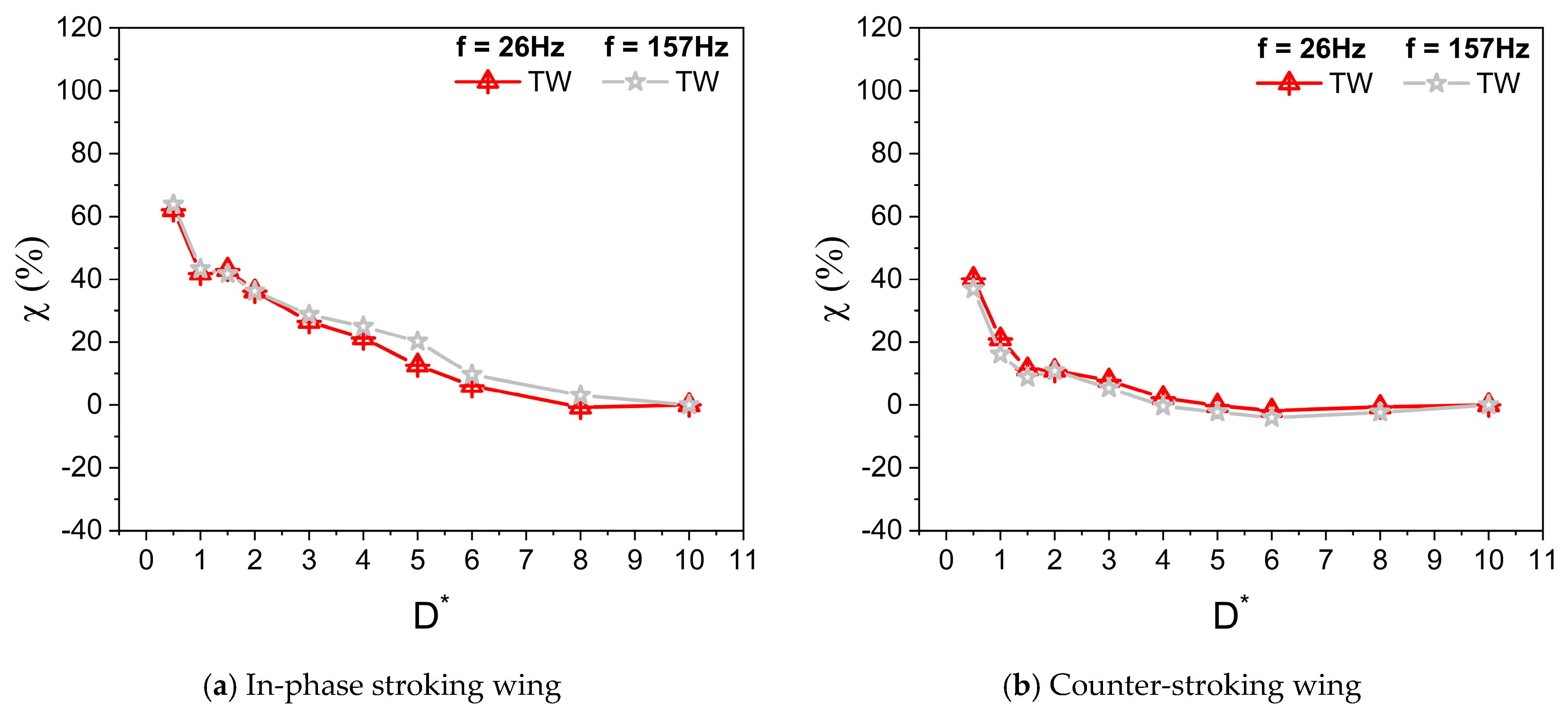
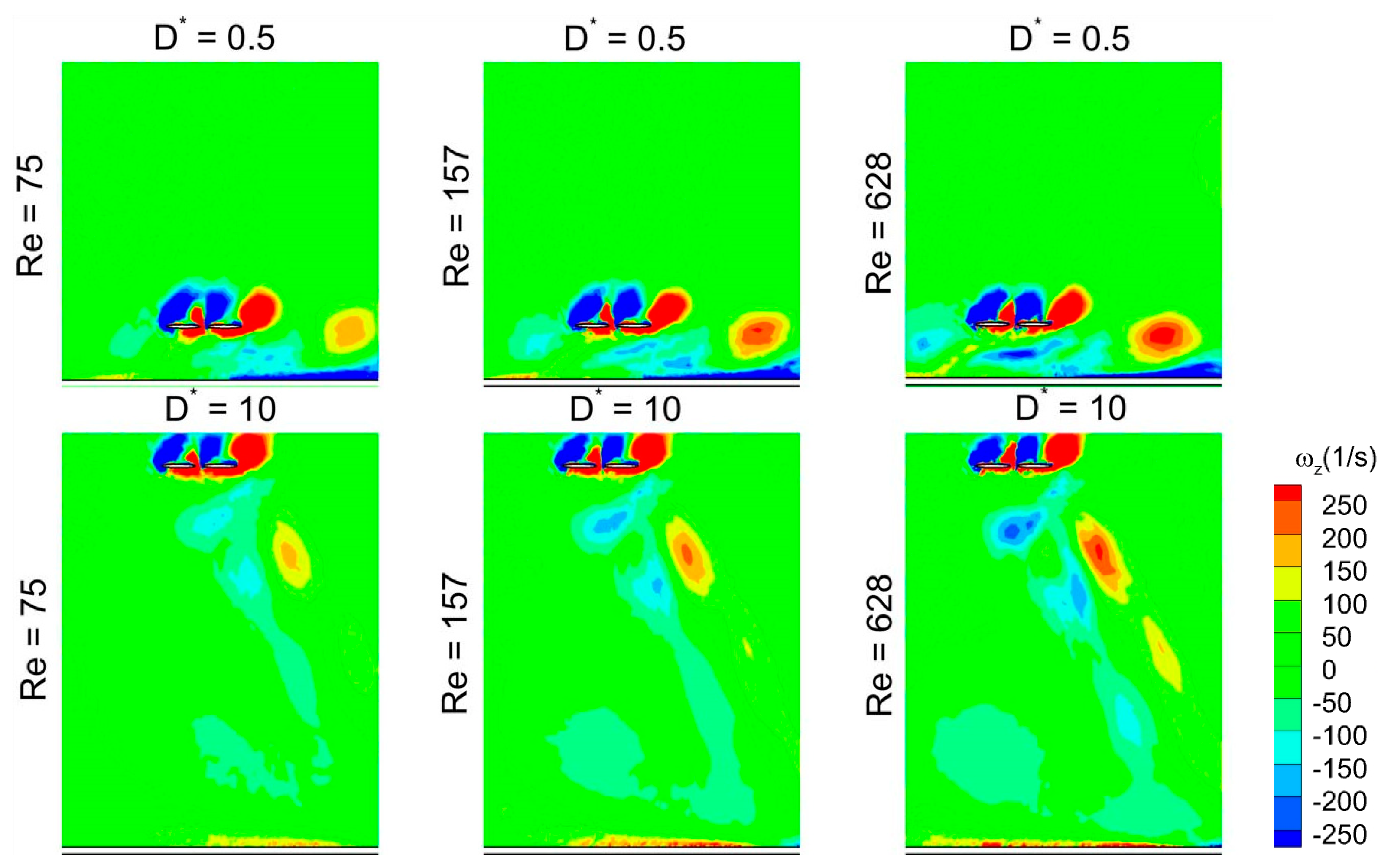
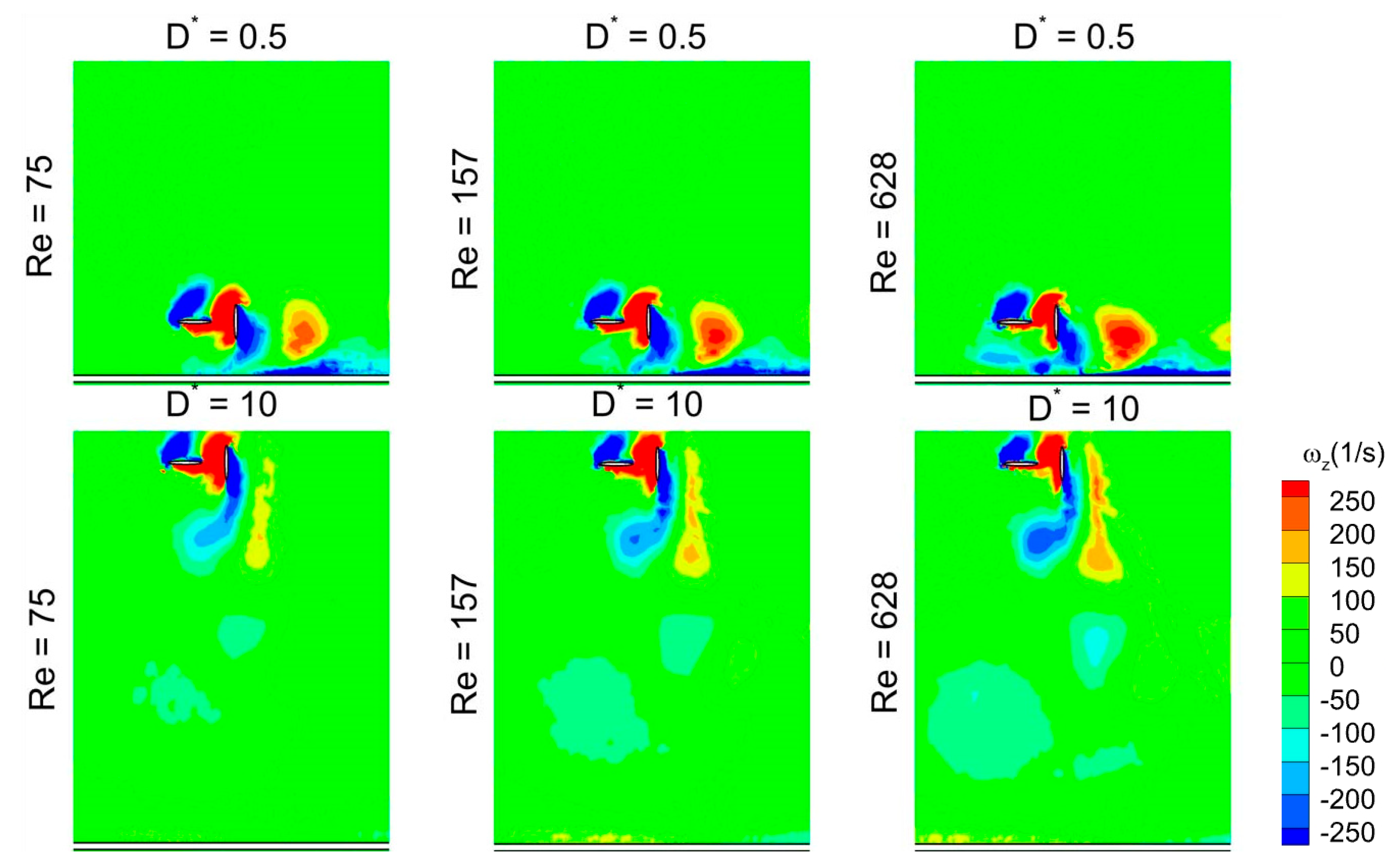
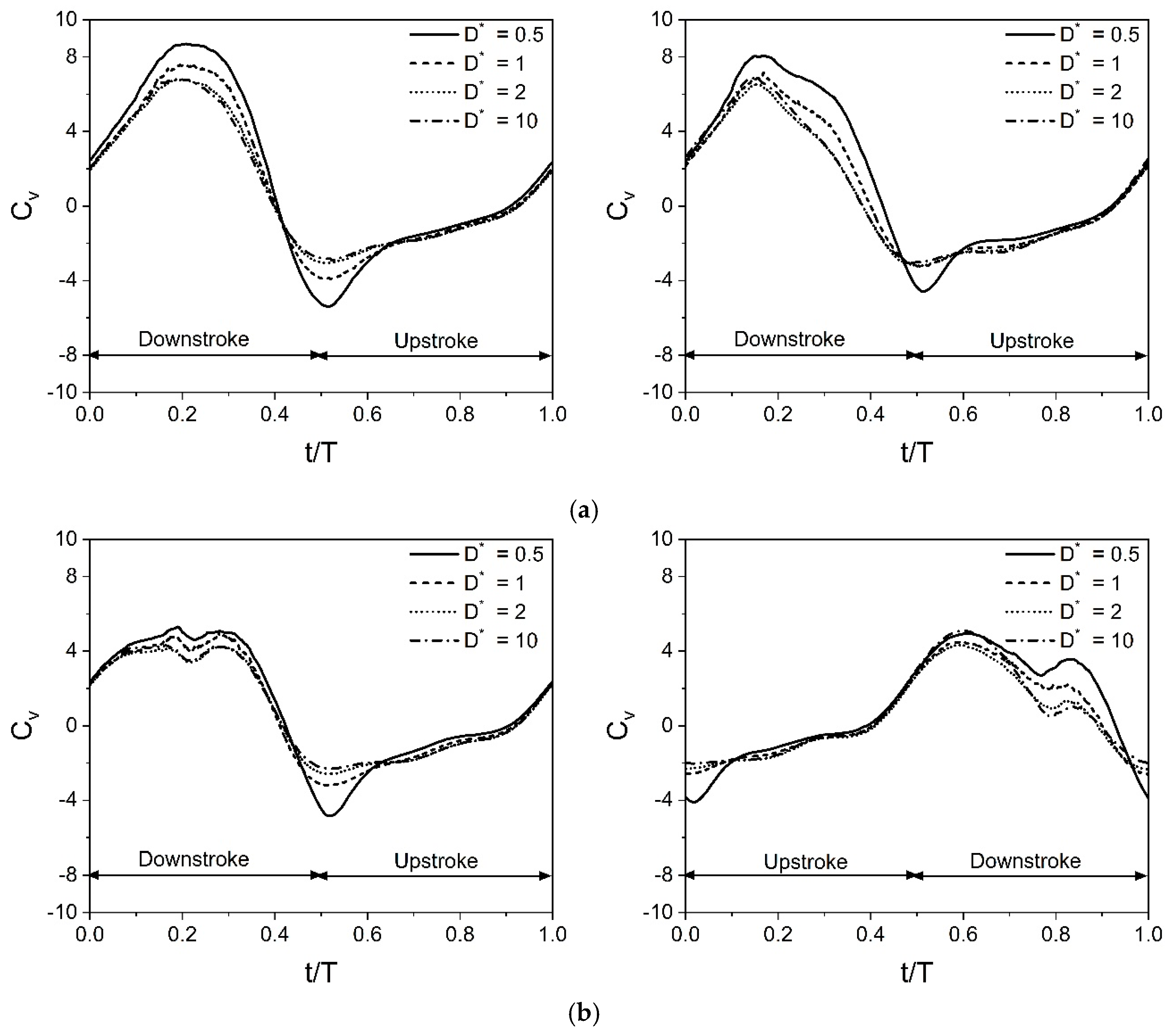
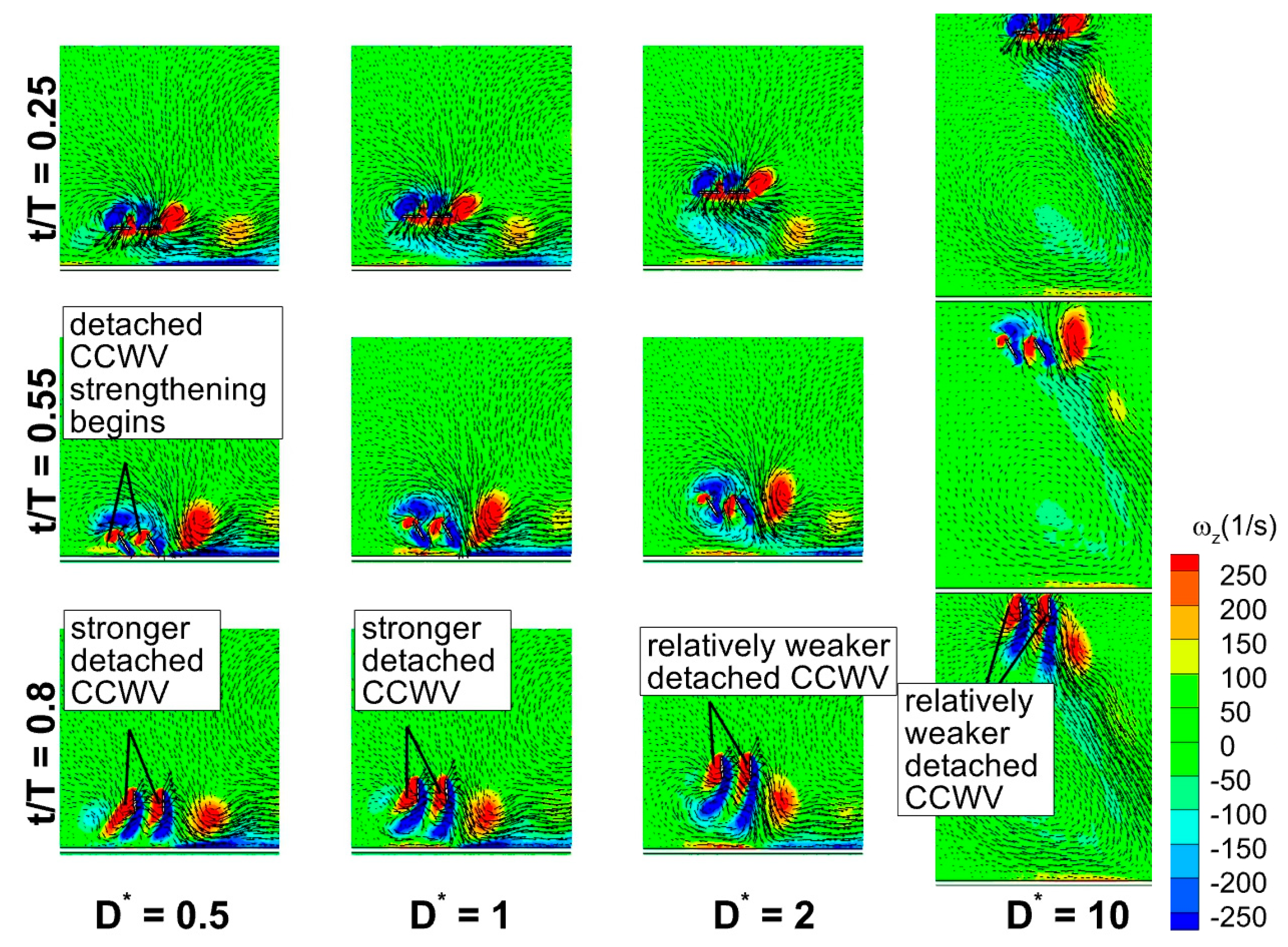
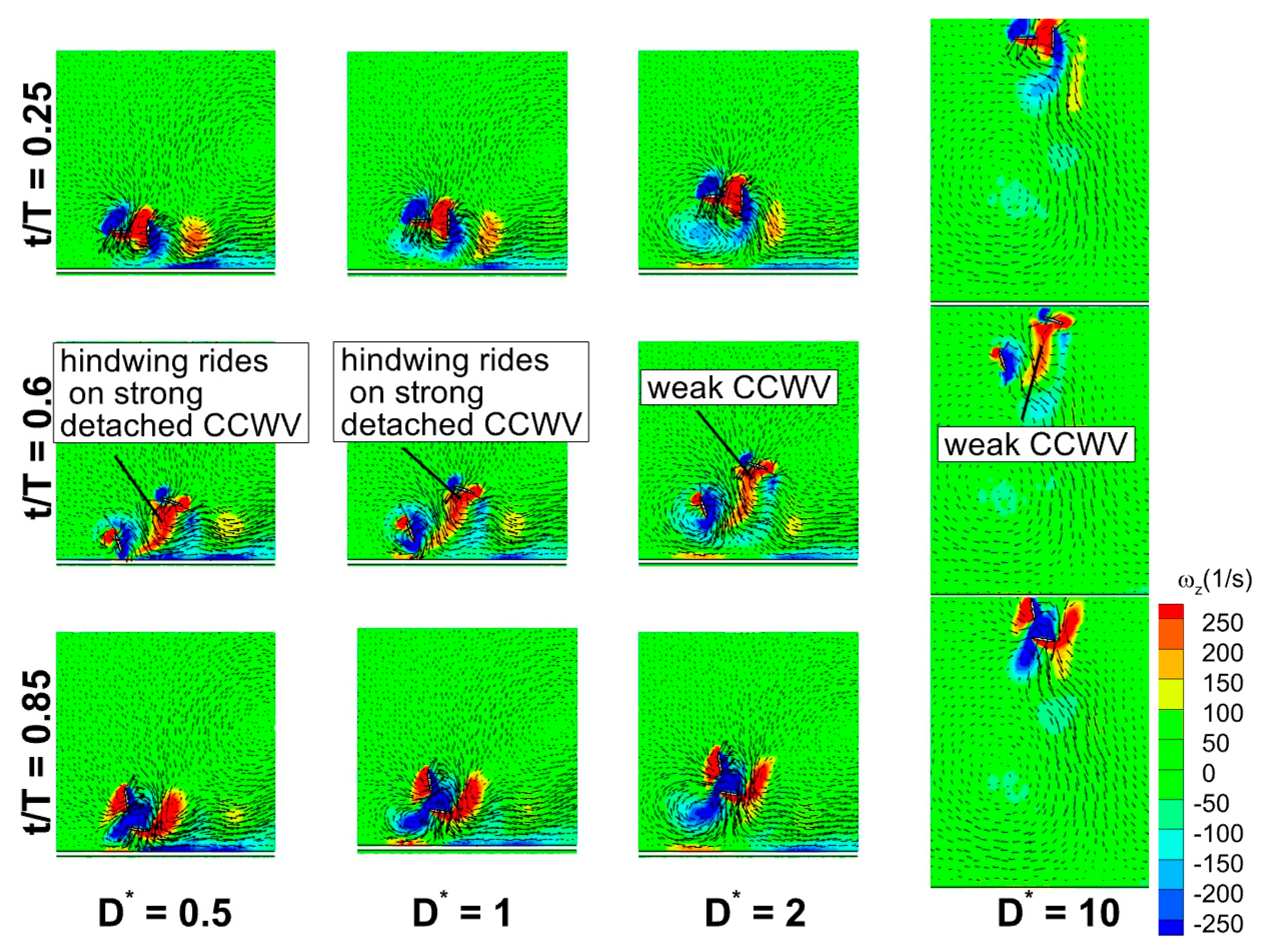
3.6. Time Histories of Cv and Vortex Structures for a Wide Range of D*
4. Conclusions
- The flapping frequency f has no effect on the vertical and horizontal force generation for both in-phase and counter-stroking patterns when the Reynolds number Re remain same.
- A large stroke amplitude Ao/c decreases vertical force generation for both in-phase and counter-stroking patterns when the Re remain same.
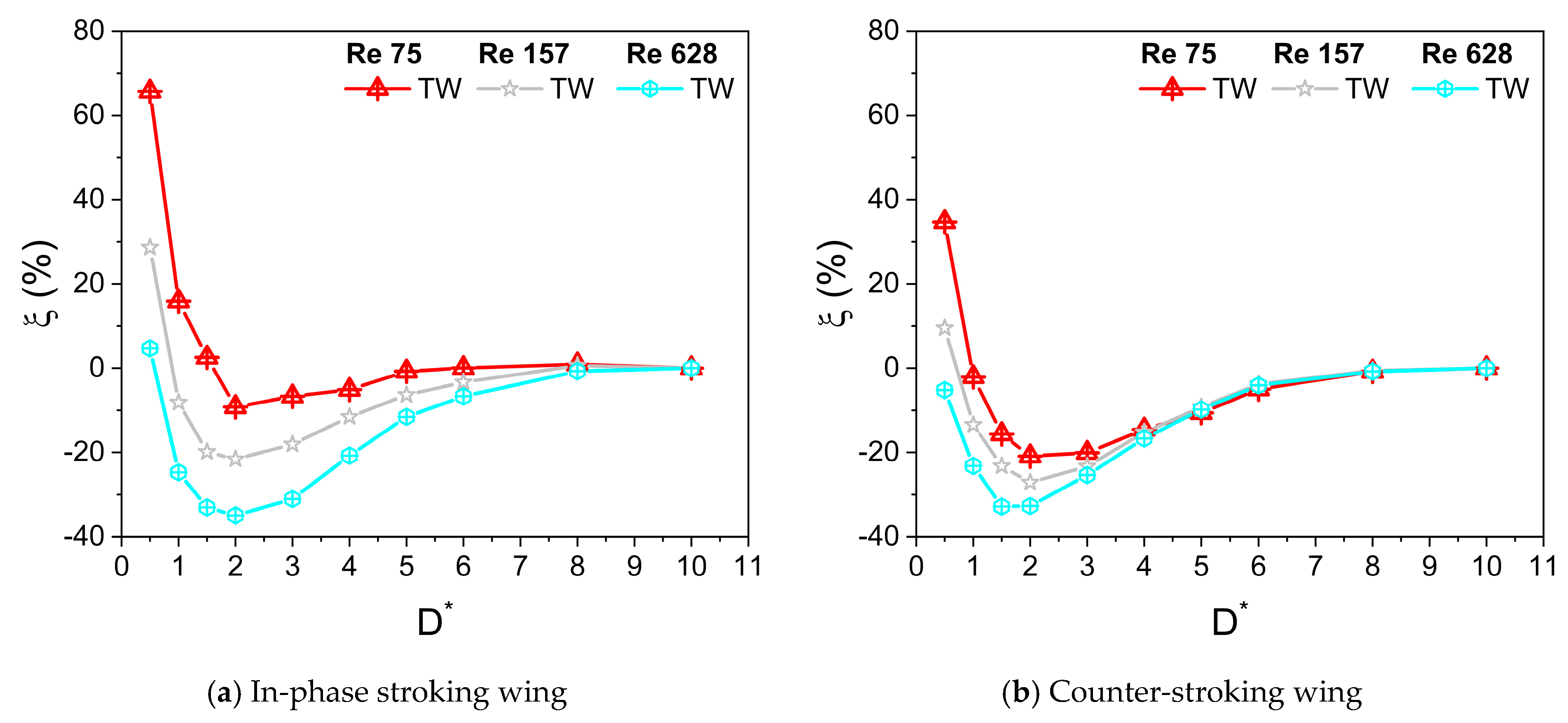
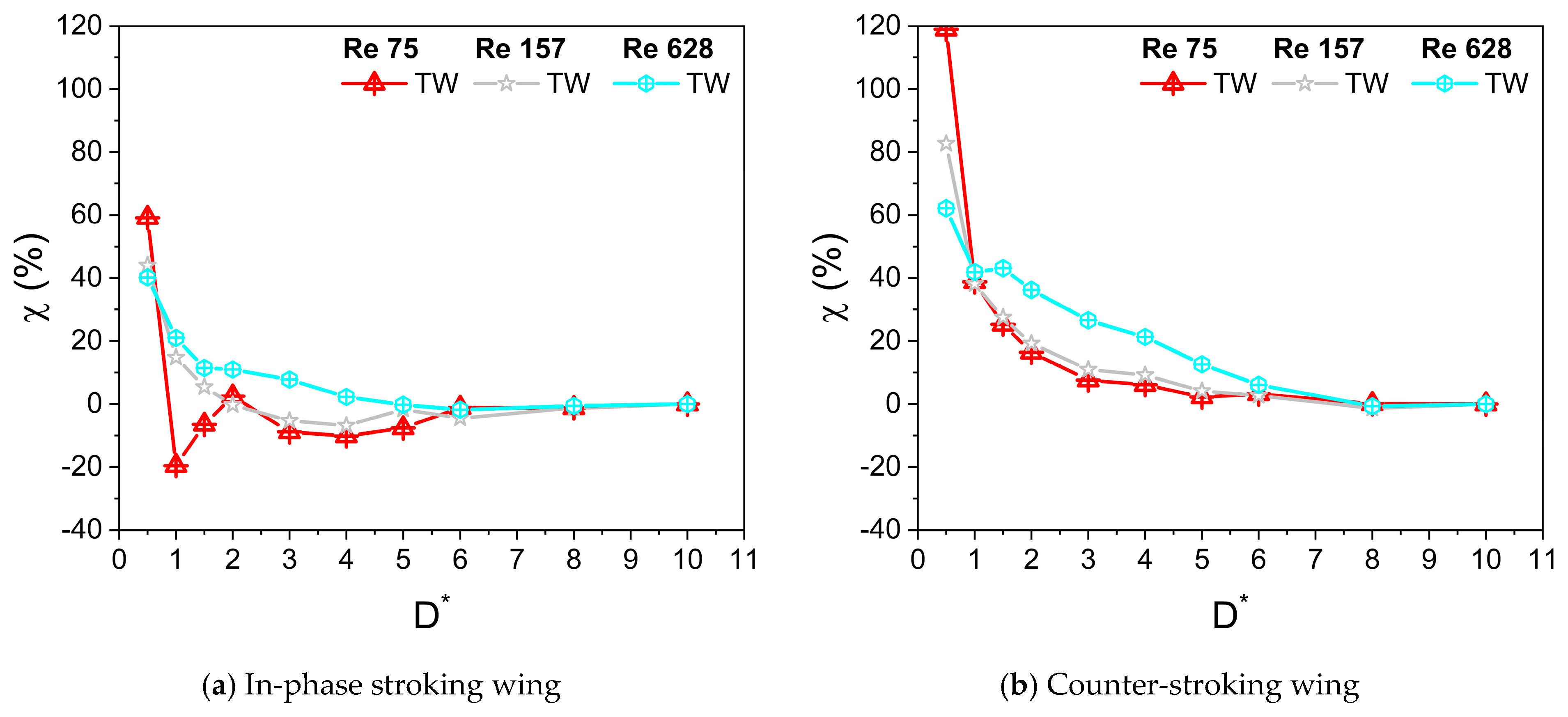
- At low Re (Re = 75) or large viscosity condition, a tremendous increase in the vertical force is observed for in-phase stroking wings when D* is extremely small (D* = 0.5). A maximum vertical force enhancement of around 65% for in-phase pattern and 35% for counter-stroking pattern is observed when D* = 0.5, as compared to D* = 10. This enhancement primarily results from the strengthening of detached vortices on the lower surface of the wings at the middle of the downstroke when the ground distance is extremely small (D* = 0.5).
- The vertical force behavior of an inclined hovering wing in the presence of the ground exhibits similarities to the findings of Gao and Lu (2008), which were observed in a normal hovering wing in ground-effect. Three distinct types characterize the vertical force behavior of the inclined hovering wing: force enhancement, force reduction, and force recovery.
- The wing–wing interaction and secondary rebound vortex, caused by wing–ground interaction, play a key role in vertical force generation. The wing–ground vortex interaction has a positive influence on the vertical and horizontal force generation for the in-phase and counter-stroking wings.
- In general, the vertical and horizontal force generated by the in-phase stroking wing is greater than the counter-stroking wing across all studied Re.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAV | Micro-Aerial Vehicle |
| LEV | Leading-Edge Vortex |
| IB-LBM | Immersed Boundary-Lattice Boltzmann Method |
| NACA | National Advisory Committee for Aeronautics |
| AOA | Angle of Attack |
| PISO | Pressure Implicit with Split Operator algorithm |
| FW | Fore Wing |
| HW | Hind Wing |
| TW | Tandem Wing |
| CWV | Clock Wise Vortex |
| CCWV | Counter Clock Wise Vortex |
References
- Khalid, M.S.U.; Akhtar, I.; Dong, H. Hydrodynamics of a tandem fish school with asynchronous undulation of individuals. J. Fluids Struct. 2016, 66, 19–35. [Google Scholar] [CrossRef]
- Weihs, D. The hydrodynamics of dolphin drafting. J. Biol. 2004, 3, 8. [Google Scholar] [CrossRef]
- Trenchard, H.; Perc, M. Energy saving mechanisms, collective behavior and the variation range hypothesis in biological systems: A review. Biosystems 2016, 147, 40–66. [Google Scholar] [CrossRef]
- Rayner, J.M. On the aerodynamics of animal flight in ground effect. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1991, 334, 119–128. [Google Scholar] [CrossRef]
- Finn, J.; Carlsson, J.; Kelly, T.; Davenport, J. Avoidance of headwinds or exploitation of ground effect—Why do birds fly low? J. Field. Ornithol. 2012, 83, 192–202. [Google Scholar] [CrossRef]
- Nowroozi, B.N.; Strother, J.A.; Horton, J.M.; Summers, A.P.; Brainerd, E.L. Whole-body lift and ground effect during pectoral fin locomotion in the northern spearnose poacher (Agonopsis vulsa). Zoology 2009, 112, 393–402. [Google Scholar] [CrossRef] [PubMed]
- Pesavento, U.; Wang, Z.J. Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 2009, 103, 118102. [Google Scholar] [CrossRef]
- Rüppell, G. Kinematic analysis of symmetrical flight manoeuvres of Odonata. J. Exp. Biol. 1989, 144, 13–42. [Google Scholar] [CrossRef]
- Wang, Z.J. The role of drag in insect hovering. J. Exp. Biol. 2004, 207, 4147–4155. [Google Scholar] [CrossRef]
- Mao, S.; Gang, D.U. Lift and power requirements of hovering insect flight. Acta. Mech. Sin. 2003, 19, 458–469. [Google Scholar] [CrossRef]
- Sun, M.; Wang, J.; Xiong, Y. Dynamic flight stability of hovering insects. Acta. Mech. Sin. 2007, 23, 231–246. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Chang, C.C.; Chu, C.C. Revisiting the aerodynamics of hovering flight using simple models. J. Fluid Mech. 2009, 623, 121–148. [Google Scholar] [CrossRef]
- Sudhakar, Y.; Vengadesan, S. Flight force production by flapping insect wings in inclined stroke plane kinematics. Comput. Fluids 2010, 39, 683–695. [Google Scholar] [CrossRef]
- Jones, S.K.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift vs. drag based mechanisms for vertical force production in the smallest flying insects. J. Theor. Biol. 2015, 384, 105–120. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, C.; Xie, P. Numerical investigation on aerodynamic performance of a 2-D inclined hovering wing in asymmetric strokes. J. Mech. Sci. Technol. 2016, 30, 199–210. [Google Scholar] [CrossRef]
- Shanmugam, A.R.; Sohn, C.H. Systematic investigation of a flapping wing in inclined stroke-plane hovering. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 347. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Kung, C.F.; Chang, C.C.; Chu, C.C. Unsteady aerodynamics of dragonfly using a simple wing–wing model from the perspective of a force decomposition. J. Fluid Mech. 2010, 663, 233–252. [Google Scholar] [CrossRef]
- Broering, T.M.; Lian, Y. Numerical study of tandem flapping wing aerodynamics in both two and three dimensions. Comput. Fluids 2015, 115, 124–139. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Y.; Tang, H. An experimental study on the forewing–hindwing interactions in hovering and forward flights. Int. J. Heat Fluid Flow 2016, 59, 62–73. [Google Scholar] [CrossRef]
- Yang, X.; Luo, Y.; Lang, X.; Wang, W. Investigation of the aerodynamic performance of the dragonfly-inspired tandem wings considering the coupling between the stroke plane and phase difference. Aerosp. Sci. Technol. 2024, 155, 109717. [Google Scholar] [CrossRef]
- Maybury, W.J.; Lehmann, F.O. The fluid dynamics of flight control by kinematic phase lag variation between two robotic insect wings. J. Exp. Biol. 2004, 207, 4707–4726. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Cuevas, P.; Heredia, G.; Ollero, A. Characterization of the aerodynamic ground effect and its influence in multirotor control. Int. J. Aerosp. Eng. 2017, 2017, 1823056. [Google Scholar] [CrossRef]
- Xu, G.; Sun, Z.; Liu, H.; Zhou, Y.; Gong, X.; Gong, S. Identification of ground effect and intelligent control of unmanned aerial vehicles. Aerosp. Sci. Technol. 2022, 131, 107976. [Google Scholar] [CrossRef]
- Gao, T.; Lu, X.Y. Insect normal hovering flight in ground effect. Phys. Fluids 2008, 20, 087101. [Google Scholar] [CrossRef]
- Lu, H.; Lua, K.B.; Lim, T.T.; Yeo, K.S. Ground effect on the aerodynamics of a two-dimensional oscillating airfoil. Exp. Fluids 2014, 55, 1787. [Google Scholar] [CrossRef]
- Lu, H.; Lua, K.B.; Lee, Y.J.; Lim, T.T.; Yeo, K.S. Ground effect on the aerodynamics of three-dimensional hovering wings. Bioinspir. Biomim. 2016, 11, 66003. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhao, N.; Yan, W. Fluid dynamics of flapping insect wing in ground effect. J. Bionic Eng. 2014, 11, 52–60. [Google Scholar] [CrossRef]
- Wu, J.; Qiu, Y.L.; Shu, C.; Zhao, N.; Wang, X. An adaptive immersed boundary-lattice Boltzmann method for simulating a flapping foil in ground effect. Comput. Fluids 2015, 106, 171–184. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.C.; Shu, C.; Zhao, N.; Yan, W.W. Ground effect on the power extraction performance of a flapping wing biomimetic energy generator. J. Fluids Struct. 2015, 54, 247–262. [Google Scholar] [CrossRef]
- Mivehchi, A.; Dahl, J.; Licht, S. Heaving and pitching oscillating foil propulsion in ground effect. J. Fluids Struct. 2016, 63, 174–187. [Google Scholar] [CrossRef]
- Srinidhi, N.G.; Vengadesan, S. Ground effect on tandem flapping wings hovering. Comput. Fluids 2017, 152, 40–56. [Google Scholar] [CrossRef]
- Abdizadeh, G.R.; Farokhinejad, M.; Ghasemloo, S. Numerical investigation on the aerodynamic efficiency of bio-inspired corrugated and cambered airfoils in ground effect. Sci. Rep. 2022, 12, 19117. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Zhang, J.; Zhang, W. Impact of the ground effect on the energy extraction properties of a flapping wing. Ocean Eng. 2020, 209, 107376. [Google Scholar] [CrossRef]
- He, G.; Mo, W.; Gao, Y.; Wang, J.; Zhang, Z.; Yang, H.; Mao, W. Numerical study of a semi-passive oscillating hydrofoil on power-extraction with wing-in-ground effect. J. Fluids Struct. 2022, 115, 103761. [Google Scholar] [CrossRef]
- Mo, W.; He, G.; Wang, J.; Zhang, Z.; Gao, Y.; Zhang, W.; Ghassemi, H. Hydrodynamic analysis of three oscillating hydrofoils with wing-in-ground effect on power extraction performance. Ocean Eng. 2022, 246, 110642. [Google Scholar] [CrossRef]
- Mo, W.; He, G.; Wang, J.; Zhang, Z.; Wang, J.; Liu, P.; Yang, H. Hydrodynamic characteristics of wing-in-ground effect oscillating hydrofoil on power extraction performance. Energy Rep. 2024, 11, 2991–3004. [Google Scholar] [CrossRef]
- Li, Y.; Pan, Z.; Zhang, N. Numerical analysis on the propulsive performance of oscillating wing in ground effect. Appl. Ocean Res. 2021, 114, 102772. [Google Scholar] [CrossRef]
- Wang, Z.J. Two dimensional mechanism for insect hovering. Phys. Rev. Lett. 2000, 85, 2216. [Google Scholar] [CrossRef]
- Salami, E.; Ward, T.A.; Montazer, E.; Ghazali, N.N.N. A review of aerodynamic studies on dragonfly flight. Proc. Inst. Mech. Eng. Part. C J. Mech. Eng. Sci. 2019, 233, 6519–6537. [Google Scholar] [CrossRef]
- Kim, D.; Choi, H. Two-dimensional mechanism of hovering flight by single flapping wing. J. Mech. Sci. 2007, 21, 207–221. [Google Scholar] [CrossRef]
- Hou, D.; Tan, B.; Shi, B.; Zhong, Z. Aerodynamic effects of time-varying corrugations on dragonfly wings in flapping flight. Biomimetics 2024, 9, 433. [Google Scholar] [CrossRef] [PubMed]
- Lua, K.B.; Lu, H.; Zhang, X.H.; Lim, T.T.; Yeo, K.S. Aerodynamics of two-dimensional flapping wings in tandem configuration. Phys. Fluids 2016, 28, 121901. [Google Scholar] [CrossRef]
- Wu, D.; Yeo, K.S.; Lim, T.T. A numerical study on the free hovering flight of a model insect at low Reynolds number. Comput. Fluids 2014, 103, 234–261. [Google Scholar] [CrossRef]
- Shanmugam, A.R.; Sohn, C.H. Numerical investigation of the aerodynamic benefits of wing-wing interactions in a dragonfly-like flapping wing. J. Mech. Sci. Technol. 2019, 33, 2725–2735. [Google Scholar] [CrossRef]
- Moryossef, Y.; Levy, Y. Effect of oscillations on airfoils in close proximity to the ground. AIAA J. 2004, 42, 1755–1764. [Google Scholar] [CrossRef]
- Park, H.; Choi, H. Kinematic control of aerodynamic forces on an inclined flapping wing with asymmetric strokes. Bioinspir. Biomim. 2012, 7, 16008. [Google Scholar] [CrossRef]
- Mou, X.L.; Liu, Y.P.; Sun, M. Wing motion measurement and aerodynamics of hovering true hoverflies. J. Exp. Biol. 2011, 214, 2832–2844. [Google Scholar] [CrossRef]
- Wang, L.; Yeung, R.W. Investigation of full and partial ground effects on a flapping foil hovering above a finite-sized platform. Phys. Fluids 2016, 28, 71902. [Google Scholar] [CrossRef]
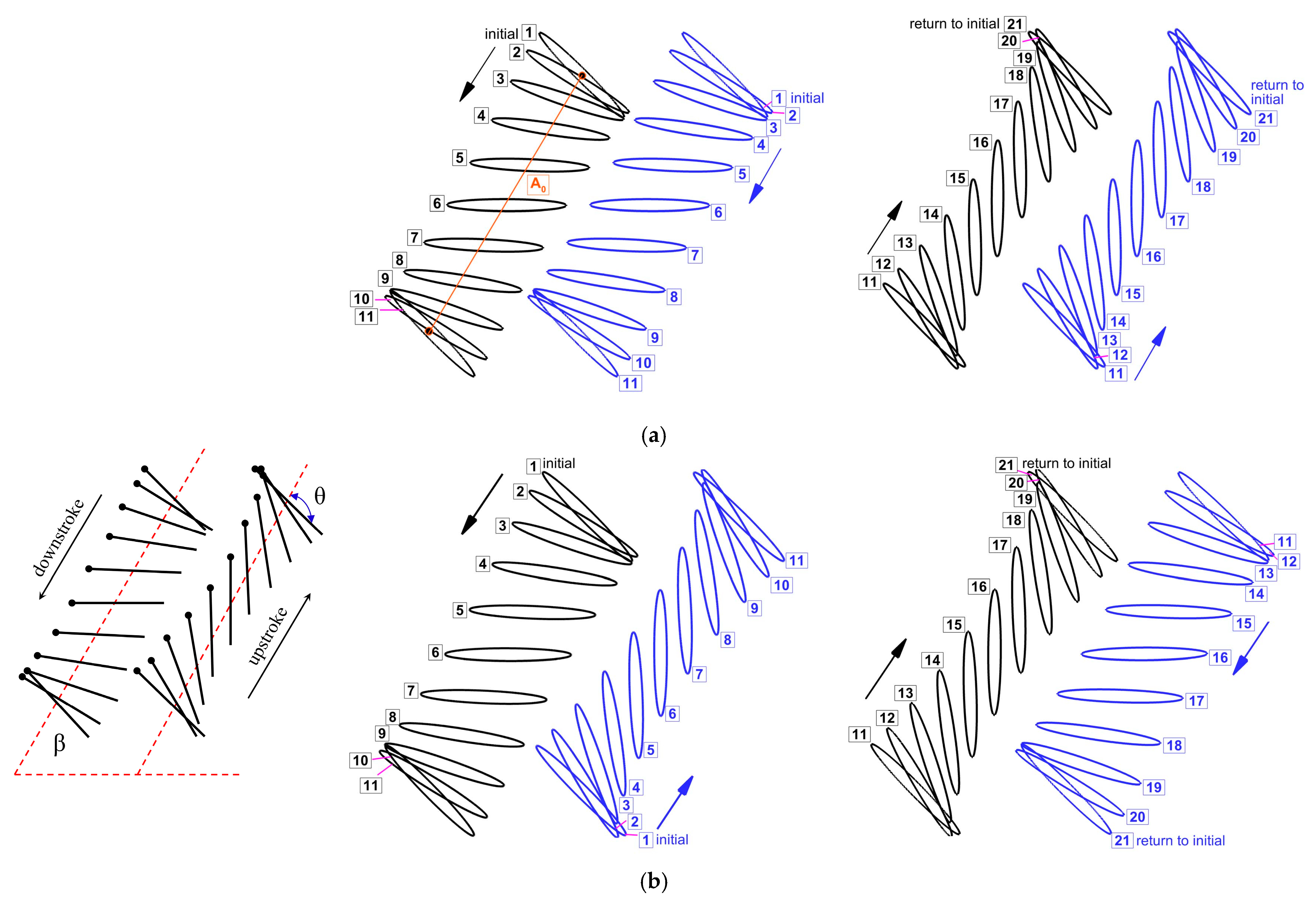

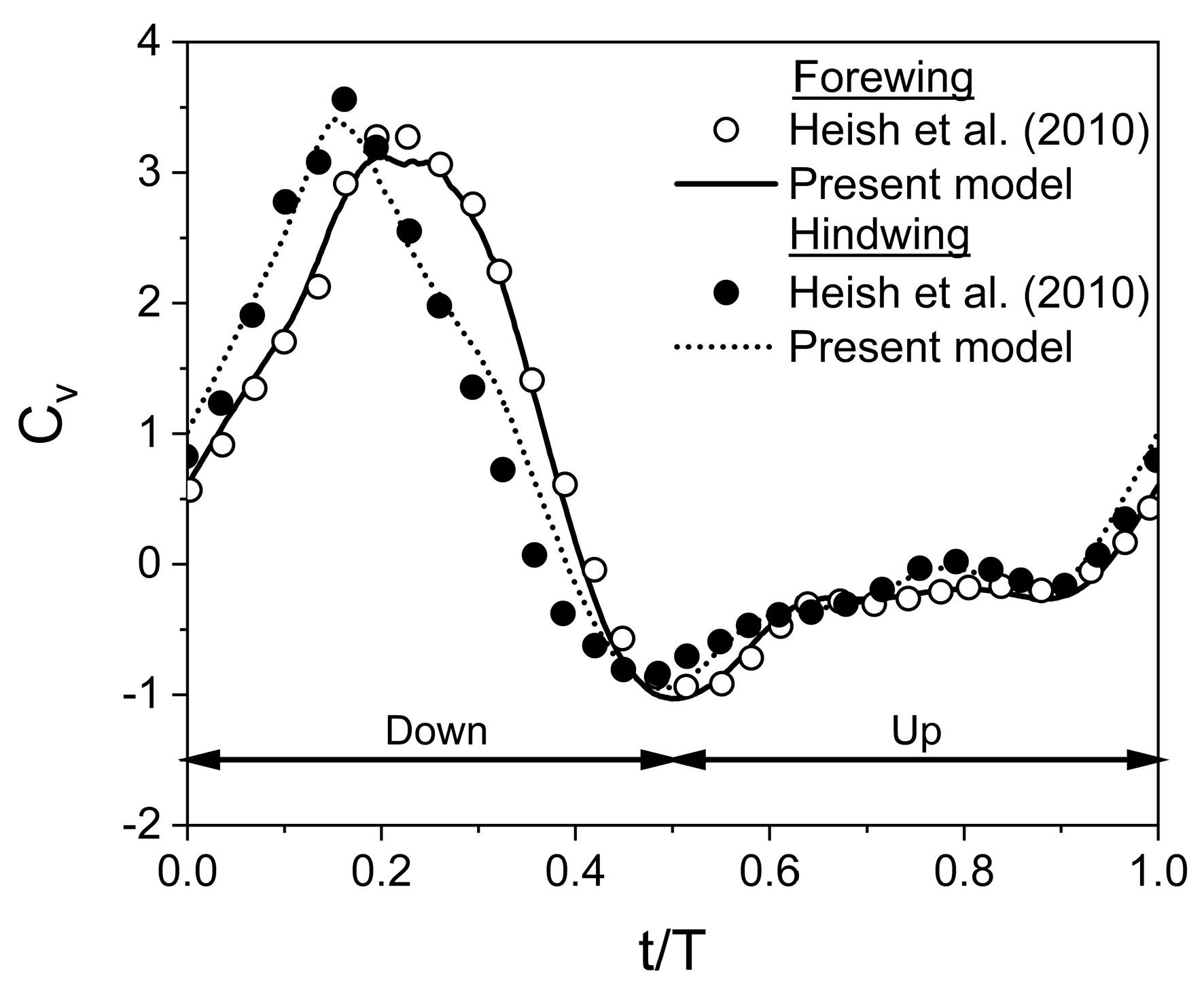
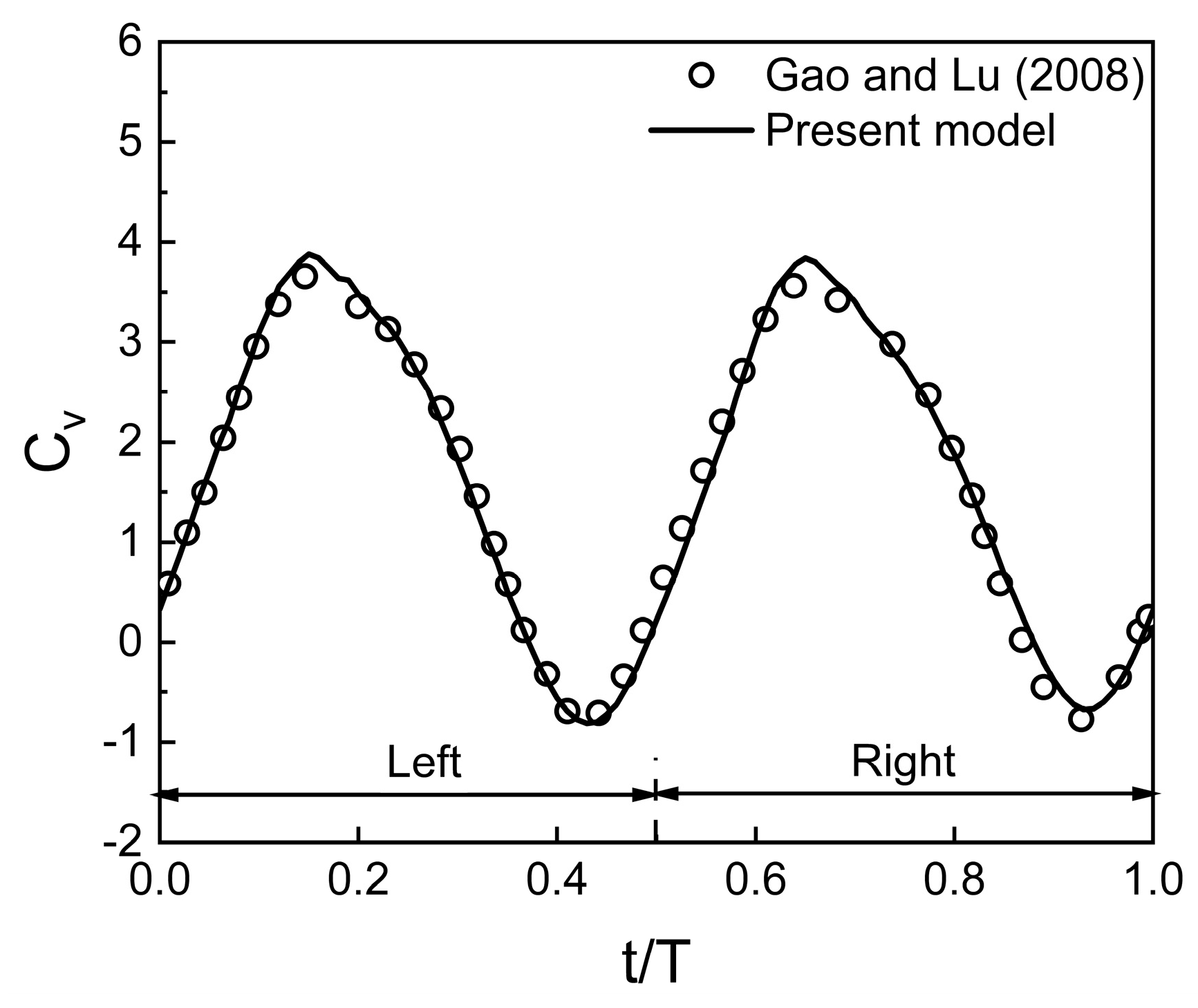
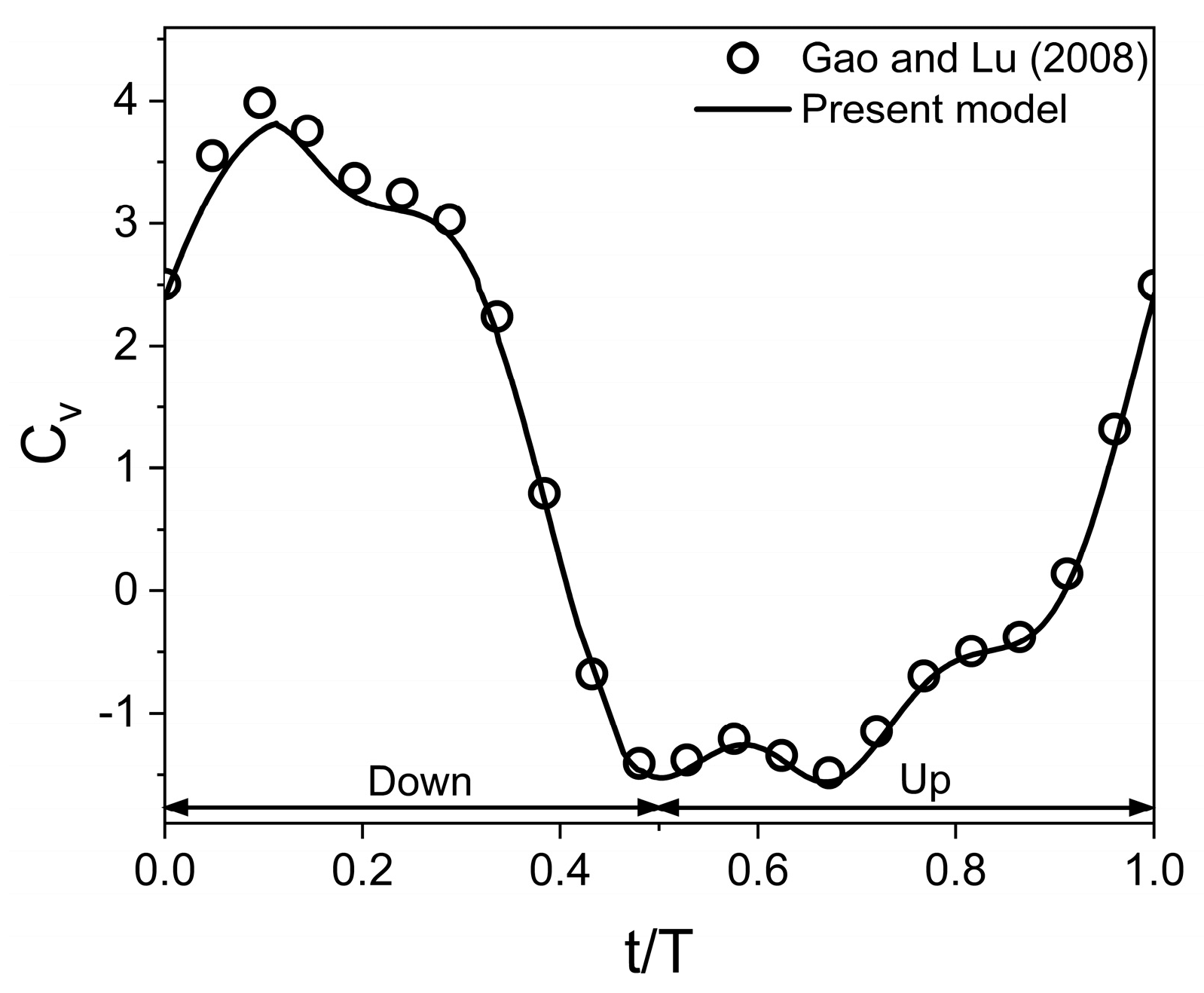




| Parameter and the Source of Data | Value |
|---|---|
| Reynolds number Re|corresponding dynamic viscosity (kg/ms) | 75|0.000333532 157|0.000159331 628|3.98327 × 10−5 |
| Flapping frequency f [10,11] | 26–157 Hz |
| Mean angle of attack αo | 45° |
| Pitch amplitude B | 45° |
| Phase difference between the translation and the rotation φ | 0° |
| Stroke plane inclination β [8,9] | 60° |
| Angle of attack AOA | Downstroke: θ° Upstroke: 180-θ° |
| Stroke amplitude Ao/c [8,9] | 2.5–5 |
| Phase difference between the forewing and the hindwing ψ [17] | 0° and 180° |
| Downstroke | |||||
|---|---|---|---|---|---|
| Stage | t/T | α° | Stage | t/T | α° |
| 1 | 0 | 45 | 7 | 0.3 | 2.20 |
| 2 | 0.05 | 31.09 | 8 | 0.35 | 8.59 |
| 3 | 0.1 | 18.55 | 9 | 0.4 | 18.55 |
| 4 | 0.15 | 8.59 | 10 | 0.45 | 31.09 |
| 5 | 0.2 | 2.20 | 11 | 0.5 | 45 |
| 6 | 0.25 | 0 | |||
| upstroke | |||||
| stage | t/T | α° | stage | t/T | α° |
| 11 | 0.5 | 45 | 17 | 0.8 | 87.80 |
| 12 | 0.55 | 58.91 | 18 | 0.85 | 81.41 |
| 13 | 0.6 | 71.45 | 19 | 0.9 | 71.45 |
| 14 | 0.65 | 81.41 | 20 | 0.95 | 58.91 |
| 15 | 0.7 | 87.80 | 21 | 1 | 45 |
| 16 | 0.75 | 90 | |||
| Grid Size (Million) | ||
|---|---|---|
| Medium (0.13) | 1.150 | 1.083 |
| Fine (0.25) | 1.203 | 1.152 |
| Refined (0.5) | 1.209 | 1.161 |
| Time-Step Size (s) | ||
| Medium (0.004T) | 1.157 | 1.097 |
| Fine (0.002T) | 1.203 | 1.152 |
| Refined (0.001T) | 1.221 | 1.174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shanmugam, A.R.; Sohn, C.H.; Park, K.S. Aerodynamic Characteristics of a Tandem Flapping Wing in Inclined Stroke Plane Hovering with Ground Effect. Biomimetics 2025, 10, 212. https://doi.org/10.3390/biomimetics10040212
Shanmugam AR, Sohn CH, Park KS. Aerodynamic Characteristics of a Tandem Flapping Wing in Inclined Stroke Plane Hovering with Ground Effect. Biomimetics. 2025; 10(4):212. https://doi.org/10.3390/biomimetics10040212
Chicago/Turabian StyleShanmugam, Arun Raj, Chang Hyun Sohn, and Ki Sun Park. 2025. "Aerodynamic Characteristics of a Tandem Flapping Wing in Inclined Stroke Plane Hovering with Ground Effect" Biomimetics 10, no. 4: 212. https://doi.org/10.3390/biomimetics10040212
APA StyleShanmugam, A. R., Sohn, C. H., & Park, K. S. (2025). Aerodynamic Characteristics of a Tandem Flapping Wing in Inclined Stroke Plane Hovering with Ground Effect. Biomimetics, 10(4), 212. https://doi.org/10.3390/biomimetics10040212






