The Two-Echelon Unmanned Ground Vehicle Routing Problem: Extreme-Weather Goods Distribution as a Case Study
Abstract
1. Introduction
2. Literature Review
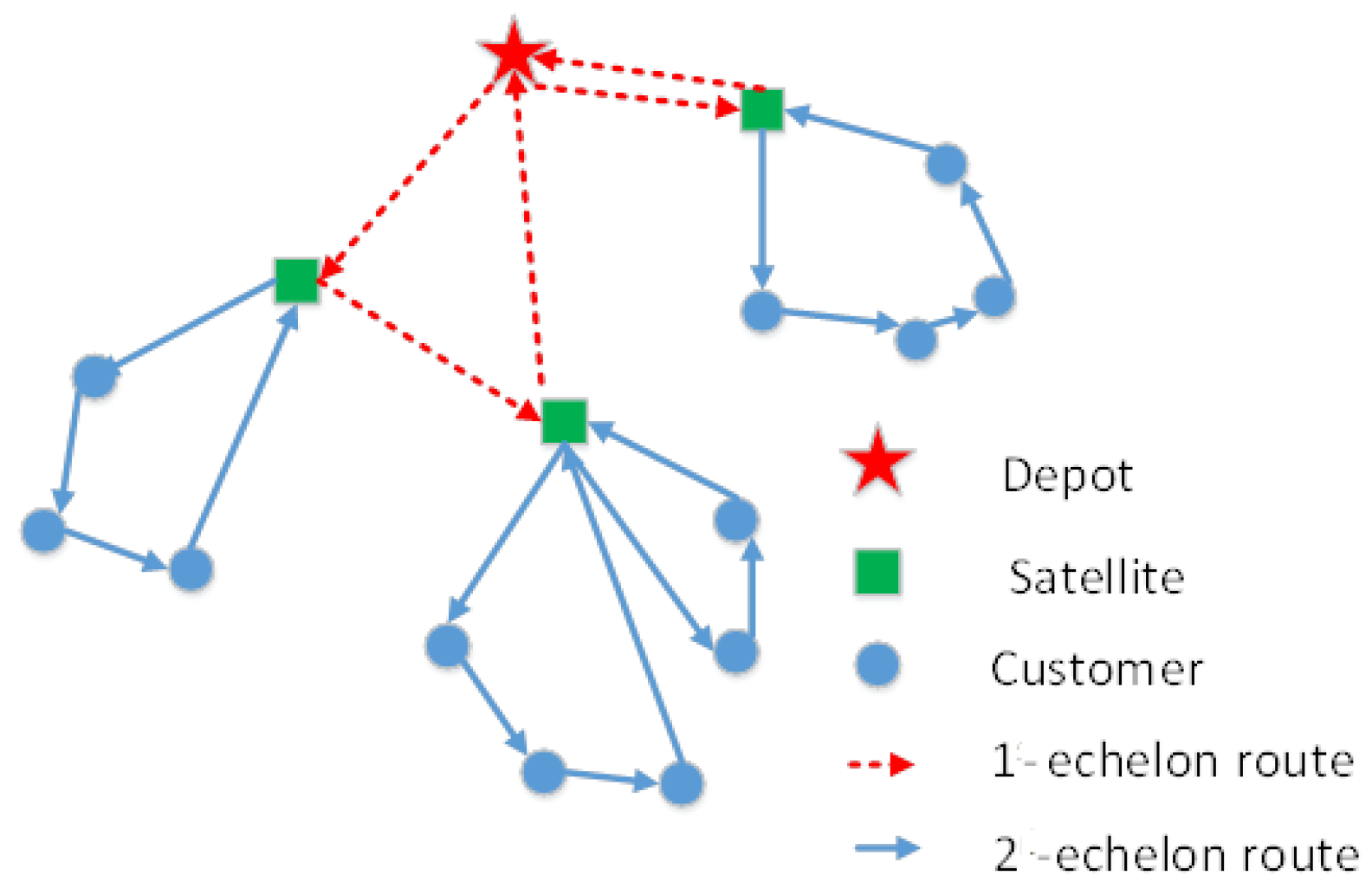
3. Problem Description
4. Mathematical Formulation
5. Solution Method
5.1. Construction of Initial Solutions
5.2. The Principle of Wild Horse Optimizer (WHO)
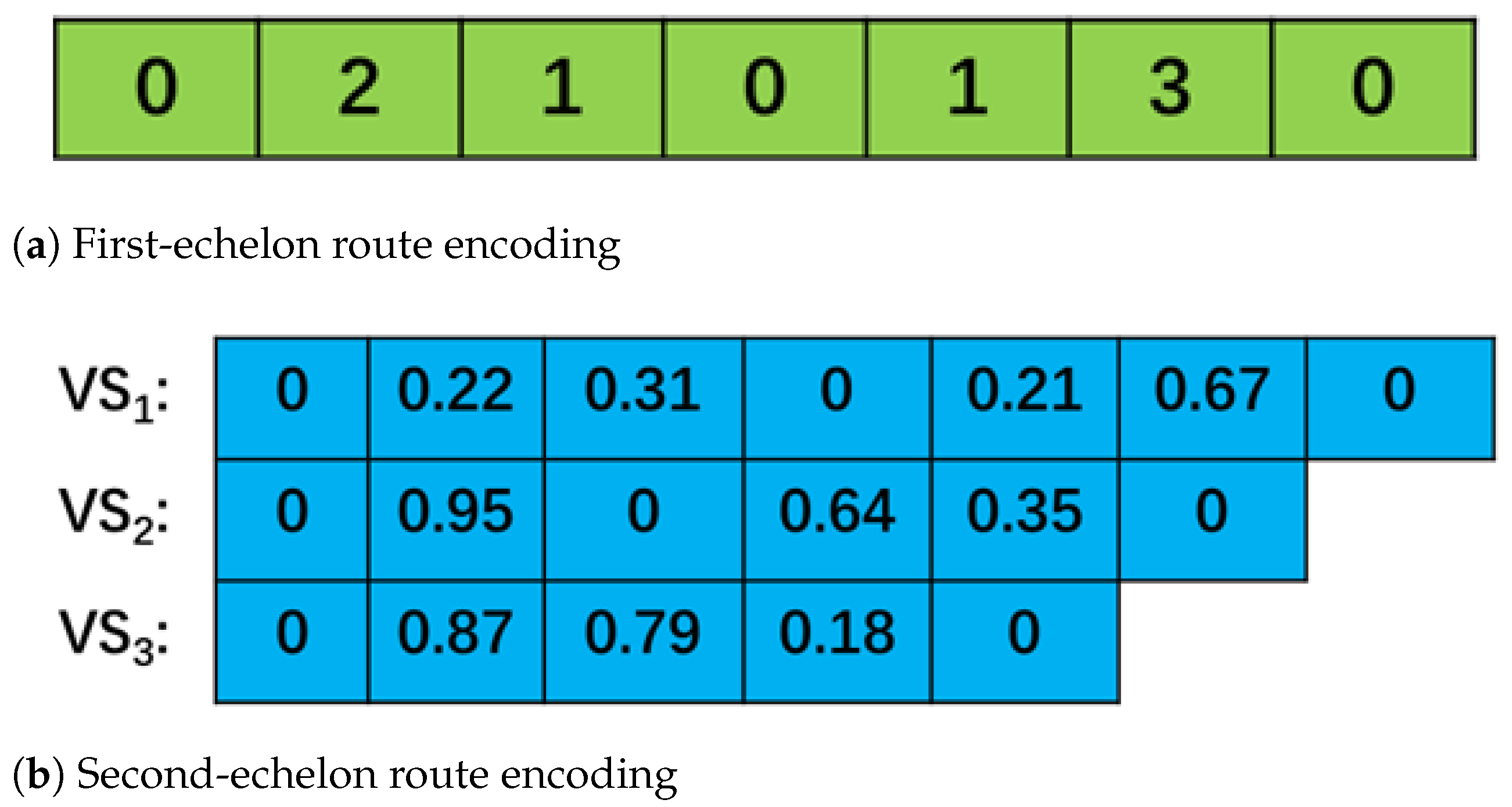
5.3. Solution Encoding and Decoding
5.4. Wild Horse State Updates
| Algorithm 1 Pseudo-code of WHO | |
| Require: Objective function | |
| Ensure: The best solution | |
| 1: | Initialize the wild horse population(), //Initialize the population. |
| 2: | =1 |
| 3: | Create groups and select leaders |
| 4: | Find the best horse as the solution // Find the global optimal value |
| 5: | while do |
| 6: | Calculate by Equation (32) // Calculate the population fitness |
| 7: | Calculate by Equation (29) |
| 8: | for do |
| 9: | Update the position of the stallion by Equation (31) |
| 10: | for do |
| 11: | Update the position of the foal by Equation (25) |
| 12: | end for |
| 13: | Select leaders // Find the optimal values for each group |
| 14: | Find the best leader // Find the global optimal value |
| 15: | end for |
| 16: | end while |
| 17: | Return global best solution |
5.5. Hybrid Artificial Bee Colony–Wild Horse Optimizer (HABC-WHO)
| Algorithm 2 Pseudo-code of HABC-WHO | |
| Require: Objective function | |
| Ensure: The best solution | |
| 1: | Initialize the wild horse population(), //Initialize the population |
| 2: | Iter=1 |
| 3: | Create groups and select leaders |
| 4: | Find the best horse as the solution // Find the global optimal value |
| 5: | while do |
| 6: | Calculate by Equation (32) // Calculate the population fitness |
| 7: | Calculate TDR by Equation (29) |
| 8: | for do |
| 9: | Update the position of stallions by Equation (31) |
| 10: | Large neighborhood operator //Apply large neighborhood operations for stallions |
| 11: | for do |
| 12: | Update the position of foals by Equation (25) |
| 13: | Large neighborhood operator //Apply large neighborhood operations for stallions |
| 14: | end for |
| 15: | Find the of each group |
| 16: | if then |
| 17: | Exchange , //The best foal in the group is exchanged with the stallion |
| 18: | end if |
| 19: | Find the best leader // Find the global optimal value |
| 20: | decoding |
| 21: | end for |
| 22: | Assign the wild horse population to the ABC population |
| 23: | Perform large neighborhood operation during the employed bee phase. |
| 24: | Update the bee colony information. |
| 25: | The best individual of ABC replaces the worst individual of WHO |
| 26: | 2-Opt operator |
| 27: | Satellite subpath crossover operator |
| 28: | if < then |
| 29: | Exchange , |
| 30: | end if |
| 31: | end while |
| 32: | Return global best solution |
5.6. Search Strategy
5.6.1. Large Neighborhood Search
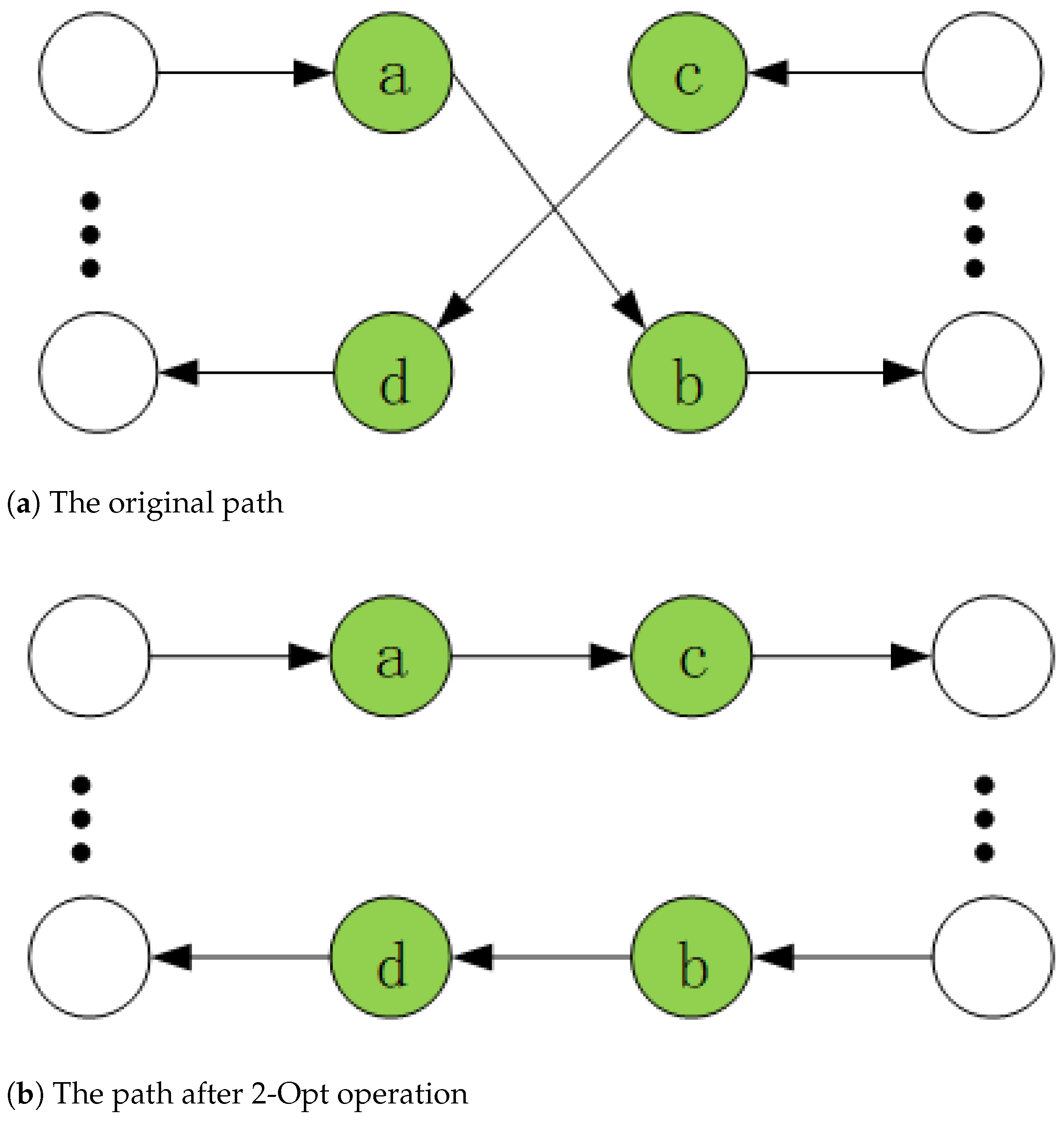
5.6.2. Two-Optimization (2-Opt) Operation
5.6.3. Satellite Subpath Crossover Strategy
6. Computational Tests
6.1. Parameter Settings for HABC-WHO
- Population size: popN = 50.
- Stallion ratio: PS = 0.2.
- Mating probability: PC = 0.13.
- Maximum number of iterations: MI = 300.
- Number of stallions: NS = popN × PS = 10.
- Number of foals: Nf = popN × (1 − PS) = 40.
- OS: Windows 10 (×64).
- CPU: Intel Core i5-11400 (2.60 GHz).
- RAM: 16 GB.
- Language: Matlab 2016B.
6.2. Experimental Verification
6.3. Time Complexity Analysis
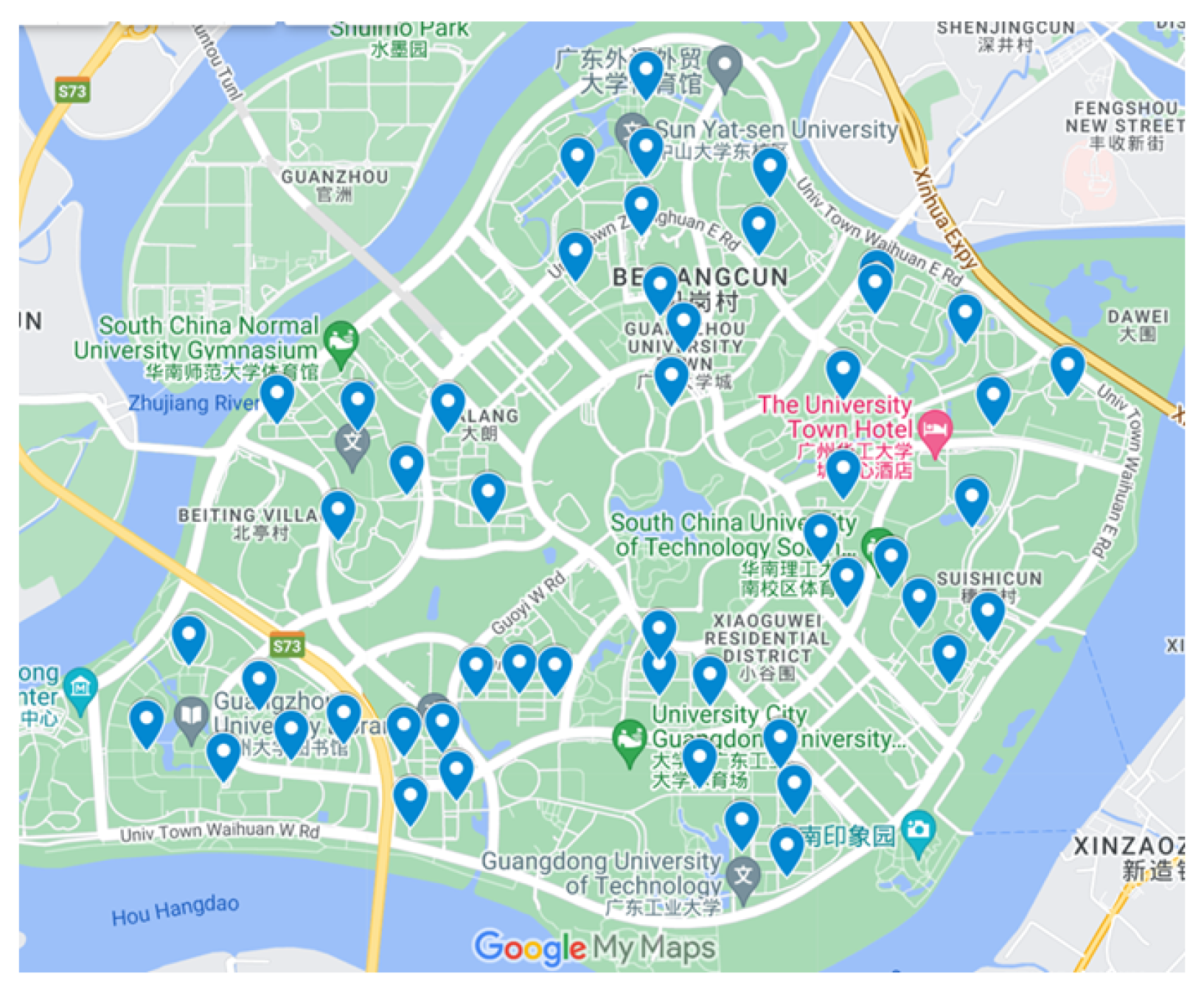
7. Application to Real-World Problem
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gevaers, R.; Van de Voorde, E.; Vanelslander, T. Characteristics of Innovations in Last-Mile Logistics—Using Best Practices, Case Studies and Making the Link with Green and Sustainable Logistics; Association for European Transport and Contributors: Antwerpen, Belgium, 2009; Volume 1, p. 21. [Google Scholar]
- Yu, S.; Puchinger, J.; Sun, S. Two-Echelon Urban Deliveries Using Autonomous Vehicles. Transport. Res. E Logist. Transp. Rev. 2020, 141, 102018. [Google Scholar] [CrossRef]
- China AGV Network. Review: These 9 Delivery Robots Are Replacing Couriers. Available online: https://www.chinaagv.com/news/detail/201705/2514.html (accessed on 23 March 2025).
- Laporte, G. Fifty Years of Vehicle Routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Jacobsen, S.K.; Madsen, O.B.G. A Comparative Study of Heuristics for a Two-Echelon Routing-Location Problem. Eur. J. Oper. Res. 1980, 5, 378–387. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild Horse Optimizer: A New Meta-Heuristic Algorithm for Solving Engineering Optimization Problems. Eng. Comput. 2021, 38, 3025–3056. [Google Scholar] [CrossRef]
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Advanced Freight Transportation Systems for Congested Urban Areas. Transp. Res. C Emerg. Technol. 2004, 12, 119–137. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J. Models and Methods for the City Logistics: The Two-Echelon Capacitated Vehicle Routing Problem. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2008. [Google Scholar]
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Models for Evaluating and Planning City Logistics Systems. Transp. Sci. 2009, 43, 432–454. [Google Scholar] [CrossRef]
- Sluijk, N.; Florio, A.M.; Kinable, J.; Dellaert, N.; Van Woensel, T. Two-Echelon Vehicle Routing Problems: A Literature Review. Eur. J. Oper. Res. 2023, 304, 865–886. [Google Scholar] [CrossRef]
- Perboli, G.; Tadei, R.; Vigo, D. The Two-Echelon Capacitated Vehicle Routing Problem: Models and Math-Based Heuristics. Transp. Sci. 2011, 45, 364–380. [Google Scholar] [CrossRef]
- Crainic, T.G.; Mancini, S.; Perboli, G.; Tadei, R. Multi-Start Heuristics for the Two-Echelon Vehicle Routing Problem. In Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2011; pp. 179–190. [Google Scholar]
- Bevilaqua, A.; Bevilaqua, D.; Yamanaka, K. Parallel Island Based Memetic Algorithm with Lin–Kernighan Local Search for a Real-Life Two-Echelon Heterogeneous Vehicle Routing Problem Based on Brazilian Wholesale Companies. Appl. Soft Comput. 2019, 76, 697–711. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The Flying Sidekick Traveling Salesman Problem: Optimization of Drone-Assisted Parcel Delivery. Transp. Res. C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Cheng, C.; Rousseau, L.M. An Exact Algorithm for the Two-Echelon Vehicle Routing Problem with Drones. Transp. Res. B Methodol. 2023, 168, 124–150. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Chen, J.; Bai, M. Two-Echelon Vehicle Routing Problem with Time Windows and Mobile Satellites. Transp. Res. B Methodol. 2020, 138, 179–201. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, P.; Thompson, R.G. A Stochastic Formulation of the Two-Echelon Vehicle Routing and Loading Bay Reservation Problem. Transp. Res. E Logist. Transp. Rev. 2023, 177, 103252. [Google Scholar] [CrossRef]
- Zhong, X.; Jiang, S.; Song, H. ABCGA Algorithm for the Two Echelon Vehicle Routing Problem. In 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC); IEEE: New York, NY, USA, 2017; Volume 1, pp. 301–308. [Google Scholar]
- Breunig, U.; Baldacci, R.; Hartl, R.F.; Vidal, T. The Electric Two-Echelon Vehicle Routing Problem. Comput. Oper. Res. 2019, 103, 198–210. [Google Scholar] [CrossRef]
- Jie, W.; Yang, J.; Zhang, M.; Huang, Y. The Two-Echelon Capacitated Electric Vehicle Routing Problem with Battery Swapping Stations: Formulation and Efficient Methodology. Eur. J. Oper. Res. 2019, 272, 879–904. [Google Scholar] [CrossRef]
- Agárdi, A.; Kovács, L.; Bányai, T. Two-Echelon Vehicle Routing Problem with Recharge Stations. Transp. Telecommun. J. 2019, 20, 305–317. [Google Scholar] [CrossRef]
- Crainic, T.G.; Errico, F.; Rei, W.; Ricciardi, N. Modeling Demand Uncertainty in Two-Tier City Logistics Tactical Planning. Transp. Sci. 2016, 50, 559–578. [Google Scholar] [CrossRef]
- Marques, G.; Sadykov, R.; Dupas, R.; Deschamps, J.C. A Branch-Cut-and-Price Approach for the Single-Trip and Multi-Trip Two-Echelon Vehicle Routing Problem with Time Windows. Transp. Sci. 2022, 56, 1598–1617. [Google Scholar] [CrossRef]
- Vincent, F.Y.; Jodiawan, P.; Schrotenboer, A.H.; Hou, M.L. The Two-Echelon Vehicle Routing Problem with Time Windows, Intermediate Facilities, and Occasional Drivers. Expert Syst. Appl. 2023, 234, 120945. [Google Scholar]
- Lehmann, J.; Winkenbach, M. A Matheuristic for the Two-Echelon Multi-Trip Vehicle Routing Problem with Mixed Pickup and Delivery Demand and Time Windows. Transp. Res. C Emerg. Technol. 2024, 160, 104522. [Google Scholar] [CrossRef]
- Dellaert, N.; Dashty Saridarq, F.; Van Woensel, T.; Crainic, T.G. Branch-and-Price–Based Algorithms for the Two-Echelon Vehicle Routing Problem with Time Windows. Transp. Sci. 2019, 53, 463–479. [Google Scholar] [CrossRef]
- Zamal, M.A.; Schrotenboer, A.H.; Van Woensel, T. The Two-Echelon Vehicle Routing Problem with Pickups, Deliveries, and Deadlines. Comput. Oper. Res. 2025, 179, 107016. [Google Scholar] [CrossRef]
- Mhamedi, T.; Andersson, H.; Cherkesly, M.; Desaulniers, G. A Branch-Price-and-Cut Algorithm for the Two-Echelon Vehicle Routing Problem with Time Windows. Transp. Sci. 2022, 56, 245–264. [Google Scholar] [CrossRef]
- Dellaert, N.; Van Woensel, T.; Crainic, T.G.; Saridarq, F.D. A Multi-Commodity Two-Echelon Capacitated Vehicle Routing Problem with Time Windows: Model Formulations and Solution Approach. Comput. Oper. Res. 2021, 127, 105154. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Zhang, Z.; Li, J. Two-Echelon Vehicle Routing Problem with Time Windows and Simultaneous Pickup and Delivery. Soft Comput. 2022, 26, 3345–3360. [Google Scholar] [CrossRef]
- Kim, B.; Jeong, H.Y.; Lee, S. Two-Echelon Collaborative Routing Problem with Heterogeneous Crowd-Shippers. Comput. Oper. Res. 2023, 160, 106389. [Google Scholar] [CrossRef]
- Al Theeb, N.; Abu-Aleqa, M.; Diabat, A. Multi-objective Optimization of Two-Echelon Vehicle Routing Problem: Vaccines Distribution as a Case Study. Comput. Ind. Eng. 2024, 187, 109590. [Google Scholar] [CrossRef]
- Grangier, P.; Gendreau, M.; Lehuédé, F.; Rousseau, L.M. An Adaptive Large Neighborhood Search for the Two-Echelon Multiple-Trip Vehicle Routing Problem with Satellite Synchronization. Eur. J. Oper. Res. 2016, 254, 80–91. [Google Scholar] [CrossRef]
- Marques, G.; Sadykov, R.; Deschamps, J.C.; Dupas, R. An Improved Branch-Cut-and-Price Algorithm for the Two-Echelon Capacitated Vehicle Routing Problem. Comput. Oper. Res. 2020, 114, 104833. [Google Scholar] [CrossRef]
- Anderluh, A.; Nolz, P.C.; Hemmelmayr, V.C.; Crainic, T.G. Multi-Objective Optimization of a Two-Echelon Vehicle Routing Problem with Vehicle Synchronization and ‘Grey Zone’ Customers Arising in Urban Logistics. Eur. J. Oper. Res. 2021, 289, 940–958. [Google Scholar] [CrossRef]
- Kergosien, Y.; Lenté, C.; Billaut, J.C.; Perrin, S. Metaheuristic Algorithms for Solving Two Interconnected Vehicle Routing Problems in a Hospital Complex. Comput. Oper. Res. 2013, 40, 2508–2518. [Google Scholar] [CrossRef]
- Bouman, P.; Agatz, N.; Schmidt, M. Dynamic Programming Approaches for the Traveling Salesman Problem with Drone. Networks 2018, 72, 528–542. [Google Scholar] [CrossRef]
- Carlsson, J.G.; Song, S. Coordinated Logistics with a Truck and a Drone. Manag. Sci. 2018, 64, 4052–4069. [Google Scholar] [CrossRef]
- Yu, K.; Budhiraja, A.K.; Buebel, S.; Tokekar, P. Algorithms and Experiments on Routing of Unmanned Aerial Vehicles with Mobile Recharging Stations. J. Field Robot. 2019, 36, 602–616. [Google Scholar] [CrossRef]
- Schermer, D.; Moeini, M.; Wendt, O. A Hybrid VNS/Tabu Search Algorithm for Solving the Vehicle Routing Problem with Drones and En Route Operations. Comput. Oper. Res. 2019, 109, 134–158. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Shao, P. Discrete Artificial Bee Colony Algorithm with Fixed Neighborhood Search for Traveling Salesman Problem. Eng. Appl. Artif. Intell. 2024, 131, 107816. [Google Scholar] [CrossRef]
- Karak, A.; Abdelghany, K. The Hybrid Vehicle-Drone Routing Problem for Pick-Up and Delivery Services. Transp. Res. Part C Emerg. Technol. 2019, 102, 427–449. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B.; Wasil, E.A. A Branch-and-Bound Approach to the Traveling Salesman Problem with a Drone. INFORMS J. Comput. 2019, 31, 335–346. [Google Scholar] [CrossRef]
- Guastaroba, G.; Speranza, M.G.; Vigo, D. Intermediate Facilities in Freight Transportation Planning: A Survey. Transp. Sci. 2016, 50, 763–789. [Google Scholar] [CrossRef]
- Cai, Y.; Fang, C.; Wu, Y.; Chen, H. A Discrete Wild Horse Optimizer for TSP. J. Comput. Eng. Appl. 2024, 60, 145–153. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Lin, S. Computer Solutions of the Traveling Salesman Problem. Bell Labs Tech. J. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Fang, C.; Cai, Y.; Wu, Y. A Discrete Wild Horse Optimizer for Capacitated Vehicle Routing Problem. Sci. Rep. 2024, 14, 21277. [Google Scholar] [CrossRef] [PubMed]



| Reference | Homogeneous Fleet | Objective | With Drone | Solution Approach | Year |
|---|---|---|---|---|---|
| Kergosien Y et al. [37] | Yes | Time | No | Genetic Algorithm, tabu search | 2013 |
| Murray C C & Chu A G [14] | Yes | Time | Yes | MILP, FSTSP | 2015 |
| Grangier P et al. [34] | Yes | Cost | No | Adaptive large neighborhood search | 2016 |
| X. Zhong et al. [19] | Yes | Cost | No | Artificial Bee Colony algorithm, Genetic Algorithm | 2017 |
| Carlsson J G, Song S [39] | Yes | Time | Yes | Horsefly algorithm | 2018 |
| Agatz N et al. [15] | Yes | Time | Yes | Integer program model, greedy partitioning heuristic | 2018 |
| Bouman P et al. [38] | yes | Cost | Yes | Dynamic programming | 2018 |
| Dellaert N et al. [27] | Yes | Cost | No | Branch-and-price algorithm | 2018 |
| Bouman P et al. [38] | Yes | Time | Yes | Dynamic programming approach, A* algorithm | 2018 |
| Yu K et al. [40] | Yes | Time | Yes | Generalized large neighborhood search solver, integer linear programming | 2019 |
| Schermer D et al. [41] | Yes | Time | Yes | VNS, tabu | 2019 |
| Breunig U et al. [20] | Yes | Cost | No | Large neighborhood search, exact mathematical programming algorithm | 2019 |
| Karak A.& Abdelghany, K [43] | Yes | Cost | Yes | Clarke and Wright algorithm | 2019 |
| Poikonen S et al. [44] | Yes | Time | Yes | Branch-and-bound | 2019 |
| Bevilaqua A et al. [13] | No | Cost | No | Lin–Kernighan heuristic | 2019 |
| Jie W et al. [21] | Yes | Cost | No | Combines a column generation and adaptive large neighborhood search | 2019 |
| Agárdi A et al. [22] | Yes | Cost | No | Hill climbing algorithm, Genetic Algorithm | 2019 |
| Marques G et al. [35] | Yes | Cost | No | Branch-cut-and-price | 2020 |
| Yu S et al. [2] | Yes | Cost | Yes | Mixed-integer program, hybrid metaheuristic | 2020 |
| Li H et al. [17] | Yes | Cost | Yes | Adaptive large neighborhood search heuristic | 2020 |
| Anderluh A et al. [36] | Yes | Cost | No | Large neighborhood search | 2021 |
| Mhamedi T et al. [29] | Yes | Cost | No | Branch-cut-and-price | 2021 |
| Dellaert N et al. [30] | Yes | Cost | No | Branch-and-price | 2021 |
| Zhou H et al. [31] | Yes | Cost | No | Variable neighborhood search, tabu search | 2022 |
| Marques G et al. [24] | Yes | Cost | No | Branch-cut-and-price | 2022 |
| Zhang L et al. [18] | No | Cost | No | Hybrid Genetic Algorithm | 2023 |
| Kim B et al. [32] | No | Cost | No | Adaptive large neighborhood search | 2023 |
| Zhou H et al. [16] | Yes | Time | Yes | Tabu search, exact branch-and-price algorithm | 2023 |
| Vincent F Y et al. [25] | Yes | Cost | No | Hybrid adaptive large neighborhood search | 2023 |
| Lehmann J & Winkenbach M [26] | Yes | Cost | No | Simulated annealing | 2024 |
| Instance | BKS | GA | DWHO | DABC-FNS | HABC-WHO | |
|---|---|---|---|---|---|---|
| Best | Best | Best | Best | Gap (%) | ||
| E-n22-k4-s06-17 | 417.07 | 424.81 | 424.81 | 417.07 | 417.07 | 0.00 |
| E-n22-k4-s08-14 | 384.96 | 386.25 | 386.25 | 384.96 | 384.96 | 0.00 |
| E-n22-k4-s09-19 | 470.60 | 476.13 | 476.13 | 476.13 | 470.72 | 0.03 |
| E-n22-k4-s10-14 | 371.50 | 375.82 | 375.82 | 373.24 | 371.39 | −0.03 |
| E-n22-k4-s11-12 | 427.22 | 456.88 | 453.66 | 427.22 | 427.22 | 0.00 |
| E-n22-k4-s12-16 | 392.78 | 425.49 | 423.55 | 392.78 | 392.78 | 0.00 |
| E-n33-k4-s01-09 | 730.16 | 774.91 | 774.41 | 774.41 | 730.16 | 0.00 |
| E-n33-k4-s02-13 | 714.63 | 848.45 | 745.27 | 736.33 | 714.64 | 0.00 |
| E-n33-k4-s03-17 | 707.41 | 875.27 | 810.61 | 731.01 | 707.32 | −0.01 |
| E-n33-k4-s04-05 | 778.73 | 850.19 | 778.76 | 758.44 | 757.91 | −2.67 |
| E-n33-k4-s07-25 | 756.84 | 778.88 | 775.66 | 746.40 | 748.76 | −1.07 |
| E-n33-k4-s14-22 | 779.05 | 844.06 | 833.12 | 824.42 | 824.42 | 5.82 |
| E-n51-k5-s02-04-17-46 | 530.76 | 594.71 | 668.87 | 571.58 | 570.31 | 7.45 |
| E-n51-k5-s02-17 | 597.49 | 650.52 | 634.17 | 597.49 | 602.72 | 0.88 |
| E-n51-k5-s06-12 | 554.80 | 607.4 | 590.89 | 567.88 | 567.18 | 2.23 |
| E-n51-k5-s11-19 | 581.64 | 693.74 | 626.01 | 612.66 | 606.30 | 4.24 |
| E-n51-k5-s27-47 | 538.22 | 612.35 | 600.82 | 564.15 | 563.92 | 4.77 |
| Instance | BKS | GA | DWHO | DABC-FNS | HABC-WHO | |
|---|---|---|---|---|---|---|
| Best | Best | Best | Best | Gap (%) | ||
| E-n22-k4-s13-14 | 526.15 | 541.36 | 541.36 | 526.15 | 526.15 | 0.00 |
| E-n22-k4-s13-16 | 521.09 | 546.23 | 546.23 | 521.77 | 518.69 | −0.46 |
| E-n22-k4-s13-17 | 496.38 | 496.38 | 496.38 | 496.38 | 496.38 | 0.00 |
| E-n22-k4-s14-19 | 498.80 | 541.45 | 506.99 | 498.80 | 498.59 | −0.04 |
| E-n22-k4-s17-19 | 512.80 | 607.42 | 577.74 | 514.53 | 514.08 | 0.25 |
| E-n22-k4-s19-21 | 520.42 | 550.67 | 527.48 | 520.42 | 520.42 | 0.00 |
| E-n33-k4-s16-22 | 634.26 | 817.25 | 788.60 | 671.55 | 666.78 | 5.13 |
| E-n33-k4-s16-24 | 666.02 | 826.11 | 781.40 | 668.81 | 666.35 | 0.05 |
| E-n33-k4-s19-26 | 680.36 | 699.35 | 691.73 | 680.46 | 680.49 | 0.02 |
| E-n33-k4-s22-26 | 680.37 | 767.73 | 761.86 | 676.63 | 680.89 | 0.08 |
| E-n33-k4-s24-28 | 670.43 | 762.31 | 756.02 | 670.86 | 670.86 | 0.06 |
| E-n33-k4-s25-28 | 650.58 | 771.73 | 712.44 | 664.55 | 651.40 | 0.13 |
| E-n51-k5-s12-18 | 690.59 | 828.23 | 698.85 | 694.23 | 692.51 | 0.28 |
| E-n51-k5-s12-41 | 683.05 | 883.95 | 715.01 | 695.58 | 693.85 | 1.58 |
| E-n51-k5-s12-43 | 710.41 | 926.04 | 757.58 | 747.49 | 745.88 | 4.99 |
| E-n51-k5-s39-41 | 728.54 | 789.74 | 752.16 | 759.53 | 746.71 | 2.49 |
| E-n51-k5-s40-41 | 723.75 | 852.68 | 729.94 | 729.94 | 730.19 | 0.89 |
| E-n51-k5-s40-43 | 752.15 | 820.71 | 779.74 | 772.75 | 757.45 | 0.70 |
| Instance | BKS | GA | DWHO | DABC-FNS | HABC-WHO | |
|---|---|---|---|---|---|---|
| Best | Best | Best | Best | Gap (%) | ||
| Instance50-s2-01 | 1590.00 | 1987.97 | 1776.11 | 1626.16 | 1590.04 | 0.00 |
| Instance50-s2-02 | 1442.00 | 1780.62 | 1497.63 | 1516.43 | 1470.23 | 1.96 |
| Instance50-s2-03 | 1603.00 | 1961.93 | 1772.37 | 1689.15 | 1602.97 | 0.00 |
| Instance50-s2-04 | 1440.77 | 1530.69 | 1484.05 | 1497.91 | 1441.78 | 0.07 |
| Instance50-s2-05 | 2188.15 | 2280.75 | 2212.14 | 2226.00 | 2200.27 | 0.55 |
| Instance50-s2-06 | 1310.80 | 1398.20 | 1313.32 | 1331.86 | 1311.12 | 0.02 |
| Instance50-s2-07 | 1486.00 | 1857.16 | 1668.14 | 1616.66 | 1486.09 | 0.01 |
| Instance50-s2-08 | 1369.78 | 1444.15 | 1371.50 | 1404.72 | 1369.78 | 0.00 |
| Instance | GA | DWHO | DABC-FNS | HABC-WHO |
|---|---|---|---|---|
| E-n22-k4-s06-17 | 4.389.41+ | 4.252.33+ | 4.171.17= | 4.171.17 |
| E-n22-k4-s08-14 | 4.041.43+ | 3.860.00+ | 3.850.00= | 3.850.00 |
| E-n22-k4-s09-19 | 5.001.70+ | 4.760.00+ | 4.761.30+ | 4.732.41 |
| E-n22-k4-s10-14 | 3.911.21+ | 3.761.17+ | 3.741.96+ | 3.711.17 |
| E-n22-k4-s11-12 | 4.656.74+ | 4.540.00+ | 4.271.07= | 4.275.83 |
| E-n22-k4-s12-16 | 4.386.49+ | 4.245.83+ | 3.934.76+ | 3.931.55 |
| E-n33-k4-s01-09 | 8.132.92+ | 7.740.00+ | 7.786.24+ | 7.341.62 |
| E-n33-k4-s02-13 | 9.082.50+ | 7.452.33+ | 7.557.56+ | 7.268.16 |
| E-n33-k4-s03-17 | 9.392.81+ | 8.111.46+ | 7.438.15+ | 7.167.77 |
| E-n33-k4-s04-05 | 9.373.66+ | 7.887.50+ | 7.624.97= | 7.602.25 |
| E-n33-k4-s07-25 | 8.352.33+ | 7.765.22+ | 7.513.32= | 7.512.98 |
| E-n33-k4-s14-22 | 9.932.57+ | 8.333.50+ | 8.284.17+ | 8.242.61 |
| E-n51-k5-s02-04-17-46 | 6.412.09+ | 6.693.50+ | 5.783.63= | 5.774.42 |
| E-n51-k5-s02-17 | 7.123.56+ | 6.355.26+ | 6.066.64- | 6.084.59 |
| E-n51-k5-s06-12 | 6.794.09+ | 5.932.34+ | 5.805.64= | 5.785.65 |
| E-n51-k5-s11-19 | 7.514.16+ | 6.271.28+ | 6.194.58+ | 6.133.46 |
| E-n51-k5-s27-47 | 6.533.48+ | 6.042.57+ | 5.847.98= | 5.826.67 |
| +/=/− | 17/0/0 | 17/0/0 | 10/6/1 |
| Instance | GA | DWHO | DABC-FNS | HABC-WHO |
|---|---|---|---|---|
| E-n22-k4-s13-14 | 5.642.06+ | 5.410.00+ | 5.261.17= | 5.261.17 |
| E-n22-k4-s13-16 | 5.544.27+ | 5.461.25+ | 5.244.31+ | 5.192.33 |
| E-n22-k4-s13-17 | 5.061.04+ | 4.965.83+ | 4.962.23+ | 4.911.17 |
| E-n22-k4-s14-19 | 5.753.28+ | 5.070.00+ | 5.023.74= | 5.012.25 |
| E-n22-k4-s17-19 | 6.271.93+ | 5.780.00+ | 5.183.15- | 5.183.96 |
| E-n22-k4-s19-21 | 5.832.74+ | 5.271.17+ | 5.299.14+ | 5.200.00 |
| E-n33-k4-s16-22 | 8.532.65+ | 7.908.75+ | 6.807.84+ | 6.671.09 |
| E-n33-k4-s16-24 | 8.471.92+ | 7.863.57+ | 6.747.60+ | 6.693.63 |
| E-n33-k4-s19-26 | 7.241.46+ | 6.922.33+ | 6.833.59= | 6.821.98 |
| E-n33-k4-s22-26 | 7.911.66+ | 7.622.33+ | 6.803.73+ | 6.787.53 |
| E-n33-k4-s24-28 | 7.771.05+ | 7.575.59+ | 6.797.56= | 6.753.02 |
| E-n33-k4-s25-28 | 8.192.51+ | 7.138.41+ | 6.704.55+ | 6.564.11 |
| E-n51-k5-s12-18 | 8.925.37+ | 7.013.24+ | 7.004.51+ | 6.982.91 |
| E-n51-k5-s12-41 | 9.193.00+ | 7.234.00+ | 7.014.95- | 7.025.28 |
| E-n51-k5-s12-43 | 1.014.44+ | 7.642.18+ | 7.565.47- | 7.575.74 |
| E-n51-k5-s39-41 | 9.887.88+ | 7.562.22+ | 7.678.00+ | 7.532.76 |
| E-n51-k5-s40-41 | 9.363.77+ | 7.426.70+ | 7.388.07+ | 7.314.55 |
| E-n51-k5-s40-43 | 8.813.47+ | 7.892.43+ | 7.849.01+ | 7.655.83 |
| +/=/− | 18/0/0 | 18/0/0 | 11/4/3 |
| Instance | GA | DWHO | DABC-FNS | HABC-WHO |
|---|---|---|---|---|
| Instance50-s2-01 | 2.09 × 103 ± 6.15 × 101+ | 1.78 × 103 ± 4.22 × 100+ | 1.64 × 103 ± 9.33 × 100+ | 1.59 × 103 ± 5.12 × 100 |
| Instance50-s2-02 | 1.91 × 103 ± 7.47 × 101+ | 1.50 × 103 ± 2.22 × 100+ | 1.52 × 103 ± 8.69 × 100+ | 1.48 × 103 ± 6.92 × 100 |
| Instance50-s2-03 | 2.08 × 103 ± 5.52 × 101+ | 1.77 × 103 ± 4.76 × 100+ | 1.70 × 103 ± 6.68 × 100+ | 1.61 × 103 ± 2.43 × 100 |
| Instance50-s2-04 | 1.64 × 103 ± 5.37 × 101+ | 1.49 × 103 ± 5.11 × 100+ | 1.50 × 103 ± 5.82 × 100+ | 1.45 × 103 ± 4.86 × 100 |
| Instance50-s2-05 | 2.41 × 103 ± 6.90 × 101+ | 2.22 × 103 ± 5.33 × 100= | 2.23 × 103 ± 7.04 × 100+ | 2.21 × 103 ± 6.32 × 100 |
| Instance50-s2-06 | 1.55 × 103 ± 7.92 × 101+ | 1.32 × 103 ± 9.77 × 100+ | 1.34 × 103 ± 8.63 × 100+ | 1.31 × 103 ± 3.89 × 100 |
| Instance50-s2-07 | 1.99 × 103 ± 7.04 × 101+ | 1.67 × 103 ± 4.05 × 100+ | 1.62 × 103 ± 8.06 × 100+ | 1.49 × 103 ± 3.48 × 100 |
| Instance50-s2-08 | 1.55 × 103 ± 5.46 × 101+ | 1.37 × 103 ± 1.27 × 100+ | 1.41 × 103 ± 8.97 × 100+ | 1.37 × 103 ± 1.27 × 100 |
| +/=/− | 8/0/0 | 7/1/0 | 8/0/0 |
| GA | DWHO | DABC-FNS | HABC-WHO |
|---|---|---|---|
| 62.36 | 52.89 | 52.89 | 51.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, C.; Cai, Y.; Wu, Y. The Two-Echelon Unmanned Ground Vehicle Routing Problem: Extreme-Weather Goods Distribution as a Case Study. Biomimetics 2025, 10, 255. https://doi.org/10.3390/biomimetics10050255
Fang C, Cai Y, Wu Y. The Two-Echelon Unmanned Ground Vehicle Routing Problem: Extreme-Weather Goods Distribution as a Case Study. Biomimetics. 2025; 10(5):255. https://doi.org/10.3390/biomimetics10050255
Chicago/Turabian StyleFang, Chuncheng, Yanguang Cai, and Yanlin Wu. 2025. "The Two-Echelon Unmanned Ground Vehicle Routing Problem: Extreme-Weather Goods Distribution as a Case Study" Biomimetics 10, no. 5: 255. https://doi.org/10.3390/biomimetics10050255
APA StyleFang, C., Cai, Y., & Wu, Y. (2025). The Two-Echelon Unmanned Ground Vehicle Routing Problem: Extreme-Weather Goods Distribution as a Case Study. Biomimetics, 10(5), 255. https://doi.org/10.3390/biomimetics10050255






