A Parameter Reduction-Based Decision-Making Method with Interval-Valued Neutrosophic Soft Sets for the Selection of Bionic Thin-Wall Structures
Abstract
:1. Introduction
2. Preliminary
3. Methods Section
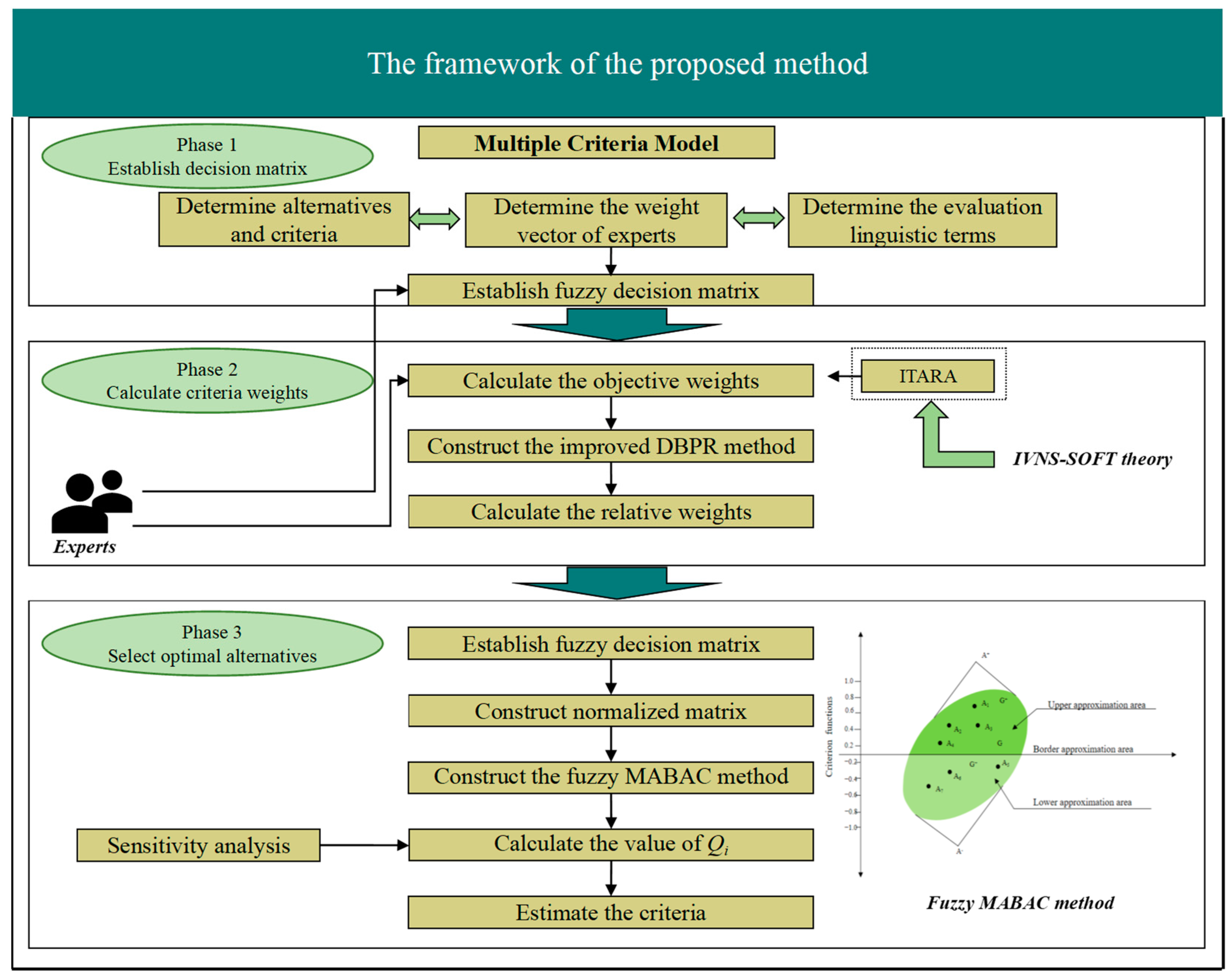
3.1. The Framework of the Proposed Solution Methodology
3.2. A Parameter Reduction Algorithm of Interval-Value Neutrosophic Soft Sets
| Algorithm 1: Distance-based parameter reduction algorithm of interval-value neutrosophic soft sets |
| Input: (F, E) (interval-valued neutrosophic soft set), E (parameter set), and threshold λ Output: (E − A) (an optimal choice considered parameter reduction in IVNS-SOFT). BEGIN 1. , for 1 ≤ i ≤ n,1 ≤ j ≤ m. 2. Let j = 1. 3. , perform the following. 4. Calculate distances for all pairs of j parameters. j = 1, 2, …, m. 5. Obtain the distance matrix D = (dkl)m×m, for 1 ≤ k ≤ m,1 ≤ l ≤ m. 6. If the distance between parameters k and l is less than the threshold λ, then perform the following. 7. Consider parameters k and l to be similar, keep one parameter and place another set A of the reduction parameters. 8. Obtain the new interval-valued neutrosophic soft set ) after parameter reduction. 9. Return ). END |
3.3. The ITARA Method with Interval-Value Neutrosophic Soft Sets
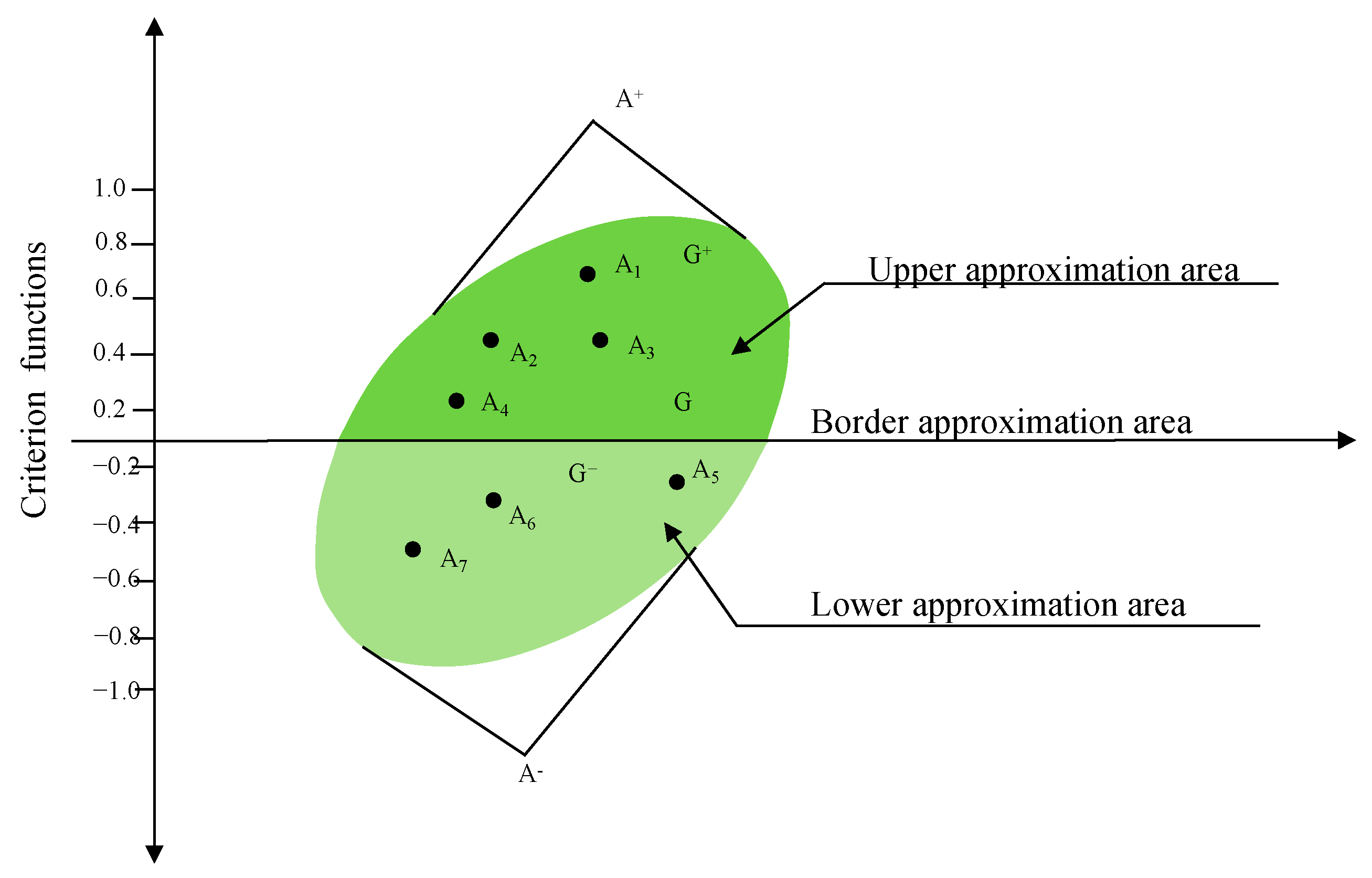
3.4. The MABAC Method with Interval-Value Neutrosophic Soft Sets
4. Results and Discussion
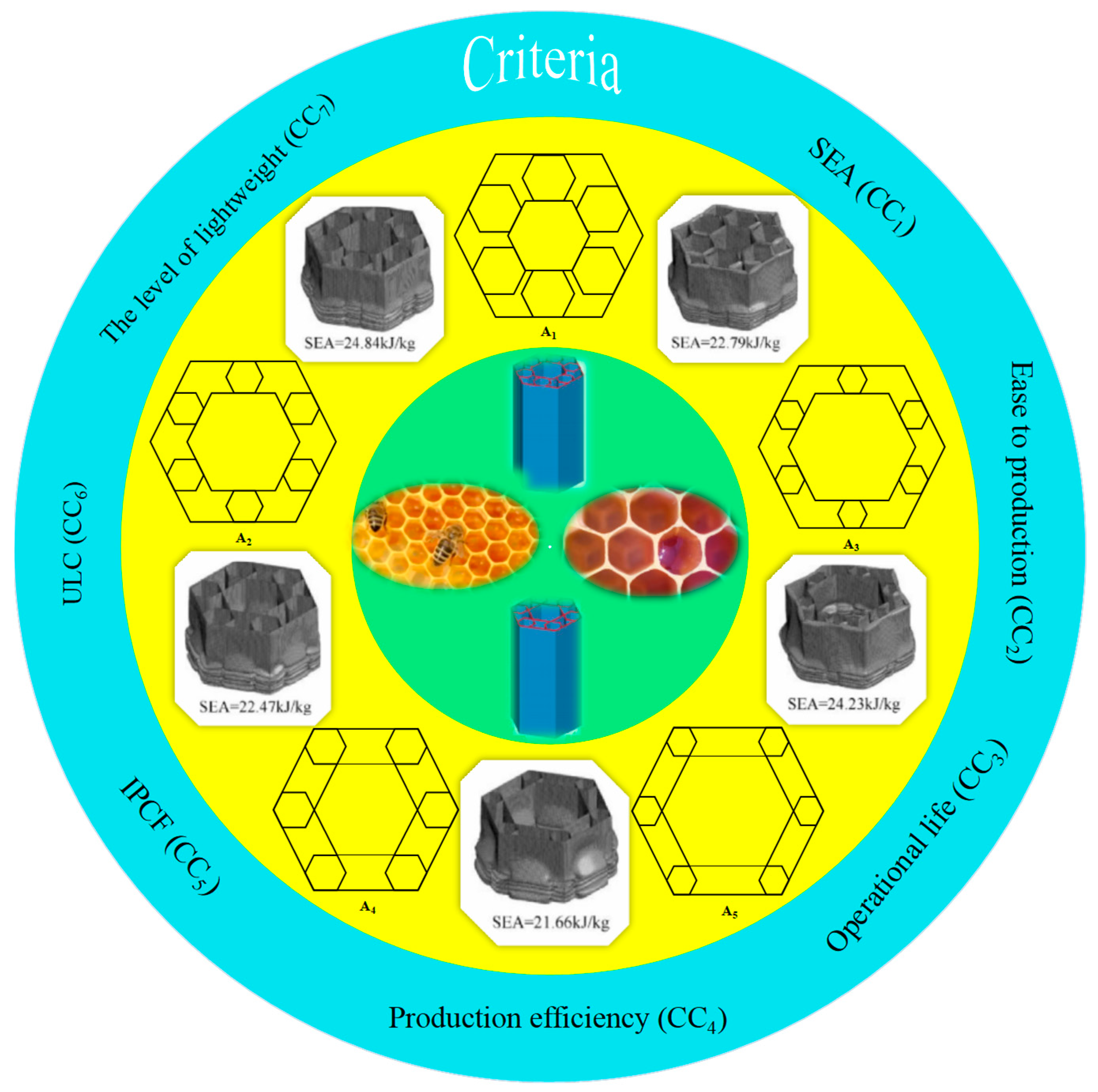
4.1. Background
4.2. Evaluation and Decision
4.3. Comparative Studies with Other Traditional Methods
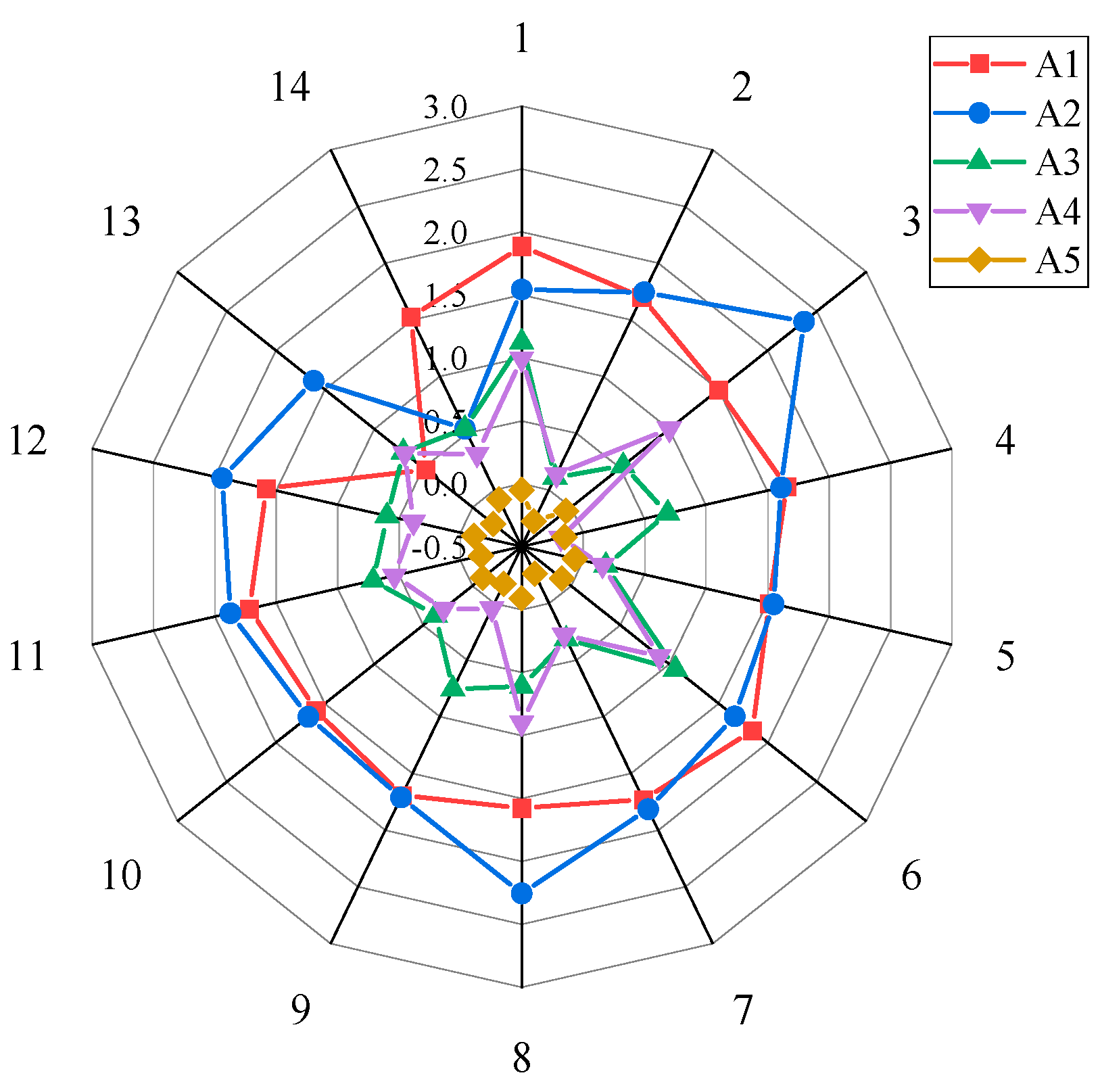
4.4. Sensitivity Analysis
5. Conclusions
- (1)
- Different design philosophies of bionic thin-wall structures lead to different performance and application scenarios.
- (2)
- Indicators of SEA, ease of production, IPCF, ULC, and lightweight levels greatly affect the process of bionic thin-wall structure selection, with weights of 0.2596, 0.0960, 0.2929, 0.3336 and 0.0179, respectively.
- (3)
- By comparing this with the four existing methods, it was found that the proposed method is reasonable and feasible to select optimal bionic thin-wall structures.
- (4)
- Through sensitivity analysis, the results found that out of 14 experiments, alternative A2 had the highest score in 10 experiments. Hence, the final result is reliable. In addition, the rank of each alternative is relatively sensitive to the criteria weights.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Meyers, M.A.; McKittrick, J.; Chen, P.-Y. Structural Biological Materials: Critical Mechanics-Materials Connections. Science 2013, 339, 773–779. [Google Scholar] [CrossRef]
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional Gradients and Heterogeneities in Biological Materials: Design Principles, Functions, and Bioinspired Applications. Prog. Mater. Sci. 2017, 88, 467–498. [Google Scholar] [CrossRef]
- Jiang, B.; Tan, W.; Bu, X.; Zhang, L.; Zhou, C.; Chou, C.C.; Bai, Z. Numerical, theoretical, and experimental studies on the energy absorption of the thin-walled structures with bio-inspired constituent element. Int. J. Mech. Sci. 2019, 164, 105173. [Google Scholar] [CrossRef]
- Abo Sabah, S.H.; Kueh, A.B.H.; Al-Fasih, M.Y. Comparative Low-Velocity Impact Behavior of Bio-Inspired and Conventional Sandwich Composite Beams. Compos. Sci. Technol. 2017, 149, 64–74. [Google Scholar] [CrossRef]
- Zou, M.; Xu, S.; Wei, C.; Wang, H.; Liu, Z. A Bionic Method for the Crashworthiness Design of Thin-Walled Structures Inspired by Bamboo. Thin-Walled Struct. 2016, 101, 222–230. [Google Scholar] [CrossRef]
- Nikkhah, H.; Crupi, V.; Baroutaji, A. Crashworthiness Analysis of Bio-Inspired Thin-Walled Tubes Based on Morpho Wings Microstructures. Mech. Based Des. Struct. Mach. 2022, 50, 3683–3700. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Zhao, J.; Ruan, D. The Axial Crushing Performance of Bio-Inspired Hierarchical Multi-Cell Hexagonal Tubes. Int. J. Mech. Sci. 2023, 239, 107880. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Wang, J.; Chen, T.; Wang, C.H. Crushing Analysis for Novel Bio-Inspired Hierarchical Circular Structures Subjected to Axial Load. Int. J. Mech. Sci. 2018, 140, 407–431. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Shi, C.; Zhou, W. Mechanical Performance of Vertex-Based Hierarchical vs Square Thin-Walled Multi-Cell Structure. Thin-Walled Struct. 2019, 134, 102–110. [Google Scholar] [CrossRef]
- Li, W.; Zhang, B.; Fan, H. Crushing Behaviors of Fractal Hexagonal Tubular Structures: Experiments and Plastic Analysis. Acta Mech. Solida Sin. 2019, 32, 713–724. [Google Scholar] [CrossRef]
- Xu, S.; Li, W.; Li, L.; Li, T.; Ma, C. Crashworthiness design and multi-objective optimization for bio-inspired hierarchical thin-walled structures. Comput. Model. Eng. Sci. 2022, 131, 929–947. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Ebrahimi, H.; Haghpanah, B.; Ghosh, R.; Ajdari, A.; Hamouda, A.M.S.; Vaziri, A. Spiderweb Honeycombs. Int. J. Solids Struct. 2015, 66, 218–227. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G. A Review of Recent Research on Bio-Inspired Structures and Materials for Energy Absorption Applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Vinayagar, K.; Ganeshan, P.; Raja, P.N.; Hussain, M.S.Z.; Kumar, P.V.; Ramshankar, P.; Mohanavel, V.; Mathankumar, N.; Raja, K.; Bezabih, T.T. Optimization of Crashworthiness Parameters of Thin-Walled Conoidal Structures. Adv. Mater. Sci. Eng. 2022, 2022, 4475605. [Google Scholar] [CrossRef]
- Fang, J.; Gao, Y.; Sun, G.; Qiu, N.; Li, Q. On Design of Multi-Cell Tubes under Axial and Oblique Impact Loads. Thin-Walled Struct. 2015, 95, 115–126. [Google Scholar] [CrossRef]
- Qiu, N.; Gao, Y.; Fang, J.; Feng, Z.; Sun, G.; Li, Q. Crashworthiness Analysis and Design of Multi-Cell Hexagonal Columns under Multiple Loading Cases. Finite Elem. Anal. Des. 2015, 104, 89–101. [Google Scholar] [CrossRef]
- Nikkhah, H.; Guo, F.; Chew, Y.; Bai, J.; Song, J.; Wang, P. The Effect of Different Shapes of Holes on the Crushing Characteristics of Aluminum Square Windowed Tubes under Dynamic Axial Loading. Thin-Walled Struct. 2017, 119, 412–420. [Google Scholar] [CrossRef]
- Pirmohammad, S.; Esmaeili Marzdashti, S. Crashworthiness Optimization of Combined Straight-Tapered Tubes Using Genetic Algorithm and Neural Networks. Thin-Walled Struct. 2018, 127, 318–332. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, D.; Wang, D.; Li, T.; Peng, Y.; Hou, L.; Li, Z. Crashworthiness of Nested Corrugation Square Energy-Absorbing Tubes with Circumferentially Cosine Profile. Mech. Adv. Mater. Struct. 2023, 1–18. [Google Scholar] [CrossRef]
- Hatefi, M.A. Indifference Threshold-Based Attribute Ratio Analysis: A Method for Assigning the Weights to the Attributes in Multiple Attribute Decision Making. Appl. Soft Comput. 2019, 74, 643–651. [Google Scholar] [CrossRef]
- Alper Sofuoğlu, M. Development of an ITARA-Based Hybrid Multi-Criteria Decision-Making Model for Material Selection. Soft Comput. 2019, 23, 6715–6725. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The Selection of Transport and Handling Resources in Logistics Centers Using Multi-Attributive Border Approximation Area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Algorithms for Interval Neutrosophic Multiple Attribute Decision-Making Based on MABAC, Similarity Measure, and EDAs. Int. J. Uncertain. Quantif. 2017, 7, 395–421. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chandel, A.; Motwani, D. Extended MABAC Method Based on Divergence Measures for Multi-Criteria Assessment of Programming Language with Interval-Valued Intuitionistic Fuzzy Sets. Granul. Comput. 2020, 5, 97–117. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Gorzałczany, M.B. A Method of Inference in Approximate Reasoning Based on Interval-Valued Fuzzy Sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, H.; Wang, D.; Yu, H.; Wang, L.; Yu, D.; Peng, Y. Preference-Based Multi-Attribute Decision-Making Method with Spherical-Z Fuzzy Sets for Green Product Design. Eng. Appl. Artif. Intell. 2023, 126, 106767. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Z.; Tian, G.; Wang, W.; Li, Z. A Hybrid QFD-Based Human-Centric Decision Making Approach of Disassembly Schemes Under Interval 2-Tuple q-Rung Orthopair Fuzzy Sets. In IEEE Transactions on Automation Science and Engineering; IEEE: New York, NY, USA, 2023; pp. 1–12. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft Set Theory—First Results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Maji, P.K. Neutrosophic Soft Set. AFMI 2013, 45, 555–562. [Google Scholar]
- Karaaslan, F.; Çağman, N. Parameter Trees Based on Soft Set Theory and Their Similarity Measures. Soft Comput. 2022, 26, 4629–4639. [Google Scholar] [CrossRef]
- Şahin, R.; Küçük, A. On Similarity and Entropy of Neutrosophic Soft Sets. J. Intell. Fuzzy Syst. 2014, 27, 2417–2430. [Google Scholar] [CrossRef]
- Deli, I. Interval-Valued Neutrosophic Soft Sets and Its Decision Making. Int. J. Mach. Learn. Cybern. 2017, 8, 665–676. [Google Scholar] [CrossRef]
- Bolturk, E.; Kahraman, C. A Novel Interval-Valued Neutrosophic AHP with Cosine Similarity Measure. Soft Comput. 2018, 22, 4941–4958. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Chen, X. Interval Neutrosophic Sets and Their Application in Multicriteria Decision Making Problems. Sci. World J. 2014, 2014, 645953. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Compromise Solution by MCDM Methods: A Comparative Analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Ye, J. Similarity Measures between Interval Neutrosophic Sets and Their Applications in Multicriteria Decision-Making. J. Intell. Fuzzy Syst. 2014, 26, 165–172. [Google Scholar] [CrossRef]
- Kong, Z.; Gao, L.; Wang, L.; Li, S. The Normal Parameter Reduction of Soft Sets and Its Algorithm. Comput. Math. Appl. 2008, 56, 3029–3037. [Google Scholar] [CrossRef]
- Khameneh, A.Z.; Kılıçman, A. Parameter Reduction of Fuzzy Soft Sets: An Adjustable Approach Based on the Three-Way Decision. Int. J. Fuzzy Syst. 2018, 20, 928–942. [Google Scholar] [CrossRef]
- Han, B.; Li, Y.; Geng, S. 0–1 Linear Programming Methods for Optimal Normal and Pseudo Parameter Reductions of Soft Sets. Appl. Soft Comput. 2017, 54, 467–484. [Google Scholar] [CrossRef]
- Ma, X.; Qin, H. A Distance-Based Parameter Reduction Algorithm of Fuzzy Soft Sets. IEEE Access 2018, 6, 10530–10539. [Google Scholar] [CrossRef]
- Barron, F.H.; Barrett, B.E. Decision Quality Using Ranked Attribute Weights. Manag. Sci. 1996, 42, 1515–1523. [Google Scholar] [CrossRef]
- Feng, Z.J.; Xie, S.C.; Ma, W.; Jing, K.K.; Wang, H. Multi-tube energy-absorbing structures with different matching patterns of heights and diaphragm spacings. Alex. Eng. J. 2022, 61, 11111–11127. [Google Scholar] [CrossRef]
- Liu, B.; Xu, X. Experimental and numerical study on crashworthiness of bionic hedgehog spine thin-walled structures. Thin-Walled Struct. 2023, 189, 110892. [Google Scholar] [CrossRef]
- Xie, S.; Wang, H.; Yang, C.; Zhou, H.; Feng, Z. Mechanical Properties of Combined Structures of Stacked Multilayer Nomex® Honeycombs. Thin-Walled Struct. 2020, 151, 106729. [Google Scholar] [CrossRef]
- Sun, G.; Pang, T.; Fang, J.; Li, G.; Li, Q. Parameterization of Criss-Cross Configurations for Multiobjective Crashworthiness Optimization. Int. J. Mech. Sci. 2017, 124–125, 145–157. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Z.; Sun, G.; Xu, F.; Huang, X. Crushing Analysis and Multiobjective Optimization for Functionally Graded Foam-Filled Tubes under Multiple Load Cases. Int. J. Mech. Sci. 2014, 89, 439–452. [Google Scholar] [CrossRef]
- Sun, G.; Li, G.; Hou, S.; Zhou, S.; Li, W.; Li, Q. Crashworthiness Design for Functionally Graded Foam-Filled Thin-Walled Structures. Mater. Sci. Eng. A 2010, 527, 1911–1919. [Google Scholar] [CrossRef]
- Pouresmaeil, H.; Shivanian, E.; Khorram, E.; Fathabadi, H.S. An Extended Method Using TOPSIS and VIKOR for Multiple Attribute Decision Making with Multiple Decision Makers and Single Valued Neutrosophic Numbers. Adv. Appl. Stat. 2017, 50, 261–292. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Wei, G.-W.; Wei, C. VIKOR Method for Interval Neutrosophic Multiple Attribute Group Decision-Making. Information 2017, 8, 144. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Approaches to Single-Valued Neutrosophic MADM Based on MABAC, TOPSIS and New Similarity Measure with Score Function. Neural Comput. Appl. 2018, 29, 939–954. [Google Scholar] [CrossRef]


| Linguistic Variable | Interval-Valued Neutrosophic Soft Number |
|---|---|
| Unimportant (UI) | <[0.1, 0.2], [0.4, 0.5], [0.6, 0.7]> |
| Ordinary level of importance (OI) | <[0.2, 0.4], [0.5, 0.6], [0.4, 0.5]> |
| Important (IM) | <[0.4, 0.6], [0.4, 0.5], [0.3, 0.4]> |
| Very important (VI) | <[0.6, 0.8], [0.3, 0.4], [0.2, 0.3]> |
| Absolutely important (AI) | <[0.7, 0.9], [0.2, 0.3], [0.1, 0.2]> |
| CC1 | CC2 | CC5 | CC6 | CC7 | |
|---|---|---|---|---|---|
| Weight | 0.2596 | 0.0960 | 0.2929 | 0.3336 | 0.0179 |
| Alt. | CC1 | CC2 | CC5 | CC6 | CC7 |
|---|---|---|---|---|---|
| A1 | 0.1523 | 0.0599 | 1.4142 | 0.1021 | 0.0006 |
| A2 | 1.4142 | 0.0599 | 0.4472 | 0.0378 | 0.0003 |
| A3 | 0.4931 | −0.0275 | 0.1407 | 0.3904 | −0.0005 |
| A4 | 0.4227 | −0.0050 | 0.4722 | −0.2096 | −0.0003 |
| A5 | 0.0000 | −0.0576 | 0.0000 | −0.0761 | −0.0005 |
| Methods | Results |
|---|---|
| SVNS-VIKOR | A1 > A2 > A4 > A3 > A5 |
| IVNS-VIKOR | A1 > A2 > A3 > A4 > A5 |
| SVNS-MABAC | A2 > A1 > A3 > A4 > A5 |
| Similarity measures between IVNSs | A2 > A1 > A3 > A4 > A5 |
| The proposed method | A2 > A1 > A3 > A4 > A5 |
| No. | Weights | Qi Value | Rank | ||||
|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | |||
| 1 | ωCC1 = 0.800, ωCC2, CC5–7 = 0.050 | 1.8864 | 1.5430 | 1.1276 | 0.9949 | −0.0479 | A1 > A2 > A3 > A4 > A5 |
| 2 | ωCC2 = 0.800,ωCC1, CC5–7 = 0.050 | 1.6988 | 1.7435 | 0.1108 | 0.1395 | −0.2756 | A2 > A1 > A4 > A3 > A5 |
| 3 | ωCC5 = 0.800, ωCC1–2, CC6–7 = 0.050 | 1.4983 | 2.3677 | 0.5298 | 1.0011 | −0.0479 | A2 > A1 > A4 > A3 > A5 |
| 4 | ωCC6 = 0.800, ωCC1–2, CC5, CC7 = 0.050 | 1.6570 | 1.6122 | 0.6896 | −0.1818 | −0.1517 | A1 > A2 > A3 > A5 > A4 |
| 5 | ωCC7 = 0.800, ωCC1–2, CC5–6 = 0.050 | 1.5173 | 1.5521 | 0.1853 | 0.1567 | −0.0654 | A2 > A1 > A3 > A4 > A5 |
| 6 | ωCC1 = 0.600, ωCC2, CC5–7 = 0.100 | 1.8433 | 1.6623 | 1.0620 | 0.8970 | −0.0914 | A1 > A2 > A3 > A4 > A5 |
| 7 | ωCC2 = 0.600,ωCC1, CC5–7 = 0.100 | 1.7298 | 1.8155 | 0.3173 | 0.2791 | −0.2617 | A2 > A1 > A3 > A4 > A5 |
| 8 | ωCC5 = 0.600, ωCC1–2, CC6–7 = 0.100 | 1.5766 | 2.2553 | 0.6117 | 0.9020 | −0.0914 | A2 > A1 > A4 > A3 > A5 |
| 9 | ωCC6 = 0.600, ωCC1–2, CC5, CC7 = 0.100 | 1.6927 | 1.7112 | 0.7573 | 0.0459 | −0.1694 | A2 > A1 > A3 > A4 > A5 |
| 10 | ωCC7 = 0.600, ωCC1–2, CC5–6 = 0.100 | 1.5899 | 1.6686 | 0.3759 | 0.2924 | −0.1036 | A2 > A1 > A3 > A4 > A5 |
| 11 | ωCC1–2, CC5–7 = 0.200 | 1.7177 | 1.8752 | 0.7124 | 0.5373 | −0.1668 | A2 > A1 > A3 > A4 > A5 |
| 12 | ωCC1–2 = 0.050, ωCC5–7 = 0.300 | 1.5810 | 1.9419 | 0.5976 | 0.3835 | −0.1103 | A2 > A1 > A3 > A4 > A5 |
| 13 | ωCC1–2 = 0.500, ωCC5–7 = 0.000 | 0.4782 | 1.6137 | 0.7027 | 0.6882 | −0.2090 | A2 > A3 > A4 > A1 > A5 |
| 14 | ωCC1–2 = 0.000, ωCC5–7 = 0.333 | 1.5262 | 0.5387 | 0.5397 | 0.3186 | −0.0852 | A1 > A3 > A2 > A4 > A5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, L.; Wang, D.; Huang, Z.; Yu, D.; Peng, Y. A Parameter Reduction-Based Decision-Making Method with Interval-Valued Neutrosophic Soft Sets for the Selection of Bionic Thin-Wall Structures. Biomimetics 2024, 9, 208. https://doi.org/10.3390/biomimetics9040208
Zhang H, Wang L, Wang D, Huang Z, Yu D, Peng Y. A Parameter Reduction-Based Decision-Making Method with Interval-Valued Neutrosophic Soft Sets for the Selection of Bionic Thin-Wall Structures. Biomimetics. 2024; 9(4):208. https://doi.org/10.3390/biomimetics9040208
Chicago/Turabian StyleZhang, Honghao, Lingyu Wang, Danqi Wang, Zhongwei Huang, Dongtao Yu, and Yong Peng. 2024. "A Parameter Reduction-Based Decision-Making Method with Interval-Valued Neutrosophic Soft Sets for the Selection of Bionic Thin-Wall Structures" Biomimetics 9, no. 4: 208. https://doi.org/10.3390/biomimetics9040208
APA StyleZhang, H., Wang, L., Wang, D., Huang, Z., Yu, D., & Peng, Y. (2024). A Parameter Reduction-Based Decision-Making Method with Interval-Valued Neutrosophic Soft Sets for the Selection of Bionic Thin-Wall Structures. Biomimetics, 9(4), 208. https://doi.org/10.3390/biomimetics9040208








