Postural Change of the Annual Cicada (Tibicen linnei) Helps Facilitate Backward Flight
Abstract
:1. Introduction
2. Materials and Methods
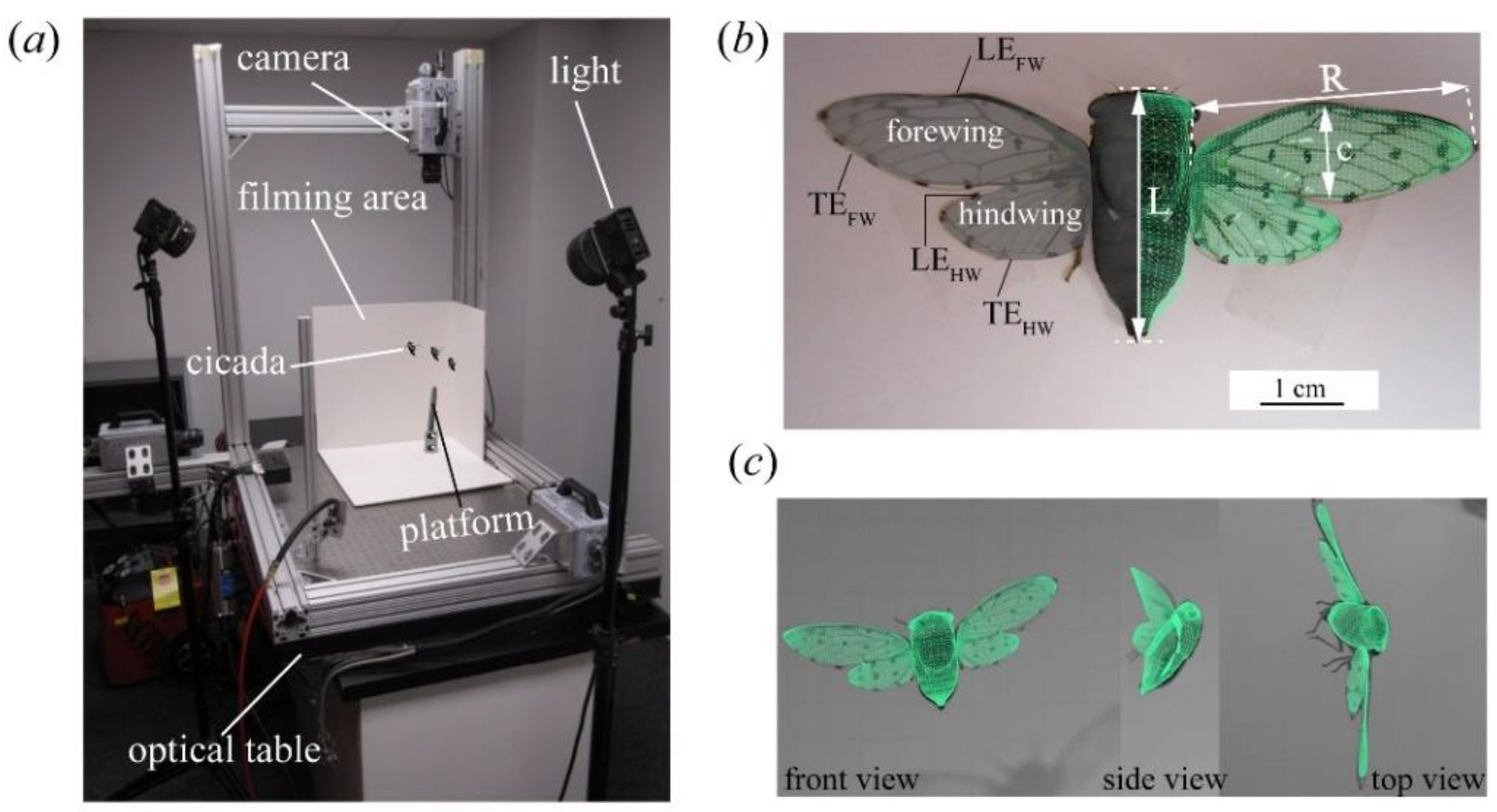
2.1. Insects, Data Acquisition, and Three-Dimensional (3D) Surface Reconstruction
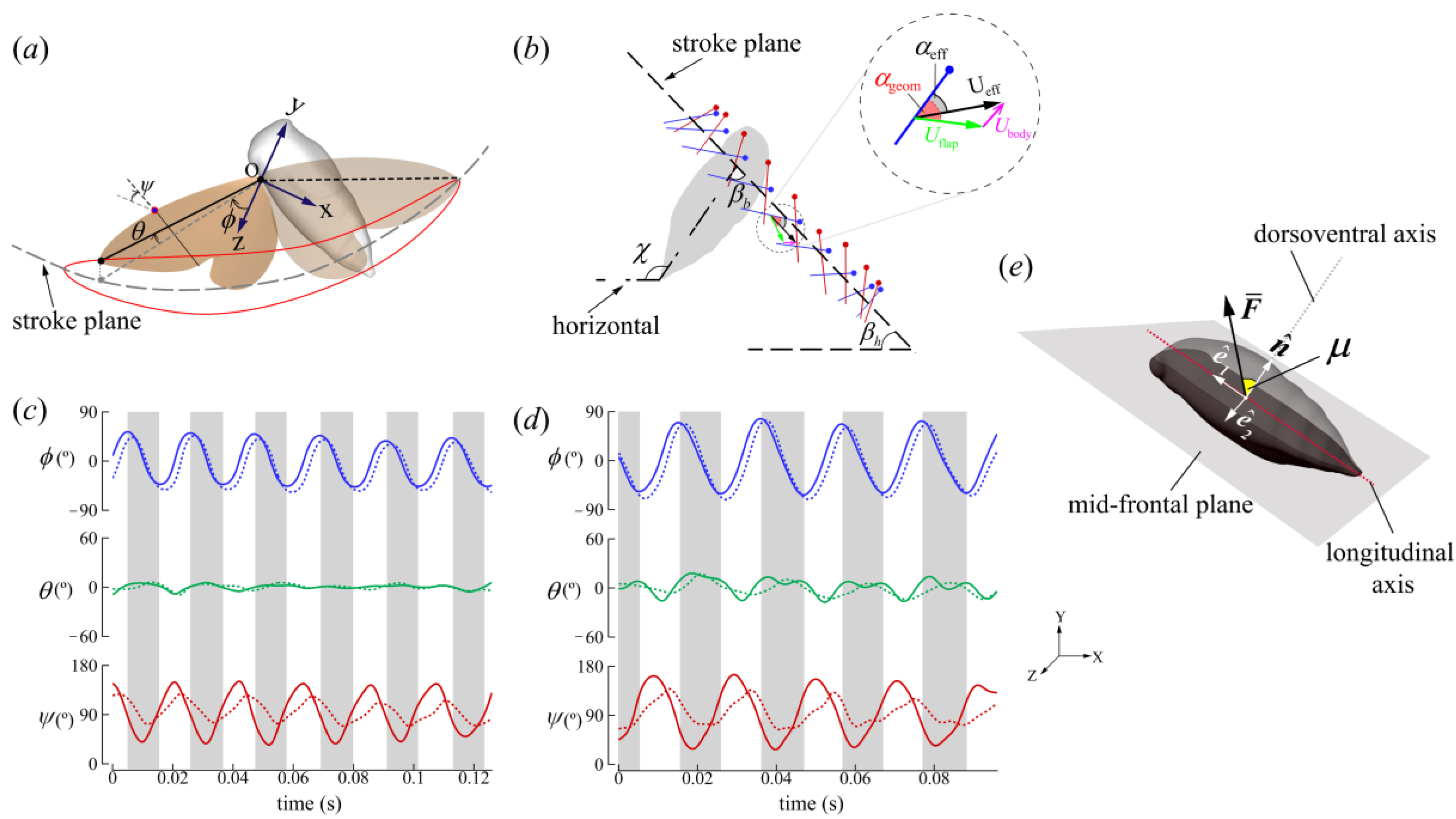
2.2. Wing Kinematics Definitions
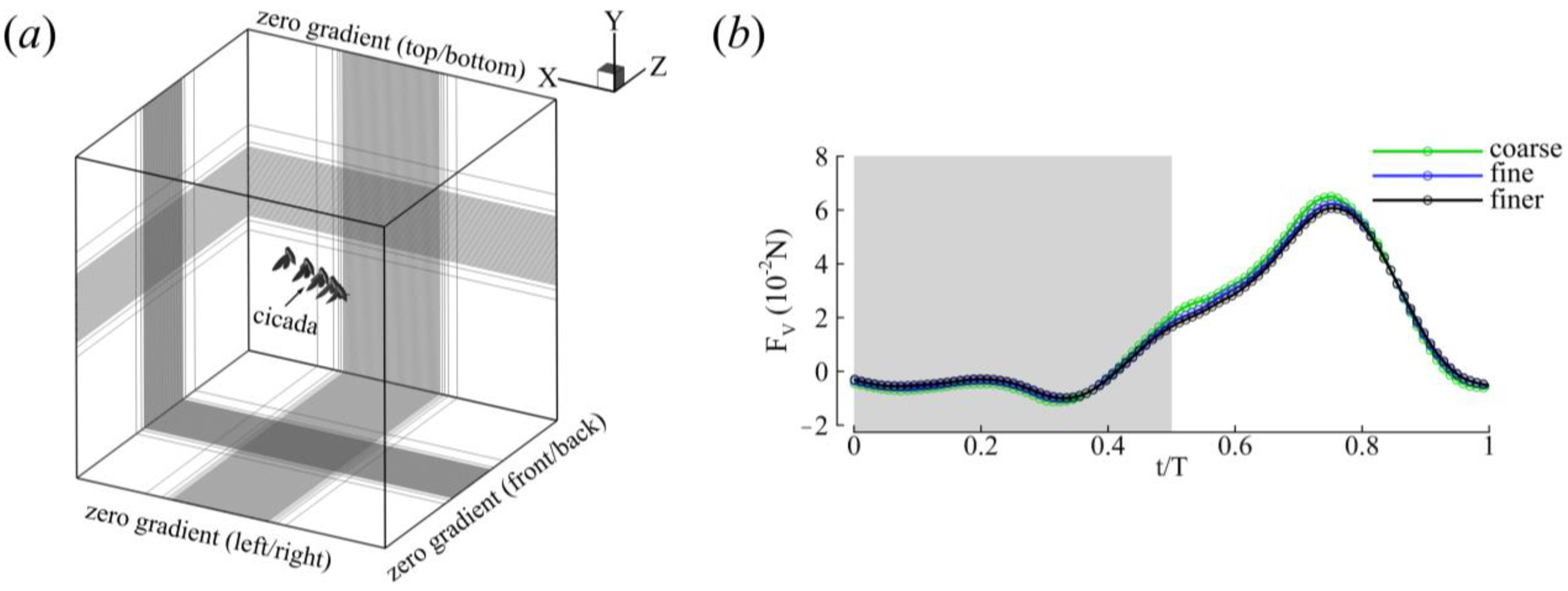
2.3. Numerical Methods and Simulation Setup
3. Results
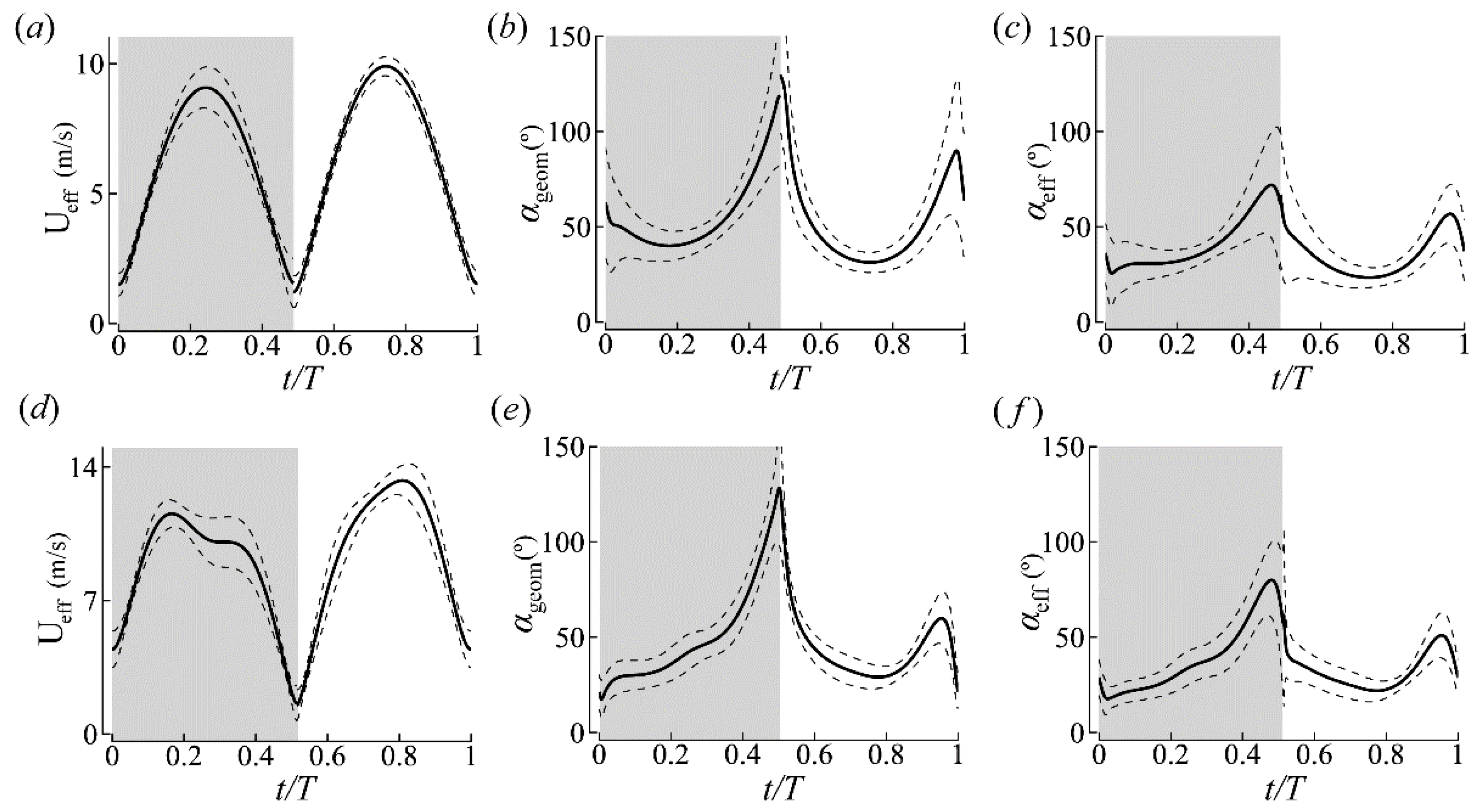
3.1. Kinematics
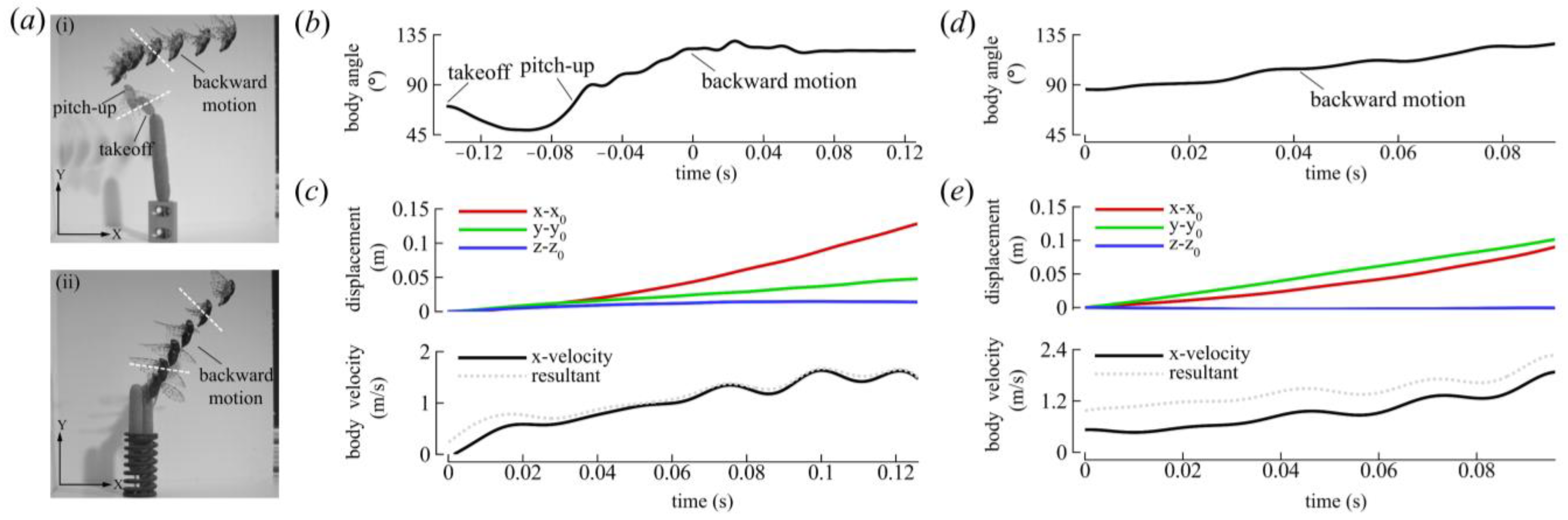
3.1.1. Body Kinematics
3.1.2. Wing Kinematics
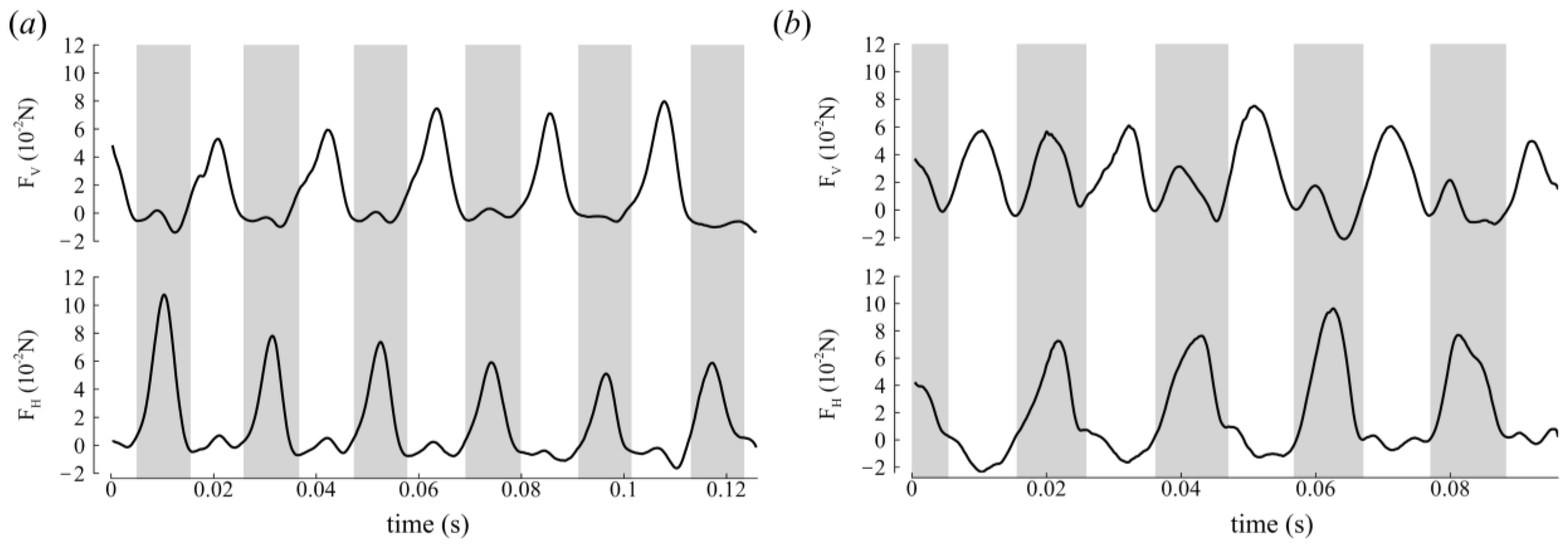
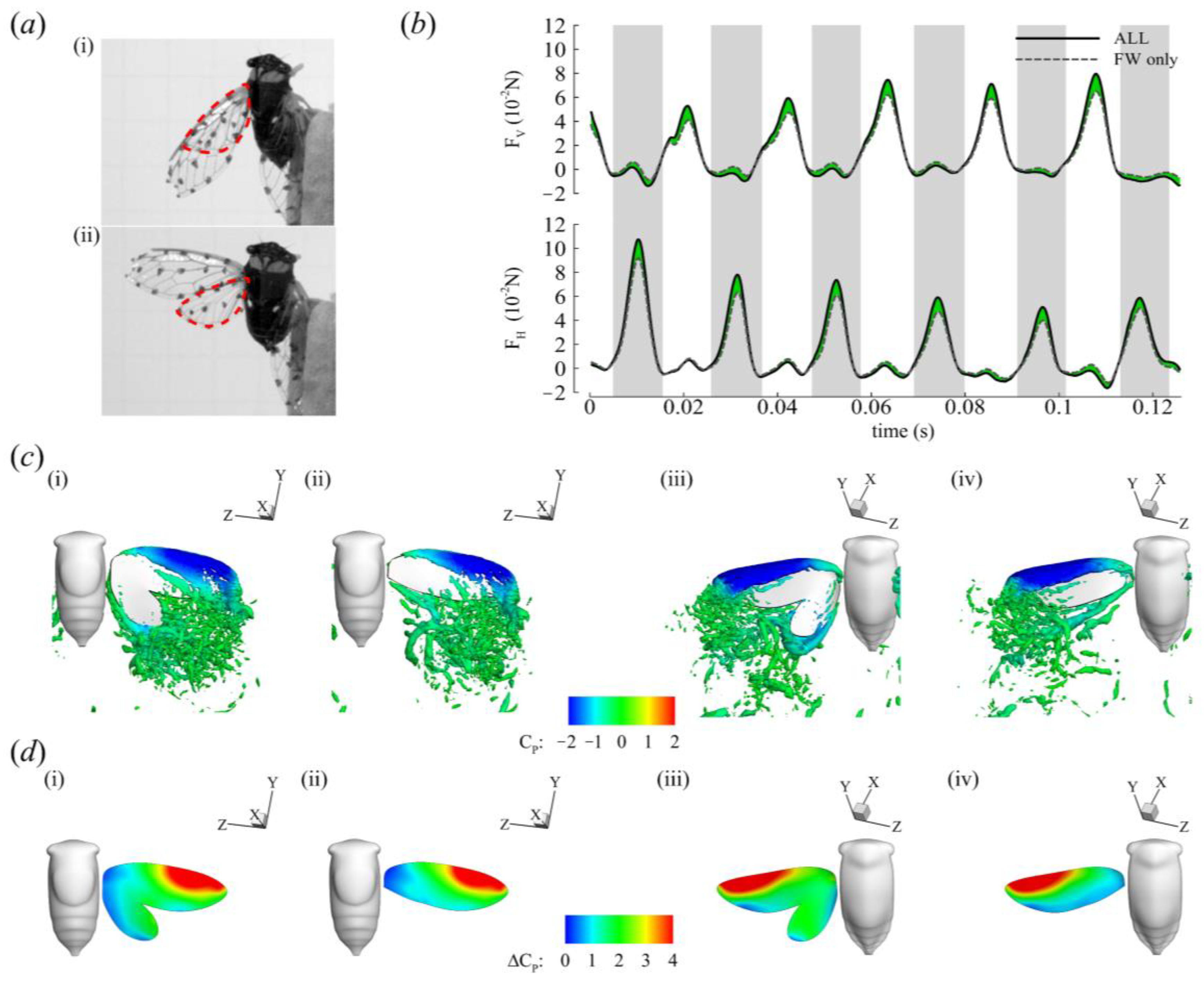
3.2. Aerodynamic Forces
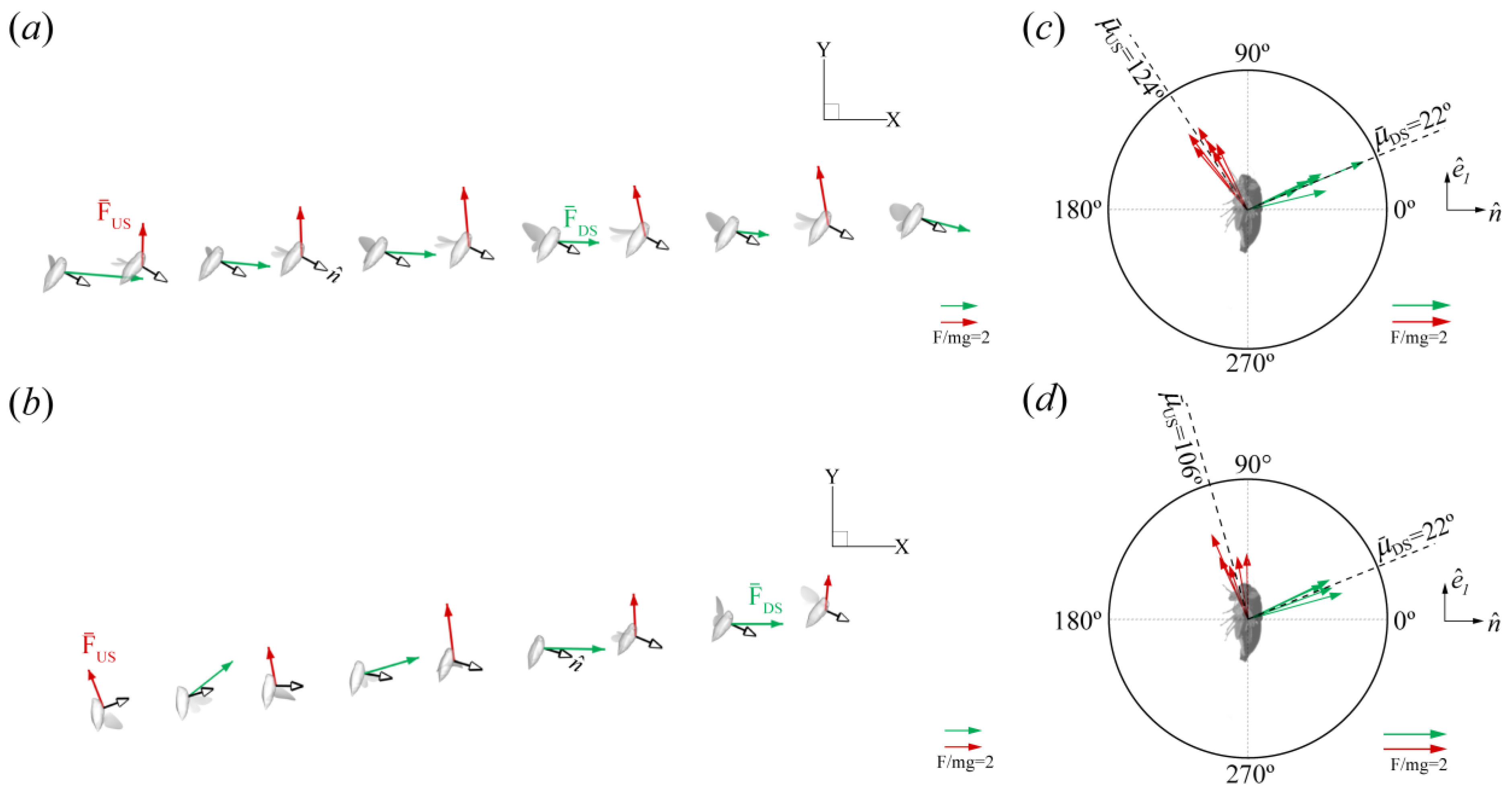
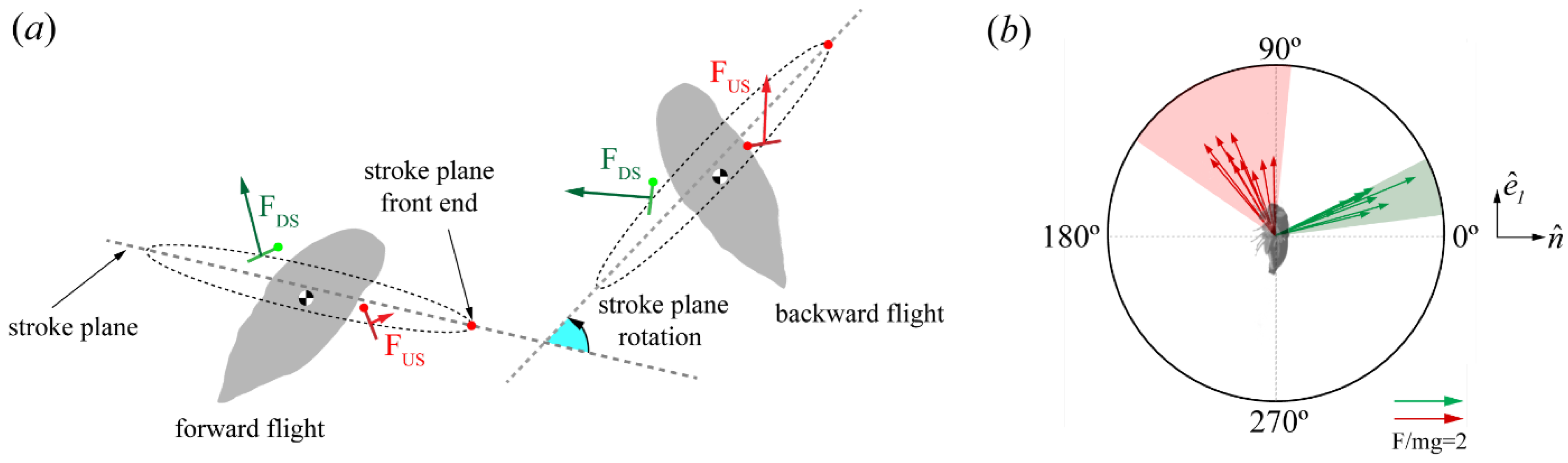
Force Orientation in the Global and Local Frames
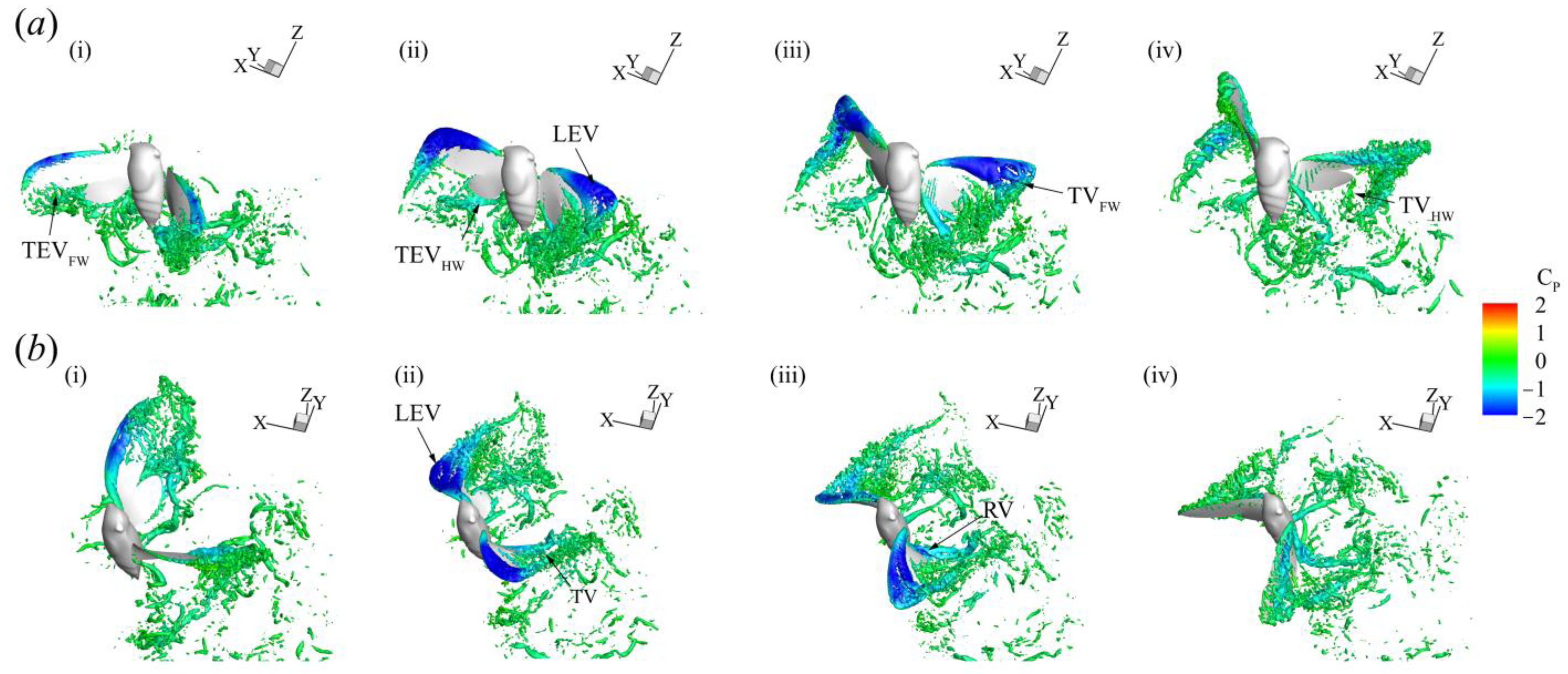
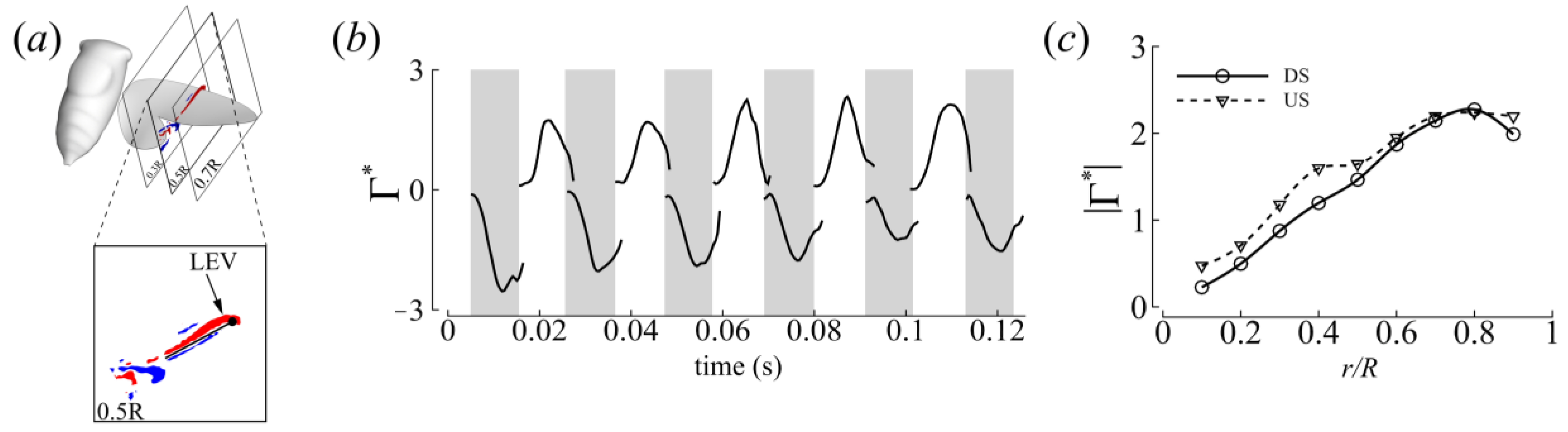
3.3. Three-Dimensional Wake Topology and Leading-Edge Vortex Strength
3.4. Roles of the Forewing and Hindwing
4. Discussion and Conclusions
| Flight Mode | J | (m/s) | (°) | (°) | (°) | DS/US | (°) | Reference | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS | US | ||||||||||||
| Forward | -- | 1.9 | 25 | -- | -- | -- | -- | -- | -- | -- | -- | -- | [52] |
| 0.32 | 2.0 | 28 | 64 | 36 * | 1.0 | -- | -- | 3.33 | 0.53 | 3.23 ‡ | 0.10 | [15] | |
| 0.32 | 2.2 | 49 | 62 | 13 * | 1.17 | 62 | 72 | 1.91 | 0.59 | 1.58 ‡ | 0.47 | [14] | |
| Backward | −0.19 | −1.0 | 122 | 73 | 46 † | 0.95 | 41 | 36 | 2.89 | 2.96 | −0.28 | 2.87 ‡ | current study |
| −0.17 | −0.94 | 107 | 69 | 37 † | 1.06 | 40 | 34 | 3.14 | 2.35 | 0.81 | 2.27 ‡ | ||
| Animal | J | (m/s) | (°) | (°) | (°) | DS/US | (°) | (°) | Reference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cockchafer beetle | -- | −1.2 | 87–115 | -- | -- | -- | -- | -- | -- | -- | [26] | |||||
| Hummingbird | 0.3 | −1.5 | 51–75 | 57–71 | −15–6 | 0.88–1.08 | -- | -- | -- | -- | [10] | |||||
| Dragonfly | 0.3 | −1.0 | 85–95 | 35 | 47 | 0.87 | 0.83 | 25 | 27 | 21 | 27 | 1.44 | 2.07 | 2.15 | 3.17 | [25] |
| Cicada | 0.2 | −1.0 | 122 | 73 | 46 | 0.95 | 41 | 36 | 2.89 | 2.96 | current study | |||||
| 0.2 | −0.9 | 86–130 | 69 | 37 | 1.06 | 40 | 34 | 3.14 | 2.35 | |||||||
| Waterlily beetle | -- | -- | 50–70 | 40–50 | 0 –30 | -- | -- | -- | -- | -- | [5] | |||||
| Butterfly | 0.3–0.4 | −0.4 to −0.8 | 85–119 | 78–86 | 0–35 | 0.82–1.45 | 53–72 | 33–51 | 1.3–2.1 | 1.3–2.6 | [24] | |||||
| DelFly II | -- | −1.0 | 70–100 | -- | -- | -- | -- | -- | -- | -- | [54] | |||||
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, M.H.; Muijres, F.T. The aerodynamics and control of free flight manoeuvres in Drosophila. Philos. Trans. R. Soc. B 2016, 371, 20150388. [Google Scholar] [CrossRef] [PubMed]
- Rüppell, G. Kinematic analysis of symmetrical flight manoeuvres of Odonata. J. Exp. Biol. 1989, 144, 13–42. [Google Scholar] [CrossRef]
- Rüppell, G.; Hilfert, D. The flight of the relict dragonfly Epiophlebia superstes (Selys) in comparison with that of the modern Odonata (Anisozygoptera: Epiophlebiidae). Odonatologica 1993, 22, 295–309. [Google Scholar]
- Mukundarajan, H.; Bardon, T.C.; Kim, D.H.; Prakash, M. Surface tension dominates insect flight on fluid interfaces. J. Exp. Biol. 2016, 219, 752–766. [Google Scholar] [CrossRef]
- Yokoi, T.; Fujisaki, K. Hesitation behaviour of hoverflies Sphaerophoria spp. to avoid ambush by crab spiders. Naturwissenschaften 2009, 96, 195–200. [Google Scholar] [CrossRef]
- Dudley, R. The Biomechanics of Insect Flight: Form, Function, Evolution; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Lannoo, M.J.; Lannoo, S.J. Why do electric fishes swim backwards? An hypothesis based on gymnotiform foraging behavior interpreted through sensory constraints. Environ. Biol. Fishes 1993, 36, 157–165. [Google Scholar] [CrossRef]
- Flammang, B.E.; Lauder, G.V. Functional morphology and hydrodynamics of backward swimming in bluegill sunfish, Lepomis macrochirus. Zoology 2016, 119, 414–420. [Google Scholar] [CrossRef] [PubMed]
- Sapir, N.; Dudley, R. Backward flight in hummingbirds employs unique kinematic adjustments and entails low metabolic cost. J. Exp. Biol. 2012, 215, 3603–3611. [Google Scholar] [CrossRef]
- Collett, M.; Graham, P.; Collett, T.S. Insect Navigation: What Backward Walking Reveals about the Control of Movement. Curr. Biol. 2017, 27, R141–R144. [Google Scholar] [CrossRef]
- Duysens, J.; Tax, A.A.; Murrer, L.; Dietz, V. Backward and forward walking use different patterns of phase-dependent modulation of cutaneous reflexes in humans. J. Neurophysiol. 1996, 76, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Zeil, J.; Wittmann, D. Visually controlled station-keeping by hovering guard bees of Trigona (Tetragonisca) angustula (Apidae, Meliponinae). J. Comp. Physiol. A 1989, 165, 711–718. [Google Scholar] [CrossRef]
- Wan, H.; Dong, H.; Gai, K. Computational investigation of cicada aerodynamics in forward flight. J. R. Soc. Interface 2015, 12, 20141116. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Dong, H.; Li, C. Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 2016, 795, 634–651. [Google Scholar] [CrossRef]
- Wang, Z.J.; Russell, D. Effect of forewing and hindwing interactions on aerodynamic forces and power in hovering dragonfly flight. Phys. Rev. Lett. 2007, 99, 148101. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C.P. The novel aerodynamics of insect flight: Applications to micro-air vehicles. J. Exp. Biol. 1999, 202, 3439–3448. [Google Scholar] [CrossRef] [PubMed]
- Bode-Oke, A.T.; Zeyghami, S.; Dong, H. Aerodynamics and flow features of a damselfly in takeoff flight. Bioinspiration Biomim. 2017, 12, 056006. [Google Scholar] [CrossRef]
- Bennet-Clark, H.C.; Daws, A.G. Transduction of mechanical energy into sound energy in the cicada cyclochila australasiae. J. Exp. Biol. 1999, 202, 1803–1817. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.S.; Simon, C. The Ecology, Behavior, and Evolution of Periodical Cicadas. Annu. Rev. Entomol. 1995, 40, 269–295. [Google Scholar] [CrossRef]
- Bartholomew, G.A.; Barnhart, M.C. Tracheal Gases, Respiratory Gas Exchange, Body Temperature and Flight in Some Tropical Cicadas. J. Exp. Biol. 1984, 111, 131–144. [Google Scholar] [CrossRef]
- Kelleher, S.M.; Habimana, O.; Lawler, J.; O’ Reilly, B.; Daniels, S.; Casey, E.; Cowley, A. Cicada Wing Surface Topography: An Investigation into the Bactericidal Properties of Nanostructural Features. ACS Appl. Mater. Interfaces 2016, 8, 14966–14974. [Google Scholar] [CrossRef] [PubMed]
- Sane, S.P.; Dieudonné, A.; Willis, M.A.; Daniel, T.L. Antennal mechanosensors mediate flight control in moths. Science 2007, 315, 863–866. [Google Scholar] [CrossRef] [PubMed]
- Bode-Oke, A.T.; Dong, H. The reverse flight of a monarch butterfly (Danaus plexippus) is characterized by a weight-supporting upstroke and postural changes. J. R. Soc. Interface 2020, 17, 202200268. [Google Scholar] [CrossRef]
- Bode-Oke, A.T.; Zeyghami, S.; Dong, H. Flying in reverse: Kinematics and aerodynamics of a dragonfly in backward free flight. J. R. Soc. Interface 2018, 15, 20180102. [Google Scholar] [CrossRef] [PubMed]
- Schneider, P. Flugmanöver der käfer. Mitteilungen Dtsch. Ges. Allg. Angew. Entomol. 1981, 3, 259–263. [Google Scholar]
- Tiegs, O.W. The flight muscles of insects-their anatomy and histology; with some observations on the structure of striated muscle in general. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 1955, 238, 221–348. [Google Scholar]
- Zeyghami, S.; Babu, N.; Dong, H. Cicada (Tibicen linnei) steers by force vectoring. Theor. Appl. Mech. Lett. 2016, 6, 107–111. [Google Scholar] [CrossRef]
- Bode-Oke, A.; Dong, H. On the Backward Flight of a Cicada: Kinematics and Aerodynamics. Bull. Am. Phys. Soc. 2018, 63. [Google Scholar]
- Ma, K.Y.; Chirarattananon, P.; Fuller, S.B.; Wood, R.J. Controlled Flight of a Biologically Inspired, Insect-Scale Robot. Science 2013, 340, 603–607. [Google Scholar] [CrossRef]
- Pfau, H. Contributions of functional morphology to the phylogenetic systematics of Odonata. Adv. Odonatol. 1991, 5, 109–141. [Google Scholar]
- Wakeling, J.; Ellington, C.P. Dragonfly flight. II. Velocities, accelerations and kinematics of flapping flight. J. Exp. Biol. 1997, 200, 557–582. [Google Scholar] [CrossRef] [PubMed]
- Ros, I.G.; Bassman, L.C.; Badger, M.A.; Pierson, A.N.; Biewener, A.A. Pigeons steer like helicopters and generate down- and upstroke lift during low speed turns. Proc. Natl. Acad. Sci. USA 2011, 108, 19990–19995. [Google Scholar] [CrossRef] [PubMed]
- Koehler, C.; Liang, Z.; Gaston, Z.; Wan, H.; Dong, H. 3D reconstruction and analysis of wing deformation in free-flying dragonflies. J. Exp. Biol. 2012, 215, 3018–3027. [Google Scholar] [CrossRef] [PubMed]
- Catmull, E.; Clark, J. Recursively generated B-spline surfaces on arbitrary topological meshes. Comput.-Aided Des. 1978, 10, 350–355. [Google Scholar] [CrossRef]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Menzer, A.; Ren, Y.; Guo, J.; Tobalske, B.W.; Dong, H. Wing Kinematics and Unsteady Aerodynamics of a Hummingbird Pure Yawing Maneuver. Biomimetics 2022, 7, 115. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Dong, H.; Zhao, K. A balance between aerodynamic and olfactory performance during flight in Drosophila. Nat. Commun. 2018, 9, 3215. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Mittal, R.; Najjar, F.M. Wake topology and hydrodynamic performance of low-aspect-ratio flapping foil. J. Fluid Mech. 2006, 566, 528–553. [Google Scholar] [CrossRef]
- Menzer, A.; Gong, Y.; Fish, F.E.; Dong, H. Bio-inspired propulsion: Towards understanding the role of pectoral fin kinematics in manta-like swimming. Biomimetics 2022, 7, 45. [Google Scholar] [CrossRef]
- Hunt, J.C.; Wray, A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. Cent. Turbul. Res. Rep. 1988, CTR-S88, 193–208. [Google Scholar]
- Brackenbury, J. Insects in Flight; Publisher: Blandford, UK, 1995. [Google Scholar]
- Willmott, A.P.; Ellington, C.P. The mechanics of flight in the hawkmoth Manduca sexta. I. Kinematics of hovering and forward flight. J. Exp. Biol. 1997, 200, 2705–2722. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The control of flight force by a flapping wing: Lift and drag production. J. Exp. Biol. 2001, 204, 2607–2626. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, Q.; Deng, X.; Sane, S.P. Aerodynamic effects of flexibility in flapping wings. J. R. Soc. Interface 2010, 7, 485–497. [Google Scholar] [CrossRef] [PubMed]
- Hsu, S.-J.; Thakur, N.; Cheng, B. Speed control and force-vectoring of bluebottle flies in a magnetically levitated flight mill. J. Exp. Biol. 2019, 222, jeb187211. [Google Scholar]
- Grodnitsky, D.L. Evolution and Classification of Insect Flight Kinematics. Evolution 1995, 49, 1158–1162. [Google Scholar] [CrossRef] [PubMed]
- Jantzen, B.; Eisner, T. Hindwings are unnecessary for flight but essential for execution of normal evasive flight in Lepidoptera. Proc. Natl. Acad. Sci. USA 2008, 105, 16636–16640. [Google Scholar] [CrossRef] [PubMed]
- Moore, T.E.; Huber, F.; Weber, T.; Klein, U.; Back, C. Interaction between visual and phonotactic orientation during flight in Magicicada cassini (Homoptera: Cicadidae). Great Lakes Entomol. 1993, 26, 3. [Google Scholar] [CrossRef]
- Caetano, J.V.; de Visser, C.C.; Remes, B.D.; De Wagter, C.; Van Kampen, E.-J.; Mulder, M. Controlled flight maneuvers of a Flapping Wing Micro Air Vehicle: A step towards the DelFly II Identification. In Proceedings of the AIAA Atmospheric Flight Mechanics (AFM) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Bomphrey, R.J.; Taylor, G.K.; Thomas, A.L.R. Smoke visualization of free-flying bumblebees indicates independent leading-edge vortices on each wing pair. Exp. Fluids 2009, 46, 811–821. [Google Scholar] [CrossRef]
- Zeyghami, S. Wing in the Loop: Integrating the Wing into Dynamics of Insect Flight. Ph.D. Thesis, Department of Mechanical and Aerospace Engineering, University of Virginia, Charlottesville, VA, USA, 2015. [Google Scholar]
- Ellington, C.P. The Aerodynamics of Flapping Animal Flight. Am. Zool. 1984, 24, 95–105. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. III. Kinematics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1984, 305, 41–78. [Google Scholar]
- Chen, D.; Kolomenskiy, D.; Nakata, T.; Liu, H. Forewings match the formation of leading-edge vortices and dominate aerodynamic force production in revolving insect wings. Bioinspiration Biomim. 2017, 13, 016009. [Google Scholar] [CrossRef]
- Sato, M.; Azuma, A. The flight performance of a damselfly Ceriagrion melanurum Selys. J. Exp. Biol. 1997, 200, 1765–1779. [Google Scholar] [CrossRef] [PubMed]
- Russell, D.B. Numerical and Experimental Investigations into the Aerodynamics of Dragonfly Flight. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2004. [Google Scholar]
- Azuma, A.; Watanabe, T. Flight Performance of a Dragonfly. J. Exp. Biol. 1988, 137, 221–252. [Google Scholar] [CrossRef]
- Hefler, C.; Noda, R.; Shyy, W.; Qiu, H. Unsteady Vortex Interactions for Performance Enhancement of a Free Flying Dragonfly. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 30 July–3 August 2017; p. 69579. [Google Scholar]
- Meng, X.; Sun, M. Wing Kinematics, Aerodynamic Forces and Vortex-wake Structures in Fruit-flies in Forward Flight. J. Bionic Eng. 2016, 13, 478–490. [Google Scholar] [CrossRef]
- Willmott, A.P.; Ellington, C.P.; Thomas, A.L. Flow visualization and unsteady aerodynamics in the flight of the hawkmoth, Manduca sexta. Philos. Trans. R. Soc. B Biol. Sci. 1997, 352, 303–316. [Google Scholar] [CrossRef]
- Aono, H.; Liu, H. Vortical Structure and Aerodynamics of Hawkmoth Hovering. J. Biomech. Sci. Eng. 2006, 1, 234–245. [Google Scholar] [CrossRef]
- Young, J.; Walker, S.M.; Bomphrey, R.J.; Taylor, G.K.; Thomas, A.L.R. Details of Insect Wing Design and Deformation Enhance Aerodynamic Function and Flight Efficiency. Science 2009, 325, 1549–1552. [Google Scholar] [CrossRef]
- Zheng, L.; Hedrick, T.L.; Mittal, R. Time-Varying Wing-Twist Improves Aerodynamic Efficiency of Forward Flight in Butterflies. PLoS ONE 2013, 8, e53060. [Google Scholar] [CrossRef]
| Species | ID | Body Weight (mg) | L (mm) | FW/HW Length (mm) | FW/HW Chord (mm) | FW/HW Area (mm2) | Flapping Frequency (Hz) |
|---|---|---|---|---|---|---|---|
| Tibicen linnei | CCD #1 | 1174 | 30 | 38/22 | 14/11 | 352/171 | 47.6 |
| CCD #2 | 1514 | 30 | 39/22 | 14/11 | 359/175 | 52.2 |
| Grid Size | (10−2 N) | (10−2 N) | |
|---|---|---|---|
| Coarse | 336 × 216 × 192 | 1.48 | 6.50 |
| Fine | 480 × 320 × 216 | 1.45 | 6.22 |
| Finer | 600 × 392 × 336 | 1.42 | 6.08 |
| ID | J | (m/s) | (°) | (°) | (°) | DS/US | (°) | (°) | (°) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS | US | DS | US | |||||||||
| CCD #1 | −0.19 | −1.0 | 122 ± 2 | 73 ± 2 | 46 ± 3 | 0.95 | 0.88 | 92 ± 5 | 56 ± 5 | 53 ± 7 | 41 ± 7 | 36 ± 5 |
| CCD #2 | −0.17 | −0.94 | 107 ± 14 | 69 ± 2 | 37 ± 13 | 1.06 | 0.83 | 133 ± 5 | 52 ± 4 | 43 ± 4 | 39 ± 5 | 32 ± 4 |
| Half Stroke | ||||
|---|---|---|---|---|
| DS 1 | −1.61 | −2.58 | 1.62 | 1.46 |
| US 1 | 0.99 | 1.76 | ||
| DS 2 | −1.22 | −2.07 | 1.18 | 1.20 |
| US 2 | 1.03 | 1.72 | ||
| DS 3 | −1.22 | −1.94 | 0.98 | 0.85 |
| US 3 | 1.25 | 2.28 | ||
| DS 4 | −1.05 | −1.80 | 0.90 | 0.76 |
| US 4 | 1.17 | 2.36 | ||
| DS 5 | −0.83 | −1.27 | 0.70 | 0.59 |
| US 5 | 1.18 | 2.16 | ||
| DS 6 | −1.03 | −1.55 |
| Insect | Flight Mode | DS Force (%) | DS Force Type | US Force (%) | US Force Type | Reference |
|---|---|---|---|---|---|---|
| Cicada | forward | 90 | vertical | 10 | horizontal | [15] |
| 80 | vertical | 20 | horizontal | [14] | ||
| backward | 49 | horizontal | 51 | vertical | current study | |
| 57 | horizontal | 43 | vertical | current study | ||
| Damselfly | forward | 84 | vertical | 16 | horizontal | [18] |
| 75 | vertical | 25 | horizontal | [56] | ||
| Dragonfly | hovering * | 77 | vertical | 23 | horizontal | [57] |
| backward | 33 | horizontal | 67 | vertical | [25] | |
| forward | 80 | vertical | 20 | horizontal | [58] | |
| 67 | vertical | 33 | horizontal | [59] | ||
| Fruit fly | forward | 61 | vertical | 39 | horizontal | [60] |
| Hawkmoth | forward | 80 | vertical | 20 | horizontal | [61] |
| hovering | 67 | vertical | 33 | horizontal | [62] | |
| Locust | forward | 84 | vertical | 14 | horizontal | [63] |
| Butterfly | forward | 74 | vertical | 26 | horizontal | [64] |
| backward | 40 | horizontal | 60 | vertical | [24] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bode-Oke, A.T.; Menzer, A.; Dong, H. Postural Change of the Annual Cicada (Tibicen linnei) Helps Facilitate Backward Flight. Biomimetics 2024, 9, 233. https://doi.org/10.3390/biomimetics9040233
Bode-Oke AT, Menzer A, Dong H. Postural Change of the Annual Cicada (Tibicen linnei) Helps Facilitate Backward Flight. Biomimetics. 2024; 9(4):233. https://doi.org/10.3390/biomimetics9040233
Chicago/Turabian StyleBode-Oke, Ayodeji T., Alec Menzer, and Haibo Dong. 2024. "Postural Change of the Annual Cicada (Tibicen linnei) Helps Facilitate Backward Flight" Biomimetics 9, no. 4: 233. https://doi.org/10.3390/biomimetics9040233
APA StyleBode-Oke, A. T., Menzer, A., & Dong, H. (2024). Postural Change of the Annual Cicada (Tibicen linnei) Helps Facilitate Backward Flight. Biomimetics, 9(4), 233. https://doi.org/10.3390/biomimetics9040233








