Post-Quantum Secure ID-Based (Threshold) Linkable Dual-Ring Signature and Its Application in Blockchain Transactions

Abstract

Ring signatures are widely used in e-voting, anonymous whistle-blowing systems, and blockchain transactions. However, due to the anonymity of ring signatures, a signer can sign the same message multiple times, potentially leading to repeated voting or double spending in blockchain transactions. To address these issues in blockchain transactions, this work constructs an identity-based linkable ring signature scheme based on the hardness of the lattice-based Module Small Integer Solution (M-SIS) assumption, which is hard even for quantum attackers. The proposed scheme is proven to be anonymous, unforgeable, linkable, and nonslanderable in the random oracle model. Compared to existing identity-based linkable ring signature (IBLRS) schemes of linear size, our signature size is relatively smaller, and this advantage is more pronounced when the number of ring members is small. We provide approximate signature size data for ring members ranging from 2 to 2048. When the number of ring members is 16 (or 512. resp.), the signature size of our scheme is 11.40 KB (or 24.68 KB, respectively). Finally, a threshold extension is given as an additional scheme with specifications and security analysis.

1. Introduction

A ring signature, first proposed [1] by Rivest et al. in 2001, allows the signer to create signatures in the name of a group include him or herself (called a ring). A ring signature is verified to come from a ring, without knowing the identity of the real signer, thus ensuring the anonymity. To meet the privacy and security needs of both parties in blockchain transactions, ring signatures have been introduced to ensuring the anonymity of transaction user identities and transaction security in the last decade or so [2,3]. The first use of ring signatures on blockchains was in the Cryptonote protocol research conducted by Saberhagen et al. [4] in 2013. The Cryptonote protocol proposed two major privacy-related properties that an anonymous e-cash system needs to satisfy: untraceability and unlinkability. To meet these requirements, the protocol uses one-time public–private key pairs to protect the privacy of the recipient in transactions and, at the same time, uses one-time ring signatures to protect the privacy of the sender. This provides an important practical case and theoretical basis for the application of ring signatures in blockchain privacy protection.

However, using ring signatures to solve the privacy protection problem on blockchains also introduces the “double-spending” problem due to its anonymity. “Double spending”, also known as double payment, refers to the situation where the same digital asset is used repeatedly. The linkable ring signature first introduced by Liu et al. [5] in 2004 provides a solution. By linking two legitimate ring signatures created by the same sender for a single message, the “double-spending” problem in blockchain technology can be solved.

Early linkable ring signatures were built based on Public Key Infrastructure (PKI), where certificate management issues increased computational costs. This issue can be solved by identity-based cryptography, which was proposed by Adi Shamir [6] in 1984. An identity-based signature (IBS) allows users to directly generate public keys from their identities, such as email addresses or usernames, without the need for certificates. Combining identity-based cryptography with linkable ring signature technology to achieve an identity-based linkable ring signature (IBLRS) is a significant topic that addresses identity authentication and key management issues while providing linkability to prevent repeated signatures. In 2006, Chow et al. [7] proposed the first IBLRS scheme based on the bilinear pairing assumption. Subsequently, numerous IBLRS schemes emerged [8,9,10,11,12,13].

However, many of the above schemes rely on traditional number-theoretic assumptions, including factoring and discrete logarithms, which become vulnerable to quantum attacks with the development of large-scale quantum computers [14,15]. So, researchers start to turn their attention to post-quantum cryptography [16]. Among the post-quantum candidates, lattice-based cryptography is the most promising one. This can be confirmed by the post-quantum algorithmic standards selected by NIST (National Institute of Standards and Technology) after years of analysis and argumentation [17]. Therefore, this work chooses to construct identity linkable ring signatures that rely on a lattice-based assumption to achieve post-quantum security, thus provide identity privacy, as well as linkability to avoid double spending in blockchain transactions.

1.1. Contributions

Based on the lattice-based hard problem, we propose an identity-based linkable dual-ring signature scheme as well as its threshold extension. Our proposal has several advantages:

(1)

It applies identity information directly for public key operations to remove the need for certificates and third-party certificate authorities, and fully demonstrates the flexibility of identity-based keys.

(2)

By adopting a dual-ring structure, it has a very short signature size, especially when the ring scale is not very large (below 2000). The “double-spending” problem in general ring signature schemes is solved by adding linkability.

(3)

The scheme proposed in this paper is based on the lattice-based M-SIS assumption and can resist quantum attacks. It is proved in the random oracle model that this scheme is correct, anonymous, unforgeable, linkable, and nonslanderable.

(4)

It presents a threshold extension with detailed explanations and security analysis.

1.2. Related Works

The first post-quantum one-time linkable ring signature was proposed by Torres et al. [18] in 2018. Le et al. [19] suggested IBLRS methods that rely on lattice-based SIS and ring-SIS. Tang et al. [20] proposed a new lattice-based IBLRS scheme in 2020, which reduced the signature size and computational complexity, making it more suitable for practical applications. Although lattice-based ring signature schemes offer more security and are particularly suitable for future quantum computing environments, they tend to have large signature sizes and high computational complexity. To further reduce the size of ring signatures, much effort has been made in recent years. Most schemes for reducing ring signature size use two methods: accumulators [21] and zero-knowledge proofs [22]. However, accumulators require a trusted setup. In 2021, Yuen et al. [23] introduced a novel type of ring signature known as the “dual-ring signature”. This signature scheme builds upon the type-T standard signature algorithm and includes a lattice-based variant of the dual-ring signature. This new structure of ring signatures significantly reduces the signature size and speeds up the signing and verification processes compared to ordinary ring signatures. In 2024, Feng et al. [24] proposed a dual-ring signature scheme based on SM2, initially converting SM2 digital signatures into Type-T, and then integrating dual-ring with a variant of SM2 digital signatures.

2. Preliminaries

2.1. Notations

Table 1 lists the related symbols. When an integer N exists for each positive integer c and, for all $x>N$, $\left|f\left(x\right)\right|<{\displaystyle \frac{1}{x^c}}$, a function $f:\mathbb{N}\to \mathbb{R}$ is said to be negligible (negl). If all probabilistic polynomial-time (PPT) algorithms cannot solve a problem with a non-negligible probability, then the problem is considered hard.

Table 1. Symbol description.

Symbol	Description
$\lambda$	security parameter
q	an odd modulus
$pp$	public parameter
$\Vert ·\Vert$	take the square root of the sum of the squares of each element
${\Vert ·\Vert }_{\infty }$	the largest absolute value among all vector elements
$\mathit{A}$	matrices that form a lattice
x	representation constant
${\mathit{s}}_{I{D}_i}$	represents the signer’s private key
$\mathbb{Z}$	integer set
${\mathcal{R}}_q$	ring ${\mathbb{Z}}_q\left[X\right]/(X^d+1)$
W	set of all user identities $W=\{I{D}_1,\cdots ,I{D}_N\}$
${\mathit{T}}_A$	the trapdoor of the lattice constituted by $\mathit{A}$
$\mathit{\tau }$	linking tag
$Sig$	represents the signature
$H_1,H_2,H_3$	collision-resistant hash functions

2.2. Lattices

Definition 1.

Let $\mathit{B}=\{{\mathit{b}}_1,\cdots ,{\mathit{b}}_n\}$ be n vectors in m-dimensional space, which are linearly independent. All integer linear combinations of the vectors in $\{{\mathit{b}}_1,\cdots ,{\mathit{b}}_n\}$ constitute lattice $L\left(\mathit{B}\right)$; that is, $\Lambda =L\left(\mathit{B}\right)=\left\{{\sum }_{i=1}^n{x}_i{\mathit{b}}_i\right|x_i\in \mathbb{Z}\}$. We call $\{{\mathit{b}}_1,\cdots ,{\mathit{b}}_n\}$ a basis of lattice $L\left(\mathit{B}\right)$.

Definition 2

(M-$SI{S}_{q,n,m,\beta }$ assumption [25]). Let q, n, m be integers and β be a positive real number. Given $\mathit{A}\in {\mathbb{R}}_q^{n\times m}$, the Module Small Integer Solution (M-SIS) assumption aims to find a vector $\mathit{z}\in {\mathbb{R}}_q^m$ such that $\mathit{Az}=0$ and $∥\mathit{z}∥<\beta$.

The M-SIS (Module-SIS) hard problem is a modular version of the SIS (Short Integer Solution) hard problem, which transforms ${\mathbb{Z}}_q$ in the SIS problem to ${\mathbb{R}}_q$. Due to the increase in the modular structure, the M-SIS problem is more computationally complex, and finding short vectors is more challenging than in the SIS problem.

2.3. Important Algorithms

In 2008, Gentry et al. [26] proposed the GPV lattice screening algorithm, which is used by most lattice-based signature schemes and mainly consists of the following three parts:

TrapGen($1^n$): Input the security parameter n; let $q=q\left(n\right)⩾3$, $m=5nlogq$, and $\sigma =\sqrt{m}·2^{\omega \left(\sqrt{logm}\right)}$. The algorithm TrapGen$\left(1^n\right)$ outputs a matrix $A\in {\mathbb{R}}_q^{n\times m}$ and a set of bases on $T\in {\mathbb{R}}_q^{m\times m}$, and satisfies $\tilde{T}=O(nlogq)$.

SampleDom($1^n,\sigma )$: Input the security parameter n and the Gaussian parameter $\sigma$. The algorithm SampleDom$(1^n,\sigma )$ selects a random vector $\mathit{v}\in$${\mathbb{Z}}^m$ according to the distribution $D_{\sigma }^m$, and with high probability satisfies $\Vert \mathit{v}\Vert \le \sigma \sqrt{m}$.

SamplePre($\mathit{A},\mathit{T},\sigma ,\mathit{y})$: Input the matrix $\mathit{A}\in {\mathbb{Z}}_q^{n\times m}$; $\mathit{T}$ is a trapdoor basis of the lattice ${\Lambda }^{\perp }$($\mathit{A}$); the parameter $\sigma \ge$ $\Vert \tilde{\mathit{T}}\Vert \omega$$\left(\sqrt{logm}\right)$; for any vector $\mathit{y}\in {\mathbb{Z}}_q^n$, the algorithm SamplePre($\mathit{A},\mathit{T},\sigma ,\mathit{y}$) outputs a random non-zero vector $\mathit{e}\in {\mathbb{Z}}_q^m$, where $\Vert \mathit{e}\Vert \le \sigma \sqrt{m}$ and $\mathit{A}\mathit{e}=\mathit{y}\left(modq\right)$.

2.4. Rejection Sampling Technique

In lattice-based digital signatures, the signer wants to output a vector z that is independent of the private key s, ensuring that z cannot be used to gain any information about the signer’s secret. In the protocol, the signer computes $z=r+ls$, where s can be the private key or randomness used for the signer’s secret, $l\leftarrow \mathcal{L}$ is a challenge polynomial, and r is a “masking” vector. To eliminate the dependence of z on s, rejection sampling can be applied [27].

As Theorem 1 shows, for any $\mathit{v}\in {\mathbb{Z}}^m$, $\sigma =\omega (\Vert \mathit{v}\Vert \sqrt{logm})$, $Pr[{\displaystyle \frac{(D_{\sigma }^m\left(z\right)}{(D_{\mathit{v},\sigma }^m\left(z\right)}}$ = $O\left(1\right):\mathit{z}\leftarrow D_{\sigma }^m]$ = $1-2^{-\omega (logm)}$.

Theorem 1.

Given a probability distribution $V=\{\mathit{v}\in {\mathbb{Z}}^m:|\left|\mathit{v}\right||<t\}$, determine $\sigma =\omega \left(t\sqrt{logm}\right)$ and $h:V\to R$. The statistical distance between the input distributions of the next two algorithms is then less than $2^{-\omega (logm)}/M$, where M = $O\left(1\right)$ is a constant:

• Distribution 1: Output $(\mathit{z},\mathit{v})$ with probability min$({\displaystyle \frac{D_{\sigma }^m\left(z\right)}{M{D}_{v,\sigma }^m\left(z\right)}},1)$; sample $\mathit{v}\leftarrow h$ and $\mathit{z}\leftarrow D_{\mathit{v},\sigma }^m$;
• Distribution 2: With a probability of ${\displaystyle \frac{1}{M}}$, the sample $\mathit{v}\leftarrow h$ and $\mathit{z}\leftarrow D_{\sigma }^m$ yields $(\mathit{z},\mathit{v})$.

Distribution 1 has a minimum probability of producing an output of ${\displaystyle \frac{1-2^{-\omega (logm)}}{M}}$.

2.5. The Forking Lemma

  In 2000, Pointcheval and Stern proposed the forking lemma [28]. Suppose $(G,\Sigma ,V)$ is a digital signature scheme with security parameter n. A is a PPT algorithm whose input only consists of public data. Let Q be the maximum number of queries that A can make to the random oracle. If A generates a valid signature $(m,{\sigma }_1,h,{\sigma }_2)$ with probability $\epsilon \ge 7Q/2^n$ within time T, then there exists an algorithm B that controls algorithm A and can generate two valid signatures $(m,{\sigma }_1,h,{\sigma }_2)$ and $(m,{\sigma }_1,h^{\prime },{\sigma }_2^{\prime })$ within expected time $T^{\prime }\le 84480TQ/\epsilon$, where $h\ne h^{\prime }$.

2.6. Dual-Ring Structure

To further shorten the ring signature size of the AOS structure [29], especially the number of responses, the dual-ring structure, an efficient approach for constructing ring signatures, is suggested by [23]. The dual-ring signature splits the AOS single-ring signature into two separate rings: the commitments ring and the challenges ring, which are connected using a hash function. A dual-ring signature consists of N challenges and one response. We further provide a high-level description of the dual-ring structure:

In Figure 1, $Com$ represents the function used by the signer. ⊙ and ⊗ are two commutative group operations. V is the verification function. The verification function is split into two parts, $V_1$ and $V_2$, and their relationship is $V=V_1\odot V_2$. Z is the response function.

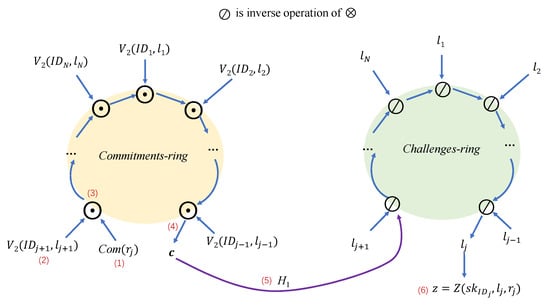
Figure 1. Structure of dual-ring structure.

(1)

The signatory selects a random number $r_j$ and generates a commitment through the Com function.

(2)

Randomly select $n-1$ challenges $c_i$, where $i\in \{1,\cdots ,j-1,j+1,\cdots ,n\}$.

(3)

Use the group operation ⊙ and functions $Com$ and $V_2$ to form a commitment ring.

(4)

Calculate the commitment c.

(5)

Link the commitment ring and the challenge ring through the hash function $H_1$.

(6)

Obtain $l_j$ through the hash value of $H_1$ and $l_i,(i\ne j)$ by group operation ⊘. Calculate the response z through the Z function.

3. Syntax and Security Model

As shown in the Figure 2, an identity-based linkable ring signature (IBLRS) scheme includes five PPT algorithms [20]:

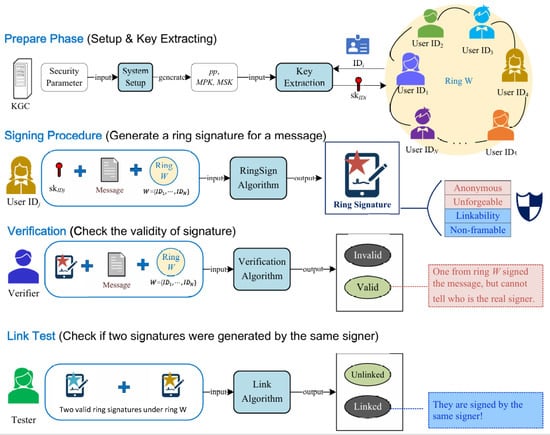
Figure 2. Definition of identity-based linkable ring signature.

(1)

Setup($\lambda$): The Key Generation Center (KGC) generates the public parameter $pp$ and the system master private key $MSK$.

(2)

KeyExt($I{D}_i,MSK,pp$): Performed by the $KGC$, this process takes the user’s identity $I{D}_i$, $MSK$, and $pp$ as input, and produces the private key ${\mathit{s}}_{I{D}_i}$ corresponding to the user’s identity $I{D}_i$.

(3)

Sign($pp,W,\mathit{\mu },{\mathit{s}}_{I{D}_j}$): Operated by the signer. Taking $pp$, a set of ring members W = $\{I{D}_1,I{D}_2,\cdots ,I{D}_N\}$, message $\mathit{\mu }$, and the private key ${\mathit{s}}_{I{D}_j}$ corresponding to the signer’s identity $I{D}_j\in W$ as input, this algorithm outputs a linkable ring signature $Sig$ on $\mathit{\mu }$ under W. The signature $Sig$ includes a linkable tag $\mathit{\tau }$.

(4)

Verify($pp,W,\mathit{\mu },Sig$): Carried out by the verifier, this process takes $pp$, the set of user identities W = $\{I{D}_1,I{D}_2,\cdots ,I{D}_N\}$ forming the ring, $\mathit{\mu }$, and $Sig$ as inputs. If the verification is successful, it outputs “1”; otherwise, it outputs “0”.

(5)

Link($Sig,Si{g}^{\prime },\mathit{\mu },W$): Taking as input two tuples, ($Sig,\mathit{\mu },W$) and (${Sig}^{\prime },\mathit{\mu },W$), this algorithm returns “linkable” or “unlinkable”.

We illustrate the security model of IBLRS through a series of interactions between attacker $\mathcal{A}$ and challenger $\mathcal{C}$. In the context of the random oracle model (ROM), attacker $\mathcal{A}$ is granted access to the RO and can issue two distinct types of queries:

(1)

Key extract query: $\mathcal{A}$ selects identity $I{D}_i$ and sends it to $\mathcal{C}$ for a private key query. $\mathcal{C}$ generate ${\mathit{s}}_{I{D}_i}$ corresponding to $I{D}_i$, and returns the result to $\mathcal{A}$.

(2)

Signing query: $\mathcal{A}$ selects a ring signature $W=(I{D}_1,I{D}_2,\cdots ,I{D}_N)$, a user identity $I{D}_j\in W,i\ne j$, and $\mathit{\mu }\in {\{0,1\}}^{*}$ to send to $\mathcal{C}$ for querying. $\mathcal{C}$ returns the generated signature $Sig$ to $\mathcal{A}$.

Definition 3

(Correctness). For any PPT attacker $\mathcal{A}$, an IBLRS scheme is correct if

$$Pr\left[Verify(pp,W,\mathit{\mu },Sig)=1|\begin{array}{c}(pp,MSK)\leftarrow Setup\left(\lambda \right)\\ {\mathit{s}}_{I{D}_i}\leftarrow KeyExt(I{D}_i,pp,MSK)\\ Sig\leftarrow Sign(pp,W,\mathit{\mu },{\mathit{s}}_{I{D}_j})\end{array}\right]=1$$

Definition 4

(Anonymity). The anonymity of IBLRS is defined by $Gam{e}_{anony}$ below:

(1) 

System Setup: Challenger $\mathcal{C}$ inputs the security parameter λ, and the KGC generates $MSK$ and $pp$. $\mathcal{C}$ sends $pp$ to $\mathcal{A}$. $\mathcal{A}$ is allowed a polynomially bounded number of queries, each query potentially dependent on previous query results.

(2) 

Query Stage: $\mathcal{A}$ adaptively carries out various queries with polynomial time bounds.

(3) 

Challenge Phase: $\mathcal{A}$ submits the message ${\mathit{\mu }}^{*}$, the ring $W=\{I{D}_1,I{D}_2,\cdots ,I{D}_N\}$, and randomly selects the user identity $I{D}_b(b\in \{0,1\})$ as $\mathcal{C}$. Note that A has not queried the private key associated to $I{D}_b$. $\mathcal{C}$ returns a signature $Si{g}^{*}=(l_1^{*},l_2^{*},\cdots ,l_N^{*},{\mathit{z}}^{*},{\mathit{\tau }}^{*})$, then sends it to $\mathcal{A}$.

(4) 

Guessing Phase: $\mathcal{A}$ outputs his or her guess $b^{\prime }$.

The advantage of $\mathcal{A}$ in $Gam{e}_{anony}$ is defined as

$$Ad{v}_{\mathcal{A}}^{anony}=|Pr\{b^{\prime }=b\}-1/2|.$$

For any PPT attacker $\mathcal{A}$, an IBLRS scheme is anonymous if the advantage $Ad{v}_{\mathcal{A}}^{anony}$ in $Gam{e}_{anony}$ is negligible.

Definition 5

(Unforgeability against insider corruption). We define the unforgeability of IBLRS through the $Gam{e}_{forge}$ below:

(1) 

System Setup: Challenger $\mathcal{C}$ inputs the security parameter λ, and the KGC generates $MSK$ and $pp$. $\mathcal{C}$ sends $pp$ to $\mathcal{A}$. $\mathcal{A}$ is allowed a polynomially bounded number of queries, each query potentially dependent on previous query results.

(2) 

Query Stage: $\mathcal{A}$ can access a polynomial-time oracle, and perform the aforementioned private key inquiries and signature inquiries.

(3) 

Forgery Stage: $\mathcal{A}$ provides (${\mathit{\mu }}^{*},W^{*},Si{g}^{*}$); if it satisfies the following conditions, then the attacker $\mathcal{A}$ wins the unforgeability $Gam{e}_{forge}$:

• $Verify({\mathit{\mu }}^{*},W^{*},{Sig}^{*})$=$“1”$;
• $\mathcal{A}$ has not queried the private key of any user in the ring $W^{*}$;
• $\mathcal{A}$ has not initiated any signature queries for (${\mathit{\mu }}^{*},W^{*}$).

The advantage of $\mathcal{A}$ winning the unforgeability game is defined as follows:

$$Ad{v}_{\mathcal{A}}^{forge}=Pr\left[\mathcal{A}winstheGam{e}_{forge}\right].$$

For any PPT attacker $\mathcal{A}$, the advantage $Ad{v}_{\mathcal{A}}^{forge}$ of winning $Gam{e}_{forge}$ is negligible.

Definition 6

(Linkability). We define the linkability of IBLRS through the $Gam{e}_{link}$ below:

(1) 

System Setup: Challenger $\mathcal{C}$ inputs the security parameter λ, and the KGC generates $MSK$ and $pp$. $\mathcal{C}$ sends $pp$ to $\mathcal{A}$. $\mathcal{A}$ is allowed a polynomially bounded number of queries, each query potentially dependent on previous query results.

(2) 

Query Stage: $\mathcal{A}$ can access a polynomial-time oracle, and perform the aforementioned private key inquiries and signature inquiries.

(3) 

Forgery Stage: $\mathcal{A}$ outputs two signatures $Si{g}_1=(l_1^{\prime },\cdots ,l_N^{\prime },{\mathit{z}}^{\prime },{\mathit{\tau }}^{\prime })$ and $Si{g}_2=(l_1^{″},\cdots ,l_N^{″},{\mathit{z}}^{″},{\mathit{\tau }}^{″})$, with linking tag $\mathit{\tau },{\mathit{\tau }}^{\prime }$. If they satisfy the following conditions, then attacker $\mathcal{A}$ wins the linkability $Gam{e}_{link}$:

• $Verify(\mathit{\mu },W,Si{g}_i)=“1”$, $i\in \{1,2\}$;
• $Link(Si{g}_1,Si{g}_2)=“unlinkabl{e}^{″}$;
• Less than two inquiries for the private key are made by attacker $\mathcal{A}$ (attacker $\mathcal{A}$ can have at most one user’s private key).

The advantage of attacker $\mathcal{A}$ winning the linkability game is defined as follows:

$$Ad{v}_{\mathcal{A}}^{link}=Pr\left[\mathcal{A}winstheGam{e}_{link}\right].$$

For any PPT attacker $\mathcal{A}$, the advantage $Ad{v}_{\mathcal{A}}^{link}$ of winning the following $Gam{e}_{link}$ is negligible.

Definition 7

(Nonslanderability). The nonslanderability of IBLRS is defined by $Gam{e}_{NS}$ below:

(1) 

System Setup: Challenger $\mathcal{C}$ inputs the security parameter λ, and the KGC generates $MSK$ and $pp$. $\mathcal{C}$ sends $pp$ to $\mathcal{A}$. $\mathcal{A}$ is allowed a polynomially bounded number of queries, each query potentially dependent on previous query results.

(2) 

Query Stage I: $\mathcal{A}$ can access a polynomial-time oracle, and perform the aforementioned private key inquiries and signature inquiries.

(3) 

Challenge: Attacker $\mathcal{A}$ sends a tuple $(\mathit{\mu },W,\mathit{\tau },I{D}_b)$ to the challenger $\mathcal{C}$, with the $I{D}_b$ not having undergone a private key query. The challenger $\mathcal{C}$ returns a signature $Si{g}^{*}$.

(4) 

Query Stage II: Similar to Query Stage I, but private key queries for $I{D}_b$ and signature queries for $(I{D}_b,\mathit{\mu })$ are not allowed.

(5) 

Slander: On μ and τ, attacker $\mathcal{A}$ produces a new signature $Si{g}^{\prime }$. If the following scenarios are met, then attacker $\mathcal{A}$ wins the nonslanderability $Gam{e}_{NS}$:

• $Verify(\mathit{\mu },W,Si{g}^{\prime })=“1”$;
• $Si{g}^{\prime }$ did not result from any queries made in Query Stage I or Query Stage II;
• $Link(Si{g}^{*},Si{g}^{\prime })=“linkable”$.

The advantage of $\mathcal{A}$ winning the nonslanderability game is defined as follows:

$$Ad{v}_{\mathcal{A}}^{NS}=Pr\left[\mathcal{A}winsGam{e}_{NS}\right].$$

For any PPT attacker $\mathcal{A}$, the advantage $Ad{v}_{\mathcal{A}}^{NS}$ of winning $Gam{e}_{NS}$ is negligible.

4. The Proposed Scheme

In this section, we first present the system model of privacy-preserving transactions on the blockchain, and then describe the construction of an identity-based linkable dual ring signature (IB-LDRS) in detail.

4.1. System Model

As Figure 3 shows, the signer with $I{D}_i$ starts the transaction and creates a ring using his or her identity and the identity information of other users in the blockchain to protect anonymity in blockchain transactions. The signer signs the transaction data using their private key. Note that it is impossible for outsiders to identify which signer created the signature since the identities of the entire ring are used in the signature generation process. The ring signature and associated transaction details are broadcast along with the transaction to the blockchain network. The ring signature is validated by other nodes on the blockchain network, confirming that a member of the ring actually created it. Thus, the ring signature protects the identity privacy of its real signer.

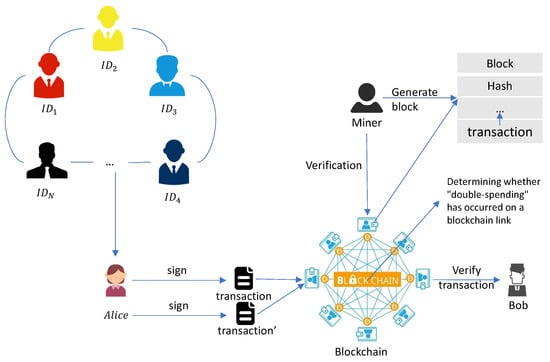
Figure 3. System model of IB-LDRS in blockchain transactions.

4.2. Parameters and Ranges

Before giving the algorithms, we first introduce the related parameters as follows: $q\ge 3$ is defined as the modulus of odd numbers, $m\ge 5nlogq$; ${\sigma }_1,{\sigma }_2$ are real numbers such that ${\sigma }_2\ge {\sigma }_1$. ${\mathcal{R}}_q$ is a ring ${\mathbb{Z}}_q\left[X\right]/(X^d+1)$ of dimension d. The set D is the collection of polynomials in ${\mathbb{Z}}_q\left[X\right]/(X^d+1)$. We define the total ring as $W=\{I{D}_1,I{D}_2,\cdots ,I{D}_N\}$. Define the following challenge space:

$$\mathcal{L}=\{l\in \mathbb{Z}\left[X\right]/(X^d+1):\parallel l{\parallel }_{\infty }=1\}$$

Observe that $\left|\mathcal{L}\right|=3^d$. When $d=128$, we have $\left|\mathcal{L}\right|=3^{128}>2^{202}$. During the computation, the polynomial coefficients need to be modulo 3. After performing the modulo operation, the polynomial coefficients will be within the range $\{-1,0,1\}$.

4.3. Construction

The proposed construction of the IB-LDRS scheme from lattices is described as follows:

IB-LDRS.Setup: The blockchain system executes Algorithm 1; this algorithm takes the security parameter $\lambda$ as input, and outputs the public parameter $pp$. $H_1$ and $H_2$ act as random oracles, and $H_3$ functions as a collision-resistant one-way function.

Algorithm 1: IB-LDRS.Setup

Input: $\lambda$. Output: $pp$. 1 define $H_1:{\{0,1\}}^{*}\to {\mathcal{R}}_q^n$, $H_2:{\{0,1\}}^{*}\to \mathcal{L}$, and $H_3:{\{0,1\}}^{*}\to {\mathcal{R}}_q^{n\times m}$; 2 generate $(\mathit{A},{\mathit{T}}_A)\leftarrow TrapGen(n,m,q)$, $\mathit{A}\in {\mathcal{R}}_q^{n\times m}$; 3 define $MSK:={\mathit{T}}_A$, $\Vert {\tilde{\mathit{T}}}_A\Vert \le O\left(\sqrt{nlogq}\right)$; 4 return $pp:=\{n,m,q,\mathit{A},H_1,H_2,H_3\}$.

IB-LDRS.KeyExt: The KGC runs Algorithm 2 to generate the user’s public and private keys; this algorithm takes the public parameters $pp=\{n,m,q,\mathit{A},H_1,H_2,H_3\}$, identity $I{D}_i$, and master private key $MSK$ as inputs; compute ${\mathit{p}}_{I{D}_i}$ using hash function $H_1\left(I{D}_i\right)$ and sample ${\mathit{s}}_{I{D}_i}$ using the $SamplePre(\mathit{A},{\mathit{T}}_A,{\sigma }_1,{\mathit{p}}_{I{D}_i})$ function. It outputs public key $I{D}_i$ and private key${\mathit{s}}_{I{D}_i}$.

Algorithm 2: IB-LDRS.KeyExt

Input: $\{I{D}_i,pp,MSK.\}$ Output: $p{k}_i,s{k}_i$. 1 compute ${\mathit{p}}_{I{D}_i}=H_1\left(I{D}_i\right)$; 2 sample ${\mathit{s}}_{I{D}_i}\leftarrow SamplePre(\mathit{A},{\mathit{T}}_A,{\sigma }_1,{\mathit{p}}_{I{D}_i})$ with trapdoor ${\mathit{T}}_A$, where ${\sigma }_1\ge \Vert {\tilde{\mathit{T}}}_A\Vert \omega \left(\sqrt{logq}\right)$, ${\mathit{s}}_{I{D}_i}\le {\sigma }_1\sqrt{md}$; 3 return: $(p{k}_i,s{k}_i)=(I{D}_i,{\mathit{s}}_{I{D}_i})$.

IB-LDRS.Sign: The transaction initiator, Alice, runs the signature Algorithm 3 to initiate a transaction; the following algorithm generates the ring signature of message $\mathit{\mu }$ based on the dual-ring architecture, given input $\mathit{\mu }$, $pp$, W. The signer’s index is $j,(1\le j\le N)$, ${\mathit{s}}_{I{D}_j}$.

Algorithm 3: IB-LDRS.Sign

Input: $pp,W,\mathit{\mu },{\mathit{s}}_{I{D}_j}$ Output: $Sig$. 1 compute ${\mathit{A}}_{com}=H_3(\mathit{A},\mathit{\mu })$; 2 define $\mathit{\tau }:={\mathit{A}}_{com}·{\mathit{s}}_{I{D}_j}$; 3 pick $\mathit{r}\leftarrow D_{{\sigma }_2}^m,\mathit{e}=\mathit{A}·\mathit{r}\in {\mathcal{R}}_q^n,l_i\leftarrow \mathcal{L},i\in \{1,\cdots ,N\}$, $i\ne j$; 4 compute $\mathit{c}=\mathit{e}-{\sum }_{i=1,i\ne j}^N{l}_i·H_1\left(I{D}_i\right)$ 5 compute $\mathit{u}={\mathit{A}}_{com}·\mathit{r}-{\sum }_{i=1,i\ne j}^N{l}_i·\mathit{\tau }$; 6 compute $l_j=H_2(\mathit{c},\mathit{\mu },W,\mathit{u})-{\sum }_{i=1,i\ne j}^N{l}_i$; 7 define and compute $\mathit{z}:=\mathit{r}+l_j·{\mathit{s}}_{I{D}_j}$; 8 if $\parallel \mathit{z}\parallel >({\sigma }_1+{\sigma }_2)\sqrt{md}$, then restart from step 3; 9 return $Sig=(l_1,l_2,\cdots ,l_N,\mathit{z},\mathit{\tau })$

   IB-LDRS.Verify: The transaction receiver, Bob, runs the verification Algorithm 4 to verify the transaction; given $pp$, W, $\mathit{\mu }$, and $Sig$, verify it by the following steps.

Algorithm 4: IB-LDRS.Verify

Input: $pp,W,\mathit{\mu },Sig$ Output: 0 or 1. 1 if    $l_i\notin \mathcal{L}$, return 0 2 if    $\parallel {\mathit{z}}^{\prime }\parallel >({\sigma }_1+{\sigma }_2)\sqrt{md}$, return 0 3 ${\mathit{A}}_{com}=H_3(\mathit{A},\mathit{\mu })$ 4 ${\mathit{c}}^{\prime }=\mathit{A}·{\mathit{z}}^{\prime }-{\sum }_{i=1}^N{l}_i·H_1\left(I{D}_i\right)$ 5 ${\mathit{u}}^{\prime }={\mathit{A}}_{com}·{\mathit{z}}^{\prime }-{\sum }_{i=1}^N{l}_i·\mathit{\tau }$ 6 check if ${\sum }_{i=1}^N{l}_i=H_2({\mathit{c}}^{\prime },\mathit{\mu },W,{\mathit{u}}^{\prime })$, if so return 1 7 else return 0

   IB-LDRS.Link: The blockchain link runs the linking Algorithm 4 to conduct “double-spending” detection. Once it receives two different and valid signatures $Sig,Si{g}^{\prime }$ to be tested, this algorithm checks whether $\mathit{\tau }\stackrel{?}{=}{\mathit{\tau }}^{\prime }$. If it does, it returns “linkable”; otherwise, it returns “unlinkable”. Note that this algorithm tests valid signatures only, because it can invoke Algorithm 4 to check the validity and reject the invalid signatures. If both of the signatures are accepted, go to Algorithm 5 to check whether they are generated by the same signer.

Algorithm 5: IB-LDRS.Link

Input: $Sig,Si{g}^{\prime }$ Output: linkable or unlinkable. 1 if $\mathit{\tau }={\mathit{\tau }}^{\prime }$, return “linkable” 2 else, return “unlinkable”

5. Security Analysis

Theorem 2

(Correctness). A linkable ring signature generated by a legitimate signature system can pass the verification of the algorithm, thereby satisfying the correctness verification.

Since it is impossible to determine whether it has been tampered with during transmission, suppose $Si{g}^{\prime }=(l_1^{\prime },l_2^{\prime },\cdots ,l_N^{\prime },{\mathit{z}}^{\prime },{\mathit{\tau }}^{\prime })$ is the signature received by the IB-LDRS.Verify Algorithm 4, $\mathit{z}=\mathit{r}+l_j·{\mathit{s}}_{I{D}_j}$, and it will be accepted by the IB-LDRS.Verify Algorithm 4 as follows.

Correctness of $\mathit{u}$:

$$\begin{array}{cc}\hfill {\mathit{u}}^{\prime }& ={\mathit{A}}_{com}·{\mathit{z}}^{\prime }-{\sum }_{i=1}^N{l}_i^{\prime }·\mathit{\tau }\hfill \\ \hfill & ={\mathit{A}}_{com}·(\mathit{r}+l_j^{\prime }·{\mathit{s}}_{I{D}_j})-{\sum }_{i=1}^N{l}_i^{\prime }·\mathit{\tau }\hfill \\ \hfill & ={\mathit{A}}_{com}·\mathit{r}+l_i^{\prime }·{\mathit{A}}_{com}·{\mathit{s}}_{I{D}_i}-{\sum }_{i=1}^N{l}_i^{\prime }·\mathit{\tau }\hfill \\ \hfill & ={\mathit{A}}_{com}·\mathit{r}-{\sum }_{i=1,i\ne j}^N{l}_i^{\prime }·\mathit{\tau }\hfill \\ \hfill & =\mathit{u}\hfill \end{array}$$

Correctness of $Sig$:

$$\begin{array}{cc}\hfill {\mathit{c}}^{\prime }& =\mathit{A}·{\mathit{z}}^{\prime }-{\sum }_{i=1}^N{l}_i^{\prime }·H_1\left(I{D}_i\right)\hfill \\ \hfill & =\mathit{A}·(\mathit{r}+l_j^{\prime }·{\mathit{s}}_{I{D}_j})-{\sum }_{i=1}^N{l}_i^{\prime }·H_1\left(I{D}_i\right)\hfill \\ \hfill & =\mathit{A}·\mathit{r}+l_j^{\prime }·\mathit{A}·{\mathit{s}}_{I{D}_j}-{\sum }_{i=1}^N{l}_i^{\prime }·H_1\left(I{D}_i\right)\hfill \\ \hfill & =\mathit{A}·\mathit{r}-{\sum }_{i=1,i\ne j}^N{l}_i^{\prime }·H_1\left(I{D}_i\right)\hfill \\ \hfill & =\mathit{c}\hfill \end{array}$$

Therefore, ${\sum }_{i=1}^N{l}_i=H_2({\mathit{c}}^{\prime },\mathit{\mu },W,{\mathit{u}}^{\prime })$ holds, and the proposed scheme meets the correctness requirement.

Theorem 3

(Unforgeability). Under the assumption of ${M-\mathit{SIS}}_{n,m+1,q,\beta }$, for any PPT attacker $\mathcal{A}$, the scheme is unforgeable under chosen message attacks and insider corruption attacks in the random oracle model, where $\beta \le 3({\sigma }_1+{\sigma }_2)\sqrt{md+1}$.

Proof. 

Let us assume that there is an attacker $\mathcal{A}$ with a non-negligible advantage $\epsilon$ that can forge signatures in polynomial time. Then, there is a challenger $\mathcal{C}$ that has a non-negligible probability of solving the M-SIS hard problem. Assume $\mathcal{C}$ has an ${\mathrm{M}-\mathrm{SIS}}_{n,m+1,q,\beta }$ instance $(\widehat{\mathit{A}},n,m,q,\beta )$ to solve, where $\widehat{\mathit{A}}\in {\mathbb{R}}_q^{n\times (m+1)}$. Finding a short vector e such that $\widehat{\mathit{Ae}}=\mathbf{0}modq$ that $\left|\right|\mathit{e}\left|\right|\le \beta$ is the aim of $\mathcal{C}$. $\mathcal{C}$ first transforms $\widehat{\mathit{A}}$ into the form $\left[\mathit{A}\right|\left|\mathit{a}\right]$, and then embeds it in the reduction algorithm. The hash functions $H_1$ and $H_2$ are random oracles. $\mathcal{C}$ establishes four lists, $L_1,L_2,L_3$, and $L_4$, which are used to store $H_1$-oracle, $H_2$-oracle, signature queries, and corruption queries, respectively. The following describes how $\mathcal{C}$ and $\mathcal{A}$ interact:

• IB-LDRS.Setup Stage: Generate system parameter $pp$. Send the system parameters $pp=\{n,m,q,\mathit{A},H_1,H_2,H_3\}$ and the ring W to $\mathcal{A}$.
• Query phase: During this phase, the attacker $\mathcal{A}$ interacts with $\mathcal{C}$ by making oracle queries to learn information about the scheme. The challenge $\mathcal{C}$ responds to the queries as follows.

  (1)

  $H_1$ oracle query: When $\mathcal{A}$ submits user $I{D}_i(i\in \left[N\right])$ to $\mathcal{C}$, for $i\ne j^{*}$, $\mathcal{C}$ checks whether $(I{D}_i,\ast ,\ast )$ exists in $L_1$: if so, it returns ${\mathit{s}}_{I{D}_i}$ to $\mathcal{A}$; if not, $\mathcal{C}$ randomly selects ${\mathit{s}}_{I{D}_i}\in {\mathcal{D}}_{\sigma }^m$, and then computes ${\mathit{p}}_{I{D}_i}=\mathit{A}·{\mathit{s}}_{I{D}_i}$, assigns ${\mathit{p}}_{I{D}_i}$ to $H_1\left(I{D}_i\right)$, and returns it to $\mathcal{A}$. $\mathcal{C}$ records it in list $L_1=(I{D}_i,{\mathit{s}}_{I{D}_i},H_1\left(I{D}_i\right))$. If $i=j^{*}$, $\mathcal{C}$ sets

  $$H_1\left(I{D}_{j^{*}}\right)=\mathit{A}·\mathit{s}+\mathit{a}$$

  (1)

  for randomly chosen $\mathit{s}\in {\mathcal{D}}_{\sigma }^m$, and returns $H\left(I{D}_{j^{*}}\right)$ to $\mathcal{A}$; $\mathcal{C}$ records it in list $L_1=(I{D}_{j^{*}},\mathit{s},H\left(I{D}_{j^{*}}\right))$.

  (2)

  $H_2$ oracle query: Upon $\mathcal{C}$ receiving an $H_2$ oracle query with message $\mathit{\mu }$, ring $W^{\prime }\in \{I{D}_1,I{D}_2,\cdots ,I{D}_N\}$, and intermediate parameters R and T to $\mathcal{C}$ from $\mathcal{A}$, $\mathcal{A}$ first searches $(\mathit{c},\mathit{\mu },W,\mathit{u},*)$ in list $L_2$; if found, it returns the corresponding hash value to $\mathcal{A}$; if not, it randomly choose a vector $l\leftarrow \mathcal{L}$, and returns l to $\mathcal{A}$. Finally, $\mathcal{C}$ records $(\mathit{c},\mathit{\mu },W,\mathit{u},l)$ in list $L_2$. This query can be made at most $q_H$ times.

  (3)

  Registration query: When $\mathcal{A}$ sends a new identity $I{D}_i\notin W$ for registration, $\mathcal{C}$ first randomly chooses ${\mathit{s}}_{I{D}_i}$ and computes $H_1\left(I{D}_i\right)=\mathit{A}·{\mathit{s}}_{I{D}_i}$ as for the $H_1$ oracle, and then returns the private key ${\mathit{s}}_{I{D}_i}$ to $\mathcal{A}$. Finally, $\mathcal{C}$ adds $I{D}_i$ to list $L_4$ and tuple $(I{D}_i,{\mathit{s}}_{I{D}_i},H_1\left(I{D}_i\right))$ to list $L_1$.

  (4)

  Signing oracle query: When $\mathcal{A}$ submits an inquiry for a ring signature on identity $I{D}_j$ of message $\mathit{\mu }$ under ring $W^{\prime }$ such that $I{D}_j\in W^{\prime }$, if $j=j^{*}$, $\mathcal{C}$ chooses random $\mathit{z}$ with $\left|\right|\mathit{z}\left|\right|\le ({\sigma }_1+{\sigma }_2)\sqrt{md}$, and random $l_1,\cdots ,l_{j-1},l_{j+1},\cdots ,l_N\in \mathcal{L}$, and computes ${\mathit{c}}^{\prime }$ and ${\mathit{u}}^{\prime }$ as in the verification algorithm. $\mathcal{C}$ calculates $l_j$ through $l_j=H_2({\mathit{c}}^{\prime },\mathit{\mu },W,{\mathit{u}}^{\prime })-{\sum }_{i=1,i\ne j}^N{l}_i$, and stores it in $L_2$, and then returns the signature $Sig=(l_1,\cdots ,l_N,\mathit{z},\mathit{\tau })$, where $\mathit{\tau }=H_3\left(\mathit{A}\right)\mathit{s}$. If $j\ne j^{*}$, $\mathcal{C}$ first checks if $W^{\prime }\in \{I{D}_1,I{D}_2,\cdots ,I{D}_N\}\cup L_4$. If not, it returns ⊥ to $\mathcal{A}$. If it does meet the condition, $\mathcal{C}$ directly checks tuple $(\mathit{\mu },I{D}_j,W^{\prime },\ast )$ in list $L_3$ and returns the signature to $\mathcal{A}$ if it does exist. Otherwise, $\mathcal{C}$ generates a new signature as in the following steps. If it does exist, $\mathcal{C}$ researches $(I{D}_j,\ast ,\ast )$ in list $L_1$. If it exists, $\mathcal{C}$ generates a ring signature $Sig=(l_1,\cdots ,l_N,\mathit{z},\mathit{\tau })$ of $\mathit{\mu }$ under $W^{\prime }$ with ${\mathit{s}}_{I{D}_i}$ by the steps in the signing algorithm. If $(I{D}_i,\ast ,\ast )$ does not exist in list $L_1$, $\mathcal{C}$ invokes the $H_1$ oracle to achieve the private key and then generates ring signature $Sig$ as before. Note that tuple $(\mathit{c},\mathit{\mu },W^{\prime },\mathit{u},l)$ should have been added to list $L_2$ by the query to $H_2$ during the generation of the ring signature, where $\mathit{c}$ is an intermediate value in signing procedures. Finally, $\mathcal{C}$ returns the signature $Sig$ of message $\mathit{\mu }$ under ring $W^{\prime }$, and then stores tuple $(\mathit{\mu },I{D}_j,W^{\prime },Sig)$ in list $L_3$.

  (5)

  Corruption query: If $\mathcal{A}$ selects a user identity $I{D}_i(i\in \left[N\right],i\ne j)$ to corrupt, $\mathcal{C}$ first checks whether $I{D}_i$ exists in list $L_4$. If it does, $\mathcal{C}$ searches $(I{D}_i,\ast ,\ast )$ in list $L_1$ and returns the corresponding private key ${\mathit{s}}_{I{D}_i}$ to $\mathcal{A}$; if it does not, $\mathcal{C}$ randomly choose ${\mathit{s}}_{I{D}_i}$ and generates $H_1\left(I{D}_i\right)$ as for the $H_1$ oracle, and then returns the private key ${\mathit{s}}_{I{D}_i}$ to $\mathcal{A}$. Finally, $\mathcal{C}$ adds $I{D}_i$ to list $L_4$, and tuple $(I{D}_i,{\mathit{s}}_{I{D}_i},H_1\left(I{D}_i\right))$ to list $L_1$. If $\mathcal{A}$ selects a user identity $I{D}_i(i\in \left[N\right],i\ne j)$ to corrupt, $\mathcal{C}$ fails and aborts.

• Forgery Stage: After polynomial queries to the oracles, $\mathcal{A}$ submits a signature $Si{g}^{*}=(l_1^{*},l_2^{*},\cdots ,l_N^{*},{\mathit{z}}^{*},{\mathit{\tau }}^{*})$ of message $\mathit{\mu }$ under ring $W^{*}$ as his or her forgery to challenger $\mathcal{C}$. The signature $Si{g}^{*}$ is considered to be a successful forgery if it satisfies the following conditions:

  (1)

  Attacker $\mathcal{A}$ never registers or corrupts any user $I{D}_i^{*}\in W^{*}$, that is, $W^{*}\cap L_4=\varnothing$;

  (2)

  Attacker $\mathcal{A}$ has not queried the signature of ${\mathit{\mu }}^{*}$ under $W^{*}$, that is, $({\mathit{\mu }}^{*},W^{*},Si{g}^{*})\notin L_3$;

  (3)

  The forgery $({\mathit{\mu }}^{*},W^{*},Si{g}^{*})$ can pass the verification algorithm, that is,

  IB-LDRS.Verify $({\mathit{\mu }}^{*},W^{*},Si{g}^{*})$=“1”.

Analysis: Assume ${\sigma }^{*}=(l_1^{*},l_2^{*},\cdots ,l_N^{*},{\mathit{z}}^{*},{\mathit{\tau }}^{*})$ is a successful forgery with probability $\epsilon$; then, the verification equation

$${\mathit{c}}^{*}={\mathit{Az}}^{*}-\sum _{I{D}_i\in W^{*}}{l}_i^{*}·H_1\left(I{D}_i\right)$$

(2)

holds from the correctness property. There must be one $l_i^{*}\in \{l_1^{*},l_2^{*},\cdots ,l_N^{*}\}$ that comes from the response of oracle $H_2$, so $({\mathit{c}}^{*},{\mathit{\mu }}^{*},W^{*},{\mathit{u}}^{*},l_j^{*})$ can be found in list $L_2$. From the general forking lemma [28], $\mathcal{C}$ can obtain another valid signature $Si{g}^{\prime }=(l_1^{\prime },l_2^{\prime },\cdots ,l_N^{\prime },{\mathit{z}}^{\prime },{\mathit{\tau }}^{\prime })$ where $Si{g}^{\prime }\ne Si{g}^{*}$ with same randomness from $\mathcal{A}$ of message ${\mathit{\mu }}^{*}$ under $W^{*}$ by rewinding the random oracle $H_2$, with a probability at least ${\displaystyle \frac{\epsilon }{q_H}}-{\displaystyle \frac{1}{3^d}}$. So, $l_i^{\prime }=l_i^{*}$ for $i\ne j$, ${\mathit{c}}^{\prime }={\mathit{c}}^{*}$, ${\mathit{r}}^{*}={\mathit{r}}^{\prime }$,$l_j^{\prime }\ne l_j^{*}$. The verification equation

$${\mathit{c}}^{\prime }=\mathit{A}{\mathit{z}}^{\prime }-\sum _{I{D}_i\in W^{\prime }}{l}_i^{\prime }·H_1\left(I{D}_i\right)$$

(3)

holds by the correctness property. Subtracting Equation (2) from Equation (3) yields the following equation:

$$\begin{array}{cc}\hfill (l_{j^{\prime }}^{\prime }-l_j^{*})H_1\left(I{D}_j\right)& =\mathit{A}({\mathit{z}}^{*}-{\mathit{z}}^{\prime })+(l_{j^{\prime }}^{\prime }-l_j^{*}){\mathit{Ar}}^{*}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & =\widehat{\mathit{A}}\left[\left(\begin{array}{c}{\mathit{z}}^{*}-{\mathit{z}}^{\prime }\\ 0\end{array}\right)+(l_{j^{\prime }}^{\prime }-l_j^{*})\left(\begin{array}{c}{\mathit{r}}^{*}\\ 0\end{array}\right)\right]\hfill \end{array}$$

(5)

Then, we multiply Equation (1) by $(l_{j^{\prime }}^{\prime }-l_j^{*})$ to achieve

$$\begin{array}{cc}\hfill (l_{j^{\prime }}^{\prime }-l_j^{*})H_1\left(I{D}_j\right)& =\mathit{A}(l_{j^{\prime }}^{\prime }-l_j^{*})\mathit{s}+(l_{j^{\prime }}^{\prime }-l_j^{*})\mathit{a}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & =\widehat{\mathit{A}}(l_{j^{\prime }}^{\prime }-l_j^{*})\left(\begin{array}{c}\mathit{s}\\ 1\end{array}\right)\hfill \end{array}$$

(7)

By subtracting Equation (7) from Equation (5), we obtain a short $\mathit{e}$ such that

$$\mathit{e}=(l_{j^{\prime }}^{\prime }-l_j^{*})\left(\begin{array}{c}\mathit{s}\\ 1\end{array}\right)-\left[\left(\begin{array}{c}{\mathit{z}}^{*}-{\mathit{z}}^{\prime }\\ 0\end{array}\right)+(l_{j^{\prime }}^{\prime }-l_j^{*})\left(\begin{array}{c}{\mathit{r}}^{*}\\ 0\end{array}\right)\right].$$

$\mathit{e}$ is a non-zero vector as its last coordinate is $(l_{j^{\prime }}^{\prime }-l_j^{*})$ which is not zero. Therefore, $\mathcal{C}$ can output a valid solution to ${\mathrm{M-SIS}}_{n,m+1,q,\beta }$, where $\beta =3({\sigma }_1+{\sigma }_2)\sqrt{md+1}$. Therefore, we can conclude that our signature algorithm is strongly unforgeable under the message chosen and the insider corruption attack. This completes the proof. □

Theorem 4

(Anonymity). The proposed IB-LDRS scheme satisfies unconditional anonymity.

Proof. 

The challenger $\mathcal{C}$ and the PPT attacker $\mathcal{A}$ interact in a game to prove the scheme’s anonymity. The attacker $\mathcal{A}$ provides $\mathcal{C}$ with a message, two identities, and a ring, after which $\mathcal{C}$ returns a signature. If $\mathcal{A}$ can guess the identity of the signer with a non-negligible probability, the scheme’s anonymity is compromised.

• IB-LDRS.Setup Stage: Determine the ring $W^{*}=\{I{D}_1,I{D}_2,\cdots ,I{D}_N\}$. Challenger $\mathcal{C}$ generates $pp$ and W for each user. Then, $\mathcal{C}$ sends $pp=\{n,m,q,\mathit{A},H_1,H_2,H_3\}$ to $\mathcal{A}$.
• Query Stage: Conduct various queries adaptively on $\mathcal{C}$ with polynomial time limits.
• Challenge Stage: $\mathcal{A}$ submits a message $\mathit{\mu }$, ring $W^{*}=\{I{D}_1^{*},I{D}_2^{*},\cdots ,I{D}_N^{*}\}$, and user identity $I{D}_b$ to $\mathcal{C}$. $\mathcal{C}$ randomly selects $b\in \{0,1\}$, computes for $i\ne j,l_i^{*}\leftarrow \mathcal{L},l_j^{*}=H_2(\mathit{c},\mathit{\mu },W^{*},\mathit{u})-{\sum }_{i=1,i\ne j}^N{l}_i^{*},{\mathit{z}}^{*}={\mathit{r}}^{*}-{\mathit{s}}_{I{D}_j}^{*}{l}_j^{*}$, and performs a ring signature $Si{g}^{*}=(l_1^{*},\cdots ,l_N^{*},{\mathit{z}}^{*},{\mathit{\tau }}^{*})$, then sends it to $\mathcal{A}$.
• Guess Stage: $\mathcal{A}$ outputs the guess $b^{\prime }$.
• Forgery Stage: To demonstrate that the probability $Ad{v}_{\mathcal{A}}^{anon}=|Pr[b^{\prime }=b]-1/2|=\epsilon$ of $\mathcal{A}$ winning the game is negligible, we only need to prove that the signature $Si{g}^{*}=\{l_1^{*},\cdots ,l_N^{*},{\mathit{z}}^{*},{\mathit{\tau }}^{*}\}$ generated by $I{D}_b$ and the signature $Si{g}^{\prime }=\{l_1^{\prime },\cdots ,l_N^{\prime },{\mathit{z}}^{\prime },{\mathit{\tau }}^{\prime }\}$ generated by $I{D}_{1-b}$ are statistically indistinguishable.

When signing $Si{g}^{*}$, $i\ne b$ results in $l_i\leftarrow \mathcal{L}$, and $i=b$ results in $l_b=H_2(\mathit{c},\mathit{\mu },W,\mathit{u})-{\sum }_{i=1,i\ne j}^N{l}_i·\mathit{\tau }$, ${\mathit{z}}^{*}=r^{*}+{\mathit{s}}_{I{D}_b}$, according to Theorem 1, ${\mathit{z}}^{*}$ and the Gaussian distribution $D_{\sigma }^{m+1}$ are statistically indistinguishable; thus, the signature $Si{g}^{*}$ is statistically indistinguishable from $D_{\sigma }^{m+1}$. Similarly, the signature $Si{g}^{\prime }$ is also statistically indistinguishable from $D_{\sigma }^{m+1}$. Therefore, $Si{g}^{*}$ and $Si{g}^{\prime }$ follow the same discrete Gaussian distribution, making them statistically indistinguishable. Consequently, the probability that $\mathcal{A}$ can determine whether $Si{g}^{*}$ was generated by $I{D}_0$ or $I{D}_1$ is negligible. □

Theorem 5

(Linkability). For any polynomial-time attacker $\mathcal{A}$, the proposed IB-LDRS scheme is linkable in the ROM.

Proof. 

The linkability of the scheme is proved by an interactive security game between challenger $\mathcal{C}$ and a PPT adversary $\mathcal{A}$.

• IB-LDRS.Setup Stage: Challenger $\mathcal{C}$ inputs the security parameter $\lambda$. Generate the public parameter $pp$. Send the system parameter $pp$ to the attacker $\mathcal{A}$.
• Inquiry Stage: Same as in the scheme’s unforgeability proof.
• Challenge Stage I: The attacker $\mathcal{A}$ provides two signatures, denoted $Si{g}_1=(l_1^{\prime },\cdots ,l_N^{\prime },{\mathit{z}}^{\prime },{\mathit{\tau }}^{\prime })$ and $Si{g}_2=(l_1^{″},\cdots ,l_N^{″},{\mathit{z}}^{″},{\mathit{\tau }}^{″})$.

Analysis. Attacker $\mathcal{A}$ uses a single private key to generate two ring signatures $Si{g}_1$ and $Si{g}_2$ for the same message with a non-negligible probability. These signatures can pass the verification algorithm and satisfy ${\mathit{\tau }}^{\prime }\ne {\mathit{\tau }}^{″}$.

$$\{\begin{array}{}\mathrm{(8)}& {\mathit{c}}^{\prime }=\mathit{A}{\mathit{z}}^{\prime }-{\displaystyle \sum _{i=1}^N}{l}_i^{\prime }·H_1\left(I{D}_i\right)\mathrm{(9)}& {\mathit{u}}^{\prime }={\mathit{A}}_{com}{\mathit{z}}^{\prime }-{\displaystyle \sum _{i=1}^N}{l}_i^{\prime }·{\mathit{\tau }}^{\prime }\end{array}$$

$$\{\begin{array}{}\mathrm{(10)}& {\mathit{c}}^{″}=\mathit{A}{\mathit{z}}^{″}-{\displaystyle \sum _{i=1}^N}{l}_i^{″}·H_1\left(I{D}_i\right)\mathrm{(11)}& {\mathit{u}}^{″}={\mathit{A}}_{com}{\mathit{z}}^{″}-{\displaystyle \sum _{i=1}^N}{l}_i^{″}·{\mathit{\tau }}^{″}\end{array}$$

We assume that ${\mathit{c}}^{\prime }$, ${\mathit{c}}^{″}$, and ${\mathit{u}}^{\prime }$ are generated by the signer’s own private key, while ${\mathit{u}}^{″}$ is forged. Simplifying the operations Equations (10) and (11) yields the following:

$$\{\begin{array}{}\mathrm{(12)}& \mathit{A}\mathit{r}-{\displaystyle \sum _{i=1,i\ne j}^N}{l}_i^{″}·H_1\left(I{D}_i\right)=\mathit{A}{\mathit{z}}^{″}-{\displaystyle \sum _{i=1}^N}{l}_i^{″}·H_1\left(I{D}_i\right)\mathrm{(13)}& {\mathit{A}}_{com}\mathit{r}-{\displaystyle \sum _{i=1,i\ne j}^N}{l}_i^{″}·{\mathit{\tau }}^{″}={\mathit{A}}_{com}{\mathit{z}}^{″}-{\displaystyle \sum _{i=1}^N}{l}_i^{″}·{\mathit{\tau }}^{″}\end{array}$$

$$\{\begin{array}{}\mathrm{(14)}& \mathit{A}·l_j^{″}·({\mathit{s}}_{I{D}_j}-{\mathit{s}}_{I{D}_j})=\mathbf{0}\mathrm{(15)}& {\mathit{A}}_{com}·l_j^{″}·({\mathit{s}}_{I{D}_j}-{\mathit{s}}_{ID}^{\prime })=\mathbf{0}\end{array}$$

From the above equations, through simple derivation, we can obtain ${\mathit{s}}_{I{D}_j}={\mathit{s}}_{ID}^{\prime }$, which leads to ${\mathit{\tau }}^{\prime }={\mathit{\tau }}^{″}$. This contradicts the assumption; thus, the signatures of the same signer on the same message can be linked.

In the event that the signer did not utilize their private key in $Si{g}_2$, then the signature is legitimately faked. According to the unforgeability of Theorem 3, challenger $\mathcal{C}$ can generate $Si{g}_2^{*}$ using the forking lemma based on forger $\mathcal{A}$’s ability. Subtracting ${\mathit{c}}^{″}$ from ${\mathit{c}}^{*}$ yields $\mathit{A}({\mathit{z}}^{″}-{\mathit{z}}^{*})=\mathbf{0}$; thus, we obtain a solution to the M-SIS hard problem. Therefore, we can conclude that legitimate signatures generated for the same message by the same signer are linkable. This completes the proof. □

Theorem 6

(Nonslanderability). The IB-LDRS is nonslanderable in the random oracle model, if the M-SIS problem is hard.

Proof. 

Challenger $\mathcal{C}$ and polynomial-time attacker $\mathcal{A}$ interact in a game to prove the nonslanderability of the scheme. We will explain that the nonslanderability relies on the scheme’s unforgeability.

In the security model of nonslanderability, attacker $\mathcal{A}$ sends a tuple $(\mathit{\mu },W,\mathit{\tau },I{D}_b)$ to challenger $\mathcal{C}$, with the $I{D}_b$ not having undergone a private key query. Challenger $\mathcal{C}$ obtains the private key ${\mathit{s}}_{I{D}_b}$ for the $ID$ by running IB-LDRS.KeyExt$(I{D}_b,pp,MSK,\mathit{\tau })$. Then, challenger $\mathcal{C}$ runs IB-LDRS.Sign$(pp,W,\mathit{\mu },{\mathit{s}}_{I{D}_b})$ to obtain the signature $Si{g}^{*}$. On the same message $\mathit{\mu }$ and tag $\mathit{\tau }={\mathit{\tau }}^{\prime }$, attacker $\mathcal{A}$ produces a new signature $Si{g}^{\prime }$.

This implies that, for any PPT attacker $\mathcal{A}$, if he or she knows ${\mathit{s}}_{I{D}_{\pi }}\in W\setminus \left\{I{D}_b\right\}$, he or she can produce a signature with the linkability tag $\mathit{\tau }$ without knowing the private key ${\mathit{s}}_{I{D}_b}$. According to the unforgeability of Theorem 3, challenger $\mathcal{C}$ can generate $Si{g}^{″}$ using the forking lemma based on forger $\mathcal{A}$’s ability. Subtracting ${\mathit{c}}^{″}$ from ${\mathit{c}}^{\prime }$ yields $\mathit{A}({\mathit{z}}^{″}-{\mathit{z}}^{\prime })=\mathbf{0}$; thus, we obtain a solution to the M-SIS hard problem. Consequently, we can state that legitimate signatures generated by the same signer for the same message ought to be connected. □

6. Performance Analysis

In this section, we will compare our scheme with other ring signature schemes, including functionality, computational overhead, and communication overhead.

6.1. Functionality Comparison

We compare the scheme’s functionality with those of other schemes in the section below. Table 2 compares five features, including post-quantum resistant (PQR), linkability (Link), identity-based (ID-based), dual-ring (DR), and hard problem assumptions (Assumption). Unlike the Yuen et al. [23] lattice-based dual-ring signature system from 2019, our scheme improves linkability and resolves the blockchain’s “double-spending” problem. The SM2-based dual-ring scheme proposed by Feng et al. [24] in 2024 is similar in structure to our scheme, but it does not possess quantum-resistant properties. Tang et al. presented [26], a scheme based on the NTRU lattice that satisfies the properties of PQR, Link, and ID-based. The two schemes [30,31] only satisfy the PQR and ID-based properties. The schemes in [20,32,33] satisfy all properties except DR. Our scheme satisfies all the functionalities aforementioned.

Table 2. Comparison of functionality.

Scheme	PQR	Link	ID-Based	DR	Assumption
[23]	√	×	×	√	M-SIS
[24]	×	√	×	√	DDH
[26]	√	√	√	×	NTRU-SIS
[30]	√	×	√	×	SIS
[31]	√	×	√	×	SIS&LWE
[33]	√	√	√	×	M-LWE&M-SIS
[20]	√	√	√	×	SIS
[32]	√	√	√	×	R-SIS
Ours	√	√	√	√	M-SIS

6.2. Comparison of Costs

We selected three schemes with similar functionalities to our proposed scheme [20,32,33] for a comparison of computational and communication overhead.

The time comparisons for $MSK$ generation, individual user $sk$ generation, and $Sig$ generation of the three schemes are shown in Table 3. Here, $\lambda$ represents the security parameter, N denotes the number of ring members, and $T_1$ represents the average time for the TrapGen algorithm. Because [33] is not identity-based, there is no such time overhead. For this part, it is represented by “/”. $T_2$ represents the average time for the SamplePre algorithm. $T_3$ represents the average time for polynomial modular multiplication. $T_4$ represents the average time for scalar multiplication. Table 3 presents a comparative analysis of the time overhead, individual user $sk$ generation time, and signature generation time for the four schemes. We ignored less time-consuming procedures like hash functions and matrix additions in favor of concentrating mostly on computationally demanding operations.

Table 3. Comparison of time costs.

Scheme	MSK-Cost	Ext-Cost	Sig-Cost
[20]	$T_1$	$T_2$	$(2N+1)T_4$
[32]	$T_1$	$T_1+m{T}_2$	$2(N+1)T_4$
[33]	/	$T_4$	$(2N+1)T_4$
Ours	$T_1$	$T_2$	$3T_3+(2N-1)T_4$

Table 4 compares the communication overhead of three schemes in terms of private key size and signature size. Our private key is generated using the SamplePre algorithm and is an m-dimensional vector multiplied by the polynomial dimension d. The private key in [20] is generated using BasisDel and SamplePre, resulting in an m-dimensional vector. The scheme in [33] uses the SampleDom algorithm to generate the private key, with the size being the same as in [20]. In our scheme, $l_i$ in the signature is a d-dimensional vector with values in the range {−1, 0, 1}, so its size is $dlog3$. The vectors $\mathit{z}$ and $\mathit{\tau }$ are m-dimensional and n-dimensional vectors, respectively, and, since the scheme is based on the M-SIS hard problem, they need to be multiplied by the polynomial dimension d. Although this makes our scheme appear larger in size compared to other schemes, the values of m and n in our scheme are very small, so the signature size is smaller compared to other schemes.

Table 4. Comparison of communication costs.

Scheme	$\left|\mathit{sk}\right|$	$\left|\mathit{Sig}\right|$
[20]	$mlogq$	$(Nm+N+n)logq$
[32]	$m·2^{\lambda }log3$	$Nm·2^{\lambda }logq+2^{\lambda }log3$
[33]	$mlogq$	$(mN+n)logq$
Ours	$mdlogq$	$Ndlog3+(m+n)dlogq$

We set the parameters $d=128$ and $q=2^{32}=4294967296$. In our signature scheme, $|l_i|=(dlog3)/8bytes$, $\left|\mathit{z}\right|=(mdlogq)/8bytes$, and $\left|\mathit{\tau }\right|=(ndlogq)/8bytes$. Here are the estimated signature sizes for this scheme with different numbers of ring members based on the parameters in [23].

In Table 5, we provide the sizes of the proposed ring signature with the increase in ring size N, as well as the sizes of responses $l_i$. “Sig Size” denotes the sizes of signature, while the “Size of $(l_1,\cdots ,l_N)$” shows the sizes of the hash values in the ring signatures. Figure 4 shows the increasing trend of communication costs with the ring scale. We can observe that, although the signature size increases linearly with the number of ring members N, the size of $\mathit{z}$ in the signature does not change significantly. When the number of ring members $N\le 64$, the signature size does not change much, and it is no more than 13 KB even when $N=64$. The size is mainly affected by the response $\mathit{z}$. Therefore, the signature size is mainly related to the number of $l_i$ values. Since the $l_i$ values are very small, the signature size does not change much as the number of ring members increases. When N reaches 128, the signature size is just under 15 KB. When N grows to 2048 and the parameters n and m are chosen to be larger, the signature size is 62.72 KB, which is still acceptable for most application scenarios.

Table 5. Communication costs (KB).

N	n	m	Sig Size	Size of $({\mathit{l}}_1,\cdots ,{\mathit{l}}_{\mathit{N}})$
2	7	15	$11.05$	$0.05$
4	7	15	$11.10$	$0.10$
8	7	15	$11.20$	$0.20$
16	7	15	$11.40$	$0.40$
32	7	15	$11.79$	$0.79$
64	7	15	$12.58$	$1.58$
128	7	15	$14.17$	$3.17$
256	7	15	$17.34$	$6.34$
512	8	16	$24.68$	$12.68$
1024	8	16	$37.36$	$25.36$
2048	8	16	$62.72$	$50.72$

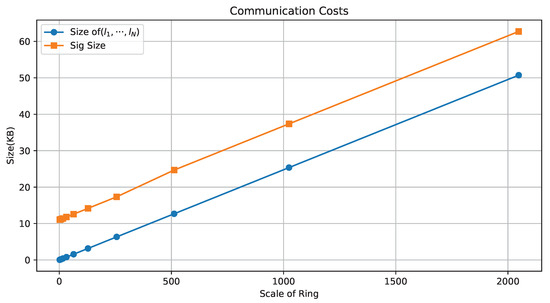
Figure 4. Communication costs with numbers of ring members.

7. Identity-Based Threshold Linkable Dual-Ring Signature

To further enhance threshold functionality, we adapt the threshold technique from [34] into our scheme, resulting in an identity-based threshold linkable dual-ring signature scheme (IB-TLDRS). Since most steps of this structure are similar to the previous scheme, we focus on the different steps.

• IB-TLDRS.Setup: Same as the setup process in Algorithm 1, except setting a threshold t.
• IB-TLDRS.KeyExt: Same as Algorithm 2.
• IB-TLDRS.Sign: Same as Algorithm 3.
• IB-TLDRS.Combine: A new algorithm required to be added in. The signer sends the generated valid signature $Sig$ to the IB-TLDRS.Combine algorithm, which then combines it into a set $(\mathit{\mu },Si{g}_0,Si{g}_1,\cdots ,Si{g}_k,W)$ and sends it to the verification algorithm IB-TLDRS.Verify.
• IB-TLDRS.Link: Same as Algorithm 5.
• IB-TLDRS.Verify: Input $(pp,W,\mathit{\mu },Si{g}_0,\cdots ,Si{g}_k)$; after parsing and verifying the signature, the verifier retrieves the successfully verified signature tag in $\Gamma$. If it is not in $\Gamma =({\mathit{\tau }}_1,\cdots ,{\mathit{\tau }}_k)$, the tag is added. Finally, if $|\Gamma |>t$, the output is 1; otherwise, the output is 0.

Specifications. Through the above method, we can obtain a new scheme with threshold functionality. For the new scheme, we only need a third party to perform the IB-LDRS.Combine algorithm after the signing procedure is completed. In the Verify algorithm, it is necessary to first verify the correctness of the signature before checking whether the threshold requirement is met.

Security Analysis. Adding threshold functionality does not affect the security. The threshold functionality mainly relies on the tags in the signature. We have already proven the linkability and nonslanderability, which ensure the security of the tags. This also demonstrates that the scheme can still ensure its security after incorporating the threshold functionality.

8. Conclusions and Future Work

Based on the lattice-based M-SIS assumption, this work constructs an efficient identity-based linkable dual-ring signature scheme, with its threshold extension additionally. The proposed scheme leverages the benefits of dual-ring signatures, which can reduce signature size effectively, especially when the number of ring members is not very large compared to other logarithmic (linkable) ring signatures. Moreover, our scheme, based on identity, simplifies key management processes, reduces computational and communication costs, and offers enhanced security in linkability compared to existing linkable ring signature schemes. Our ring signature is proved to be anonymous, unforgeable, linkable, and nonslanderable in the random oracle model. The research data further show that this work achieves a smaller signature size compared to prior schemes, effectively decreasing storage costs, even though our signature size scales linearly with the number of ring members. Finally, a threshold extension is given as an additional scheme with specifications and security analysis. Although the signature size in this scheme is very small, it increases linearly with the increase in the number of ring members. Therefore, we consider research on the construction of the logarithmic ring signature from lattices as future work.