On Advances of Anonymous Credentials—From Traditional to Post-Quantum
Abstract
1. Introduction
1.1. Our Contribution
Comparison with Kakvi et al.’s Recent Work
- Design Principles: We propose a construction-based approach to AC design principles, focusing on the structure of AC schemes. We classify AC schemes in two dimensions, the design structure and application, which helps to unify and guide the design of the AC scheme.
- Design Structures of Basic AC Schemes: We identify four design structures of the basic AC model: single-attribute AC, multi-attribute AC, multi-authority AC, and credential-modifiable AC. For each category, we identify the cryptographic primitives needed for the constructions. In addition, we highlight the associated advantages and disadvantages.
- Application-Oriented Design Principles for Practical Use: We identify four major application-oriented types of AC: traceable AC, revocable AC, delegatable AC, and decentralized AC. We outline each type’s cryptographic principles used in the key designs.
- Post-Quantum AC Schemes: Recently, with the advancement of quantum computing, cryptography research has significantly focused on post-quantum solutions. Among post-quantum cryptographic approaches, lattice-based cryptography has gained prominence, especially due to NIST standardization [8] of lattice-based key encapsulation mechanisms (KEMs) and digital signatures. As a result, the design and analysis of post-quantum AC schemes from lattices have become increasingly important. Here, we provide a qualitative and quantitative analysis of the most recent proposed lattice-based AC schemes.
- Real-World Applications: We identify the real-world applications of AC systems and provide a comparative analysis of the security notions achieved by the applications.
- Open directions including Quantum-Resistant AC Schemes: Most AC systems are based on discrete-log-related problems and will become insecure with large-scale quantum computers. We identify research gaps based on the most recent development of post-quantum AC schemes, which is not covered in Kakvi et al. [7].
1.2. Road Map
2. Evolution of Anonymous Credential Schemes
2.1. Early Development
2.1.1. Formalizing Attribute-Based Anonymous Credential Systems
- (opk,osk) ← OrgKeyGen(1λ): A probabilistic algorithm that outputs the organization’s public key opk and private key osk.
- (upk,usk) ← UserKeyGen(1λ): A probabilistic algorithm that outputs the user’s public key upk and private key usk.
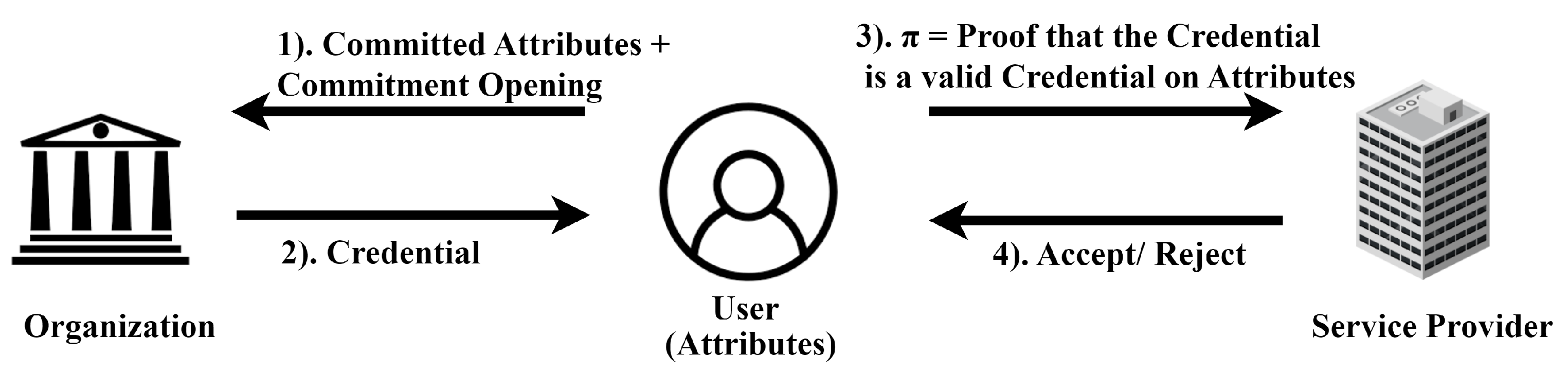
- (cred/⊥) ← (Obtain(opk, usk, A), issue(opk, upk, A)): An interactive protocol that outputs the credential (cred) over attribute set A or an error symbol ⊥.
- (1,/0, ⊥) ← (show(usk, A, D, cred), Verify(opk, D)): An interactive protocol that verifies the credential over that subset (D) of attributes (A). The protocol outputs 1 if the cred is a valid credential over D A and returns 0 otherwise.
2.1.2. Cryptographic Components for Anonymous Credential Systems
2.1.3. Summary
2.2. Enhancement from Pairing-Based Cryptography
2.3. Next-Generation Post-Quantum
2.4. Summary
3. Design and Structure of AC Schemes
3.1. AC Categorization Based on Design Structure
- Single-Attribute Anonymous Credentials: As shown in Figure 2, single-attribute AC systems were introduced in the early stages of AC development. In this type of system, users receive one credential for each attribute. While having a simple structure, this type of AC falls short in terms of efficiency; the public/private key sizes, the credential size, and/or the computational overhead of credential verification all increase linearly with the number of attributes if multiple attributes are needed, i.e., users must demonstrate knowledge of each credential for every attribute [52].
- Multi-Attribute Anonymous Credentials: This category, as depicted by Figure 1, refers to the AC systems in which users have multiple attributes, such as name, age, university, and more, being able to obtain a single credential for all of these attributes [16]. Two main types within this category exist: (1) selective disclosure (s) of attributes and (2) proving relations (r) of attributes during the verification process. Selective disclosure allows users to share a subset of their attributes with verifiers while keeping the remaining attributes concealed [18,23,46]. In contrast, proving relationships enables users to demonstrate the connection between their attributes to the verifier [13,22,38].
- Multi-Authority Anonymous Credentials: Both above AC schemes struggle to deal with situations where users hold credentials from multiple issuers and prove their knowledge of each signature to a verifier. This potentially results in larger credential sizes, e.g., linear with the number of issuers, due to separate credentials to be received from different issuers. To address this challenge, aggregate signatures are adopted in the AC system design. AC incorporated with aggregate signatures is depicted in Figure 5. It allows users to combine credentials from multiple organizations into a single credential. The crucial advantage of these schemes is that even when aggregating several signatures, they still end up with a constant-sized credential that is the same length as a single credential, keeping the prover cost independent of the number of issuers while still allowing verification of validities of the credentials [23].
- Credential-Modifiable Anonymous Credentials: This category, as depicted in Figure 6, represents a type of AC system that allows users to modify or hide certain parts of the issued credentials. It is used to overcome challenges encountered when requiring users to present the entire credential or the originally received credential to the verifier. Firstly, self-blinding or re-randomizable signature schemes [46,53] are the primary cryptographic primitives used for this type of AC. Once a user obtains a credential from an issuer, the user can randomize the credential into a new credential under the same attributes. Hence, they often make the AC system multi-show-unlinkable. Secondly, redactable [22,39] or sanitizable [40] signatures are the main cryptographic primitives that enable credentials to be modifiable. They introduce the ability to conceal or remove specific parts of the credential selectively while proving the validity of the remaining information. Similarly, sanitizable signatures allow, once a credential for ℓ number of attributes is received, the user (known as a sanitizer) to modify the signature for k out of ℓ attributes. The most efficient approach lies in constant-size redactable/sanitizable AC systems instead of linearly growing ones, which are particularly beneficial for applications such as membership or age verification.
3.2. AC Categorization Based on Additional Properties
3.2.1. Traceable Anonymous Credentials (TACs)
3.2.2. Revocable Anonymous Credentials (RACs)
- Setting Expiry Dates: This is the type of RAC where the credential issuer sets expiration dates for each credential, which becomes outdated after a specific period. Therefore, the user has to request a new credential from the issuer once it expires, which is inefficient because the user has to request new credentials every time they expire. However, if the issuer introduces a mechanism to update all the credentials without user interaction, the user will be able to download the updated version before the authentication. The protocol proposed by Camenisch et al. [42] introduces a method to update the credential once issued without requiring interaction between the user and the issuer.
- Blacklist/Whitelist: An additional entity, referred to as the revocation authority (RA), is introduced for the purpose of revocation. This entity may be a trusted third party (TTP), issuer, or verifier. Each credential is associated with a unique identifier, which can be categorized under a whitelist or a blacklist. The RA is responsible for maintaining a list of valid identifiers, known as a whitelist, or a list of invalid identifiers, known as a blacklist. Following the completion of the verification process by the user, the verifier will proceed to confirm whether the user’s credentials are present in the whitelist or absent from the blacklist. However, the revocation mechanism can also be implemented without relying on a trusted third party (TTP), as introduced by [55,56].
- Cryptographic Accumulator-Based: The construction of an RAC requires the RA to maintain a large list of identifiers (serial numbers) and continuously update the list, which is sometimes inefficient. To overcome this challenge, dynamic accumulators are introduced [57] to help the RA distribute a short accumulated value instead of a large set of identifiers. The term dynamic refers to an RA being able to add or delete identifiers to the accumulator, and it outputs a short value independent of the number of identifiers. Moreover, the term universal accumulator refers to accumulators which support membership proofs. The accumulator-based RAC systems operate as follows: Each credential is associated with a serial number, and the RA outputs the accumulated value of valid or invalid serial numbers, which it then publishes. When a user goes through the credential verification process, additionally, the user must prove that their credential has not been revoked. Hence, the user must prove that the serial number associated with their credential is included in the accumulated value of valid serial numbers. Alternatively, if the RA publishes the accumulated value of invalid serial numbers, the user must show that their serial number is not included in that accumulated value. Hence, the user has to prove the membership or non-membership of the accumulated value using a zero-knowledge proof [58,59,60] during the credential Show protocol.
- Verifier-Local Revocation (VLR): Verifier-local revocation (VLR) is commonly used for group signatures [34,61,62] and was later introduced for anonymous credentials [63]. Here, a trusted third party (TTP) or RA maintains and publishes a list of tokens associated with each credential. Users reveal the proof of knowledge of their tokens to the verifier during authentication. Then, the service provider (verifier) downloads the list of tokens associated with revoked credentials and checks whether the presented token has been revoked.
- Verifiable Encryption (VE): Verifiable encryption is a public key encryption scheme in which a prover can encrypt a piece of information using the public key of the receiver, and then the prover can convince a third party that the encrypted data satisfy certain properties. The VE-based RAC systems work as follows. In this type, a trusted revocation authority (RA) is involved, and the RA has a public–secret key pair. Let each credential be associated with a unique identifier; the user encrypts the credential identifier using the public key of the RA. After that, the user shares the encrypted version of the credential identifier with the verifier during the credential (Show, Verify) protocol. The verifier does not have direct access to the identifier but knows the encrypted version, so it cannot be decrypted. However, the verifier needs to confirm that the identifier has not been associated with a revoked credential. To achieve this, the verifier sends a request to the RA to check the validity of the identifier. The RA then decrypts the identifier using their secret key, checks whether it is on the revocation list, and informs the verifier about its revocation status. This method ensures that verifiers can verify the validity of credentials [64,65]; however, in VE-based RAC systems, the user put full trust in the RA.
3.2.3. Delegatable Anonymous Credentials (DACs)
3.2.4. Decentralized Anonymous Credentials
3.2.5. Summary of AC Additional Properties
4. Security of Anonymous Credentials
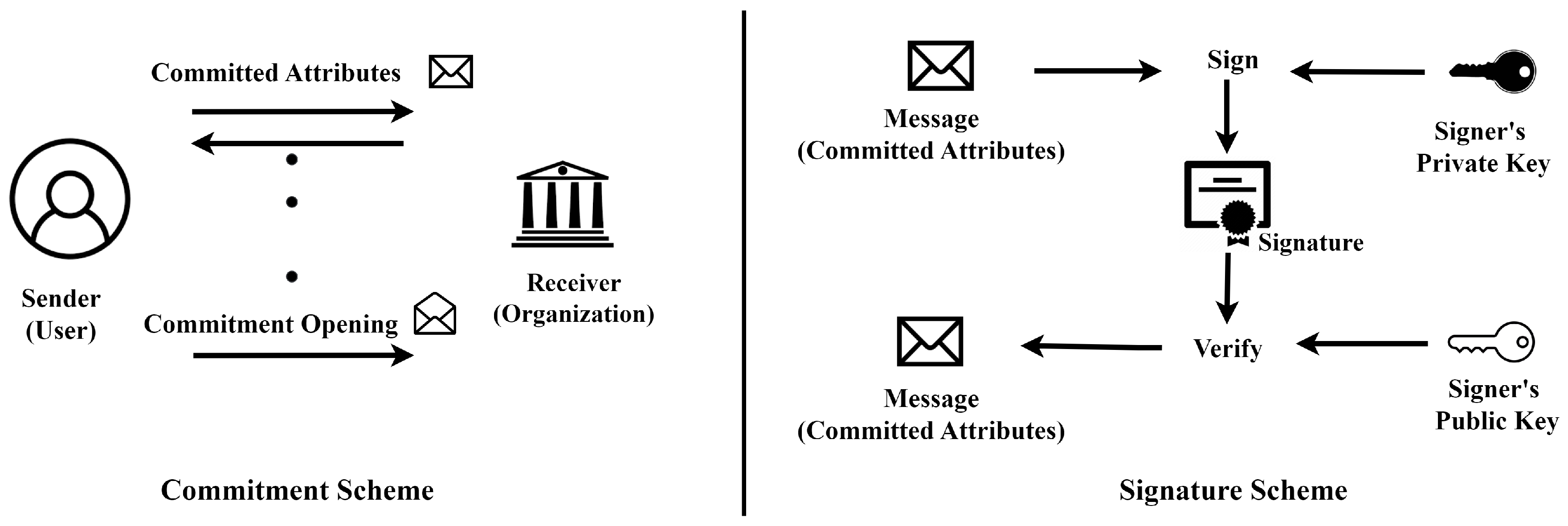
- Commitment Scheme: hiding, binding;
- Signature Scheme: EUF-CMA security;
- Zero-Knowledge Proof System: completeness, soundness, zero Knowledge.
5. Performance Analysis
6. Discussion
6.1. Real-World Applications
6.2. Open Directions
- The current literature indicates that the credential sizes of these lattice-based schemes are comparatively large compared to existing schemes. Interested readers can focus on minimizing the credential sizes of quantumly secure AC schemes.
- Although several AC systems have been proposed for specific properties in pairing-based cryptography, only a few designs have been proposed for lattice-based cryptography. Interested readers may explore constructions for properties such as revocability, traceability, signer hiding, and delegation in lattice-based AC systems.
- Although aggregate, redactable, and sanitizable signatures have been used in pairing-based designs, it is worth investigating their suitability for quantum-secure AC systems.
- To the best of our knowledge, the existing AC systems based on lattices remain less efficient than the classical and pairing-based AC systems and are not practical enough. Researchers are encouraged to address this gap and explore innovative solutions in developing quantum-resistant AC schemes for practical, real-world applications.
7. Conclusions
Funding
Conflicts of Interest
Abbreviations
| AC | Anonymous Credential |
| TAC | Traceable Anonymous Credential |
| RAC | Revocable Anonymous Credential |
| DAC | Delegatable Anonymous Credential |
| TA | Tracing Authority |
| RA | Revocation Authority |
| ZKPs | Zero-Knowledge Proofs |
References
- Diffie, W.; Hellman, M.E. New directions in cryptography. In Democratizing Cryptography: The Work of Whitfield Diffie and Martin Hellman; Association for Computing Machinery: New York, NY, USA, 2022; pp. 365–390. [Google Scholar]
- Garman, C.; Green, M.; Miers, I. Decentralized anonymous credentials. In Network and Distributed System Security (NDSS) Symposium; The Internet Society: San Diego, CA, USA, 2013. [Google Scholar]
- Pussewalage, H.S.G.; Oleshchuk, V.A. An anonymous delegatable attribute-based credential scheme for a collaborative e-health environment. ACM Trans. Internet Technol. (TOIT) 2019, 19, 1–22. [Google Scholar] [CrossRef]
- Bourse, F.; Pointcheval, D.; Sanders, O. Divisible e-cash from constrained pseudo-random functions. In Proceedings of the Advances in Cryptology–ASIACRYPT 2019: 25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; Proceedings, Part I 25. Springer: Berlin/Heidelberg, Germany, 2019; pp. 679–708. [Google Scholar]
- Canard, S.; Gouget, A. Divisible e-cash systems can be truly anonymous. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Barcelona, Spain, 20–24 May 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 482–497. [Google Scholar]
- Chaum, D. Security without identification: Transaction systems to make big brother obsolete. Commun. ACM 1985, 28, 1030–1044. [Google Scholar] [CrossRef]
- Kakvi, S.A.; Martin, K.M.; Putman, C.; Quaglia, E.A. SoK: Anonymous Credentials. In Proceedings of the International Conference on Research in Security Standardisation, Lyon, France, 22–23 April 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 129–151. [Google Scholar]
- Alagic, G.; Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Liu, Y.K.; Miller, C.; et al. Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Chaum, D.; Evertse, J.H. A secure and privacy-protecting protocol for transmitting personal information between organizations. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, 18–22 August 1985; Springer: Berlin/Heidelberg, Germany, 1986; pp. 118–167. [Google Scholar]
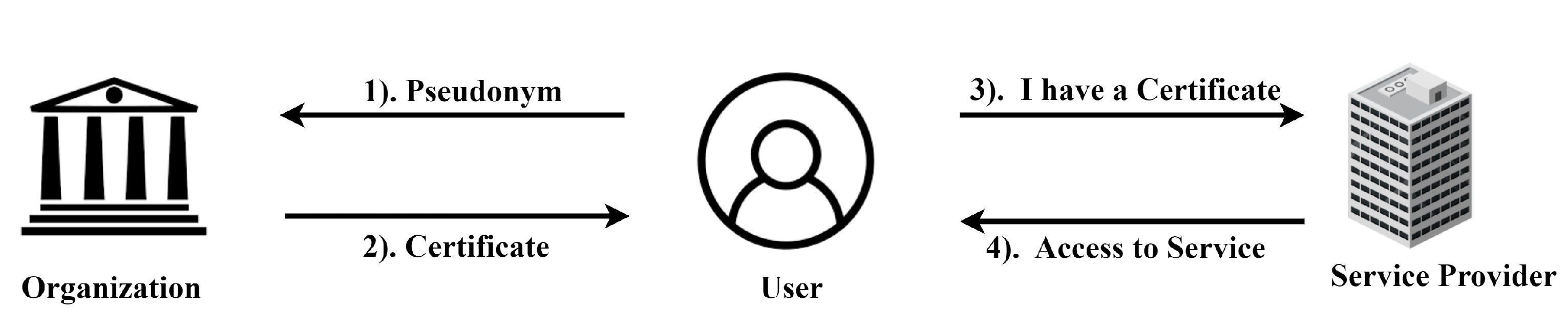
- Chen, L. Access with pseudonyms. In Proceedings of the International Conference on Cryptography: Policy and Algorithms, Brisbane, QLD, Australia, 3–5 July 1995; Springer: Berlin/Heidelberg, Germany, 1995; pp. 232–243. [Google Scholar]
- Lysyanskaya, A.; Rivest, R.L.; Sahai, A.; Wolf, S. Pseudonym systems. In Proceedings of the Selected Areas in Cryptography: 6th Annual International Workshop, SAC’99, Kingston, ON, Canada, 9–10 August 1999; Springer: Berlin/Heidelberg, Germany, 2000; pp. 184–199. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. A signature scheme with efficient protocols. In Proceedings of the Security in Communication Networks: Third International Conference, SCN 2002, Amalfi, Italy, 11–13 September 2002; Revised Papers 3. Springer: Berlin/Heidelberg, Germany, 2003; pp. 268–289. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. Signature schemes and anonymous credentials from bilinear maps. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 56–72. [Google Scholar]
- Lysyanskaya, A. Signature Schemes and Applications to Cryptographic Protocol Design. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2002. [Google Scholar]
- Brands, S. Rethinking Public Key Infrastructures and Digital Certificates: Building in Privacy; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Camenisch, J.; Groß, T. Efficient attributes for anonymous credentials. ACM Trans. Inf. Syst. Secur. (TISSEC) 2012, 15, 1–30. [Google Scholar] [CrossRef]
- Fuchsbauer, G.; Hanser, C.; Slamanig, D. Structure-preserving signatures on equivalence classes and constant-size anonymous credentials. J. Cryptol. 2019, 32, 498–546. [Google Scholar] [CrossRef]
- Bootle, J.; Lyubashevsky, V.; Nguyen, N.K.; Sorniotti, A. A framework for practical anonymous credentials from lattices. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–24 August 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 384–417. [Google Scholar]
- Lai, Q.; Liu, F.H.; Lysyanskaya, A.; Wang, Z. Lattice-based Commit-Transferrable Signatures and Applications to Anonymous Credentials. Cryptol. ePrint Arch. 2023, preprint. [Google Scholar]
- Jeudy, C.; Roux-Langlois, A.; Sanders, O. Lattice signature with efficient protocols, application to anonymous credentials. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–24 August 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 351–383. [Google Scholar]
- Sanders, O. Efficient redactable signature and application to anonymous credentials. In Proceedings of the IACR International Conference on Public-Key Cryptography, Edinburgh, UK, 4–7 May 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 628–656. [Google Scholar]
- Hébant, C.; Pointcheval, D. Traceable constant-size multi-authority credentials. Inf. Comput. 2023, 293, 105060. [Google Scholar] [CrossRef]
- Chaum, D.; Pedersen, T. Wallet databases with observers. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 1992; pp. 89–105. [Google Scholar]
- Fujisaki, E.; Okamoto, T. A practical and provably secure scheme for publicly verifiable secret sharing and its applications. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Espoo, Finland, 31 May–4 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 32–46. [Google Scholar]
- Naor, M. Bit commitment using pseudorandomness. J. Cryptol. 1991, 4, 151–158. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Fiat, A.; Shamir, A. How to prove yourself: Practical solutions to identification and signature problems. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, 18–22 August 1985; Springer: Berlin/Heidelberg, Germany, 1986; pp. 186–194. [Google Scholar]
- Schnorr, C.P. Efficient signature generation by smart cards. J. Cryptol. 1991, 4, 161–174. [Google Scholar] [CrossRef]
- Bellare, M.; Micali, S. How to sign given any trapdoor function. In Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; pp. 32–42. [Google Scholar]
- Damgård, I.B. Payment systems and credential mechanisms with provable security against abuse by individuals. In Proceedings of the Conference on the Theory and Application of Cryptography, Davos, Switzerland, 25–27 May 1988; Springer: Berlin/Heidelberg, Germany, 1988; pp. 328–335. [Google Scholar]
- Camenisch, J.; Stadler, M. Proof Systems for General Statements about Discrete Logarithms; Technical Report; Department of Computer Science, ETH Zurich: Zürich, Switzerland, 1997. [Google Scholar]
- Boneh, D.; Boyen, X.; Shacham, H. Short group signatures. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 41–55. [Google Scholar]
- Boneh, D.; Shacham, H. Group signatures with verifier-local revocation. In Proceedings of the 11th ACM Conference on Computer and Communications Security, Washington, DC, USA, 25–29 October 2004; pp. 168–177. [Google Scholar]
- Groth, J.; Sahai, A. Efficient non-interactive proof systems for bilinear groups. In Proceedings of the Advances in Cryptology–EUROCRYPT 2008: 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, 13–17 April 2008; Proceedings 27. Springer: Berlin/Heidelberg, Germany, 2008; pp. 415–432. [Google Scholar]
- Groth, J. Efficient fully structure-preserving signatures for large messages. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Auckland, New Zealand, 29 November–3 December 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 239–259. [Google Scholar]
- Canard, S.; Lescuyer, R. Anonymous credentials from (indexed) aggregate signatures. In Proceedings of the 7th ACM workshop on Digital Identity Management, Chicago, IL, USA, 21 October 2011; pp. 53–62. [Google Scholar]
- Tan, S.Y.; Groß, T. Monipoly—An expressive q-SDH-based anonymous attribute-based credential system. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Virtual Event, 7–11 December 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 498–526. [Google Scholar]
- Camenisch, J.; Dubovitskaya, M.; Haralambiev, K.; Kohlweiss, M. Composable and modular anonymous credentials: Definitions and practical constructions. In Proceedings of the Advances in Cryptology–ASIACRYPT 2015: 21st International Conference on the Theory and Application of Cryptology and Information Security, Auckland, New Zealand, 29 November–3 December 2015; Proceedings, Part II 21. Springer: Berlin/Heidelberg, Germany, 2015; pp. 262–288. [Google Scholar]
- Canard, S.; Lescuyer, R. Protecting privacy by sanitizing personal data: A new approach to anonymous credentials. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 7–10 May 2013; pp. 381–392. [Google Scholar]
- Hanser, C.; Slamanig, D. Structure-preserving signatures on equivalence classes and their application to anonymous credentials. In Proceedings of the Advances in Cryptology–ASIACRYPT 2014: 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, Taiwan, 7–11 December 2014; Proceedings, Part I 20. Springer: Berlin/Heidelberg, Germany, 2014; pp. 491–511. [Google Scholar]
- Camenisch, J.; Kohlweiss, M.; Soriente, C. Solving revocation with efficient update of anonymous credentials. In Proceedings of the International Conference on Security and Cryptography for Networks, Amalfi, Italy, 13–15 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 454–471. [Google Scholar]
- Belenkiy, M.; Camenisch, J.; Chase, M.; Kohlweiss, M.; Lysyanskaya, A.; Shacham, H. Randomizable proofs and delegatable anonymous credentials. In Proceedings of the Advances in Cryptology-CRYPTO 2009: 29th Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 108–125. [Google Scholar]
- Mir, O.; Slamanig, D.; Bauer, B.; Mayrhofer, R. Practical delegatable anonymous credentials from equivalence class signatures. Proc. Priv. Enhancing Technol. 2023, 2023, 488–513. [Google Scholar] [CrossRef]
- Bobolz, J.; Eidens, F.; Krenn, S.; Ramacher, S.; Samelin, K. Issuer-hiding attribute-based credentials. In Proceedings of the Cryptology and Network Security: 20th International Conference, CANS 2021, Vienna, Austria, 13–15 December 2021; Proceedings 20. Springer: Berlin/Heidelberg, Germany, 2021; pp. 158–178. [Google Scholar]
- Connolly, A.; Lafourcade, P.; Perez Kempner, O. Improved constructions of anonymous credentials from structure-preserving signatures on equivalence classes. In Proceedings of the IACR International Conference on Public-Key Cryptography, Virtual Event, 8–11 March 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 409–438. [Google Scholar]
- Argo, S.; Güneysu, T.; Jeudy, C.; Land, G.; Roux-Langlois, A.; Sanders, O. Practical Post-Quantum Signatures for Privacy. In Proceedings of the 2024 on ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, UT, USA, 14–18 October 2024. [Google Scholar]
- Libert, B.; San Ling, F.M.; Nguyen, K.; Wang, H. Signature Schemes with Efficient Protocols and Dynamic Group Signatures from Lattice Assumptions. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016. [Google Scholar]
- Boyen, X. Lattice Mixing and Vanishing Trapdoors: A Framework for Fully Secure Short Signatures and More. In Public Key Cryptography-PKC 2010; Nguyen, P.Q., Pointcheval, D., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6056, pp. 499–517. [Google Scholar]
- del Pino, R.; Katsumata, S. A new framework for more efficient round-optimal lattice-based (partially) blind signature via trapdoor sampling. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–18 August 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 306–336. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In Proceedings of the Advances in Cryptology—EUROCRYPT 2001: International Conference on the Theory and Application of Cryptographic Techniques, Innsbruck, Austria, 6–10 May 2001; Proceedings 20. Springer: Berlin/Heidelberg, Germany, 2001; pp. 93–118. [Google Scholar]
- Blazy, O.; Chevalier, C.; Renaut, G.; Ricosset, T.; Sageloli, E.; Senet, H. Efficient Implementation of a Post-Quantum Anonymous Credential Protocol. In Proceedings of the 18th International Conference on Availability, Reliability and Security, Benevento, Italy, 29 August–1 September 2023; pp. 1–11. [Google Scholar]
- Ringers, S.; Verheul, E.; Hoepman, J.H. An efficient self-blindable attribute-based credential scheme. In Proceedings of the Financial Cryptography and Data Security: 21st International Conference, FC 2017, Sliema, Malta, 3–7 April 2017; Revised Selected Papers 21. Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–20. [Google Scholar]
- Wu, W. Efficient and Traceable Anonymous Credentials on Smart Cards. Comput. Inf. Sci. 2022, 15, 1–58. [Google Scholar] [CrossRef]
- Tsang, P.P.; Au, M.H.; Kapadia, A.; Smith, S.W. Blacklistable anonymous credentials: Blocking misbehaving users without TTPs. In Proceedings of the 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 28–31 October 2007; pp. 72–81. [Google Scholar]
- Tsang, P.P.; Au, M.H.; Kapadia, A.; Smith, S.W. BLAC: Revoking repeatedly misbehaving anonymous users without relying on TTPs. ACM Trans. Inf. Syst. Secur. (TISSEC) 2010, 13, 1–33. [Google Scholar] [CrossRef]
- Camenisch, J.; Lysyanskaya, A. Dynamic accumulators and application to efficient revocation of anonymous credentials. In Proceedings of the Advances in Cryptology—CRYPTO 2002: 22nd Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2002; Proceedings 22. Springer: Berlin/Heidelberg, Germany, 2002; pp. 61–76. [Google Scholar]
- Camenisch, J.; Kohlweiss, M.; Soriente, C. An accumulator based on bilinear maps and efficient revocation for anonymous credentials. In Proceedings of the Public Key Cryptography–PKC 2009: 12th International Conference on Practice and Theory in Public Key Cryptography, Irvine, CA, USA, 18–20 March 2009; Proceedings 12. Springer: Berlin/Heidelberg, Germany, 2009; pp. 481–500. [Google Scholar]
- Baldimtsi, F.; Camenisch, J.; Dubovitskaya, M.; Lysyanskaya, A.; Reyzin, L.; Samelin, K.; Yakoubov, S. Accumulators with applications to anonymity-preserving revocation. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy (EuroS&P), Paris, France, 26–28 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 301–315. [Google Scholar]
- Acar, T.; Nguyen, L. Revocation for delegatable anonymous credentials. In Proceedings of the International Workshop on Public Key Cryptography, Taormina, Italy, 6–9 March 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 423–440. [Google Scholar]
- Ateniese, G.; Song, D.; Tsudik, G. Quasi-efficient revocation of group signatures. In Proceedings of the Financial Cryptography: 6th International Conference, FC 2002 Southampton, Bermuda, UK, 11–14 March 2002; Revised Papers 6. Springer: Berlin/Heidelberg, Germany, 2003; pp. 183–197. [Google Scholar]
- Zaverucha, G.M.; Stinson, D.R. Group testing and batch verification. In Proceedings of the International Conference on Information Theoretic Security, Shizuoka, Japan, 3–6 December 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 140–157. [Google Scholar]
- Camenisch, J.; Drijvers, M.; Hajny, J. Scalable revocation scheme for anonymous credentials based on n-times unlinkable proofs. In Proceedings of the 2016 ACM on Workshop on Privacy in the Electronic Society, Vienna, Austria, 24–28 October 2016; pp. 123–133. [Google Scholar]
- Camenisch, J.; Shoup, V. Practical verifiable encryption and decryption of discrete logarithms. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 126–144. [Google Scholar]
- Backes, M.; Camenisch, J.; Sommer, D. Anonymous yet accountable access control. In Proceedings of the 2005 ACM Workshop on Privacy in the Electronic Society, Alexandria, VA, USA, 7 November 2005; pp. 40–46. [Google Scholar]
- Tsang, P.P.; Kapadia, A.; Cornelius, C.; Smith, S.W. Nymble: Blocking misbehaving users in anonymizing networks. IEEE Trans. Dependable Secur. Comput. 2009, 8, 256–269. [Google Scholar] [CrossRef]
- Lueks, W.; Alpár, G.; Hoepman, J.H.; Vullers, P. Fast revocation of attribute-based credentials for both users and verifiers. Comput. Secur. 2017, 67, 308–323. [Google Scholar] [CrossRef]
- Verheul, E.R. Practical backward unlinkable revocation in fido, german e-id, idemix and u-prove. Cryptol. ePrint Arch. 2016, preprint. [Google Scholar]
- Chase, M.; Lysyanskaya, A. On signatures of knowledge. In Proceedings of the Advances in Cryptology-CRYPTO 2006: 26th Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2006; Proceedings 26. Springer: Berlin/Heidelberg, Germany, 2006; pp. 78–96. [Google Scholar]
- Chase, M.; Kohlweiss, M.; Lysyanskaya, A.; Meiklejohn, S. Malleable signatures: New definitions and delegatable anonymous credentials. In Proceedings of the 2014 IEEE 27th computer security foundations symposium, Vienna, Austria, 19–22 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 199–213. [Google Scholar]
- Yang, R.; Au, M.H.; Xu, Q.; Yu, Z. Decentralized blacklistable anonymous credentials with reputation. Comput. Secur. 2019, 85, 353–371. [Google Scholar] [CrossRef]
- Lin, C.; He, D.; Zhang, H.; Shao, L.; Huang, X. Privacy-enhancing decentralized anonymous credential in smart grids. Comput. Stand. Interfaces 2021, 75, 103505. [Google Scholar] [CrossRef]
- Blömer, J.; Bobolz, J.; Diemert, D.; Eidens, F. Updatable anonymous credentials and applications to incentive systems. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 1671–1685. [Google Scholar]
- Chase, M.; Meiklejohn, S.; Zaverucha, G. Algebraic MACs and keyed-verification anonymous credentials. In Proceedings of the 2014 ACM Sigsac Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 1205–1216. [Google Scholar]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 136–145. [Google Scholar]
- Bellare, M.; Rogaway, P. Random oracles are practical: A paradigm for designing efficient protocols. In Proceedings of the 1st ACM Conference on Computer and Communications Security, Fairfax, VA, USA, 3–5 November 1993; pp. 62–73. [Google Scholar]
- Shoup, V. Lower bounds for discrete logarithms and related problems. In Proceedings of the Advances in Cryptology—EUROCRYPT’97: International Conference on the Theory and Application of Cryptographic Techniques, Konstanz, Germany, 11–15 May 1997; Proceedings 16. Springer: Berlin/Heidelberg, Germany, 1997; pp. 256–266. [Google Scholar]
- Hébant, C.; Pointcheval, D. Traceable Constant-Size Multi-authority Credentials. In Proceedings of the Security and Cryptography for Networks, Amalfi, Italy, 12–14 September 2022; Galdi, C., Jarecki, S., Eds.; Springer: Cham, Switzerland, 2022; pp. 411–434. [Google Scholar]
- Fuchsbauer, G. Automorphic signatures in bilinear groups and an application to round-optimal blind signatures. Cryptol. ePrint Arch. 2009, preprint. [Google Scholar]
- Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108. [Google Scholar]
- Yang, R.; Au, M.H.; Zhang, Z.; Xu, Q.; Yu, Z.; Whyte, W. Efficient lattice-based zero-knowledge arguments with standard soundness: Construction and applications. In Proceedings of the Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; Proceedings, Part I 39. Springer: Berlin/Heidelberg, Germany, 2019; pp. 147–175. [Google Scholar]
- Lyubashevsky, V.; Nguyen, N.K.; Plançon, M. Lattice-based zero-knowledge proofs and applications: Shorter, simpler, and more general. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–18 August 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 71–101. [Google Scholar]
- Baum, C.; Damgård, I.; Lyubashevsky, V.; Oechsner, S.; Peikert, C. More efficient commitments from structured lattice assumptions. In Proceedings of the International Conference on Security and Cryptography for Networks, Amalfi, Italy, 5–7 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 368–385. [Google Scholar]
- Peikert, C.; Shiehian, S. Noninteractive zero knowledge for NP from (plain) learning with errors. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2022; Springer: Berlin/Heidelberg, Germany, 2019; pp. 89–114. [Google Scholar]
- Agrawal, S.; Kirshanova, E.; Stehlé, D.; Yadav, A. Practical, round-optimal lattice-based blind signatures. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 39–53. [Google Scholar]
- Paquin, C.; Zaverucha, G. U-Prove Cryptographic Specification v1. 1; Technical Report; Microsoft Corporation: Redmond, WA, USA, 2011. [Google Scholar]
- Bichsel, P.; Camenisch, J. Mixing identities with ease. In Proceedings of the Policies and Research in Identity Management: Second IFIP WG 11.6 Working Conference, IDMAN 2010, Oslo, Norway, 18–19 November 2010; Proceedings 2. Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–17. [Google Scholar]
- Hesse, J.; Singh, N.; Sorniotti, A. How to Bind Anonymous Credentials to Humans. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023; pp. 3047–3064. [Google Scholar]
- Doesburg, J.; Jacobs, B.; Ringers, S. Using IRMA for Small Scale Digital Elections. Bachelor Thesis, Radboud University, Nijmegen, The Netherlands, 2020. [Google Scholar]
- Camenisch, J.; Van Herreweghen, E. Design and implementation of the idemix anonymous credential system. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, 18–22 November 2002; pp. 21–30. [Google Scholar]
- Godtschalk, L. Accountability and Access Control using Anonymous Credentials; Eindhoven University of Technology: Eindhoven, The Netherlands, 2022. [Google Scholar]
- Rosenberg, M.; White, J.; Garman, C.; Miers, I. zk-creds: Flexible anonymous credentials from zksnarks and existing identity infrastructure. In Proceedings of the 2023 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–24 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 790–808. [Google Scholar]
- Camenisch, J.; Drijvers, M.; Lehmann, A. Universally composable direct anonymous attestation. In Proceedings of the Public-Key Cryptography–PKC 2016: 19th IACR International Conference on Practice and Theory in Public-Key Cryptography, Taipei, Taiwan, 6–9 March 2016; Proceedings, Part II 19. Springer: Berlin/Heidelberg, Germany, 2016; pp. 234–264. [Google Scholar]
- Förster, D.; Kargl, F.; Löhr, H. PUCA: A pseudonym scheme with user-controlled anonymity for vehicular ad-hoc networks (VANET). In Proceedings of the 2014 IEEE Vehicular Networking Conference (VNC), Paderborn, Germany, 3–5 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 25–32. [Google Scholar]
- Kaaniche, N.; Laurent, M. Attribute-based signatures for supporting anonymous certification. In Proceedings of the Computer Security–ESORICS 2016: 21st European Symposium on Research in Computer Security, Heraklion, Greece, 26–30 September 2016; Proceedings, Part I 21. Springer: Berlin/Heidelberg, Germany, 2016; pp. 279–300. [Google Scholar]
- Hajnỳ, J. Anonymous Authentication for Smartcards. Radioengineering 2010, 19, 363–368. [Google Scholar]
- Brickell, E.; Camenisch, J.; Chen, L. Direct anonymous attestation. In Proceedings of the 11th ACM conference on Computer and Communications Security, Washington, DC, USA, 25–29 October 2004; pp. 132–145. [Google Scholar]
- Bichsel, P.; Camenisch, J.; Groß, T.; Shoup, V. Anonymous credentials on a standard java card. In Proceedings of the 16th ACM conference on Computer and communications security, Chicago, IL, USA, 9–13 November 2009; pp. 600–610. [Google Scholar]
- Matetic, S.; Schneider, M.; Miller, A.; Juels, A.; Capkun, S. {DelegaTEE}: Brokered delegation using trusted execution environments. In Proceedings of the 27th USENIX Security Symposium (USENIX Security 18), Baltimore, MD, USA, 15–17 August 2018; pp. 1387–1403. [Google Scholar]
- Camenisch, J.; Drijvers, M.; Dubovitskaya, M. Practical UC-secure delegatable credentials with attributes and their application to blockchain. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 683–699. [Google Scholar]
- Mateu, V.; Sebé, F.; Valls, M. Constructing credential-based E-voting systems from offline E-coin protocols. J. Netw. Comput. Appl. 2014, 42, 39–44. [Google Scholar] [CrossRef]
- Boudgoust, K.; Takahashi, A. Sequential half-aggregation of lattice-based signatures. In Proceedings of the European Symposium on Research in Computer Security, Hague, The Netherlands, 25–29 September 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 270–289. [Google Scholar]
- El Bansarkhani, R.; Buchmann, J. Towards lattice based aggregate signatures. In Proceedings of the Progress in Cryptology–AFRICACRYPT 2014: 7th International Conference on Cryptology in Africa, Marrakesh, Morocco, 28–30 May 2014; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 2014; pp. 336–355. [Google Scholar]
- Lu, X.; Yin, W.; Wen, Q.; Jin, Z.; Li, W. A lattice-based unordered aggregate signature scheme based on the intersection method. IEEE Access 2018, 6, 33986–33994. [Google Scholar] [CrossRef]





| Property | Description | Mechanism |
|---|---|---|
| Non-transferability [51] | Credentials should not be transferable between users. | Certification authority (CA) is introduced. |
| Traceability [23,40,54]. | Ability to trace credentials to prevent misuse. | Tracing authority (TA) is introduced. |
| Revocability [42,58] | Revoke outdated credentials. | Revocation mechanism is introduced |
| Delegation [43,44,69,70] | Users can delegate credentials to other users. | A delegation chain/list is introduced. |
| Issuer Hiding [45,46] | The identity of the credential issuer is hidden. | A set of acceptable issuers/the signing key space is introduced by the verifier (verification policy). |
| Updatable [73] | After the credential was issued, its attributes were modified. | A protocol (update function) is introduced between the issuer and the user. |
| Self-Blinding [18] | The credential is randomized by the user before showing. | A randomizable signature scheme is utilized. |
| Keyed Verification [74] | The issuer of credentials is also the verifier. | A shared key/algebraic MAC is used between the issuer and verifier. |
| Property | Requirement | Cryptographic Primitives |
|---|---|---|
| Unforgeability | It should be infeasible to forge credentials. Malicious provers must be prevented. | Signature Scheme: EUF-CMA security ZK Proof System: Soundness |
| Anonymity | Attributes must not be leaked to the issuer. The secret key must not be leaked. | Commitment Scheme: Hiding Zero-Knowledge Proof System |
| Unlinkability | Different showings of the credentials cannot be linked. | Zero-Knowledge Proof System/Self Blindable |
| Scheme | Main Assumptions | Setting | (KB) | Model | |
|---|---|---|---|---|---|
| [51] | sRSA, DDH | SM | |||
| [13] | sRSA | SM | |||
| [14] | LRSW, DDH | BG | SM | ||
| [37] | q-ADHSDH, DDH | BG | ROM | ||
| [40] | DL, DDH, SDH | BG | ROM | ||
| [39] | CDH, q-SDH, SXDH | BG | CRS | ||
| [53] | LRSW | BG | SM | ||
| [18] | DDH, q-co-DL | BG | GGM | ||
| [22] | DDH, DL | BG | GGM | ||
| [78] | DL, DDH | BG | GGM | ||
| [38] | q-(co-)SDH, SDH | BG | SM | ||
| [46] | DDH, q-co-DL | BG | SM |
| Scheme | Assumption | Commitment | Signature | ZKPs |
|---|---|---|---|---|
| [21] | MSIS/MLWE | Ajtai [80] | [48] * | [81,82] |
| [20] | MSIS/RLWE | BDLOP [83], ABDLOP [82] | CTS [20] | [84] |
| [19] | NTRU- | ABDLOP [82] | [85] | [50] |
| [47] | MSIS/MLWE | ABDLOP | [21] * | [82] |
| Scheme | Assumption | Setting | (KB) | (KB) | (KB) | Security Model |
|---|---|---|---|---|---|---|
| [21] | MSIS/MLWE | standard | 117.103 | 261 | 306.103 | ROM |
| [21] | MSIS/MLWE | module | 276.48 | 317 | 724 | ROM |
| [20] | MSIS/RLWE | structured | 440 | 236.56 | 372.56 | ROM * |
| [20] | MSIS/RLWE | structured | 276.5 | 16,711.68 | 25,364.48 | ROM |
| [19] | NTRU | 17 | 243 | 473 | ROM | |
| [19] | Int-NTRU | 3.5 | 62 | 107 | ROM | |
| [47] | MSIS/MLWE | module | 49.91 | 6.81 | 80 | ROM |
| AC Security Properties | Real-World Applications |
|---|---|
| Non-Transferability | E-Voting |
| Revocation | KYC Verification, Membership Revocation |
| Traceability | Smart Cards, Digital Cash |
| Selective attribute disclosure | Digital ID, Healthcare Systems |
| Delegation | Access Control, Transactions in Blockchain |
| Authenticity | Anonymous Survey |
| Verifiability | E-Voting |
| Transparency | E-Voting |
| Exculpability | Cryptocurrencies, Digital Cash |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chathurangi, M.; Li, Q.; Foo, E. On Advances of Anonymous Credentials—From Traditional to Post-Quantum. Cryptography 2025, 9, 8. https://doi.org/10.3390/cryptography9010008
Chathurangi M, Li Q, Foo E. On Advances of Anonymous Credentials—From Traditional to Post-Quantum. Cryptography. 2025; 9(1):8. https://doi.org/10.3390/cryptography9010008
Chicago/Turabian StyleChathurangi, Madusha, Qinyi Li, and Ernest Foo. 2025. "On Advances of Anonymous Credentials—From Traditional to Post-Quantum" Cryptography 9, no. 1: 8. https://doi.org/10.3390/cryptography9010008
APA StyleChathurangi, M., Li, Q., & Foo, E. (2025). On Advances of Anonymous Credentials—From Traditional to Post-Quantum. Cryptography, 9(1), 8. https://doi.org/10.3390/cryptography9010008





