Investigating the Individual Performances of Coupled Superconducting Transmon Qubits
Abstract
:1. Introduction
2. Results
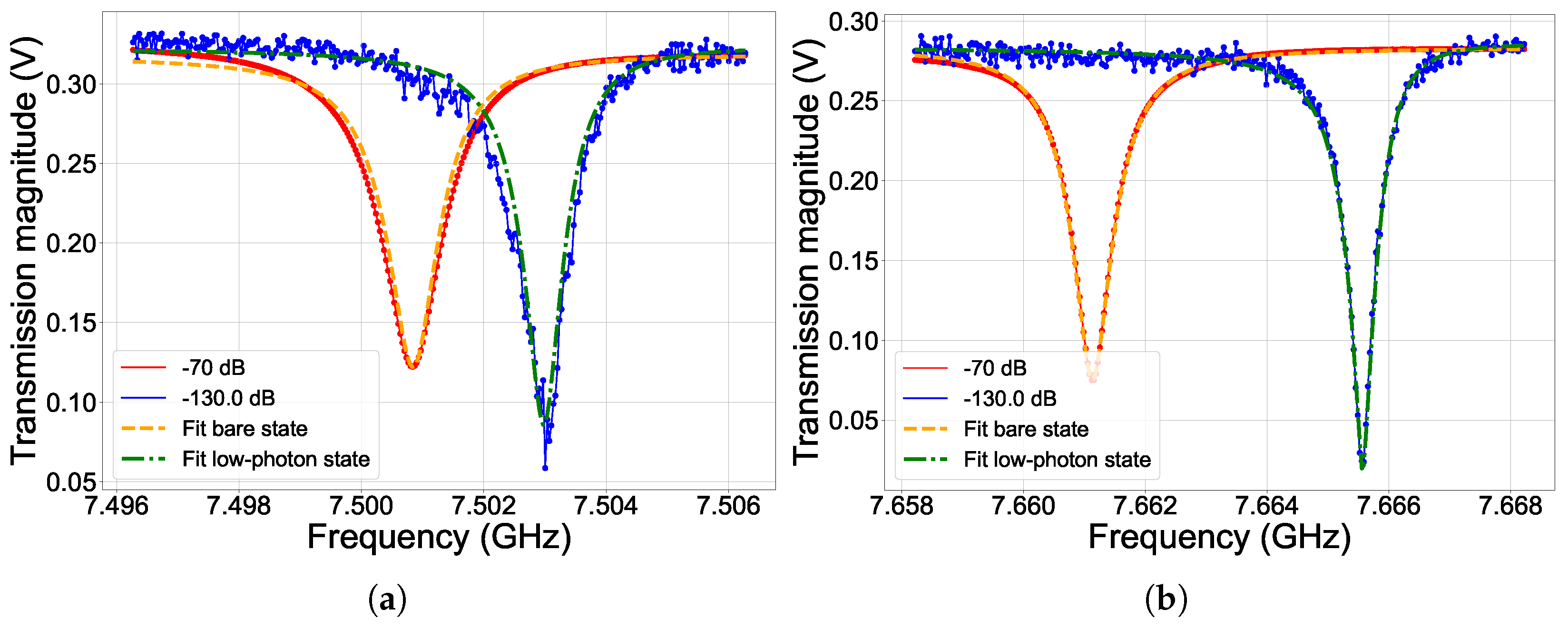
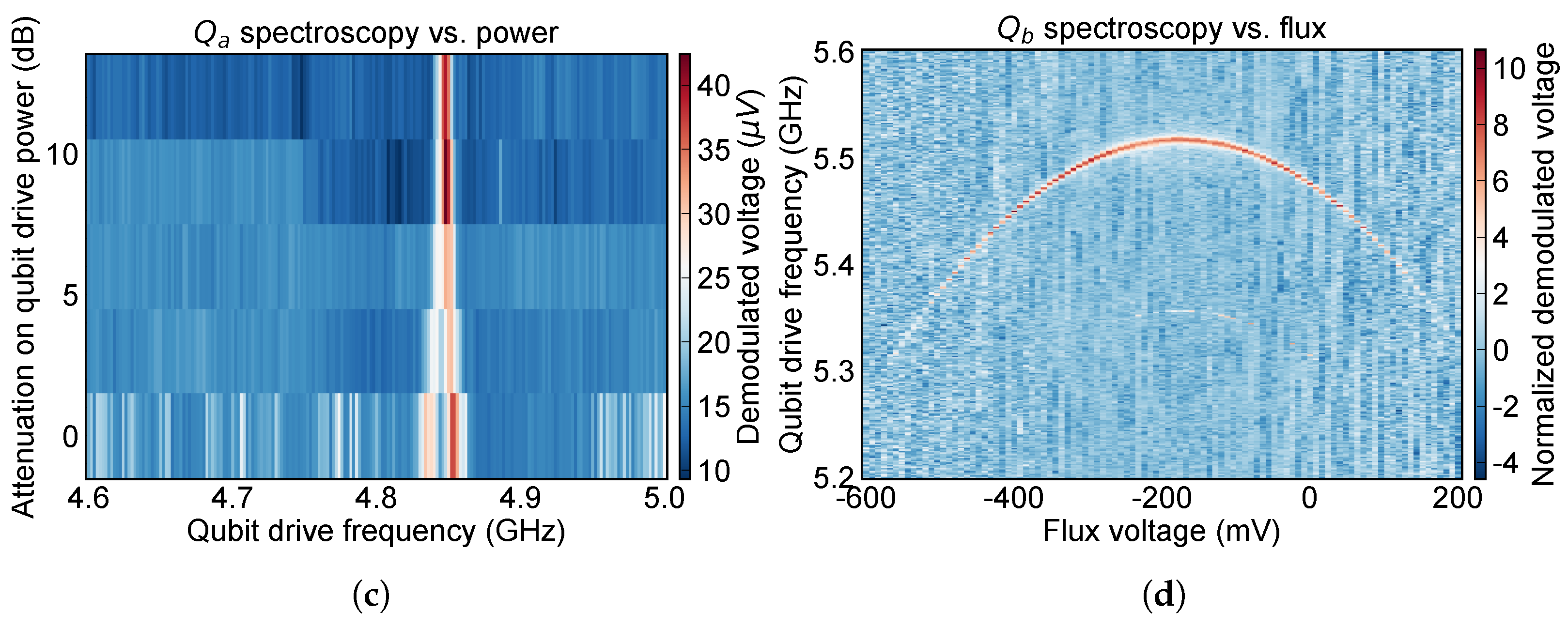
2.1. Read-Out Resonator and Qubit Spectroscopy
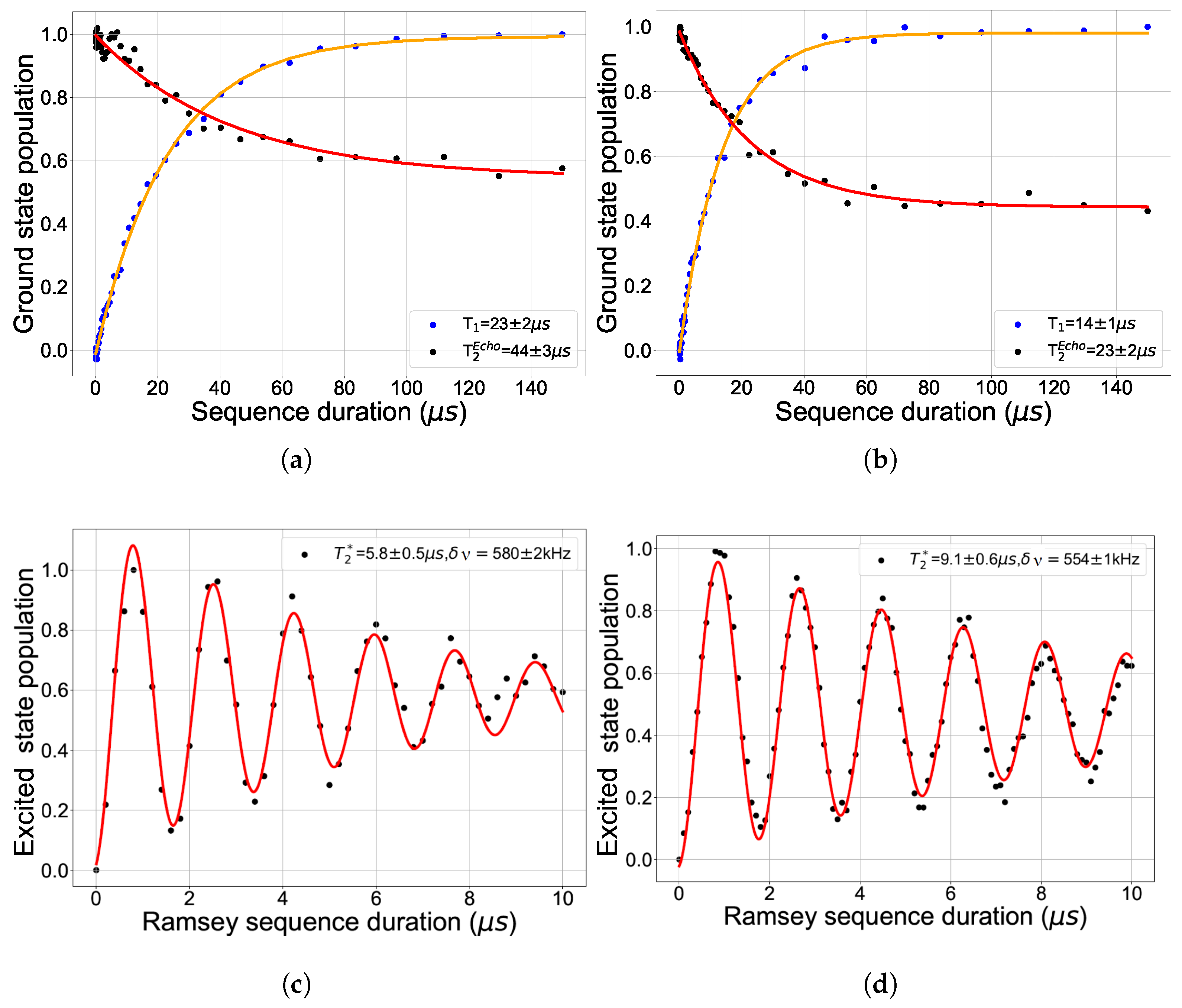
2.2. Relaxation and Coherence Properties
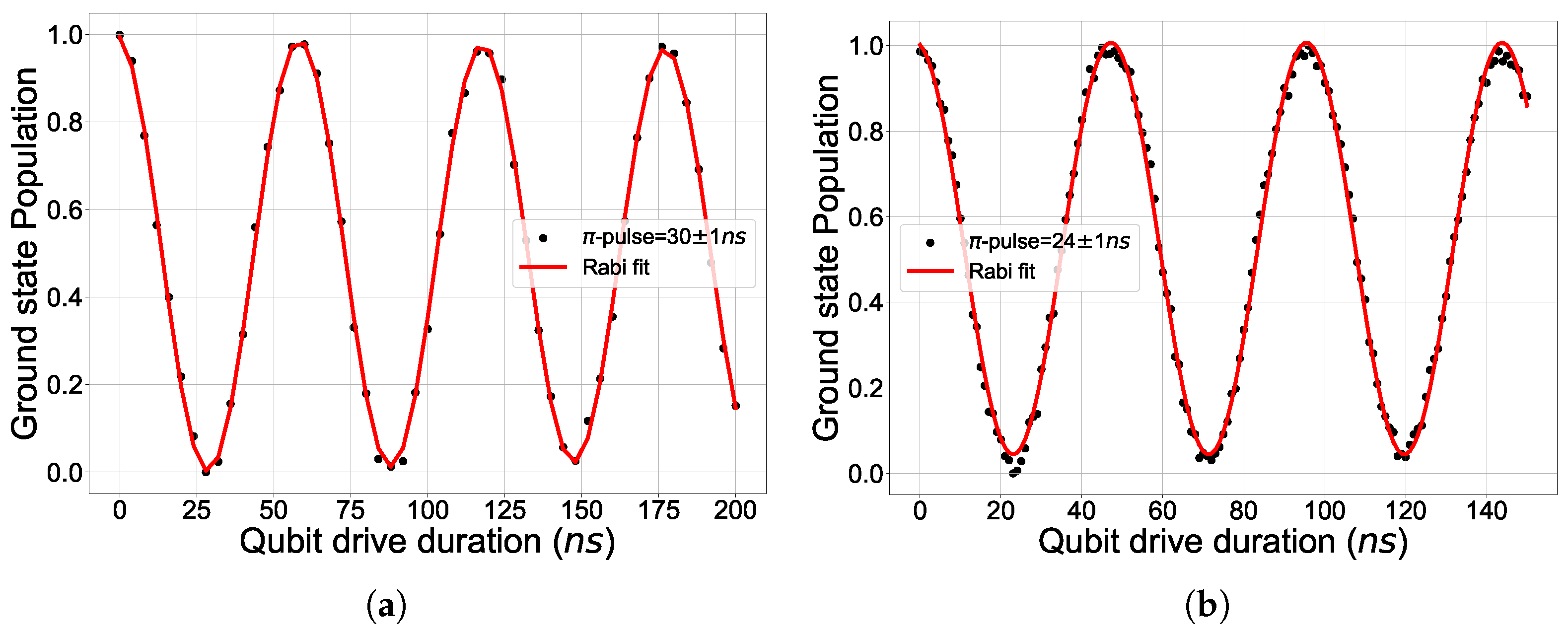
2.3. Control-Pulses Optimization
2.4. Single-Qubit Gate Fidelities
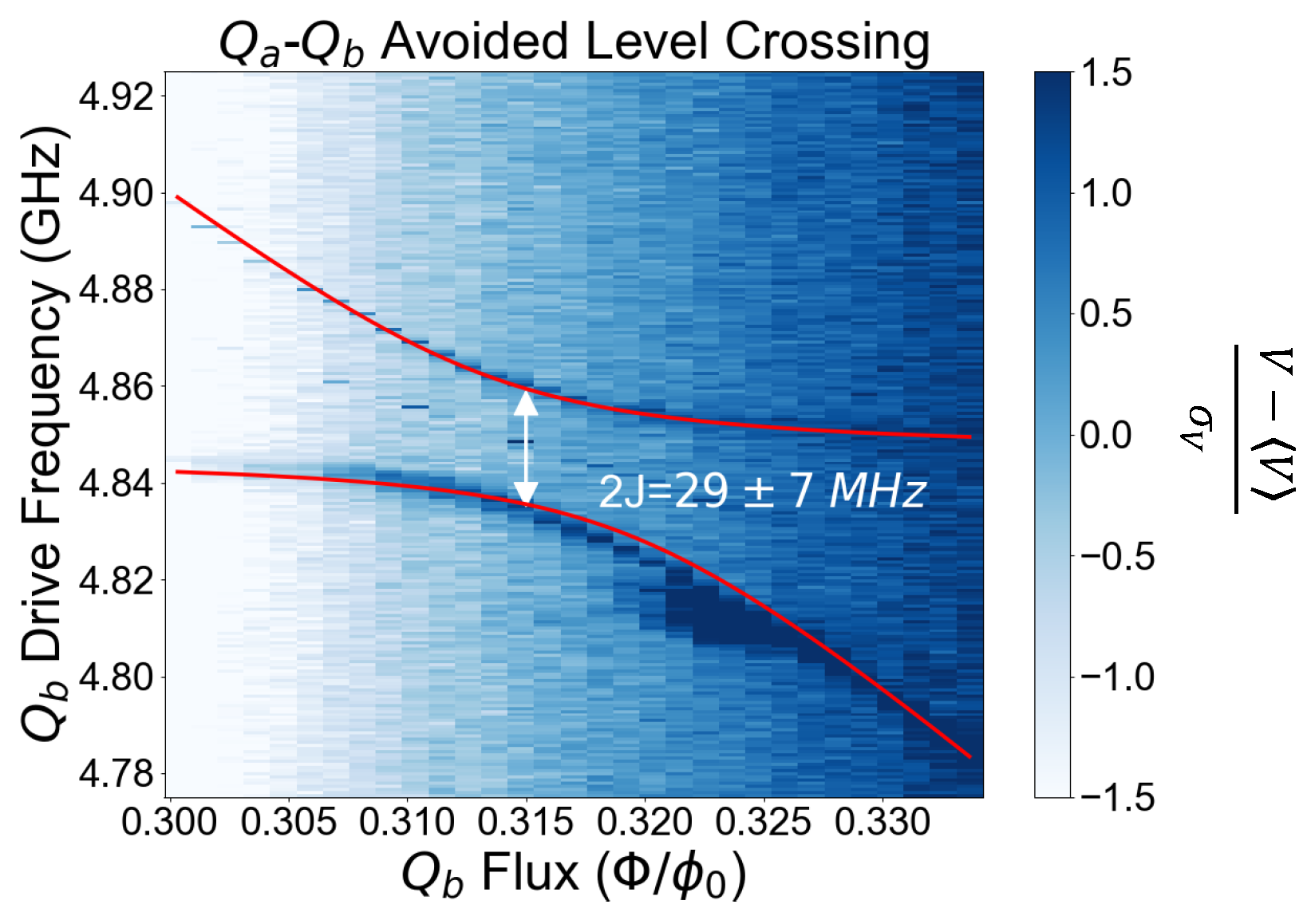
2.5. Evidence of Two-Qubit Coupling
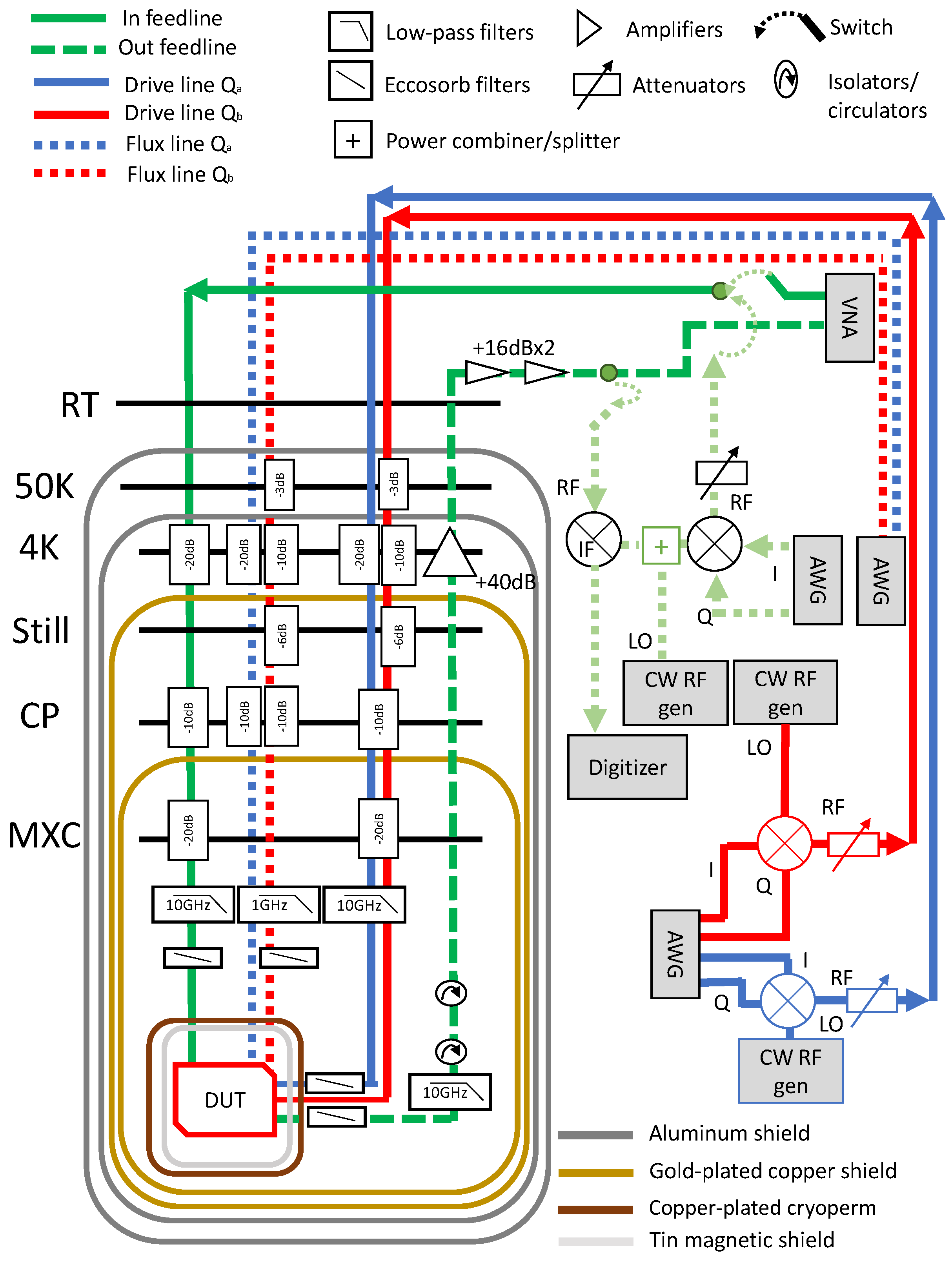
3. Materials and Methods
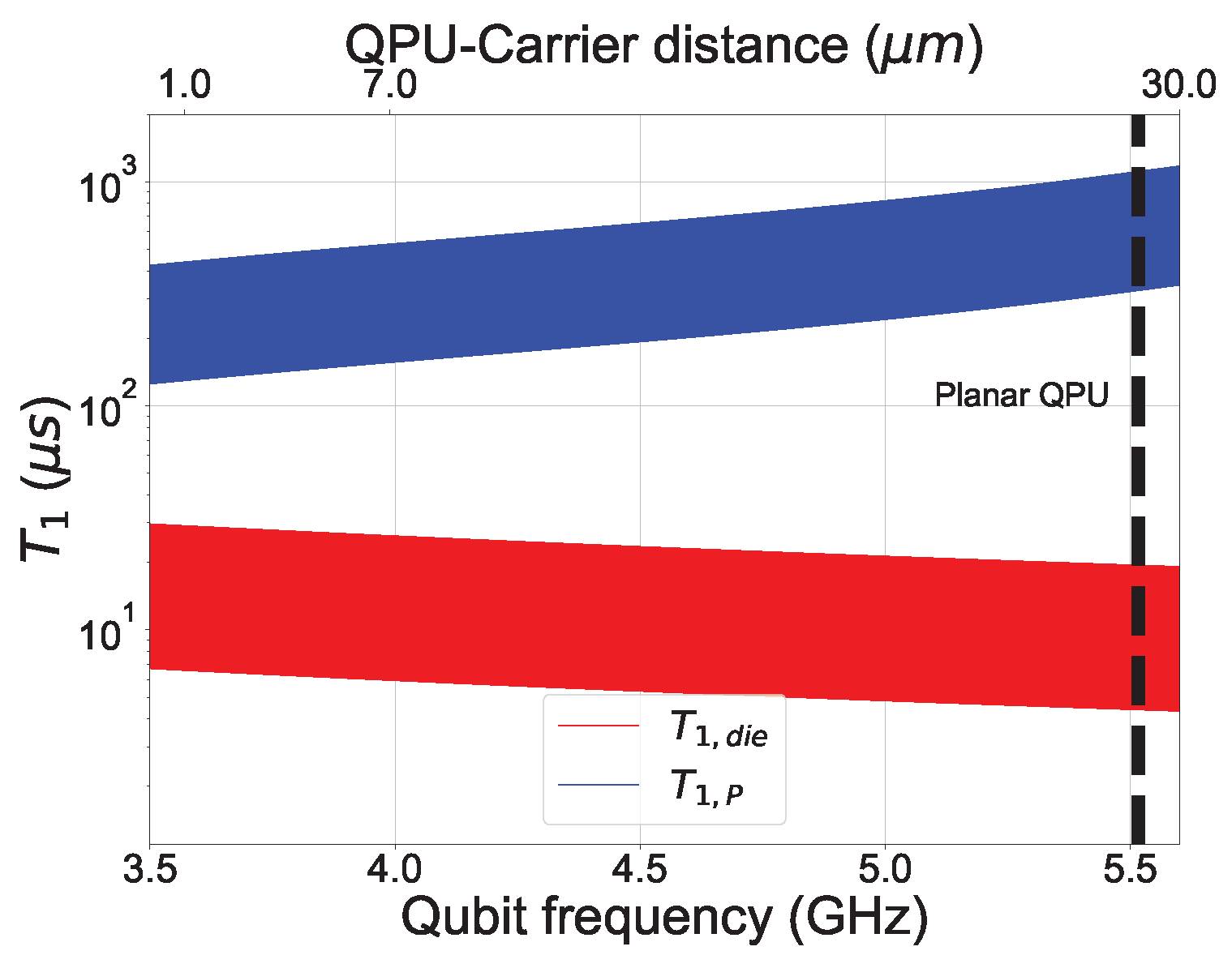
4. Discussion and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Fowler, A.G.; Mariantoni, M.; Martinis, J.M.; Cleland, A.N. Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A 2012, 86, 032324. [Google Scholar] [CrossRef] [Green Version]
- Gambetta, J.M.; Chow, J.M.; Steffen, M. Building logical qubits in a superconducting quantum computing system. NPJ Quantum Inf. 2017, 3, 2. [Google Scholar] [CrossRef] [Green Version]
- Versluis, R.; Poletto, S.; Khammassi, N.; Tarasinski, B.; Haider, N.; Michalak, D.J.; Bruno, A.; Bertels, K.; DiCarlo, L. Scalable Quantum Circuit and Control for a Superconducting Surface Code. Phys. Rev. Appl. 2017, 8, 034021. [Google Scholar] [CrossRef] [Green Version]
- Campbell, E.T.; Terhal, B.M.; Vuillot, C. Roads towards fault-tolerant universal quantum computation. Nature 2017, 549, 172–179. [Google Scholar] [CrossRef] [Green Version]
- Egan, L.; Debroy, D.M.; Noel, C.; Risinger, A.; Zhu, D.; Biswas, D.; Newman, M.; Li, M.; Brown, K.R.; Cetina, M.; et al. Fault-tolerant control of an error-corrected qubit. Nature 2021, 598, 281–286. [Google Scholar] [CrossRef]
- Krinner, S.; Lacroix, N.; Remm, A.; Di Paolo, A.; Genois, E.; Leroux, C.; Hellings, C.; Lazar, S.; Swiadek, F.; Herrmann, J.; et al. Realizing repeated quantum error correction in a distance-three surface code. Nature 2022, 605, 669–674. [Google Scholar] [CrossRef]
- Webster, P.; Vasmer, M.; Scruby, T.R.; Bartlett, S.D. Universal fault-tolerant quantum computing with stabilizer codes. Phys. Rev. Res. 2022, 4, 013092. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, Y.; Huang, H.L.; Zhang, Y.; Wu, D.; Guan, H.; Zhu, Q.; Wei, Z.; He, T.; Cao, S.; et al. Realization of an Error-Correcting Surface Code with Superconducting Qubits. Phys. Rev. Lett. 2022, 129, 030501. [Google Scholar] [CrossRef]
- Marques, J.F.; Varbanov, B.M.; Moreira, M.S.; Ali, H.; Muthusubramanian, N.; Zachariadis, C.; Battistel, F.; Beekman, M.; Haider, N.; Vlothuizen, W.; et al. Logical-qubit operations in an error-detecting surface code. Nat. Phys. 2022, 18, 80–86. [Google Scholar] [CrossRef]
- Koch, D.; Torrance, A.; Kinghorn, D.; Patel, S.; Wessing, L.; Alsing, P.M. Simulating Quantum Algorithms Using Fidelity and Coherence Time as Principle Models for Error. arXiv 2019, arXiv:1908.04229. [Google Scholar]
- Bravyi, S.; Dial, O.; Gambetta, J.M.; Gil, D.; Nazario, Z. The future of quantum computing with superconducting qubits. J. Appl. Phys. 2022, 132, 160902. [Google Scholar] [CrossRef]
- Abad, T.; Fernández-Pendás, J.; Frisk Kockum, A.; Johansson, G. Universal Fidelity Reduction of Quantum Operations from Weak Dissipation. Phys. Rev. Lett. 2022, 129, 150504. [Google Scholar] [CrossRef] [PubMed]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162–167. [Google Scholar] [CrossRef] [Green Version]
- Blais, A.; Huang, R.S.; Wallraff, A.; Girvin, S.M.; Schoelkopf, R.J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 2004, 69, 062320. [Google Scholar] [CrossRef] [Green Version]
- Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef] [Green Version]
- Oliver, W.D.; Welander, P.B. Materials in superconducting quantum bits. MRS Bull. 2013, 38, 816–825. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.H.; Chakram, S.; Kim, S.E.; Mujid, F.; Ray, A.; Gao, H.; Park, C.; Zhong, Y.; Muller, D.A.; Schuster, D.I.; et al. Two-Dimensional Material Tunnel Barrier for Josephson Junctions and Superconducting Qubits. Nano Lett. 2019, 19, 8287–8293. [Google Scholar] [CrossRef]
- Place, A.P.M.; Rodgers, L.V.H.; Mundada, P.; Smitham, B.M.; Fitzpatrick, M.; Leng, Z.; Premkumar, A.; Bryon, J.; Vrajitoarea, A.; Sussman, S.; et al. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 2021, 12, 1779. [Google Scholar] [CrossRef]
- Blais, A.; Grimsmo, A.L.; Girvin, S.M.; Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 2021, 93, 025005. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Xu, H.; Li, Z.; Wang, J.; Yang, Z.; Mi, Z.; Liang, X.; Su, T.; Yang, C.; et al. Towards practical quantum computers: Transmon qubit with a lifetime approaching 0.5 milliseconds. NPJ Quantum Inf. 2022, 8, 3. [Google Scholar] [CrossRef]
- Manucharyan, V.E.; Koch, J.; Glazman, L.I.; Devoret, M.H. Fluxonium: Single Cooper-Pair Circuit Free of Charge Offsets. Science 2009, 326, 113–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, L.B.; Lin, Y.H.; Somoroff, A.; Mencia, R.; Grabon, N.; Manucharyan, V.E. High-Coherence Fluxonium Qubit. Phys. Rev. X 2019, 9, 041041. [Google Scholar] [CrossRef] [Green Version]
- Somoroff, A.; Ficheux, Q.; Mencia, R.A.; Xiong, H.; Kuzmin, R.V.; Manucharyan, V.E. Millisecond coherence in a superconducting qubit. arXiv 2021, arXiv:2103.08578. [Google Scholar]
- Dogan, E.; Rosenstock, D.; Guevel, L.L.; Xiong, H.; Mencia, R.A.; Somoroff, A.; Nesterov, K.N.; Vavilov, M.G.; Manucharyan, V.E.; Wang, C. Demonstration of the Two-Fluxonium Cross-Resonance Gate. arXiv 2022, arXiv:2204.11829. [Google Scholar]
- Sevilla, J.; Riedel, C.J. Forecasting timelines of quantum computing. arXiv 2020, arXiv:2009.05045. [Google Scholar]
- IBM Unveils 400 Qubit-Plus Quantum Processor and Next-Generation IBM Quantum System Two. 2022. Available online: https://newsroom.ibm.com/2022-11-09-IBM-Unveils-400-Qubit-Plus-Quantum-Processor-and-Next-Generation-IBM-Quantum-System-Two (accessed on 1 February 2023).
- Krinner, S.; Storz, S.; Kurpiers, P.; Magnard, P.; Heinsoo, J.; Keller, R.; Lütolf, J.; Eichler, C.; Wallraff, A. Engineering cryogenic setups for 100-qubit scale superconducting circuit systems. EPJ Quantum Technol. 2019, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- George, R.E.; Senior, J.; Saira, O.P.; Pekola, J.P.; de Graaf, S.E.; Lindström, T.; Pashkin, Y.A. Multiplexing Superconducting Qubit Circuit for Single Microwave Photon Generation. J. Low Temp. Phys. 2017, 189, 60–75. [Google Scholar] [CrossRef] [Green Version]
- Shan, Z.; Zhu, Y.; Zhao, B. A high-performance compilation strategy for multiplexing quantum control architecture. Sci. Rep. 2022, 12, 7132. [Google Scholar] [CrossRef]
- Braginski, A.I. Superconductor Electronics: Status and Outlook. J. Supercond. Nov. Magn. 2019, 32, 23–44. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Liang, F.T.; Xu, Y.; Sun, L.H.; Guo, C.; Liao, S.K.; Peng, C.Z. Scalable and customizable arbitrary waveform generator for superconducting quantum computing. AIP Adv. 2019, 9, 115309. [Google Scholar] [CrossRef]
- Pauka, S.J.; Das, K.; Kalra, R.; Moini, A.; Yang, Y.; Trainer, M.; Bousquet, A.; Cantaloube, C.; Dick, N.; Gardner, G.C.; et al. A cryogenic CMOS chip for generating control signals for multiple qubits. Nat. Electron. 2021, 4, 64–70. [Google Scholar] [CrossRef]
- Potočnik, A.; Brebels, S.; Verjauw, J.; Acharya, R.; Grill, A.; Wan, D.; Mongillo, M.; Li, R.; Ivanov, T.; Winckel, S.V.; et al. Millikelvin temperature cryo-CMOS multiplexer for scalable quantum device characterisation. Quantum Sci. Technol. 2021, 7, 015004. [Google Scholar] [CrossRef]
- Parker, M. Controlling qubits with cryogenic devices. Nat. Electron. 2022, 5, 125. [Google Scholar] [CrossRef]
- Howe, L.; Castellanos-Beltran, M.A.; Sirois, A.J.; Olaya, D.; Biesecker, J.; Dresselhaus, P.D.; Benz, S.P.; Hopkins, P.F. Digital Control of a Superconducting Qubit Using a Josephson Pulse Generator at 3 K. PRX Quantum 2022, 3, 010350. [Google Scholar] [CrossRef]
- Lecocq, F.; Quinlan, F.; Cicak, K.; Aumentado, J.; Diddams, S.A.; Teufel, J.D. Control and readout of a superconducting qubit using a photonic link. Nature 2021, 591, 575–579. [Google Scholar] [CrossRef]
- Larsen, T.W.; Petersson, K.D.; Kuemmeth, F.; Jespersen, T.S.; Krogstrup, P.; Nygård, J.; Marcus, C.M. Semiconductor-Nanowire-Based Superconducting Qubit. Phys. Rev. Lett. 2015, 115, 127001. [Google Scholar] [CrossRef] [Green Version]
- de Lange, G.; van Heck, B.; Bruno, A.; van Woerkom, D.J.; Geresdi, A.; Plissard, S.R.; Bakkers, E.P.A.M.; Akhmerov, A.R.; DiCarlo, L. Realization of Microwave Quantum Circuits Using Hybrid Superconducting-Semiconducting Nanowire Josephson Elements. Phys. Rev. Lett. 2015, 115, 127002. [Google Scholar] [CrossRef] [Green Version]
- Wiedenmann, J.; Bocquillon, E.; Deacon, R.S.; Hartinger, S.; Herrmann, O.; Klapwijk, T.M.; Maier, L.; Ames, C.; Brüne, C.; Gould, C.; et al. 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat. Commun. 2016, 7, 10303. [Google Scholar] [CrossRef] [Green Version]
- Manousakis, J.; Altland, A.; Bagrets, D.; Egger, R.; Ando, Y. Majorana qubits in a topological insulator nanoribbon architecture. Phys. Rev. B 2017, 95, 165424. [Google Scholar] [CrossRef] [Green Version]
- Karzig, T.; Knapp, C.; Lutchyn, R.M.; Bonderson, P.; Hastings, M.B.; Nayak, C.; Alicea, J.; Flensberg, K.; Plugge, S.; Oreg, Y.; et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 2017, 95, 235305. [Google Scholar] [CrossRef] [Green Version]
- Gül, Ö.; Zhang, H.; Bommer, J.D.S.; de Moor, M.W.A.; Car, D.; Plissard, S.R.; Bakkers, E.P.A.M.; Geresdi, A.; Watanabe, K.; Taniguchi, T.; et al. Ballistic Majorana nanowire devices. Nat. Nanotechnol. 2018, 13, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Kroll, J.G.; Uilhoorn, W.; van der Enden, K.L.; de Jong, D.; Watanabe, K.; Taniguchi, T.; Goswami, S.; Cassidy, M.C.; Kouwenhoven, L.P. Magnetic field compatible circuit quantum electrodynamics with graphene Josephson junctions. Nat. Commun. 2018, 9, 4615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casparis, L.; Connolly, M.R.; Kjaergaard, M.; Pearson, N.J.; Kringhøj, A.; Larsen, T.W.; Kuemmeth, F.; Wang, T.; Thomas, C.; Gronin, S.; et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotechnol. 2018, 13, 915–919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kunakova, G.; Surendran, A.P.; Montemurro, D.; Salvato, M.; Golubev, D.; Andzane, J.; Erts, D.; Bauch, T.; Lombardi, F. Topological insulator nanoribbon Josephson junctions: Evidence for size effects in transport properties. J. Appl. Phys. 2020, 128, 194304. [Google Scholar] [CrossRef]
- Ahmad, H.G.; Minutillo, M.; Capecelatro, R.; Pal, A.; Caruso, R.; Passarelli, G.; Blamire, M.G.; Tafuri, F.; Lucignano, P.; Massarotti, D. Coexistence and tuning of spin-singlet and triplet transport in spin-filter Josephson junctions. Commun. Phys. 2022, 5, 2. [Google Scholar] [CrossRef]
- Ahmad, H.G.; Brosco, V.; Miano, A.; Di Palma, L.; Arzeo, M.; Montemurro, D.; Lucignano, P.; Pepe, G.P.; Tafuri, F.; Fazio, R.; et al. Hybrid ferromagnetic transmon qubit: Circuit design, feasibility, and detection protocols for magnetic fluctuations. Phys. Rev. B 2022, 105, 214522. [Google Scholar] [CrossRef]
- Likharev, K.K.; Semenov, V.K. RSFQ logic/memory family: A new Josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appl. Supercond. 1991, 1, 3–28. [Google Scholar] [CrossRef]
- Mukhanov, O.A. Energy-Efficient Single Flux Quantum Technology. IEEE Trans. Appl. Supercond. 2011, 21, 760–769. [Google Scholar] [CrossRef]
- Tanaka, M.; Kitayama, A.; Koketsu, T.; Ito, M.; Fujimaki, A. Low-Energy Consumption RSFQ Circuits Driven by Low Voltages. IEEE Trans. Appl. Supercond. 2013, 23, 1701104. [Google Scholar] [CrossRef]
- Mukhanov, O.A. Digital electronics. In Handbook of Superconductivity, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2022; pp. 702–709. [Google Scholar]
- Liebermann, P.J.; Wilhelm, F.K. Optimal Qubit Control Using Single-Flux Quantum Pulses. Phys. Rev. Appl. 2016, 6, 024022. [Google Scholar] [CrossRef] [Green Version]
- McDermott, R.; Vavilov, M.G.; Plourde, B.L.T.; Wilhelm, F.K.; Liebermann, P.J.; Mukhanov, O.A.; Ohki, T.A. Quantum–classical interface based on single flux quantum digital logic. Quantum Sci. Technol. 2018, 3, 024004. [Google Scholar] [CrossRef] [Green Version]
- Mukhanov, O.; Kirichenko, A.; Howington, C.; Walter, J.; Hutchings, M.; Vernik, I.; Yohannes, D.; Dodge, K.; Ballard, A.; Plourde, B.L.T.; et al. Scalable Quantum Computing Infrastructure Based on Superconducting Electronics. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), Francisco, CA, USA, 7–11 December 2019; pp. 31.2.1–31.2.4. [Google Scholar] [CrossRef]
- Takeuchi, N.; Ozawa, D.; Yamanashi, Y.; Yoshikawa, N. An adiabatic quantum flux parametron as an ultra-low-power logic device. Supercond. Sci. Technol. 2013, 26, 035010. [Google Scholar] [CrossRef]
- Govia, L.C.G.; Pritchett, E.J.; Xu, C.; Plourde, B.L.T.; Vavilov, M.G.; Wilhelm, F.K.; McDermott, R. High-fidelity qubit measurement with a microwave-photon counter. Phys. Rev. A 2014, 90, 062307. [Google Scholar] [CrossRef] [Green Version]
- Opremcak, A.; Pechenezhskiy, I.V.; Howington, C.; Christensen, B.G.; Beck, M.A.; Leonard, E.; Suttle, J.; Wilen, C.; Nesterov, K.N.; Ribeill, G.J.; et al. Measurement of a superconducting qubit with a microwave photon counter. Science 2018, 361, 1239–1242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Howington, C.; Opremcak, A.; McDermott, R.; Kirichenko, A.; Mukhanov, O.A.; Plourde, B.L.T. Interfacing Superconducting Qubits With Cryogenic Logic: Readout. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Opremcak, A.; Liu, C.H.; Wilen, C.; Okubo, K.; Christensen, B.G.; Sank, D.; White, T.C.; Vainsencher, A.; Giustina, M.; Megrant, A.; et al. High-Fidelity Measurement of a Superconducting Qubit Using an On-Chip Microwave Photon Counter. Phys. Rev. X 2021, 11, 011027. [Google Scholar] [CrossRef]
- Di Palma, L.; Miano, A.; Mastrovito, P.; Massarotti, D.; Arzeo, M.; Pepe, G.; Tafuri, F.; Mukhanov, O. Discriminating the phase of a weak coherent tone with a flux-switchable superconducting circuit. 2023; under revision. [Google Scholar]
- Conner, C.; Biengait, A.; Chang, H.; Chou, M.; Dumur, E.; Grebel, J.; Peairs, G.; Povey, R.; Yan, H.; Zhong, Y.; et al. Superconducting qubits in a flip-chip architecture. Appl. Phys. Lett. 2021, 118, 232602. [Google Scholar] [CrossRef]
- Smith, K.N.; Ravi, G.S.; Baker, J.M.; Chong, F.T. Scaling Superconducting Quantum Computers with Chiplet Architectures. In Proceedings of the 2022 55th IEEE/ACM International Symposium on Microarchitecture (MICRO), Chicago, IL, USA, 1–5 October 2022. [Google Scholar] [CrossRef]
- Thomas, C.; Michel, J.P.; Deschaseaux, E.; Charbonnier, J.; Souil, R.; Vermande, E.; Campo, A.; Farjot, T.; Rodriguez, G.; Romano, G.; et al. Superconducting routing platform for large-scale integration of quantum technologies. Mater. Quantum Technol. 2022, 2, 035001. [Google Scholar] [CrossRef]
- Kosen, S.; Li, H.X.; Rommel, M.; Shiri, D.; Warren, C.; Grönberg, L.; Salonen, J.; Abad, T.; Biznárová, J.; Caputo, M.; et al. Building blocks of a flip-chip integrated superconducting quantum processor. Quantum Sci. Technol. 2022, 7, 035018. [Google Scholar] [CrossRef]
- Leonard, E.; Beck, M.A.; Nelson, J.; Christensen, B.; Thorbeck, T.; Howington, C.; Opremcak, A.; Pechenezhskiy, I.; Dodge, K.; Dupuis, N.; et al. Digital Coherent Control of a Superconducting Qubit. Phys. Rev. Appl. 2019, 11, 014009. [Google Scholar] [CrossRef] [Green Version]
- Yorozu, S.; Miyazaki, T.; Semenov, V.; Nakamura, Y.; Hashimoto, Y.; Hinode, K.; Sato, T.; Kameda, Y.; Tsai, J.S. Sub-Kelvin single flux quantum control circuits and multi-chip packaging for supporting superconducting qubit. J. Phys. Conf. Ser. 2006, 43, 1417. [Google Scholar] [CrossRef] [Green Version]
- Yohannes, D.; Amparo, D.; Chernyashevskyy, O.; Mukhanov, O.; Renzullo, M.; Talalaeskii, A.; Vernik, I.; Vivalda, J.; Walter, J. System and Method for Superconducting Multi-Chip Module. Patent No. US11121302B2, 14 September 2019. [Google Scholar]
- Yohannes, D.; Vernik, I.; Jordan, C.; Truitt, P.; Kirichenko, A.; Salim, A.J.; Katam, N.; Mukhanov, O. Interconnections between Quantum Computing Module and Non-Quantum Processing Modules in Quantum Computing Systems. Patent No. US20220237495A1, 28 July 2021. [Google Scholar]
- Mukhanov, O.A.; Kirichenko, A.F.; Vernik, I.V.; Nevirkovets, I.P.; Kadin, A.M. System and Method for Cryogenic Hybrid Technology Computing and Memory. Patent No. US10950299B1, 16 March 2022. [Google Scholar]
- Probst, S.; Song, F.B.; Bushev, P.A.; Ustinov, A.V.; Weides, M. Efficient and robust analysis of complex scattering data under noise in microwave resonators. Rev. Sci. Instrum. 2015, 86, 024706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef] [Green Version]
- Naghiloo, M. Introduction to experimental quantum measurement with superconducting qubits. arXiv 2019, arXiv:1904.09291. [Google Scholar]
- Chen, Z.; Kelly, J.; Quintana, C.; Barends, R.; Campbell, B.; Chen, Y.; Chiaro, B.; Dunsworth, A.; Fowler, A.G.; Lucero, E.; et al. Measuring and Suppressing Quantum State Leakage in a Superconducting Qubit. Phys. Rev. Lett. 2016, 116, 020501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucero, E.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Katz, N.; Neeley, M.; O’Connell, A.D.; Wang, H.; Cleland, A.N.; Martinis, J.M. High-Fidelity Gates in a Single Josephson Qubit. Phys. Rev. Lett. 2008, 100, 247001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chow, J.M.; DiCarlo, L.; Gambetta, J.M.; Motzoi, F.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Optimized driving of superconducting artificial atoms for improved single-qubit gates. Phys. Rev. A 2010, 82, 040305. [Google Scholar] [CrossRef] [Green Version]
- Pokharel, B.; Anand, N.; Fortman, B.; Lidar, D.A. Demonstration of Fidelity Improvement Using Dynamical Decoupling with Superconducting Qubits. Phys. Rev. Lett. 2018, 121, 220502. [Google Scholar] [CrossRef] [Green Version]
- Werninghaus, M.; Egger, D.J.; Roy, F.; Machnes, S.; Wilhelm, F.K.; Filipp, S. Leakage reduction in fast superconducting qubit gates via optimal control. NPJ Quantum Inf. 2021, 7, 14. [Google Scholar] [CrossRef]
- Chow, J.M.; Gambetta, J.M.; Tornberg, L.; Koch, J.; Bishop, L.S.; Houck, A.A.; Johnson, B.R.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Randomized Benchmarking and Process Tomography for Gate Errors in a Solid-State Qubit. Phys. Rev. Lett. 2009, 102, 090502. [Google Scholar] [CrossRef] [Green Version]
- Grier, D.; Schaeffer, L. The Classification of Clifford Gates over Qubits. Quantum 2022, 6, 734. [Google Scholar] [CrossRef]
- Wallman, J.J.; Barnhill, M.; Emerson, J. Robust characterization of leakage errors. New J. Phys. 2016, 18, 043021. [Google Scholar] [CrossRef] [Green Version]
- Sheldon, S.; Bishop, L.S.; Magesan, E.; Filipp, S.; Chow, J.M.; Gambetta, J.M. Characterizing errors on qubit operations via iterative randomized benchmarking. Phys. Rev. A 2016, 93, 012301. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Wallman, J.J.; Hincks, I.; Laflamme, R. Independent state and measurement characterization for quantum computers. Phys. Rev. Res. 2021, 3, 033285. [Google Scholar] [CrossRef]
- Reed, M. Entanglement and Quantum Error Correction with Superconducting Qubits. Ph.D. Thesis, Faculty of the Graduate School of Yale University, New Haven, CT, USA, May 2013. [Google Scholar]
- Motzoi, F.; Gambetta, J.M.; Rebentrost, P.; Wilhelm, F.K. Simple Pulses for Elimination of Leakage in Weakly Nonlinear Qubits. Phys. Rev. Lett. 2009, 103, 110501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krantz, P.; Bengtsson, A.; Simoen, M.; Gustavsson, S.; Shumeiko, V.; Oliver, W.D.; Wilson, C.M.; Delsing, P.; Bylander, J. Single-shot read-out of a superconducting qubit using a Josephson parametric oscillator. Nat. Commun. 2016, 7, 11417. [Google Scholar] [CrossRef] [Green Version]
- Theis, L.S.; Motzoi, F.; Machnes, S.; Wilhelm, F.K. Counteracting systems of diabaticities using DRAG controls: The status after 10 years(a). Europhys. Lett. 2018, 123, 60001. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.Y.; Rol, M.A.; Touzard, S.; Wang, C. Practical Guide for Building Superconducting Quantum Devices. PRX Quantum 2021, 2, 040202. [Google Scholar] [CrossRef]
- Babu, A.P.; Tuorila, J.; Ala-Nissila, T. State leakage during fast decay and control of a superconducting transmon qubit. NPJ Quantum Inf. 2021, 7, 30. [Google Scholar] [CrossRef]
- Chao, R.; Reichardt, B.W. Fault-tolerant quantum computation with few qubits. NPJ Quantum Inf. 2018, 4, 42. [Google Scholar] [CrossRef] [Green Version]
- Majer, J.; Chow, J.M.; Gambetta, J.M.; Koch, J.; Johnson, B.R.; Schreier, J.A.; Frunzio, L.; Schuster, D.I.; Houck, A.A.; Wallraff, A.; et al. Coupling superconducting qubits via a cavity bus. Nature 2007, 449, 443–447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sillanpää, M.A.; Park, J.I.; Simmonds, R.W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 2007, 449, 438–442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.I.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.M.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Filipp, S.; Göppl, M.; Fink, J.M.; Baur, M.; Bianchetti, R.; Steffen, L.; Wallraff, A. Multimode mediated qubit-qubit coupling and dark-state symmetries in circuit quantum electrodynamics. Phys. Rev. A 2011, 83, 063827. [Google Scholar] [CrossRef] [Green Version]
- Ferraro, E.; Rei, D.; Paris, M.; De Michielis, M. Universal set of quantum gates for the flip-flop qubit in the presence of 1/f noise. EPJ Quantum Technol. 2022, 9, 2. [Google Scholar] [CrossRef]
- Ganzhorn, M.; Salis, G.; Egger, D.J.; Fuhrer, A.; Mergenthaler, M.; Müller, C.; Müller, P.; Paredes, S.; Pechal, M.; Werninghaus, M.; et al. Benchmarking the noise sensitivity of different parametric two-qubit gates in a single superconducting quantum computing platform. Phys. Rev. Res. 2020, 2, 033447. [Google Scholar] [CrossRef]
- Huang, H.L.; Wu, D.; Fan, D.; Zhu, X. Superconducting quantum computing: A review. Sci. China Inf. Sci. 2020, 63, 180501. [Google Scholar] [CrossRef]
- Torosov, B.T.; Vitanov, N.V. Robust high-fidelity coherent control of two-state systems by detuning pulses. Phys. Rev. A 2019, 99, 013424. [Google Scholar] [CrossRef] [Green Version]
- Peterson, J.P.; Sarthour, R.S.; Laflamme, R. Enhancing Quantum Control by Improving Shaped-Pulse Generation. Phys. Rev. Appl. 2020, 13, 054060. [Google Scholar] [CrossRef]
- Güngördü, U.; Kestner, J.P. Robust quantum gates using smooth pulses and physics-informed neural networks. Phys. Rev. Res. 2022, 4, 023155. [Google Scholar] [CrossRef]
- Wang, C.; Axline, C.; Gao, Y.Y.; Brecht, T.; Chu, Y.; Frunzio, L.; Devoret, M.H.; Schoelkopf, R.J. Surface participation and dielectric loss in superconducting qubits. Appl. Phys. Lett. 2015, 107, 162601. [Google Scholar] [CrossRef] [Green Version]
- Groszkowski, P.; Koch, J. Scqubits: A Python package for superconducting qubits. Quantum 2021, 5, 583. [Google Scholar] [CrossRef]
- Chitta, S.P.; Zhao, T.; Huang, Z.; Mondragon-Shem, I.; Koch, J. Computer-aided quantization and numerical analysis of superconducting circuits. New J. Phys. 2022, 24, 103020. [Google Scholar] [CrossRef]
- Bruno, A.; Poletto, S.; Dicarlo, L. Superconducting Microwave-Frequency vias for Mult-Planar Quantum Circuits. Patent No. WO2017155531A1, 14 September 2017. [Google Scholar]



| at SS (GHz) | |||
| at SS (MHz) | - | ||
| (bare state) (GHz) | |||
| (GHz) | |||
| g (MHz) | |||
| s) | |||
| s) | |||
| s) | at kHz | at kHz | |
| (MHz) |
| K | |
| w | 12 m |
| 4 m | |
| 112 × 10 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, H.G.; Jordan, C.; van den Boogaart, R.; Waardenburg, D.; Zachariadis, C.; Mastrovito, P.; Georgiev, A.L.; Montemurro, D.; Pepe, G.P.; Arthers, M.; et al. Investigating the Individual Performances of Coupled Superconducting Transmon Qubits. Condens. Matter 2023, 8, 29. https://doi.org/10.3390/condmat8010029
Ahmad HG, Jordan C, van den Boogaart R, Waardenburg D, Zachariadis C, Mastrovito P, Georgiev AL, Montemurro D, Pepe GP, Arthers M, et al. Investigating the Individual Performances of Coupled Superconducting Transmon Qubits. Condensed Matter. 2023; 8(1):29. https://doi.org/10.3390/condmat8010029
Chicago/Turabian StyleAhmad, Halima Giovanna, Caleb Jordan, Roald van den Boogaart, Daan Waardenburg, Christos Zachariadis, Pasquale Mastrovito, Asen Lyubenov Georgiev, Domenico Montemurro, Giovanni Piero Pepe, Marten Arthers, and et al. 2023. "Investigating the Individual Performances of Coupled Superconducting Transmon Qubits" Condensed Matter 8, no. 1: 29. https://doi.org/10.3390/condmat8010029
APA StyleAhmad, H. G., Jordan, C., van den Boogaart, R., Waardenburg, D., Zachariadis, C., Mastrovito, P., Georgiev, A. L., Montemurro, D., Pepe, G. P., Arthers, M., Bruno, A., Tafuri, F., Mukhanov, O., Arzeo, M., & Massarotti, D. (2023). Investigating the Individual Performances of Coupled Superconducting Transmon Qubits. Condensed Matter, 8(1), 29. https://doi.org/10.3390/condmat8010029











