Design and Optimization of Potentially Low-Cost and Efficient MXene/InP Schottky Barrier Solar Cells via Numerical Modeling
Abstract
1. Introduction
2. Numerical Modeling and Simulation Methodology
3. Results and Discussions
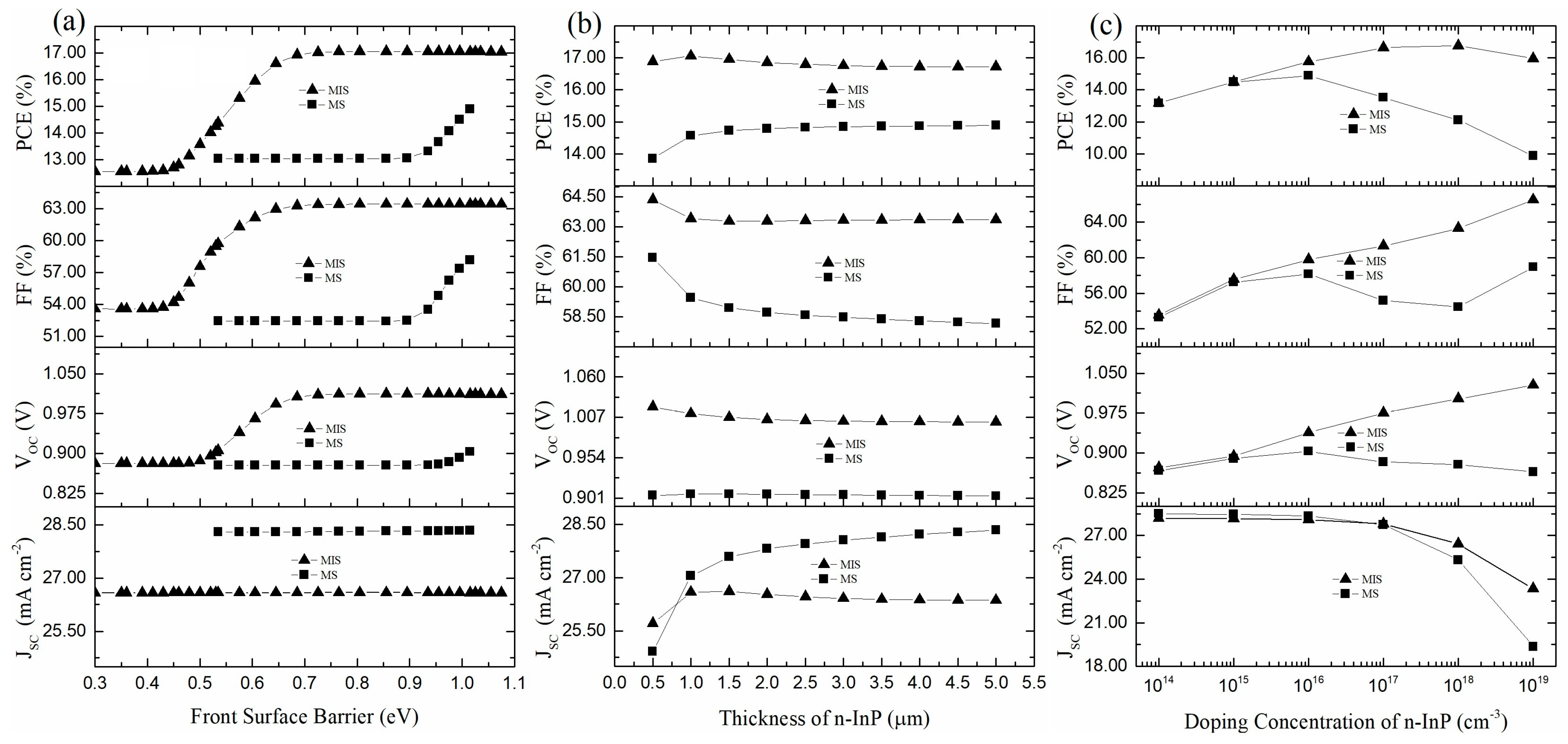
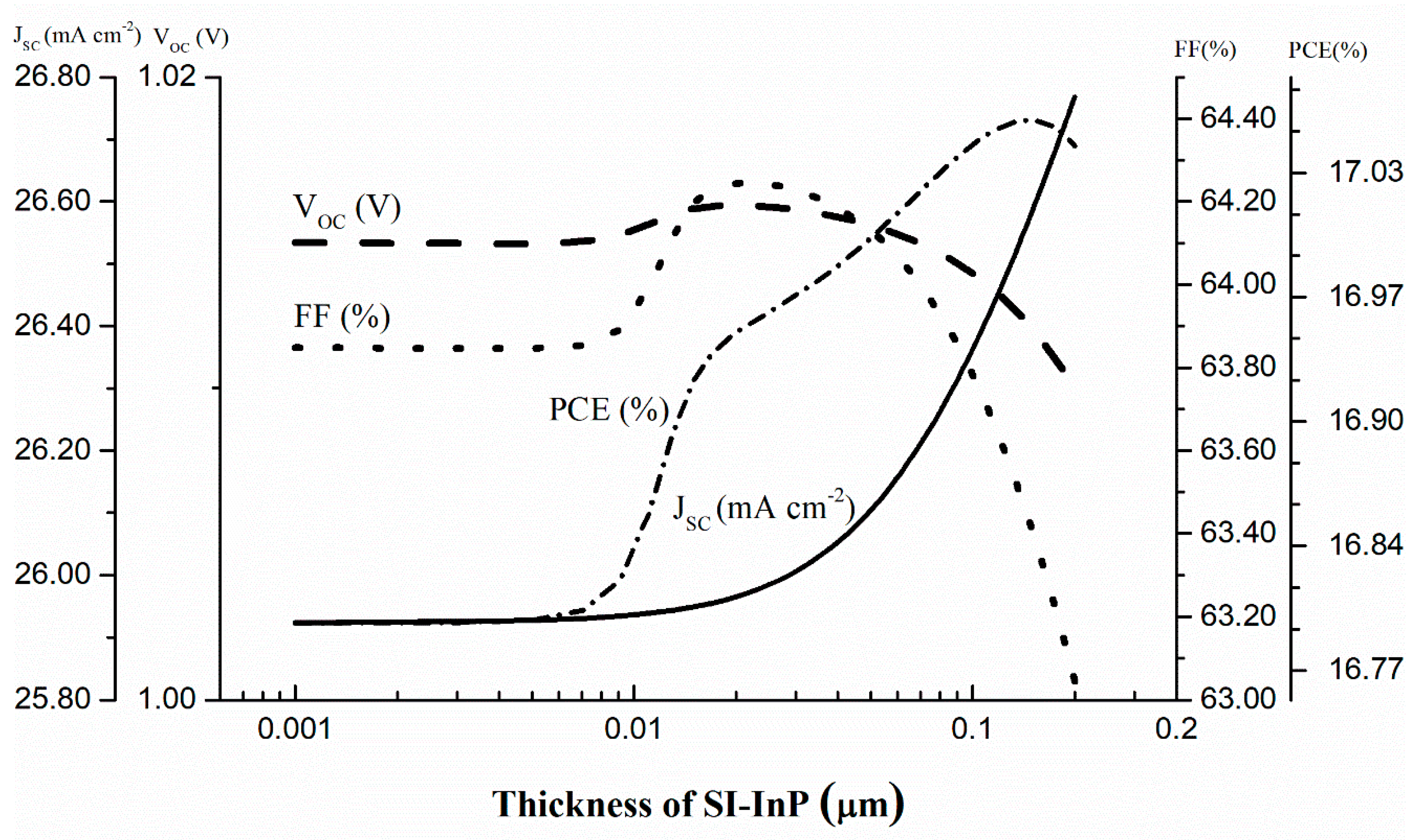
3.1. Optimization of MS and MIS Structures
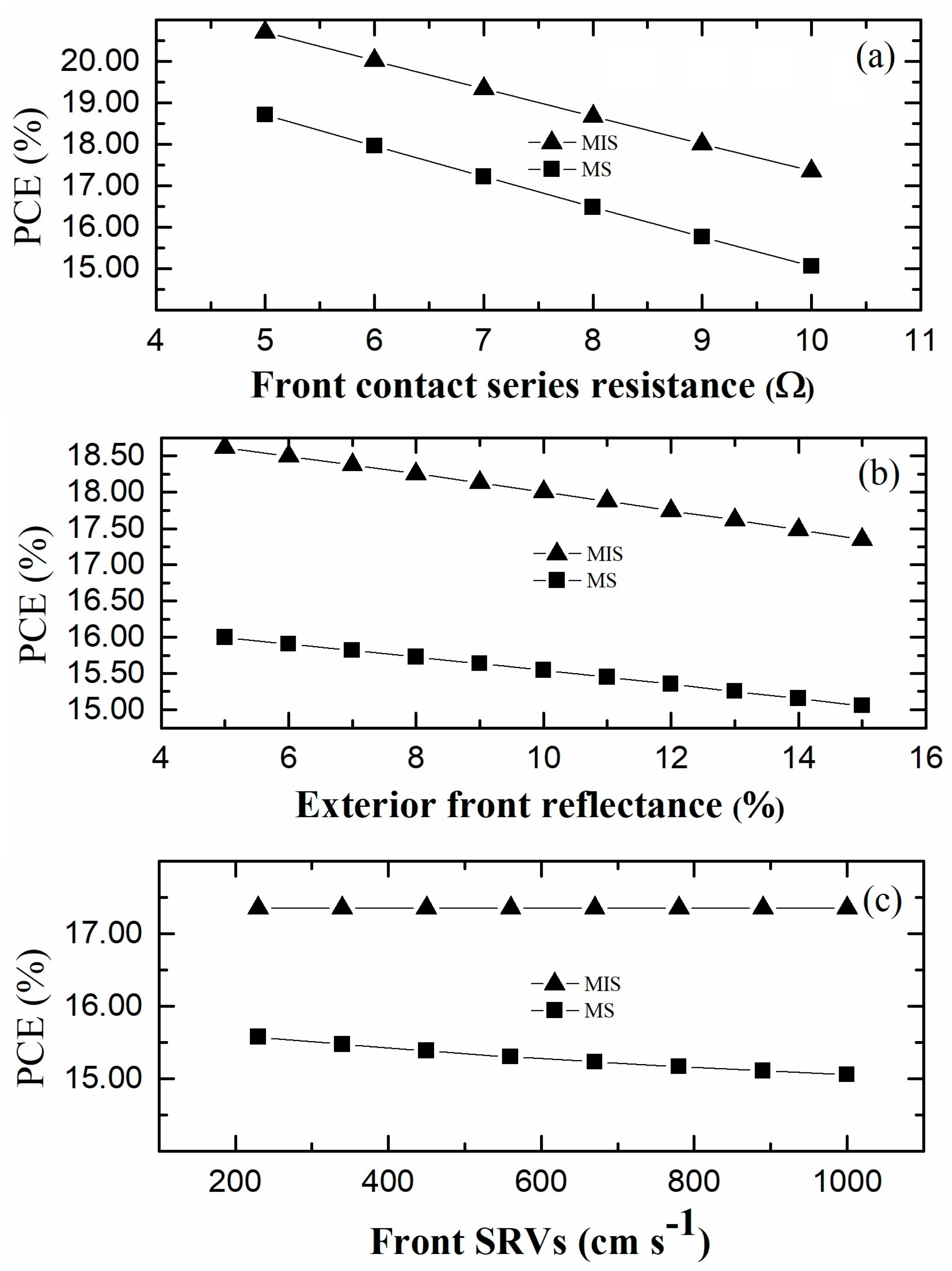
3.2. Performance Sensitivity to Optimization Parameters
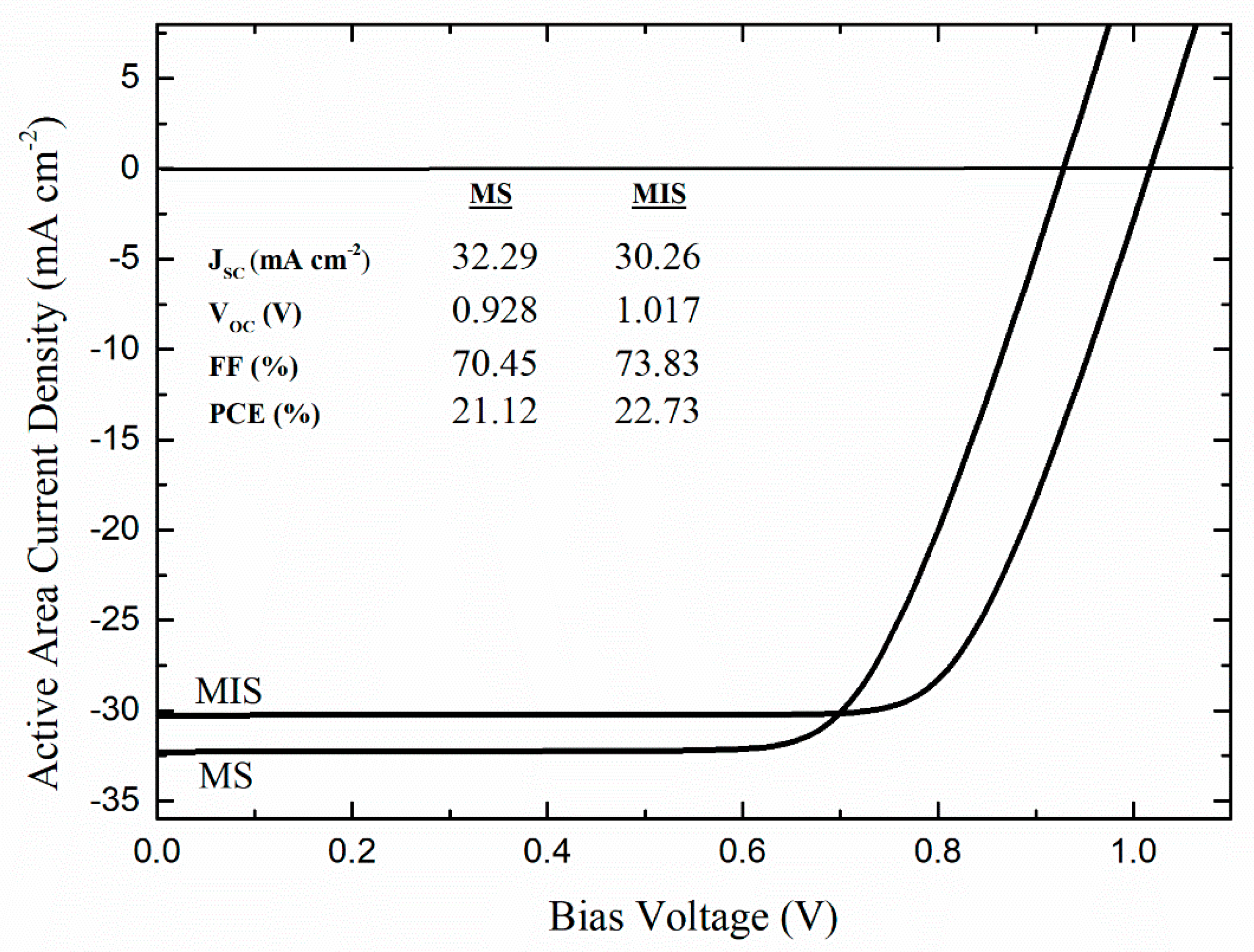
3.3. Possible Performance Gains
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ang, T.-Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strategy Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Chee, A.K.-W. On current technology for light absorber materials used in highly efficient industrial solar cells. Renew. Sustain. Energy Rev. 2023, 173, 113027. [Google Scholar] [CrossRef]
- Yamaguchi, M. Radiation-resistant solar cells for space use. Sol. Energy Mater. Sol. Cells 2001, 68, 31–53. [Google Scholar] [CrossRef]
- Matthew, P.L.; Myles, A.S.; John, F.G.; Robert, J.W. Analytical modeling of III-V solar cells close to the fundamental limit. In Proceedings of the SPIE OPTO Conference, San Francisco, CA, USA, 7 March 2014; p. 898114. [Google Scholar]
- Gupta, B.; Shehata, M.M.; Lee, Y.; Black, L.E.; Ma, F.; Hoex, B.; Jagadish, C.; Tan, H.H.; Karuturi, S. Unveiling the Role of H2 Plasma for Efficient InP Solar Cells. Sol. RRL 2023, 7, 2200868. [Google Scholar] [CrossRef]
- Ward, J.S.; Remo, T.; Horowitz, K.; Woodhouse, M.; Sopori, B.; VanSant, K.; Basore, P. Techno-economic analysis of three different substrate removal and reuse strategies for III-V solar cells. Prog. Photovolt. Res. Appl. 2016, 24, 1284–1292. [Google Scholar] [CrossRef]
- Wanlass, M.U.S. Systems and Methods for Advanced Ultra-High-Performance InP Solar Cells. U.S. Patent 9,590,131B2, 7 March 2017. [Google Scholar]
- Green, M.A.; Dunlop, E.D.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Siefer, G.; Hao, X. Solar cell efficiency tables (version 62). Prog. Photovolt. Res. Appl. 2023, 31, 651–663. [Google Scholar] [CrossRef]
- Rühle, S. Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Sree Harsha, K.S.; Bachmann, K.J.; Schmidt, P.H.; Spencer, E.G.; Thiel, F.A. n-indium tin oxide/p-indium phosphide solar cells. Appl. Phys. Lett. 1977, 30, 645–646. [Google Scholar] [CrossRef]
- Coutts, T.J.; Pearsall, N.M.; Tarricone, L. The influence of input power on the performance of rf sputtered ITO/InP solar cells. J. Vac. Sci. Technol. B Microelectron. Process. Phenom. 1984, 2, 140–144. [Google Scholar] [CrossRef]
- Li, X.; Wanlass, M.W.; Gessert, T.A.; Emery, K.A.; Coutts, T.J. High-efficiency indium tin oxide/indium phosphide solar cells. Appl. Phys. Lett. 1989, 54, 2674–2676. [Google Scholar] [CrossRef]
- Rosenwaks, Y.; Li, X.; Coutts, T.J. Characterization of heat-treated ITO/InP solar cells. J. Vac. Sci. Technol. A 1997, 15, 2354–2358. [Google Scholar] [CrossRef]
- Yoshikawa, A.; Sakai, Y. High efficiency n-CdS/p-InP solar cells prepared by the close-spaced technique. Solid-State Electron. 1977, 20, 133–137. [Google Scholar] [CrossRef]
- Bettini, M.; Bachmann, K.J.; Buehler, E.; Shay, J.L.; Wagner, S. Preparation of CdS/InP solar cells by chemical vapor deposition of CdS. J. Appl. Phys. 1977, 48, 1603–1606. [Google Scholar] [CrossRef]
- Purica, M.; Budianu, E.; Rusu, E.; Arabadji, P. Electrical properties of the CdS/InP heterostructures for photovoltaic applications. Thin Solid Film. 2006, 511–512, 468–472. [Google Scholar] [CrossRef]
- Yin, X.; Battaglia, C.; Lin, Y.; Chen, K.; Hettick, M.; Zheng, M.; Chen, C.-Y.; Kiriya, D.; Javey, A. 19.2% Efficient InP Heterojunction Solar Cell with Electron-Selective TiO2 Contact. ACS Photonics 2014, 1, 1245–1250. [Google Scholar] [CrossRef]
- Raj, V.; dos Santos, T.S.; Rougieux, F.; Vora, K.; Lysevych, M.; Fu, L.; Mokkapati, S.; Tan, H.H.; Jagadish, C. Indium phosphide based solar cell using ultra-thin ZnO as an electron selective layer. J. Phys. D Appl. Phys. 2018, 51, 395301. [Google Scholar] [CrossRef]
- Raj, V.; Rougieux, F.; Fu, L.; Tan, H.H.; Jagadish, C. Design of Ultrathin InP Solar Cell Using Carrier Selective Contacts. IEEE J. Photovolt. 2020, 10, 1657–1666. [Google Scholar] [CrossRef]
- Kamimura, K.; Suzuki, T.; Kunioka, A. InP (MIS) Schottky Barrier Solar Cells. Jpn. J. Appl. Phys. 1980, 19, 203. [Google Scholar] [CrossRef]
- Pande, K.P. Characteristics of MOS solar cells built on (n-type) InP substrates. IEEE Trans. Electron Devices 1980, 27, 631–634. [Google Scholar] [CrossRef]
- Kamimura, K.; Suzuki, T.; Kunioka, A. Metal-insulator semiconductor Schottky-barrier solar cells fabricated on InP. Appl. Phys. Lett. 1981, 38, 259–261. [Google Scholar] [CrossRef]
- Li, Y.; Yu, M.; Cheng, Q. Improved performance of graphene/n-GaAs heterojunction solarcells by introducing an electron-blocking/hole-transporting layer. Mater. Res. Express 2019, 6, 016202. [Google Scholar] [CrossRef]
- Fonash, S.J. Solar Cell Device Physics; Elsevier Inc.: Boston, MA, USA, 2010; p. 381. [Google Scholar]
- Har-Lavan, R.; Cahen, D. 40 Years of Inversion Layer Solar Cells: From MOS to Conducting Polymer/Inorganic Hybrids. IEEE J. Photovolt. 2013, 3, 1443–1459. [Google Scholar] [CrossRef]
- Kuphal, E. Low resistance ohmic contacts to n- and p-InP. Solid-State Electron. 1981, 24, 69–78. [Google Scholar] [CrossRef]
- Alnassar, M.S.N. Discovering new pathways to improved performance of TFSA-doped single-layer graphene/n-Si Schottky barrier solar cells: A detailed numerical study. Optik 2024, 299, 171640. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, L.; Liu, B.; Gao, H.; Zhang, Y.; Yan, H.; Song, X. Graphene/Si Schottky solar cells: A review of recent advances and prospects. RSC Adv. 2019, 9, 863–877. [Google Scholar] [CrossRef]
- Yin, X.; Tang, C.S.; Zheng, Y.; Gao, J.; Wu, J.; Zhang, H.; Chhowalla, M.; Chen, W.; Wee, A.T.S. Recent developments in 2D transition metal dichalcogenides: Phase transition and applications of the (quasi-)metallic phases. Chem. Soc. Rev. 2021, 50, 10087–10115. [Google Scholar] [CrossRef]
- Naguib, M.; Kurtoglu, M.; Presser, V.; Lu, J.; Niu, J.; Heon, M.; Hultman, L.; Gogotsi, Y.; Barsoum, M.W. Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2. Adv. Mater. 2011, 23, 4248–4253. [Google Scholar] [CrossRef]
- Guo, Z.; Gao, L.; Xu, Z.; Teo, S.; Zhang, C.; Kamata, Y.; Hayase, S.; Ma, T. High Electrical Conductivity 2D MXene Serves as Additive of Perovskite for Efficient Solar Cells. Small 2018, 14, 1802738. [Google Scholar] [CrossRef]
- Yu, L.; Bati, A.S.R.; Grace, T.S.L.; Batmunkh, M.; Shapter, J.G. Ti3C2Tx (MXene)-Silicon Heterojunction for Efficient Photovoltaic Cells. Adv. Energy Mater. 2019, 9, 1901063. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, J.; Sun, P.; Zeng, Q.; Deng, X.; Mo, Y.; Chen, J.; Zheng, Y.; Wang, W.; Li, G. Air-stable MXene/GaAs heterojunction solar cells with a high initial efficiency of 9.69%. J. Mater. Chem. A 2021, 9, 16160–16168. [Google Scholar] [CrossRef]
- Clugston, D.A.; Basore, P.A. PC1D version 5: 32-bit solar cell modeling on personal computers. In Proceedings of the Conference Record of the Twenty Sixth IEEE Photovoltaic Specialists Conference, Anaheim, CA, USA, 29 September–3 October 1997; pp. 207–210. [Google Scholar]
- Kc, D.; Shah, D.K.; Akhtar, M.S.; Park, M.; Kim, C.Y.; Yang, O.B.; Pant, B. Numerical Investigation of Graphene as a Back Surface Field Layer on the Performance of Cadmium Telluride Solar Cell. Molecules 2021, 26, 3275. [Google Scholar] [CrossRef] [PubMed]
- Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Chandran, J.; Stojcevski, A.; Subramanian, M.; Marnadu, R.; Alfaify, S.; Shkir, M. Optimization of Mono-Crystalline Silicon Solar Cell Devices Using PC1D Simulation. Energies 2021, 14, 4986. [Google Scholar] [CrossRef]
- Parajuli, D.; Kc, D.; Khattri, K.B.; Adhikari, D.R.; Gaib, R.A.; Shah, D.K. Numerical assessment of optoelectrical properties of ZnSe–CdSe solar cell-based with ZnO antireflection coating layer. Sci. Rep. 2023, 13, 12193. [Google Scholar] [CrossRef] [PubMed]
- Alnassar, M.S.N. Utilization of open-source software in teaching the physics of P-N diodes. Comput. Appl. Eng. Educ. 2023, 31, 867–883. [Google Scholar] [CrossRef]
- Jain, R.K.; Flood, D.J. Effects of recombination parameters in p+n indium phosphide solar cells. Sol. Energy Mater. Sol. Cells 1997, 45, 51–55. [Google Scholar] [CrossRef]
- Piprek, J.; Boer, K.W. InP solar cell improvement by inverse delta-doping. In Proceedings of the First IEEE World Conference on Photovoltaic Energy Conversion—WCPEC (A Joint Conference of PVSC, PVSEC and PSEC), Waikoloa, HI, USA, 5–9 December 1994; pp. 1818–1821. [Google Scholar]
- Weinberg, I. InP solar cells for use in space. Sol. Cells 1990, 29, 225–244. [Google Scholar] [CrossRef]
- Bugajski, M.; Lewandowski, W. Concentration-dependent absorption and photoluminescence of n-type InP. J. Appl. Phys. 1985, 57, 521–530. [Google Scholar] [CrossRef]
- Sotoodeh, M.; Khalid, A.H.; Rezazadeh, A.A. Empirical low-field mobility model for III–V compounds applicable in device simulation codes. J. Appl. Phys. 2000, 87, 2890–2900. [Google Scholar] [CrossRef]
- Pearsall, T.P. Properties, Processing and Applications of Indium Phosphide; INSPEC/The Institution of Electrical Engineers: London, UK, 2000; p. 300. [Google Scholar]
- Vidimari, F.; Pellegrino, S.; Caldironi, M.; Paola, A.D.; Chen, R. High resistivity layers in InP obtained by Co or Fe ion implantation and LPE regrowth. In Proceedings of the Third International Conference Indium Phosphide and Related Materials, Cardiff, UK, 8–11 April 1991; pp. 500–503. [Google Scholar]
- Sze, S.M.; Ng, K.K. The Physics of Semiconductor Devices; John Wiley & Sons, Inc.: New York, NY, USA, 2007; p. 815. [Google Scholar]
- McIntosh, K.R.; Baker-Finch, S.C. OPAL 2: Rapid optical simulation of silicon solar cells. In Proceedings of the Conference 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 000265–000271. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1985; p. 804. [Google Scholar]
- Aspnes, D.E.; Studna, A.A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Phys. Rev. B 1983, 27, 985–1009. [Google Scholar] [CrossRef]
- Schroder, D.K.; Meier, D.L. Solar cell contact resistance—A review. IEEE Trans. Electron Devices 1984, 31, 637–647. [Google Scholar] [CrossRef]
- Levinshtein, M.; Rumyantsev, S.; Shur, M. Handbook Series on Semiconductor Parameters; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1996; p. 232. [Google Scholar]
- Khazaei, M.; Arai, M.; Sasaki, T.; Ranjbar, A.; Liang, Y.; Yunoki, S. OH-terminated two-dimensional transition metal carbides and nitrides as ultralow work function materials. Phys. Rev. B 2015, 92, 075411. [Google Scholar] [CrossRef]
- Jain, R.K.; Flood, D.J. Design modeling of high-efficiency p/sup +/-n indium phosphide solar cells. IEEE Trans. Electron Devices 1993, 40, 224–227. [Google Scholar] [CrossRef]
- Brandhorst, H.W.; Flood, D.J. The Past, Present and Future of Space Photovoltaics. In Proceedings of the IEEE 4th World Conference on Photovoltaic Energy Conference, Waikoloa, HI, USA, 7–12 May 2006; pp. 1744–1749. [Google Scholar]
- Yahia, A.H.; Wanlass, M.W.; Coutts, T.J. Modeling and simulation of InP homojunction solar cells. In Proceedings of the Conference Record of the Twentieth IEEE Photovoltaic Specialists Conference, Las Vegas, NV, USA, 26–30 September 1988; pp. 702–707. [Google Scholar]
- Ding, K.; Zhang, X.; Ning, L.; Shao, Z.; Xiao, P.; Ho-Baillie, A.; Zhang, X.; Jie, J. Hue tunable, high color saturation and high-efficiency graphene/silicon heterojunction solar cells with MgF2/ZnS double anti-reflection layer. Nano Energy 2018, 46, 257–265. [Google Scholar] [CrossRef]
- Wang, P.; Li, X.; Xu, Z.; Wu, Z.; Zhang, S.; Xu, W.; Zhong, H.; Chen, H.; Li, E.; Luo, J.; et al. Tunable graphene/indium phosphide heterostructure solar cells. Nano Energy 2015, 13, 509–517. [Google Scholar] [CrossRef]
- Keavney, C.J.; Spitzer, M.B. Indium phosphide solar cells made by ion implantation. Appl. Phys. Lett. 1988, 52, 1439–1440. [Google Scholar] [CrossRef]
- Goldman, D.A.; Murray, J.; Munday, J.N. Nanophotonic resonators for InP solar cells. Opt. Express 2016, 24, A925–A934. [Google Scholar] [CrossRef] [PubMed]
- Aho, T.; Aho, A.; Tukiainen, A.; Polojärvi, V.; Salminen, T.; Raappana, M.; Guina, M. Enhancement of photocurrent in GaInNAs solar cells using Ag/Cu double-layer back reflector. Appl. Phys. Lett. 2016, 109, 251104. [Google Scholar] [CrossRef]
- McEvoy, A.; Castaner, L.; Markvart, T. Solar Cells: Materials, Manufacture and Operation; Elsevier Inc.: London, UK, 2012. [Google Scholar]
- Greenaway, A.L.; Boucher, J.W.; Oener, S.Z.; Funch, C.J.; Boettcher, S.W. Low-Cost Approaches to III–V Semiconductor Growth for Photovoltaic Applications. ACS Energy Lett. 2017, 2, 2270–2282. [Google Scholar] [CrossRef]
- Zheng, M.; Horowitz, K.; Woodhouse, M.; Battaglia, C.; Kapadia, R.; Javey, A. III-Vs at scale: A PV manufacturing cost analysis of the thin film vapor–liquid–solid growth mode. Prog. Photovolt. Res. Appl. 2016, 24, 871–878. [Google Scholar] [CrossRef]
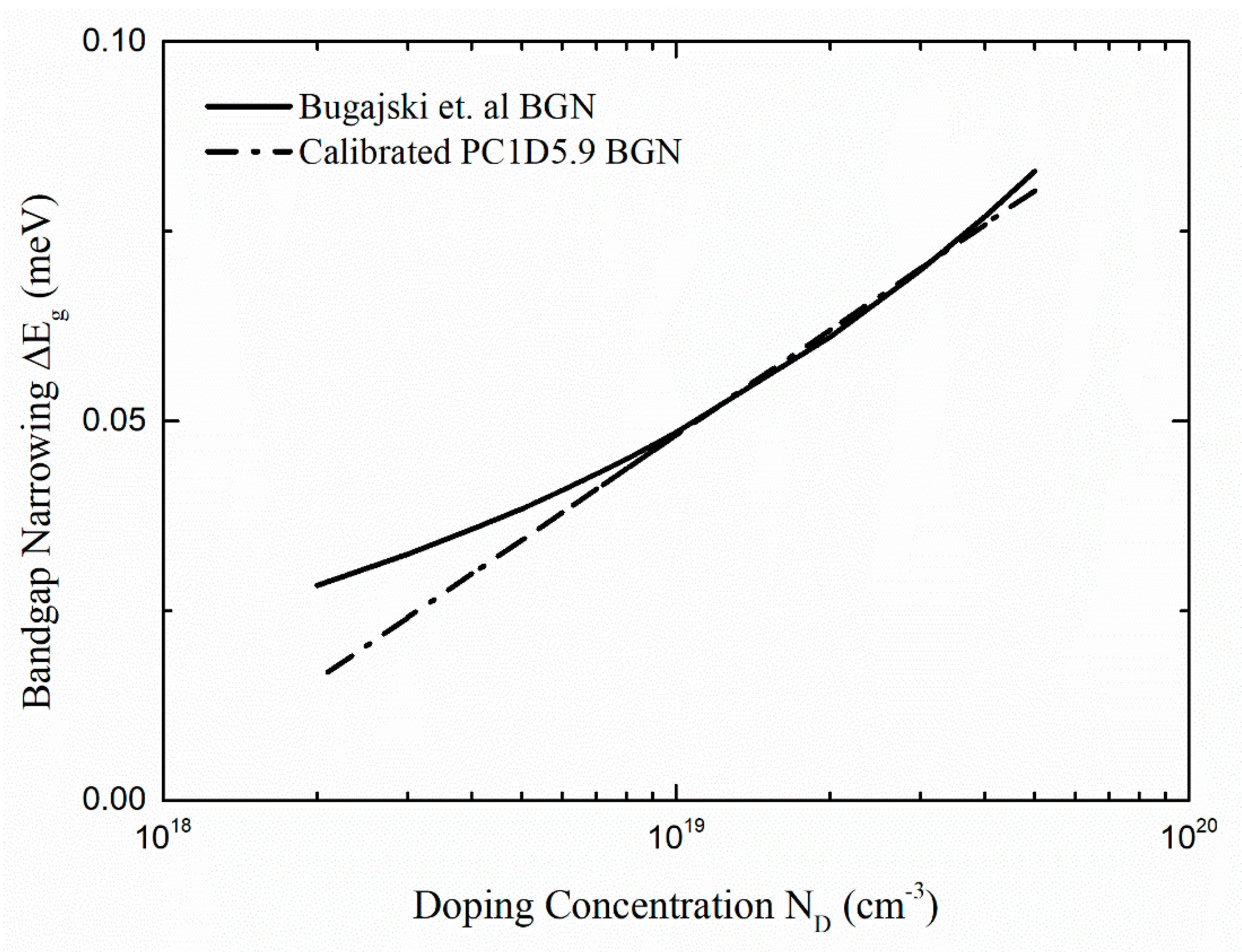
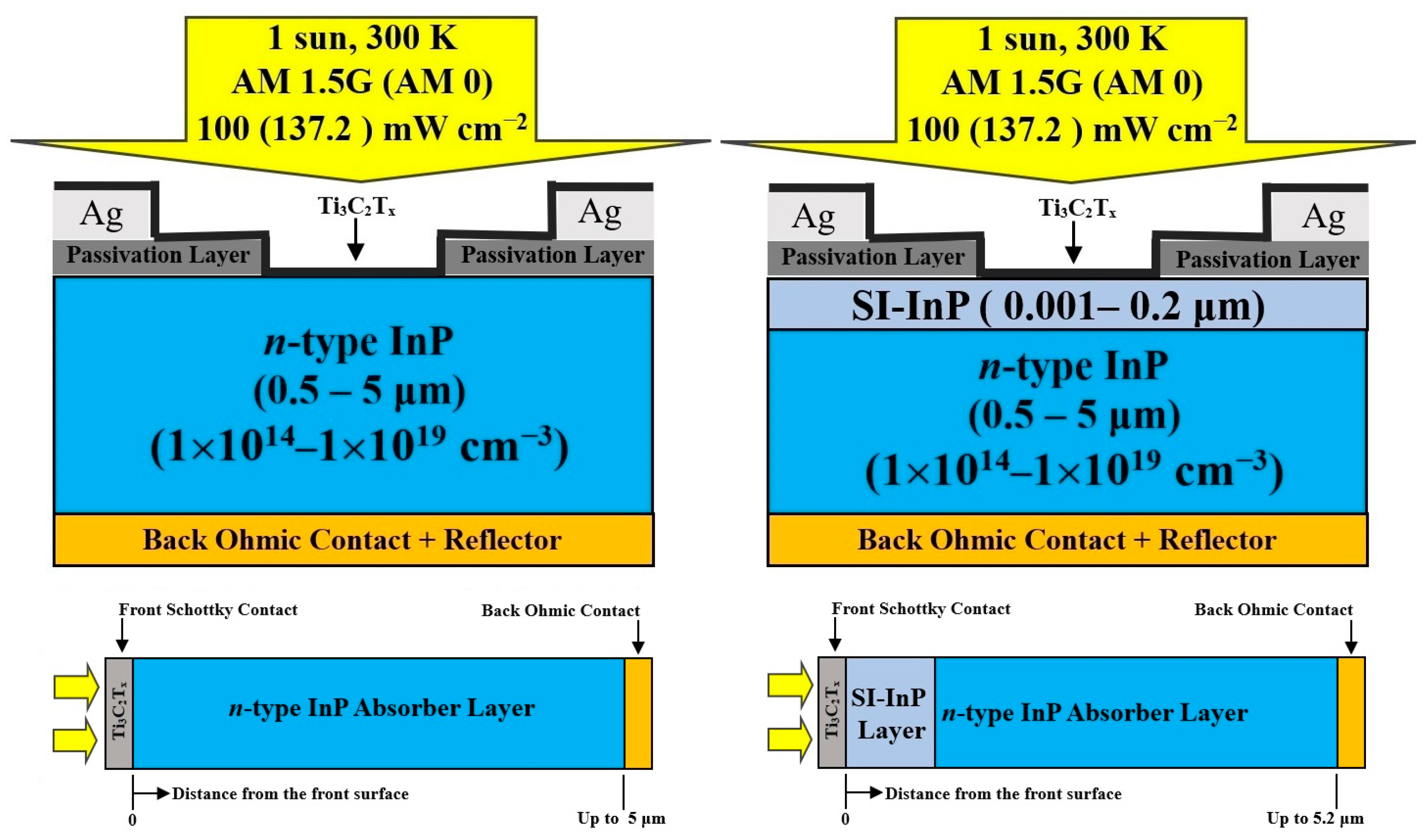
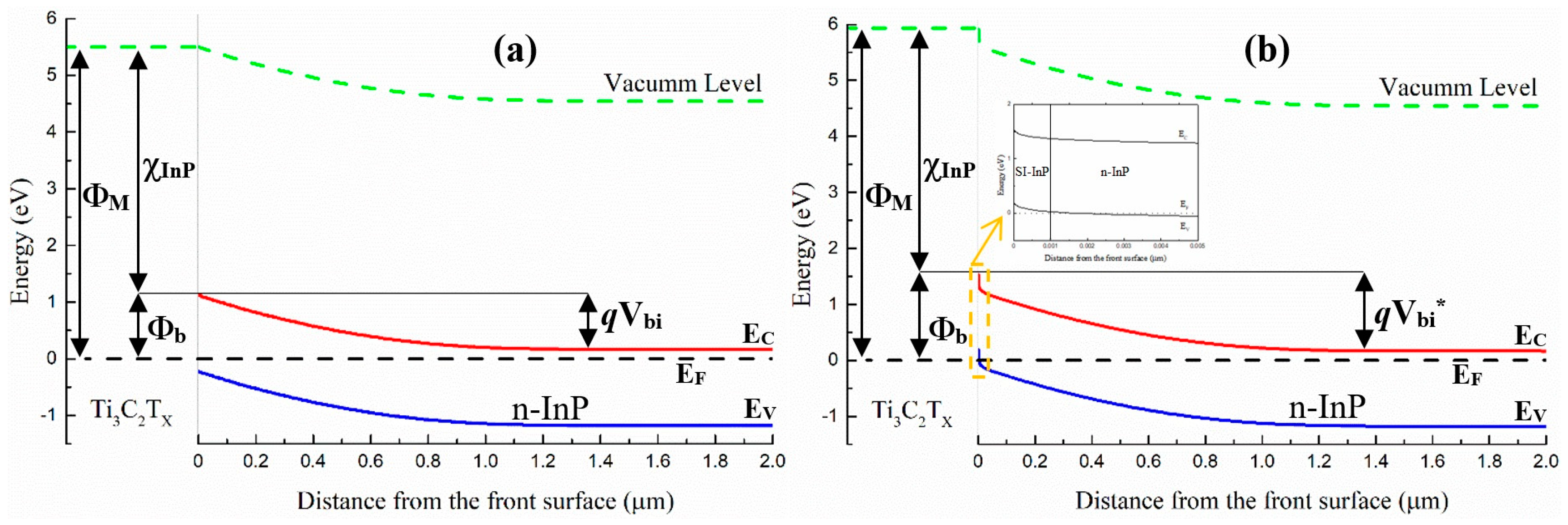
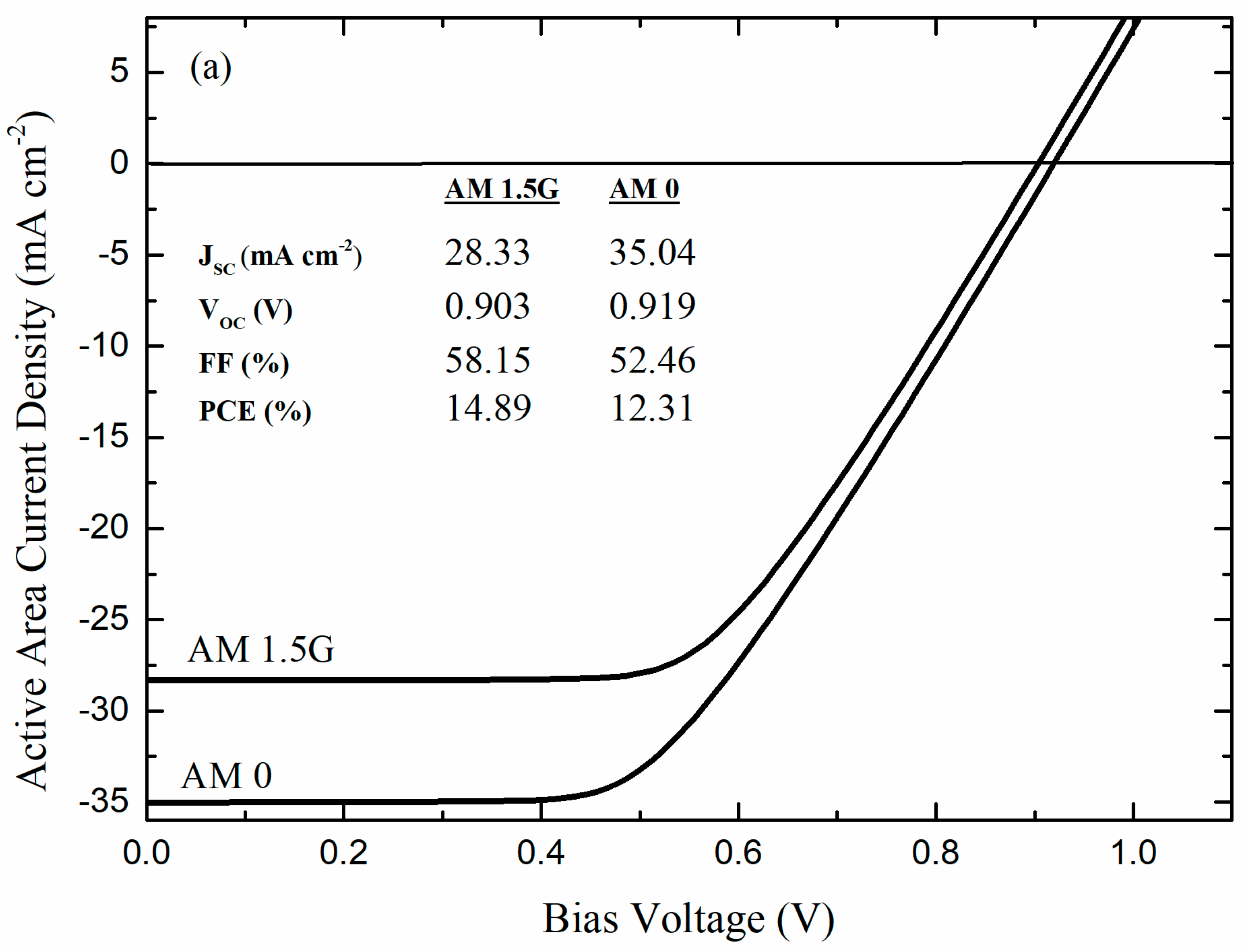

| Parameter | μmax (cm2/Vs) | μmin (cm2/Vs) | Nref (cm−3) | α | β1 | β2 | β3 | β4 | vsat (cm/s) |
|---|---|---|---|---|---|---|---|---|---|
| Electrons | 5200 | 400 | 3 × 1017 | 0.47 | 0 | −2 | 3.25 | 0 | 2.6 × 107 |
| Holes | 170 | 10 | 4.87 × 1017 | 0.47 | 0 | −2 | 3 | 0 | 2.6 × 107 |
| Device Parameters | ||
| Parameter | Value | Reference |
| Front surface barrier (qVbi) † | 0.956 eV * | Ti3C2Tx TCE thin film [33] |
| Exterior front reflectance | 15% ** | According to [33] |
| Front contact resistance | 10 Ω ** | Ti3C2Tx TCE thin film [33] |
| Back contact resistance | 0.1 Ω | Assuming good ohmics [50] |
| Region Parameters (n-InP) | ||
| Parameter | Value | Reference |
| Bandgap | 1.344 eV | According to [51] |
| Electron affinity | 4.38 eV | According to [51] |
| Thickness | 3 μm * | Initial simulation |
| Mobility | Variable | According to [43] |
| Dielectric constant | 12.61 | According to [51] |
| Refractive index | Variable | (using inp.inr file) |
| Absorption coefficient | Variable | (using inp300.abs file) |
| Intrinsic concentration (300 K) | 1.3 × 107 cm−3 | According to [51] |
| Doping concentration (ND) | 1 × 1015 cm−3 * | Initial simulation |
| Bulk recombination lifetimes | 1 μs | According to [44] |
| Front SRVs (Sn and Sp) | 1000 cm s−1 ** | According to [44] |
| Back SRVs (Sn and Sp) | 1000 cm s−1 | According to [44] |
| Region Parameters (SI-InP) | ||
| Parameter | Value | Reference |
| Thickness | 0.001 μm * | Initial simulation |
| Resistivity | 10 MΩ·cm | Semi-insulating layer [45] |
| Front SRVs (Sn and Sp) | 1000 cm s−1 ** | According to [44] |
| Excitation Parameters | ||
| Parameter | Value | |
| Spectrum | AM 1.5G and AM 0 | |
| Constant intensity | 100 mW cm−2 and 137.2 mW cm−2 | |
| Temperature | 300 K | |
| PC1D Design Parameter | Schottky Barrier Solar Cell Structure | |||
|---|---|---|---|---|
| MS | MIS | |||
| AM 1.5G | AM 0 | AM 1.5G | AM 0 | |
| Front surface barrier qVbi (eV) | 1.015 | 1.075 | 0.865 | 0.865 |
| Thickness of n-InP (μm) | 5 | 2.5 | 1 | 1 |
| Doping conc. of n-InP (cm−3) | 1 × 1016 | 1 × 1017 | 1 × 1018 | 1 × 1018 |
| Thickness of SI-InP (μm) | - | - | 0.15 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnassar, M.S.N. Design and Optimization of Potentially Low-Cost and Efficient MXene/InP Schottky Barrier Solar Cells via Numerical Modeling. Condens. Matter 2024, 9, 17. https://doi.org/10.3390/condmat9010017
Alnassar MSN. Design and Optimization of Potentially Low-Cost and Efficient MXene/InP Schottky Barrier Solar Cells via Numerical Modeling. Condensed Matter. 2024; 9(1):17. https://doi.org/10.3390/condmat9010017
Chicago/Turabian StyleAlnassar, Mohammad Saleh N. 2024. "Design and Optimization of Potentially Low-Cost and Efficient MXene/InP Schottky Barrier Solar Cells via Numerical Modeling" Condensed Matter 9, no. 1: 17. https://doi.org/10.3390/condmat9010017
APA StyleAlnassar, M. S. N. (2024). Design and Optimization of Potentially Low-Cost and Efficient MXene/InP Schottky Barrier Solar Cells via Numerical Modeling. Condensed Matter, 9(1), 17. https://doi.org/10.3390/condmat9010017









