Simple Model for Tc and Pairing Symmetry Changes in Sr2RuO4 Under (100) Uniaxial Strain
Abstract
:1. Introduction
2. Materials and Methods
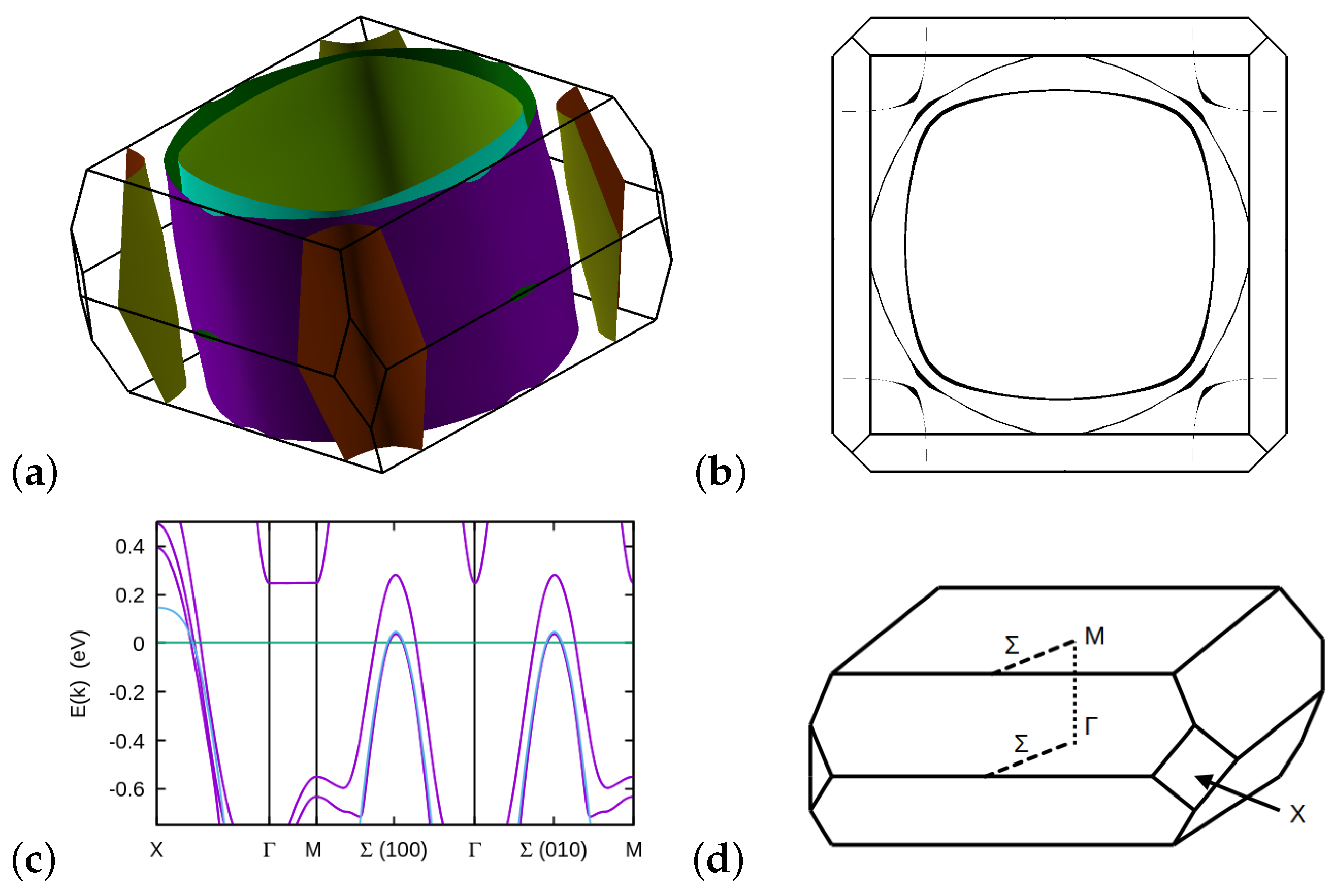
2.1. Normal State Band Structure
2.2. -Band Tight Binding Model
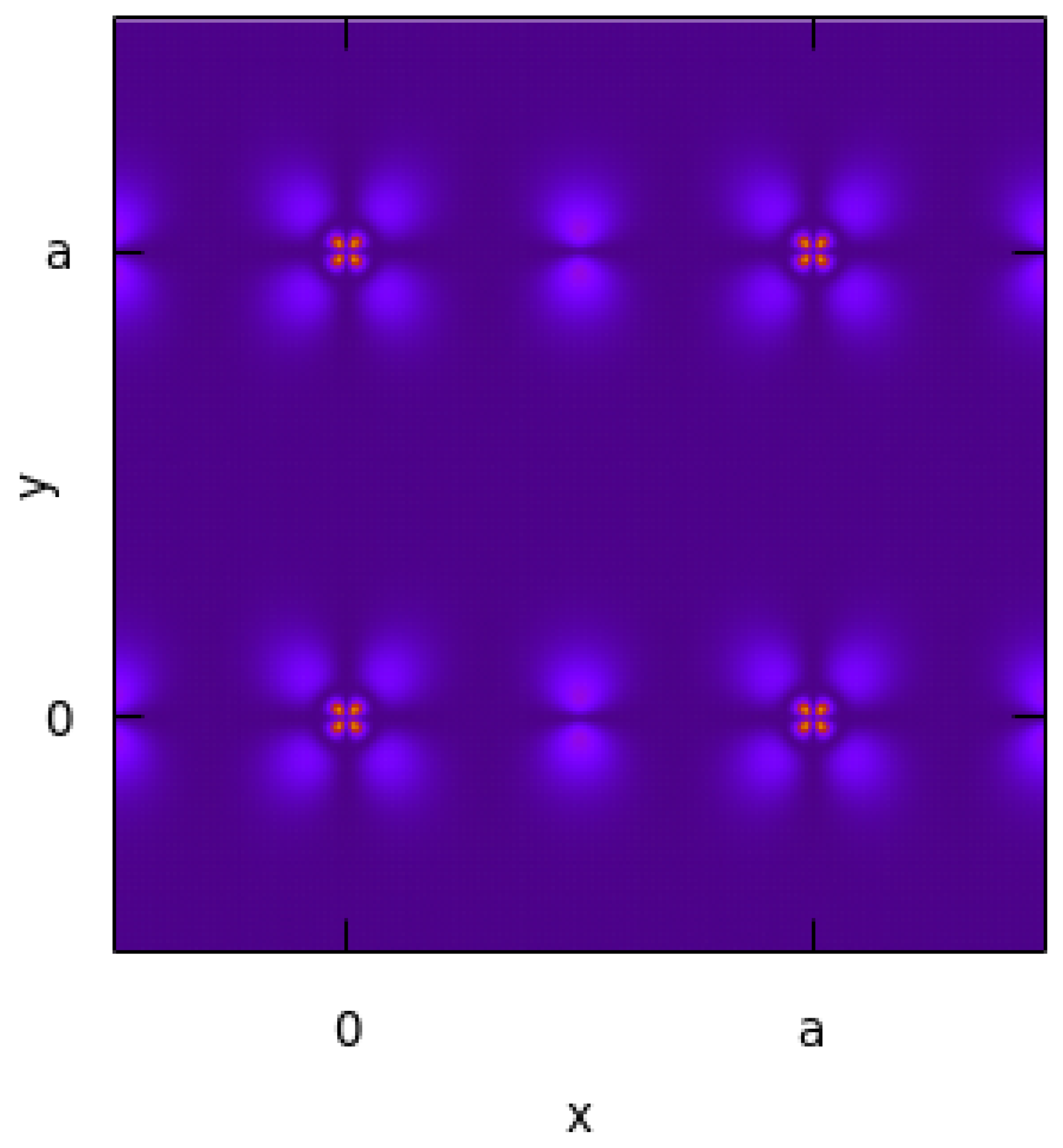
2.3. Fermi Liquid Theory and Pairing
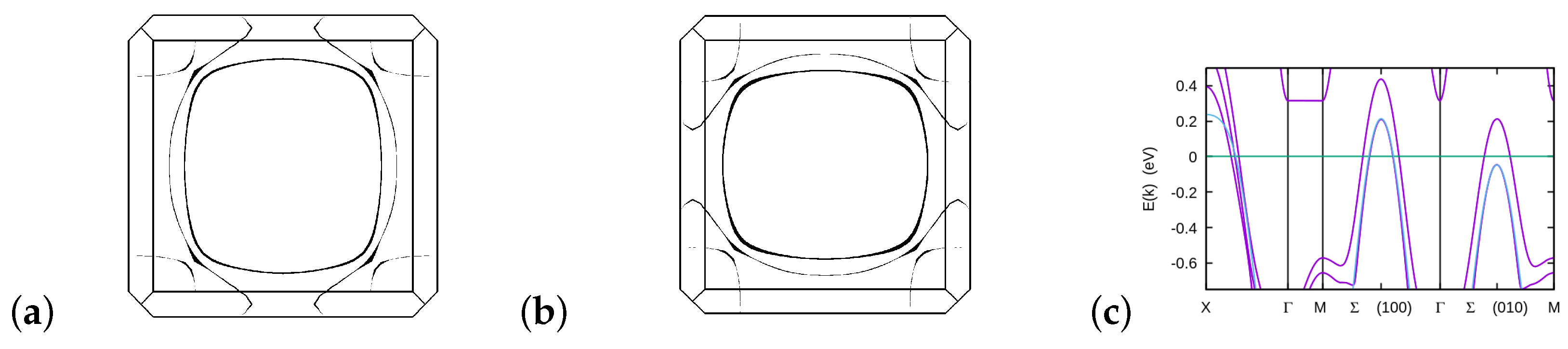
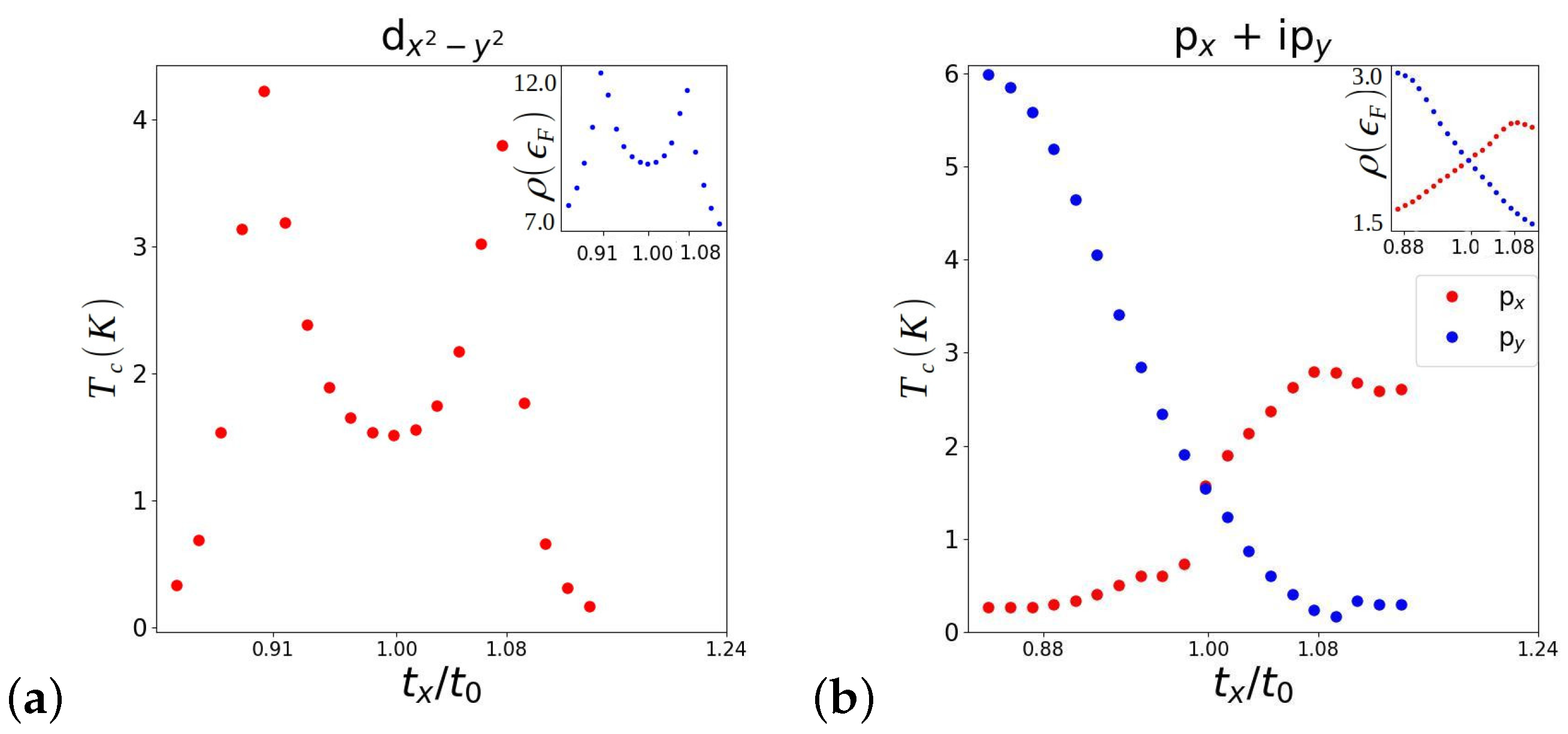
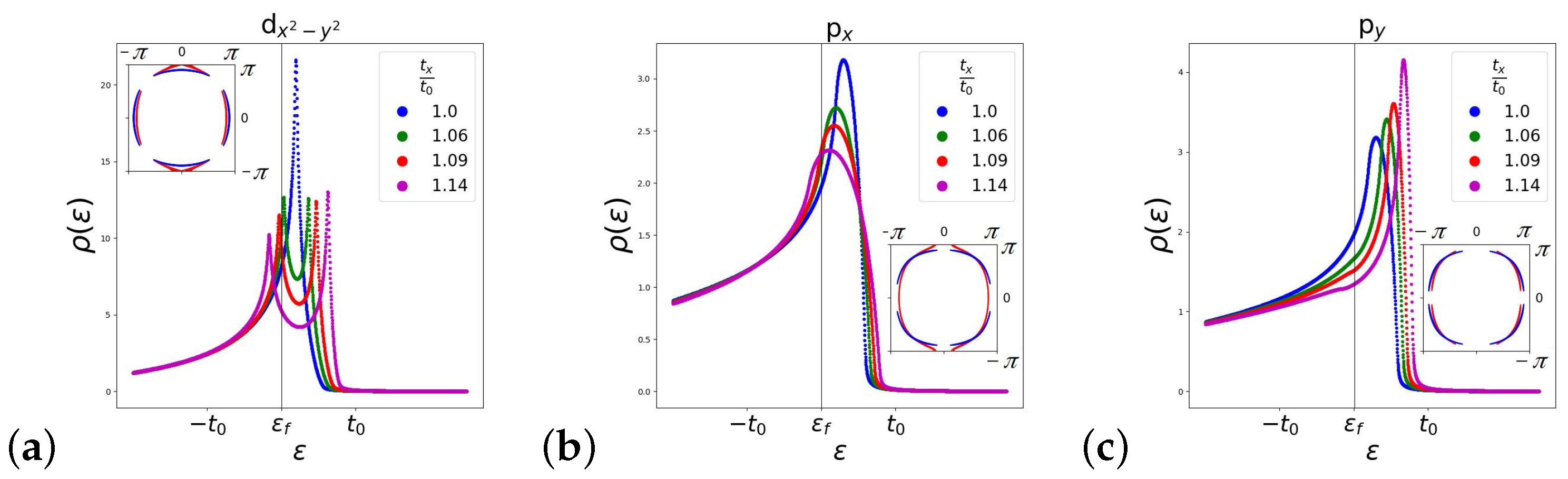
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TRSB | Time-reversal symmetry breaking |
| DOS | Density of states |
| SOC | Spin–orbit coupling |
| BCS | Bardeen–Cooper–Scrieffer |
References
- Mackenzie, A.P.; Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 2003, 74, 657–712. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Scaffidi, T.; Hicks, C.W.; Maeno, Y. Even odder after twenty-three years: The superconducting order parameter puzzle of Sr2RuO4. Npj Quantum Mater. 2008, 2, 40. [Google Scholar] [CrossRef]
- Maeno, Y.; Yonezawa, S.; Ramirez, A. Still Mystery after All These Years—Unconventional Superconductivity of Sr2RuO4. J. Phys. Soc. Jpn. 2024, 93, 062001. [Google Scholar] [CrossRef]
- Rice, T.M.; Sigrist, M. Sr2RuO4—An electronic analog of He-3. J. Phys.-Condens. Matter 1995, 7, L643–L648. [Google Scholar] [CrossRef]
- Mazin, I.I.; Singh, D.J. Competitions in layered ruthenates: Ferromagnetism versus antiferromagnetism and triplet versus singlet pairing. Phys. Rev. Lett. 1999, 82, 4324–4327. [Google Scholar] [CrossRef]
- Nomura, T.; Yamada, K. Perturbation theory of spin-triplet superconductivity for Sr2RuO4. J. Phys. Soc. Jpn. 2000, 69, 3678–3688. [Google Scholar] [CrossRef]
- Eremin, I.; Manske, D.; Ovchinnikov, S.G.; Annett, J.F. Unconventional superconductivity and magnetism in Sr2RuO4 and related materials. Ann. Phys. 2004, 13, 149–174. [Google Scholar] [CrossRef]
- Raghu, S.; Kapitulnik, A.; Kivelson, S.A. Hidden Quasi-one-dimensional superconductivity in Sr2RuO4. Phys. Rev. Lett. 2010, 105, 136401. [Google Scholar] [CrossRef]
- Røising, H.S.; Scaffidi, T.; Flicker, F.; Lange, G.F.; Simon, S.H. Superconducting order of Sr2RuO4 from a three-dimensional microscopic model. Phys. Rev. Res. 2019, 1, 033108. [Google Scholar] [CrossRef]
- Kugler, F.B.; Zingl, M.; Strand, H.U.R.; Lee, S.B.; von Delft, J.; Georges, A. Strongly Correlated Materials from a Numerical Renormalization Group Perspective: How the Fermi-Liquid State of Sr2RuO4 Emerges. Phys. Rev. Lett. 2020, 124, 016401. [Google Scholar] [CrossRef]
- Roig, M.; Rømer, A.T.; Kreisel, A.; Hirschfeld, P.J.; Andersen, B.M. Superconductivity in multiorbital systems with repulsive interactions: Hund’s pairing versus spin-fluctuation pairing. Phys. Rev. B 2022, 106, L100501. [Google Scholar] [CrossRef]
- Scaffidi, T. Degeneracy between even- and odd-parity superconductivity in the quasi-one-dimensional Hubbard model and implications for Sr2RuO4. Phys. Rev. B 2023, 107, 014505. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Haselwimmer, R.K.W.; Tyler, A.W.; Lonzarich, G.G.; Mori, Y.; Nishizaki, S.; Maeno, Y. Extremely Strong Dependence of Superconductivity on Disorder in Sr2RuO4. Phys. Rev. Lett. 1998, 80, 161, Erratum in Phys. Rev. Lett. 1998, 80, 3890.. [Google Scholar] [CrossRef]
- Deguchi, K.; Mao, Z.Q.; Yaguchi, H.; Maeno, Y. Gap Structure of the Spin-Triplet Superconductor Sr2RuO4 Determined from the Field-Orientation Dependence of the Specific Heat. Phys. Rev. Lett. 2004, 92, 047002. [Google Scholar] [CrossRef] [PubMed]
- Hassinger, E.; Bourgeois-Hope, P.; Taniguchi, H.; René de Cotret, S.; Grissonnanche, G.; Anwar, M.S.; Maeno, Y.; Doiron-Leyraud, N.; Taillefer, L. Vertical Line Nodes in the Superconducting Gap Structure of Sr2RuO4. Phys. Rev. X 2017, 7, 011032. [Google Scholar] [CrossRef]
- Sharma, R.; Edkins, S.D.; Wang, Z.; Kostin, A.; Sow, C.; Maeno, Y.; Mackenzie, A.P.; Davis, J.C.S.; Madhavan, V. Momentum-resolved superconducting energy gaps of Sr2RuO4 from quasiparticle interference imaging. Proc. Natl. Acad. Sci. USA 2020, 117, 5222. [Google Scholar] [CrossRef]
- Pustogow, A.; Luo, Y.; Chronister, A.; Su, Y.-S.; Sokolov, D.A.; Jerzembeck, F.; Mackenzie, A.P.; Hicks, C.W.; Kikugawa, N.; Raghu, S.; et al. Constraints on the superconducting order parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. Nature 2019, 574, 72–75. [Google Scholar] [CrossRef]
- Petsch, A.N.; Zhu, M.; Enderle, M.; Mao, Z.Q.; Maeno, Y.; Mazin, I.I.; Hayden, S.M. Reduction of the spin susceptibility in the superconducting state of Sr2RuO4 observed by polarized neutron scattering. Phys. Rev. Lett. 2020, 125, 217004. [Google Scholar] [CrossRef]
- Gupta, R.; Saunderson, T.; Shallcross, S.; Gradhand, M.; Quintanilla, J.; Annett, J. Superconducting subphase and substantial knight shift in Sr2RuO4. Phys. Rev. B 2020, 102, 235203. [Google Scholar] [CrossRef]
- Gupta, R.; Shallcross, S.; Quintanilla, J.; Gradhand, M.; Annett, J. Distinguishing dxz + idyz and dx2−y2 pairing in Sr2RuO4 by high magnetic field H-T phase diagrams. Phys. Rev. B 2022, 106, 115126. [Google Scholar] [CrossRef]
- Luke, G.M.; Fudamoto, Y.; Kojima, K.M.; Larkin, M.I.; Merrin, J.; Nachumi, B.; Uemura, Y.J.; Maeno, Y.; Mao, Z.Q.; Mori, Y.; et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature 1998, 394, 558–561. [Google Scholar] [CrossRef]
- Xia, J.; Maeno, Y.; Beyersdorf, P.T.; Fejer, M.M.; Kapitulnik, A. High resolution polar kerr effect measurements of Sr2RuO4: Evidence for broken time-reversal symmetry in the superconducting state. Phys. Rev. Lett. 2006, 97, 167002. [Google Scholar] [CrossRef] [PubMed]
- Benhabib, S.; Lupien, C.; Paul, I.; Berges, L.; Dion, M.; Nardone, M.; Zitouni, A.; Mao, Z.Q.; Maeno, Y.; Georges, A.; et al. Ultrasound evidence for a two- component superconducting order parameter in Sr2RuO4. Nat. Phys. 2020, 17, 194–198. [Google Scholar] [CrossRef]
- Ghosh, S.; Shekhter, A.; Jerzembeck, F.; Kikugawa, N.; Sokolov, D.A.; Brando, M.; Mackenzie, A.P.; Hicks, C.W.; Ramshaw, B.J. Thermodynamic evidence for a two- component superconducting order parameter in Sr2RuO4. Nat. Phys. 2020, 17, 199–204. [Google Scholar] [CrossRef]
- Suh, H.G.; Menke, H.; Brydon, P.M.R.; Timm, C.; Ramires, A.; Agterberg, D.F. Stabilizing even-parity chiral superconductivity in Sr2RuO4. Phys. Rev. Res. 2020, 2, 032023(R). [Google Scholar] [CrossRef]
- Kivelson, S.A.; Yuan, A.C.; Ramshaw, B.; Thomale, R. A proposal for reconciling diverse experiments on the superconducting state in Sr2RuO4. Npj Quantum Mater. 2020, 5, 43. [Google Scholar] [CrossRef]
- Hicks, C.W.; Brodsky, D.O.; Yelland, E.A.; Gibbs, A.S.; Bruin, J.A.N.; Barber, M.E.; Edkins, S.D.; Nishimura, K.; Yonezawa, S.; Maeno, Y.; et al. Strong increase of tc of Sr2RuO4 under both tensile and compressive strain. Science 2014, 344, 283. [Google Scholar] [CrossRef]
- Steppke, A.; Zhao, L.; Barber, M.E.; Scaffidi, T.; Jerzembeck, F.; Rosner, H.; Gibbs, A.S.; Maeno, Y.; Simon, S.H.; Mackenzie, A.P.; et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science 2017, 355, 148. [Google Scholar] [CrossRef]
- Barber, M.E.; Gibbs, A.S.; Maeno, Y.; Mackenzie, A.P.; Hicks, C.W. Resistivity in the vicinity of a van hove singularity: Sr2RuO4 under uniaxial pressure. Phys. Rev. Lett. 2018, 120, 076602. [Google Scholar] [CrossRef]
- Barber, M.E.; Lechermann, F.; Streltsov, S.V.; Skornyakov, S.L.; Ghosh, S.; Ramshaw, B.J.; Kikugawa, N.; Sokolov, D.A.; Mackenzie, A.P.; Hicks, C.W.; et al. Role of correlations in determining the Van Hove strain in Sr2RuO4. Phys. Rev. B 2019, 100, 245139. [Google Scholar] [CrossRef]
- Li, Y.-S.; Kikugawa, N.; Sokolov, D.A.; Jerzembeck, F.; Gibbs, A.S.; Maeno, Y.; Hicks, C.W.; Schmalian, J.; Nicklas, M.; Mackenzie, A.P. High-sensitivityheat-capacity measurements on Sr2RuO4 under uniaxial pressure. Proc. Natl. Acad. Sci. USA 2021, 118, e2020492118. [Google Scholar] [CrossRef] [PubMed]
- Grinenko, V.; Ghosh, S.; Sarkar, R.; Orain, J.-C.; Nikitin, A.; Elender, M.; Das, D.; Guguchia, Z.; Bruckner, F.; Barber, M.E.; et al. Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 2021, 17, 748–754. [Google Scholar] [CrossRef]
- Li, Y.-S.; Garst, M.; Schmalian, J.; Ghosh, S.; Kikugawa, N.; Sokolov, D.A.; Hicks, C.W.; Jerzembeck, F.; Ikeda, M.S.; Hu, Z.; et al. Elastocaloric determination of the phase diagram of Sr2RuO4. Nature 2022, 607, 276. [Google Scholar] [CrossRef]
- Burganov, B.; Adamo, C.; Mulder, A.; Uchida, M.; King, P.D.C.; Harter, J.W.; Shai, D.E.; Gibbs, A.S.; Mackenzie, A.P.; Uecker, R.; et al. Strain Control of Fermiology and Many-Body Interactions in Two-Dimensional Ruthenates. Phys. Rev. Lett. 2016, 116, 197003. [Google Scholar] [CrossRef]
- Sunko, V.; Morales, E.A.; Marković, I.; Barber, M.E.; Milosavljević, D.; Mazzola, F.; Sokolov, D.A.; Kikugawa, N.; Cacho, C.; Dudin, P.; et al. Direct observation of a uniaxial stress-driven Lifshitz transition in Sr2RuO4. Npj Quantum Mater. 2019, 4, 46. [Google Scholar] [CrossRef]
- Watson, C.A.; Gibbs, A.S.; Mackenzie, A.P.; Hicks, C.W.; Moler, K.A. Micron-scale measurements of low anisotropic strain response of local Tc in Sr2RuO4. Phys. Rev. B 2018, 98, 094521. [Google Scholar] [CrossRef]
- Grinenko, V.; Das, D.; Gupta, R.; Zinkl, B.; Kikugawa, N.; Maeno, Y.; Hicks, C.W.; Klauss, H.-H.; Sigrist, M.; Khasanov, R. Unsplit superconducting and time reversal symmetry breaking transitions in Sr2RuO4 under hydrostatic pressure and disorder. Nat. Commun. 2021, 12, 3920. [Google Scholar] [CrossRef]
- Jerzembeck, F.; Røising, H.S.; Steppke, A.; Rosner, H.; Sokolov, D.A.; Kikugawa, N.; Scaffidi, T.; Simon, S.H.; Mackenzie, A.P.; Hicks, C.W. The superconductivity of Sr2RuO4 under c-axis uniaxial stress. Nat. Comms. 2022, 13, 4596. [Google Scholar] [CrossRef] [PubMed]
- Vollhardt, D.D.; Woelfle, P. The Superfluid Phases Of Helium 3; CRC Press: London, UK, 1990. [Google Scholar]
- Scaffidi, T.; Romers, J.C.; Simon, S.H. Pairing symmetry and dominant band in Sr2RuO4. Phys. Rev. B 2014, 89, 220510R. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Zhang, F.C.; Rice, T.M.; Wang, Q.-H. Theory of the evolution of superconductivity in Sr2RuO4 under anisotropic strain. Npj Quantum Mater. 2017, 2, 12. [Google Scholar] [CrossRef]
- Scaffidi, T. Weak-Coupling Theory of Topological Superconductivity; Springer Thesis; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Rømer, A.T.; Kreisel, A.; Müller, M.A.; Hirschfeld, P.J.; Eremin, I.M.; Andersen, B.M. Theory of strain-induced magnetic order and splitting of Tc and TTRSB in Sr2RuO4. Phys. Rev. B 2020, 102, 054506. [Google Scholar] [CrossRef]
- Beck, S.; Hampel, A.; Zingl, M.; Timm, C.; Ramires, A. Effects of strain in multiorbital superconductors: The case of Sr2RuO4. Phys. Rev. Res. 2022, 4, 023060. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- The Elk Code. Available online: http://elk.sourceforge.net/ (accessed on 22 October 2024).
- Chmaissem, O.; Jorgensen, J.D.; Shaked, H.; Ikeda, S.; Maeno, Y. Thermal expansion and compressibility of Sr2RuO4. Phys. Rev. B 1998, 57, 5067. [Google Scholar] [CrossRef]
- Pavarini, E.; Mazin, I. First-principles study of spin-orbit effects and NMR in Sr2RuO4. Phys. Rev. B 2006, 74, 035115, Erratum in Phys. Rev. B 2007, 76, 079901.. [Google Scholar] [CrossRef]
- Autieri, C.; Cuoco, M.; Noce, C. Structural and electronic properties of heterostructures Sr2RuO4/Sr3Ru2O7. Phys. Rev. B 2014, 89, 075102. [Google Scholar] [CrossRef]
- Paglione, J.; Lupien, C.; MacFarlane, W.A.; Perz, J.M.; Taillefer, L.; Mao, Z.Q.; Maeno, Y. Elastic tensor of Sr2RuO4. Phys. Rev. B 2002, 65, 220506(R). [Google Scholar] [CrossRef]
- Zhitomirsky, M.E.; Rice, T.M. Interband Proximity Effect and Nodes of Superconducting Gap in Sr2RuO4. Phys. Rev. Lett. 2001, 87, 057001. [Google Scholar] [CrossRef]
- Røising, H.S.; Wagner, G.; Roig, M.; Rømer, A.T.; Andersen, B.M. Heat capacity double transitions in time-reversal symmetry broken superconductors. Phys. Rev. B 2022, 106, 174518. [Google Scholar] [CrossRef]
- Rozbicki, E.J.; Annett, J.F.; Souquet, J.-R.; Mackenzie, A.P. Spin–orbit coupling and k-dependent Zeeman splitting in strontium ruthenate. J. Phys. Condens. Matter. 2011, 23, 094201. [Google Scholar] [CrossRef]
- Curtis, M. Effects of Strain Induced Topological Changes on the Superconducting Critical Temperature. Ph.D. Thesis, University of Bristol, Bristol, UK, 2024. [Google Scholar]

| Symmetry Rep. | Name | |
|---|---|---|
| d-wave | ||
| chiral | ||
| mixed | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curtis, M.; Gradhand, M.; Annett, J.F. Simple Model for Tc and Pairing Symmetry Changes in Sr2RuO4 Under (100) Uniaxial Strain. Condens. Matter 2024, 9, 44. https://doi.org/10.3390/condmat9040044
Curtis M, Gradhand M, Annett JF. Simple Model for Tc and Pairing Symmetry Changes in Sr2RuO4 Under (100) Uniaxial Strain. Condensed Matter. 2024; 9(4):44. https://doi.org/10.3390/condmat9040044
Chicago/Turabian StyleCurtis, Macauley, Martin Gradhand, and James F. Annett. 2024. "Simple Model for Tc and Pairing Symmetry Changes in Sr2RuO4 Under (100) Uniaxial Strain" Condensed Matter 9, no. 4: 44. https://doi.org/10.3390/condmat9040044
APA StyleCurtis, M., Gradhand, M., & Annett, J. F. (2024). Simple Model for Tc and Pairing Symmetry Changes in Sr2RuO4 Under (100) Uniaxial Strain. Condensed Matter, 9(4), 44. https://doi.org/10.3390/condmat9040044






