Stern Duct with NACA Foil Section Designed by Resistance and Self-Propulsion Simulation for Japan Bulk Carrier
Abstract
:1. Introduction
- V and V (Verification and Validation) analysis.
- a.
- Resistance simulation without the original duct;
- b.
- Resistance simulation with the original duct;
- c.
- Open-water propeller test (OPT) simulation;
- d.
- Self-propulsion simulation with the original duct.
- 2.
- Resistance simulation with various duct designs with a NACA four-digit series foil section.
- 3.
- Self-propulsion simulation with the optimized duct selected from the stage 2 result.
2. Methods
2.1. Numerical Schemes
2.2. Geomtry and Test Conditions
2.3. Domain and Boundary Conditions
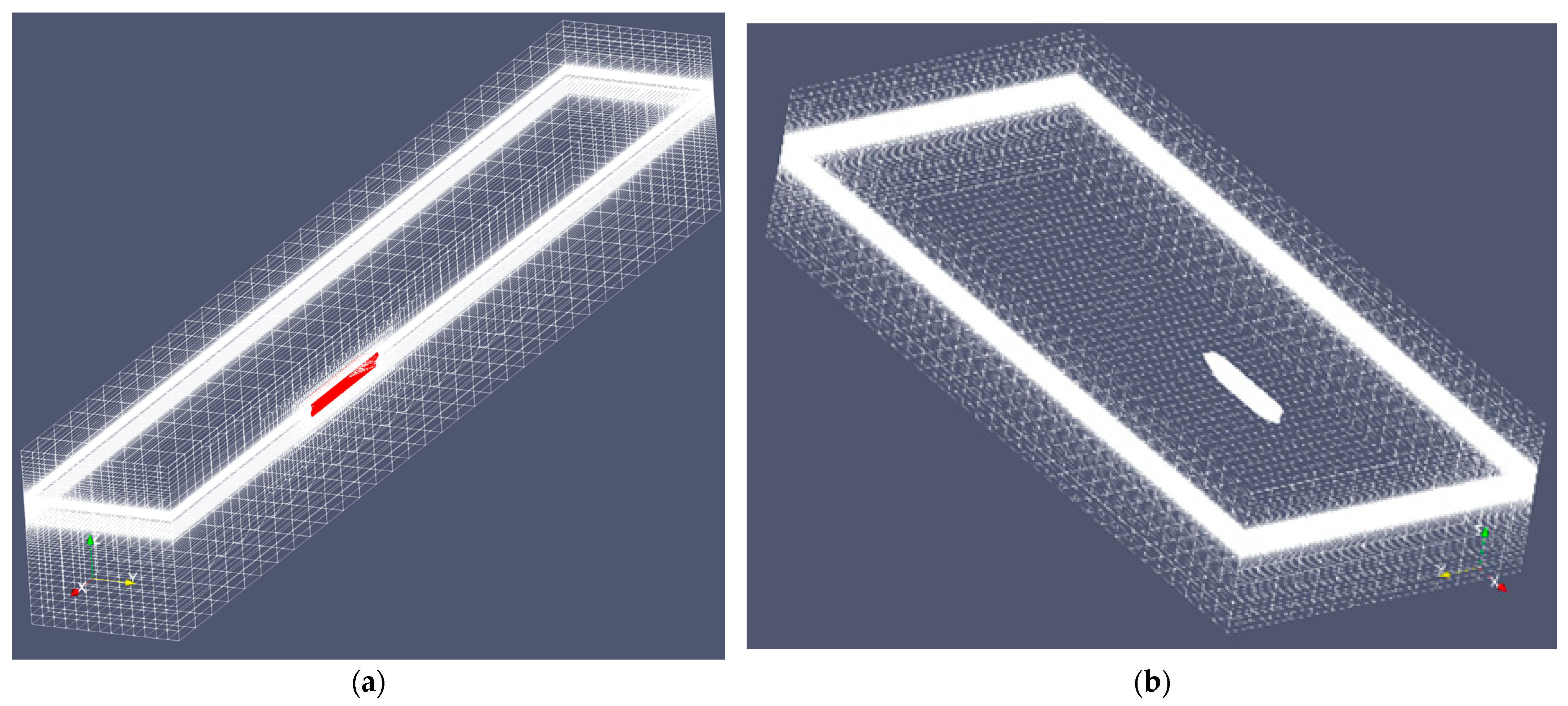
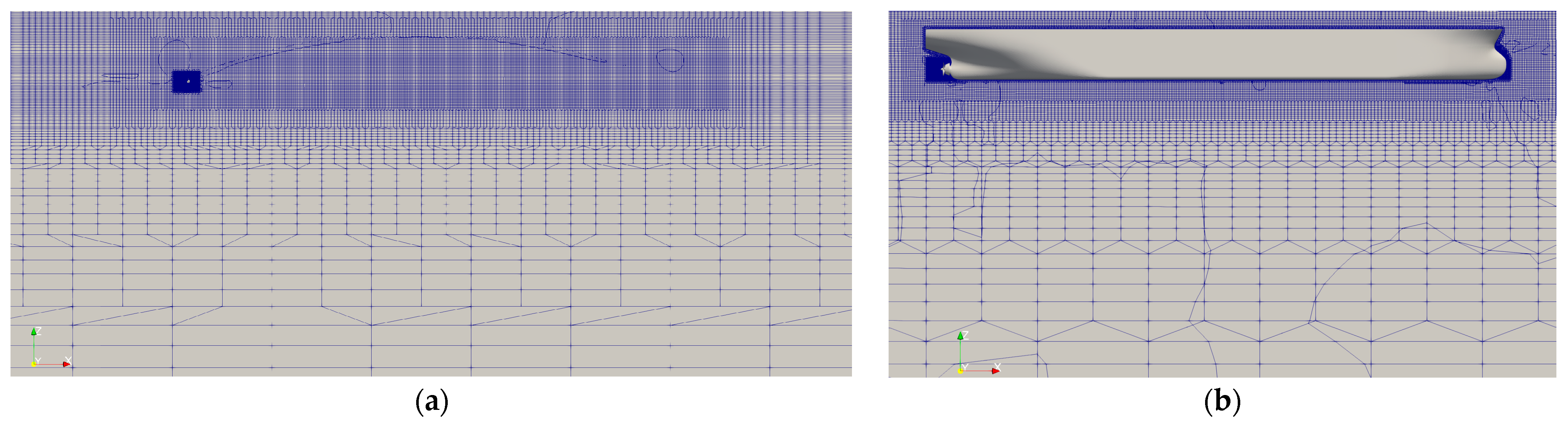
2.4. Unstructured Grid Generation
3. Results
3.1. V and V (Verification and Validation)
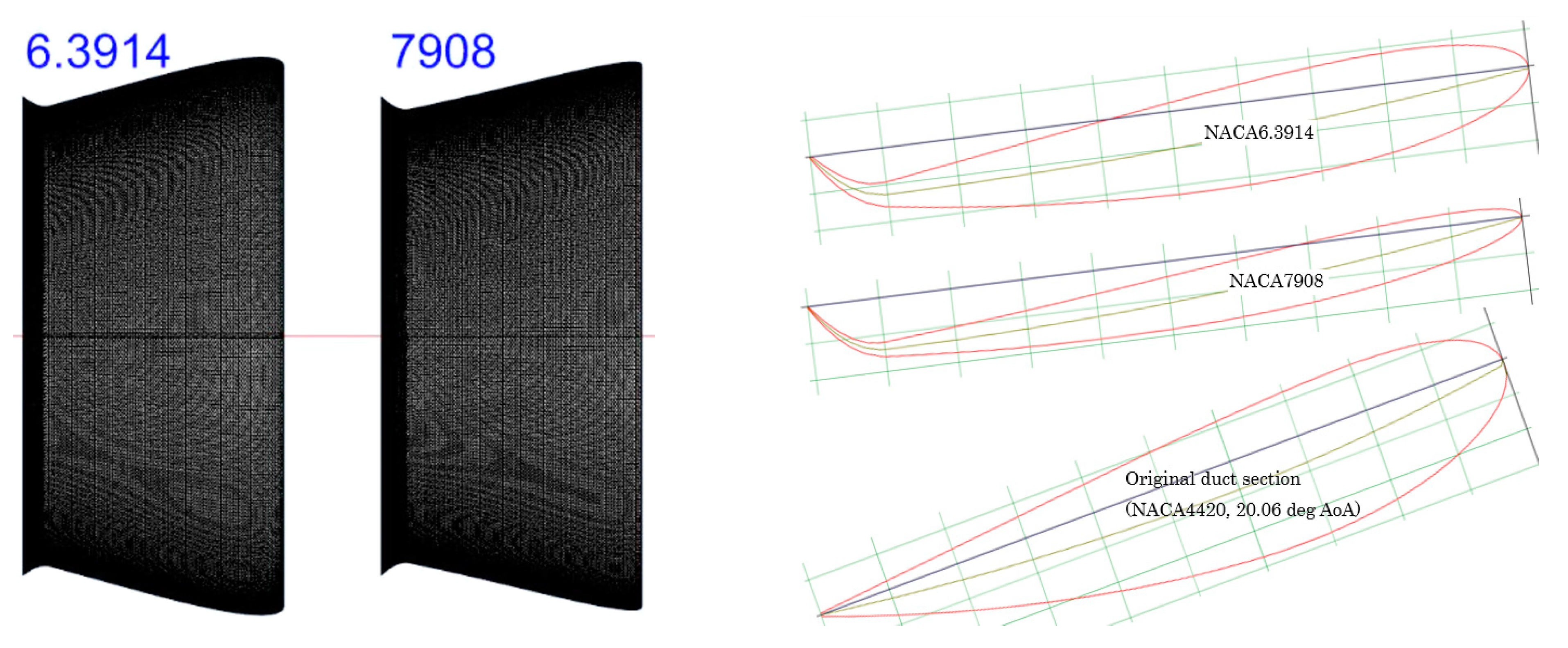
3.2. Duct Design by Resistance Test
- Maximum camber, e.g., NACA m420 series. Test m = 1~9 and found NACA 6.320 and NACA7420 the best;
- Location of the maximum camber. Test NACA6.3p20 and 7p20 with p = 1~9 and found p = 9 the best for both;
- Maximum thickness. Test NACA 6.39xx with xx = 8~23 and 79xx with xx = 4~24.
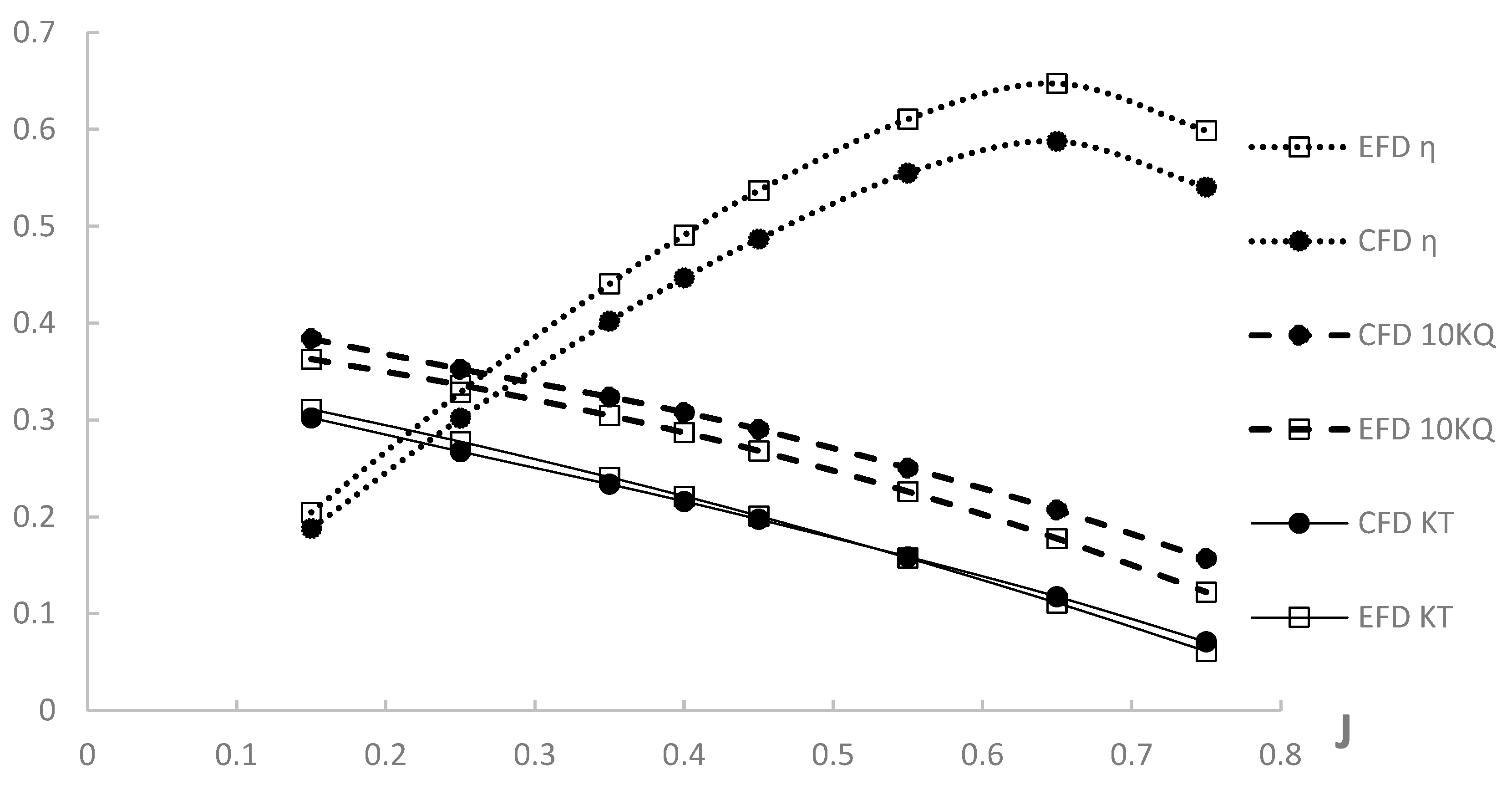
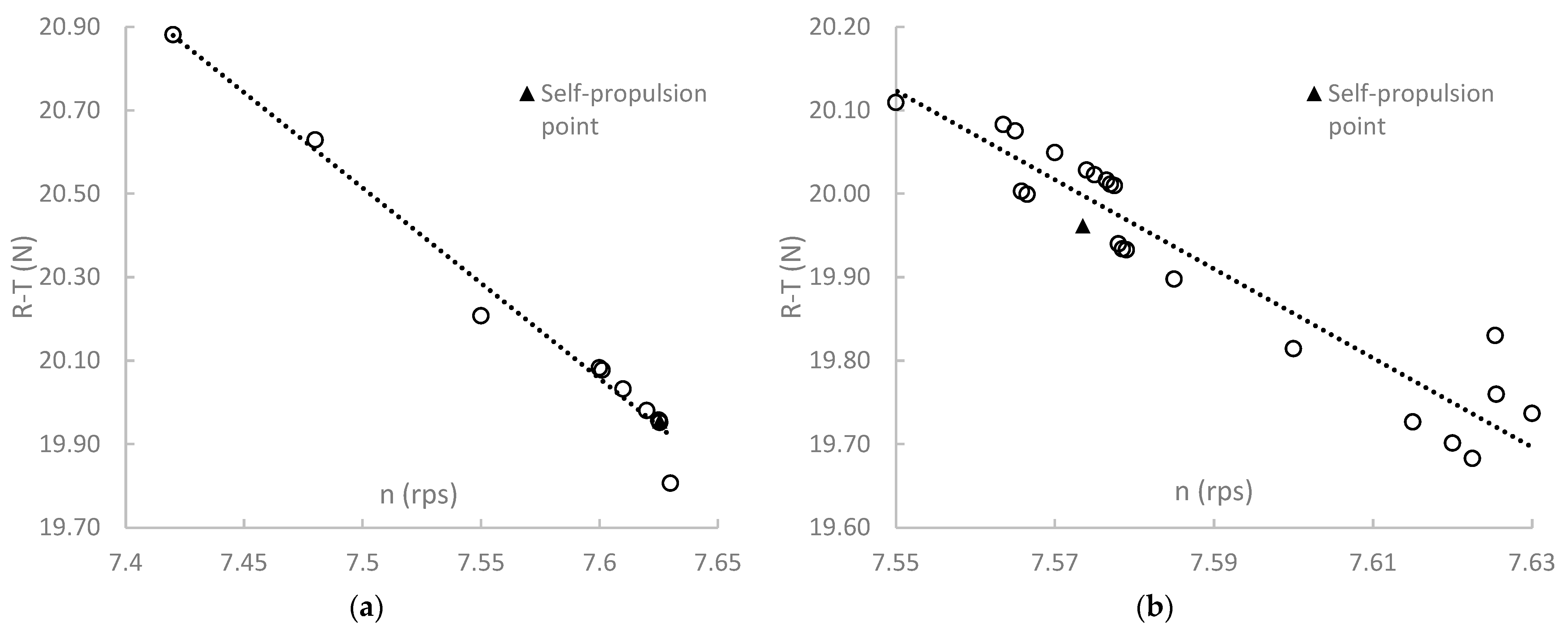
3.3. Self-Propulsion Simulation
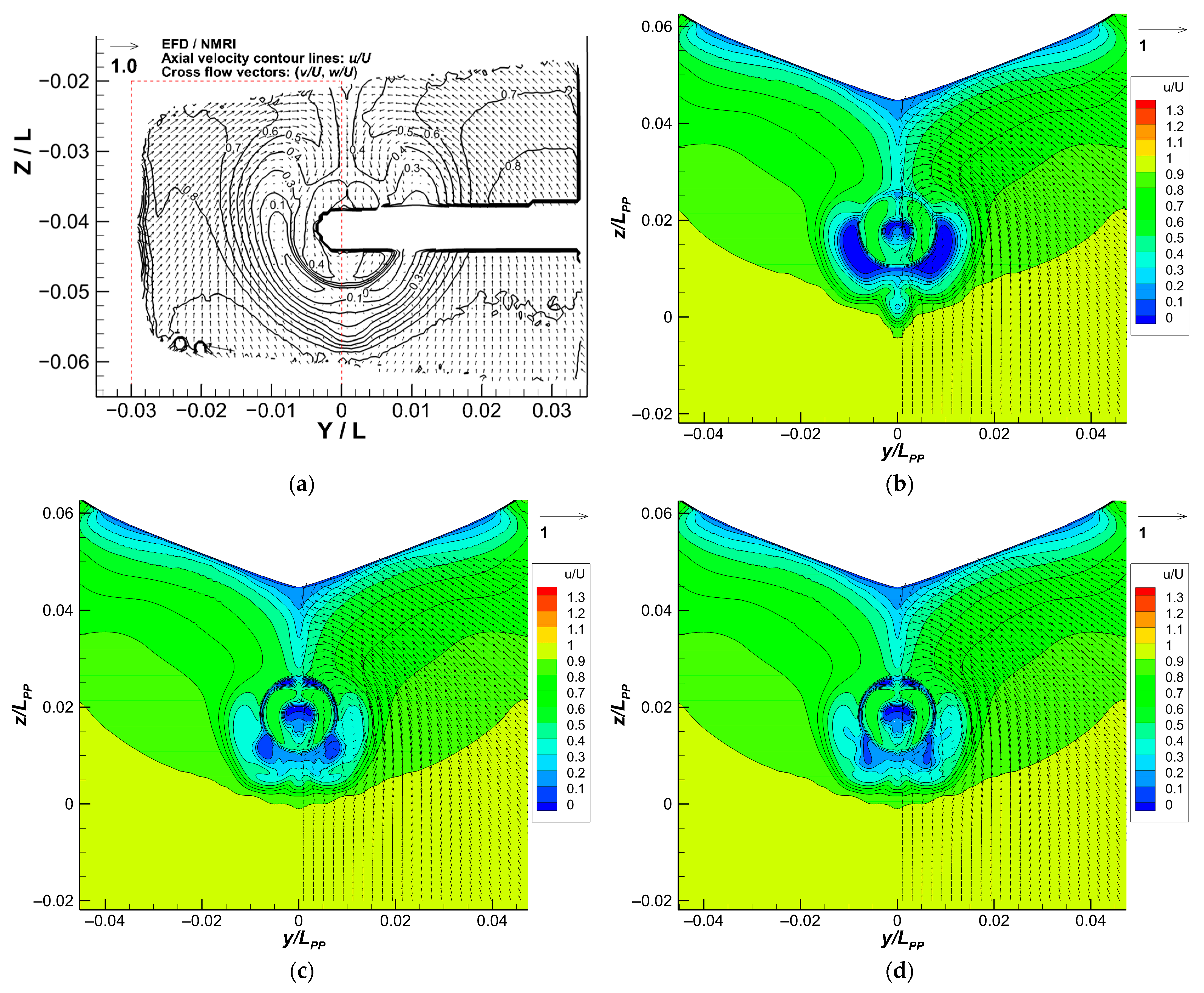
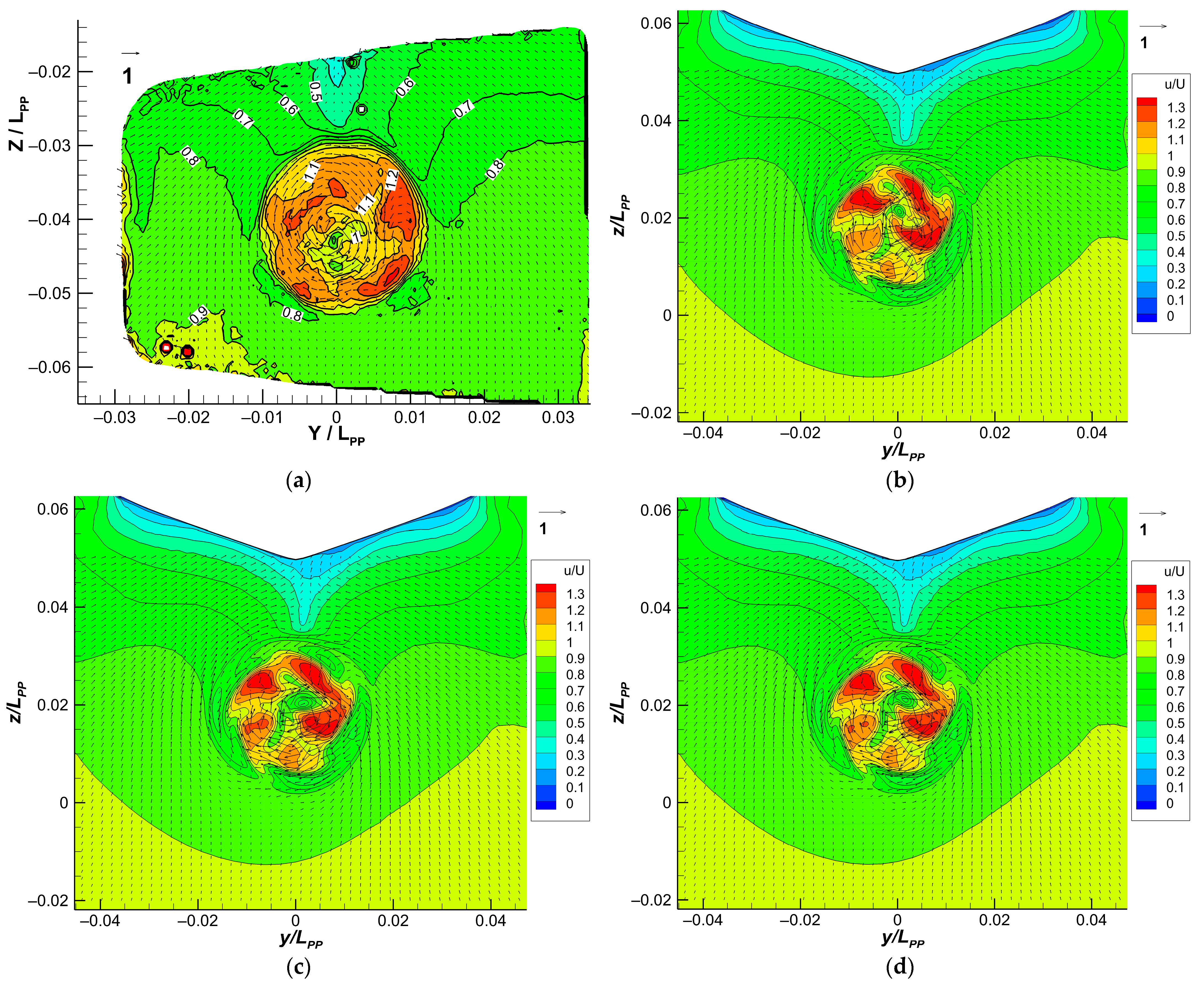
3.4. Nominal and Propeller Wake Field
3.5. Pressure Coefficient Distribution
3.6. Grid Sensitivity for Optimal Ducts
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1 − t | thrust deduction |
| 1 − w | wake factor |
| ANN | Artificial Neural Network |
| AOA | angle of attack |
| AP | Aft Particulars |
| BEM | Boundary Element Method |
| BSD | Blade efficiency improving Stator Duct |
| BWL | waterline beam, ship beam |
| c | Foil chord length |
| CB | block coefficient |
| CFD | Computational Fluid Dynamics |
| CP | Pressure coefficient |
| CT | Total ship resistance coefficient with or without duct |
| D | Propeller diameter, experimental value or data |
| DHP | delivered horsepower |
| DTC | Duisburg Test Case |
| Dwater | Domain water depth |
| DWT | Deadweight Tonnage |
| E%D | error |
| EHP | effective horsepower |
| EFD | Experimental Fluid Dynamics |
| ETS | Emissions Trading System |
| EU | European Union |
| FCFs | flow control fins |
| FP | Front Particulars |
| Fr | Froude number |
| Hair | Domain air par height |
| HZN | Hitachi Zosen Nozzle |
| IGES | Initial Graphics Exchange Specification |
| IHIMU | Ishikawajima-Harima Heavy Industries & Marine United Inc. |
| ITTC | International Towing Tank Conference |
| Ja | advance coefficient |
| JBC | Japan Bulk Carrier |
| k | turbulent kinematic energy |
| KQ | propeller torque coefficient |
| KT | propeller thrust coefficient |
| L, LPP | length between particulars |
| Ldownstram | Domain length after ship AP |
| Lside | Domain length to the side |
| Lupstram | Domain length before ship FP |
| m | Foil camber |
| MIDP | Mitsui Integrated Duct |
| MOGA | Multi-Objective Genetic Algorithm |
| MRF | Multi-Reference Frame |
| n | propeller rotation rate |
| NACA | National Advisory Committee for Aeronautics |
| NG, Ntotal | total grid number |
| NSGA-II | Non-Dominating Sorting Genetic Algorithm-II |
| OpenFOAM | open-source field and manipulation |
| OPT | Openwater Propeller Test |
| p | static pressure, position of maximal camber |
| P/D | pitch ratio |
| total pressure | |
| PIMPLE | PISO + SIMPLE |
| PISO | pressure implicit with splitting of operator |
| POD | proper orthogonal decomposition |
| PSD | pre-swirl ducts |
| PSS | pre-swirl stators |
| r | propeller radius |
| R | Ship resistance |
| RANS | Reynolds-averaged Navier–Stokes equations |
| duct radius | |
| Re | Reynolds number |
| grid convergence indicator | |
| rps | revolutions per sec |
| SBDO | Simulation-based design optimization |
| SDS-F | Semi-Duct System with contra-Fins |
| SFC | Skin Friction Correction |
| Si | simulation value for i = 1, 2, 3 |
| SILD | Sumitomo Integrated Lammeren Duct |
| SIMPLE | semi-implicit method for pressure linked equations |
| SST | Shear Stress Transport |
| t | ship draft, foil thickness |
| T | Propeller Thrust |
| T2015 | Tokyo 2015 Workshop on CFD in Ship Hydrodynamics |
| TEU | Twenty-foot Equivalent Unit (container size and cargo capacity) |
| THP | thrust horsepower |
| U | Model ship speed |
| u/U | Non-dimensional axial flow velocity |
| Ud | Experimental uncertainty |
| Ug | Grid uncertainty |
| Ui | Iterative uncertainty |
| Uv | Validation uncertainty |
| V and V | Verification and Validation |
| VOF | Volume of Fluid |
| WED | Wake Equalizing Duct |
| x | Longitudinal position |
| y+ | non-dimensional wall distance |
| Efficiency, propeller open water efficiency | |
| propeller behind-hull efficiency | |
| quasi-propulsive, propeller propulsive efficiency | |
| hull efficiency | |
| relative rotative efficiency | |
| viscous turbulence | |
| ω | Specific turbulent dissipation rate |
References
- JAPAN Bulk Carrier (JBC), Tokyo 2015 a Workshop on CFD in Ship Hydrodynamics. Available online: https://t2015.nmri.go.jp/jbc_gc.html (accessed on 28 February 2025).
- Schneekluth Hydrodynamik GmbH. Available online: https://www.schneekluth.com/en/ (accessed on 4 April 2025).
- Sanoyas Shipbuilding Co., Ltd. Available online: https://www.sanoyas.skdy.co.jp/technology (accessed on 4 April 2025).
- Gougoulidis, G.; Vasileiadis, N. An Overview of Hydrodynamic Energy Efficiency Improvement Measures. In Proceedings of the 5th International Symposium on Ship Operations, Athens, Greece, 28–29 May 2015. [Google Scholar]
- Lee, J.-T.; Kim, M.-C.; Suh, J.-C.; Kim, S.-H.; Choi, J.-K. Development of a preswirl stator-propeller system for improvement of propulsion efficiency: A symmetric stator propulsion system. J. Soc. Nav. Archit. Korea 1992, 29, 132–145. [Google Scholar]
- Park, S.; Oh, G.; Rhee, S.H.; Koo, B.Y.; Lee, H. Full scale wake prediction of an energy saving device by using computational fluid dynamics. Ocean Eng. 2015, 101, 254–263. [Google Scholar] [CrossRef]
- Guiard, T.; Leonard, S. The Becker Mewis Duct®-Challenges in Full-Scale Design and new Developments for Fast Ships. In Proceedings of the 3rd International Symposium on Marine Propulsors, Launceston, Australia, 5–8 May 2013. [Google Scholar]
- Elangovan, M. Hydrodynamic Energy Devices to Improve the Efficiency of Propulsion System in AUVs. Int. Res. J. Adv. Sci. Hub 2020, 2, 18–22. [Google Scholar] [CrossRef]
- Andersson, J.; Shiri, A.A.; Bensow, R.E.; Yixing, J.; Chengsheng, W.; Gengyao, Q.; Deng, G.; Queutey, P.; Xing-Kaeding, Y.; Horn, P.; et al. Ship-scale CFD benchmark study of a pre-swirl duct on KVLCC2. Appl. Ocean Res. 2022, 123, 103134. [Google Scholar] [CrossRef]
- Falchi, M.; Aloisio, G. On the Effect of Energy Saving Devices on the Wake Hydrodynamics of a Bulk Carrier Model. In Proceedings of the Thirty-First International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021. [Google Scholar]
- Schuiling, B.; van Terwisga, T. Hydrodynamic working principles of Energy Saving Devices in ship propulsion systems. Int. Shipbuild. Prog. 2017, 63, 255–290. [Google Scholar] [CrossRef]
- Narita, H.; Yagi, H.; Johnson, H.D.; Breves, L.R. Development and full scale experiences of a novel integrated duct propeller. SNAME Trans. 1981, 89, 319–346. [Google Scholar]
- Kitazawa, T.; Hukino, M.; Fujimoto, T.; Ueda, K. Increase in the propulsive efficiency of a ship with the installation of a nozzle immediately forward of the propeller. J. Kansai Soc. Nav. Archit. Jpn. 1982, 184, 73–78. [Google Scholar]
- Schneekluth, H. Wake equalizing duct. Nav. Archit. 1986, 103, 147–150. [Google Scholar]
- Sasaki, N.; Aono, T. Energy saving device “SILD”. J. Shipbuild. Jpn. 1997, 45, 47–50. [Google Scholar]
- Inukai, Y.; Itabashi, M.; Sudo, Y.; Takeda, T.; Ochi, F. Energy saving device for ship IHIMU semicircular duct. IHI Eng. Rev. 2007, 40, 59–63. [Google Scholar]
- Mewis, F. A novel power saving device for full form vessels. In Proceedings of the First International Symposium on Marine Propulsors (SMP’09), Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- Energy-Saving Technology. Available online: https://global.kawasaki.com/en/mobility/marine/technology/energy_saving.html (accessed on 28 February 2025).
- Schuiling, B. The design and numerical demonstration of a new energy saving device. In Proceedings of the 16th Numerical Towing Tank Symposium (NUTTS 2013), Mulheim, Germany, 2–4 September 2013. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model, in: Turbulence, Heat and Mass Transfer. In Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003; pp. 625–632. [Google Scholar]
- Nicorelli, G.; Villa, D.; Gaggero, S. Pre-swirl ducts, pre-swirl fins and wake-equalizing ducts for the DTC hull: Design and scale effects. J. Mar. Sci. Eng. 2023, 11, 1032. [Google Scholar] [CrossRef]
- Sakamoto, N.; Kawanami, Y.; Hinatsu, M.; Uto, S. Viscous CFD analysis of stern duct installed on panamax bulk carrier in model and full scale. In Proceedings of the 15th International Conference on Computer and IT Applications in the Maritime Industries, Lecce, Italy, 9–11 May 2016. [Google Scholar]
- Tahara, Y.; Peri, D.; Campana, E.F.; Stern, F. Computational fluid dynamics-based multiobjective optimization of a surface combatant using a global optimization method. J. Mar. Sci. Technol. 2008, 13, 95–116. [Google Scholar] [CrossRef]
- Tahara, Y.; Norisada, K.; Yamane, M.; Takai, T. Development and demonstration of CAD/CFD/optimizer integrated simulation-based design framework by using high-fidelity viscous free-surface RANS equation solver. J. Jpn. Soc. Nav. Archit. Ocean Eng. 2008, 7, 171–184. [Google Scholar] [CrossRef]
- Lee, M.-K.; Lee, I. Optimal Design of Flow Control Fins for a Small Container Ship Based on Machine Learning. J. Mar. Sci. Eng. 2023, 11, 1149. [Google Scholar] [CrossRef]
- Diez, M.; Serani, A.; Campana, E.F.; Goren, O.; Sarioz, K.; Danisman, D.B.; Grigoropoulos, G.; Aloniati, E.; Visonneau, M.; Queutey, P.; et al. Multi-objective hydrodynamic optimization of the DTMB 5415 for resistance and seakeeping. In Proceedings of the 13th International Conference on Fast Sea Transportation (FAST 2015), Washington, DC, USA, 1–4 September 2015. [Google Scholar]
- Grigoropoulos, G.; Campana, E.; Diez, M.; Serani, A.; Goren, O.; Sariöz, K.; Danisman, D.B.; Visonneau, M.; Queutey, P.; Abdel-Maksoud, M.; et al. Mission-based hull-form and propeller optimization of a transom stern destroyer for best performance in the sea environment. In Proceedings of the VII International Conference on Computational Methods in Marine Engineering (MARINE2017), Nantes, France, 15–17 May 2017. [Google Scholar]
- Guo, J.; Zhang, Y.; Chen, Z.; Feng, Y. CFD-based multi-objective optimization of a waterjet-propelled trimaran. Ocean Eng. 2020, 195, 106755. [Google Scholar] [CrossRef]
- Wie, D.-E.; Kim, D.-J. The Design Optimization of a Flow Control Fin Using CFD. J. Soc. Nav. Archit. Korea 2012, 49, 174–181. [Google Scholar] [CrossRef]
- Vesting, F.; Bensow, R. Propeller Optimisation Considering Sheet Cavitation and Hull Interaction. In Proceedings of the Second International Symposium on Marine Propulsors (SMP’11), Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Vázquez-Santos, A.; Camacho-Zamora, N.; Hernández-Hernández, J.; Herrera-May, A.L.; Santos-Cortes, L.d.C.; Tejeda-del-Cueto, M.E. Numerical Analysis and Validation of an Optimized B-Series Marine Propeller Based on NSGA-II Constrained by Cavitation. J. Mar. Sci. Eng. 2024, 12, 205. [Google Scholar] [CrossRef]
- Zhai, S.; Jin, S.; Chen, J.; Liu, Z.; Song, X. CFD-based multi-objective optimization of the duct for a rim-driven thruster. Ocean Eng. 2022, 264, 112467. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Chandar, D. Ship specific optimization of pre-duct energy saving devices using reduced order models. Appl. Ocean Res. 2023, 131, 103449. [Google Scholar] [CrossRef]
- Furcas, F.; Vernengo, G.; Villa, D.; Gaggero, S. Design of wake equalizing ducts using RANSE-based SBDO. Appl. Ocean Res. 2020, 97, 102087. [Google Scholar] [CrossRef]
- Wu, P.-C.; Chang, C.-W.; Huang, Y.-C. Design of Energy-Saving Duct for JBC to Reduce Ship Resistance by CFD Method. Energies 2022, 15, 6484. [Google Scholar] [CrossRef]
- ITTC Recommended Procedures and Guidelines 7.5-03-01-01: Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures. Available online: https://ittc.info/media/4184/75-03-01-01.pdf (accessed on 20 September 2008).
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London, London, UK, 2002. [Google Scholar]
- Holzmann, T. The numerical algorithms: SIMPLE, PISO and PIMPLE. In Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: Loeben, Germany, 2006; pp. 93–121. [Google Scholar]





| U = (u,v,w) | p | ω | α | |||
|---|---|---|---|---|---|---|
| Hull | movingWallVelocity | fixedFluxPressure | nutkWallFunction | kqRWallFunction | omegaWallFunction | zeroGradient |
| Propeller Duct | movingWallVelocity | fixedFluxPressure | nutLowReWallFunction | kLowReWallFunction | omegaWallFunction | zeroGradient |
| Inlet | fixedValue | fixedFluxPressure | fixedValue | fixedValue | fixedValue | fixedValue |
| Outlet | outletPhaseMeanVelocity | zeroGradient | zeroGradient | inletOutlet | inletOutlet | variableHeightFlowRate |
| Top | pressureInletOutletVelocity | prghEntrainmentPressure | zeroGradient | inletOutlet | inletOutlet | inletOutlet |
| Bottom Mid-plane Sides | SymmetryPlane | |||||
| Case 1.1 | Case 1.2 | OPT | Case 1.6 | |
|---|---|---|---|---|
| Coarse grid | 321,463 | 581,168 | 493,679 | 790,082 |
| Medium grid | 1,245,900 | 1,547,393 | 1,422,479 | 2,125,520 |
| Fine grid | 2,263,181 | 3,989,685 | 3,733,057 | 5,192,505 |
| Resistance | Self-Propulsion | |||
|---|---|---|---|---|
| NACA 7908 | NACA 6.3914 | NACA 7908 | NACA 6.3914 | |
| Coarse grid | 551,138 | 551,677 | 765,272 | 763,202 |
| Medium grid | 1,481,464 | 1,488,405 | 2,071,378 | 2,073,981 |
| Fine grid | 3,886,754 | 3,886,754 | 5,073,662 | 5,083,935 |
| Case 1.1 | Case 1.2 | OPT (J = 0.4) | Case 1.6 | ||||
|---|---|---|---|---|---|---|---|
| 1000CT | 1000CT | KT | KQ | 1000CT | KT | KQ | |
| S1 | 4.3642 | 4.3272 | 0.2160 | 0.03079 | 5.0053 | 0.2375 | 0.02762 |
| S2 | 4.4031 | 4.3989 | 0.2108 | 0.02976 | 5.0474 | 0.2344 | 0.02759 |
| S3 | 4.6327 | 4.6671 | 0.2022 | 0.02870 | 5.5656 | 0.2131 | 0.02587 |
| D | 4.289 | 4.263 | 0.2214 | 0.02871 | 4.762 | 0.233 | 0.0295 |
| 0.03884 | 0.07164 | 0.0052 | 0.0103 | 0.04211 | 0.00313 | 0.000023 | |
| 0.22967 | 0.26818 | 0.0087 | 0.0106 | 0.51815 | 0.02132 | 0.001727 | |
| 0.16912 | 0.26713 | 0.5982 | 0.9679 | 0.08128 | 0.1471 | 0.01361 | |
| E%D | 1.76% | 1.51% | 2.43% | −7.25% | 5.11% | 1.96% | 6.37% |
| Ug | 0.05562 | 0.05801 | 0.04351 | 135% | 0.12496 | 0.09756 | 0.07219 |
| Ud | 1% | 1% | Not provided | Not provided | 1% | Not provided | Not provided |
| Ui | 0.00046 | 0.00108 | 7.8 | 6.01 | 0.0026 | 0.0108 | 0.00738 |
| Uv | 5.6516% | 5.8877% | 4.4199% | 135% | 12.5385% | 9.8163% | 7.2567% |
| J | η | E%D of η | Average y+ | ||||
|---|---|---|---|---|---|---|---|
| 0.15 | 0.3023 | 0.3839 | 0.1880 | 2.87% | 5.78% | 8.19% | 4.98 |
| 0.25 | 0.2675 | 0.3526 | 0.3019 | 3.67% | 4.90% | 8.17% | 5.00 |
| 0.35 | 0.2337 | 0.3238 | 0.4020 | 3.01% | 6.28% | 8.75% | 5.03 |
| 0.4 | 0.2160 | 0.3078 | 0.4466 | 2.45% | 7.22% | 9.02% | 5.07 |
| 0.45 | 0.1975 | 0.2905 | 0.4869 | 1.74% | 8.32% | 9.29% | 5.12 |
| 0.55 | 0.1588 | 0.2506 | 0.5549 | 0.72% | 10.83% | 9.12% | 5.23 |
| 0.65 | 0.1177 | 0.2072 | 0.5877 | 5.85% | 16.59% | 9.21% | 5.32 |
| 0.75 | 0.0711 | 0.1571 | 0.5405 | 15.86% | 28.36% | 9.74% | 5.42 |
| Original Duct | NACA 7908 Duct | Diff. from Orig. | NACA 6.3914 Duct | Diff. from Orig. | |
|---|---|---|---|---|---|
| n (rps) | 7.5 | 7.62542 | −1.67% | 7.5735 | 0.98% |
| 10KQ | 0.276 | 0.267604 | 3.12% | 0.267699 | 3.08% |
| KT | 0.238 | 0.223 | 6.30% | 0.225 | 5.46% |
| 1000CT | 5.005 | 4.925 | 1.60% | 4.918 | 1.74% |
| 1w | 0.464 | 0.520 | 12.07% | 0.509 | 9.70% |
| 1t | 0.740 | 0.730 | 1.35% | 0.732 | 1.08% |
| Va | 0.546 | 0.614 | 12.45% | 0.600 | 9.89% |
| EHP 1 (W) | 19.754 | 18.911 | 4.27% | 18.902 | 4.31% |
| DHP 2 (W) | 25.194 | 25.654 | 1.83% | 25.143 | 0.20% |
| THP 3 (W) | 12.379 | 13.479 | 8.89% | 13.144 | 6.18% |
| 1.596 | 1.403 | 12.09% | 1.438 | 9.90% | |
| 0.449 | 0.487 | 8.46% | 0.481 | 7.13% | |
| 0.784 | 0.737 | 5.99% | 0.752 | 4.08% | |
| 1.094 | 1.079 | 1.37% | 1.087 | 0.64% | |
| 0.491 | 0.525 | 6.92% | 0.523 | 6.52% |
| NACA7908 Duct | NACA6.3914 Duct | |||||||
|---|---|---|---|---|---|---|---|---|
| Resistance Test | Self-Propulsion Test (Propeller Rotational Rate = 7.5 rps) | Resistance Test | Self-Propulsion Test (Propeller Rotational Rate = 7.5 rps) | |||||
| 1000CT | 1000CT | KT | KQ | 1000CT | 1000CT | KT | KQ | |
| S1 = D * | 4.2431 | 4.9098 | 0.2232 | 0.0265 | 4.2429 | 4.9193 | 0.2250 | 0.0266 |
| S2 | 4.3130 | 4.9327 | 0.2192 | 0.0262 | 4.3083 | 4.9311 | 0.2191 | 0.0262 |
| S3 | 4.5724 | 5.4231 | 0.1974 | 0.0243 | 4.5282 | 5.4413 | 0.1988 | 0.0244 |
| 0.06993 | 0.04657 | 0.00403 | 0.00033 | 0.06535 | 0.01176 | 0.00591 | 0.00045 | |
| 0.25934 | 0.02284 | 0.02183 | 0.00189 | 0.21991 | 0.51024 | 0.02028 | 0.00174 | |
| 0.26966 | 0.04657 | 0.18471 | 0.17502 | 0.29715 | 0.02305 | 0.29179 | 0.25990 | |
| Ug | 0.05620 | 0.11907 | 0.10008 | 0.07425 | 0.04621 | 0.12667 | 0.08078 | 0.06089 |
| Ui | 0.00120 | 0.00173 | 0.00887 | 0.01054 | 0.00119 | 0.00142 | 0.00026 | 0.00025 |
| Uv | 5.6206% | 11.905% | 10.008% | 7.425% | 4.6211% | 12.667% | 8.078% | 6.089% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.-C.; Yeh, T.-C.; Wang, Y.-C. Stern Duct with NACA Foil Section Designed by Resistance and Self-Propulsion Simulation for Japan Bulk Carrier. Inventions 2025, 10, 32. https://doi.org/10.3390/inventions10020032
Wu P-C, Yeh T-C, Wang Y-C. Stern Duct with NACA Foil Section Designed by Resistance and Self-Propulsion Simulation for Japan Bulk Carrier. Inventions. 2025; 10(2):32. https://doi.org/10.3390/inventions10020032
Chicago/Turabian StyleWu, Ping-Chen, Tzu-Chi Yeh, and Yu-Cheng Wang. 2025. "Stern Duct with NACA Foil Section Designed by Resistance and Self-Propulsion Simulation for Japan Bulk Carrier" Inventions 10, no. 2: 32. https://doi.org/10.3390/inventions10020032
APA StyleWu, P.-C., Yeh, T.-C., & Wang, Y.-C. (2025). Stern Duct with NACA Foil Section Designed by Resistance and Self-Propulsion Simulation for Japan Bulk Carrier. Inventions, 10(2), 32. https://doi.org/10.3390/inventions10020032







