Abstract
This paper presents a control strategy that is applied in turning control for decentralized electric vehicles known as the electronic differential system. The conventional mechanical differential has drawbacks, such as bulkiness and slow response. The electric system response is not only ten times faster than its mechanical counterpart, but its accurate control even reduces the loss of power from the motor to the wheel. Through the turning radius from the steering angle command that the driver gives, the controller can distribute torque to each wheel. After controlling each wheel’s rotation, the vehicle can turn in neutral steering. The results show that this strategy can be effectively employed on urban roads.
1. Introduction
1.1. Background and Motivation
In recent years, the rising awareness of the need to protect the environment has accelerated an increase in hybrid vehicle and pure electric vehicle (EV) production. In addition to environmental protection, electric vehicles operate with high efficiency [1,2]. Compared to conventional gasoline vehicles, decentralized-drive electric vehicles achieve nimble response because of the high efficiency of motor propulsion. In addition, the motor can be controlled individually, which shows certain flexibility regarding the system implementations. Through the given torque difference to each wheel, the electronic differential system (EDS) facilitates different steering behaviors [3,4,5]. Basically, EDS is the fundamental system of autonomous emergency braking. Moreover, vehicles that are equipped with more advanced assistive technologies are of interest due to the developments in the automotive industry.
The companies that use pure electric vehicles, such as Starship Technologies in the United Kingdom, have developed “STARPSHIP” robots [6] that can transfer a commodity fully autonomously. Moreover, the automatic handling robot Kiva from Amazon has been utilized in automated factories [7]. Among the similar mobility platforms, vehicles that have no steering mechanism have become a trend. This can not only effectively reduce the steering radius but also the maintenance of the operation.
The paper is organized as follows: Section 1.2 reviews some literature about intelligent vehicle technologies and points out the advantages of electric vehicles. Section 2 mentions the materials from the software in use and the related vehicle model and principles of steering. Section 3 shows the simulation method and results. Finally, we summarize this study in Section 4.
1.2. Related Studies
The popular study topics in intelligent vehicles, such as Electronic Stability Control (ESC), Anti-lock Braking System (ABS), Adaptive Cruise Control (ACC), and Autonomous Emergency Braking (AEB) have been investigated worldwide. Additionally, EDS, a related subsystem of ABS, is popular for controlling the In-Wheel Motor (IWM) electric vehicle [8] because it can facilitate the control of each wheel sufficiently to reach neutral steering.
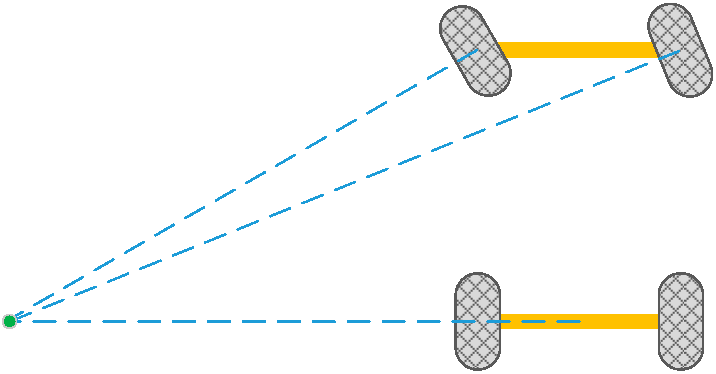
Generally, when the vehicle is in operation, Ackermann steering geometry [9], shown in Figure 1, is often referenced. This mechanism is designed to avoid the tires that slip sideways when following the path around a curve. Because the rear wheels are fixed, the center point must be on a line that has an extension line from the rear axle. Intersecting the axes of the front wheels on this line also requires that the inside front wheel is turned when steering through a greater angle than the outside wheel.
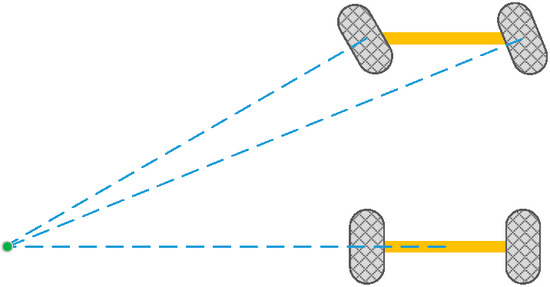
Figure 1.
Ackermann steering geometry.
From the investigation in [10], common EDS approaches need the steering angle command to control any wheel speed discrepancies. Four motors of only the front wheels can be turned and consequently require EDS. The kernel of the EDS is the control algorithm. Some research uses fuzzy logic to achieve the specific tasks in various conditions and improve directional stability [11,12]. In previous studies [13,14], the concept of torque distributions was proposed by using robust motion control based on fast and accurate in-wheel motor dynamics. The performance in these studies inspired the enhancement of lateral vehicle stability shown in this paper.
2. Proposed Approach
2.1. Model Construction
In order to construct the system, we use CarSim software to build the virtual vehicle. CarSim delivers the most accurate, detailed, and efficient methods for simulating the performance of different kinds of vehicles. Under the verification by automotive engineers, CarSim has gradually become the preferred tool for analyzing vehicle dynamics, controllers, calculating a car’s performance characteristics, and evaluating new strategies. Many famous automobile manufacturers, such as General Motors and TOYOTA, utilize this software as the first step in prototype evaluations. It can connect to MATLAB/Simulink to build up the feedback system for evaluation in the simulations. In this paper, we use MATLAB/Simulink to set up our controller and utilize CarSim to set up the vehicle plant. Then, we employ the plotting tools of MATLAB to help us to verify the performance.
2.2. System Structure
This paper proposed a new EDS for the four-wheel drive EV without a steering link in the front wheels. Basically, due to the lack of steering link in the front wheels, the differential-steered vehicle requires a mechanism to initiate a yaw-moment for turning. Hence, many approaches propose their solutions based on vehicle dynamics, intelligent control, or wheel slip control. Similar to these solutions, the proposed approach initiates the yaw-moment by the difference of wheel speed control. Unlike these sophisticated solutions, the proposed approach provides an easy way to proceed with the needed yaw-moment. Additionally, it is feasible for urban driving. In this paper, we regard the approach as a turnkey solution. The main idea is easy and effective. When the vehicle requires steering by turning, this mechanism is responsible for creating a minor spin. The action is basically responsible for helping the tires to produce certain deformation and initiate the needed lateral forces. It is suitable for the vehicle with an operator, but not for delicate steering scenarios.
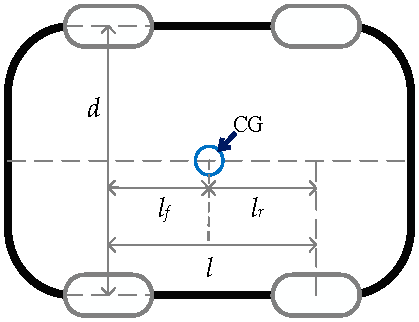
The vehicle parameters of the E-Class Mercedes-Benz was adopted in CarSim for simulation. The vehicle parameters are shown in Table 1, and the vehicle model is shown in Figure 2. Note that in this figure, the CG stands for the Center of Gravity. Note that, a four-passenger EV which has a mass of less than 2000 kg is considered in this study.

Table 1.
Vehicle parameters of E-Class.
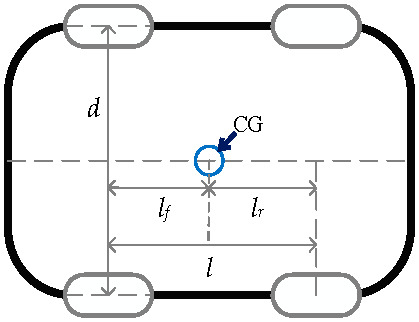
Figure 2.
Vehicle model.
2.3. Longitudinal Vehicle Dynamics
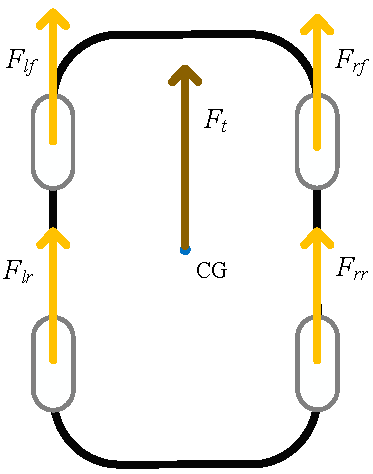
In this subsection, the vehicle dynamics of longitudinal motion is explained. The vehicle dynamics are shown in Figure 3, ignored the inertial torque of wheel. The equations of the vehicle in longitudinal vehicle motion can be represented by
where T is the torque of the wheel, r is the wheel radius, F is the driving force, V is the velocity of the vehicle, and ω is presented as the wheel velocity. The subscript i and j can be replaced by l and r, which mean left and right wheel, respectively. j can be replaced by f and r, which mean front and rear wheel, respectively. Note that the total driving force Ft is defined in Equation (2).
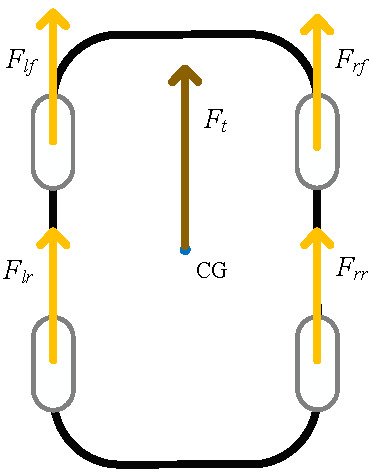
Figure 3.
Schematic view of a vehicle dynamics model.
In general conditions, consider that the friction coefficient between the tire and the road is a function of slip ratio λ, and it is defined as
where is the small constant value to avoid a meaningless equation.
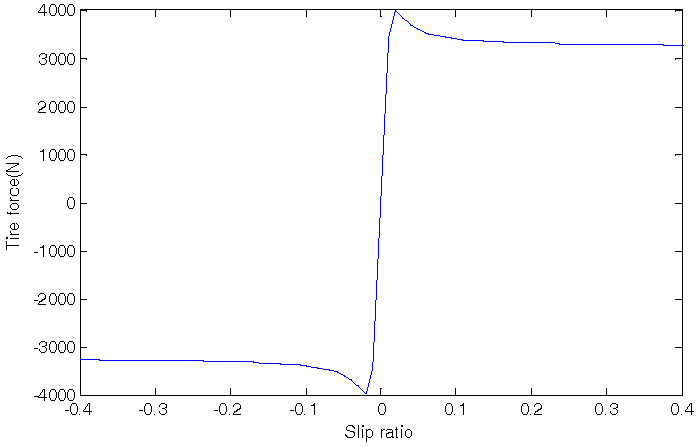
The slip ratio λ has a relationship with the coefficient of friction µ [15]. In Figure 4 [16], when the slip ratio is small, it can be regarded as linear to the friction coefficient. The tire force in this small-slip region can then be modeled as
where Nij is the normal force. The driving force could be defined as
where Cij is the longitudinal tire stiffness parameters of the tires. In this paper, because tests are carried out on a high friction road, it is assumed that the slip ratio is small. Therefore, the longitudinal tire stiffness parameter Ċij is constant. Furthermore, the coefficient Ċij depends on the road condition, and is represented by
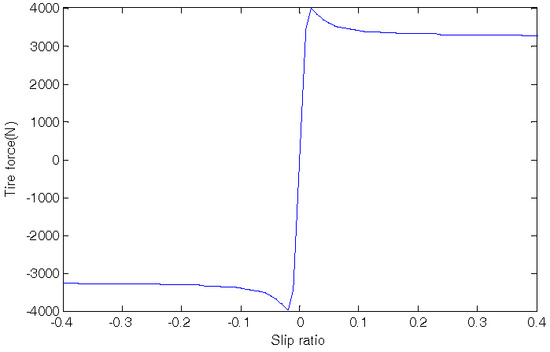
Figure 4.
Magic formula of tire force curve.
2.4. Distribution Method
Studies [17,18] indicate that acceleration and deceleration that could transfer the exact position in CG. Through the concept of distributing the driving torque, the slip ratio of the wheel should be minimized to compress the energy consumption. This paper proposes a new system structure that distributes the torque to the right and left wheels, based on the centrifugal force. Note that the unified unit follows the SI standard.
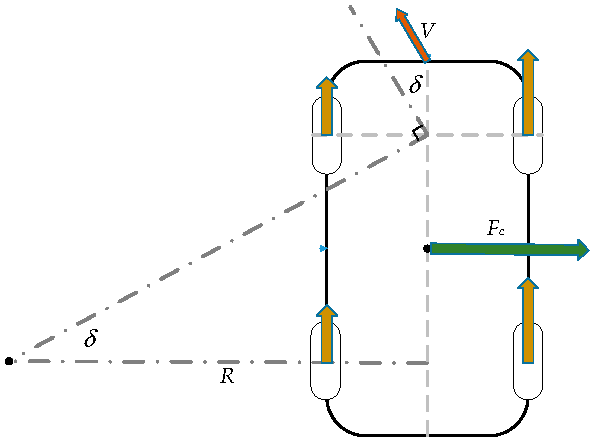
As shown in Figure 5, when a vehicle makes a turn, it will cause a fictitious force known as centrifugal force because of inertia, and this force will lead to the CG shift. Similarly to the aforementioned discussions, after moving the center of gravity, the need for torque in the inside or outside wheel will be different. Let the whole vehicle be treated as a rigid body and the centrifugal force can be represented as
where Fc is the centrifugal force caused by inertia, M is the whole mass of vehicle, ν is the velocity of vehicle and presented by meters per second, and R is the turning radius that calculated from the steering angle and the units is meter. δ is the steering angle and its unit is radians.
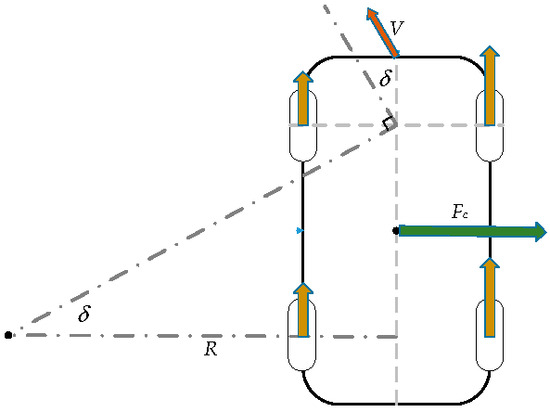
Figure 5.
Vehicle turning geometry.
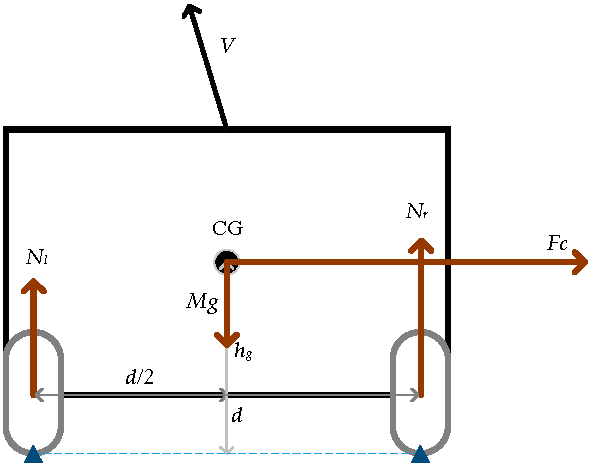
When the vehicle turns, the center of gravity will shift because of centrifugal force and the distances between inside and outside wheel. If the forces were different in the left and right motors, it could make the vehicle turn smoothly. From the rear-view of vehicle (Figure 6), if we consider the bottom of the right wheel as the fulcrum and calculate the total torque of the vehicle, we can get
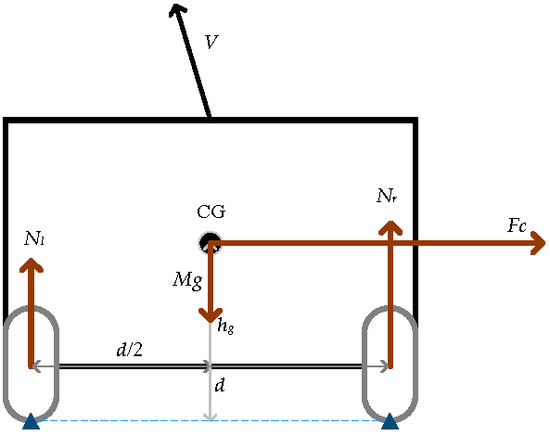
Figure 6.
Rear-view of vehicle.
Similarly, if we consider the bottom of the left wheel as the fulcrum and calculate the total torque of the vehicle, we can obtain
where M is the vehicle mass, g is gravity acceleration, d is the width of the vehicle wheel from right to left, and h is the height of the center of gravity. Substituting Equation (8) into Equations (11) and (13), we have
Herein, consider the torque distribution. Recalling Equation (1) gives us
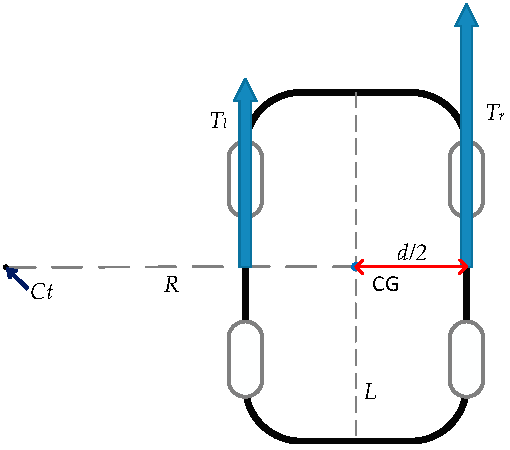
where Tl equal to Tlf +Tlr, means the total torque to the left wheel after distribution, and Tr is the total torque to the right wheel after distribution, that is Tr = Trf + Trr. Thus, regarding the driving force, Fl = Flf + Flr and Fr =Frf + Frr. The need for torque in the left and right wheels can be seen in Figure 7. After the distribution of total torque, the traction force to the front and rear wheels can be obtained. Note that in Figure 7, Ct is the turning center, and the required torque of both the inside and outside wheels can be presented as
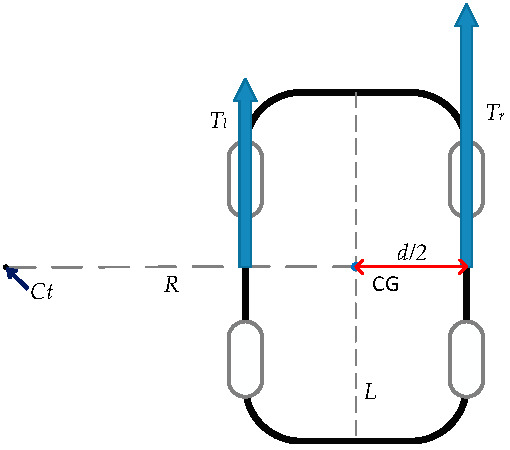
Figure 7.
Torque distribution scheme.
In the proposed system, the following algorithm is employed.
Note that the differential algorithm for motion and orientation control involves two constants, (W1, W2) which are introduced to allow for the association between two different physical quantities and to make the turning control more flexible. Consequently, without the turning mechanism in the front wheels, four-wheel drive electric vehicles still can make a turn by the presented torque distributions.
3. Results
3.1. Slip Ratio
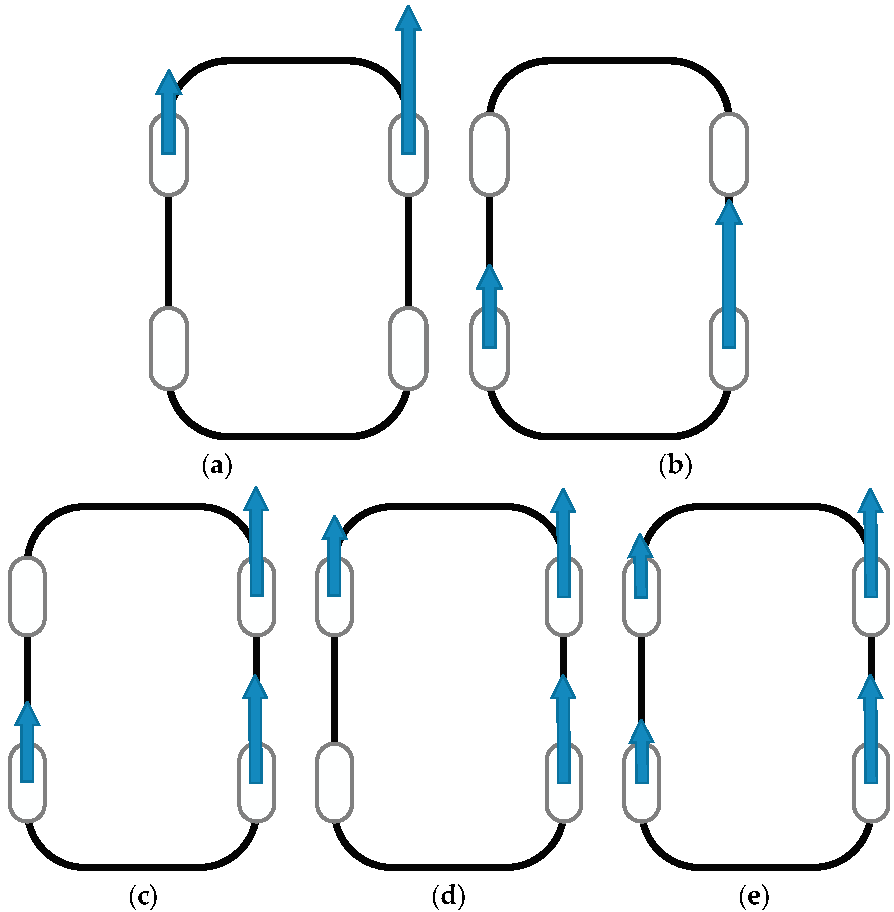
The following evaluations are carried out by simulations in CarSim. According to the torque distribution method in Section 2.4, during a left turn, the wheel on the outside should receive more torque than the inner one. It will be affected by front and rear allocation. The torque distribution method can be discussed as follows: (a) front wheel drive only; (b) rear wheel drive only; (c) inside front wheel is not activated; (d) inside rear wheel is not activated; (e) four-wheel drive. Figure 8 shows the formations mentioned above when the vehicle turns left.
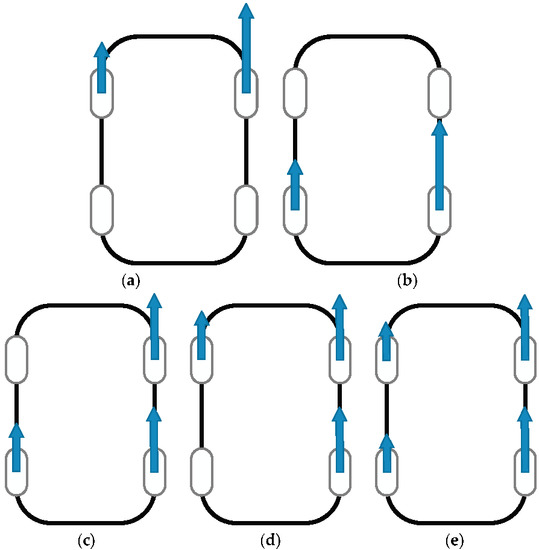
Figure 8.
Torque distributions for different cases. (a) Front wheel drive only; (b) Rear wheel drive only; (c) Inside front wheel is not activated; (d) Inside rear wheel is not activated; (e) Four-wheel drive.
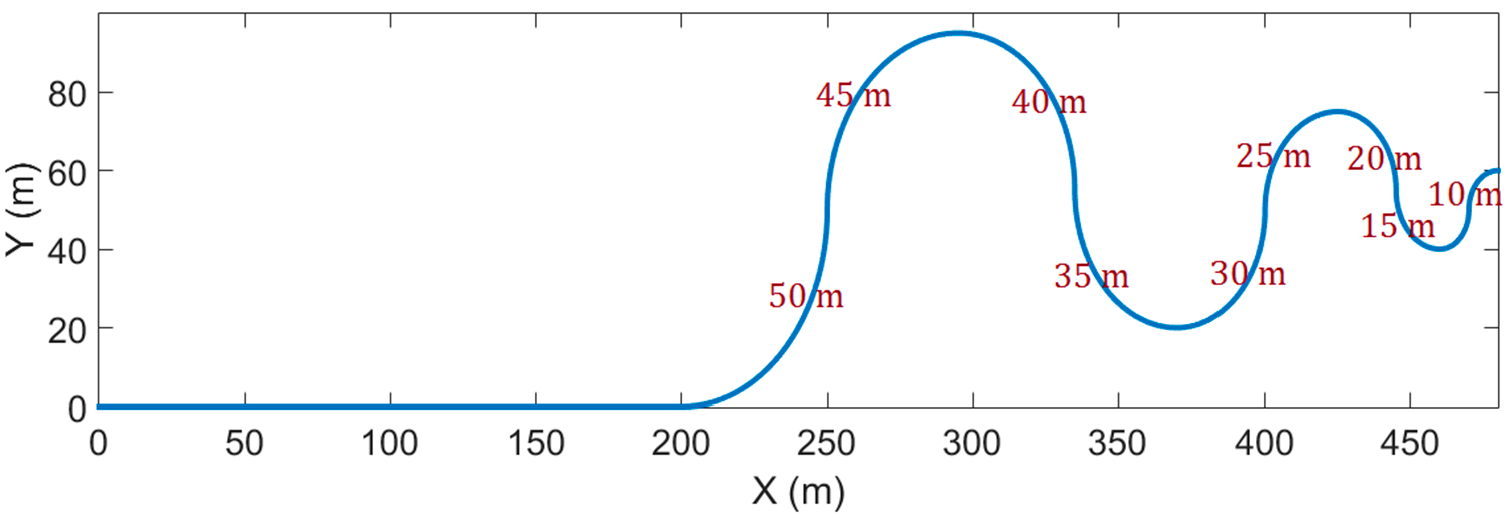
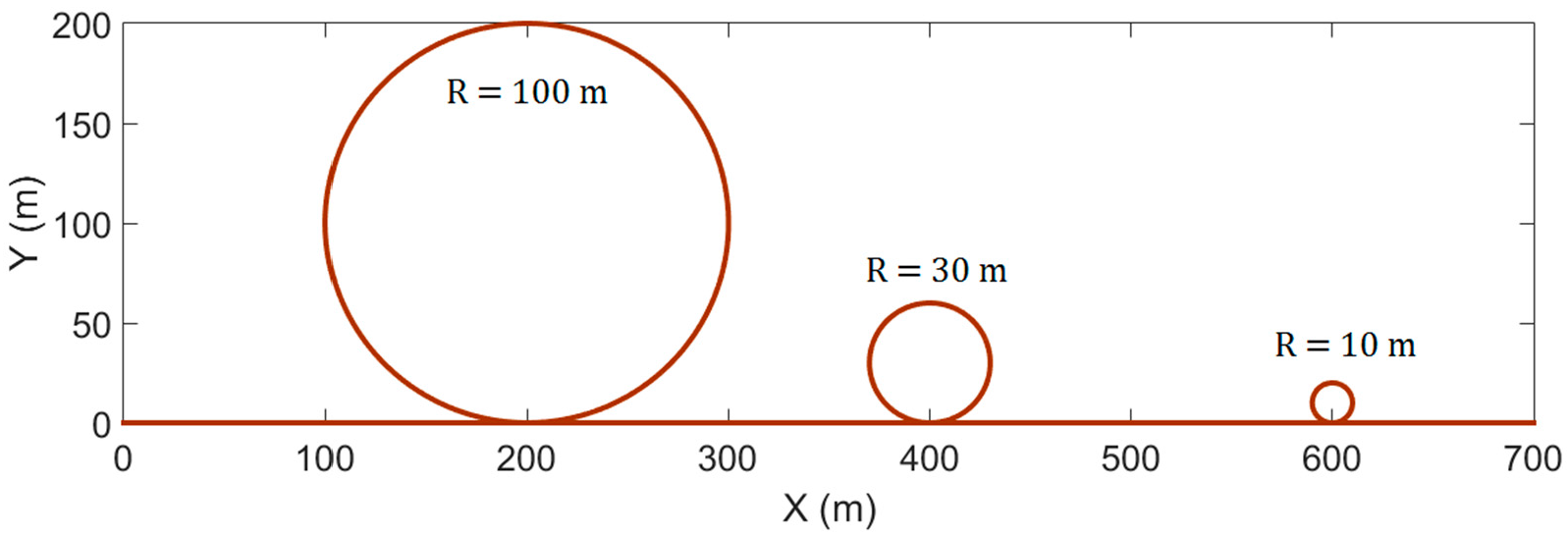
The test path-1 is as shown in Figure 9. To reach and maintain a speed of 40 km/h, the first 200 m of the test path are straight. After that, there are continuous curves that have turning radii from 50 to 10 m. The relation factors of W1 and W2 are set as 1.
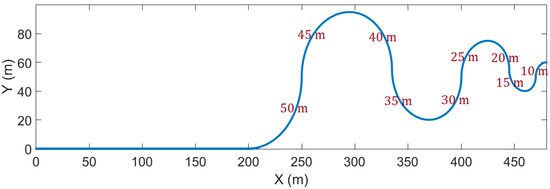
Figure 9.
Test path-1.
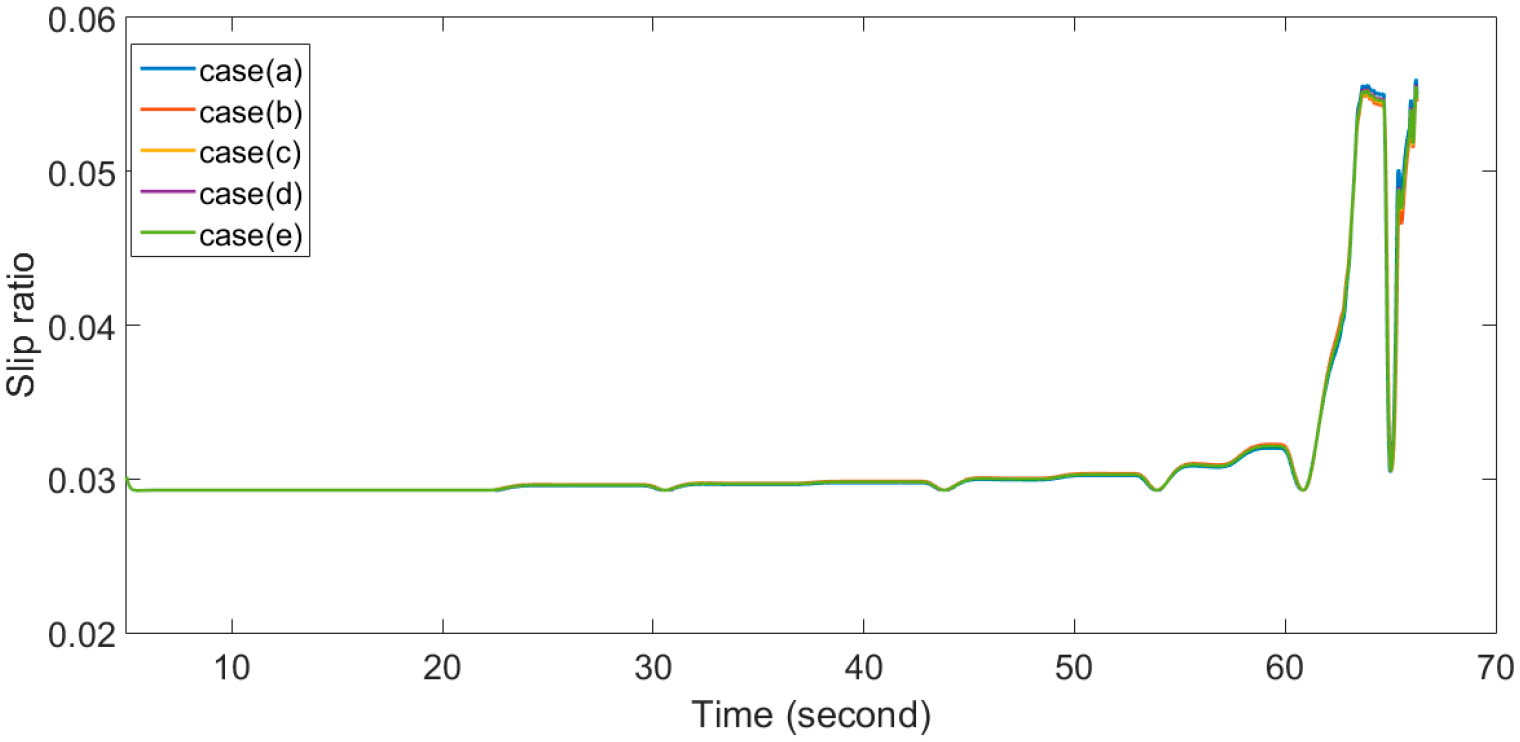
The slip ratios of all tests are shown in Figure 10. From the simulation results, the slip ratio of the proposed vehicle is regulated well. Clearly, from Figure 10, the slip ratio is always less than 0.1, which means that none of the wheels skidded during the tests.
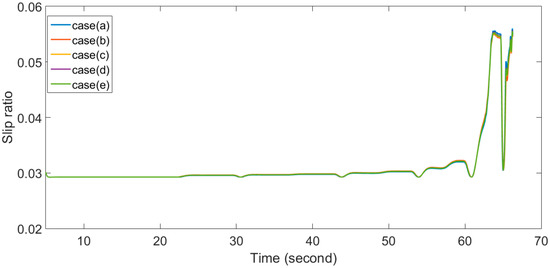
Figure 10.
Slip ratio.
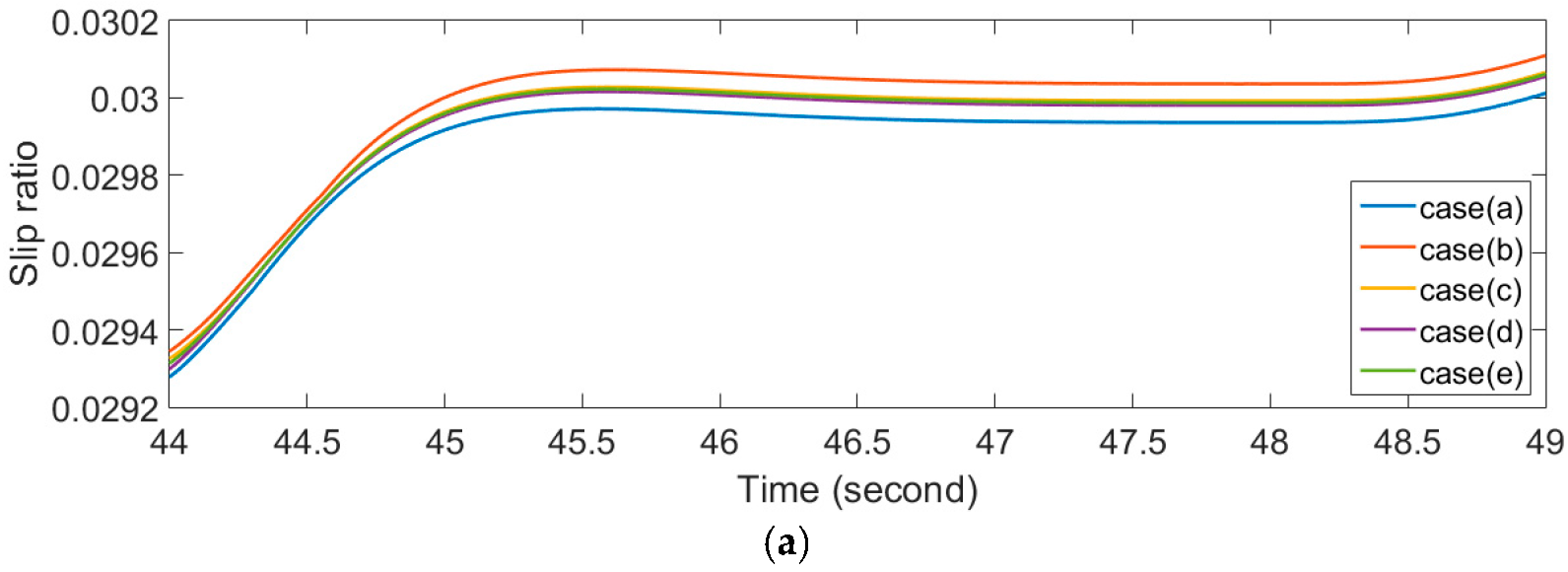
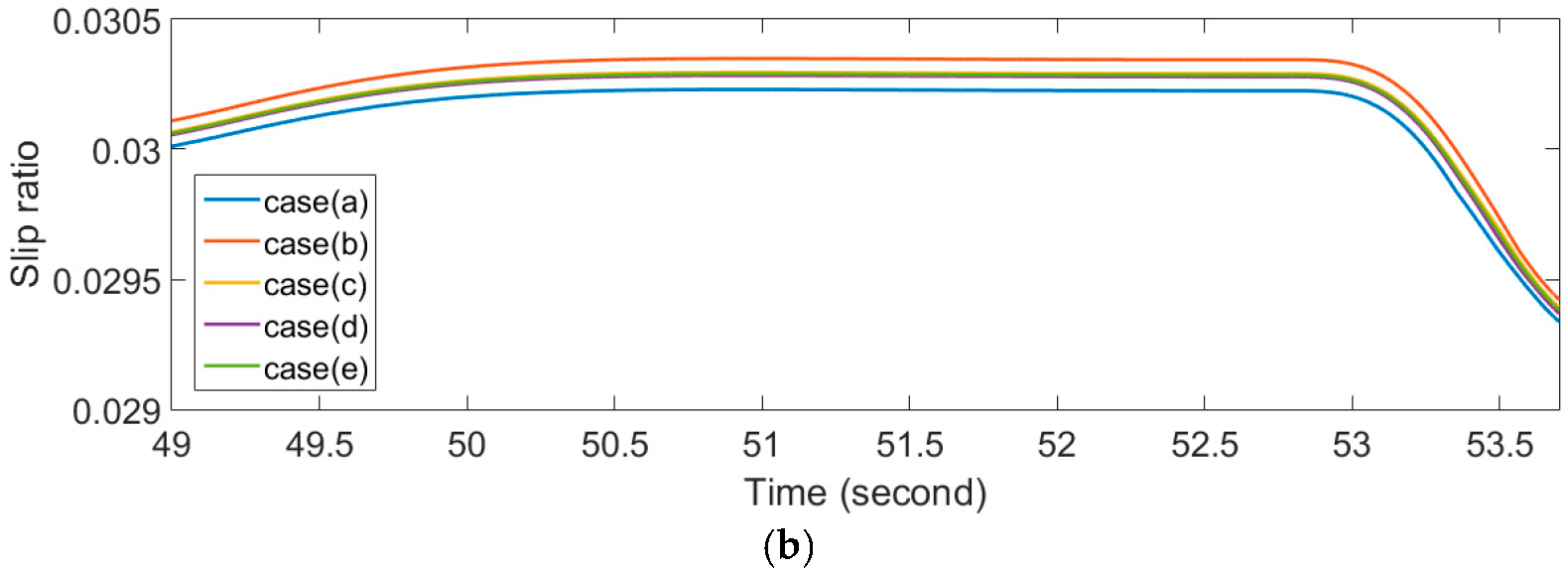
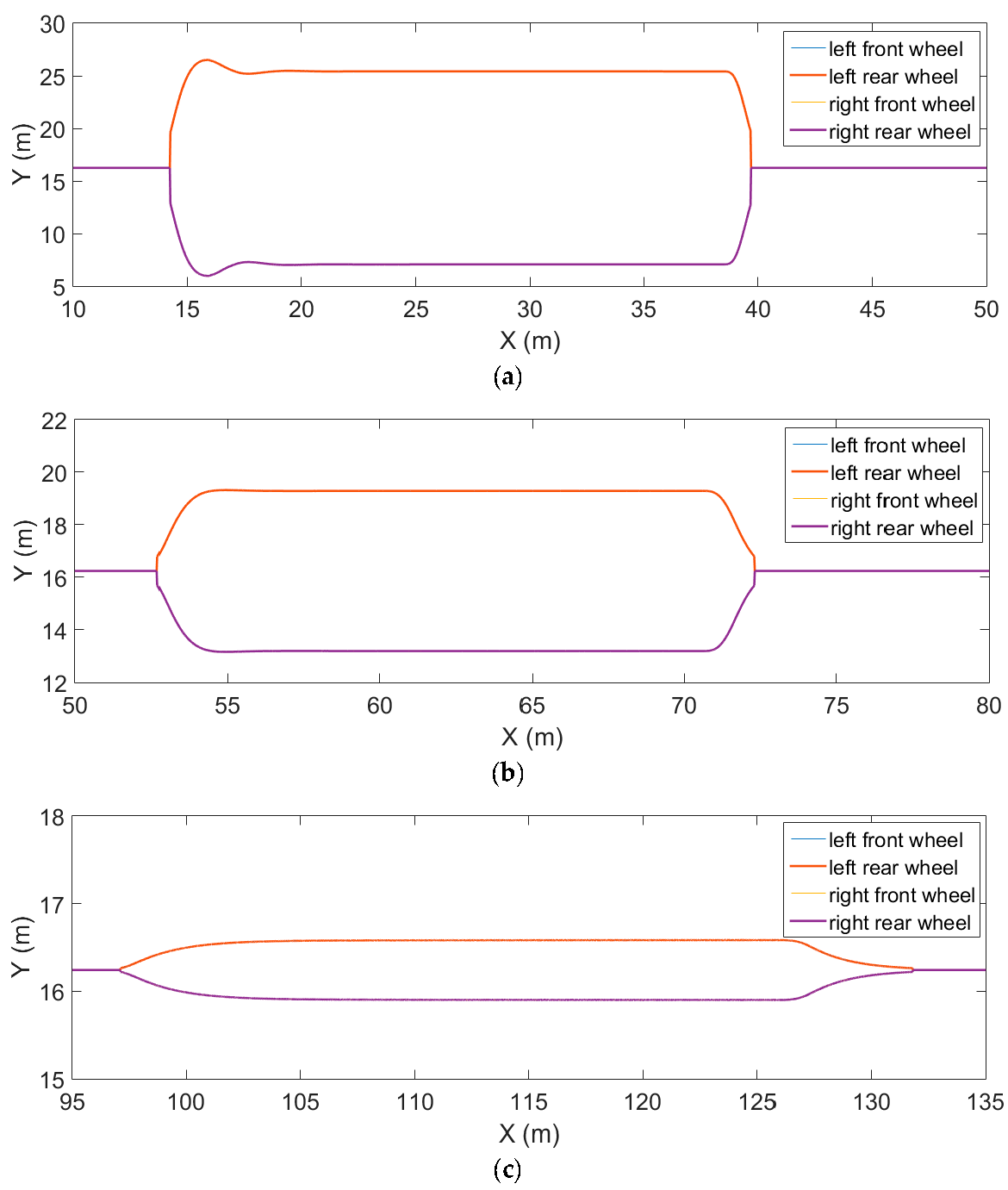
The slip ratio on the left and right turns is pertinent to this investigation. Choose a left turn section with a turning radius equal to 30 m and a right turn section with a turning radius equal to 25 m. The results are shown in Figure 11, from which we can see case (b) whether there is a discrepancy when the vehicle turns left or right. Referring to (6), in the case where longitudinal tire stiffness and the normal force are fixed, it is obvious that the larger slip ratio, the bigger the driving force.
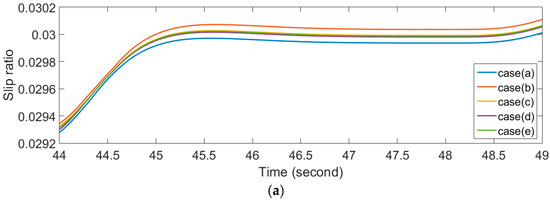
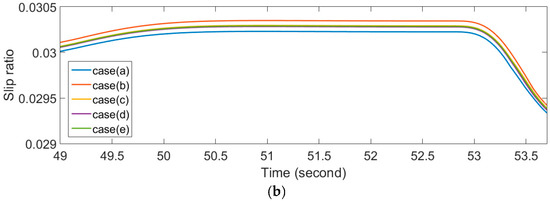
Figure 11.
Slip ratio of specific sections. (a) Turning left section; (b) Turning right section.
3.2. Torque Distribution
In order to test the proposed torque distribution method on common roads, the test path-2 shown in Figure 12 was adopted. The path is a road with a high-speed section, a medium-speed section, and a low-speed section. In the high-speed section, we simulate a highway road, so the vehicle speed is fixed at about 25 m/s (equal to 90 km/h), and the turning radius on the road is 100 m. In the medium-speed section, we simulate general inner-city driving; thus, the vehicle speed is fixed at about 10 m/s (equal to 36 km/h) when vehicle makes a turn, and the turning radius on the road is 30 m. In the low-speed section, we simulate the road conditions in the countryside and set the turning radius to 10 m. The vehicle speed is fixed at 2 m/s (equal to 7.2 km/h) while the vehicle turns.
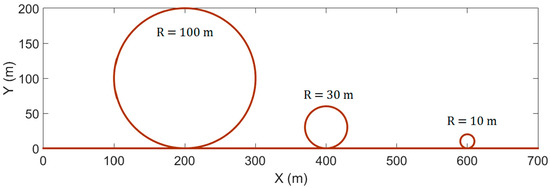
Figure 12.
Test path-2.
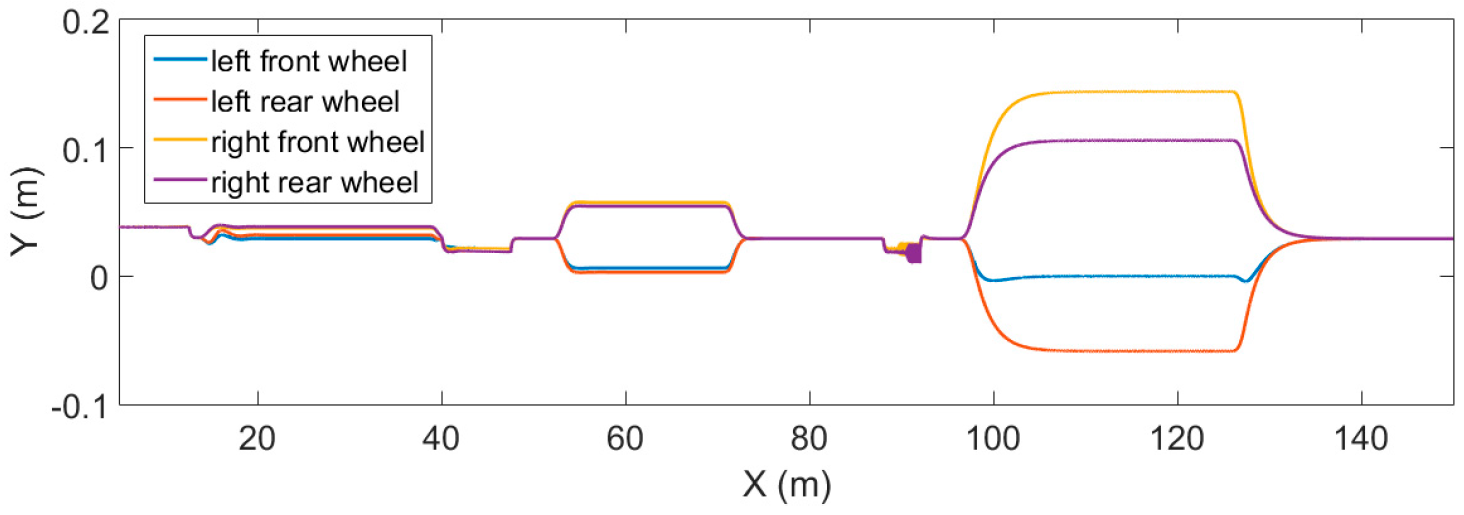
Firstly, as shown in Figure 13, the slip ratio is small enough throughout the test drives to be regarded as non-existent. From the above equations, we know that the higher the speed while the vehicle is turning, the bigger the torque difference should be, and the larger the turning radius, the smaller the torque difference will be. Figure 14 shows the simulation results of torque distributions for different wheels while the vehicle is turning.
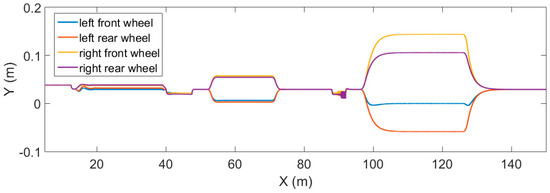
Figure 13.
Slip ratio in test path-2.
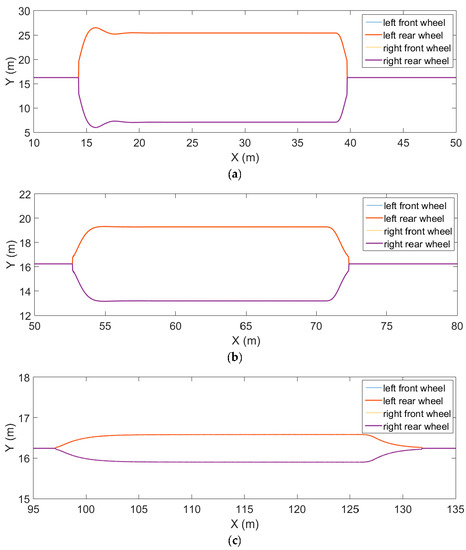
Figure 14.
Torque distributions for different wheels. (a) High-speed section; (b) Medium-speed section; (c) Low-speed section.
4. Conclusions
Electronic differential systems (EDS) have some benefits, such as faster response and more precise control than conventional differential. In this paper, an appropriate controller has been applied to test vehicle turning. The results have shown that the proposed torque distribution scheme has the ability to smoothen the turning and sustain more stability while steering. Using the proposed method, the driving distribution force to the left and right wheels can be solved effectively. Verification of the proposed approach by simulation has shown that the performance is effective for urban steering.
Acknowledgments
This work was supported by Metals Industry Research and Development Center (MIRDC) of Taiwan and Ministry of Science and Technology (MOST) of Taiwan, under projects MIRDC-106-EC-17-A-25-0803, MOST 106-2218-E-006-023, and MOST 106-2221-E-024-013.
Author Contributions
Yu-Chen Chang and Jia-Sheng Hu initiated and discussed the research problem; Jia-Sheng Hu, Jinn-Feng Jiang, Tsu-Kun Chang, and Hung-Yuan Wei conceived and developed the methods; Chuan-Yi Lu and Wei-Chun Chen performed the simulations; Yu-Chen Chang and Jia-Sheng Hu analyzed the data; Yu-Chen Chang and Jia-Sheng Hu prepared and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Chan, C.C.; Chau, K.T. Modern Electric Vehicle Technology; Oxford University Press: London, UK, 2001; ISBN 978-0198504160. [Google Scholar]
- Folgado, J.; Valtchev, S.S.; Coito, F. Electronic differential for electric vehicle with evenly split torque. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 1204–1209. [Google Scholar]
- Zhao, Y.E.; Zhang, J.W.; Guan, X.Q. Modeling and simulation of electronic differential system for an electric vehicle with two-motor-wheel drive. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 1209–1214. [Google Scholar]
- Wu, X.; Xu, M.; Wang, L. Differential speed steering control for four-wheel independent driving electric vehicle. Int. J. Mater. Mech. Manuf. 2013, 1, 355–359. [Google Scholar]
- STARSHIP. Available online: https://www.starship.xyz/ (accessed on 3 December 2017).
- Kiva Systems. Available online: http://www.mwpvl.com/html/kiva_systems.html (accessed on 3 December 2017).
- Yıldırım, M.; Öksüztepe, E.; Tanyeri, B.; Kürüm, H. Design of Electronic Differential System for an Electric Vehicle with in-wheel motor. In Proceedings of the 2016 IEEE Power and Energy Conference at Illinois (PECI), Urbana, IL, USA, 19–20 February 2016; pp. 1–5. [Google Scholar]
- Zhao, S.; Zhao, J.S.; Feng, Z.J. Design of a Pair of Noncircular Gears Meeting Ackermann Steering Principle. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 11–13 March 2011; pp. 217–221. [Google Scholar]
- Yin, D.; Sun, N.; Shan, D.; Hu, J.-S. A multiple data fusion approach to wheel slip control for decentralized electric vehicles. Energies 2017, 10, 461. [Google Scholar] [CrossRef]
- Hu, J.; Wu, J.; Peng, H.; Peng, Q.; Huang, Q. Application of Fuzzy Logic Algorithm for Optimization of Control Strategy in Electric Vehicles. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 2042–2045. [Google Scholar]
- Mirzaei, M.; Mirzaeinejad, H. Fuzzy scheduled optimal control of integrated vehicle braking and steering systems. IEEE/ASME Trans. Mechatron. 2017, 22, 2369–2379. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar]
- Hu, J.S.; Wang, Y.; Fujimoto, H.; Hori, Y. Robust yaw stability control for in-wheel motor electric vehicles. IEEE/ASME Trans. Mechatron. 2017, 22, 1360–1370. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Veh. Syst. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control, 2nd ed.; Springer: New York, NY, USA, 2012; pp. 87–98, 359–366. ISBN 978-1-4614-1432-2. [Google Scholar]
- Wang, Y.; Fujimoto, H.; Hara, S. Torque distribution-based range extension control system for longitudinal motion of electric vehicles by LTI modeling with generalized frequency variable. IEEE/ASME Trans. Mechatron. 2016, 21, 443–452. [Google Scholar]
- Fujimoto, H.; Harada, S. Model-based range extension control system for electric vehicles with front and rear driving—Braking force distributions. IEEE Trans. Ind. Electron. 2015, 62, 3245–3254. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).