Efficient Protection Scheme Based on Y-Source Circuit Breaker in Bi-Directional Zones for MVDC Micro-Grids
Abstract
:1. Introduction
2. Proposed Topology (Coupled-Inductor Y-Source Impedance Bi-Directional Circuit Breaker)
2.1. Breaker Operation
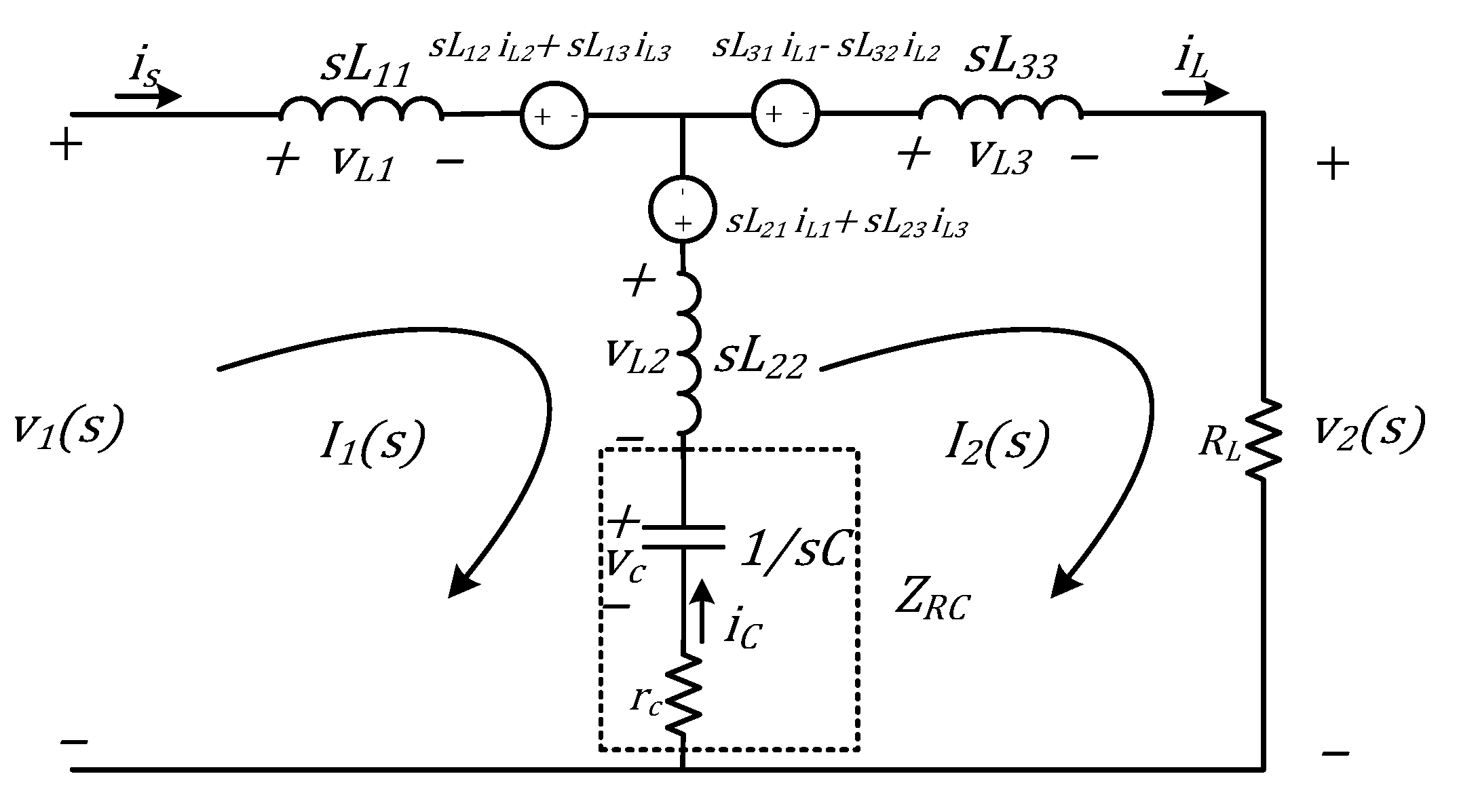
2.2. Circuit Breaker Analysis
2.3. Circuit Breaker Design
2.3.1. Infinite Fault Conductance Slope Rate
2.3.2. Linear Fault Conductance Slope Rate
2.3.3. The Effect of Turns-Ratio on knull
3. Results and Discussions
3.1. Coupled-Inductor Y-Source Impedance Bi-Directional Circuit Breaker
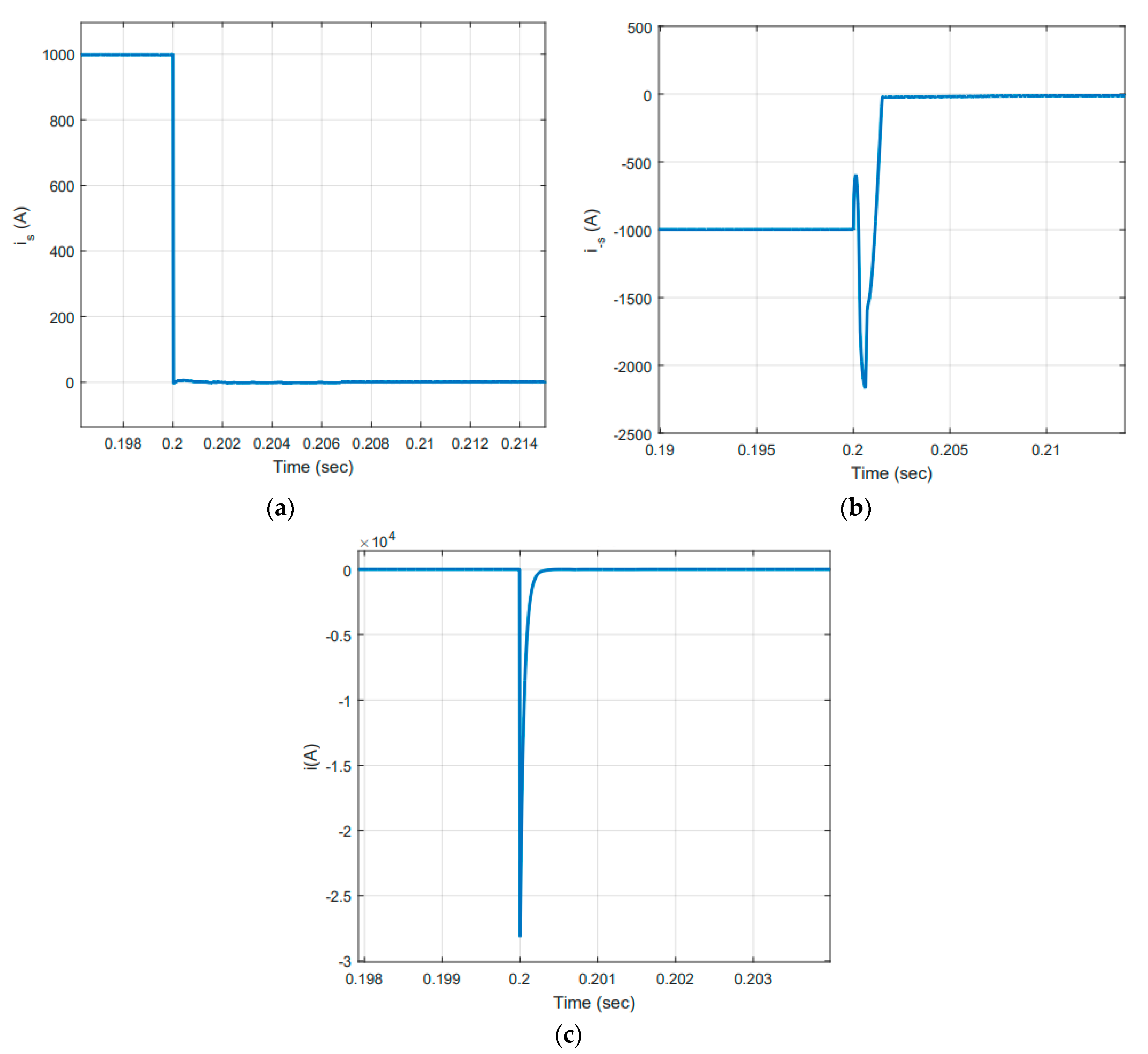
3.1.1. Fault Interruption
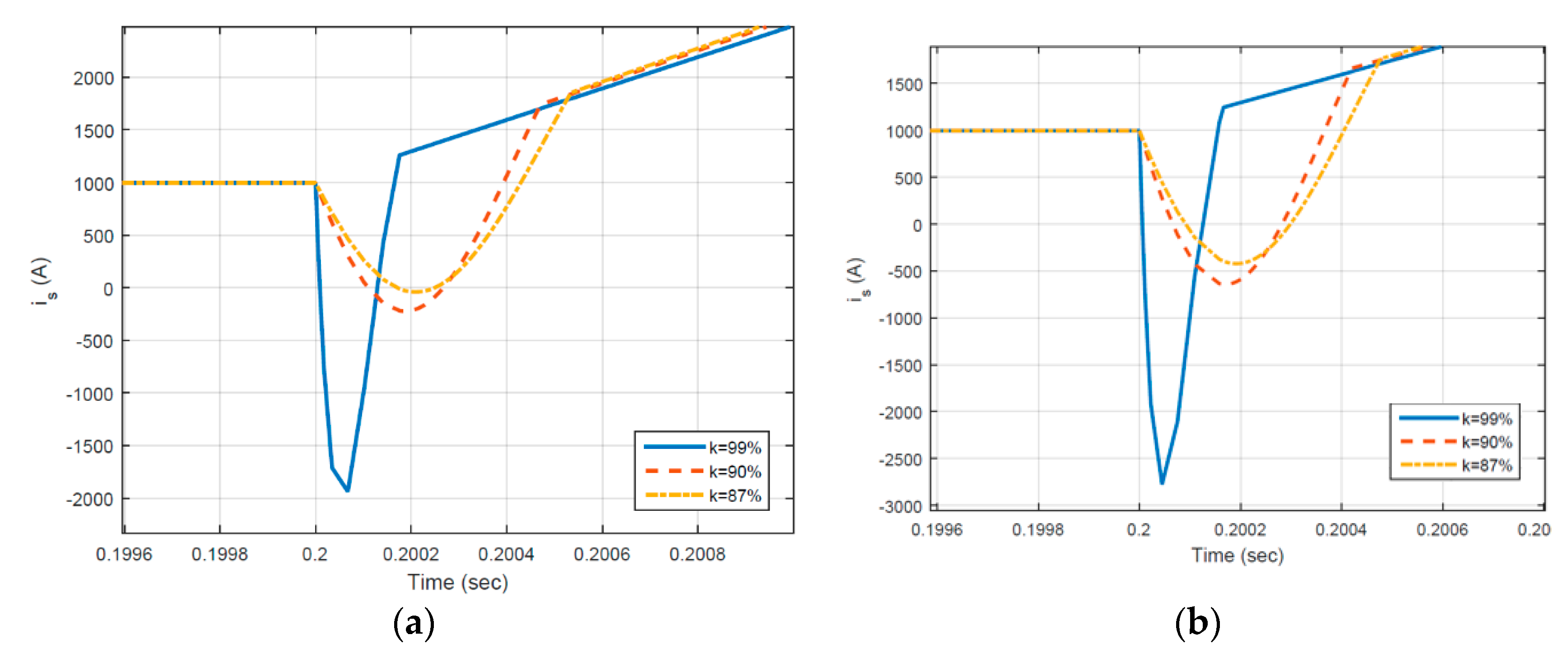
3.1.2. Load Change
3.2. Developed Y-Source Bi-Directional Circuit Breaker
3.2.1. Positive Pole-to-Ground Fault
3.2.2. Negative Pole-to-Ground Fault
3.2.3. Pole-to-Pole Fault
3.3. Y-Source Breaker Deployment into MVDC Micro-Grid (Case Study)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Zhang, B.; Zhao, S.; Liang, L.; Chen, Y. Design of an IGBT-series-based solid-state circuit breaker for battery energy storage system terminal in solid-state transformer. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 6677–6682. [Google Scholar]
- Cui, S.; Hu, J.; De Doncker, R.W. Fault-Tolerant Operation of a TLC-MMC Hybrid DC-DC Converter for Interconnection of MVDC and HVdc Grids. IEEE Trans. Power Electron. 2020, 35, 83–93. [Google Scholar] [CrossRef]
- Shi, Y.; Li, H. Isolated Modular Multilevel DC–DC Converter with DC Fault Current Control Capability Based on Cur-rent-Fed Dual Active Bridge for MVDC Application. IEEE Trans. Power Electron. 2018, 33, 2145–2161. [Google Scholar] [CrossRef]
- IEEE Std 1709–1018. IEEE Recommended Practice for 1 kV to 35 kV Medium-Voltage DC Power Systems on Ships; IEEE: New York, NY, USA, 2018; pp. 1–54. [Google Scholar]
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Keshavarzi, D.; Ghanbari, T.; Farjah, E. A Z-Source-Based Bidirectional DC Circuit Breaker with Fault Current Limitation and Interruption Capabilities. IEEE Trans. Power Electron. 2016, 32, 6813–6822. [Google Scholar] [CrossRef]
- Corzine, K.A. Circuit breaker for DC micro grids. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015. [Google Scholar]
- Li, C.; Nie, Z.; Li, H.; Zhang, Y. A novel solid-state protection scheme for DC system. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2039–2042. [Google Scholar]
- Maqsood, A.; Corzine, K. Z-source Dc circuit breakers with coupled inductors. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1905–1909. [Google Scholar]
- Lin, W.; Jovcic, D.; Nguefeu, S. Saad, H. Modelling of high-power hybrid DC circuit breaker for grid-level studies. IET Power Electron. 2016, 9, 237–246. [Google Scholar] [CrossRef]
- Salomonsson, D.; Soder, L.; Sannino, A. Protection of Low-Voltage DC Microgrids. IEEE Trans. Power Deliv. 2009, 24, 1045–1053. [Google Scholar] [CrossRef]
- Cuzner, R.M.; Venkataramanan, G. The status of DC micro-grid protection. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Baran, M.E.; Mahajan, N.R. Overcurrent Protection on Voltage-Source-Converter-Based Multiterminal DC Distribution Systems. IEEE Trans. Power Deliv. 2007, 22, 406–412. [Google Scholar] [CrossRef]
- Tennakoon, S.; McEwan, P. Short-circuit interruption performance of thyristor circuit breakers. In Proceedings of the 1994 IEEE Applied Power Electronics Conference and Exposition—ASPEC’94, Orlando, FL, USA, 13–17 February 1994. [Google Scholar]
- Corzine, K. Dc micro grid protection with the z-source breaker. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Bolanowski, B.; Wojcik, F. A fast DC hybrid circuit breaker. In Proceedings of the IEE Colloquium on Electronic-Aided Current-Limiting Circuit Breaker Developments and Applications, London, UK, 22 November 1989. [Google Scholar]
- Meyer, C.; Kowal, M.; De Doncker, R. Circuit breaker concepts for future high-power DC-applications. In Proceedings of the Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; Volume 2, pp. 860–866. [Google Scholar]
- Hirayama, S.Y. Zero-Current Arc-Suppression DC Circuit Breaker. U.S. Patent 4,740,858, 26 April 1988. [Google Scholar]
- Niwa, Y.; Matsuzaki, J.; Yokokura, K. The basic investigation of the high-speed VCB and its application for the DC power system. In Proceedings of the 23rd International Symposium on Discharges and Electrical Insulation in Vacuum, Bucharest, Romania, 15–19 September 2008; Volume 1, pp. 107–112. [Google Scholar] [CrossRef]
- Lawes, D.; Ran, L.; Xu, Z. Design of a solid-state D.C. circuit breaker for light rail transit power supply network. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 350–357. [Google Scholar]
- Shen, Z.J.; Sabui, G.; Miao, Z.; Shuai, Z. Wide-Bandgap Solid-State Circuit Breakers for DC Power Systems: Device and Circuit Considerations. IEEE Trans. Electron Devices 2015, 62, 294–300. [Google Scholar] [CrossRef]
- Maqsood, A.; Corzine, K. DC Microgrid Protection: Using the Coupled-Inductor Solid-State Circuit Breaker. IEEE Electrif. Mag. 2016, 4, 58–64. [Google Scholar] [CrossRef]
- Corzine, K.A.; Ashton, R.W. A New Z-Source DC Circuit Breaker. IEEE Trans. Power Electron. 2012, 27, 2796–2804. [Google Scholar] [CrossRef]
- Corzine, K.A.; Ashton, R.W. Structure and analysis of the Z-source MVDC breaker. In Proceedings of the 2011 IEEE Electric Ship Technologies Symposium, Alexandria, VA, USA, 10–13 April 2011; pp. 334–338. [Google Scholar]
- Chang, A.H.; Avestruz, A.-T.; Leeb, S.B.; Kirtley, J.L. Design of DC system protection. In Proceedings of the 2013 IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA, 22–24 April 2013; pp. 500–508. [Google Scholar]
- Chang, A.H.; Sennett, B.R.; Avestruz, A.-T.; Leeb, S.B.; Kirtley, J.L. Analysis and Design of DC System Protection Using Z-Source Circuit Breaker. IEEE Trans. Power Electron. 2016, 31, 1036–1049. [Google Scholar] [CrossRef]
- Maqsood, A.; Overstreet, A.; Corzine, K.A. Modified Z-source DC Circuit Breaker Topologies. IEEE Trans. Power Electron. 2016, 31, 7394–7403. [Google Scholar] [CrossRef]
- Al-Khafaf, H.; Asumadu, J. Γ-Z-source DC circuit breaker operation with variable coupling coefficient k. In Proceedings of the 2017 IEEE International Conference on Electro Information Technology (EIT), Lincoln, NE, USA, 14–17 May 2017; pp. 492–496. [Google Scholar]
- Al-Khafaf, H.; Asumadu, J. Bi-directional Y-Source DC Circuit Breaker Design and Analysis Under Different Conditions of Coupling. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; pp. 1–6. [Google Scholar]
- Al-Khafaf, H.; Asumadu, J. Y-Source Bi-directional DC Circuit Breaker. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 20–24 May 2018. [Google Scholar]
- Witulski, A. Introduction to modeling of transformers and coupled inductors. IEEE Trans. Power Electron. 1995, 10, 349–357. [Google Scholar] [CrossRef]
- Saleh, K.A.; Hooshyar, A.; El-Saadany, E.F. Ultra-High-Speed Traveling-Wave-Based Protection Scheme for Medi-um-Voltage DC Microgrids. IEEE Trans. Smart Grid 2019, 10, 1440–1451. [Google Scholar] [CrossRef]
- Monad, M.; Gavriluta, C.; Luna, A.; Candela, J.I.; Rodriguez, P. Centralized Protection Strategy for Medium Voltage DC Microgrids. IEEE Trans. Power Deliv. 2017, 32, 430–440. [Google Scholar] [CrossRef]
- Li, W.; Monti, A.; Ponci, F. Fault detection and classification in medium fault detection and classification in medium wavelets and artificial neural networks. IEEE Trans. Instrum. Meas. 2014, 63, 2651–2665. [Google Scholar] [CrossRef]
- Li, H.; Li, W.; Luo, M.; Monti, A. Design of Smart MVDC Power Grid Protection. IEEE Trans. Instrum. Meas. 2011, 60, 3035–3046. [Google Scholar] [CrossRef]
- Tang, L.; Ooi, B.-T. Locating and Isolating DC Faults in Multi-Terminal DC Systems. IEEE Trans. Power Deliv. 2007, 22, 1877–1884. [Google Scholar] [CrossRef]











| SCR Gates | i1 and i2 Direction | |
|---|---|---|
| Positive | Negative | |
| G1 | 1 | 0 |
| G2 | 0 | 1 |
| G3 | 1 | 0 |
| G4 | 0 | 1 |
| Parameters | Values | Description |
|---|---|---|
| L1 | 1000 µH | Self-inductance |
| L2 | 250 µH | Self-inductance [23] |
| L3 | 1000 µH | Self-inductance |
| C, rc | 100 µF, 0.2 Ω | Capacitance, Equivalent Series Resistance (ESR) [23] |
| V1 | 6 kV | Input voltage [25] |
| RL | 6 Ω | Load resistance [25] |
| Rf | 10 m Ω | Fault resistance [7] |
| Coupling Coefficient (k) | Source Current (A) | |
|---|---|---|
| N1/N2 = 2 | N1/N2 = √8 | |
| 99% | −1937.384 | −2777 |
| 90% | −223 | −643 |
| 87% | −40.25 | −422.5 |
| Circuit Breaker Numbers | Type |
|---|---|
| CB3, CB4, CB6, CB7, CB8, CB9, CB11, CB12, CB14, CB16, CB24, and CB25 | Unidirectional |
| CB1, CB2, CB5, CB10, CB13, CB15, CB17, CB18, CB19, CB20, CB21, CB22, CB23, and CB26 | Bi-directional |
| Paired Breakers | Location | Paired Breakers | Location |
|---|---|---|---|
| CB11, CB16 | Bus 10–Bus 11 | CB17, CB18 | Bus 10–Bus 8 |
| CB14, CB12 | Bus 5–Bus 12 | CB19, CB20 | Bus 6–Bus 8 |
| CB1, CB2 | Bus 1–Bus 2 | CB5, CB21 | Bus 5–Bus 6 |
| CB4, CB25 | Bus 2–Bus 4 | CB22, CB23 | Bus 2–Bus 6 |
| CB3, CB24 | Bus 2–Bus 3 | CB10, CB15 | Bus 5–Bus 10 |
| CB6, CB7 | Bus 6–Bus 7 | CB26, CB13 | Bus 2–Bus 5 |
| CB8, CB9 | Bus 8–Bus 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-khafaf, H.; Asumadu, J. Efficient Protection Scheme Based on Y-Source Circuit Breaker in Bi-Directional Zones for MVDC Micro-Grids. Inventions 2021, 6, 18. https://doi.org/10.3390/inventions6010018
Al-khafaf H, Asumadu J. Efficient Protection Scheme Based on Y-Source Circuit Breaker in Bi-Directional Zones for MVDC Micro-Grids. Inventions. 2021; 6(1):18. https://doi.org/10.3390/inventions6010018
Chicago/Turabian StyleAl-khafaf, Haider, and Johnson Asumadu. 2021. "Efficient Protection Scheme Based on Y-Source Circuit Breaker in Bi-Directional Zones for MVDC Micro-Grids" Inventions 6, no. 1: 18. https://doi.org/10.3390/inventions6010018
APA StyleAl-khafaf, H., & Asumadu, J. (2021). Efficient Protection Scheme Based on Y-Source Circuit Breaker in Bi-Directional Zones for MVDC Micro-Grids. Inventions, 6(1), 18. https://doi.org/10.3390/inventions6010018





