Load Losses and Short-Circuit Resistances of Distribution Transformers According to IEEE Standard C57.110

Abstract

Load losses determine transformers’ efficiency and life, which are limited by overheating and deterioration of their elements. Since these losses can be characterized by short-circuit resistances, in this article, we have developed expressions for the short-circuit resistances of three-phase transformers according to IEEE Standard C57.110. Imposing the condition that these resistances must cause load losses of the transformer, two types of short-circuit resistance have been established: (1) the effective resistance of each phase ($R_{cc,z}$) and (2) the effective short-circuit resistance of the transformer ($R_{cc,ef}$). The first is closely related to the power loss distribution within the transformer. The second is just a mathematical parameter. Applying these resistances to the 630 kVA oil-immersed distribution transformer of a residential network, we have concluded that both types of resistances determine the total load losses of the transformer. However, only $R_{cc,z}$ accurately provides the load losses in each phase. $R_{cc,ef}$ can give rise to errors more significant than 16% in calculating these losses, depending on imbalances in the harmonic currents.

1. Introduction

Three-phase transformers are essential machines for the operation and stability of power systems. They interconnect electrical networks with different voltage levels, transferring electrical energy from generation centers (large power transformers) to consumption points (distribution transformers), and their use is growing due to the strong demand for energy in today’s societies. However, in their operation, these machines waste energy in the core and windings [1,2], which reached worldwide values of 1181 TWh in 2020 and could be higher than 1845 TWh in 2040 according to estimates provided by the organization United for Efficiency (U4E) [2], patronized by the United Nations. These energy losses raise the temperature of the transformers and cause the following adverse effects:

• emission of greenhouse gases [2,3,4,5],
• deterioration in the properties of the core material and insulation, reducing the transformer’s life [6,7],
• decrease in power transmission capacity [6,7].

Core losses ($P_0$) are little affected by voltage harmonics [8], and their values are usually considered the same as those provided by the manufacturers. Winding losses or load losses ($P_{cc}$) are caused by the circulation of currents through the primary and secondary windings of the transformer [9].

When the transformers supply non-linear loads, the load losses can be calculated by applying IEEE Standard C57.110-2018 [10,11,12,13] and other well-known standards [14,15,16,17,18,19,20]. Alternatively, the load losses of three-phase transformers can be determined with the use of short-circuit resistances ($R_{cc}$) according to the well-known equation [21,22]:

$$P_{cc}=R_{cc} · \left(I_A^2+I_B^2+I_C^2\right)$$

(1)

in which ($I_A, I_B, I_C$) are the RMS values of the currents measured in each phase ($z=A,B,C$) of the primary or secondary winding depending on $R_{cc}$, which is the short-circuit resistance referred to the primary or secondary winding.

The short-circuit resistances determine not only the load losses but also efficiency and proper operation of the transformers. These parameters, jointly with the short-circuit reactance, determine the short-circuit impedances that limit the values of short-circuit currents and their adverse effects on the transformer windings due to vibrations [23,24,25,26] and electromagnetic forces [27,28,29,30].

References [31,32,33,34,35] establish different methods for determining a transformer’s short-circuit impedances, but none specifies expressions for the short-circuit resistances as a function of the harmonic frequencies.

In 2023, L. Sima et al. [36] established expressions for the short-circuit resistance of three-phase transformers feeding non-linear loads. L. Sima et al. worked with a transformer model like the one depicted in Figure 1, which is implicit in IEEE Standard C57.110-2018 [10]. As we know, the paper published by L. Sima et al. is the only one in the technical literature that develops short-circuit resistances with values depending on harmonic frequencies.

The short-circuit resistance referred to as the primary winding ($R_k$) developed by L. Sima et al. by direct application of IEEE Standard C57.110-2018 [10] is expressed as follows:

$$R_k=\frac{P_K}{I_p^2}=R_{DC}+R_{EC}+R_{OSL}$$

(2)

where $P_K$ represents the total load losses of the transformer defined by this standard, and $I_p$ is the combined RMS value of the three currents of the primary winding, that is, $I_p^2=I_{pA}^2+I_{pB}^2+I_{pC}^2$.

The short-circuit resistance of L. Sima et al. ($R_k$), as indicated by Equation (2), is the sum of three resistances: $R_{DC}, R_{EC}$, and $R_{OSL}$ (Figure 1). Each characterizes the load losses caused by the three power phenomena present in the operation of three-phase transformers, as established by IEEE Standard C57.110-2018 [10].

In Equation (2), $R_{DC}$ [37] is the combined direct current (or ohmic) resistance of the primary ($R_{DCp}$) and secondary ($R_{DCs}$) windings of the transformer:

$$R_{DC}=R_{DCp}+r_u^2{R}_{DCs}=\frac{P_{DC}}{I_p^2}$$

(3)

where $r_u\cong V_p/V_{s0}$ is the transformation ratio, approximately defined by the quotient between the primary ($V_p$) and the no-load secondary ($V_{s0}$) voltages. The resistance $R_{DC}$ characterizes the load losses ($P_{DC}$) when direct currents circulate through the transformer windings.

The resistance $R_{EC}$ due to the combined skin effects of the primary ($R_{ECp}$) and secondary ($R_{ECs}$) windings of the transformer

$$R_{EC}=R_{ECp}+r_u^2{R}_{ECs}=\frac{P_{EC}}{I_p^2}$$

(4)

causes the eddy current losses ($P_{EC}$), which are expressed by IEEE Standard C57.110-2018 as follows:

$$P_{EC}=P_{ECN} · {\displaystyle \sum }_{h=1}^{\infty }{h}^2{\left(\frac{I_{ph}}{I_{pN}}\right)}^2$$

(5)

where $P_{ECN}$ is the value of the eddy current losses at the nominal frequency ($f_N=50-60 \mathrm{Hz}$), $I_{ph}$ is the RMS value of the harmonic of order $h=f_h/f_1$ of the transformer’s primary currents, and $I_{pN}$ is the rated RMS value of these currents.

The short-circuit resistance $R_{OSL}$ is obtained by L. Sima et al. from Equation (2) as:

$$R_{OSL}=R_k-R_{DC}-R_{EC}$$

(6)

As explained by L. Sima et al. [36], $R_{OSL}$ is not defined in the primary or secondary windings, unlike the previous two ($R_{DC}$ and $R_{EC}$), since its losses do not cause additional heating in the windings, but in the tank and other metallic parts of the transformers.

Reference [36] constitutes the first approximation in the technical literature in the study of short-circuit resistances of transformers feeding non-linear loads according to IEEE Standard C57.110-2018.

The direct relationship between the short-circuit resistances and the load losses of the three-phase transformers, implicit in Equations (1) and (2), allows the use of these resistances as indicators for monitoring the operating status of these machines, as well as being sufficient to determine deterioration caused by overheating. To do this, the short-circuit resistance expressions must provide the correct values of the load losses in each phase of the windings, regardless of the type of currents and their RMS values in the three phases.

The short-circuit resistances referred to as “primary” by L. Sima et al. ($R_k$) can determine the total load losses of three-phase transformers according to IEEE Standard C57.110-2018; however, they do not correctly determine the load losses in each phase of the transformer, as will be demonstrated in this article. This is because the expressions for the short-circuit resistances of L. Sima et al. are established using both the total load losses included in IEEE Standard C57.110-2018 [10] and the combined RMS values of the primary currents ($I_p$).

To avoid the errors that these two technologies introduce in the calculation of the load losses of each phase of the three-phase transformers, the expressions for the effective short-circuit resistances of each phase ($R_{cc,z}$) have been developed in the second section of this article (Materials and Methods) referring to the secondary winding of the transformer. These resistances constitute the main novelty of this paper and are unpublished in the technical literature. The expressions of the resistances $R_{cc,z}$ have been established by imposing the condition that they must dissipate the actual load losses of each phase of the transformer according to IEEE Standard C57.110-2018 ($P_{cc,z}$), when each phase’s secondary currents ($I_{sz}$) flow through them. Because IEEE Standard C57.110-2018 [10] does not include the expressions for $P_{cc,z}$, before developing the resistances $R_{cc,z}$, the expressions for the phase load losses ($P_{cc,z}$) have been obtained by adapting the expressions of the total load losses included in this standard [5,10] as another novelty of the article.

Likewise, in the second section of the article, the expressions for the effective short-circuit resistance of the transformer ($R_{cc,ef}$) have been developed, referring to the secondary winding. These short-circuit resistances have been defined following the same procedure used by L. Sima et al. in [36], but using the secondary combined currents ($I_s$) instead of the primary currents ($I_p$). That is, $R_{cc,ef}$ are the short-circuit resistances of L. Sima et al. ($R_k$) referred to as secondary ($R_k^{\prime }$). Thus, $R_{cc,ef}$ and $R_k$ have the same properties and disadvantages.

In the third section of the article (Results), the short-circuit resistances referred to as secondary ($R_{cc,z}$ and $R_{cc,ef}$) developed in Section 2, are calculated from the measurements carried out by a Fluke 435 Series II analyzer on the secondary of a 630 kVA, immersed in oil, and three-phase distribution transformer, which supplies a moderately distorted residential area. In the fourth section (Discussion), the effective short-circuit resistances $R_{cc,z}$, and $R_{cc,ef}$ are used to calculate the load losses in each phase ($P_{cc,z}$) and total ($P_{cc}$) in the analyzed distribution transformer of Section 3. The results demonstrate that both short-circuit resistances determine the same values of total load losses ($P_{cc}$) as IEEE Standard C57.110-2018; however, only the load losses calculated with $R_{cc,z}$ match the load losses determined in each phase applying the standard. The use of $R_{cc,ef}$ and $R_k$ resistances determine errors in the values of $P_{cc,z}$ greater than 16% for the analyzed distribution transformer. The fifth section summarizes the main conclusions.

2. Materials and Methods

The expressions for the total load losses of three-phase transformers ($P_{cc}$) with non-linear loads that were obtained in [5] by adaptation of IEEE Standard C57.110-2018 are used in this section to establish the transformer load losses for each phase ($P_{cc,z}$). Based on these losses, the expressions for the effective short-circuit resistances of each phase ($R_{cc,z}$) and the effective short-circuit resistance of the transformer ($R_{cc,ef}$) are developed.

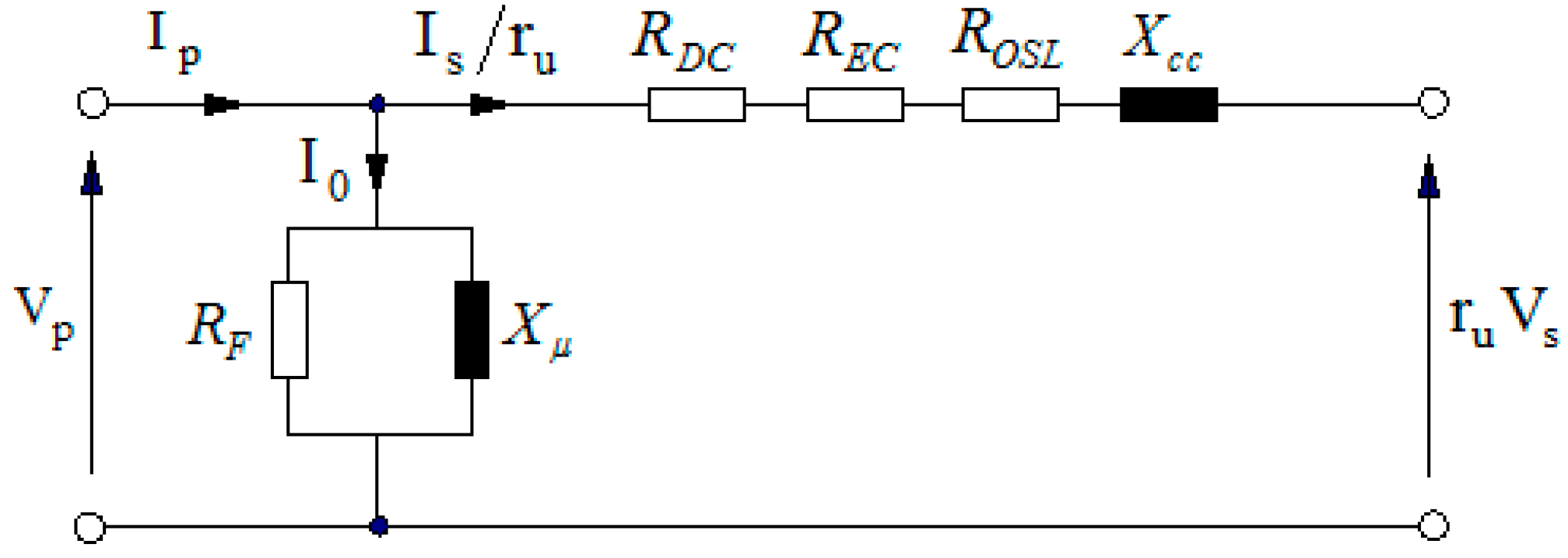
2.1. Load Losses of Three-Phase Transformers Adapted from IEEE Standard C57.110-2018

According to IEEE Standard C57.110-2018 [10], the load losses ($P_{cc}$) of three-phase transformers are expressed as the sum of three losses:

$$P_{cc}=P_{DC}+P_{EC}+P_{OSL}$$

(7)

Each of these losses is due to three different phenomena, which occur because of the circulation of currents through the transformer windings:

• $P_{DC}$ are the power losses by Joule effect that would be produced when direct currents circulate through the transformer windings [37].
• $P_{EC}$ are the eddy current losses due to the skin phenomenon in the conductors of the coils.
• $P_{OSL}$ are the other stray losses that originate in the tank and other metallic parts of the transformer due to electromagnetic induction.

The direct current losses ($P_{DC}$) are determined, in general, as follows [5]:

$$P_{DC}=\frac{1}{3}·P_{DCN}{\displaystyle \sum }_{z=A,B,C}{\displaystyle \sum }_{h_z=1}^{h_{z,max}}{\left(\frac{I_{hz}}{I_{sN}}\right)}^2$$

(8)

where

• $P_{DCN}$ are the nominal losses in direct current.
• $I_{sN}$ is the rated RMS value of the secondary currents of the transformer.
• $I_{hz}$ is the RMS value of the harmonic of order $h_z=f_{hz}/f_1$ ($f_{hz}$ = harmonic frequency, $f_1$ = 50–60 Hz is the fundamental frequency) of each phase ($z=A,B,C$) of the secondary currents.
• $h_{z,max}$ is the order of the highest-frequency harmonic used in the calculation.

The losses caused by the skin effect ($P_{EC}$) are proportional to the square of the RMS values of each phase harmonic current ($I_{hz}$) and frequency according to the following expression [5]:

$$P_{EC}=\frac{1}{3}·P_{ECN}{\displaystyle \sum }_{z=A,B,C}{\displaystyle \sum }_{h_z=1}^{h_{z,max}}{h}_z^2·{\left(\frac{I_{hz}}{I_{sN}}\right)}^2$$

(9)

where $I_{sN}$, $I_{hz}$, $h_z$ and $h_{z,max}$ have the meanings previously indicated and $P_{ECN}$ represents the nominal losses due to the skin effect, measured with the nominal secondary currents ($I_{sN}$), at the fundamental frequency.

The losses produced by the eddy currents induced in the metallic parts of the transformer ($P_{OSL}$) are obtained as follows [5]:

$$P_{OSL}=\frac{1}{3}·P_{OSLN}{\displaystyle \sum }_{z=A,B,C}{\displaystyle \sum }_{h_z=1}^{h_{z,max}}{h}_z^{0.8}·{\left(\frac{I_{hz}}{I_{sN}}\right)}^2$$

(10)

where $P_{OSLN}$ is the nominal value of these losses, measured when the transformers operate with the nominal secondary currents ($I_{sN}$), at the fundamental frequency.

Transformer manufacturers usually provide nominal load losses ($P_{DCN}$, $P_{ECN}$, $P_{OSLN}$). Their sum is equal to the nominal load losses of the transformer ($P_{ccN}=P_{DCN}+P_{ECN}+P_{OSLN}$) included in the manufacturer catalogues. However, sometimes manufacturers do not provide the individual values of $P_{ECN}$ and $P_{OSLN}$, but rather provide them together ($P_{SLN}=P_{ECN}+P_{OSLN}$). On these occasions, IEEE Standard C57.90^TM [38] establishes that $P_{ECN}=0.33·P_{SLN}$ and $P_{OSLN}=0.66·P_{SLN}$ in oil-immersed transformers, $P_{ECN}=0.66·P_{SLN}$ and $P_{OSLN}=0.33·P_{SLN}$ in dry-type transformers.

Substituting expressions (8)–(10) in Equation (7), the total load losses ($P_{cc}$) adapted from IEEE Standard C57.110-2018 [10] for three-phase transformers with unbalanced and non-linear loads can be calculated as [5]:

$$P_{cc}={\displaystyle \sum }_{z=A,B,C}{P}_{cc,z}=\frac{1}{3}·{\displaystyle \sum }_{z=A,B,C}{\displaystyle \sum }_{h_z=1}^{h_{z,max}}\left(P_{DCN}+P_{ECN}·h_z^2+P_{OSN}·h_z^{0.8}\right)·{\left(\frac{I_{hz}}{I_{sN}}\right)}^2$$

(11)

From the above expression, the load losses of each phase ($z=A,B,C$) can be determined as follows:

$$P_{cc,z}=\frac{1}{3}·{\displaystyle \sum }_{h_z=1}^{h_{z,max}}\left(P_{DCN}+P_{ECN}·h_z^2+P_{OSLN}·h_z^{0.8}\right)·{\left(\frac{I_{hz}}{I_{sN}}\right)}^2$$

(12)

2.2. Short-Circuit Resistances Referred to Secondary of Three-Phase Transformers

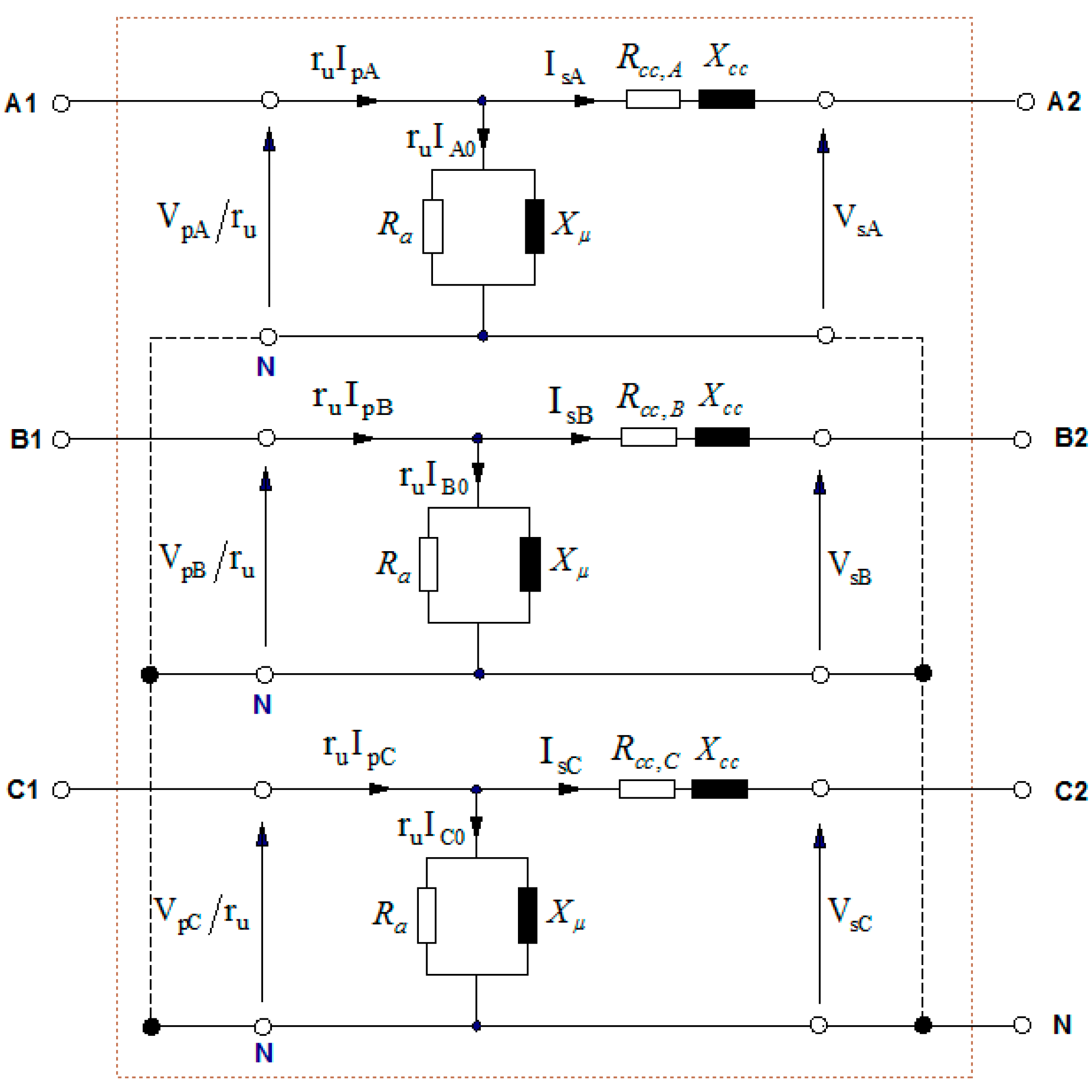
2.2.1. Effective Short-Circuit Resistance for Each Phase of the Transformer

The effective short-circuit resistances ($R_{cc,z}$) referred to as the secondary could be defined for each phase ($z=A,B,C$) of the transformer as those that would produce the same load losses in each phase ($P_{cc,z}$), that is:

$$P_{cc,z}=R_{cc,z}·{\displaystyle \sum }_{h_z=1}^{h_{z,max}}{I}_{hz}^2$$

(13)

Matching the last equation and (12), it turns out that:

$$R_{cc,z}=R_{DCN}+R_{ECN}\frac{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{h}_z^2·I_{hz}^2}{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{I}_{hz}^2}+R_{OSLN}\frac{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{h}_z^{0.8}·I_{hz}^2}{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{I}_{hz}^2}$$

(14)

being the loss coefficients of each phase ($z=A,B,C$) caused by the eddy currents in the windings ($F_{HL}^z$) and in other parts of the transformer ($F_{HL-STR}^z$), respectively,

$$F_{HL}^z=\frac{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{h}_z^2·I_{hz}^2}{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{I}_{hz}^2} F_{HL-STR}^z=\frac{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{h}_z^{0.8}·I_{hz}^2}{{{\displaystyle \sum }}_{h_z=1}^{h_{z,max}}{I}_{hz}^2}$$

(15)

and $R_{DCN}$, $R_{ECN}$, and $R_{OLSN}$ are the nominal short-circuit resistances, which characterize the nominal direct current losses ($P_{DCN}$), the nominal eddy current losses ($P_{ECN}$), and the rated other stray losses ($P_{OSLN}$), according to the following expressions.

$$R_{DCN}=\frac{P_{DCN}}{3·I_{sN}^2} R_{ECN}=\frac{P_{ECN}}{3·I_{sN}^2} R_{OSLN}=\frac{P_{OSLN}}{3·I_{sN}^2}$$

(16)

Therefore,

$$R_{cc,z}=R_{DCN}+R_{ECN}·F_{HL}^z+R_{OSLN}·F_{HL-STR}^z=R_{DCN}+R_{EC,z}+R_{OSL,z}$$

(17)

where

$$R_{EC,z}=R_{ECN}·F_{HL}^z R_{OSL,z}=R_{OSLN}·F_{HL-STR}^z$$

(18)

are the short-circuit resistances due to the phenomena of the eddy current ($R_{EC,z}$) and other stray losses ($R_{OSL,z}$) in each phase of the transformer. The values depend on the order ($h_z$) and the RMS values ($I_{hz}$) of the current harmonics of each secondary phase, as observed in Equation (14). Therefore, the short-circuit resistances $R_{EC,z}$ and $R_{OSL,z}$ are responsible for:

• the increase in the short-circuit resistance of the transformer feeding non-linear loads, and
• the different values of the short-circuit resistances in each phase of the transformer with non-linear loads, not foreseen by L. Sima et al. in Equation (2).

From Equations (14) and (17), it can also be seen that the direct current short-circuit resistance ($R_{DCN}$) is independent of the frequencies and RMS values of the harmonic currents.

The effective short-circuit resistance of each phase ($R_{cc,z}$) is a physical parameter, since its values accurately determine the load losses originating in each phase of the transformer ($P_{cc,z}$), which can be interchangeably calculated with Equations (12) and (13). These short-circuit resistances make it possible to calculate the total load losses of the three-phase transformers according to the following expression derived from (11).

$$P_{cc}={\displaystyle \sum }_{z=A,B,C}{P}_{cc,z}={\displaystyle \sum }_{z=A,B,C}\left(R_{cc,z}·{\displaystyle \sum }_{h_z=1}^{h_{z,max}}{I}_{hz}^2\right)$$

(19)

Figure 2 shows the actual operating model of the transformer based on the effective short-circuit resistance of each phase. The elements included in this equivalent model of the three-phase transformer have the following physical meanings.

-

$R_{cc,A}, R_{cc,B}$ and $R_{cc,C}$ are the effective short-circuit resistances referring to each phase of the secondary, which represents the load losses in each phase of the three-phase transformers ($P_{cc,A}, P_{cc,B}, P_{cc,C}$) according to IEEE Standard C57.110-2018 [10], caused by the circulation of currents ($I_{sA}, I_{sB}, I_{sC}$) through each phase of the secondary winding. These resistances usually have different values in each phase when currents are distorted.

-

$X_{cc}$ is the short-circuit reactance referred to as the secondary, representing the transformer’s scattered magnetic fluxes. This reactance has the same value in the three phases, because it depends only on the harmonic frequencies, not the current RMS values.

-

$R_a$ is the resistance that represents the transformer’s core losses. This resistance has the same value in each phase because it is not practically affected by the voltage harmonic frequencies.

-

$X_{\mu }$ is the magnetic reactance, which represents the main magnetic flux of the transformers and drives its electromotive forces. This reactance usually has the same values in each phase because of the same reasons indicated for $X_{cc}$.

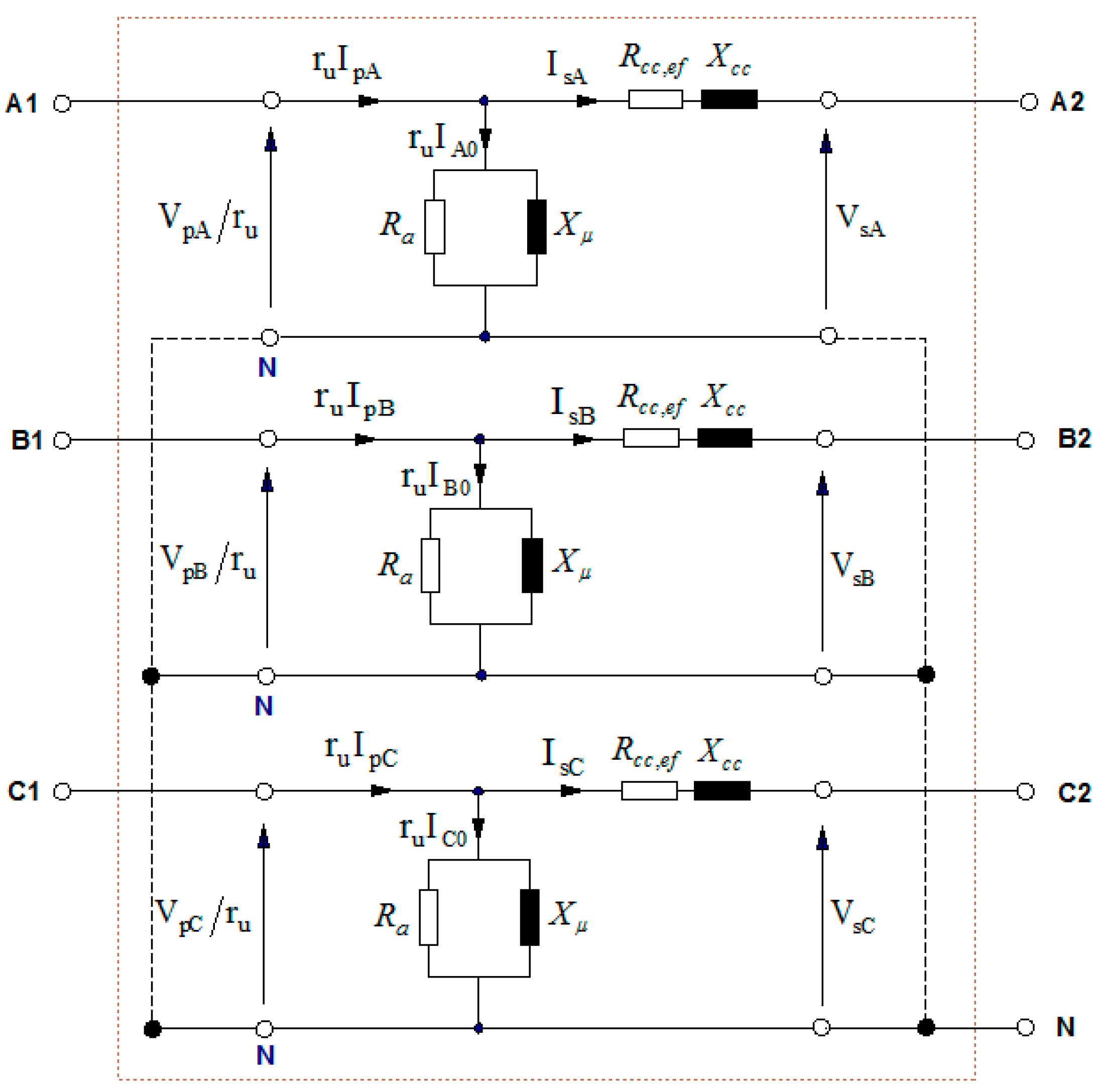
2.2.2. Effective Short-Circuit Resistance of the Transformer

Similarly to the short-circuit resistances of each phase ($R_{cc,z}$), an effective short-circuit resistance of the transformer ($R_{cc,ef}$) can be defined. The short-circuit resistance $R_{cc,ef}$ determines the total load losses of the transformer according to the following expression:

$$P_{cc}=R_{cc,ef}·{\displaystyle \sum }_{h=1}^{h_{max}}{I}_h^2$$

(20)

$I_h$ being the combined RMS value of the harmonic currents of order $h_z$:

$$I_h=\sqrt{{\displaystyle \sum }_{z=A,B,C}{I}_{hz}^2}$$

(21)

Matching expressions (11) and (20) and considering that there are usually harmonics of the same frequencies in the three phases of the transformer, the expression for the effective short-circuit resistance of the transformer ($R_{cc,ef}$) is obtained, as follows:

$$R_{cc,ef}=R_{DCN}+R_{ECN}\frac{{{\displaystyle \sum }}_{h=1}^{h_{max}}{h}^2·I_h^2}{{{\displaystyle \sum }}_{h=1}^{h_{max}}{I}_h^2}+R_{OSN}\frac{{{\displaystyle \sum }}_{h=1}^{h_{max}}{h}^{0.8}·I_h^2}{{{\displaystyle \sum }}_{h=1}^{h_{max}}{I}_h^2}=R_{DCN}+R_{ECN}·F_{HL}+R_{OSN}·F_{HL-STR}$$

(22)

where

$$F_{HL}=\frac{{{\displaystyle \sum }}_{h=1}^{h_{max}}{h}^2·I_h^2}{{{\displaystyle \sum }}_{h=1}^{h_{max}}{I}_h^2} F_{HL-STR}=\frac{{{\displaystyle \sum }}_{h=1}^{h_{max}}{h}^{0.8}·I_h^2}{{{\displaystyle \sum }}_{h=1}^{h_{max}}{I}_h^2}$$

(23)

are the transformer loss factors included in IEEE Standard C57.110-2018.

According to Equation (22), the effective short-circuit resistance of the transformer ($R_{cc,ef}$) usually has the same values in the three phases (Figure 3), because this parameter has been established using the values of the combined currents ($I_h$). Thus, the circulation of the phase currents through these resistances gives values of the losses in each phase that are different from those calculated with Equations (12) and (13). This result shows that $R_{cc,ef}$ is a merely mathematical parameter and that the three-phase transformer model based on these resistances (Figure 3) is not related to the actual operation of these machines.

For the above reasons, the resistances $R_{cc,ef}$ can only be used to calculate the total load losses of the transformers ($P_{cc}$), according to expression (20).

The effective short-circuit resistance of the transformer ($R_{cc,ef}$) coincides with the short-circuit resistance of L. Sima et al. ($R_k$) [36], referred to as the secondary ($R_k^{\prime }$), i.e.,

$$R_{cc,ef}=\frac{R_k}{r_u^2}=R_k^{\prime }$$

(24)

Therefore, $R_k$ has the same drawbacks found for $R_{cc,ef}$.

3. Results

The expressions for the losses and short-circuit resistances developed in Section 2.2 are used in this section to calculate the values of the load losses and short-circuit resistances of a 630 kVA distribution transformer when feeding to the low-voltage (LV) installations of residential consumers (homes) in a town near the city of Valencia (Spain). The RMS values and harmonic content of the currents absorbed by these installations were recorded by a Fluke 435 Series II analyzer, which was connected to the secondary of the transformer. The measurements were carried out at one-hour intervals over a week between 7 November and 13 November 2022.

The distribution transformer is oil-immersed with Dyn11 connections from the manufacturer Ormazabal, with nominal features summarized in

Table 1. Ratings of the distribution transformer from the manufacturer Ormazabal.

POWER (kVA)	${\mathit{P}}_{\mathit{D}\mathit{C}\mathit{N}}$ (W)	${\mathit{P}}_{\mathit{E}\mathit{C}\mathit{N}}$ (W)	${\mathit{P}}_{\mathit{O}\mathit{S}\mathit{N}}$ (W)	Secondary Rated Current (A)	Transformation Ratio (${\mathit{r}}_{\mathit{u}}$)
630	5900	200	400	866	24,000/420 V

.

The currents measured by the Fluke analyzer in the secondary phases of the transformer confirm the presence of unbalanced and non-linear loads in the residential installations. The imbalances are deduced from the RMS values of the fundamental-frequency currents recorded in each phase ($z=A,B,C$) throughout the 24 h of 11 November 2022 (Figure 4a). The non-linear loads are denoted by the total harmonic distortion (Figure 4b) of the currents measured in each secondary phase ($THDi{\%}_z$) by the Fluke analyzer as the quotient between the RMS value of all harmonics without the fundamental and the total RMS value of that phase current.

Table 2. RMS values of the harmonic currents at 6:55 PM on 11 November 2022.

Frequency (Hz)	Harmonic Order (h)	Secondary Currents (A)
		A-Phase	B-Phase	C-Phase	Combined (${\mathit{I}}_{\mathit{h}}$)
50	1	278.345	403.233	305.503	577.412
100	2	14.32	9.571	13.518	21.895
150	3	4.093	10.877	2.129	11.815
200	4	14.884	3.562	13.036	20.103
250	5	33.541	16.762	6.983	38.141
300	6	16.088	7.711	16.159	24.070
350	7	19.980	18.350	10.392	29.050
400	8	22.621	15.445	23.481	36.078
450	9	20.366	19.781	22.514	36.234
500	10	14.689	11.486	12.990	22.725
550	11	10.203	2.713	5.895	12.091
600	12	10.452	4.591	9.289	14.717
650	13	4.393	7.096	13.158	15.581
700	14	11.194	2.962	12.144	16.780
750	15	14.002	4.085	15.535	21.309
800	16	14.919	5.887	12.204	20.153
850	17	33.999	22.709	38.182	55.942
900	18	21.875	11.785	20.646	32.305
950	19	10.553	7.124	10.106	16.255
1000	20	7.195	2.759	8.437	11.426
1050	21	7.697	3.225	8.727	12.075
1100	22	7.760	1.113	9.491	12.310
1150	23	9.949	4.723	9.599	14.609
1200	24	13.225	3.168	12.903	18.746
1250	25	11.977	9.367	9.618	17.991
TOTAL		289.75	406.50	314.23	589.86

and

Table 3. RMS values of the harmonic currents at 0:55 AM on 11 November 2022.

Frequency (Hz)	Harmonic Order (h)	Secondary Currents (A)
		A-Phase	B-Phase	C-Phase	Combined (${\mathit{I}}_{\mathit{h}}$)
50	1	195.165	195.462	226.837	357.4210
100	2	13.411	16.062	15.774	26.2042
150	3	17.034	12.235	29.030	35.8133
200	4	16.350	17.177	20.707	31.4825
250	5	29.179	21.472	14.281	38.9411
300	6	6.029	14.787	8.218	17.9593
350	7	12.464	14.051	20.427	27.7497
400	8	7.344	6.755	6.903	12.1332
450	9	7.639	7.147	10.946	15.1409
500	10	3.483	6.534	2.550	7.8311
550	11	13.709	5.117	4.123	15.2026
600	12	3.437	4.745	3.060	6.6099
650	13	3.948	4.927	6.909	9.3593
700	14	1.423	2.793	0.139	3.1377
750	15	4.454	4.767	3.878	7.5895
800	16	1.929	1.979	2.086	3.4625
850	17	1.667	1.766	2.033	3.1671
900	18	1.998	1.404	1.454	2.8420
950	19	1.317	1.087	0.936	1.9473
1000	20	1.118	0.910	0.902	1.7004
1050	21	0.937	0.721	0.619	1.3345
1100	22	0.882	0.949	0.541	1.4040
1150	23	1.002	0.819	0.883	1.5666
1200	24	1.134	0.924	0.991	1.7668
1250	25	0.772	0.902	0.633	1.3454
TOTAL		200.622	200.107	232.255	366.38

summarize the RMS values of the first 25 harmonics, including the fundamental, of the currents recorded in the three secondary phases of the transformer at 6:55 p.m. and 0:55 a.m. on 11 November 2022. Based on the RMS values of the fundamental-frequency currents in the three phases of the secondary (Figure 4a) on 11 November 2022, it is observed that the transformer operates with more significant imbalances at 6:55 p.m. (Table 2) than at 0:55 a.m. (Table 3).

In addition, these residential installations were similarly distorted in both analyzed cases, with values of $THDi{\%}_z$ in each phase ($z=A,B,C$), as follows (Figure 4b): 24.17%, 17.63%, and 25.36%, respectively, at 6:55 p.m. and 27.81%, 24.32%, and 24.18%, respectively, at 0:55 a.m. (Table 2 and Table 3).

Table 4. Loss factors of each phase and total corresponding to the cases analyzed.

	A-Phase		B-Phase		C-Phase		Transformer
	${\mathit{F}}_{\mathit{H}\mathit{L}}$	${\mathit{F}}_{\mathit{H}\mathit{L}-\mathit{S}\mathit{T}\mathit{R}}$	${\mathit{F}}_{\mathit{H}\mathit{L}}$	${\mathit{F}}_{\mathit{H}\mathit{L}-\mathit{S}\mathit{T}\mathit{R}}$	${\mathit{F}}_{\mathit{H}\mathit{L}}$	${\mathit{F}}_{\mathit{H}\mathit{L}-\mathit{S}\mathit{T}\mathit{R}}$	${\mathit{F}}_{\mathit{H}\mathit{L}}$	${\mathit{F}}_{\mathit{H}\mathit{L}-\mathit{S}\mathit{T}\mathit{R}}$
Case 1 (Table 2)	14.6768	1.4645	3.4485	1.09	12.9388	1.3815	8.8511	1.2631
Case 2 (Table 3)	3.07619	1.15411	2.70159	1.12849	2.37866	1.11319	2.68413	1.13002

summarizes the values of the loss factors corresponding to the two cases analyzed: (1) consumption at 6:55 PM, with significant current imbalances (Table 2), and (2) consumption at 0:55 AM, with slight current imbalances (Table 3). The loss factors of each phase and the total of the transformer have been calculated according to Equations (15) and (23), respectively.

Table 5. Transformer short-circuit resistances corresponding to the cases analyzed.

	${\mathit{R}}_{\mathit{c}\mathit{c},\mathit{A}}$ ($\mathbf{m}\mathsf{\Omega }$)	${\mathit{R}}_{\mathit{c}\mathit{c}, \mathit{B}}$ ($\mathbf{m}\mathsf{\Omega }$)	${\mathit{R}}_{\mathit{c}\mathit{c},\mathit{C}}$ ($\mathbf{m}\mathsf{\Omega }$)	${\mathit{R}}_{\mathit{c}\mathit{c}, \mathit{e}\mathit{f}}$ ($\mathbf{m}\mathsf{\Omega }$)
Case 1 (Table 2)	4.1874	3.1227	4.1802	3.6337
Case 2 (Table 3)	3.1010	3.0672	3.0317	3.0619

shows the values of the short-circuit resistances $R_{cc,z}$ and $R_{cc,ef}$, calculated with Equations (17) and (22), respectively, with the values of the nominal resistances $R_{DCN}=2.262 \mathrm{m}\mathsf{\Omega }$, $R_{ECN}=0.088 \mathrm{m}\mathsf{\Omega }$, and $R_{OSLN}=0.177 \mathrm{m}\mathsf{\Omega }$, obtained from (16), being the nominal secondary current $I_{sN}=866 \mathrm{A}$ (Table 1).

From Table 4 and Table 5, obtained for similarly distorted loads as those indicated in Table 2 and Table 3, it is verified that:

(1)

the values of loss factors and short-circuit resistances increase with the imbalances of the current harmonics, and

(2)

the effective short-circuit resistances ($R_{cc,z}$) have values different in each phase ($z=A,B,C$) and are different from the effective short-circuit resistance of the transformer ($R_{cc,ef}$); these differences increase with the imbalances in the harmonics, as noted in case 1.

4. Discussion

In this section, our short-circuit resistances of three-phase transformers have been compared with those developed by L. Sima et al. [36], which is the only known work in the technical literature that develops an expression for the short-circuit resistance of transformers based on IEEE Standard C57.110-2018.

Table 6. RMS values, in amperes (A), of transformer secondary and primary currents corresponding to the cases analyzed.

	${\mathit{I}}_{\mathit{s}\mathit{A}}$	${\mathit{I}}_{\mathit{s}\mathit{B}}$	${\mathit{I}}_{\mathit{s}\mathit{C}}$	${\mathit{I}}_{\mathit{s}}$	${\mathit{I}}_{\mathit{p}}$
Case 1 (Table 2)	289.75	406.50	314.23	589.86	10.322
Case 2 (Table 3)	200.622	200.107	232.255	366.38	6.411

summarizes the RMS values of the currents of each secondary phase ($I_{sA}, I_{sB}, I_{sC}$), as well as the combined RMS value of the currents of the three phases of the secondary ($I_s$) and the primary ($I_p$). The RMS values of the currents of each secondary phase ($I_{sA}, I_{sB}, I_{sC}$) were obtained by the Fluke 435 Series II analyzer and are summarized in Table 2 and Table 3 for each of the analyzed cases. The combined RMS value of the three secondary phases ($I_s$) is also indicated in Table 2 and Table 3, and was obtained as follows:

$$I_s=\sqrt{I_{sA}^2+I_{sB}^2+I_{sC}^2}$$

(25)

The combined RMS values of the currents of the primary phases ($I_p$) indicated in Table 6 were calculated as:

$$I_p\approx \frac{I_s}{r_u}$$

(26)

where $r_u\approx V_p/V_{s0}$ is the transformation ratio of the transformer.

It is observed in

Table 7. Transformer load losses, in watts (W), using IEEE Standard C57.110 and the effective short-circuit resistances in the two analyzed cases.

	Total Losses Using IEEE Std.C57.110	Total Losses Using ${\mathit{R}}_{\mathit{c}\mathit{c},\mathit{e}\mathit{f}}$	Losses Using ${\mathit{R}}_{\mathit{c}\mathit{c},\mathit{z}}$
			A-Phase	B-Phase	C-Phase	Total
Case 1 (Table 2)	1264.321	1264.321	351.558	516.005	396.758	1264.321
Case 2 (Table 3)	411.011	411.011	124.814	122.658	163.539	411.011

that the total load losses have the same values in each of the analyzed cases (1264.321 W, in case 1, and 411.011, in case 2), either using IEEE Standard C57.110-2018 with Equation (11), or applying Equation (19) with the effective short-circuit resistances of each phase ($R_{cc,A}, R_{cc,B}, R_{cc,C}$), or using Equation (20), with the effective short-circuit resistance of the transformer ($R_{cc,ef}$).

The short-circuit resistance referred to the primary $R_k$ developed by L. Sima et al. relates the total load losses defined by IEEE Standard C57.110 with the primary current ($I_p$), as indicated in Equation (2). Substituting the calculated values of the total load losses according to IEEE Standard C57.110, included in Table 7, and the RMS value of the combined primary currents, indicated in Table 6, the short-circuit resistances of L. Sima et al. referred to the primary ($R_k$) and the secondary ($R_k^{\prime }$) have the values indicated in

Table 8. Short-circuit resistances of L. Sima in the cases analyzed.

	Referred to Primary (${\mathit{R}}_{\mathit{k}}, \mathsf{\Omega }$)	Referred to Secondary (${\mathit{R}}_{\mathit{k}}^{\prime }, \mathbf{m}\mathsf{\Omega }$)
Case 1 (Table 2)	11.865	3.6337
Case 2 (Table 3)	9.998	3.0619

.

Comparing the values of the short-circuit resistance of L. Sima et al., referred to as the secondary ($R_k^{\prime }$), indicated in Table 8, with those of our effective short-circuit resistance of the transformer ($R_{cc,ef}$), summarized in Table 5, it is noted that they are identical. This result shows that our $R_{cc,ef}$ is the L. Sima short-circuit resistance referred to as the secondary of the transformer, as had been advanced in Equation (24).

Table 9. Load losses in watts (W), and relative loss errors calculated in each phase of the transformer with $R_{cc,ef}$ instead of with $R_{cc,A}, R_{cc,B}, R_{cc,C}$.

	Load Losses (W)				Relative Loss Errors (%)
	A-Phase	B-Phase	C-Phase	Total	A-Phase	B-Phase	C-Phase
Case 1 (Table 2)	305.073	600.448	358.800	1264.321	13.222	−16.365	9.567
Case 2 (Table 3)	123.239	122.607	165.165	411.011	1.262	0.042	−0.994

shows the values of the load losses that would be obtained in each phase of the transformer using the effective short-circuit resistance $R_{cc,ef}$ (or the short-circuit resistance of L. Sima—$R_k^{\prime }$) instead of the effective short-circuit resistances of each phase ($R_{cc,A}, R_{cc,B}, R_{cc,C}$).

Comparing the values of the losses in each phase indicated in Table 7 with those shown in Table 9, essential differences are observed at 6:55 PM of greater than 16%. These high errors in the calculation of the load losses of each phase confirm that the resistances $R_{cc,ef}$ and $R_k$ are parameters not related to the energy phenomena that occur in the phases of the transformer, and thus these resistances should not be used to calculate the load losses of each phase of the transformers.

Specifically, it has been verified in this section that:

(1)

The load losses calculated with our short-circuit resistances, referred to as the secondary of the three-phase transformers, developed in Section 2.2, are equal to those resulting from applying the IEEE Standard C57.110-2018.

(2)

The short-circuit resistance of L. Sima, referred to as secondary ($R_k^{\prime }$), coincides with our effective short-circuit resistance ($R_{cc,ef}$), referred to as the primary of the transformer.

(3)

In general, the effective short-circuit resistance of the transformer ($R_{cc,ef}$) and therefore the resistance of L. Sima et al. cannot be used to calculate the load losses of each phase.

5. Conclusions

Efficiency, warm-up, and power transmission capacity, among other quantities that determine the proper steady-state operation of electrical transformers, depend on the values of load losses. In three-phase transformers, load losses can be calculated either by applying IEEE Standard C57.110 or by using short-circuit resistances derived from that standard. The last procedure has been used by L. Sima et al. with the development of their short-circuit resistance, referred to as the primary ($R_k$).

In this article, two types of short-circuit resistance referring to the secondary have been developed, deduced from IEEE Standard C57.110: (1) the effective short-circuit resistance of each phase ($R_{cc,z}$) and (2) the effective short-circuit resistance of the transformer ($R_{cc,ef}$). The total load losses of three-phase transformers ($P_{cc}$) can be calculated by any of these resistances, which have their own properties and applications.

In our opinion:

• The effective short-circuit resistances of the transformer ($R_{cc,ef}$) and therefore the short-circuit resistances of L. Sima et al. ($R_k$) are mathematical parameters unrelated to the energy phenomena of the transformer. The use of these resistances gives rise to errors in the calculation of the load losses in the transformer phases ($P_{cc,z}$), which increase with the harmonic imbalances. This fact has been verified in the operation of the transformer of an actual residential distribution network feeding two very differently unbalanced loads, both with the same $THDi\%\approx 25\%$. We have verified that if the loads are slightly unbalanced, the errors in the calculation of $P_{cc,z}$ barely exceed 1% in some phases, while with moderately unbalanced loads, the errors exceed 16% (Table 9).
• Based on the above, the effective short-circuit resistances of the transformer ($R_{cc,ef}$) can only be used to calculate the total load losses of three-phase transformers according to IEEE Standard C57.110, but their use is not suitable for monitoring the operation of three-phase transformers.
• The effective short-circuit resistances of each phase ($R_{cc,z}$) can be used to monitor the operating status of three-phase transformers. Both resistances are related to the energy phenomena that manifest in the transformer, since with them, the load losses of each phase ($P_{cc,z}$) and total ($P_{cc}$) of the transformer can be accurately calculated.
• The effective short-circuit resistances of each phase ($R_{cc,z}$) define the accurate operating model of three-phase transformers, represented in Figure 2.

6. Patents

This article has been based on our patent P202330968—“Use of short-circuit resistors, procedure and device for monitoring the operating state of a three-phase transformer in service”—lodged with the Spanish Patent and Trademark Agency.