Decoupler-Based Feedback Control Strategy for Interlinking Converter in a Hybrid Microgrid
Abstract
:1. Introduction
- Mode 1—ideal mode: both subgrids are able to meet their respective demands independently.
- Mode 2—AC to DC power transfer: the DC source is unable to meet its demand, and the additional requirement will be transferred through the IC from the AC side.
- Mode 3—DC to AC power transfer: the AC source is unable to meet its demand, and the additional requirement will be transferred through the IC from the DC side.
- To design and develop an efficient feedback-based decoupling control system for a hybrid microgrid that can address the instability in the interlinking converter due to cross-coupling between the inner control loops in the inverter section.
- To design the compensators for the control loops and develop the overall transfer function model of the inverter with a filter section using the direct synthesis method.
- To design an enhanced droop control strategy for the hybrid microgrid based on a normalization scheme by integrating with the decoupling-based control system to ensure accurate active power sharing between the subgrids subject to load transients.
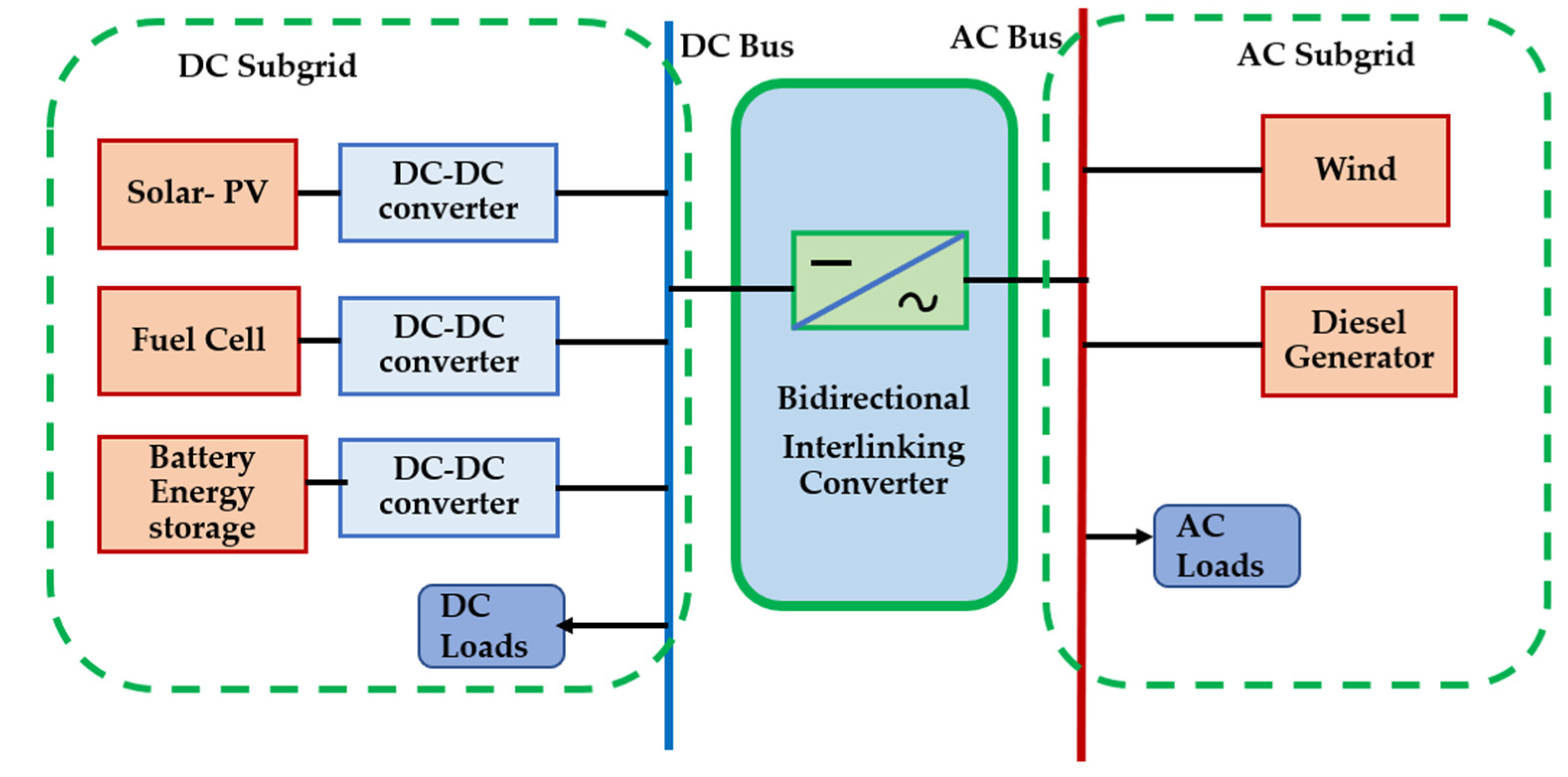
2. Modeling of the Proposed System
2.1. AC Subgrid
2.2. DC Subgrid
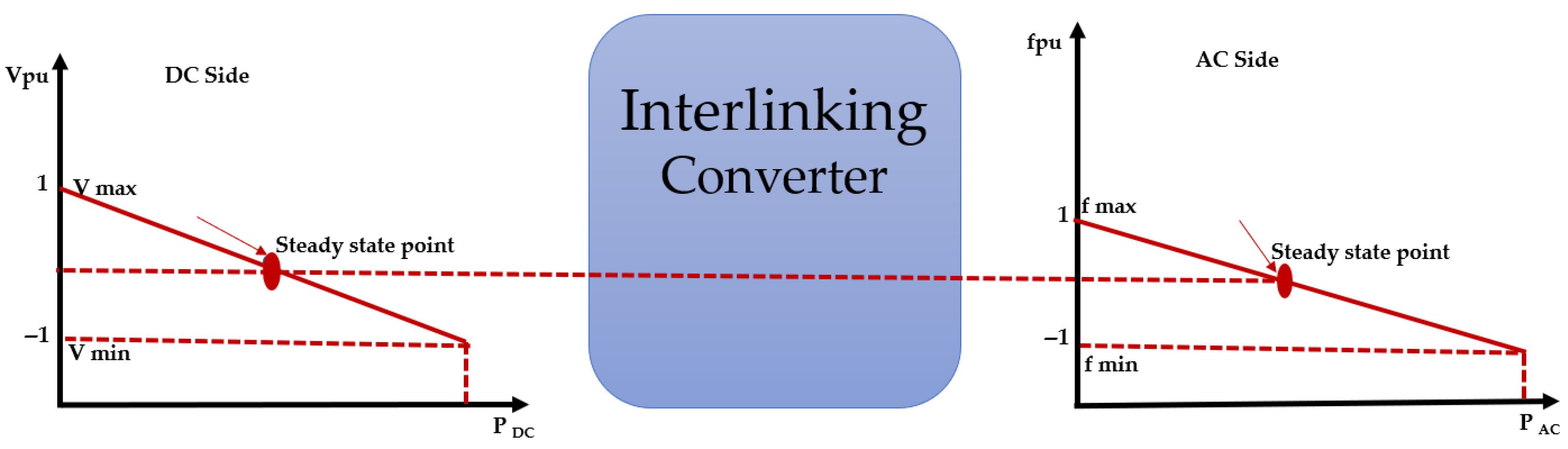
- When is less than , the condition indicates that the DC subgrid needs active power support, and the IC transfers a definite amount of power from the AC sub-grid to the DC subgrid, settling the merged characteristics at the steady-state points indicated by the dotted line in Figure 3.
- When is less than , the condition indicates that the AC subgrid needs active power support, and the IC transfers a definite amount of power from the DC subgrid to the AC subgrid, so that the merged characteristics settle at the steady-state points.
- For , both subgrids are able to meet their loads independently and do not need any external active power support.
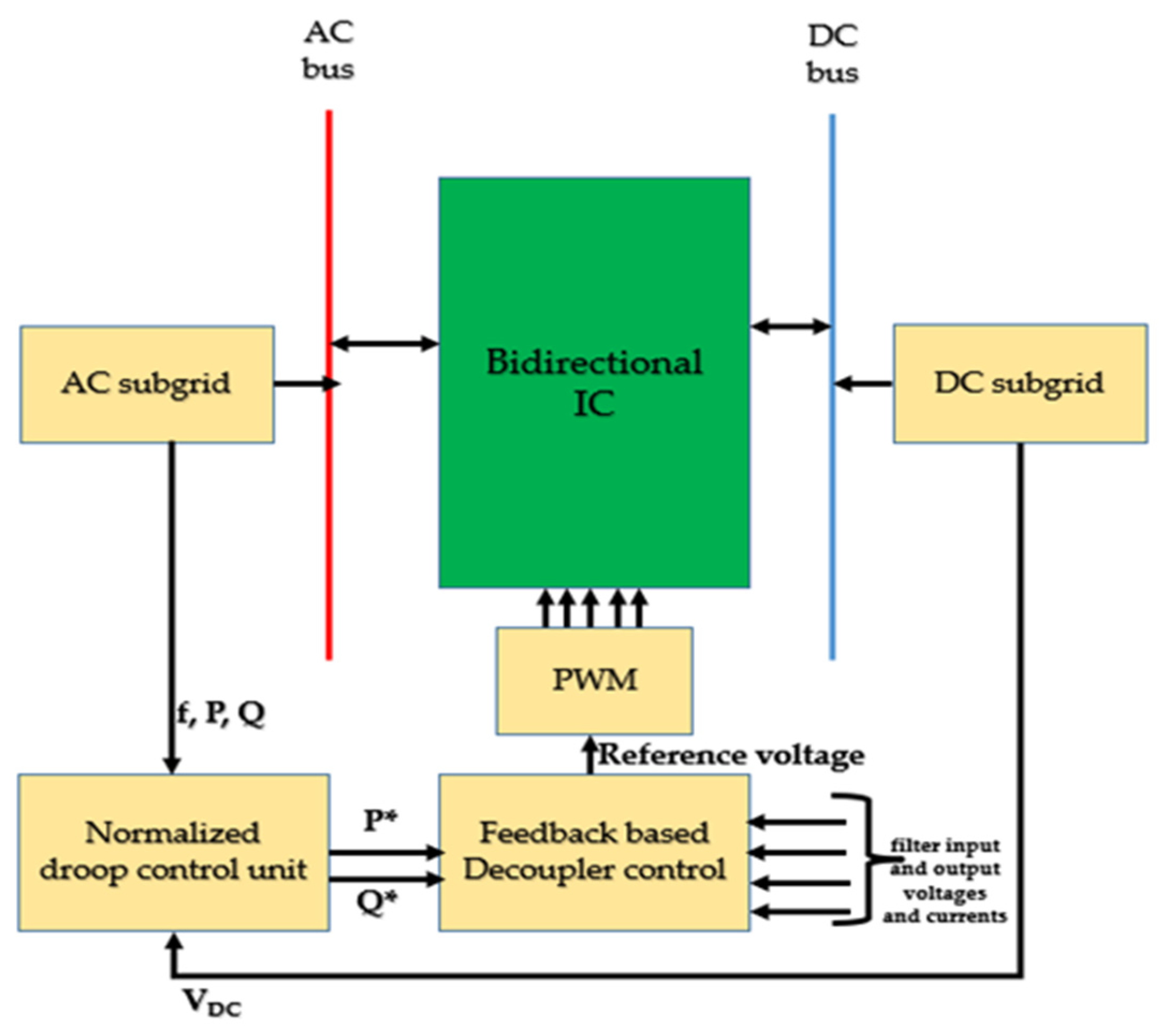
3. Proposed Control Strategy
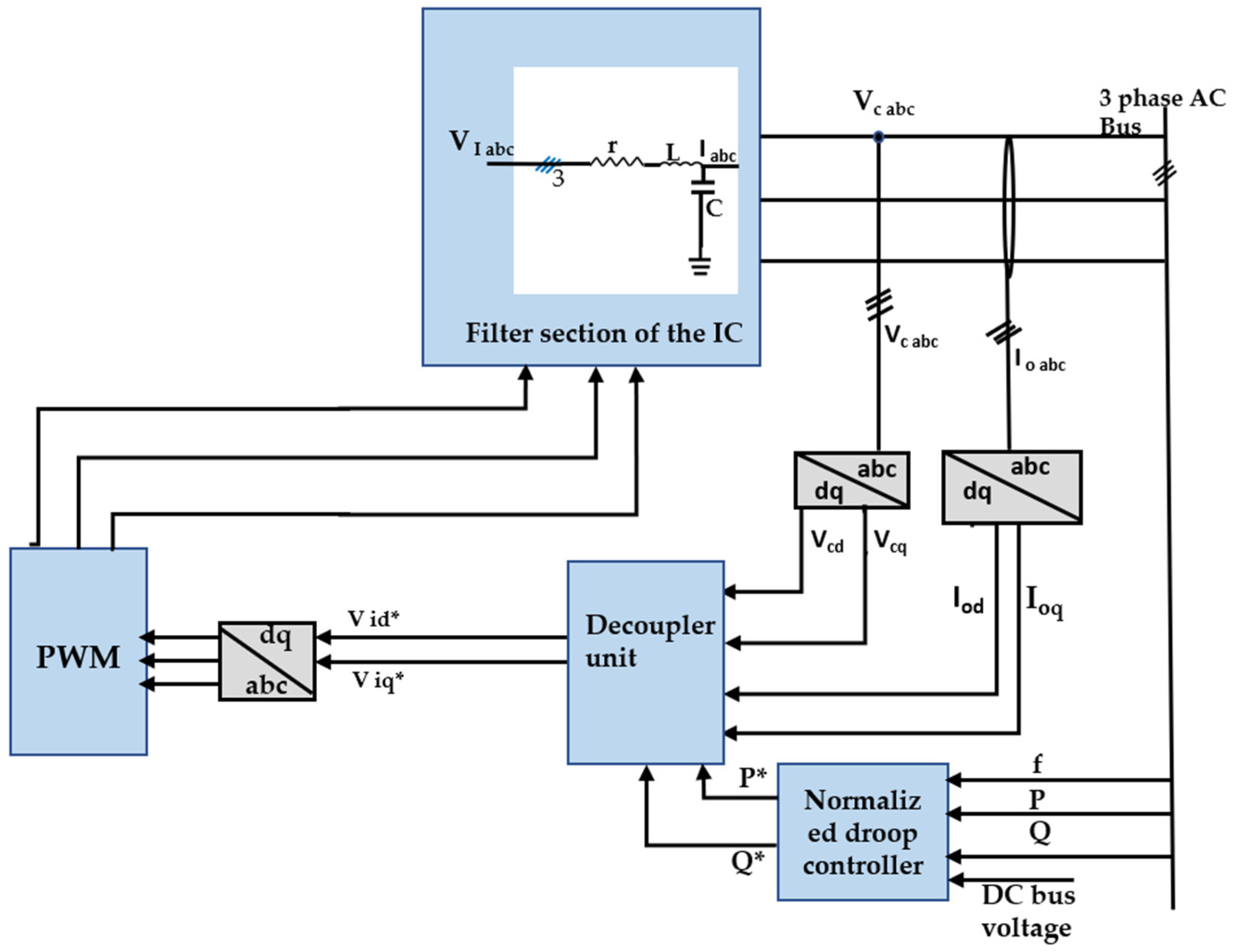
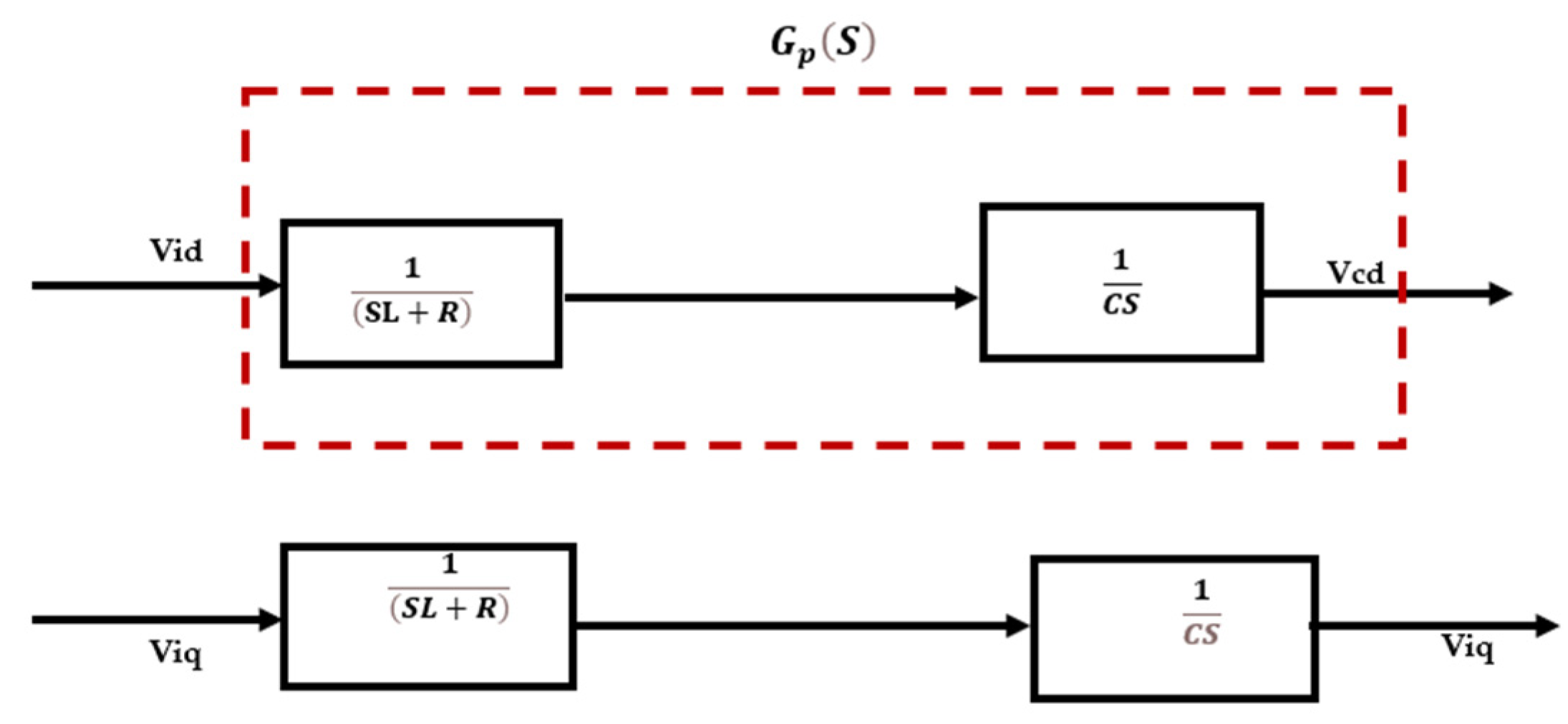
3.1. Linearized Model of the IC with the Filter Section
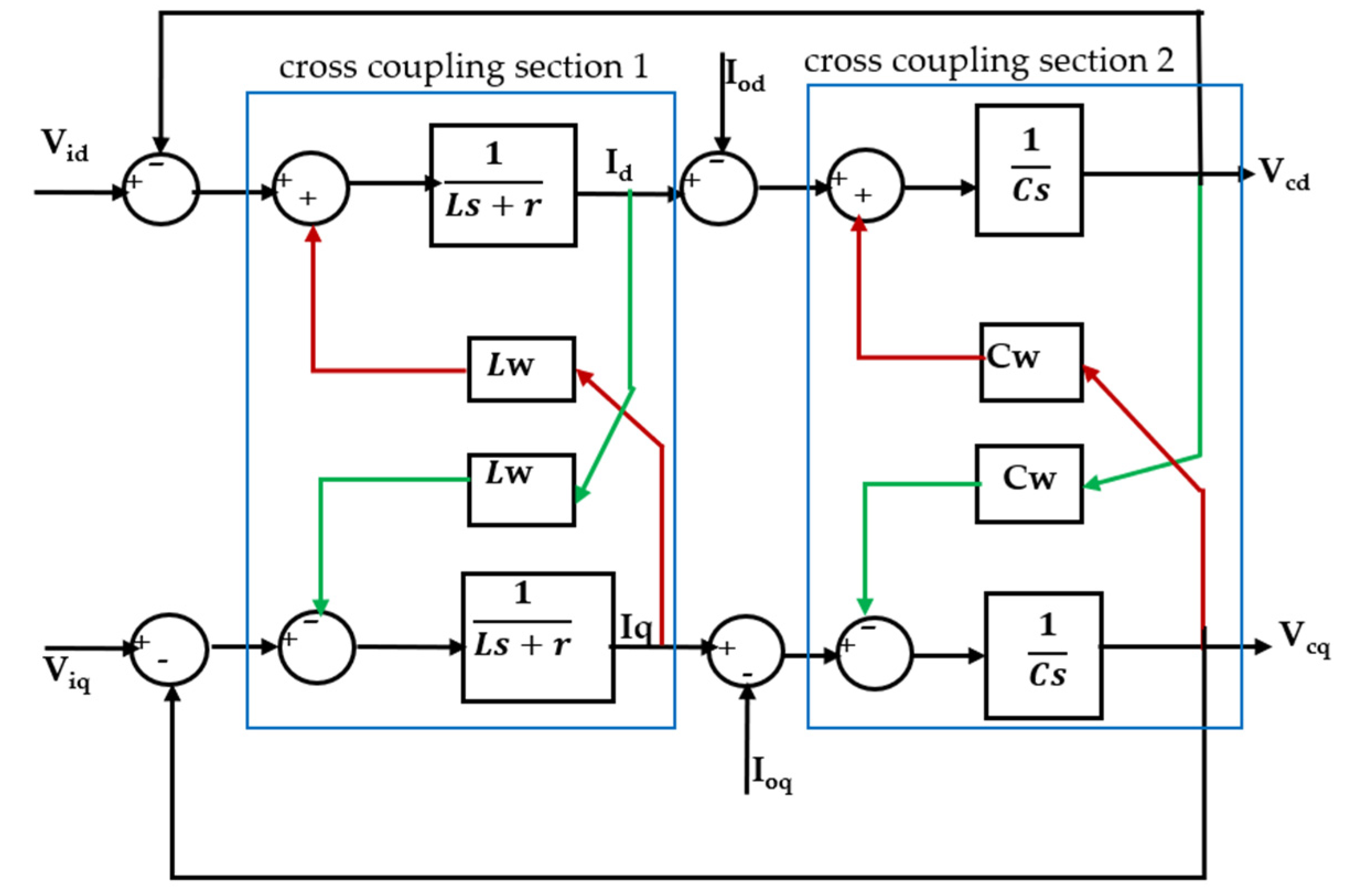
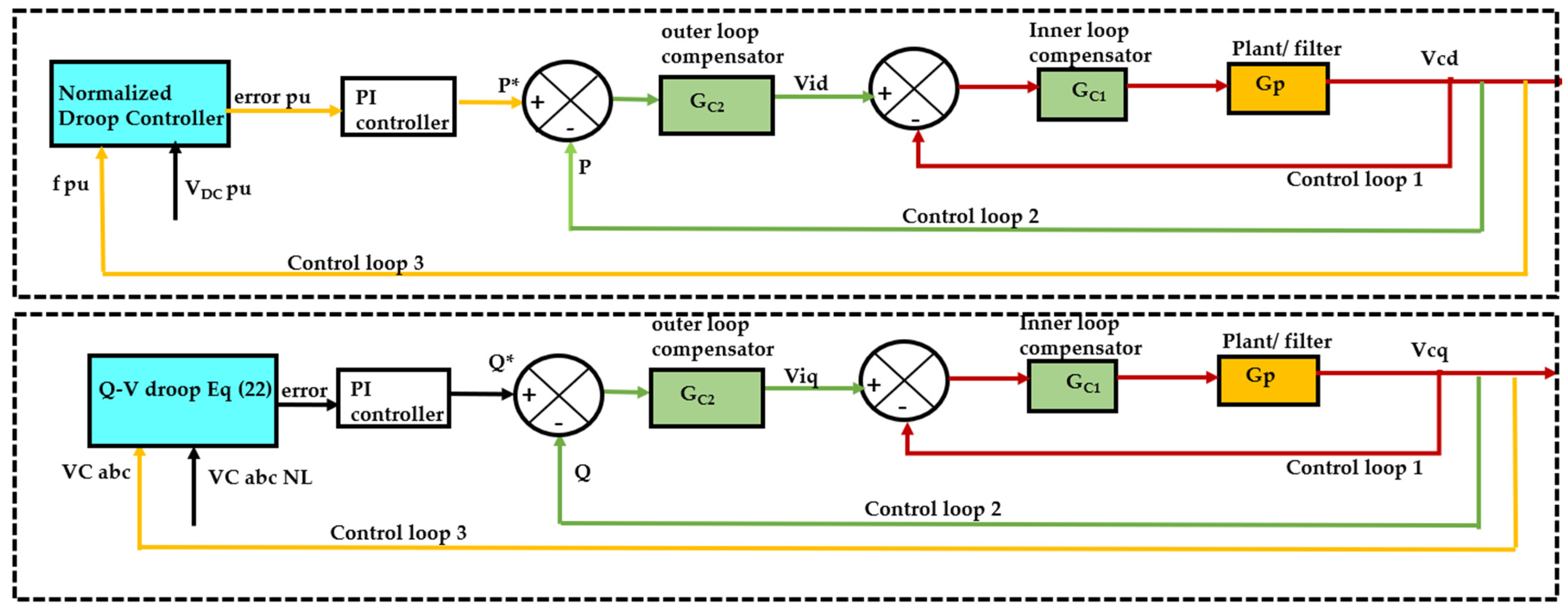
3.2. Design of Decoupling Matrix-Based Feedback Control Unit
3.2.1. Design of Decoupling Matrices
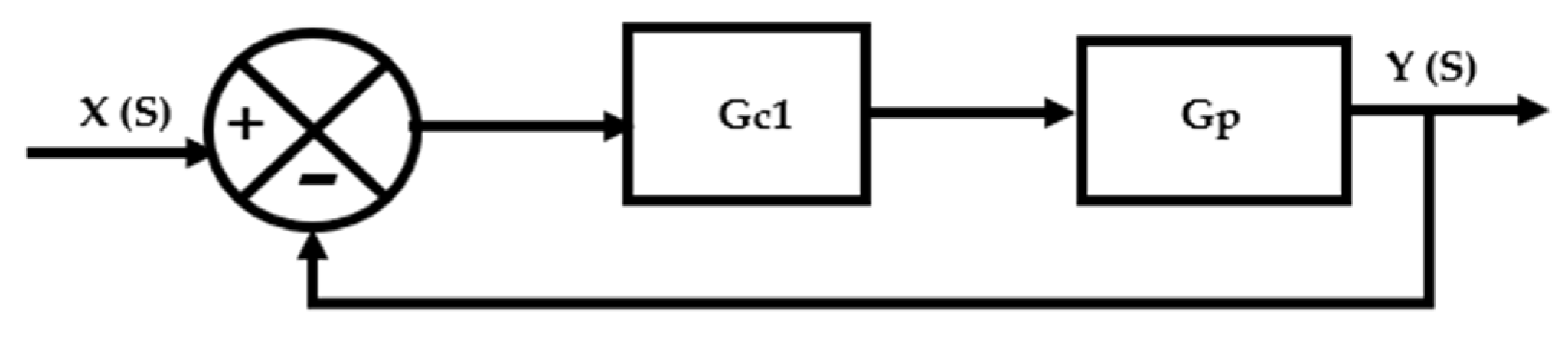
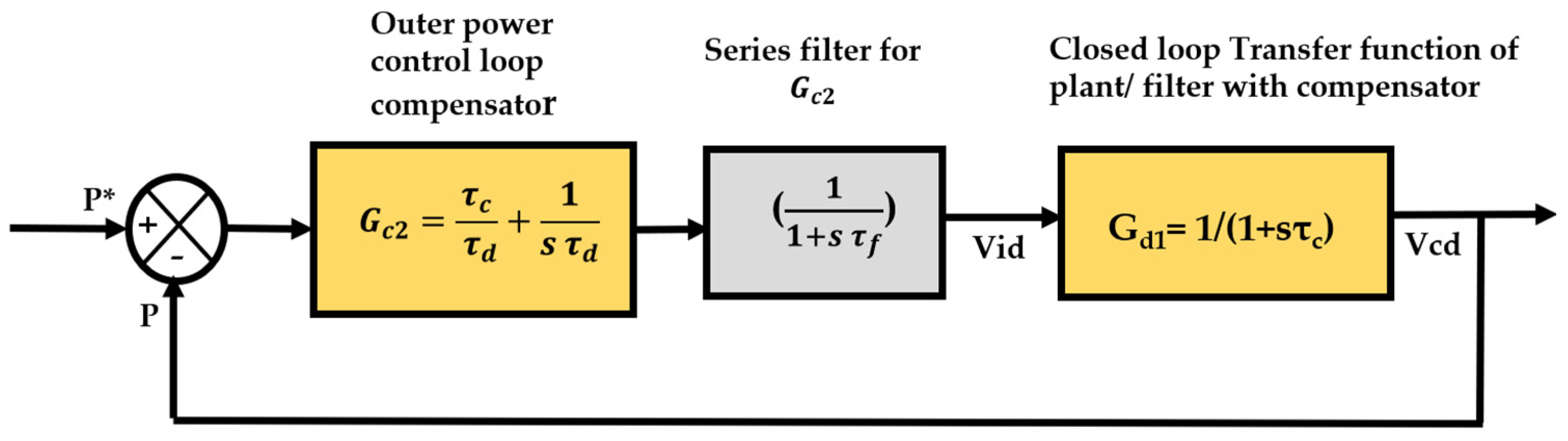
3.3. Design of the Closed-Loop Transfer Function Model by Direct Synthesis Method
- The desired closed-loop transfer function for the inner voltage control loop and outer power control loop without time delay is assumed in the first-order time constant form as = 1/(1 + sτ).
- Assuming the plant transfer function as Gp and the series compensator as Gc, the closed-loop transfer function is expressed in the form = ( )/(1 + ).
- Since and are known, we can derive the transfer function for in PI, PD, or PID forms.
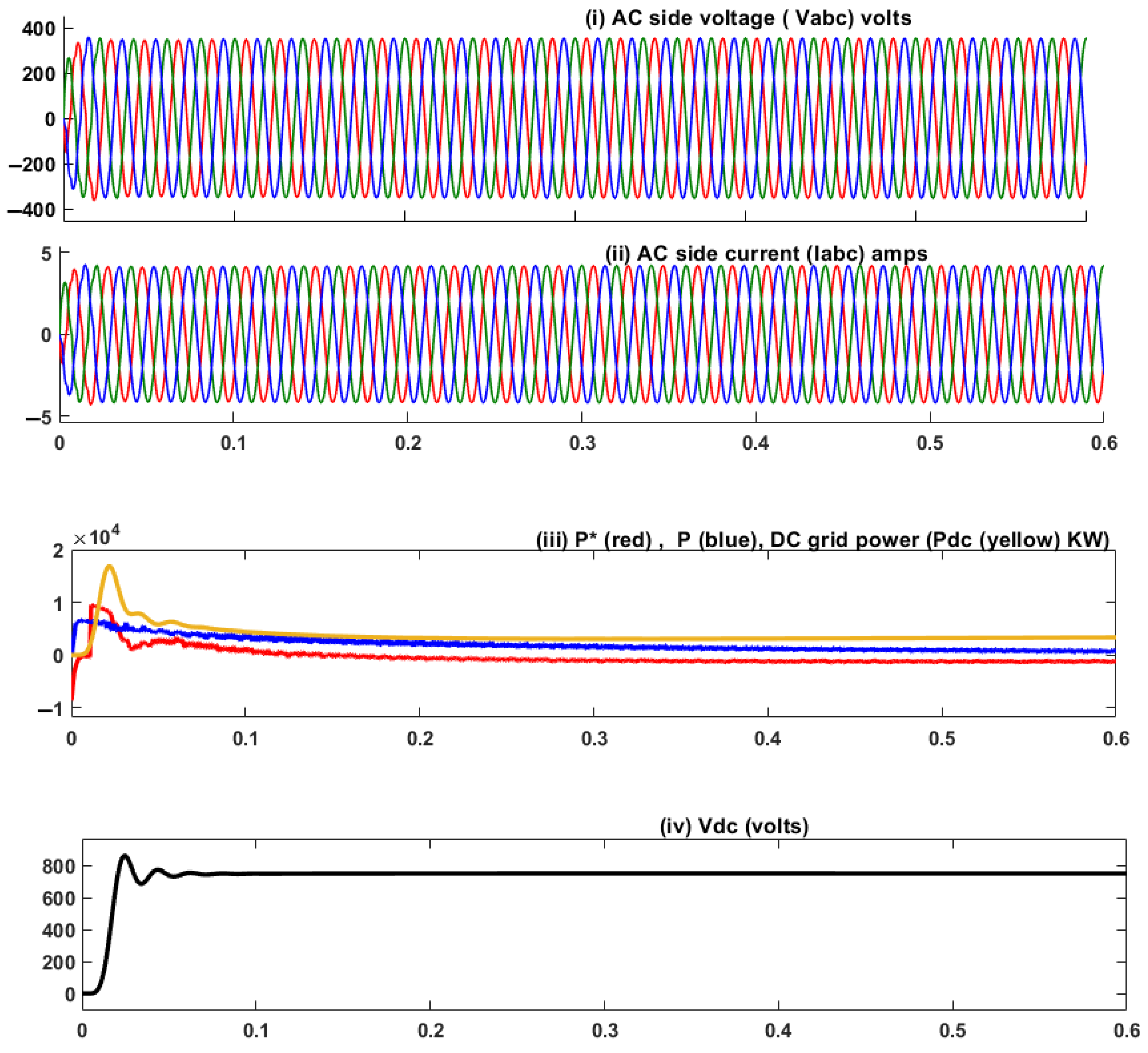
4. Results and Discussions
4.1. Analysis of Results
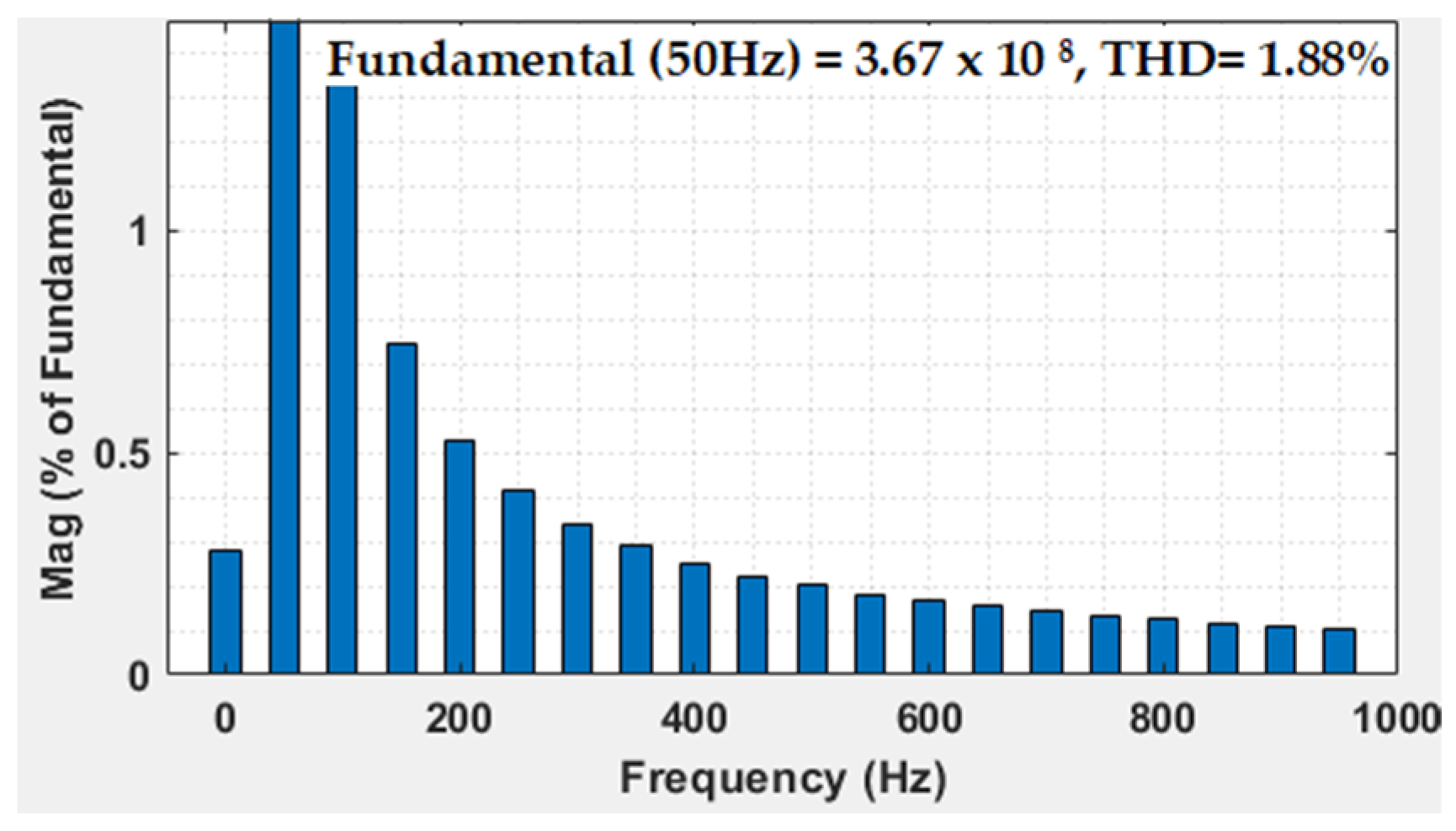
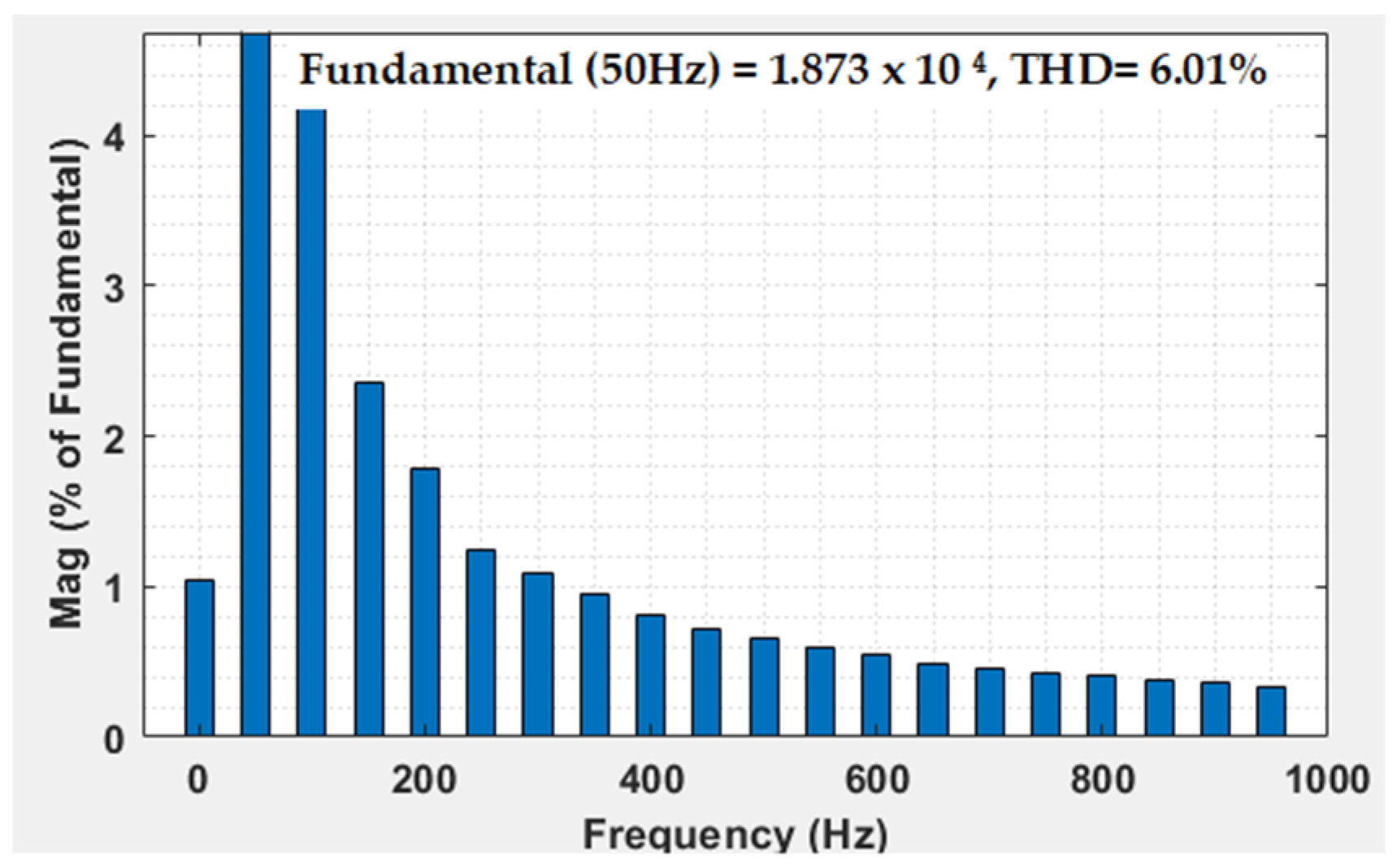
4.1.1. T.H.D Analysis
4.1.2. Comparison of Error Indices with the Designed Controller Parameters and Optimal Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shahgholian, G. A brief review on microgrids: Operation, applications, modeling, and control. Int. Trans. Electr. Energy Syst. 2021, 31, e12885. [Google Scholar] [CrossRef]
- Tabatabaei, N.M.; Kabalci, E.; Bizon, N. (Eds.) Microgrid Architectures, Control and Protection Methods; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Nithara, P.V.; Anand, R. Comparative analysis of different control strategies in Microgrid. Int. J. Green Energy 2021, 18, 1249–1262. [Google Scholar]
- Bharath, K.R.; Choutapalli, H.; Kanakasabapathy, P. Control of bidirectional DC-DC converter in renewable based DC microgrid with improved voltage stability. Int. J. Renew. Energy Res. 2018, 8, 871–877. [Google Scholar]
- Sanampudi, N.; Kanakasabapathy, P. Integrated voltage control and frequency regulation for stand-alone micro-hydro power plant. Mater. Today Proc. 2021, 46, 5027–5031. [Google Scholar] [CrossRef]
- Mishra, S.; Viral, R.K. Introduction to Hybrid AC/DC Microgrids. In Microgrids; Academic Press: Cambridge, MA, USA, 2022; pp. 159–189. [Google Scholar]
- Wang, P.; Xiao, J.; Jin, C.; Han, X.; Qin, W. Hybrid ac/dc Micro-Grids: Solution for High Efficient Future Power Systems. In Sustainable Power Systems; Springer: Singapore, 2017; pp. 23–40. [Google Scholar]
- Barik, A.K.; Jaiswal, S.; Das, D.C. Recent trends and development in hybrid microgrid: A review on energy resource planning and control. Int. J. Sustain. Energy 2021, 41, 308–322. [Google Scholar] [CrossRef]
- Sreelekshmi, R.S.; Amitha, P.; Manjula, G.N. Control and operation of microgrid connected Hybrid Energy Storage System. In Proceedings of the 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 7–8 April 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Song, Y.; Hill, D.J.; Liu, T. Impact of DG connection topology on the stability of inverter-based microgrids. IEEE Trans. Power Syst. 2019, 34, 3970–3972. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamoun, N.; Khaidar, M.; Zine-Dine, K. Review of control and energy management approaches in micro-grid systems. Energies 2020, 14, 168. [Google Scholar] [CrossRef]
- Rangu, S.K.; Lolla, P.R.; Dhenuvakonda, K.R.; Singh, A.R. Recent trends in power management strategies for optimal operation of distributed energy resources in microgrids: A comprehensive review. Int. J. Energy Res. 2020, 44, 9889–9911. [Google Scholar] [CrossRef]
- Eajal, A.A.; Yazdavar, A.H.; El-Saadany, E.F.; Ponnambalam, K. On the Loadability and Voltage Stability of Islanded AC–DC Hybrid Microgrids During Contingencies. IEEE Syst. J. 2019, 13, 4248–4259. [Google Scholar] [CrossRef]
- Eajal, A.A.; Muda, H.; Aderibole, A.; Al Hosani, M.; Zeineldin, H.; El-Saadany, E.F. Stability evaluation of AC/DC hybrid microgrids considering bidirectional power flow through the interlinking converters. IEEE Access 2021, 9, 43876–43888. [Google Scholar] [CrossRef]
- Khodabakhsh, J.; Moschopoulos, G. Simplified hybrid AC–DC microgrid with a novel interlinking converter. IEEE Trans. Ind. Appl. 2020, 56, 5023–5034. [Google Scholar] [CrossRef]
- Shen, X.; Tan, D.; Shuai, Z.; Luo, A. Control Techniques for Bidirectional Interlinking Converters in Hybrid Microgrids: Leveraging the advantages of both ac and dc. IEEE Power Electron. Mag. 2019, 6, 39–47. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Q.; Guerrero, J.M. Effect of frequency coupling on stability analysis of a grid-connected modular multilevel converter system. Energies 2021, 14, 6580. [Google Scholar] [CrossRef]
- Wang, L.; Fu, X.; Wong, M.-C.W. Operation and Control of a Hybrid Coupled Interlinking Converter for Hybrid AC/Low Voltage DC Microgrids. IEEE Trans. Ind. Electron. 2020, 68, 7104–7114. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and analysis of harmonic stability in an ac power-electronics-based power system. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Chen, Z. Autonomous control of inverter-interfaced distributed generation units for harmonic current filtering and resonance damping in an islanded microgrid. IEEE Trans. Ind. Appl. 2013, 50, 452–461. [Google Scholar] [CrossRef] [Green Version]
- Nair, D.R.; Nair, M.G.; Thakur, T. A Smart Microgrid System with Artificial Intelligence for Power-Sharing and Power Quality Improvement. Energies 2022, 15, 5409. [Google Scholar] [CrossRef]
- Hussain, M.N.; Melath, G.; Agarwal, V. An Active Damping Technique for PI and Predictive Controllers of an Interlinking Converter in an Islanded Hybrid Microgrid. IEEE Trans. Power Electron. 2020, 36, 5521–5529. [Google Scholar] [CrossRef]
- Khongkhachat, S.; Khomfoi, S. A Sliding Mode Control Strategy for a Grid-Supporting and Grid-Forming Power Converter in Autonomous AC Microgrids. Int. Rev. Electr. Eng. 2019, 14, 118. [Google Scholar] [CrossRef]
- John, G.K.; Sindhu, M.R.; Nambiar, T.N.P. Hybrid VSI Compensator for AC/DC Microgrid. In 2019 IEEE Region 10 Symposium (TENSYMP); IEEE: New York, NY, USA, 2019; pp. 738–743. [Google Scholar]
- Aryani, D.R.; Song, H. Coordination control strategy for AC/DC hybrid microgrids in stand-alone mode. Energies 2016, 9, 469. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Shan, Y.; Xu, Y.; Guerrero, J.M. A coordinated control of hybrid ac/dc microgrids with PV-wind-battery under variable generation and load conditions. Int. J. Electr. Power Energy Syst. 2018, 104, 583–592. [Google Scholar] [CrossRef] [Green Version]
- Suchetha, C.; Ramprabhakar, J. Optimization Techniques for Operation and Control of Microgrids–Review. J. Green Eng. 2018, 8, 621–644. [Google Scholar] [CrossRef] [Green Version]
- Ramezani, M.; Li, S.; Golestan, S. Analysis and controller design for stand-alone VSIs in synchronous reference frame. IET Power Electron. 2017, 10, 1003–1012. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Van, T.L.; Nawaz, A.; Natsheh, A. Feedback Linearization-Based Control Strategy for Interlinking Inverters of Hybrid AC/DC Microgrids with Seamless Operation Mode Transition. Energies 2021, 14, 5613. [Google Scholar] [CrossRef]
- Rezaei, M.H.; Akhbari, M. Power decoupling capability with PR controller for Micro-Inverter applications. Int. J. Electr. Power Energy Syst. 2021, 136, 107607. [Google Scholar] [CrossRef]
- Aljohani, T.M.; Ebrahim, A.F.; Mohammed, O. Hybrid microgrid energy management and control based on metaheuristic-driven vector-decoupled algorithm considering intermittent renewable sources and electric vehicles charging lot. Energies 2020, 13, 3423. [Google Scholar] [CrossRef]
- Azab, M. High performance decoupled active and reactive power control for three-phase grid-tied inverters using model predictive control. Prot. Control. Mod. Power Syst. 2021, 6, 25. [Google Scholar] [CrossRef]
- Li, B.; Zhou, L. Power decoupling method based on the diagonal compensating matrix for VSG-controlled parallel inverters in the microgrid. Energies 2017, 10, 2159. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Zhao, H.; Cai, H.; Shi, J.; He, X. Power decoupling strategy based on ‘virtual negative resistor for inverters in low voltage microgrids. IET Power Electron. 2016, 9, 1037–1044. [Google Scholar] [CrossRef]
- Wang, C.; Deng, C.; Li, G. Control Strategy of Interlinking Converter in Hybrid Microgrid Based on Line Impedance Estimation. Energies 2022, 15, 1664. [Google Scholar] [CrossRef]
- Wang, H.; Li, W.; Yue, Y.; Zhao, H. Distributed Economic Control for AC/DC Hybrid Microgrid. Electronics 2021, 11, 13. [Google Scholar] [CrossRef]
- Sun, L.; You, F. machine learning and data-driven techniques for the control of smart power generation systems: An uncertainty handling perspective. Engineering 2021, 7, 1239–1247. [Google Scholar] [CrossRef]






| Block | Transfer Function |
|---|---|
| Plant/Filter | |
| Compensator for control loop1 (inner voltage control) | |
| Closed loop transfer function of inner voltage control | |
| Filter transfer function in series with | |
| Compensator for control loop2 (outer power control) | where, |
| Overall closed loop transfer function of inner voltage control and outer power control. |
| Parameter | Value |
|---|---|
| R | 10 ohms |
| L | 0.0017 H |
| C | 1.2 × 10−4 F |
| (Nominal amplitude) | 325 V |
| VDC (Nominal Value) | 750 V |
| DC side Capacitor | 4800 × 10 −6 F |
| Rated Power (DC side) | 10 KW |
| Rated Power (DC side) | 10 KW |
| PI Controller Parameters | Integral Square Error (ISE) | Integral Absolute Square Error (IAE) | Integral Absolute Time Square Error (ITSE) |
|---|---|---|---|
| With designed values. Kp = 0.1 and Ki = 1000 | 0.0009075 | 0.001568 | 6.27 × 10−7 |
| With optimized values tuned by P.S.O. Kp = 814.7 and Ki = 905.79 | 7.48 × 10−7 | 0.0001171 | 6.45 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nair, R.P.; Ponnusamy, K. Decoupler-Based Feedback Control Strategy for Interlinking Converter in a Hybrid Microgrid. Designs 2023, 7, 91. https://doi.org/10.3390/designs7040091
Nair RP, Ponnusamy K. Decoupler-Based Feedback Control Strategy for Interlinking Converter in a Hybrid Microgrid. Designs. 2023; 7(4):91. https://doi.org/10.3390/designs7040091
Chicago/Turabian StyleNair, Rekha P., and Kanakasabapathy Ponnusamy. 2023. "Decoupler-Based Feedback Control Strategy for Interlinking Converter in a Hybrid Microgrid" Designs 7, no. 4: 91. https://doi.org/10.3390/designs7040091
APA StyleNair, R. P., & Ponnusamy, K. (2023). Decoupler-Based Feedback Control Strategy for Interlinking Converter in a Hybrid Microgrid. Designs, 7(4), 91. https://doi.org/10.3390/designs7040091







