Computational Fluid Dynamics Heat Transfer Analysis of Double Pipe Heat Exchanger and Flow Characteristics Using Nanofluid TiO₂ with Water

Abstract

A device called a heat exchanger is used to exchange heat transfer between two fluids with different temperatures. Because of its durability and ability to handle high-pressure application, the concentric double pipe heat exchangers are widely utilized for numerous industrial applications. To conserve pumping power energy, many researchers were involved in study of the nanoparticles to be embedded in the fluid, which will enrich the fluid thermal conductivity and surface area. This article demonstrates the flow characteristics and convective heat transfer of nanofluids containing 0.2, 0.4 and 0.6 of vol% TiO₂ nanoparticles dispersed in water under turbulent conditions, which mainly can be used for cooling nuclear reactors applications. Reynolds numbers varying from 4000 to 18,000 are examined numerically. The convective heat transfer coefficient results of the nanofluid agree well against experimental data, which are slightly more than that of base water at 1.94%. The results of the numerical model showed that the convective heat transfer coefficient of nanofluids will increase when the Reynolds and volume fraction increases. By increasing the temperature of the annular hot water, the heat transfer rate will increase, showing no major impact to the convective heat transfer coefficient of nanofluids. A generalised solution predicting the convective heat transfer coefficient for extensive nanoparticle materials is proposed. The conclusion of the empirical equation is tested among published data and the results are highly congruent, confirming the strength of the gamma equation.

1. Introduction

Heat exchangers come in a series of selections, one of which is the double pipe heat exchanger. By using convection within the fluid and conduction through the double pipe wall that separates the fluids, this device permits the exchange of heat between two fluids. A double tube heat exchanger was invented in the late 1940s, and since then, all studies broadly support its application in moving toward substantial improvement [1]. The advent of the double tube heat exchanger has an allowable transfer of thermal energy mainly between hot and cold fluids, mostly in concentric tubes in different configurations, which at the beginning were parallel and then changed to counterflows [1]. While many experimental and numerical investigations have been carried out [2,3,4,5], the majority of these studies concentrate on identifying the parameters that affect thermal performance, such as the operating temperature, inner and outer Reynolds numbers, volume fractions, dispersed nanoparticle shape, and thermal conductivity. The effect of nanoparticle shape has attracted the interest of many researchers, who find that the nanofluids heat transfer properties are responsive to the shape of nanoparticles [6,7]. Lin et al. [8] found that nanofluids containing rod-like nanoparticles at higher Reynolds numbers more effectively improve the heat transfer due to the larger aspect ratio. Not only the shape of the particle but also its size was found to be central in enhancing the thermal conductivity of nanofluids. Pak and Cho [9] concluded that heat transfer performance was enhanced through a better selection of particles with a larger size and higher thermal conductivity. They found that particles of γ-Al₂O₃ and TiO₂ could be well dispersed consistently at pH values of 3 and 10, respectively, and the Nusselt number was found to increase when the volume fraction and Reynolds number increased, since the main parameter influencing the heat transfer performance is thermal conductivity. Dayou et al. [10] conducted thermal performance comparisons between (MWCNT) and (GnP) nanofluids. The heat transfer coefficients of graphene nameplate (GnP) nanofluids are found to be much greater than the multiwall carbon nanotube (MWCNT) nanofluids at the particular concentration and the flow rates. Furthermore, Dayou et al. pointed out that to enhance the thermal performance of the nanofluids, an appropriate size and shape of carbon nanoparticles and nanofluid concentration must be chosen. In contrast, El-Behery et al. [11] numerically examined a component of nanofluids. By increasing the nanoparticles volume concentration of (Al₂O₃, CuO, TiO₂ and ZnO), the heat transfers and pressure drop increase. Also, their finding specified that when the Reynolds number increases, the average heat transfer coefficient and effectiveness increase significantly. Additionally, Lin et al. [12] concluded that not only increasing the Reynolds number, particle volume concentration, and particle diameter will increase the Nusselt number of nanofluids, also the dispersed particles must be distributed uniformly to save energy. The majority of these studies pay more attention to figuring out the variables that affect the convective heat transfer coefficient, which is directly proportional to the Nusselt number, meaning that by increasing the Nusselt number, the convective heat transfer coefficient of the nanofluids also increases. The dimensionless parameters that influence the Nusselt number excessively are the Reynolds number and the Prandtl number: Both of them have a direct influence on the Nusselt number, which then directly impacts the convective heat transfer coefficient. The Nusselt number is a crucial dimensionless number which affects heat transfer efficiency and describes a physical limit between the conductive and convective heat transfer within the fluids. To determine it, numerical software such as ANSYS/Fluent^® (i.e., ANSYS Fluent Release 15.0), computational fluid dynamics (CFD) code [13] must be used to perform the post-processing operation or an expensive experimental setup must be conducted. Therefore, this research aims to perform the validation by a numerical approach on an experimental work that enhances the TiO₂/water nanofluid heat transfer in a counterflow double tube heat exchanger and to estimate and validate the heat transfer coefficient by correlating numerous parameters in nondimensional form. These correlations can cover a wide range of applications and optimise the period involved in estimating the output parameters, such as heat transfer coefficients, instead of running computational models or conducting costly experiments.

2. Modelling

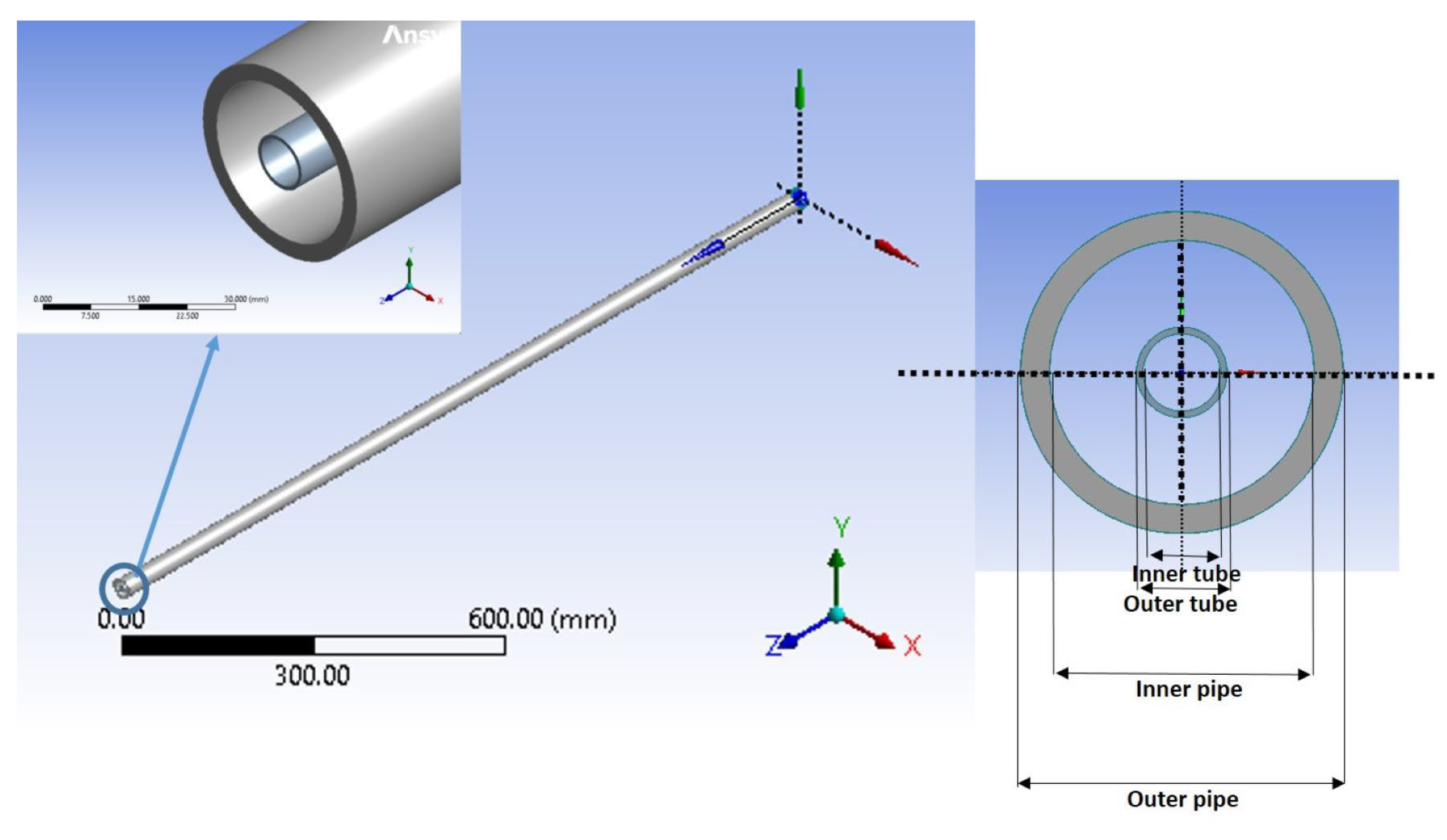
2.1. Geometry

A heat exchanger with a double pipe was modelled through the ANSYS/Fluent^® CFD (i.e., ANSYS Fluent Release 15.0), code so that both the inner and outer flow were considered. All measurements were taken as per the experimental system [14]. The inner copper tubing had an 8.13 mm inner tube diameter and a 9.53 mm outer tube diameter, while the outer PVC pipe had a 27.8 mm inner pipe diameter and a 33.9 mm outer pipe diameter. The nanofluid flowing inside the tube and the hot water flowed in the annular had a total length of 1.5 m long, as shown in Figure 1.

2.2. Mesh Development

This model was made using a quadrilateral structured mapped mesh type, which was based on the real measurements and geometry of the double pipe heat exchanger. A smaller element mesh was required in some area to capture crucial flow behaviour, such as the viscous and thermal boundary layers near the outer and the inner walls, with the progression of the grid spacing size employed as needed to avoid any artificial numerical effect. In connection with the current investigation, a sequence of grid refinements was carried out to verify that the outcome was grid-independent; from these results, 105,840 cells and 106,555 nodes, distributed as shown in Figure 2, were sufficient in order to convey the pertinent principle of thermal and viscous flow.

Table 1. Grid independence study.

Grid	Mesh Nodes	Mesh Elements	Twall (Wall Temperature)	h (Convective Heat Transfer Coefficient)
1	42,330	41,910	299.28326	11,032.24565
2	53,680	53,200	299.30795	10,624.9118
3	75,330	74,740	299.32455	10,347.64332
4	96,005	95,340	299.34390	10,052.82923
5	106,555	105,840	299.34387	10,052.16872

illustrates more detail on the grid independence studies.

2.3. Numerical Method

As of the double pipe heat exchanger’s axisymmetric geometry, which was earlier defined, it is likely to use ANSYS/Fluent^® CFD (i.e., ANSYS Fluent Release 15.0), to solve the governing partial differential equations in two-dimensional and to find the thermal flow field at the inner tube and annular region based on the flowing assumptions

• The flow is steady and incompressible.
• The thermo-physical properties of the fluid are temperature independent.
• The flow is turbulent.

In this model, a single-phase model was applied to study the turbulent forced convection flow of a nanofluid in a concentric double pipe heat exchanger. Therefore, a Shear Stress Transport (SST) k-ω turbulence model is chosen for this analysis, as the k-ω turbulence model provides a decent estimation of the flow performance near the wall boundary layer. The Continuity, Momentum, and Energy that govern this model are described as follows [15].

$$\mathrm{Continuity}: \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$\begin{array}{c}\mathrm{Momentum}:\\ \mathrm{X}\text{-}\mathrm{component}:\rho u\frac{\partial u}{\partial x}+\rho v\frac{\partial u}{\partial y}=-\frac{\partial P}{\partial x}+\mu \left[\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right]\end{array}$$

(2)

$$\begin{array}{c}\mathrm{Momentum}:\\ \mathrm{Y}\text{-}\mathrm{component}:\rho u\frac{\partial v}{\partial x}+\rho v\frac{\partial v}{\partial y}=-\frac{\partial P}{\partial y}-\rho g_y+\mu \left[\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right]\end{array}$$

(3)

$$\mathrm{Energy}:\rho C_{ p}u\frac{\partial T}{\partial x}+\rho C_{ p}v\frac{\partial T}{\partial y}=k\left[\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right]$$

(4)

These calculations were made subject to the boundary conditions shown in the following subsection.

2.4. Boundary Conditions

The real parameters from the experimental system were used to define the boundary conditions [14], and the double pipe heat exchanger’s boundary conditions were as follows:

• Inner tube inlet–imposed mass flow rate (mass flow rate inlet);
• Inner tube outlet–imposed pressure (pressure outlet);
• Outer pipe inlet–imposed mass flow rate (mass flow rate inlet);
• Outer pipe outlet–imposed pressure (pressure outlet);
• Tube centreline–axis of symmetry (axis);
• Double pipe heat exchanger walls (wall).

The mass flow rate of the (nanofluid) inner tube was extracted out from the given experimental Reynolds number (5000, 6700, 8000, 9900, 11,400, 13,000, 14,600 and 16,200) using the following equation:

$$Re=\frac{4 \dot{m}}{\pi D_{ tube }{\mu }_{ nf}}$$

(5)

where the mass flow rate of the (hot water) annular is kept at 3 LPM. The tube inlet temperature for the (nanofluids) is 298.15 K, and the annular inlet temperature for the (hot water) varies between 308.15 and 323.15 K.

3. Data Reduction Equations

3.1. Thermal and Physical Properties of Nanofluids

To begin initially the numerical model after imposing the boundary conditions, the effective thermal properties such as specific heat, density, thermal conductivity and viscosity at numerous temperatures must be determined for both nanofluids and hot water [16]. Therefore, the specific heat, density, thermal conductivity and viscosity of the hot water are evaluated by the following equations:

$${\rho }_f=-3\times {10}^{-3}{T}_{avg}^2+{1.505T}_{avg}+ 816.781$$

(6)

$$C_{pf}=-4.63\times {10}^{-5}{T}_{avg}^3+0.0552T_{avg}^2-{20.86T}_{avg}+6719.637$$

(7)

$${\mu }_f=2.414\times {10}^{-5}\times {10}^{247.8/(T_{avg}-140)}$$

(8)

$$k_f=0.6067\left(-1.26523+3.704\left(\frac{T_{avg}}{298.15}\right)-1.43955{\left(\frac{T_{avg}}{298.15}\right)}^2\right)$$

(9)

Equations (6)–(9) can be used to evaluate the density, specific heat, viscosity and thermal conductivity of the water, respectively. Once the thermal properties have been determined for the base fluid and hot water, the following relations define the thermophysical properties such as specific heat, density, thermal conductivity and viscosity of nanofluids (pure water containing TiO₂ nanoparticles with a diameter of 21 nm) based on the known thermophysical property and volume concentration of the TiO₂ nanoparticles.

$${\rho }_{nf}=(1-\varphi ){\rho }_{bf}+\varphi {\rho }_p$$

(10)

$$C{p}_{nf}=(1-\varphi )C{p}_{bf}+\varphi C{p}_p$$

(11)

Equations (10) and (11) are constant-value temperature independent densities based on nanoparticle volume concentration and the specific heat of the nanofluid, respectively.

The TiO₂/water nanofluid thermal conductivity and the viscosity can be approximated by the following:

$$\frac{k_{nf}}{k_{bf}}=0.8938{(1+\varphi )}^{1.37}{(1+\frac{T_{nf}}{70})}^{0.2777}{(1+\frac{d_p}{150})}^{-0.0336}{(\frac{{\alpha }_p}{{\alpha }_{bf}})}^{0.01737}$$

(12)

$$\frac{{\mu }_{nf}}{{\mu }_{bf}}={(1+\varphi )}^{11.3}{(1+\frac{T_{nf}}{70})}^{-0.038}{(1+\frac{d_p}{170})}^{-0.061}$$

(13)

where Equations (12) and (13) are developed using the experimental data of various investigators by Sharma et al. [17] to estimate the thermal conductivity and viscosity for water-based nanofluids, respectively. The equations are valid for a temperature unit going from 20 to 70 °C, nanoparticles having a volume concentration less than 4.0%, and the diameter of the particle scaling from 20 to 150 nm [11]. The values of the thermophysical properties of water and TiO₂ nanofluid are shown in

Table 2. The values of thermophysical properties of water and nanomaterials @ 298.15K.

Thermophysical Properties	Density kg/m3	Thermal Conductivity W/m·K	Specific Heat J/kg·K	Dynamic Viscosity Pa·s
Water	998.816	0.606226774	4180.02945	0.000890439
TiO2 (21 nm)	4250	8.953	686.2	NA

.

The impact of the turbulent transport between the walls and within the flow was taken into consideration for the current study using the Shear Stress Transport (SST) k-ω turbulence model with a coupled explicit solver. ANSYS/Fluent^® (i.e., ANSYS Fluent Release 15.0), was used to apply all pertinent boundary conditions, such as an axisymmetric condition along the double pipe heat exchanger centreline and the previously mentioned inlet conditions. The solver was then run until convergence with residuals of 10⁻⁶ on mass, momentum and energy, reporting no backflow at any cell on the pressure outlet boundaries.

3.2. Heat Transfer Coefficient, Heat Transfer Rate and Nusselt Number

To evaluate the thermal performance of the double pipe heat exchangers, and to better understand the physical processes involved in heat transfer, it was necessary to investigate parameters such as the heat transfer coefficient. The following are the main parameters that have a direct influence on the heat transfer process [18]:

$$h_{nf}=\frac{Q_{avg}}{A(T_{wall}-T_{nf})}$$

(14)

where A = πD_tubeL and Q_avg is the average heat transfer rate between hot water and nanofluid, which can be defined as follows:

$$Q_{avg}=\frac{Q_w+Q_{nf}}{2}$$

(15)

The heat transfer rates from the heating fluid into nanofluid can be calculated by the following:

$$Q_w={\dot{m}}_{w}C{p}_w{(T_{in}-T_{out})}_w$$

(16)

$$Q_{nf}={\dot{m}}_{nf}C{p}_{nf}{(T_{out}-T_{in})}_{nf}$$

(17)

Once the average heat transfer rate (Q_avg), wall temperature (T_wall) and nanofluids bulk temperature (T_nf) are defined:

$$T_{nf}=\frac{T_{in}+T_{out}}{2}$$

(18)

The convective heat transfer coefficient of the nanofluids can be calculated as well as the Nusselt number (Nu) using the following equation:

$$N{u}_{nf}=\frac{h_{nf}{D}_{tube}}{k_{nf}}$$

(19)

4. Results and Discussion

The main objective of this study is to show a numerical validation for the heat transfer coefficient of (water–TiO₂) nanofluids running in a horizontal counterflow double tube heat exchanger in turbulent flow conditions at 4000 to 18,000 Reynolds numbers. Furthermore, the correlations established by Pak and Cho [9] and Xuan and Li [19] are compared with the numerical results to calculate the nanofluid Nusselt number as defined below.

The Pak and Cho correlation is defined as

$$N{u}_{nf}=0.021{Re}_{nf}^{0.8}{Pr}_{nf}^{0.5}$$

(20)

The Xuan and Li correlation is defined as

$$N{u}_{nf}=0.0059(1.0+7.6286{\varphi }^{0.6886}P{e}_{nf}^{0.001}){Re}_{nf}^{0.9238}{Pr}_{nf}^{0.4}$$

(21)

The Reynolds, Prandtl and Peclet numbers of the nanofluid are defined as

$${Re}_{nf}=\frac{{\rho }_{nf}u{D}_{tube}}{{\mu }_{nf}}$$

(22)

$${Pr}_{nf}=\frac{{\mu }_{nf}C{p}_{nf}}{k_{nf}}$$

(23)

$$P{e}_{nf}=\frac{u{d}_p}{{\alpha }_{nf}}$$

(24)

where the a_nf is the nanofluid thermal diffusivity and can be defined as follows:

$${\alpha }_{nf}=\frac{k_{nf}}{{\rho }_{nf}C{p}_{nf}}$$

(25)

These equations calculate the nondimensional parameters like the Reynolds number, Prandtl number and Peclet number of the nanofluid.

Table 3. Effective thermophysical parameters of the nanofluid @ 298.15K.

Volume Fraction φ	Density kg/m3	Specific Heat J/kg.K	Dynamic Viscosity Pa.s	Thermal Conductivity W/m.K
0.2 vol.%	1005.31885	4150.48902	0.000900264	0.623608995
0.4 vol.%	1011.821217	4121.328268	0.000920779	0.625314903
0.6 vol.%	1018.323584	4092.53992	0.00094172	0.627022068

illustrates the values of effective thermophysical parameters of the nanofluid at different volume fractions.

The volume fractions used for this study are 0.2, 0.4 and 0.6% volume of the TiO₂ nanoparticles dispersed in water. The additional operating conditions used are as follows:

• The nanofluid Reynolds number varies from 4000 to 18,000.
• The temperature of the nanofluid is 298.15 K.
• The hot water flow rate is 3.0 LPM.
• The hot water temperature is 308.15 K, 313.15 K and 323.15 K.

The numerical model’s findings are verified against experimental data in the subsection that follows.

4.1. Convective Heat Transfer Coefficient

Based on the experimental work conducted by Duangthongsuk et al. [14], the numerical model was validated and compared with Equations (20) and (21), which were recognised by Pak and Cho and by Xuan and Li.

Figure 3 shows satisfactory consistency between the model results and the experimental data for predicting the Nusselt number. Moreover, both numerical and experimental results showed disagreement with the predicted data calculated by Xuan and Li’s correlation. However, both are closer to the value predicted by Pak and Cho’s correlation. To seek more validation for the numerical model, the pressure drop (ΔP) of the inner tube was determined from the numerical model and compared with the experimental data, as can be seen in Figure 4.

Figure 4 shows a remarkable agreement between the numerical model and the findings of the previous works in predicting the pressure drop as a function of the Reynolds number of the nanofluids. Both illustrated that by increasing the Reynolds number, the higher pressure drop will be accrued due to the loss of the energy [20]. Increasing the Reynolds numbers of the nanofluids will consistently increase the heat transfer coefficient of nanofluids, as can be seen in Figure 5.

Figure 5 illustrates the comparison of the convective heat transfer coefficient attained from base fluid (water) and that from the 0.2% volume of TiO₂ nanoparticles dispersed in water. The numerical result showed an elevation of the nanofluid convective heat transfer coefficient compared to the (water) base fluid at a higher Reynolds number, which agrees very well with published data with low-volume fractions. Since the numerical model yields a good agreement compared to the experimental data, this study will be extended to examine more volume fractions. Figure 6 represents the effect of TiO₂/water nanofluids on the convective heat transfer coefficient in the inner tube. Increasing volume concentrations of TiO₂/water nanofluids generate variations in the heat transfer coefficient at higher nanofluids Reynolds numbers. The heat transfer coefficients are found to be 1.9%, 2.7% and 3.5% for 0.2%, 0.4% and 0.6% volume concentrations, respectively, which are greater than water at the Reynolds number of 16,200.

These improvements are because of the boost of the nanofluids’ thermal conductivity. Changing the hot water temperature showed no major impact on the convective heat transfer coefficient of nanofluids. However, as illustrated in Figure 7, these changes can only be seen for the heat transfer rate of nanofluids with the same operating conditions.

Therefore, increasing the heat transfer rate does not lead to an increase in the heat transfer coefficient, where many parameters have a direct influence, as can be illustrated at Equation (14). Indeed, the determination of the convective heat transfer coefficient of nanofluids is a challenging mission requiring either running numerical solutions using the finite volume method (FVM) such as ANSYS/Fluent^® software (i.e., ANSYS Fluent Release 15.0), or conducting a sophisticated experimental setup with multiple parameters involved in the heat transfer process. Essentially, numerical modelling of the determination of the convective heat transfer coefficient of nanofluids is cumbersome and demands amended analysis practices. Therefore, nondimensional analysis can offer a general solution that predicts the convective heat transfer coefficient of nanofluids, as described in the next subsection.

4.2. Nondimensional Study of the Convective Heat Transfer Coefficient

One of the most important output parameters in the heat transfer process is the convective heat transfer coefficient. The convective heat transfer coefficient can be influenced by a wide range of independent parameters, including the flow rate, nanoparticle properties and base fluids. To comprehend the heat transfer process, it is necessary to identify the independent parameters (inputs) that have substantial impact on the major dependent variable (output), which is the convective heat transfer coefficient. These parameters’ nondimensional form, which covers a wide range of heat transfer process operation, is crucial for reducing the dimension of the parameter space. These independent parameters were cast in nondimensional form, and the number of nondimensional parameters needed was determined using the Buckingham π Theorem [21] in order to ascertain which of them significantly affected the convective heat transfer coefficient. The convective heat transfer coefficient can be determined directly from the Nusselt number, as can be seen from Equation (19), where the Nusselt number is a function of the Reynolds number, the Prandtl number and a host of additional independent factors, and the purpose for Nusselt number can be expressed in written form:

$$\frac{h_{nf}{D}_{tube}}{k_{nf}}=f({Re}_{nf},{Pr}_{nf},\frac{{\alpha }_p}{{\alpha }_{nf}})$$

(26)

where the Nusselt number (Nu) of the nanofluid is a function of three π terms: the Reynolds number (Re), the Prandtl number (Pr) and the ratio of nanoparticle to nanofluid thermal diffusivity (α_p/α_nf). Dividing the thermal diffusivity ratio by Re and Pr, the following relation defines the symbol gamma (γ), which defines the new π term:

$$\gamma =\frac{{\left({\alpha }_p/{\alpha }_{nf}\right)}^{1/3}}{{Re}_{nf}{Pr}_{nf}}$$

(27)

With this new parameter, the following nondimensional relation was proposed:

$$Nu=f(\gamma )$$

(28)

Equation (28) shows only one independent nondimensional parameter, the Nusselt number, and all the runs out of the CFD model were collapsed into a single curve, as shown in Figure 8.

Figure 8 shows the nondimensional result of predicting the Nusselt number of nanofluids. The results represent a single curve with one scaled equation. Moreover, the gamma (γ) has a profound influence on fitting the data into a single curve. The function of gamma (γ) describes the Nusselt number of nanofluids. The functions define the thermal diffusivity ratio by the Reynolds number and the Prandtl number. This confirms that increasing the Reynolds number leads to a lower value of gamma (γ), resulting in higher Nusselt numbers of nanofluids being obtained and vice versa. As stated before, the main goal of this study is to demonstrate numerical validation for the heat transfer coefficient and define simple empirical equations that can be used to govern the heat transfer coefficient of nanofluids for a wide range of applications. Thus, the use of gamma (γ) as a suitable independent variable can provide an excellent means of controlling the heat transfer coefficient of nanofluids over a wide range. A curve fit must be used on the plot in order to extract the function from the preceding plot. Excel 2021 software was used to accomplish the curve fitting. As shown in Figure 8, the power function was utilized to provide the desired curve fitting.

Since all data obtained from the CFD model collapse into a single curve, one has to examine the gamma (γ) function against the published data to check the validity of the empirical equation. Therefore, data have been taken from serval publications for comparison. Dayou et al. [10] provided data to examine the thermal performance of MWCNT/water nanofluid flows in a concentric pipe heat exchanger with flow rates varying from 1.5 to 2.5 LPM of nanofluid. Also, the data provided by Azmi et al. [22] concluded that the SiO₂ nanofluid gives a maximum experimental heat transfer coefficient, which increases with increasing nanoparticle volume fractions up to 3.0% volume. Furthermore, Bose et al. [23] provided data to examine the convective heat transfer coefficient of the Cu/water nanofluids under uniform wall heat flux flowing via a circular tube. All these data have been used to evaluate the empirical equation for the independent variable gamma (γ), to determine the nanofluid Nusselt number and then to estimate the value of heat transfer coefficients the nanofluids, as can be seen in Figure 9.

The experimental/numerical data provided by [10], [22], and [23], and the curve fit predictions exhibit exceptional consistency, as seen in Figure 9. The independent variable gamma (γ) governs all variable parameters in an extraordinarily straightforward equation, which can then predict the value of the nanofluids heat transfer coefficients regardless of different heat exchanger geometries, turbulent flow ($Re\ge 4000$), and any other thermal parameters of a wide range of nanoparticles properties. The correlation generated for the study’s CFD data revealed suitable agreement when determining the nanofluid heat transfer coefficients. The finding indicates that the proposed correlation is appropriate in anticipating convective heat transfer coefficients especially for lower values of Nu. Furthermore, it provides a proper generalized solution in a prediction of the convective heat transfer coefficients for a wide range of different nanoparticle material properties. Indeed, the power function provided by Excel software provides consequential curve fitting for the numerical model. However, with access to experimental data, this function can be effectively tuned by proper data reduction to estimate the desired value of the coefficient and exponent. Finally, this correlation is highly esteemed by the professionals involved in designing the heat exchanger given that the correlation provides instant, reliable ways to obtain the heat transfer coefficients and the parameters needed to obtain the intended outcomes without running sophisticated numerical modelling or conducting onerous experimental setups.

5. Conclusions

In this study, numerical validation was conducted for experimental data to determine the thermal performance of TiO₂ nanofluids, flowing in a horizontal counterflow double tube heat exchanger under turbulent flow conditions at Reynolds numbers ranging from 4,000 to 18,000. The finding above demonstrates that CFD tools like ANSYS/Fluent^® (i.e., ANSYS Fluent Release 15.0), offers a strong way to acquire a solid grasp of heat transfer performance and validation across a broad range of operating conditions. The numerical results validate that the use of TiO₂-water nanofluid partially gives higher heat transfer coefficients than a base fluid does. Also, the result predicted from the numerical model agrees very well with experimental findings, and the Xuan and Li correlation for predicting the Nusselt number does not apply to a TiO₂ nanofluid. However, Pak and Cho’s correlation agrees very well with both experimental and numerical findings. Additional validation of the numerical model showed that the change in temperature of the hot water only increases the heat transfer rate, which will not add significance to the heat transfer coefficient of nanofluid. The numerical results showed that with an increase in the Reynolds number and volume concentration, the convective heat transfer coefficient of nanofluids increases. However, the numerical finding cannot predict the convective heat transfer coefficient for a wide range of nanoparticle material properties in a solo run. Thus, the results of this investigation introduce a new method for estimating the nanofluid heat transfer coefficient reliably and straightforwardly. By introducing and analysing a set of nondimensional parameters that were verified against a variety of publicity available data, nondimensional correlation that is broadly applicable was produced. When calculating the output parameters, like the nanofluid heat transfer coefficient, for a given set of independent parameters, experts in the heat transfer process can save a significant amount of time and effort by utilizing these correlations. These estimations can be acquired without the need to perform laborious experimental or run extensive, complex finite difference models.