Seismic Risk of Infrastructure Systems with Treatment of and Sensitivity to Epistemic Uncertainty
Abstract
:1. Introduction
- Cause or hazard: regional seismicity.
- Physical damage: fragility of vulnerable components as a function of local seismic intensities.
- Functional consequences: network flow analysis for the considered systems.
- Impact: injured, fatalities, displaced population, economic loss.
2. Treatment of and Sensitivity to Epistemic Uncertainty
2.1. Modelling of Input Epistemic Uncertainty
- Epistemic uncertainty on model form (Type I): a logic tree is commonly used, composed of a chain of sequential modules, the latter intended as groups of parallel branches or choices. In this framework, alternative models Θ, corresponding to logic tree branches within each module, are considered in each step of the analysis. Individual simulations are carried out for each different combination of sequential branches (i.e., of models), thus yielding multiple results, for instance in terms of mean annual frequency (MAF) of exceedance curves of a performance metric. Weights, summing up to one, are attached to branches to indicate subjective degrees of belief of the analyst in each model. This is common practice in probabilistic seismic hazard analysis (PSHA), where a typical uncertainty in model form is represented by the ground motion prediction equation (GMPE). The outcome is usually expressed in terms of mean hazard curve over the logic tree, obtained as a weighted average of the curves from all branches (Bommer and Scherbaum, 2008) [8]. Upper and lower fractile curves and/or a confidence interval around the mean curve are often computed based on the set of curves from the tree, so as to quantify the effect of epistemic uncertainty on the results.
- Epistemic uncertainty on model parameters (Type II): each model parameter θ is modelled with a random variable, whose distribution describes its epistemic uncertainty. (a) The parameters (e.g., the maximum magnitude Mmax) are arranged in a hierarchical model together with aleatory uncertainty (e.g., the magnitude M). In this case, only one simulation is carried out and the risk analysis provides a single result (i.e., a single MAF curve of a performance metric, for instance), embedding the effects of both aleatory and epistemic uncertainty (e.g., Franchin and Cavalieri, 2015 [18], Su et al., 2020 [19], Morales-Torres et al., 2016 [20]). This approach prevents the analyst from properly treating Type II epistemic uncertainty, in terms of computing confidence intervals or fractiles, and identifying distinct contributions of input aleatory and epistemic uncertainty within the output uncertainty (refer to Figure 8 for an example). (b) Alternatively, the risk analysis is repeated for discrete values of each parameter θ (e.g., 16%, 50% and 84% fractiles). This approach, involving a higher associated computational effort, allows one, however, to arrange parameters in a logic tree, as done for Type I uncertainty. Since the discrete values of the model parameters are values from a probability distribution, their choice, as well as that of the corresponding weights attached to tree branches, could be assigned, for instance, according to Miller and Rice (1983) [21].
- Epistemic uncertainty of both Type I and II: (a) The analyst can decide to adopt approach (2a) for Type II uncertainty. This cheaper approach leads to carrying out the expectation over all sources of uncertainty, presenting the results as the mean over the logic tree. However, in this case, confidence intervals or fractiles would refer only to part of the total epistemic uncertainty (i.e., the one related to models). (b) The second option, involving approach (2b) for Type II uncertainty, consists of building an expanded logic tree for the treatment of both Type I and II uncertainties.
2.2. Case of Correlated Parameter Values
- The extreme values of all parameters are obtained from their marginal distributions. Based on this, a sufficiently accurate discretisation of the parameter supports is carried out, thus building a grid of points.
- The joint CDF and probability density function (pdf) are evaluated at all grid points, using the parameters of the multivariate distribution (e.g., normal with mean vector μX and covariance matrix Cxx).
- For each desired fractile of the joint distribution, corresponding to a CDF value F*, the points characterised by CDF = F* are extracted, as displayed with cyan dots in Figure 2a with reference to the example described above and the 50% fractile. The same cyan dots are also shown in Figure 2b, each with its joint pdf value. The accuracy in this step is of course a function of the discretisation employed in step #1 and the tolerance fixed for CDF around F*.
- Among the extracted points, the desired fractile of the joint distribution is selected as the one with the highest value of the joint pdf, as shown with a black dot in Figure 2b. The same selected point is also shown in Figure 2a. The selected set of values is the most likely parameter set; as such, it is not supposed to lead to extreme combinations of values and, in the case of fragility parameters, to intersection of fragility curves related to different limit states.
2.3. Quantification of Output Uncertainty Due to the Epistemic Component
2.4. Sensitivity to Input Epistemic Uncertainty
3. Application
3.1. Hazard, Vulnerability and Performance Metric for Gas System
3.2. The Synthetic City
3.3. Adopted Logic Tree
- Mmax for all the seismic sources
- (a)
- 6.5 {0.4};
- (b)
- 7.0 {0.6}
- GMPE
- Fractiles of both residual terms in the HAS fragility model
- (a)
- 91.5% {0.25};
- (b)
- 50% {0.5};
- (c)
- 8.5% {0.25}.
- Fractiles of joint normal distribution of fragility curve parameters for RC buildings
- (a)
- 91.5% {0.25};
- (b)
- 50% {0.5};
- (c)
- 8.5% {0.25}.
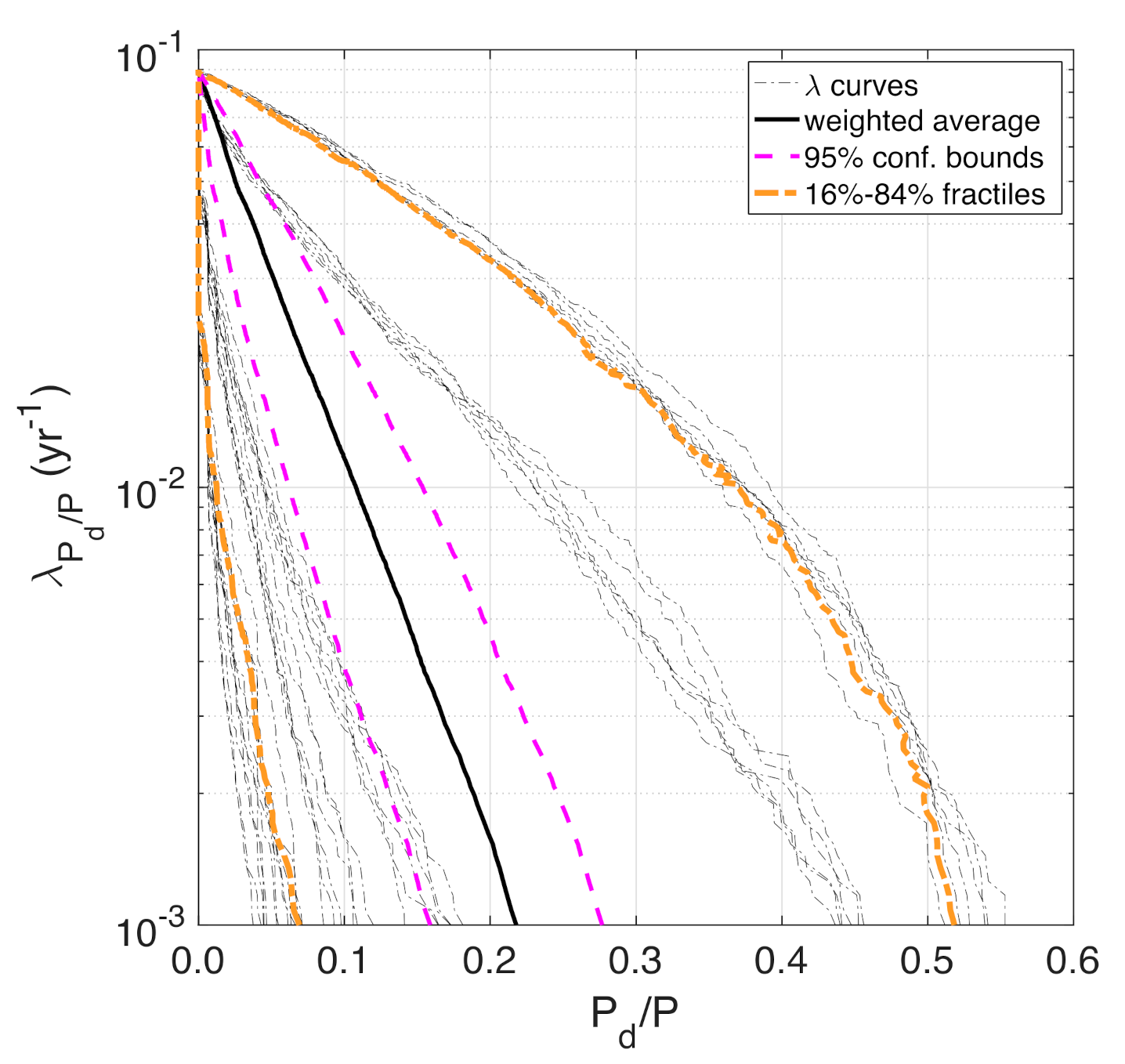
3.4. Results and Discussion
- The IMs of interest (i.e., PGA, PGV and PGD) at vulnerable components’ sites are estimated using the OOFIMS hazard module;
- The damage state of the components at risk, belonging to both gas and building systems, is estimated through the adopted fragility models;
- The connectivity and operational state are assessed for the damaged gas network;
- The gas system’s performance is estimated through the adopted flow-based metric;
- A second performance metric of interest for this application is computed, namely, the displaced population, Pd. In the implemented model, people can be displaced from their homes either because of direct physical damage (building usability) or because of lack of basic services/utilities (building habitability), resulting from damage to interdependent utility systems (only gas system in this case). See Franchin and Cavalieri (2015) [18] for further details.
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Der Kiureghian, A.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Gokkaya, B.U.; Baker, J.W.; Deierlein, G.G. Quantifying the impacts of modeling uncertainties on the seismic drift demands and collapse risk of buildings with implications on seismic design checks. Earthq. Eng. Struct. Dyn. 2016, 45, 1661–1683. [Google Scholar] [CrossRef]
- Rokneddin, K.; Ghosh, J.; Dueñas-Osorio, L.; Padgett, J.E. Uncertainty Propagation in Seismic Reliability Evaluation of Aging Transportation Networks. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Petty, M.D. Calculating and Using Confidence Intervals for Model Validation. In Proceedings of the 2012 Fall Simulation Interoperability Workshop, Orlando, FL, USA, 10–14 September 2012. [Google Scholar]
- Visser, H.; Folkert, R.J.M.; Hoekstra, J.; De Wolff, J.J. Identifying key sources of uncertainty in climate change projections. Clim. Chang. 2000, 45, 421–457. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Bommer, J.J.; Scherbaum, F. The use and misuse of logic trees in probabilistic seismic hazard analysis. Earthq. Spectra 2008, 24, 997–1009. [Google Scholar] [CrossRef]
- Zhang, H.; Mullen, R.L.; Muhanna, R.L. Interval Monte Carlo methods for structural reliability. Struct. Saf. 2010, 32, 183–190. [Google Scholar] [CrossRef]
- Alam, M.S.; Barbosa, A.R. Probabilistic seismic demand assessment accounting for finite element model class uncertainty: Application to a code-designed URM infilled reinforced concrete frame building. Earthq. Eng. Struct. Dyn. 2018, 47, 2901–2920. [Google Scholar] [CrossRef]
- Tate, E.; Muñoz, C.; Suchan, J. Uncertainty and sensitivity analysis of the HAZUS-MH flood model. Nat. Hazards Rev. 2015, 16, 04014030. [Google Scholar] [CrossRef]
- Cavalieri, F.; Franchin, P. Treatment of and Sensitivity to Epistemic Uncertainty in Seismic Risk Assessment of Infrastructures. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP13), Seoul, Korea, 26–30 May 2019. [Google Scholar]
- Cavalieri, F. Steady-state flow computation in gas distribution networks with multiple pressure levels. Energy 2017, 121, 781–791. [Google Scholar] [CrossRef]
- Cavalieri, F. Seismic risk assessment of natural gas networks with steady-state flow computation. Int. J. Crit. Infrastruct. Prot. 2020, 28, 100339. [Google Scholar] [CrossRef]
- Franchin, P.; Cavalieri, F. OOFIMS (Object-Oriented Framework for Infrastructure Modelling and Simulation). Available online: https://sites.google.com/a/uniroma1.it/oofims/home/ (accessed on 13 October 2020).
- MATLAB® R2019b; The MathWorks Inc.: Natick, MA, USA, 2019.
- SYNER-G Collaborative Research Project, Funded by the European Union within Framework Programme 7 (2007–2013), under Grant Agreement No. 244061, 2012. Available online: http://www.syner-g.eu/ (accessed on 13 October 2020).
- Franchin, P.; Cavalieri, F. Probabilistic assessment of civil infrastructure resilience to earthquakes. Comput. Civ. Infrastruct. Eng. 2015, 30, 583–600. [Google Scholar] [CrossRef]
- Su, L.; Li, X.L.; Jiang, Y.P. Comparison of methodologies for seismic fragility analysis of unreinforced masonry buildings considering epistemic uncertainty. Eng. Struct. 2020, 205, 110059. [Google Scholar] [CrossRef]
- Morales-Torres, A.; Escuder-Bueno, I.; Altarejos-García, L.; Serrano-Lombillo, A. Building fragility curves of sliding failure of concrete gravity dams integrating natural and epistemic uncertainties. Eng. Struct. 2016, 125, 227–235. [Google Scholar] [CrossRef] [Green Version]
- Miller III, A.C.; Rice, T.R. Discrete approximations of probability distributions. Manag. Sci. 1983, 29, 352–362. [Google Scholar] [CrossRef]
- Yilmaz, C.; Silva, V.; Weatherill, G. Probabilistic framework for regional loss assessment due to earthquake-induced liquefaction including epistemic uncertainty. Soil Dyn. Earthq. Eng. 2020, 106493. [Google Scholar] [CrossRef]
- Benjamin, J.R.; Cornell, C.A. Probability, Statistics, and Decision for Civil Engineers; McGraw Hill, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Merz, B.; Thieken, A.H. Flood risk curves and uncertainty bounds. Nat. Hazards 2009, 51, 437–458. [Google Scholar] [CrossRef]
- Celik, O.C.; Ellingwood, B.R. Seismic fragilities for non-ductile reinforced concrete frames–Role of aleatoric and epistemic uncertainties. Struct. Saf. 2010, 32, 1–12. [Google Scholar] [CrossRef]
- Celarec, D.; Ricci, P.; Dolšek, M. The sensitivity of seismic response parameters to the uncertain modelling variables of masonry-infilled reinforced concrete frames. Eng. Struct. 2012, 35, 165–177. [Google Scholar] [CrossRef]
- Porter, K.A.; Beck, J.L.; Shaikhutdinov, R.V. Sensitivity of building loss estimates to major uncertain variables. Earthq. Spectra 2002, 18, 719–743. [Google Scholar] [CrossRef] [Green Version]
- Pourreza, F.; Mousazadeh, M.; Basim, M.C. An efficient method for incorporating modeling uncertainties into collapse fragility of steel structures. Struct. Saf. 2021, 88, 102009. [Google Scholar] [CrossRef]
- Easa, S.M.; Ma, Y.; Liu, S.; Yang, Y.; Arkatkar, S. Reliability Analysis of Intersection Sight Distance at Roundabouts. Infrastructures 2020, 5, 67. [Google Scholar] [CrossRef]
- Sevieri, G.; De Falco, A.; Marmo, G. Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams. Infrastructures 2020, 5, 22. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Cremen, G.; Baker, J.W. Variance-based sensitivity analyses and uncertainty quantification for FEMA P-58 consequence predictions. Earthq. Eng. Struct. Dyn. 2020. [Google Scholar] [CrossRef]
- Crowley, H.; Bommer, J.J.; Pinho, R.; Bird, J. The impact of epistemic uncertainty on an earthquake loss model. Earthq. Eng. Struct. Dyn. 2005, 34, 1653–1685. [Google Scholar] [CrossRef]
- Tyagunov, S.; Pittore, M.; Wieland, M.; Parolai, S.; Bindi, D.; Fleming, K.; Zschau, J. Uncertainty and sensitivity analyses in seismic risk assessments on the example of Cologne, Germany. Nat. Hazards Earth Syst. Sci. 2014, 14, 1625–1640. [Google Scholar] [CrossRef] [Green Version]
- Bensi, M.; Weaver, T. Evaluation of tropical cyclone recurrence rate: Factors contributing to epistemic uncertainty. Nat. Hazards 2020, 103, 3011–3041. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
- Sobol’, I.M. Sensitivity analysis for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Sallaberry, C.J.; Helton, J.C. An introduction to complete variance decomposition. Shock Vib. Dig. 2006, 38, 542–543. [Google Scholar]
- Cannavó, F. Sensitivity analysis for volcanic source modeling quality assessment and model selection. Comput. Geosci. 2012, 44, 52–59. [Google Scholar] [CrossRef]
- Bovo, M.; Buratti, N. Evaluation of the variability contribution due to epistemic uncertainty on constitutive models in the definition of fragility curves of RC frames. Eng. Struct. 2019, 188, 700–716. [Google Scholar] [CrossRef]
- Searle, S.R.; Casella, G.; McCulloch, C.E. Variance Components; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 978-0-470-00959-8. [Google Scholar]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, F.K.; Nossent, J.; Sarrazin, F.; Pianosi, F.; van Griensven, A.; Wagener, T.; Bauwens, W. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model. Environ. Model. Softw. 2017, 91, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Weatherill, G.; Esposito, S.; Iervolino, I.; Franchin, P.; Cavalieri, F. Framework for Seismic Hazard Analysis of Spatially Distributed Systems. In SYNER-G: Systemic Seismic Vulnerability and Risk Assessment of Complex Urban, Utility, Lifeline Systems and Critical Facilities: Methodology and Applications; Pitilakis, K., Franchin, P., Khazai, B., Wenzel, H., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 31, pp. 57–88. [Google Scholar] [CrossRef]
- ALA (American Lifelines Alliance). Seismic Fragility Formulations for Water Systems. Part 1—Guideline; ASCE-FEMA: Reston, VA, USA, 2001. [Google Scholar]
- NIBS; FEMA. HAZUSMH MR4 Multi-Hazard Loss Estimation Methodology—Earthquake Model—Technical Manual; FEMA: Washington, DC, USA, 2007. [Google Scholar]
- Wang, Y.; O’Rourke, T.D. Seismic Performance Evaluation of Water Supply Systems; Technical Report MCEER-08-0015; MCEER: Buffalo, NY, USA, 2008. [Google Scholar]
- Dueñas-Osorio, L. Interdependent Response of Networked Systems to Natural Hazards and Intentional Disruptions. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2005. [Google Scholar]
- Crowley, H.; Colombi, M.; Silva, V. Epistemic Uncertainty in Fragility Functions for European RC Buildings. In SYNER-G: Typology Definition and Fragility Functions for Physical Elements at Seismic Risk; Pitilakis, K., Crowley, H., Kaynia, A.M., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, pp. 95–109. [Google Scholar]
- Akkar, S.; Bommer, J.J. Empirical equations for the prediction of PGA, PGV and spectral accelerations in Europe, the Mediterranean region and the Middle East. Seismol. Res. Lett. 2010, 81, 195–206. [Google Scholar] [CrossRef] [Green Version]
- Boore, D.M.; Atkinson, G.M. Ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods between 0.01 s and 10.0 s. Earthq. Spectra 2008, 24, 99–138. [Google Scholar] [CrossRef] [Green Version]
- Gabbianelli, G.; Cavalieri, F.; Nascimbene, R. Seismic vulnerability assessment of steel storage pallet racks. Ing. Sismica 2020, 37, 18–40. [Google Scholar]
- Franchin, P.; Lupoi, A.; Noto, F.; Tesfamariam, S. Seismic fragility of reinforced concrete girder bridges using Bayesian belief network. Earthq. Eng. Struct. Dyn. 2016, 45, 29–44. [Google Scholar] [CrossRef]









| Yield | Collapse | |||
|---|---|---|---|---|
| μlnY | σlnY | μlnC | σlnC | |
| Mean | −1.832 | 0.474 | −1.091 | 0.485 |
| CoV (%) | 33 | 21 | 48 | 24 |
| Yield | Collapse | ||||
|---|---|---|---|---|---|
| μlnY | σlnY | μlnC | σlnC | ||
| Yield | μlnY | 1 | 0.158 | 0.783 | 0.033 |
| σlnY | 0.158 | 1 | 0.118 | 0.614 | |
| Collapse | μlnC | 0.783 | 0.118 | 1 | −0.453 |
| σlnC | 0.033 | 0.614 | −0.453 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavalieri, F.; Franchin, P. Seismic Risk of Infrastructure Systems with Treatment of and Sensitivity to Epistemic Uncertainty. Infrastructures 2020, 5, 103. https://doi.org/10.3390/infrastructures5110103
Cavalieri F, Franchin P. Seismic Risk of Infrastructure Systems with Treatment of and Sensitivity to Epistemic Uncertainty. Infrastructures. 2020; 5(11):103. https://doi.org/10.3390/infrastructures5110103
Chicago/Turabian StyleCavalieri, Francesco, and Paolo Franchin. 2020. "Seismic Risk of Infrastructure Systems with Treatment of and Sensitivity to Epistemic Uncertainty" Infrastructures 5, no. 11: 103. https://doi.org/10.3390/infrastructures5110103
APA StyleCavalieri, F., & Franchin, P. (2020). Seismic Risk of Infrastructure Systems with Treatment of and Sensitivity to Epistemic Uncertainty. Infrastructures, 5(11), 103. https://doi.org/10.3390/infrastructures5110103







