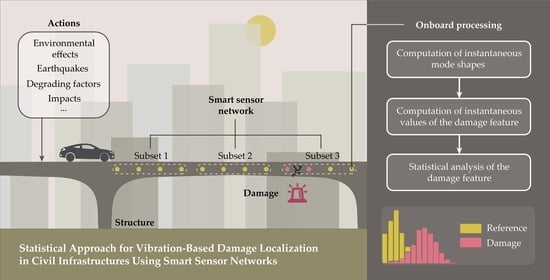
Statistical Approach for Vibration-Based Damage Localization in Civil Infrastructures Using Smart Sensor Networks

Abstract

One of the most discussed aspects of vibration-based structural health monitoring (SHM) is how to link identified parameters with structural health conditions. To this aim, several damage indexes have been proposed in the relevant literature based on typical assumptions of the operational modal analysis (OMA), such as stationary excitation and unlimited vibration record. Wireless smart sensor networks based on low-power electronic components are becoming increasingly popular among SHM specialists. However, such solutions are not able to deal with long data series due to energy and computational constraints. The decentralization of processing tasks has been shown to mitigate these issues. Nevertheless, traditional damage indicators might not be suitable for onboard computations. In this paper, a robust damage index is proposed based on a damage sensitive feature computed in a decentralized fashion, suitable for smart wireless sensing solutions. The proposed method is tested on a numerical benchmark and on a real case study, namely the S101 bridge in Austria, a prestressed concrete bridge that has been artificially damaged for research purposes. The results obtained show the potential of the proposed method to monitor the conditions of civil infrastructures.

1. Introduction

Civil infrastructure management requires the development of methods to acquire knowledge about the structural conditions and make decisions about the interventions needed to achieve the required structural performance. Structural health monitoring (SHM) systems provide information about the structural state that can support decisions about maintenance interventions. This knowledge enables the optimization of the allocation of resources based on the actual structural needs rather than scheduled ahead based on a fixed time plan.

Damage identification based on ambient vibration data is one of the most effective SHM technologies that allows the continuous acquisition of the structural response and the identification of its state using bespoke damage identification algorithms [1]. In literature, several data-driven and model-based methods have been proposed to this aim. Data-driven methods do not need a physical model and use signal processing to extract information about damage, generally enabling damage detection and localization. To quantify damage, methods based on the updating of numerical models are needed. The indicators used to identify the existence, location, and severity are often defined in terms of modal parameters extracted from vibration data. Maeck et al. [2] and Pandey et al. [3] used the modal curvature, Stubbs et al. [4] the strain energy, and Limongelli [5] and Domaneschi [6] the interpolation error.

An important component of vibration-based methods is the data management chain that leads from measurements collected on the structure to indicators of the structural state through the interpretation and analysis of the acquired data. The data management chain includes data acquisition, transmission, storage, and processing, and its efficiency depends on the characteristics of the technological components deployed to perform such operations.

Notwithstanding their undoubtful advantages, the adoption of SHM systems is not yet widespread. One of the reasons is the difficulty of estimating, before their installation, the return over the investment they provide [7,8,9]. This makes the infrastructure owners skeptical about the investment. Further to this, the initial cost of a traditional SHM system can be very high due to the need for wires to connect the sensors to a central monitoring station for data transmission [10]. Since the late 1990s, many wireless sensing prototypes with onboard processing capacity have been developed [11]. The aim was to reduce both data transmission and processing costs. One of the main issues when using wireless technologies is the limited power supply of the communication channels, which have to rely on batteries or energy harvesting systems.

In civil engineering, periodic inspections are generally enough to monitor the onset and evolution of damage or degradation phenomena. However, in some cases the real-time estimation of the structural health state becomes of the utmost importance, for example in the aftermath of a natural or manmade disaster. In the literature, algorithms based on QR decomposition, Jacobi rotations, and tridiagonalization approaches [12,13,14] have been proposed to decompose a matrix of structural responses into its eigenspace. Eigenvectors define the set of basis functions that are most efficient to describe data variability and can thus be employed for both data reduction strategies and modal identification. However, most of these methods are unsuitable for real-time implementation if they are applied on successive batches of samples, especially when large data volumes must be processed through edge computing onboard dense wireless sensor networks. First-order eigen perturbation (FOEP) techniques have been proposed to update the eigenspace in a recursive framework, thus being appropriate for real-time processing. Higher-order stabilized perturbation approaches have also been recently proposed, aimed at achieving higher levels of accuracy by efficiently tackling the issue of closely spaced eigenvalues [15]. However, the computational cost of these methods is still prohibitive for edge computing onboard low-power sensing nodes. Considering, e.g., the method based on recursive correlation analysis (RCCA) presented in [16], the most demanding part related to the eigenspace update has a computational complexity in the order of $O\left(d^3\right)$ per input sample, with $d$ indicating the number of eigenvectors of the block covariance matrix of structural responses. Other recursive approaches are typically characterized by similar complexity [17]. Moreover, most of the aforementioned methods require data collected from all the instrumented locations to be processed simultaneously and in a centralized fashion. This necessitates an accurate synchronization and high data transmission rate, which might be challenging for large and densely instrumented structures, especially when wireless sensor networks are employed.

Additionally, the complex network topologies necessary to avoid coverage issues in large civil structures pose several challenges that may affect the efficiency of battery-powered devices. An effective solution to these issues consists of the decentralization of processing tasks (e.g., filtering and compression) to reduce the volume of data transmitted. In the last years, researchers have developed distributed computing platforms with smart sensing nodes that can collect and process small datasets, thereby reducing both the volume of transmitted data and the power consumption of the sensing system. Yun et al. proposed a method based on wavelet entropy analysis [18], while Sadhu and Narasimhan introduced a decentralized filtering approach based on the stationary wavelet packet transform (SWPT) [19]. Wang and Chen pursued the online identification of time-varying structural features employing a recursive HHT-based procedure [20].

To further improve energy efficiency, a piece of research has been devoted to removing the comparison step between the current estimate and the “baseline” state in continuous monitoring strategies. Such methods are addressed as “baseline free” methods [21].

The constraints relevant to reduced volumes of data lead to short, nonstationary vibration signals that do not comply with the principal underlying assumptions of operational modal analysis (OMA) [22]. To overcome this problem, innovative algorithms for the identification of instantaneous vibration parameters have been developed and successfully applied to civil structures [23,24,25]. The application of these algorithms provides near real-time estimates of the modal parameters that can be used to extract instantaneous information about the structural state. In Reference [26], a novel decentralized approach for instantaneous identification of modal parameters was presented, involving a computational cost of $O\left(pN\right)$ per input sample, onboard each node, where $p$ is the number of identified modes and $N$ is the length of the filters employed in the procedure. In Reference [27], Quqa et al. used instantaneous values of the modal parameters computed through the identification method proposed in Reference [26] to estimate a local approximation of the instantaneous values of the interpolation error [5]. The drawback of instantaneous estimates is related to the high level of uncertainty introduced by varying operational and environmental conditions that may affect the values of the damage features, thereby hampering an accurate damage identification. The use of statistical models built using large datasets enables the reduction of false or missing indication of damage. In Reference [28], the statistical interpolation damage indicator (SIDI) was proposed for this aim. The SIDI is a function of the statistical distributions of the interpolation error in the damaged and reference conditions of the structure and requires the availability of datasets relevant to these two conditions. The estimation of the SIDI requires the availability of large datasets that enable the identification of the statistical distribution of the damage feature and, from that, the computation of the damage index. This prevents a prompt estimation of the damage index due to the requirement of a large dataset that requires some time to be acquired.

In this paper, a new method for the timely computation of a statistical indicator of damage is proposed. The indicator is extracted from short vibrational responses recorded by smart decentralized networks of sensors. In this context, the term “short” refers to a length of few minutes that enables onboard processing. For instance, for the S101 bridge, adopted as a case study in this paper, the recording length is 330 s. The proposed method is expected to detect and localize damage due to a localized reduction of stiffness between a reference and an inspection state. It integrates the method for the identification of instantaneous modal parameters proposed in Reference [27] with the procedure for damage identification based on the SIDI presented in Reference [28].

The major advantages of the proposed method include:

• The possibility of onboard computation of the damage index at selected nodes, which autonomously and timely send alarm messages, without requiring complex transmission/synchronization strategies to convey data to a central processing unit.
• A limited wireless transmission rate thanks to the onboard computation of the damage index and the implementation of adaptive downsampling of the structural responses before transmission. The aim is to extract and transmit only the frequency bands containing the relevant information.
• The data-driven nature of the approach, which does not involve any model of the structure (either analytical or numerical, e.g., finite element models), thereby reducing the computational effort.

The method is demonstrated on a numerical benchmark, for which several damage scenarios were modeled, and on the S101 bridge in Austria, for which ambient vibration data measured in a number of damage states are available for research purposes [29].

The paper is organized as follows. Section 2 presents the procedure for the instantaneous identification of modal parameters. Section 3 describes the computation of the damage sensitive feature, namely the interpolation error (Section 3.1), a decentralized algorithm for its computation in smart sensor networks (Section 3.2), and the procedure for real-time identification of the novel damage index. Section 4 and Section 5 are devoted to the case studies and the relevant discussion. A discussion of the results obtained and the conclusion section end the paper.

2. Instantaneous Identification of Modal Parameters

Clustered filter banks (CFBs) have been recently proposed to identify instantaneous modal parameters of operating civil infrastructures. In Reference [26], a two-step procedure is presented for this aim. Specifically, (1) a bank of bandpass filters (the CFB) is formed selecting the values of the cutoff frequencies that enable the extraction of separate modal contributions from the recorded response, and (2) the convolution of the recorded responses with the CFBs is carried out to obtain signals with a narrow frequency content, each representative of a single modal component. The obtained narrow-band signals are analyzed to identify instantaneous frequency and amplitude estimates. Although a fully adaptive variant of this technique was recently demonstrated to be effective when dealing with strongly time-varying systems [30], the decentralized nature of the CFB-based method has been shown to be particularly suitable for distributed smart sensing systems and effective to identify structural damage when slight frequency variations are involved. In the following, the basic principles useful for the construction of CFBs are reported. Interested readers can refer to [26] for more details.

Step 1. A training signal ${\overline{x}}_i\left[t\right]$ of length $s$ is collected at each ($i$-th) instrumented location (with $i=1,\dots ,I$) and transmitted to a central node. A wavelet packet transform (WPT) is applied to each of the $I$ signals, generating $I$ sets of $2^n$ wavelet components $w_{i,k}\left[t\right]$, where $k=1,\dots ,2^n$ indicates the frequency sub-band index and $n$ is the level of the WPT. The $k$-th wavelet component $w_{i,k}\left[t\right]$ is thus a filtered version of the $i$-th response ${\overline{x}}_i\left[t\right]$, obtained using a narrow bandpass filter with impulse response $b_k\left[h\right]$ and cutoff frequencies $f_{low}=\left(k-1\right)F_s/2^n$ and $f_{high}=k{F}_s/2^n$, where $F_s$ is half of the sampling frequency of ${\overline{x}}_i\left[t\right]$. It should be noted that the set of filtered signals $w_{i,k}\left[t\right]$ obtained, considering all the components from $k=1$ to $k=2^n$, provides a representation of the original signal in the time-frequency domain.

In analogy with the operating deflection shapes (ODSs) used in traditional OMA, herein the instantaneous sub-band shape (SBS) vectors ${\mathsf{\phi }}_k\left[t\right]$ are defined. The component of the $k$-th SBSs at the $i$-th instrumented location is:

$${\phi }_{i,k}\left[t\right]=\frac{w_{i,k}\left[t\right]}{w_{r,k}\left[t\right]}$$

(1)

where $r$ represents the location chosen as a reference to normalize all the SBSs. If the impulse response $b_k\left[h\right]$ of the $k$-th filter has a narrow frequency band, i.e., the level of the transform $n$ is sufficiently high, in the frequency regions close to a resonant frequency of the structure, the SBSs of neighboring wavelet components ${\mathsf{\phi }}_k\left[t\right]$ and ${\mathsf{\phi }}_{k+1}\left[t\right]$ are similar to each other. This similarity can be quantified using the Modal Assurance Criterion (MAC). A similar approach is adopted in the framework of the enhanced frequency domain decomposition (EFDD) technique for the extraction of resonant peaks in the power spectra of analyzed signals [31].

Evaluating the MAC between each couple of consecutive instantaneous SBSs, $2^n-1$ values (namely, $m_k\left[t\right]$) in the range from 0 to 1 are calculated as

$$m_k\left[t\right]=\frac{{\left|{\mathsf{\phi }}_k^{\mathrm{T}}\left[t\right]{\mathsf{\phi }}_{k+1}\left[t\right]\right|}^2}{\left({\mathsf{\phi }}_k^{\mathrm{T}}\left[t\right]{\mathsf{\phi }}_k\left[t\right]\right)\left({\mathsf{\phi }}_{k+1}^{\mathrm{T}}\left[t\right]{\mathsf{\phi }}_{k+1}\left[t\right]\right)}$$

(2)

where elements close to 1 indicate the presence of similar neighboring SBSs. The set of instantaneous $m_k\left[t\right]$ values is defined in [30] as the modal assurance distribution (MAD). The average of the SBSs computed according to Equation (1) using a training signal of $s$ samples reads:

$${\overline{\phi }}_{i,k}=\frac{1}{s}{\displaystyle \sum }_{t=1}^s{\phi }_{i,k}\left[t\right]$$

(3)

Using ${\overline{\phi }}_{i,k}$, a set of average MAC values, $m_k$ can be calculated and employed to partition the filters $b_k\left[h\right]$ into clusters that generate response contributions associated with different modal responses. In particular, a set of bandpass filters that generate $m_k\ge \eta$, with $\eta$ a user-defined threshold can be merged into a single “clustered” filter ${\overline{b}}_j\left[h\right],$ associated with the $j$-th structural vibration mode.

Step 2. Upon generating the CFB, the ${\overline{b}}_j\left[h\right]$ filters can be applied to the new incoming signal $x_i\left[t\right]$ in order to extract decoupled modal responses at each instrumented location independently from the others. The $j$-th modal response extracted at the $i$-th physical point can be obtained as

$$y_{i,j}\left[t\right]={\displaystyle \sum }_{h=0}^{N-1}{x}_i\left[t-h\right]{\overline{b}}_j\left[h\right]$$

(4)

where $N$ is the length of ${\overline{b}}_j\left[h\right]$. It should be noted that since $y_{i,j}\left[t\right]$ is monocomponent, the Hilbert transform can be applied to calculate its instantaneous frequency, which can be assumed as the instantaneous natural frequency of the structure, and amplitude, which can be employed to calculate an instantaneous estimate of the structural mode shape as:

$${\varphi }_{i,j}\left[t\right]=\frac{y_{i,j}\left[t\right]}{y_{r,j}\left[t\right]}$$

(5)

3. Damage Identification Method

3.1. The Damage Sensitive Feature: Interpolation Error

The Interpolation error method (IM) was proposed by Limongelli [32], and it can be used to localize damage on an instrumented structure. To do that, the method exploits the properties of interpolating cubic splines. Specifically, the IM assumes that an increase of interpolation error occurs at the damaged locations. The IM was originally formulated in terms of ODSs [33], but it can also be applied using mode shapes retrieved from OMA, see, e.g., Reference [34].

To find the interpolation error $E_{i,j}$ at a given location $i$ for a single mode shape $j$, a cubic spline interpolation line is passed through all the measured points of the mode shape except the point $i$. The location $i$ is one of the $i=1, \dots ,I$ instrumented locations, that is the locations in which a sensor has been installed, whereas the mode shape $j$ is one of the $j=1, \dots ,J$ identified mode shapes. The interpolation error at location $i$ for the mode shape $j$ is computed as the absolute value of the difference between the real value of the mode shape at that location ${\varphi }_{j,i}$ and the interpolated value ${\widehat{\varphi }}_{j,i}$, according to Equation (6).

$$E_{i,j}=\left|{\varphi }_{j,i}-{\widehat{\varphi }}_{j,i}\right|$$

(6)

The root sum squared of the interpolation errors $E_{i,j}$ computed at the location $i$ for $j=1,\dots ,J$ can be used to combine the interpolation errors at that location. In this way, a single damage sensitive feature is computed at each instrumented location, accounting for the contributions from multiple mode shapes, see Equation (7).

$$E_i=\sqrt{{\displaystyle \sum }_{j=1}^J{E}_{i,j}{}^2}=\sqrt{{\displaystyle \sum }_{j=1}^J{\left|{\varphi }_{j,i}-{\widehat{\varphi }}_{j,i}\right|}^2}$$

(7)

The increase of the interpolation error $E_i$ between the reference and a possibly damage scenario highlights the occurrence of damage at the location $i$. It should be noted that, due to its definition, the estimation of the interpolation error at the boundaries of the sensed interval (e.g., first and last instrumented location) is prone to considerable inaccuracies [35].

3.2. The Decentralized Algorithm: Clamped-Clump Interpolation Method

In applications involving wireless sensing nodes, data transmission is typically the most energy-consuming operation compared to sensing and other simple tasks, which are generally performed onboard distributed monitoring systems. Therefore, the centralized estimation of the interpolation error may be particularly challenging, especially considering large civil infrastructures where multi-hop transmissions, i.e., multiple levels of transmissions would be necessary. On the other hand, the use of a decentralized topology network entails a reduction of the transmitted data, since the evaluation of the damage index can be achieved considering small subsets of sensors.

Recently, the clump interpolation method (CIM) and its enhanced variant, the clamped-clump interpolation method (C²IM), have been proposed for damage identification for applications involving wireless sensor networks. This method computes the damage sensitive feature, i.e., the interpolation error, using a limited number of components of the mode shapes [27]. Specifically, sensing nodes are organized into subsets based on their spatial distribution, such that the sensors in each subset can reach a subset “head” node (one for each subset) through wireless transmission. Following an initialization phase (Step 1) consisting of network formation and estimation of baseline parameters, all the nodes in a subset can transmit the extracted modal responses to the subset head, where the interpolation error can be calculated instantaneously for each instrumented location (Step 2). At each subset head, only the responses extracted at the locations included within the specific subset are available, and thus the spline interpolation is performed using partial estimates of the mode shapes. Interested readers can refer to [27] for an exhaustive theoretical background on CIM and C²IM. To make the paper self-contained, the principal aspects of the C²IM are herein summarized.

Step 1. A CFB for the extraction of decoupled modal responses is generated as shown in Section 2 in a centralized process. Moreover, applying the filter of the $j$-th mode to the training signal, the instantaneous mode shape can be calculated using Equation (5). The average of the instantaneous estimates of the mode shape, calculated in the training interval, is assumed as the “baseline” mode shape of the $j$-th mode. The slope of the baseline mode shape at the instrumented locations is obtained using a finite difference method (i.e., forward, backward, or central) and used to set the boundary conditions for the spline interpolation at the edges of each subset. Finally, the baseline interpolation error is evaluated at this step, for later use to estimate the damage index onboard the nodes.

At the end of the first step, the CFB is transmitted to each sensing node in the network, while the baseline parameters are transmitted to the subset heads. Step 1 should be performed at the beginning of the procedure and whenever the CFB becomes no more suitable to filter the structural response due to substantial variations in the modes of the monitored structure (e.g., after considerable damage or temperature variation).

Step 2. Following the initialization, each node is able to collect and filter the structural response using the CFB generated in Step 1. Decoupled modal responses are instantaneously evaluated and sent to the reference subset head. Here, partial mode shapes are calculated using Equation (5), and the interpolation error is evaluated by imposing the continuity of the interpolating function and of its first and second derivatives at all the knots (i.e., the interpolation points). The slope of the mode shapes evaluated in Step 1 is used to define the rotation at the boundaries of the interpolation domain.

In Reference [27], the mode shapes used in the calculation of the interpolation error are obtained employing a median filter (i.e., at each time, the component of the modal shape is assumed as the median value computed on the previous samples) onboard the subset head. However, this process may be energy consuming if the kernel of the filter is particularly wide, affecting network efficiency.

Since the value of the interpolation error cannot be accurately computed at the boundaries of each subset, several network configurations are considered in order to have, for each sensor, at least one configuration where it is not placed at the boundary. In this study, to calculate the damage sensitive feature at all possible locations, the sensor subsets are reorganized at defined time intervals by switching between two different options. In particular, these two options have subset boundaries at different locations. It should be noted that interferences due to the overlap of subsets of sensors can be addressed using algorithms such as the carrier-sense multiple access (CSMA) strategy [36].

3.3. The Damage Index: Modified Statistical Interpolation Damage Index

The CFB-based identification method allows the instantaneous identification of modal parameters of an instrumented structure. As described in Section 2, this is accomplished by extracting narrow-band components of the recorded responses using a bank of bandpass filters. In the case of decentralized sensor networks, partial estimates of structural mode shapes can be used to feed the C²IM, which is discussed in Section 3.2. Each instantaneous estimate of modal parameters provides a sample of the damage sensitive feature. Statistical characterization of it can thus be obtained considering the entire processed signal.

In Reference [28], the Statistical Interpolation Damage Index (SIDI) was proposed to identify the location of the damage. The SIDI, at a given location $i$, is defined in terms of the distribution of the damage feature $E_i$ defined in Equation (7). In the following, the suffix $i$ is dropped for clarity of notation, and the symbol $E$ is used to indicate the interpolation error at the generic instrumented location $i$. The suffix $S$ is used to indicate the generic inspection state of the structure, whereas the suffix $R$ indicates the reference scenario. Therefore, $E_S$ is the damage feature at location $i$ when the structure is in state $S$. The damage feature in a generic state $S$ is re-defined as the probability of exceedance of a fixed threshold $E_T$, as follows:

$$PT{E}_S\left(E_T\right)={{\displaystyle \int }}_{E_T}^{\infty }{f}_{E_s}\left(E\right)dE=1-F_{E_S}\left(E_T\right)$$

(8)

where $f_{E_s}\left(E\right)$ and $F_{E_S}\left(E_T\right)$ are the probability density function (PDF) and the cumulative distribution function, respectively, of the damage feature $E$ in state $S$. To better clarify the meaning of probability of threshold exceedance (PTE), two distributions which represent the PDFs of the damage feature (interpolation error $E$) in the reference (green) and inspection states (red) are reported in Figure 1. The green and red patterns correspond to the PTEs in the reference and the generic state $S$, respectively.

The damage index $SIDI$ is defined in Equation (9) as the positive variation the probability of threshold exceedance $PT{E}_S\left(E_T\right)$ in the state $S$, with respect to the value in the reference state $PT{E}_R\left(E_T\right)$.

$${\mathrm{SIDI}}_{\mathrm{S}}\left(E_T\right)=\frac{PT{E}_S\left(E_T\right)-PT{E}_R\left(E_T\right)}{{\overline{PTE}}_R\left(E_T\right)}\ge 0$$

(9)

Negative values of the SIDI are discarded, since they indicate a decrease of the damage feature that may occur only at locations where damage is not increased. In Figure 1, the SIDI corresponds to the difference between the red and green areas normalized with respect to the probability of non-detection in the reference scenario ${\overline{PTE}}_R\left(E_T\right)$. This is the area under the greed curve at the left of the threshold. The normalization leads to values of the damage index between 0 and 1 for, respectively, the reference and severely damaged states.

In Reference [28], the value of the threshold $E_T$ is defined in terms of a given probability of threshold exceedance $\alpha$ in the reference scenario, which corresponds to the probability of false alarm. A value equal to 5% of the probability of false alarm $\alpha$ was chosen to define the threshold.

$$PT{E}_R\left(E_T\right)={{\displaystyle \int }}_{E_T}^{\infty }{f}_{E_R}dE=1-F_{E_R}\left(E_T\right)=\alpha$$

(10)

In this paper, a variant of the SIDI is proposed to increase its sensitivity to damage. To this aim, the threshold is automatically chosen as the value that maximizes the absolute value of the numerator of Equation (9), and the denominator is modified to obtain a value that decreases with damage, thus leading to an increase of the index.

The value of the threshold $E_T$ that maximizes the numerator of Equation (9) can be found as the value that zeroes its first derivative:

$$\frac{d\left[PT{E}_S\left(E\right)-PT{E}_R\left(E\right)\right]}{dE}=0$$

(11)

Writing the probability of threshold exceedance PTE in terms of the cumulative distribution $F_E$, the condition that zeroes the first derivative of the numerator in Equation (9) reads:

$$\frac{d\left[1-F_{E_S}\left(E\right)-1+F_{E_R}\left(E\right)\right]}{dE}=\frac{d}{dE}{{\displaystyle \int }}_E^{\infty }\left[f_{E_R}\left(E\right)-f_{E_S}\left(E\right)\right]dE=0$$

(12)

Therefore, the value of the threshold $E_T$ is chosen as the value of $E$ for which the PDFs of the damage sensitive feature in state $R$ and in state $S$ present the same value:$f_{E_R}\left(E\right)=f_{E_S}\left(E\right)$. Among the possible solutions of Equation (11), the value corresponding to the absolute maximum of the numerator in Equation (9) is chosen to increase the sensitivity to damage. The criterium used to select the threshold is illustrated in Figure 2. This value of $E_T$ changes with state $S$, namely, it increases with damage. The denominator of Equation (9) is the area to the left of the threshold $E_T$ that increases with the threshold, therefore with damage. This means that the damage index becomes less and less sensitive at the increase of damage. To make the damage index more effective, in the modified version of the SIDI proposed in this paper, the denominator of Equation (9) is changed in ${\overline{PTE}}_S\left(E_T\right)$. This value decreases with damage, thereby increasing the sensitivity to damage of the damage index. Thus, the Modified Statistical Interpolation Damage Index (MSIDI) in the inspection state S is defined as follows:

$${\mathrm{MSIDI}}_{\mathrm{S}}\left(E_T\right)=\frac{PT{E}_S\left(E_T\right)-PT{E}_R\left(E_T\right)}{{\overline{PTE}}_S\left(E_T\right)}$$

(13)

where the threshold is defined as discussed above. Different from the SIDI proposed in Reference [28], the MSIDI is not limited between 0 and 1 and does not present an upper bound. It is highlighted that the computation of the MSIDI does not require complex mathematical operations and, therefore, it can be considered suitable for onboard computations.

4. Numerical Benchmark

4.1. Description of the Structure

The numerical benchmark examined in this study is a 2D single-span beam represented in Figure 3. The beam is modelled using the commercial software SAP2000 [37]. The beam length is L = 12.5 m, and its height is h = 0.40 m. The material properties are: modulus of elasticity E = 20 GPa, Poisson’s ratio ν = 0.3, and mass density ρ = 2500 kg/m³. The beam model is composed of quadrilateral thick shell elements. The discretization scheme is 100 elements in the longitudinal direction and four elements in the vertical direction for a total of 400 finite elements. The beam is supported at three nodes at both ends. An arbitrary thickness is assigned to the beam, since the dynamic behavior of this type of structure is not influenced by this parameter when performing 2D analysis.

The choice of this structure is motivated by the possibility to focus on the investigation of the proposed method performance under several damage scenarios characterized by different severity levels and locations.

Five single damage types (d1 to d5) are simulated, as displayed in Figure 3. Damage is modelled through the removal of one or more finite elements that entail a local reduction of the flexural stiffness. Damage types d1–d3 present a damage located at midspan, whereas for Damage types d4–d5 and d6–d7, damage is concentrated at ¼L and ¾L, respectively. A total of nine damage scenarios (DS) are simulated, considering combinations of single damage type according to

Table 1. Simulated damage scenarios.

Damage Scenarios	Damage Type
DS1	d1
DS2	d2
DS3	d3
DS4	d4
DS5	d5
DS6	d4, d6
DS7	d5, d6
DS8	d5, d7
DS9	d1, d4, d6

.

4.2. Subsets of Sensors and Data Processing

The dynamic response of the beam to white noise is computed through linear time history analyses carried out in the reference and in all the considered damage states. The structural response in terms of vertical absolute accelerations is assumed to be recorded by vertical accelerometers deployed at 13 locations along the beam axis. Each signal has a length of 400 s and is sampled at 100 Hz. Each acceleration record is corrupted by introducing a zero-mean white noise component with a standard deviation of 5% with respect to that of the uncorrupted signal.

Two different decentralized sensor subset configurations named C1 and C2 and illustrated in Figure 4 are investigated. The two configurations have a symmetric layout and organize the 13 sensors with some overlaps. The nodes can be programmed to automatically switch the network layout between configurations C1 and C2. These two configurations are meant to comply with the main requirement of smart wireless sensing networks (i.e., low energy consumption). Moreover, their joint use overcomes the problems related to the computation of the spline interpolation at the boundaries of each subset. To minimize energy consumption, the distance between sensors should be as short as possible. In this case, we considered subsets of 3–4 close by sensors. The boundary problem is solved by organizing the sensors in a way that leaves at the boundary different sensors in C1 with respect to C2.

The response at one location of the beam, computed for length of 400 s in the reference state, is employed for the construction of the first CBF and the computation of the boundary conditions according to the procedure outlined in Section 2. The stationary WPT with a decomposition level 6 is used to calculate the initial wavelet components employed to generate the CFB. Specifically, the 22nd order Fejér–Korovkin function is chosen as a mother wavelet. The filter bank obtained automatically using the procedure described in Section 2 selects the first mode of the structure (7.12 Hz in the reference configuration). The sampling frequency of the filtered signal can be reduced to have Nyquist frequency equal to 25 Hz (downsampling of a factor 2), thus enhancing the energy efficiency of battery-powered nodes. The instantaneous first mode shape is then extracted using Equation (3). The considered damage scenarios entail very small variations of the natural frequencies; thereby, the same CFB was used for all the inspection intervals, eliminating the updating of the filter bank.

4.3. Results

This section describes the results obtained by applying the proposed damage localization method on the numerical benchmark. The instantaneous values of the first mode shape are used to compute the interpolation error as described in Section 3.2. Figure 5 displays the distributions of the instantaneous values of the damage feature at location n. 7, midspan, for the different damage scenarios. The results in Figure 5 are obtained considering the configuration C2, where sensor 7 is placed within the boundaries of the subsets. The number of available samples of the interpolation error in each scenario is equal to the sampling frequency (50 Hz upon downsampling) times the length of the signal (400 s). Therefore, for each scenario, 20,000 ($50 \mathrm{Hz}·400 \mathrm{s}$) samples of the interpolation error $E$ are estimated. In scenarios DS1–DS3 and DS9, damage is located at midspan (location 7), and, as shown in Figure 5, for these scenarios, the distribution of the interpolation error shifts toward the right of the plots consistently with the increase of the damage feature at this location.

Following Reference [28], the interpolation error can be considered lognormally distributed. The parameters of the distributions of the interpolation error in the different damage scenarios are estimated using the method of moments [38], equating the moments computed using the available samples of interpolation error and the moments of the lognormal distribution. The estimated lognormal distributions are used to compute the MSIDI for different damage scenarios.

The threshold value can be calculated by imposing the derivative of the numerator of Equation (9) equal to zero, which for the case of lognormal distributed damage sensitive feature reads:

$$\frac{d\left[PT{E}_S\left(E\right)-PT{E}_U\left(E\right)\right]}{dE}=\frac{e^{-\frac{{\left(\ln E-{\mu }_S\right)}^2}{2{\sigma }_S}}}{\sqrt{2\pi }{\sigma }_{S}E}-\frac{e^{-\frac{{\left(\ln E-{\mu }_U\right)}^2}{2{\sigma }_U}}}{\sqrt{2\pi }{\sigma }_{U}E}=0$$

(14)

where ${\mu }_U$ and ${\sigma }_U$ are the parameters of the (lognormal) distribution of $E$ in the reference state, and ${\mu }_S$ and ${\sigma }_S$ are the parameters of the (lognormal) distribution of $E$ in the inspection state. In particular, among the solutions that can be obtained solving Equation (14), the value that maximizes $\left|PTE\left(S\right)-PTE\left(U\right)\right|$ should be selected. Since the derivative shown in Equation (14) presents a close form equation, little onboard computation effort is required to compute the threshold value.

Figure 6 displays the values of the proposed damage localization index, the MSIDI, for the two sensor subset configurations, C1 and C2, and different damage scenarios, from DS1 to DS9. In Figure 6, the MSIDI is set to zero in the locations in which it presents negative values. The combination of the two sensor subset configurations allows the correct localization of damage in the case of both single and multiple damage scenarios.

5. S101 Bridge

5.1. Description of the Bridge and Monitoring System

The case study investigated in this paper is the S101 bridge in Reibersdorf, west of Vienna, Austria, see Figure 7. The bridge was built in the early 1960s and was demolished in 2008. The reasons for the demolition were the enlargement of the underneath motorway A1 Westautobahn and the overall bad conservation conditions.

The bridge had three spans and a post-tensioned concrete deck integral with the piers. The total length of the bridge was 56 m. The central span was 32 m long, while each side span had a length of 12 m. The deck was constituted by a double-webbed t-beam variable height ranging from 0.9 m at mid-span to 1.7 m in correspondence of the piers.

Before its demolition, the bridge has been artificially damaged for research purposes for three consecutive days from December 10 to December 13. The data retrieved from this benchmark have been analyzed by several research groups [34,39,40]. Their analysis and results constitute a benchmark against which the results of the MSIDI proposed in this paper are checked.

Two main types of damage have been inflicted to the structure, namely, (i) the cut and progressive lowering of the northwestern pier and (ii) the cut of several tendons in the deck. The first type of damage was intended to simulate settlement and the second one to simulate the loss of prestress. During the simulation of damage, the dynamic response of the structure has been continuously recorded at 500 Hz using 15 three-directional FBA-23 force balance accelerometers from Kinemetrics deployed along the bridge deck according to Figure 8. In particular, the sensitivity of the sensors is 2.5 V/g under a full-scale range of 1 g, and they have a resolution of 10⁻⁶ g. Raw data were logged using a 16-bit analog-to-digital converter (ADC).

During the test, the bridge was closed to traffic. Nevertheless, the roadway beneath the bridge was in use. The temperature did not change significantly during the test, being stable in the range −3°/−4°.

Four damage scenarios are considered in this study, which relate to the settlement of the pier, namely, the cut of the pier (Scenario A), 1 cm lowering (Scenario B), 2 cm lowering (Scenario C), and 3 cm lowering (Scenario D). The dynamic response of the bridge was recorded also in the reference scenario (Scenario U) before damage was inflicted. The pier was first unloaded, lifting the deck with a hydraulic jack. Then, it was cut at the base and lowered in progressive steps, releasing the pressure in the jack.

During the tests, carried out during three consecutive days and under negligible temperature variations, the 15 sensors measured acceleration at 500 Hz rate in three orthogonal directions. The results reported herein are obtained by analyzing the vertical accelerations. Data from each one of the damage scenarios were divided into several partial records, corresponding to 330 s each.

5.2. Subsets of Sensors and Data Processing

In this study, the vertical accelerations measured by the 14 sensors placed on the West side of the bridge (i.e., accelerometers from 1 to 14 in Figure 8) are employed to apply the proposed damage localization method. Acceleration records are downsampled at 50 Hz before applying the proposed procedure. As for Scenario U, five datasets, each corresponding to 330 s of measurement, are considered. For each damaged scenario, only one signal is considered. Therefore, the length of the acceleration time histories is 1650 s ($=5·330 \mathrm{s}$) for Scenario U and 330 s for the four damage scenarios (from Scenario A to D). The rationale behind the choice of different records length is that, at the beginning of the monitoring period, it is possible to collect a large amount of data to fix the reference behavior of the structure. Instead, during the inspection state, it is necessary to minimize the amount of collected data and therefore the acquisition length to limit energy consumption in case wireless smart sensors are used.

Two different decentralized sensor subset configurations are studied, named C1 and C2, as illustrated in Figure 9. The reasons that guided the choice of these configurations are similar to those described in Section 4.2 for the numerical benchmark.

A training signal of 330 s is employed for the construction of the first CBF and the boundary conditions according to the procedure outlined in Section 2. An update of the CFB is performed at the occurrence of each further damage scenario to effectively track the shifts of the vibration modes. As in the previous case study, the stationary WPT (using a 22-nd order Fejér–Korovkin function) with a decomposition level 6 is used to calculate the initial wavelet components employed to generate the CFB. Two vertical bending modes, with frequencies equal to respectively 3.98 and 9.61 Hz, and one torsional mode with frequency 6.18 Hz (in the reference state), are used to calculate the interpolation error.

5.3. Results

This section describes the results obtained by applying the proposed method on the S101 bridge. The instantaneous mode shapes are used to compute the interpolation error as described in Section 3.2. Figure 10 displays the distributions of the instantaneous values of the interpolation error at location n. 10, close to the settled pier, relevant to the different damage scenarios. The results in Figure 10 are computed considering the two subsets of sensor subset configurations displayed in Figure 9. For each damage scenario, 16,500 ($=50 \mathrm{Hz}·330 \mathrm{s}$) samples of the interpolation error $E$ are estimated. Instead, 82,500 ($=50 \mathrm{Hz}·1650 \mathrm{s}$) samples of the interpolation error are available in the reference state. It is observed that the distribution of the interpolation error shifts toward the right of the plots as the severity of damage increases.

Figure 11 shows the distributions of the instantaneous values of the interpolation error computed for sensor 5, which is far from the damage location. It can be noted that the distribution of the interpolation error computed in the reference and in the different damage scenarios (from A to D) do not differ significantly.

The computation of the MSIDI is carried out using the methodology presented in Section 4.3. for the case of the numerical benchmark: the distributions of the interpolation error are estimated using the method of moments, assuming that it can be considered lognormally distributed, whereas the threshold values $E_T$ are calculated according to Equation (14).

Figure 12 presents the values of the MSIDI computed for the two sensor subset configurations and different damages scenarios. In Figure 12, the MSIDI is set to zero in the locations in which it presents negative values. The highest values of the MSIDI are reached at sensors 9–11, which is in the proximity of the lowered pier. As for configuration C2, it is noted that sensor 11 is located at the external knots of subsets 3 and 4; therefore, the MSIDI cannot be estimated in that location. For this reason, the highest values of the damage index are in the area surrounding sensor 11.

6. Discussion

The damage localization method proposed in the paper was applied to a numerical benchmark and to the S101 bridge to demonstrate its feasibility. The method comprises the following operations:

(1)

Computation of instantaneous mode shapes using CFBs. The mode shapes are estimated using the responses over subsets of sensors organized according to different configurations.

(2)

Computation of instantaneous values of the damage feature, i.e., the interpolation error, at the inner sensors of each subset using the clamped-clump interpolation method.

(3)

Computation of a novel damage index, i.e., the MSIDI, from the statistical distributions of the interpolation error in the reference and the inspection state.

Results show that:

• The damage, i.e., losses of stiffness, can be correctly detected and localized by the proposed method, see Figure 6 and Figure 12.
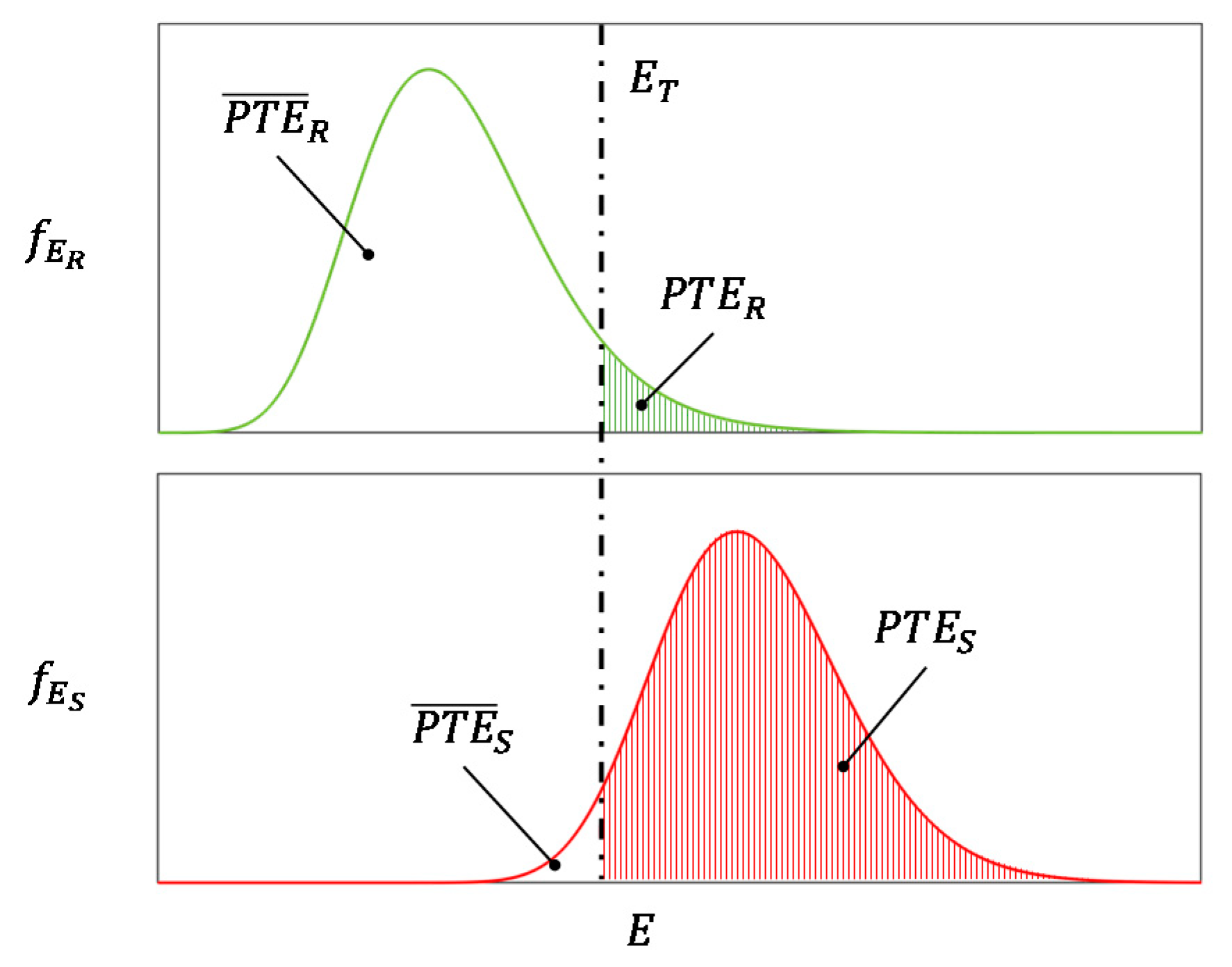
• In the damaged scenarios, the damage feature increases at the damage locations with respect to the reference condition. Conversely, the damage feature in the reference and the inspection state are similar at non-damaged locations. This is exemplified in Figure 5, Figure 10, and Figure 11, which display the histogram plot of the damage feature for different damage scenarios and at several sensor locations. It is noted, qualitatively, that the overlapping area between the distribution of the interpolation error in the reference and the damaged scenarios decreases as the magnitude of damage increases.
• For single damage scenarios, the values of the MSIDI in general increase according to the increasing severity of the damage. This is clearly shown by the comparison of DS1, DS3, and DS2 corresponding to increasing losses of stiffness at the same location (see the first row of Figure 6). This is directly linked to the definition of the damage indicator, see Equation (13).
• The same stiffness loss corresponds to different values of the damage index depending on the location of the damage. This is shown, for example, by the comparison of DS1 and DS4 or DS2 and DS5 corresponding to the same damage severity but different values of the damage feature.
• For multiple damage scenarios (e.g., DS9 in Figure 6), the detection of certain damages can be hindered by damages at other locations. This is not only due to the dependence of the damage index on the damage location (remarked at the previous point), but also on the dependence of the damage feature at a given location on damage at other locations. This is shown for example by the comparison between DS6 and DS9. In the second scenario, there is a further damaged section at midspan, but the value of the damage index at the central damage location is lower with respect to the others. This suggests that damage at midspan affects the values of the damage indexes at the other two locations.
• The comparison of the results obtained herein with those reported in Reference [28] using the SIDI show the higher sensitivity of the MSIDI with respect to the former version of the damage index.

The proposed method, based on the MSIDI, has been developed integrating a method for the identification of instantaneous modal parameters proposed in Reference [27] with the procedure for damage identification presented in Reference [28]. To further integrate the two procedures, the MSIDI introduces some modifications that simplify its application and improve results:

• The threshold value $E_T$ used to compare the distribution of the interpolation error in the MSIDI is automatically determined, which simplifies the computation of the damage index.
• The evaluation of the damage features is carried out considering two different sensor subset configurations. This overcomes the difficulties related to the computation of the damage feature at the boundaries of the subsets.

7. Conclusions

In this paper, a damage localization method based on the extraction and the processing of instantaneous values of the mode shapes from short time series is proposed.

The identification of the instantaneous mode shapes and the decentralized estimation of the instantaneous values of the damage feature are carried out using, respectively, the clamped-clump interpolation method (C²IM) and the clustered filter banks (CFB)-based method previously proposed by the authors. Damage localization is achieved through a new damage index, the Modified Statistical Interpolation Damage Index (MSIDI), proposed as an improved version of the existing SIDI. The proposed method is tested using both artificial data simulated with a numerical benchmark and real data recorded on the S101 bridge in Austria.

The MSIDI presents several advantages with respect to existing methods for damage localization: (a) it can be applied using short signals in near real time, thereby enabling a prompt damage localization; (b) it can be applied automatically, switching between different sensor configurations to enhance its robustness; (c) the modified version of the damage index exhibits a higher sensitivity to damage with respect to its original version.

The method is particularly appropriate for smart sensing applications based on wireless technologies, since the estimation of the damage index does not require complex mathematical operations and therefore is suitable for onboard computations.