Basic Study on the Proposal of New Measures to Improve the Ductility of RC Bridge Pier and Their Effectiveness
Abstract
1. Introduction
2. Proposed DE Pier
2.1. Ductility
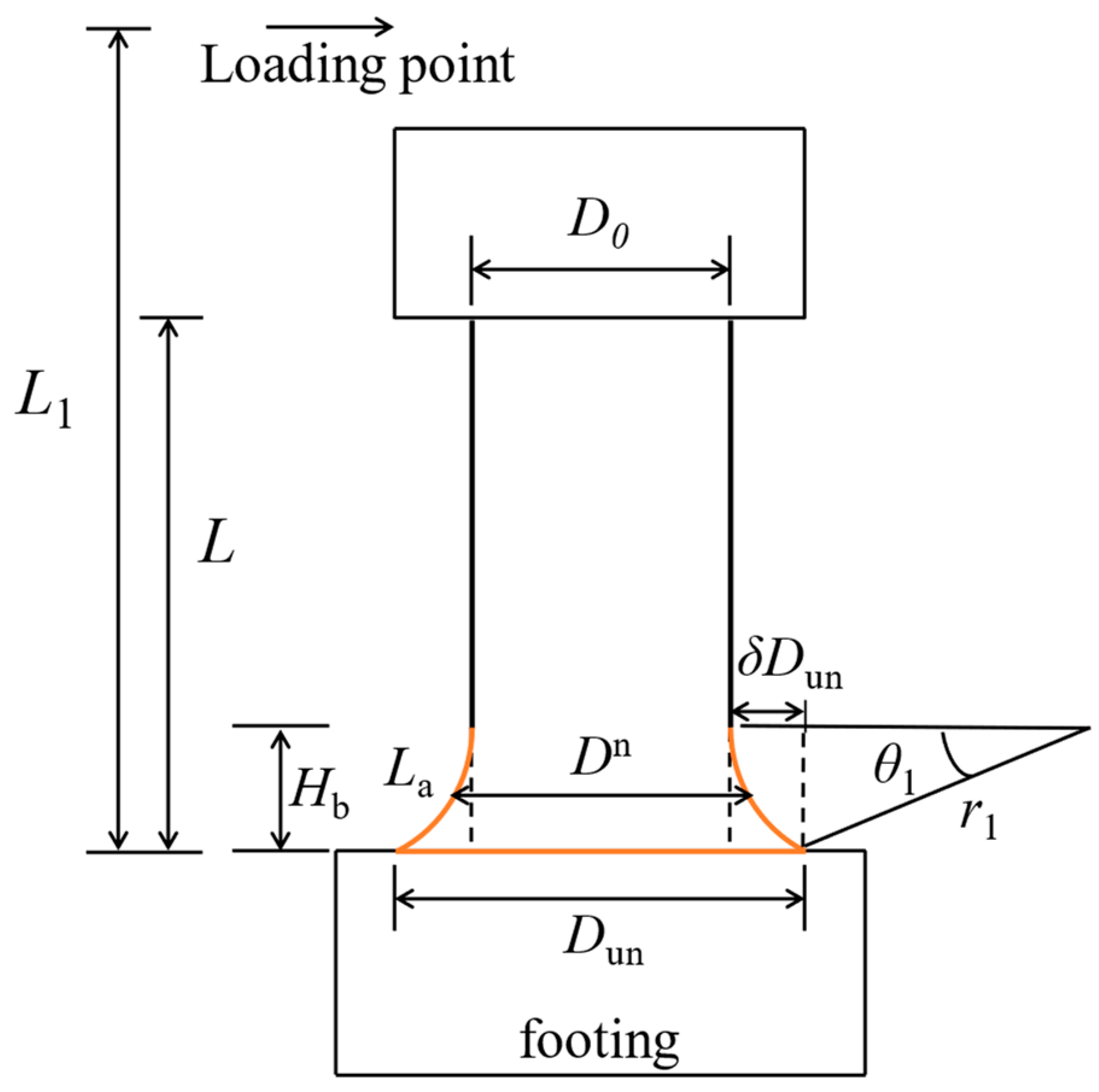
2.2. Design Concept
2.3. Detail of Design Process
2.3.1. Step 1: Setting Targeted Displacement and Determining the Displacement Due to Plastic Hinge Rotation
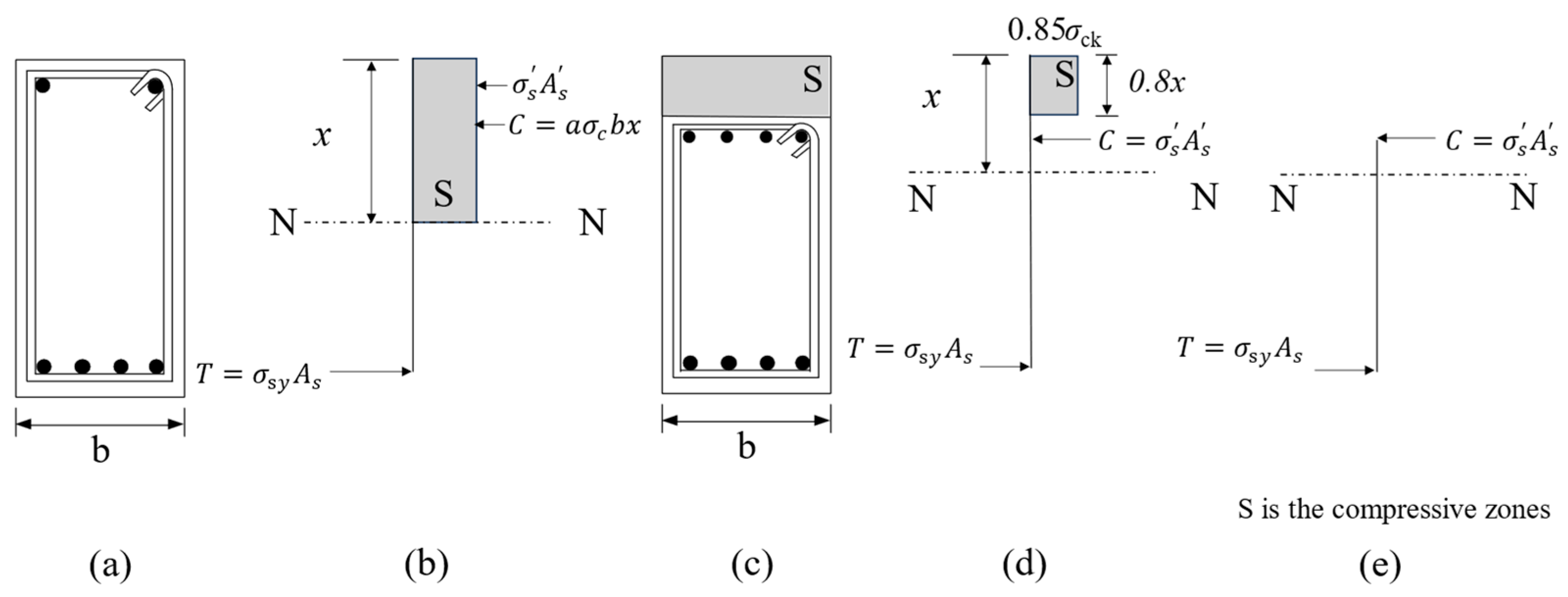
2.3.2. Step 2: Determining Plastic Hinge Length, Bending Reinforcement Intervals, and Curvature
2.3.3. Step 3: Determine the Sectional Height Dun of the DE Pier
2.3.4. Step 4: Check Whether the Pre-Deformed Rebars Are in the Strain Hardening or Not
2.3.5. Step 5: Determine the Effective Height and Iterative Calculations for DE Piers
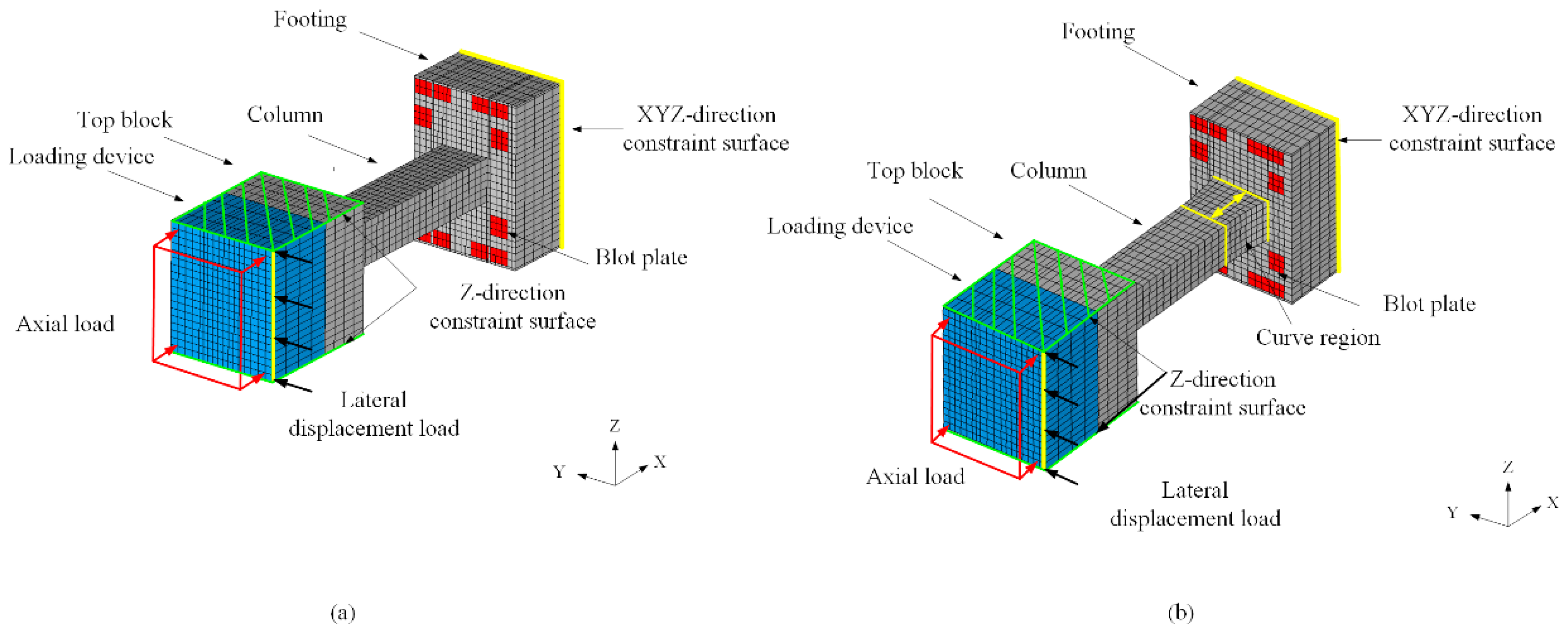
3. Test Specimen and Procedure
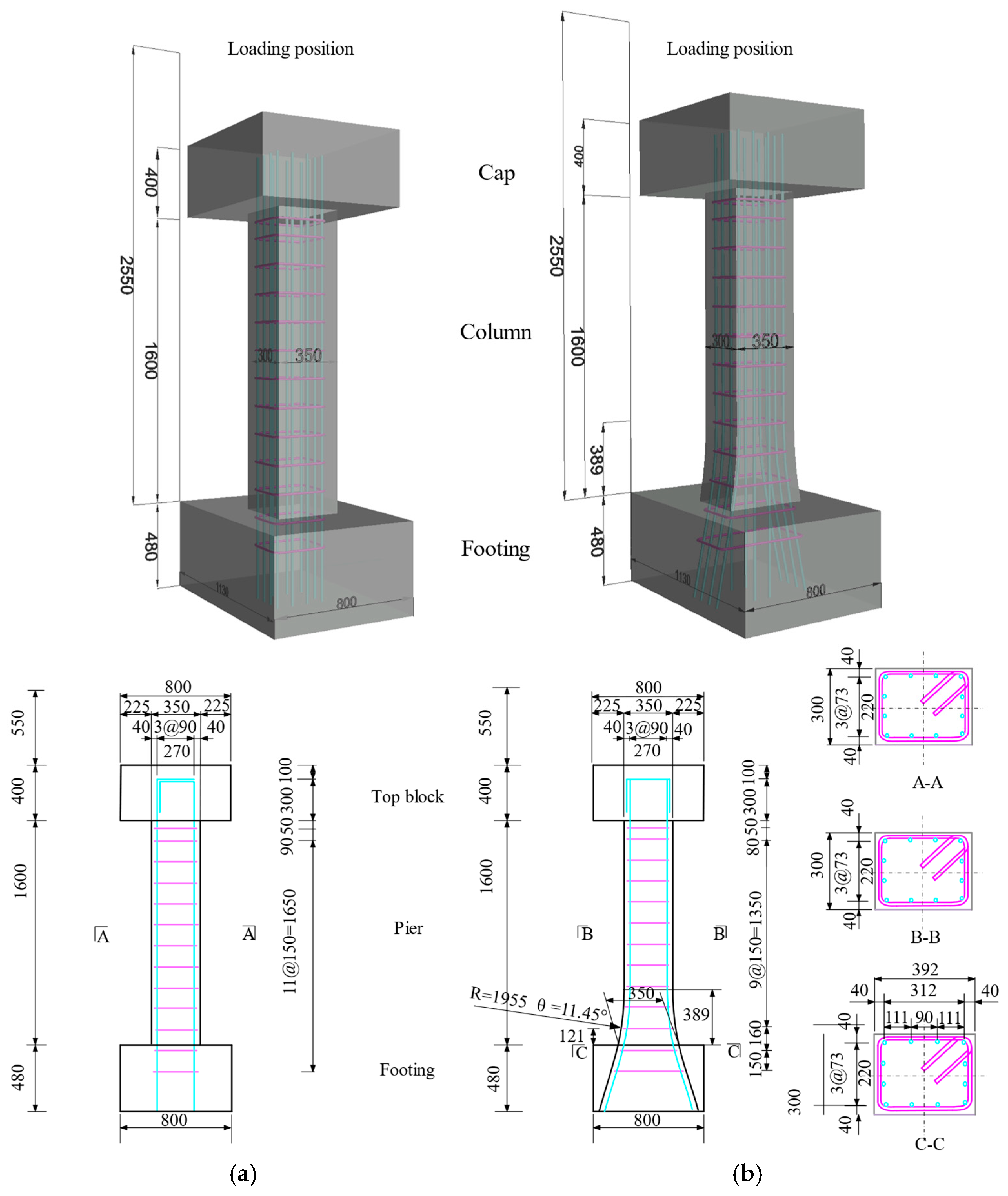
3.1. Detail of Test Specimens
3.2. Material Mechanical Properties
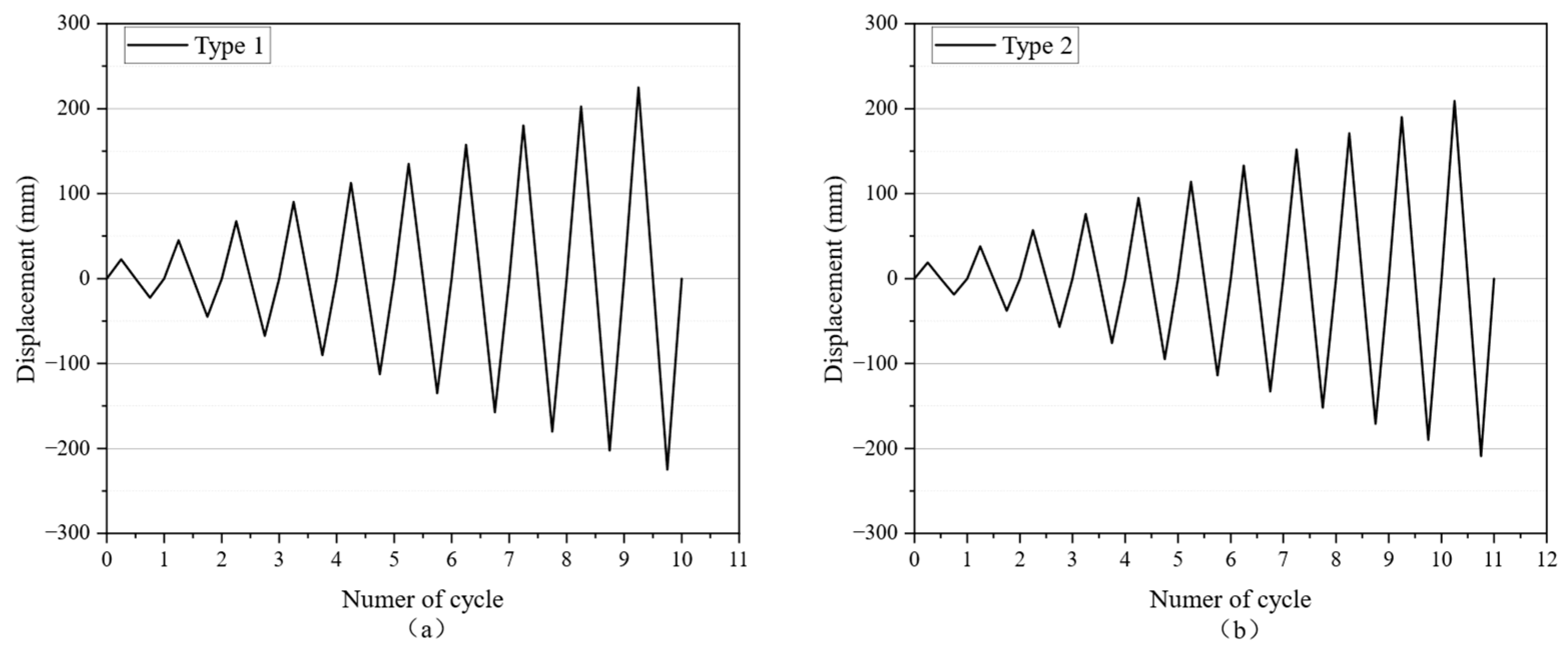
3.3. Test Procedure
4. Summary of Experimental Results
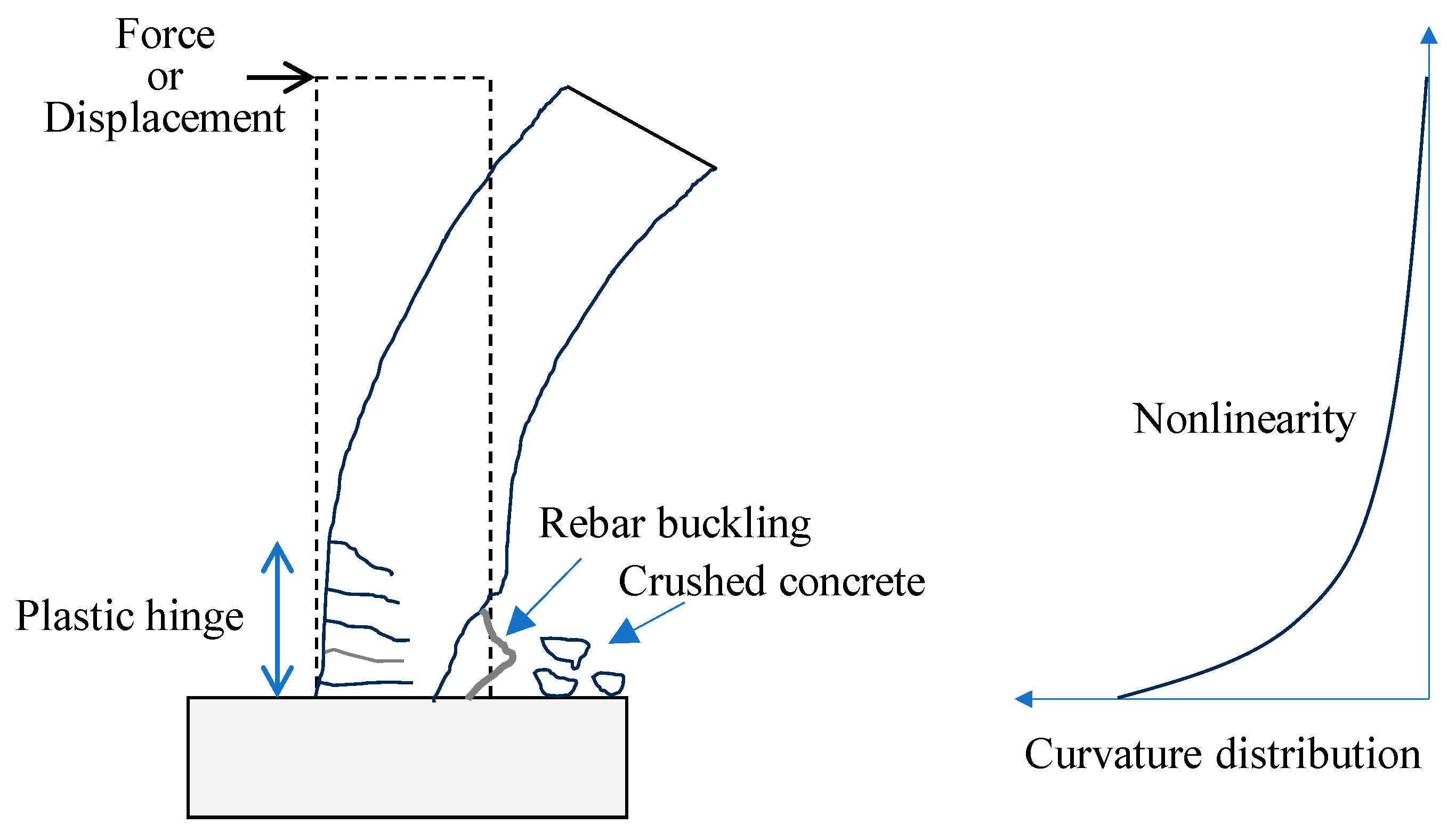
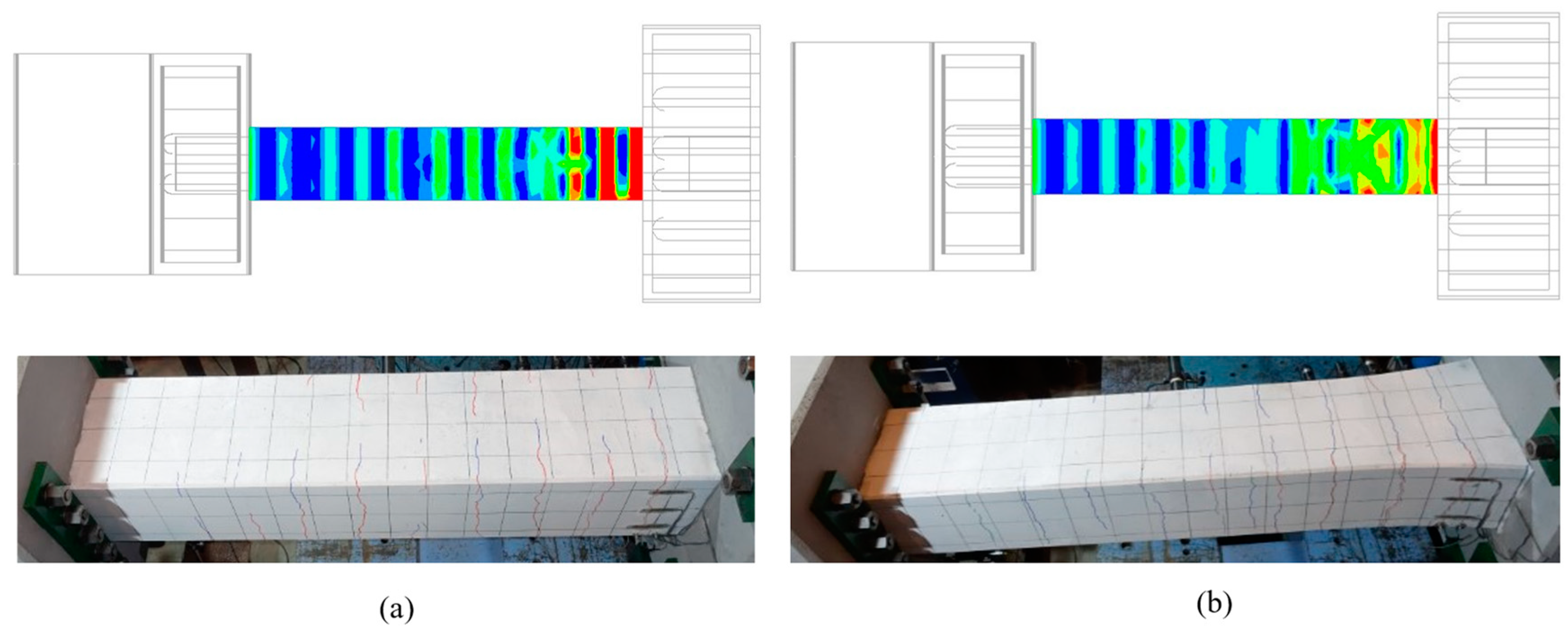
4.1. Experimental Observation
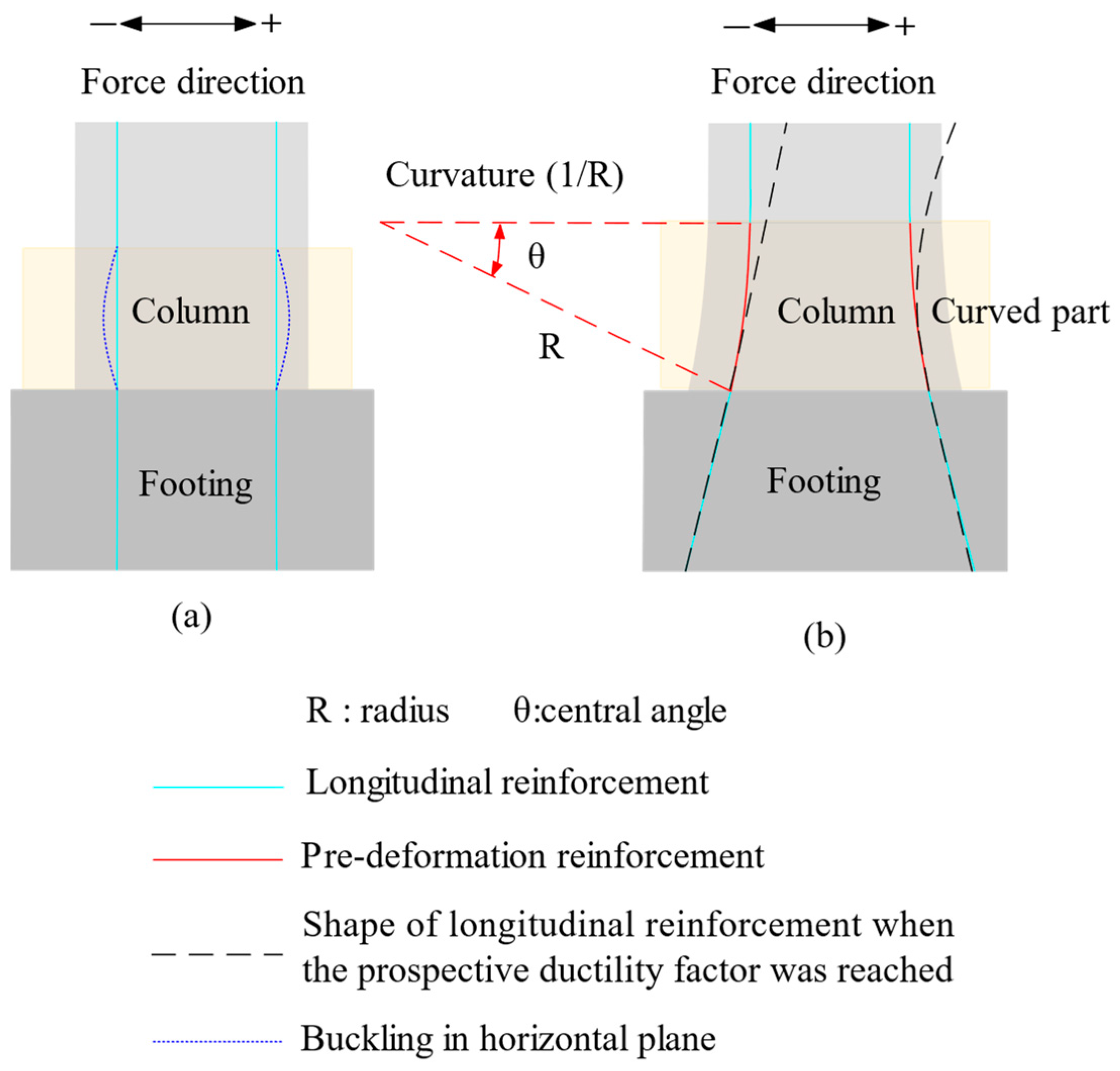
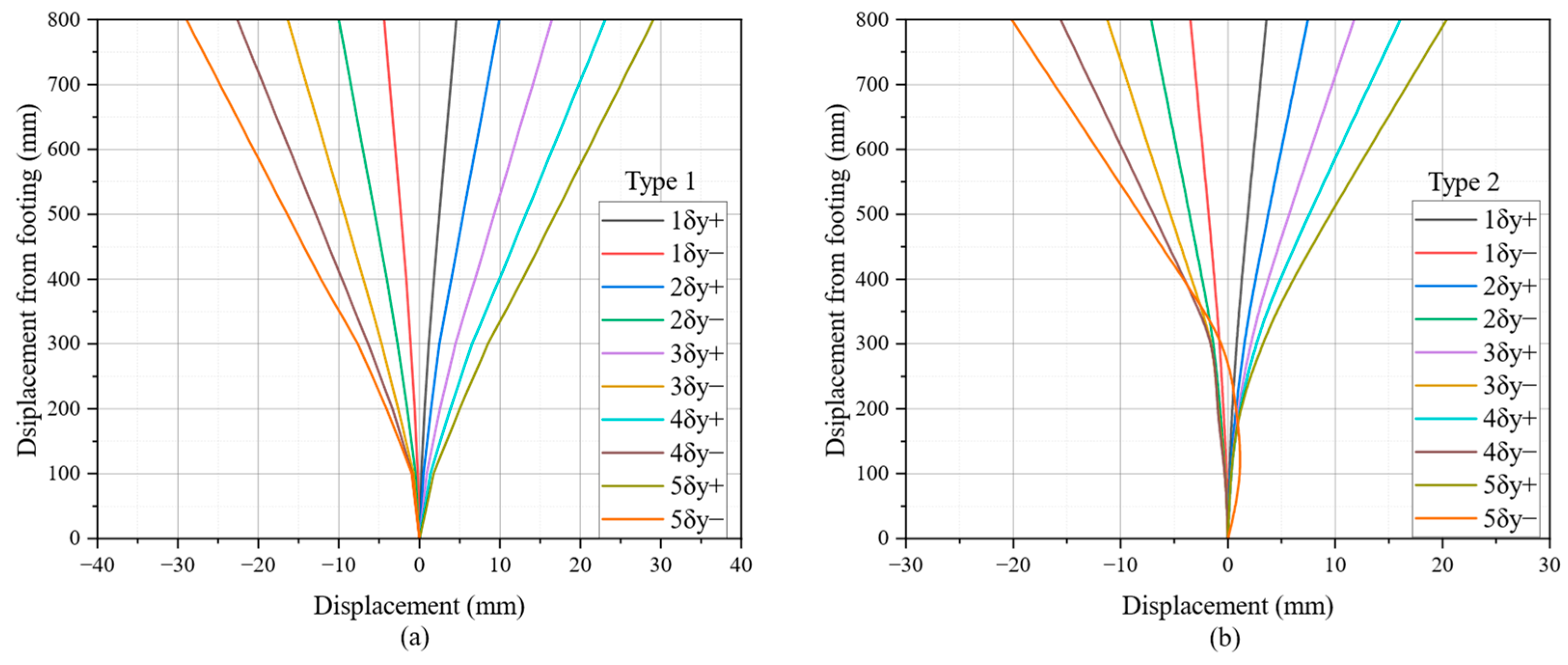
4.2. Horizontal Displacement and Plastic Hinge of Piers
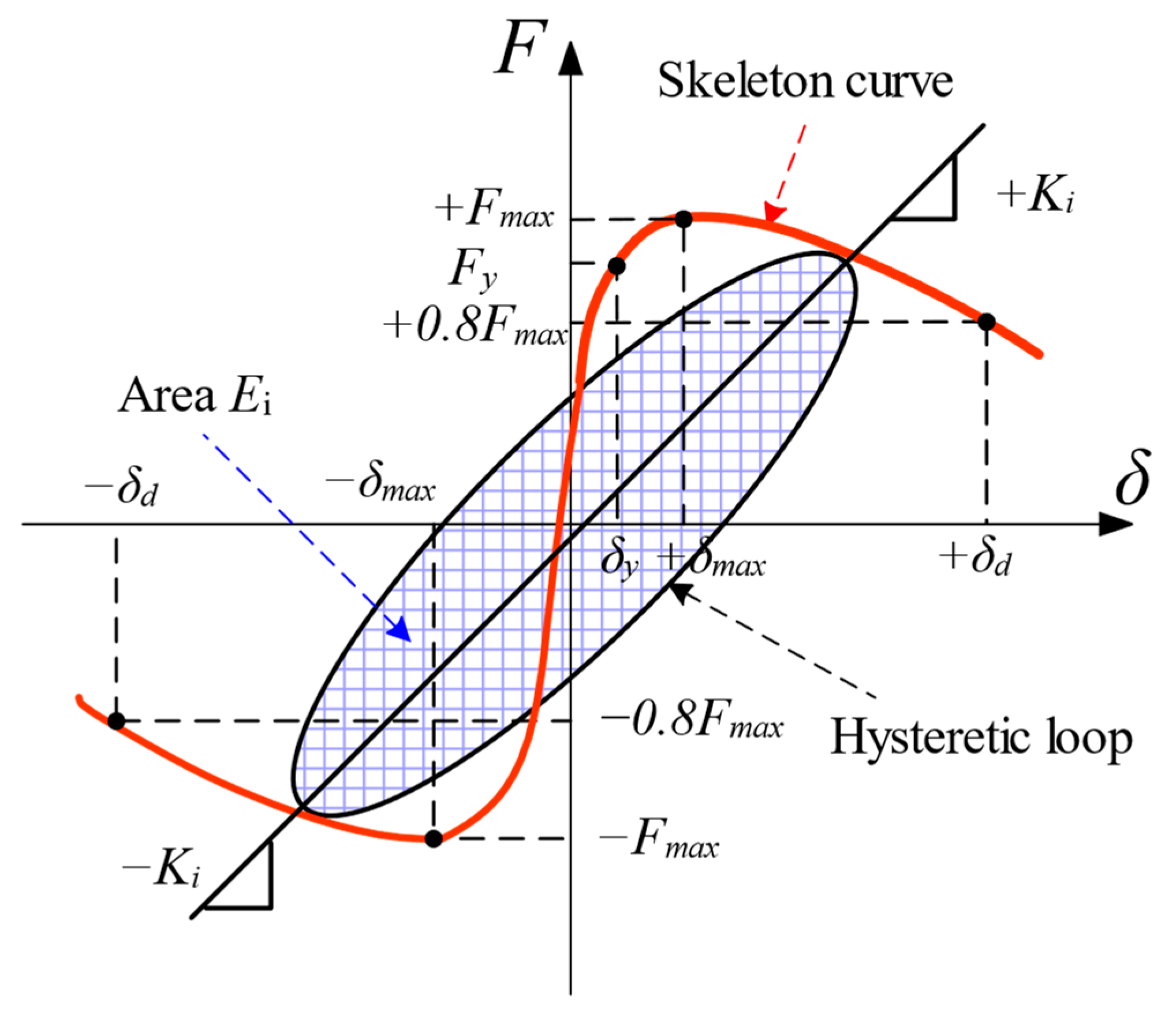
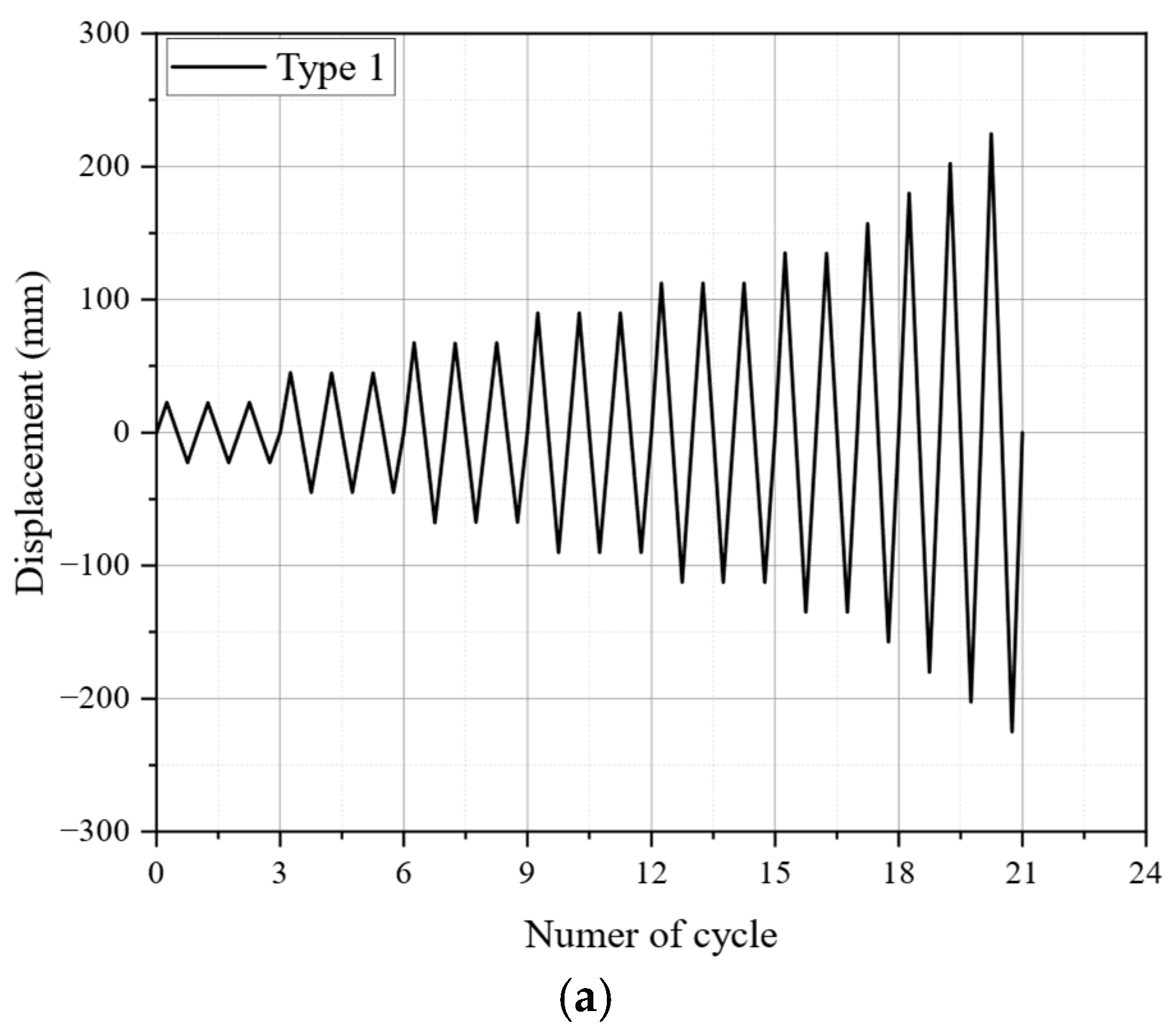
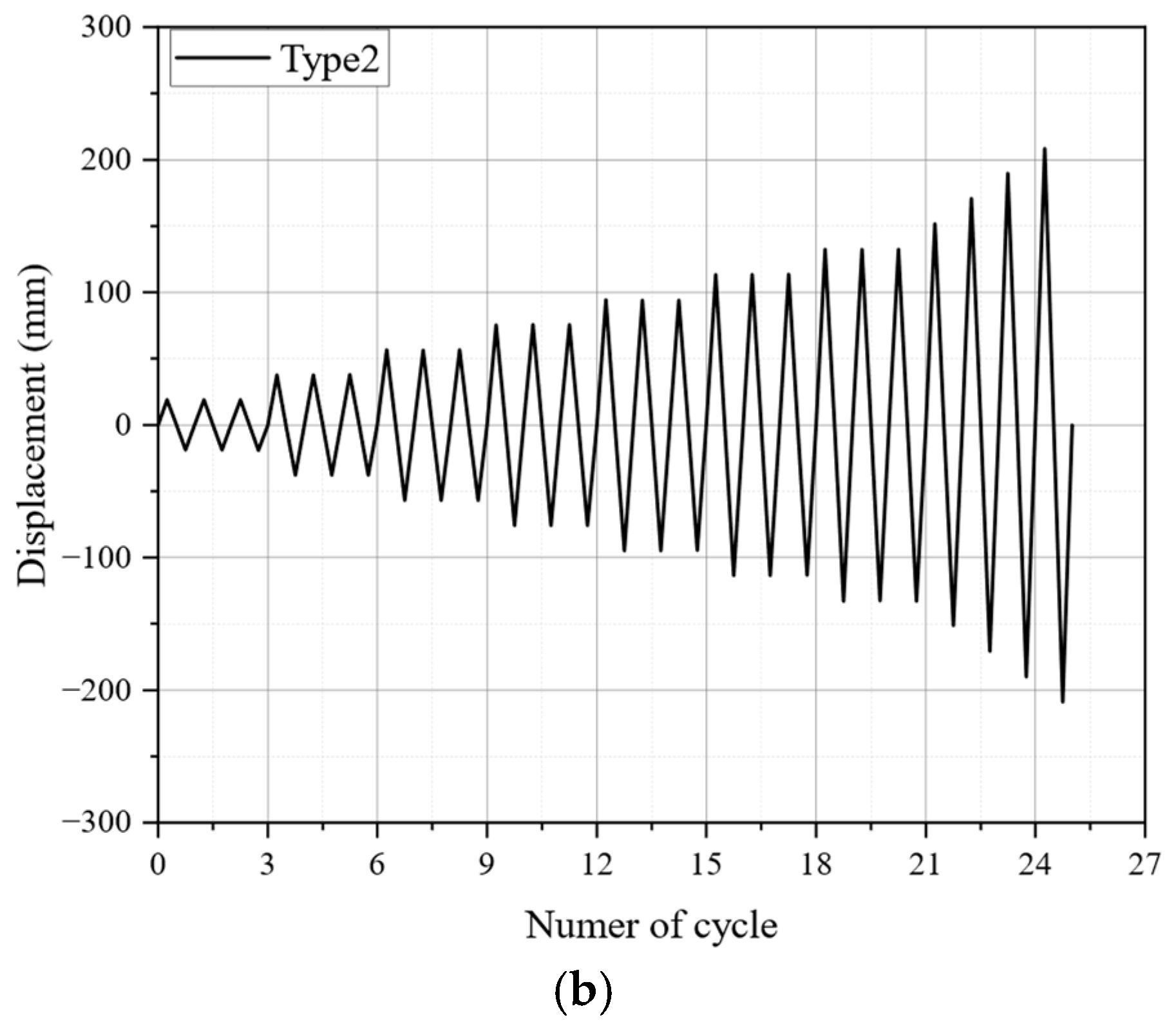
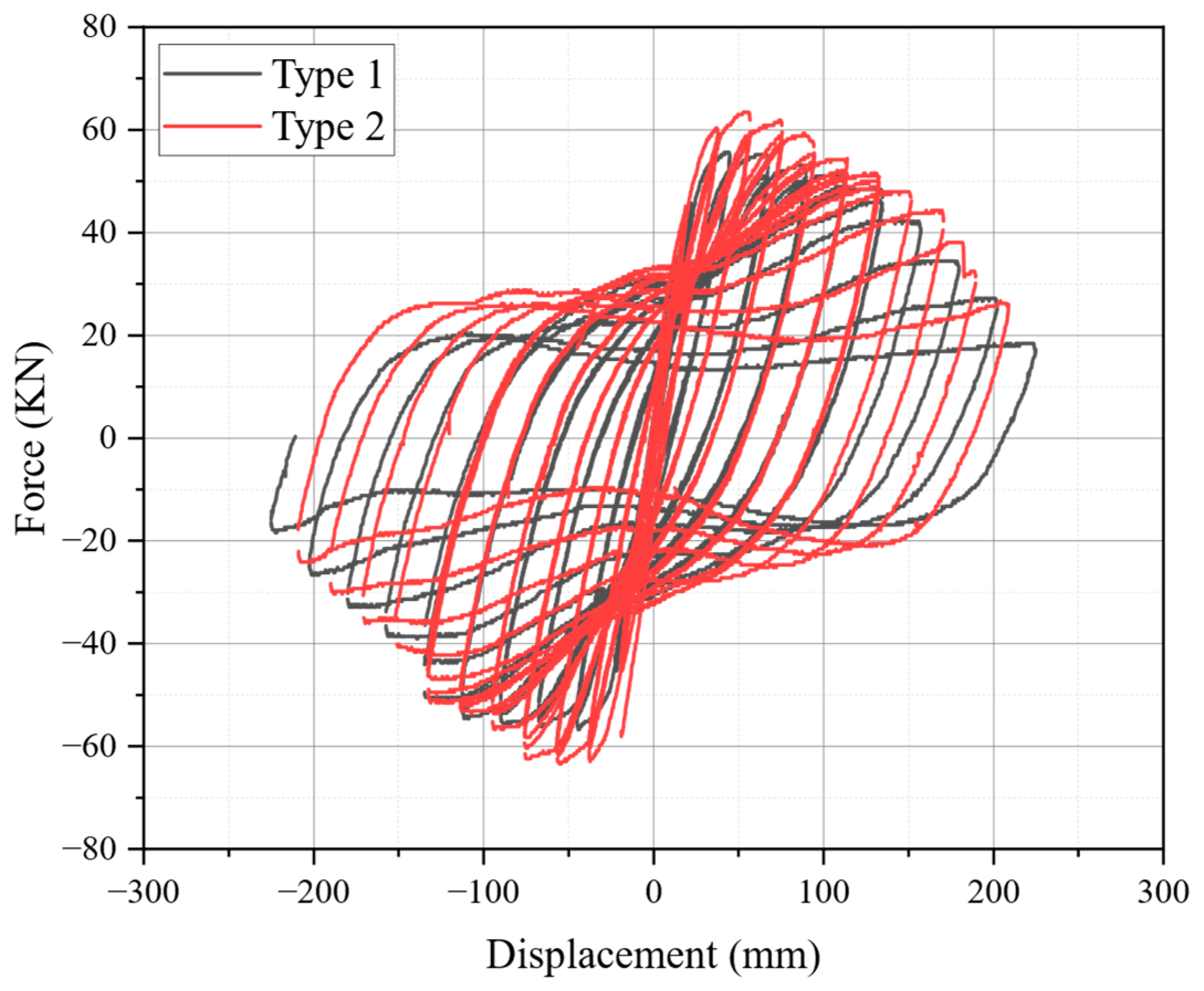
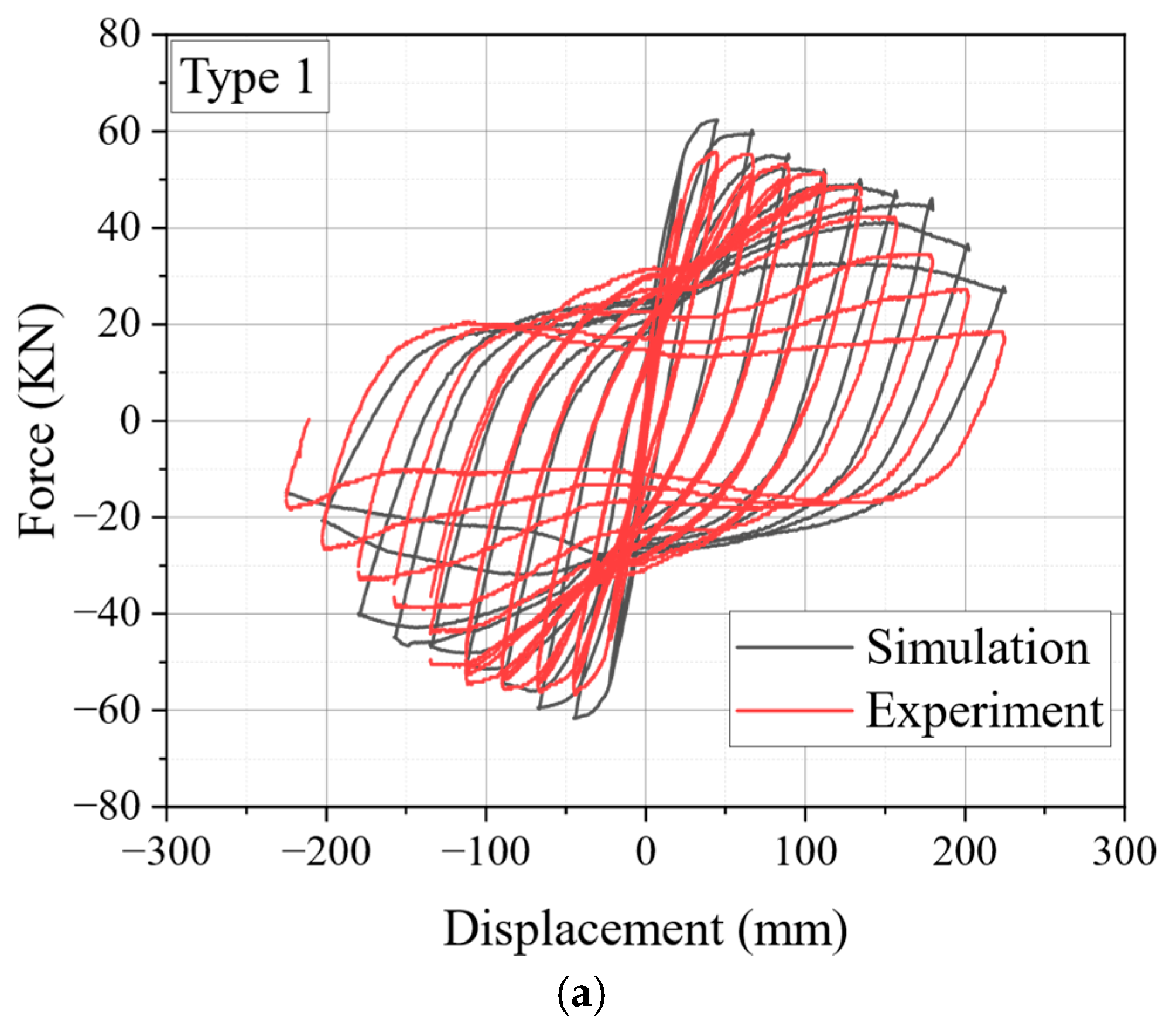
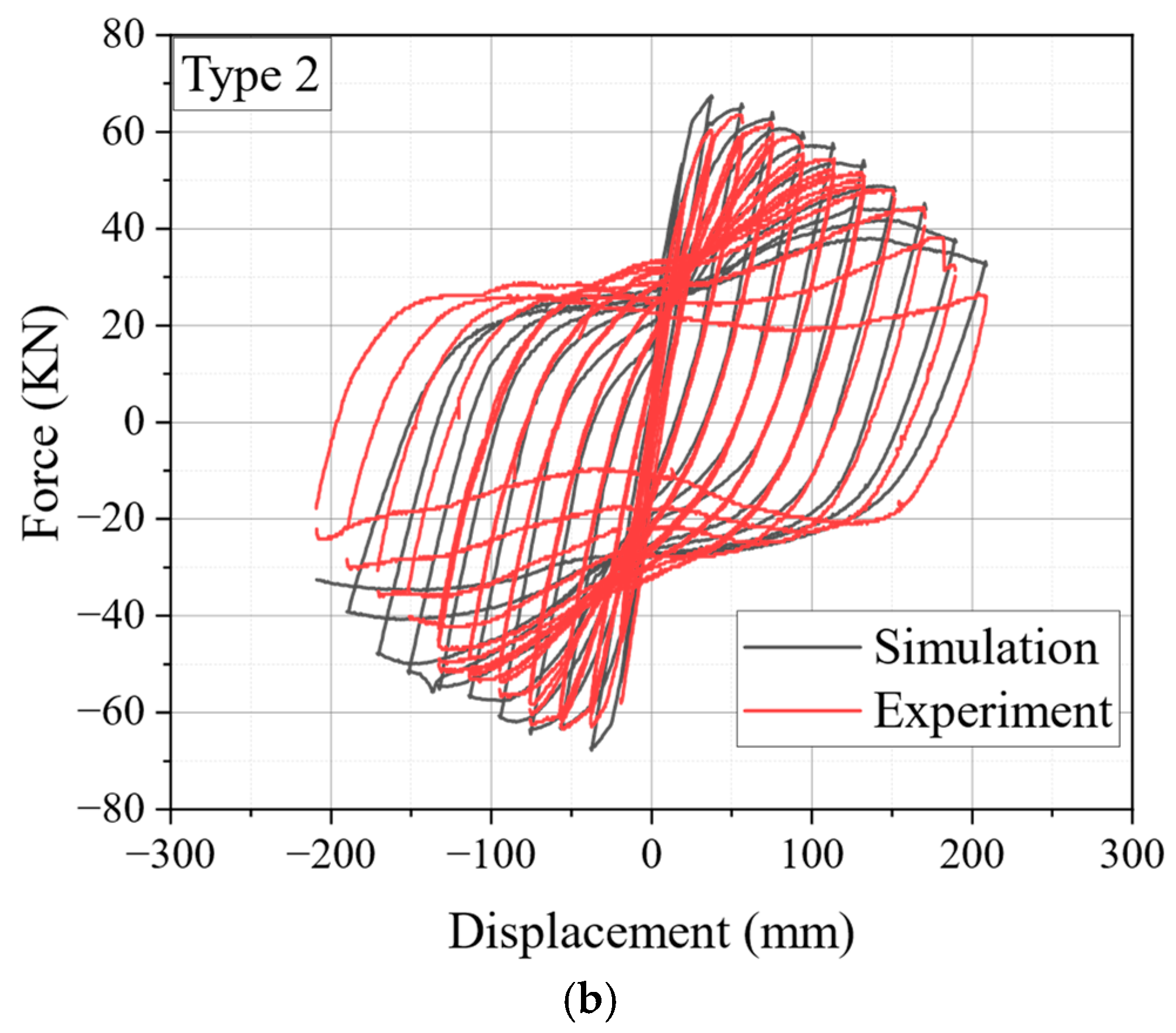
4.3. Hysteresis Curves
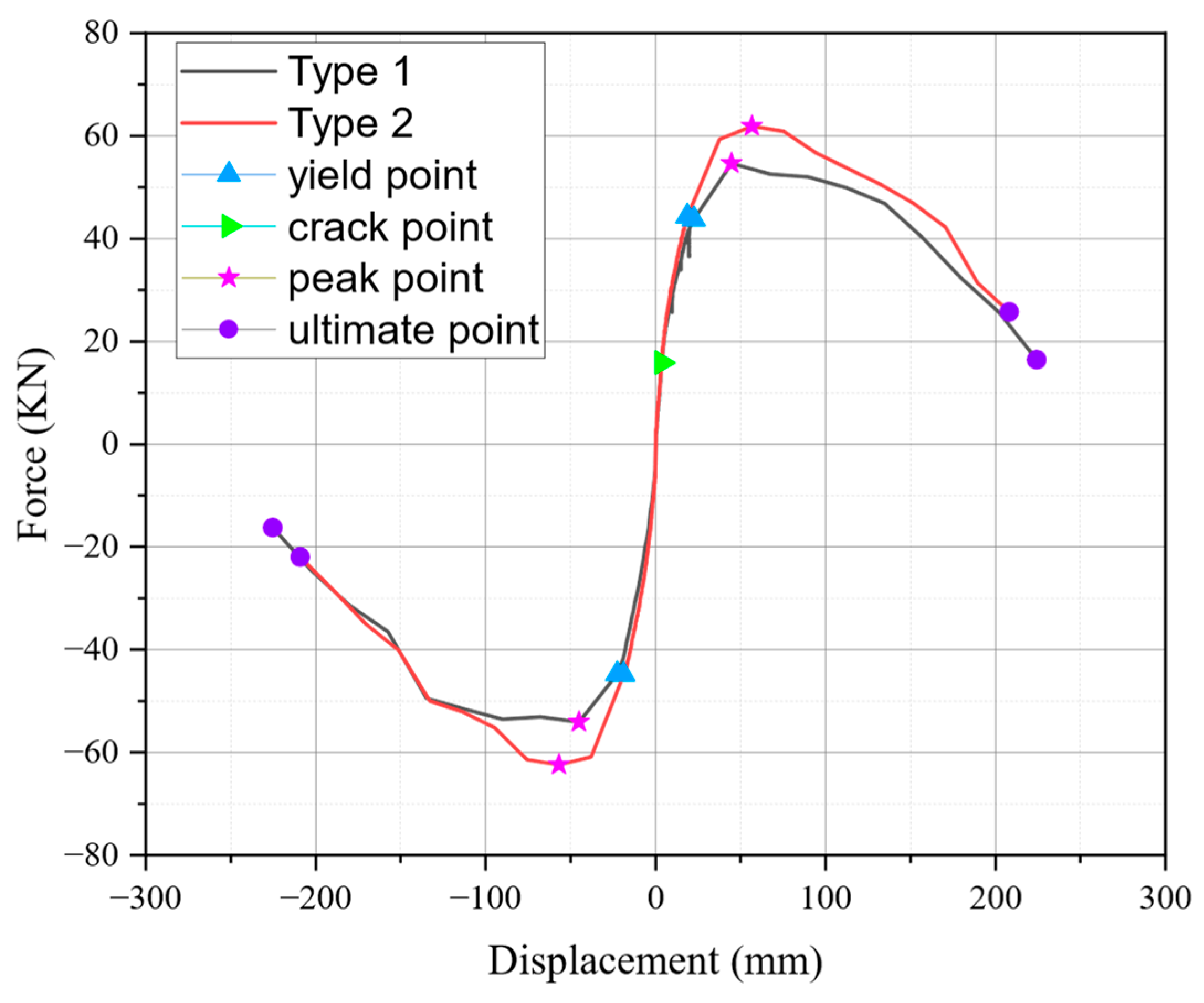
4.4. Skeleton Curve
4.5. Stiffness Degradation
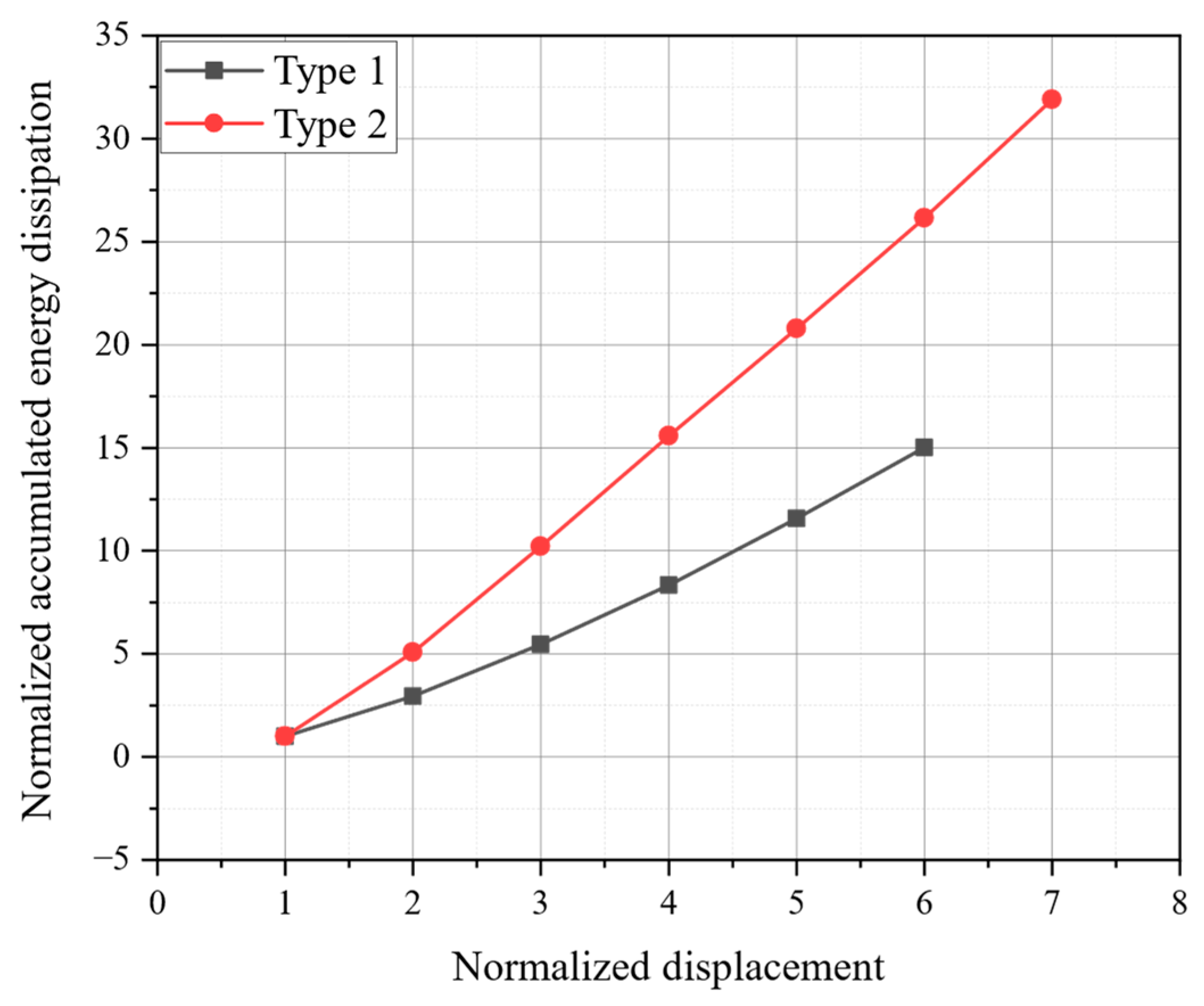
4.6. Energy Dissipation
4.7. Ductility Analysis
5. Finite Element Analysis
5.1. Overview of the Finite Element Model and Loading History
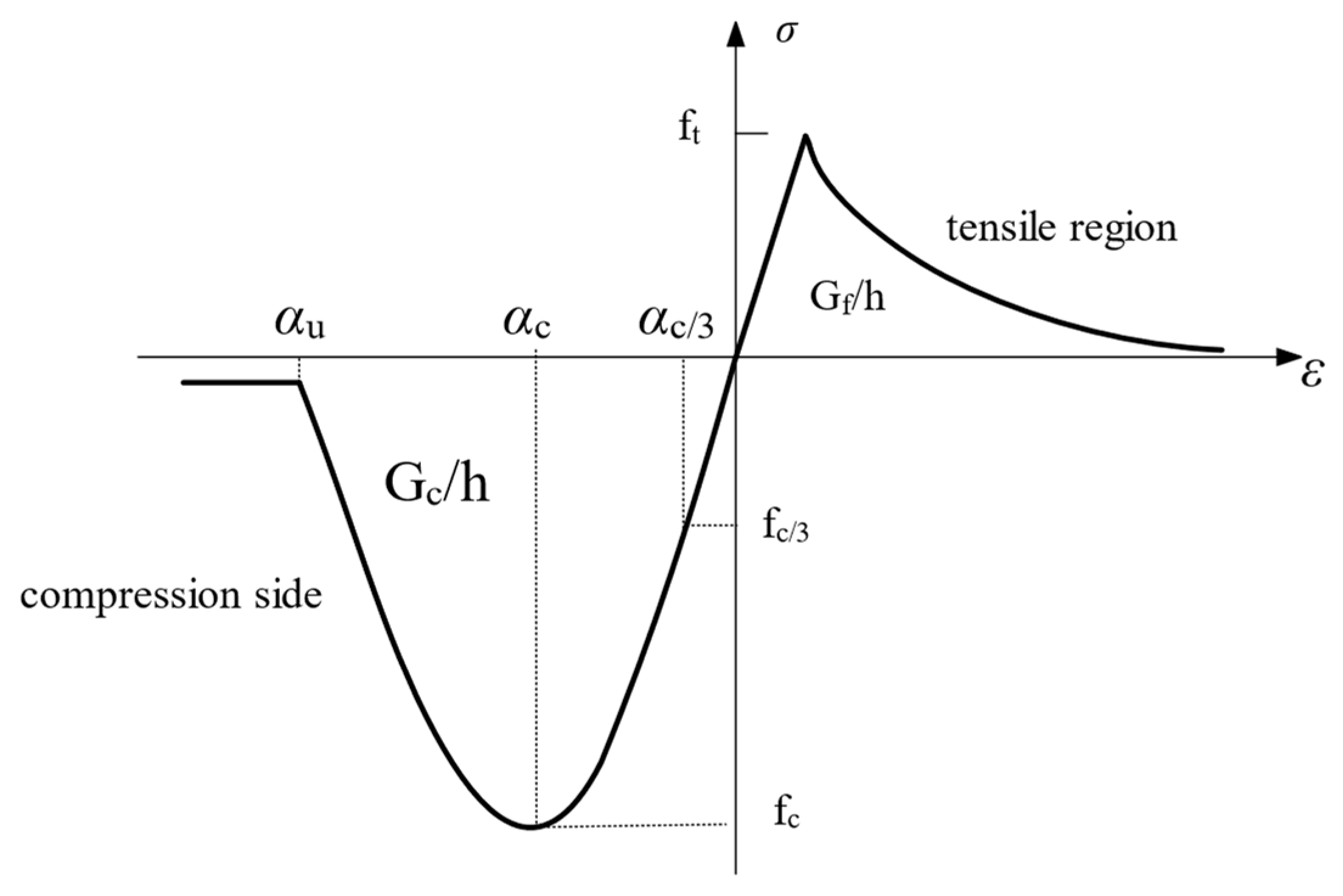
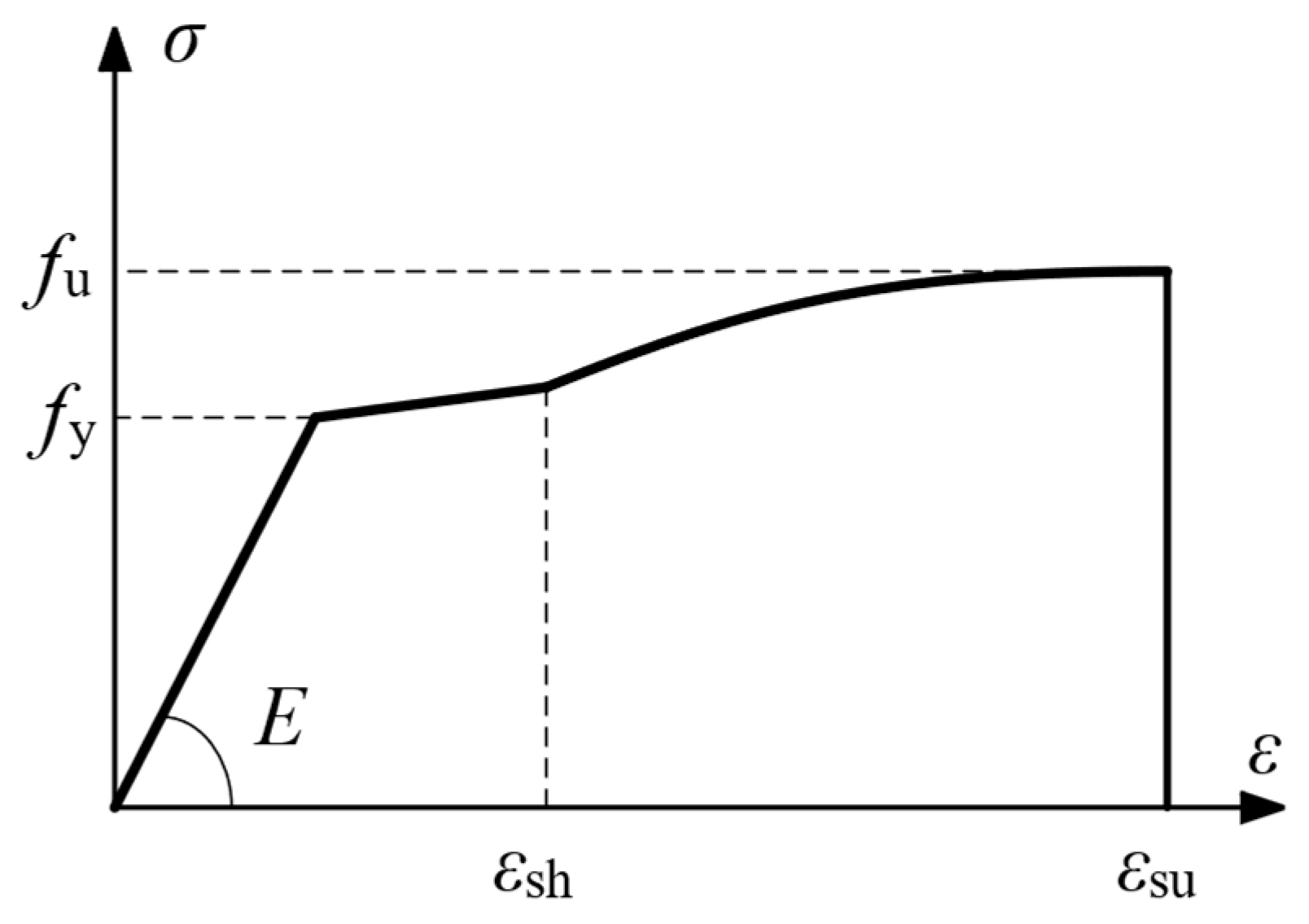
5.2. Material Model
5.2.1. Concrete
5.2.2. Rebars
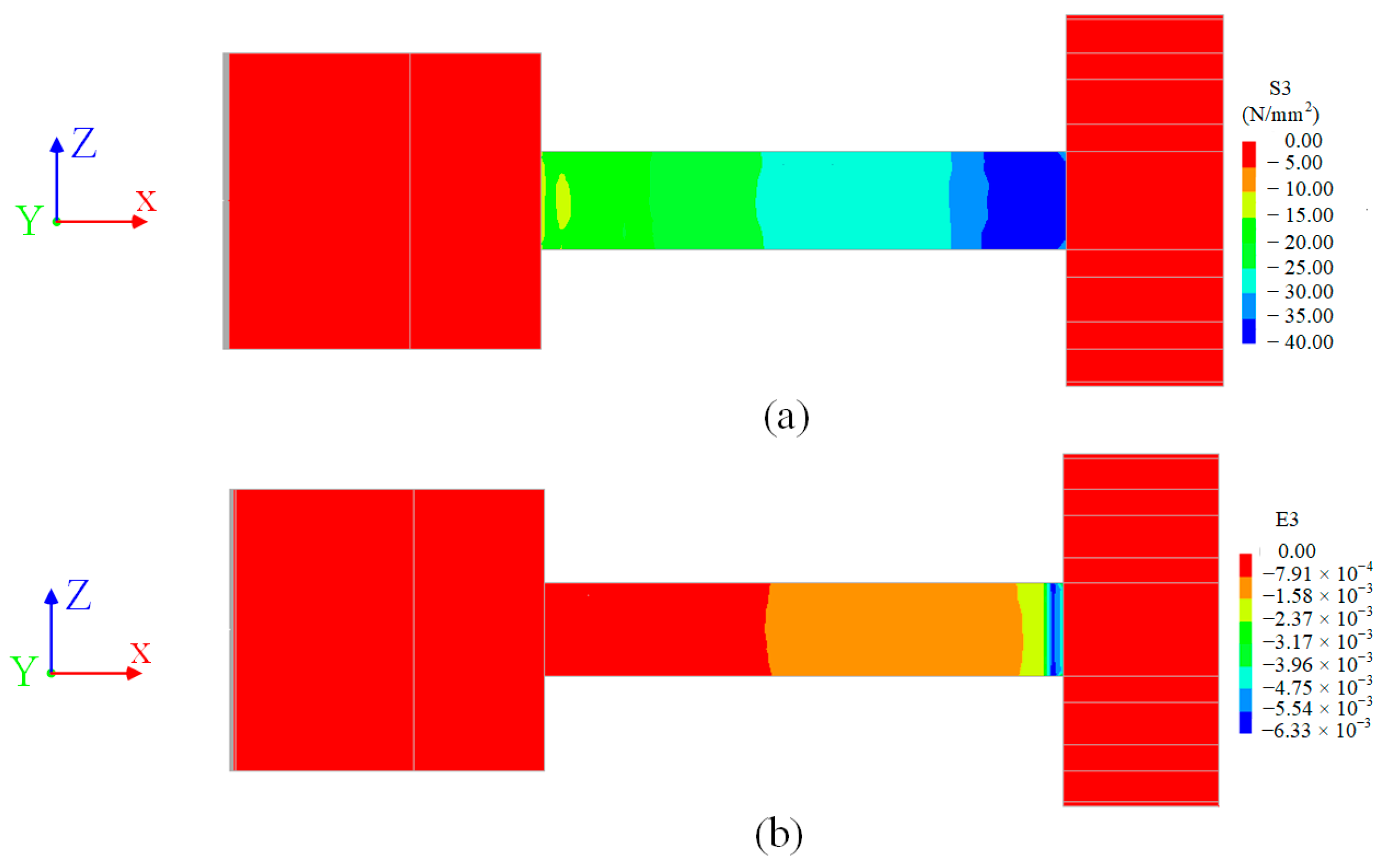
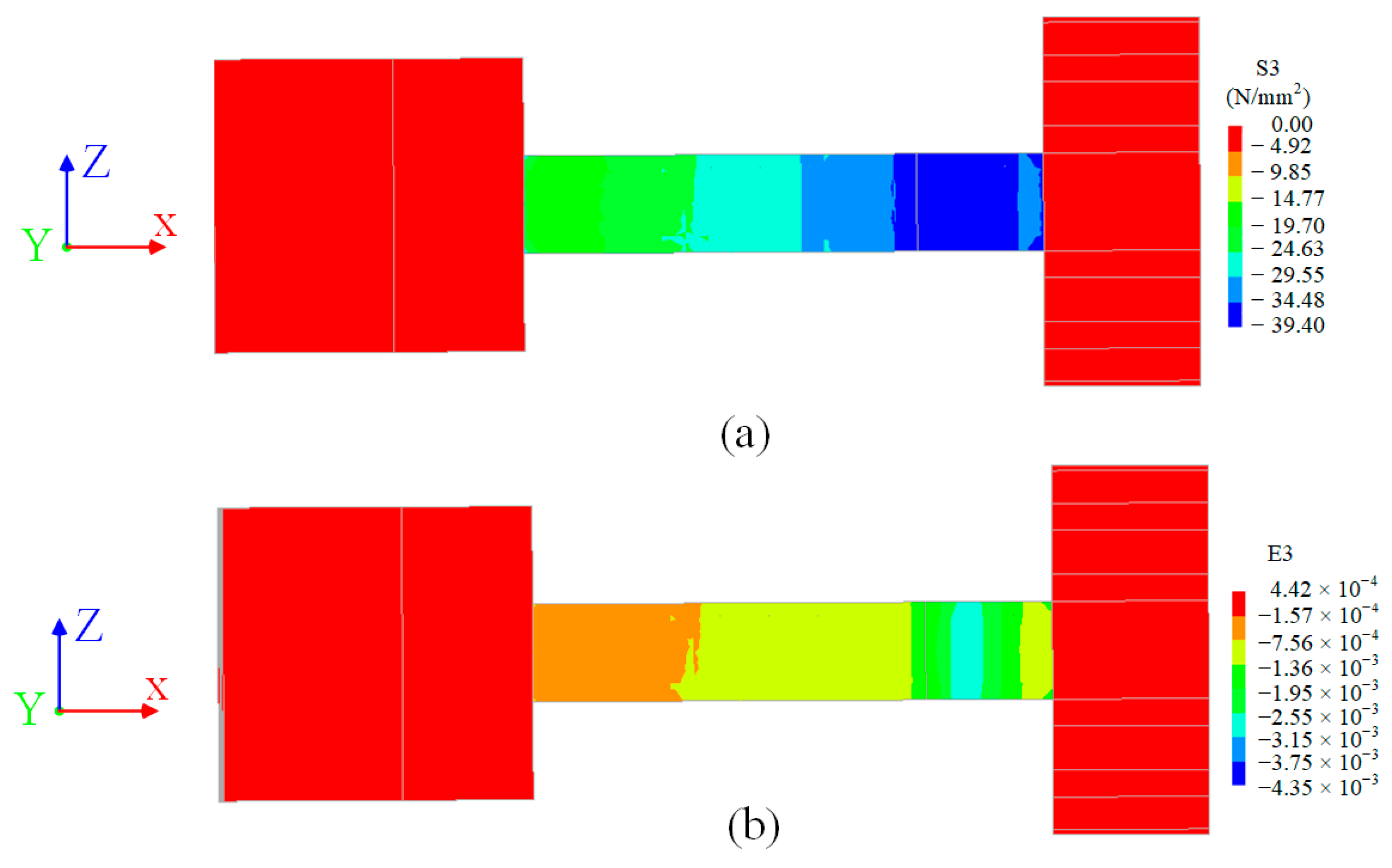
5.3. Validation of the Numerical Model
6. Conclusions
- (1)
- As a novel approach to enhance ductility, this paper proposes a method utilizing inwardly bent longitudinal reinforcement to mitigate in-plane buckling. The method offers a simple and cost-effective construction solution while improving seismic performance.
- (2)
- It was clarified that the RC pier with the proposed method had a plastic hinge part at a distance from the footing. It was indicated that the pre-deformed positions and curvature of the longitudinal reinforcements influenced the position of the plastic hinge.
- (3)
- The outcomes of the reversed cyclic load tests demonstrated that the proposed method enhanced energy dissipation capacity and stiffness. Furthermore, the load-carrying capacity increased by 14% and ductility improved by 11%. However, achieving greater ductility beyond this 11% improvement may require additional design adjustments. Additionally, although the technique successfully mitigated in-plane buckling, out-of-plane buckling of the longitudinal reinforcement was observed, indicating the need for further refinement to address this issue and enhance overall ductility.
- (4)
- FEM analysis revealed that it may be reasonable to deduce the other factors that influenced the ductility of the specimens by using the same material parameters mentioned above.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Milić, P.; Kušter Marić, M. Climate change effect on durability of bridges and other infrastructure. Građevinar Časopis Hrvat. Saveza Građevinskih Inženjera 2023, 75, 893–906. [Google Scholar]
- Jing, D.H.; Yu, T.; Liu, X.D. New configuration of transverse reinforcement for improved seismic resistance of rectangular RC columns: Concept and axial compressive behavior. Eng. Struct. 2016, 111, 383–393. [Google Scholar] [CrossRef]
- Dang, V.H.; François, R. Prediction of ductility factor of corroded reinforced concrete beams exposed to long term aging in chloride environment. Cem. Concr. Compos. 2014, 53, 136–147. [Google Scholar] [CrossRef]
- Stone, W.C.; Cheok, G.S. Inelastic Behavior of Full-Scale Bridge Piers Subjected to Cyclic Loading; Technical Report; U.S. Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1989; Volume 27.
- Park, R. Ductile design approach for reinforced concrete frames. Earthq. Spectra 1986, 2, 565–619. [Google Scholar] [CrossRef]
- Park, R. Ductility evaluation from laboratory and analytical testing. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2–9 August 1988; Volume 8, pp. 605–616. [Google Scholar]
- Sharma, U.K.; Bhargava, P.; Singh, S.P.; Kaushik, S.K. Confinement reinforcement design for plain and fibre reinforced high strength concrete columns. J. Adv. Concr. Technol. 2007, 5, 113–127. [Google Scholar] [CrossRef][Green Version]
- Paulay, T.; Priestley, M.N. Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley: New York, NY, USA, 1992; Volume 768. [Google Scholar]
- Yuen, T.Y.; Kuang, J.S.; Ho, D.Y. Ductility design of RC columns. Part 1: Consideration of axial compression ratio. HKIE Trans. 2016, 23, 230–244. [Google Scholar] [CrossRef]
- Yuen, T.Y.; Kuang, J.S.; Ho, D.Y. Ductility design of RC columns. Part 2: Extent of critical zone and confinement reinforcement. HKIE Trans. 2017, 24, 42–53. [Google Scholar] [CrossRef]
- Fischer, G.; Li, V.C. Effect of matrix ductility on deformation behavior of steel-reinforced ECC flexural members under reversed cyclic loading conditions. Struct. J. 2002, 99, 781–790. [Google Scholar]
- Kim, S.; Jeong, Y.; Kwon, M.; Kim, J. Ductile behavior of RC column reinforced with Velcro seismic reinforcement system (VSRS). Structures 2022, 44, 796–808. [Google Scholar] [CrossRef]
- Zhang, D.; Li, N.; Li, Z.X.; Xie, L. Experimental investigation and confinement model of composite confined concrete using steel jacket and prestressed steel hoop. Constr. Build. Mater. 2020, 256, 119399. [Google Scholar] [CrossRef]
- He, A.; Cai, J.; Chen, Q.J.; Liu, X.; Xue, H.; Yu, C. Axial compressive behaviour of steel-jacket retrofitted RC columns with recycled aggregate concrete. Constr. Build. Mater. 2017, 141, 501–516. [Google Scholar] [CrossRef]
- Choi, E.; Park, J.; Nam, T.H.; Yoon, S.J. A new steel jacketing method for RC columns. Mag. Concr. Res. 2009, 61, 787–796. [Google Scholar] [CrossRef]
- Islam, N.; Hoque, M. Strengthening of reinforced concrete columns by steel jacketing: A state of review. Asian Trans. Eng. 2015, 5, 6–14. [Google Scholar]
- Ibrahim, R.S.; Al-Zuhairi, A.H. Behavior of RC columns strengthened by combined (CFRP and steel jacket). Mater. Today Proc. 2022, 61, 1126–1134. [Google Scholar] [CrossRef]
- Parvin, A.; Brighton, D. FRP composites strengthening of concrete columns under various loading conditions. Polymers 2014, 6, 1040–1056. [Google Scholar] [CrossRef]
- Mo, Y.L.; Yeh, Y.K.; Hsieh, D.M. Seismic retrofit of hollow rectangular bridge columns. J. Compos. Constr. 2004, 8, 43–51. [Google Scholar] [CrossRef]
- Iacobucci, R.D.; Sheikh, S.A.; Bayrak, O. Retrofit of square concrete columns with carbon fiber-reinforced polymer for seismic resistance. Struct. J. 2003, 100, 785–794. [Google Scholar]
- Li, B.; Zohrevand, P.; Mirmiran, A. Cyclic behavior of FRP concrete bridge pier frames. J. Bridge Eng. 2013, 18, 429–438. [Google Scholar] [CrossRef]
- Wu, G.; Lü, Z.T.; Wu, Z.S. Strength and ductility of concrete cylinders confined with FRP composites. Constr. Build. Mater. 2006, 20, 134–148. [Google Scholar] [CrossRef]
- Parvin, A.; Wang, W. Behavior of FRP jacketed concrete columns under eccentric loading. J. Compos. Constr. 2001, 5, 146–152. [Google Scholar] [CrossRef]
- De Luca, A.; Nardone, F.; Matta, F.; Nanni, A.; Lignola, G.P.; Prota, A. Structural evaluation of full-scale FRP-confined reinforced concrete columns. J. Compos. Constr. 2011, 15, 112–123. [Google Scholar] [CrossRef]
- Koshiishi, M. High-Ductility RC Beam Structure. Japan Patent No. 6152975, 28 June 2017. [Google Scholar]
- Almeida, J.A.; Bandelt, M.J. Plastic hinge length in reinforced HPFRCC beams and columns. Eng. Struct. 2024, 315, 118345. [Google Scholar] [CrossRef]
- Sun, X.F. Mechanics of Materials (I); Higher Education Press: Beijing, China, 2018. [Google Scholar]
- Ishibashi, T.; Tshutoshi, T.; Kobayashi, K.; Yoshida, T.; Umihara, T. Study on evaluation of ductility of reinforced concrete columns subjected to reversed cyclic loading with large deformations. Trans. Jpn. Soc. Civ. Eng. 2002, 711, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing. Bull. New Zealand Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, L.; Elchalakani, M.; Cai, J. Cyclic loading test for reinforced concrete columns strengthened with high strength engineered cementitious composite jacket. Eng. Struct. 2023, 278, 115571. [Google Scholar] [CrossRef]
- Ghayeb, H.H.; Sulong, N.R.; Razak, H.A.; Mo, K.H. Enhancement of seismic behaviour of precast beam-to-column joints using engineered cementitious composite. Eng. Struct. 2022, 255, 113932. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI J. 1986, 83, 219–231. [Google Scholar]
- Selby, R.G. Three-Dimensional Constitutive Relations for Reinforced Concrete. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1995. [Google Scholar]
- Taerwe, L.; Matthys, S. Fib Model Code for Concrete Structures 2010; Ernst & Sohn, Wiley: Weinheim, Germany, 2013. [Google Scholar]
- Dodd, L.L.; Restrepo-Posada, J.I. Model for predicting cyclic behavior of reinforcing steel. J. Struct. Eng. 1995, 121, 433–445. [Google Scholar] [CrossRef]







| Type 1 | Type 2 | |||
|---|---|---|---|---|
| Sample | Compressive Strength (N/mm2) | Split Tensile Strength (N/mm2) | Compressive Strength (N/mm2) | Split Tensile Strength (N/mm2) |
| #1 | 39.6 | 3.24 | 39.2 | 2.82 |
| #2 | 40.4 | - | 39.6 | - |
| Average | 40.0 | 3.24 | 39.4 | 2.82 |
| Specimens | Yield Strength (N/mm2) | Tensile Strength (N/mm2) | Elongation (%) |
|---|---|---|---|
| Type 1 | 404 | 549 | 21 |
| Type 2 | 400 | 567 | 20 |
| Load Phase | Force (KN) | Displacement (mm) | K (KN/mm) | Esum (KN ∗ mm) | η | λc | |||
|---|---|---|---|---|---|---|---|---|---|
| +F | −F | +δ | −δ | ||||||
| Type 1 | 1 | 43.77 | −44.80 | 22.44 | −22.49 | 1.97 | 419.68 | 1.00 | 1.00 |
| 2 | 54.63 | −54.11 | 44.823 | −45.073 | 1.21 | 2466.02 | 0.61 | 2.94 | |
| 3 | 52.56 | −53.08 | 67.31 | −67.6094 | 0.78 | 6864.41 | 0.40 | 5.45 | |
| 4 | 52.04 | −53.60 | 89.65 | −90.046 | 0.59 | 13,989.00 | 0.30 | 8.33 | |
| 5 | 49.98 | −51.53 | 112.08 | −112.582 | 0.45 | 24,286.85 | 0.23 | 11.57 | |
| 6 | 46.87 | −49.46 | 134.82 | −134.819 | 0.36 | 37,816.60 | 0.18 | 15.02 | |
| Type 2 | 1 | 44.32 | −44.84 | 18.79 | −18.79 | 2.37 | 193.43 | 1.00 | 1.00 |
| 2 | 59.33 | −60.88 | 37.68 | −37.98 | 1.59 | 1960.42 | 0.67 | 5.07 | |
| 3 | 61.91 | −62.43 | 56.67 | −56.77 | 1.10 | 5922.43 | 0.46 | 10.21 | |
| 4 | 60.87 | −61.39 | 75.36 | −75.75 | 0.81 | 12,046.00 | 0.34 | 15.57 | |
| 5 | 56.74 | −55.19 | 94.34 | −94.79 | 0.60 | 20,091.07 | 0.25 | 20.77 | |
| 6 | 53.63 | −52.08 | 113.23 | −113.73 | 0.47 | 30,355.18 | 0.20 | 26.15 | |
| 7 | 50.53 | −50.01 | 132.32 | −132.77 | 0.38 | 43,199.59 | 0.16 | 31.90 | |
| Specimen | Ductility Displacement (mm) | Yield Displacement (mm) | Ductility | ||
|---|---|---|---|---|---|
| positive | negative | Average | |||
| Type 1 | 145.34 | −145.61 | 145.48 | 22.5 | 6.47 |
| Type 2 | 137.61 | −132.90 | 135.26 | 18.8 | 7.19 |
| Parameters | Type 1 | Type 2 | |
|---|---|---|---|
| Young’s modulus (N/mm2) | 34,100 | 34,100 | |
| Poisson’s ratio | 0.167 | 0.167 | |
| Tensile behavior | Tensile curve | Exponential | Exponential |
| Tensile strength (N/mm2) | 3.24 | 2.82 | |
| Fracture energy (N/mm) | 0.147 | 0.146 | |
| Compressive behavior | Compressive curve | Parabolic | Parabolic |
| Compressive behavior (N/mm2) | 40 | 39.4 | |
| Compressive energy (N/mm) | 36.75 | 36.5 | |
| Compressive behavior | Residual compressive strength (N/mm2) | 5 | 10 |
| Parameters | Longitudinal Reinforcement | Stirrup | ||
|---|---|---|---|---|
| Type 1 | Type 2 | Type 1 | Type 2 | |
| Young’s modulus (N/mm2) | 200,000 | 200,000 | 200,000 | 200,000 |
| Yield stress (N/mm2) | 404 | 400 | 388 | 388 |
| Strain at the end of yield plateau | 1.25% | 1.25% (0.35%-pre-deformation) | 1.25% | 1.25% |
| Ultimate strain | 0.17 | 0.17 | 0.23 | 0.23 |
| Peak stress (N/mm2) | 549 | 567 | 542 | 542 |
| Parameters | Steel Bar |
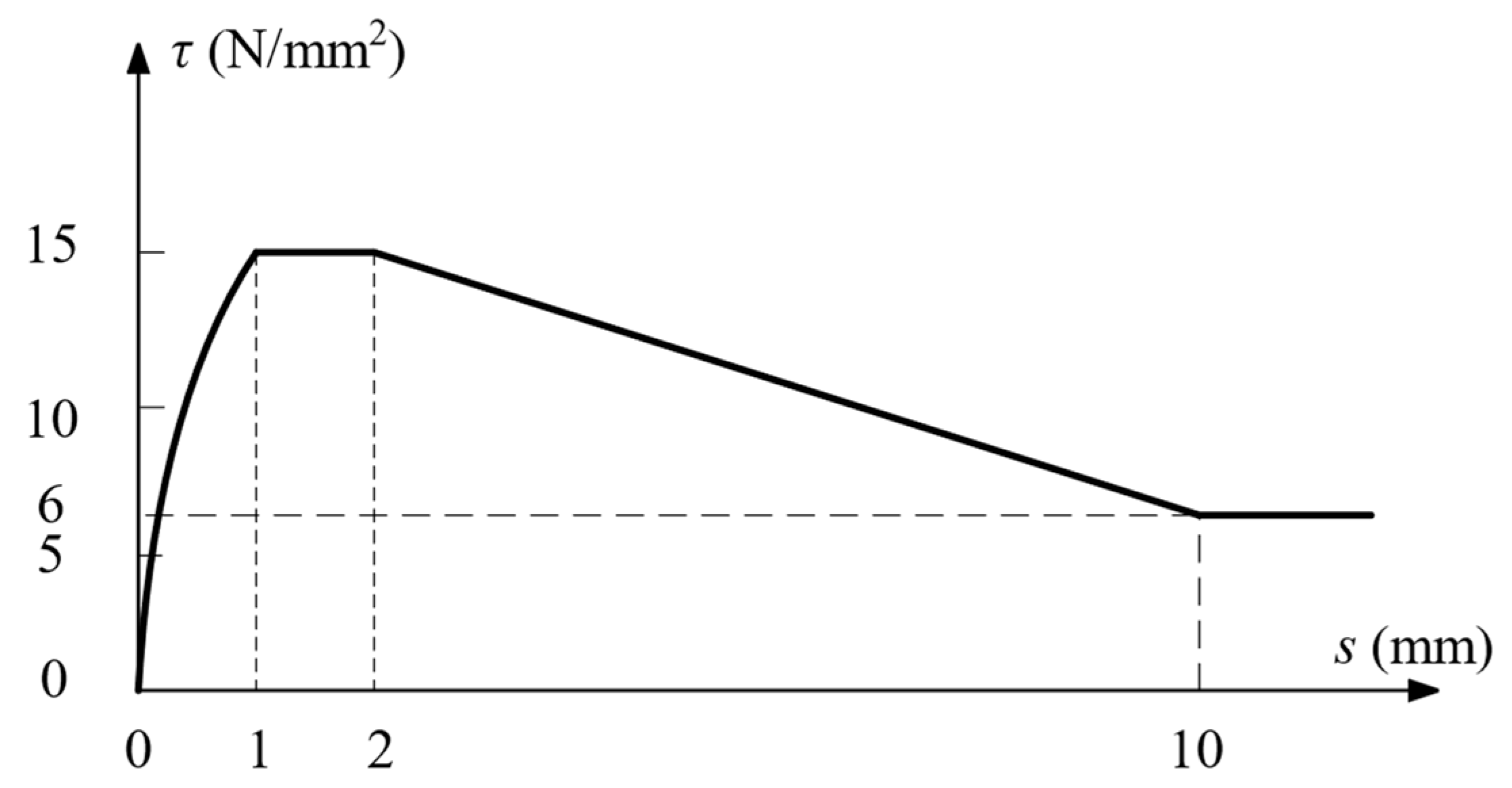
|---|---|
| Bond-slip interface failure model | CEB-FIB 2010 bond-slip function |
| Normal stiffness modulus (N/mm3) | 1000 |
| Shear stiffness modulus (N/mm3) | 100 |
| Maximum shear stress (N/mm2) | 15 |
| Ultimate shear stress (N/mm2) | 6 |
| Relative slip section (mm) | 1 |
| Relative slip section (mm) | 2 |
| Relative slip section (mm) | 10 |
| Exponent alpha | 0.4 |
| Parameters | Type 1 | Type 2 | ||
|---|---|---|---|---|
| Simulation | Experiment | Simulation | Experiment | |
| (mm) | 120.23 | 145.47 | 132.60 | 135.26 |
| (mm) | 24 | 22.5 | 24.32 | 18.8 |
| (KN) | 61.97 | 54.37 | 67.19 | 62.17 |
| 5.01 | 6.47 | 5.45 | 7.19 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamai, H.; Wang, W.; Sonoda, Y.; Koshiishi, M. Basic Study on the Proposal of New Measures to Improve the Ductility of RC Bridge Pier and Their Effectiveness. Infrastructures 2024, 9, 197. https://doi.org/10.3390/infrastructures9110197
Tamai H, Wang W, Sonoda Y, Koshiishi M. Basic Study on the Proposal of New Measures to Improve the Ductility of RC Bridge Pier and Their Effectiveness. Infrastructures. 2024; 9(11):197. https://doi.org/10.3390/infrastructures9110197
Chicago/Turabian StyleTamai, Hiroki, Wenming Wang, Yoshimi Sonoda, and Masami Koshiishi. 2024. "Basic Study on the Proposal of New Measures to Improve the Ductility of RC Bridge Pier and Their Effectiveness" Infrastructures 9, no. 11: 197. https://doi.org/10.3390/infrastructures9110197
APA StyleTamai, H., Wang, W., Sonoda, Y., & Koshiishi, M. (2024). Basic Study on the Proposal of New Measures to Improve the Ductility of RC Bridge Pier and Their Effectiveness. Infrastructures, 9(11), 197. https://doi.org/10.3390/infrastructures9110197






