Strength and Deformation of Concrete-Encased Grouting-Filled Steel Tubes Columns Exposed to Monotonic Quasi-Static Loading Conditions
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Matrix Specifications
2.2. Materials Properties
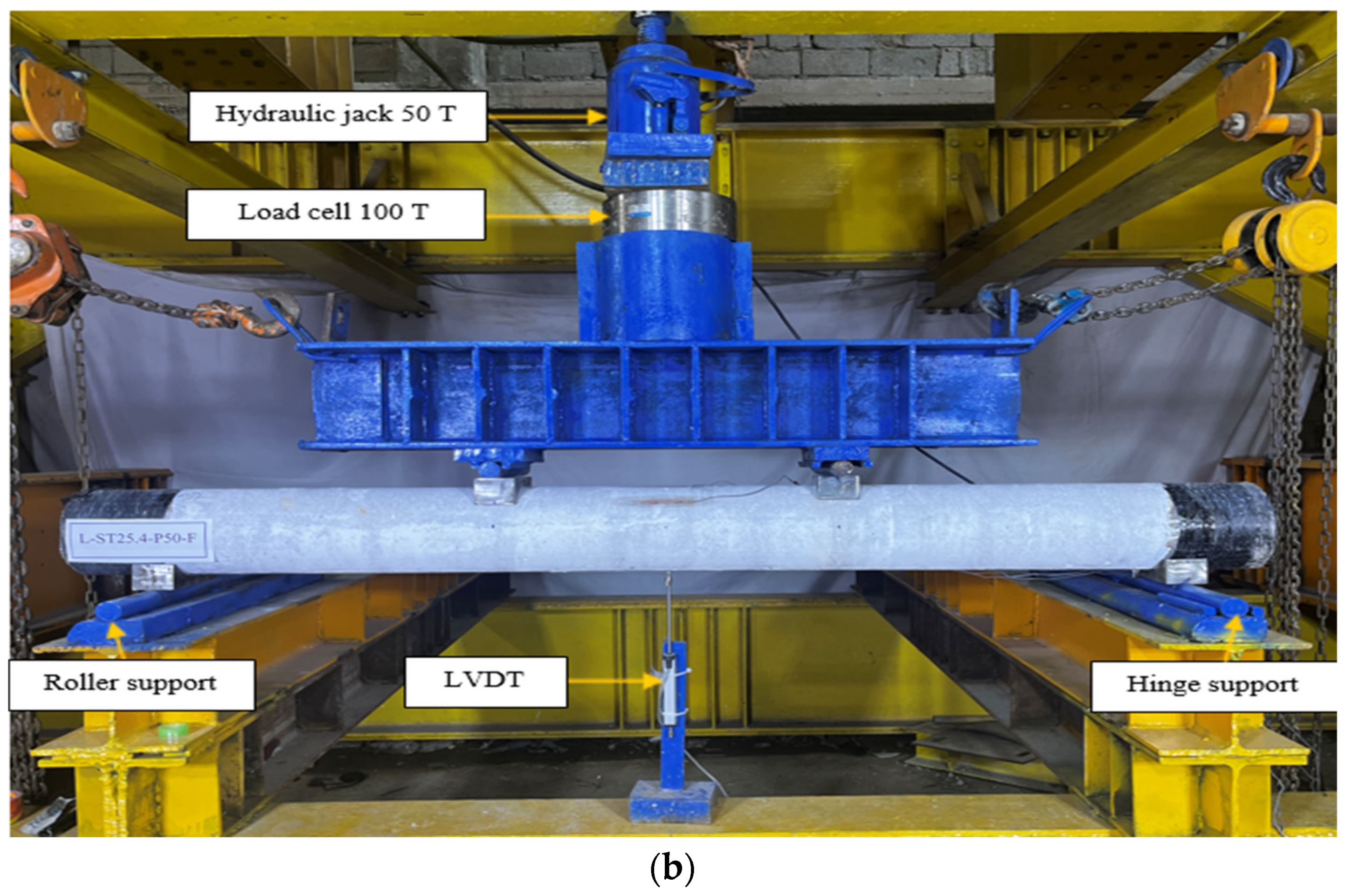
2.3. Setup Details of Tested Specimens
3. Numerical Part of the Study
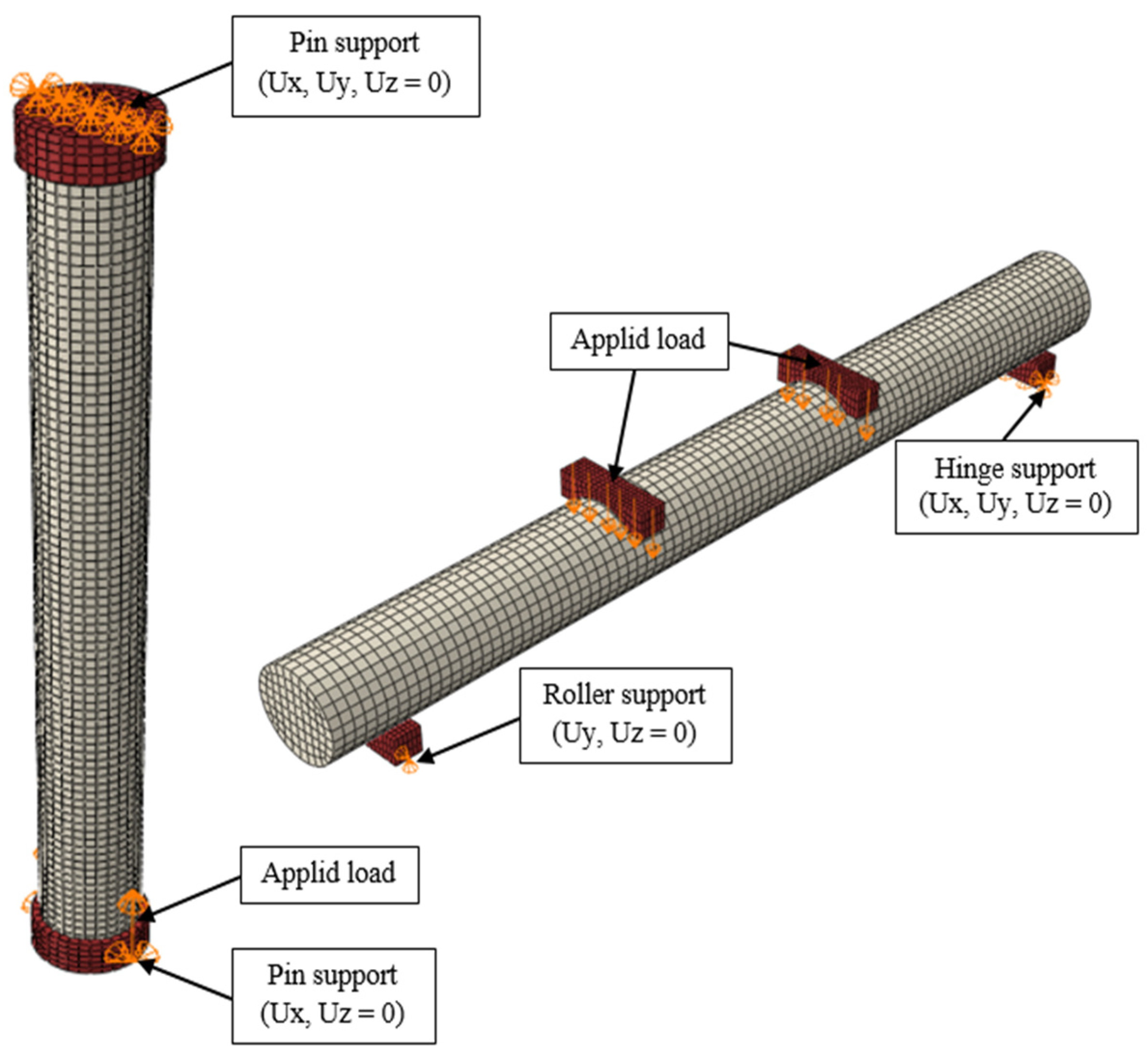
3.1. FE Modeling and Boundary Conditions
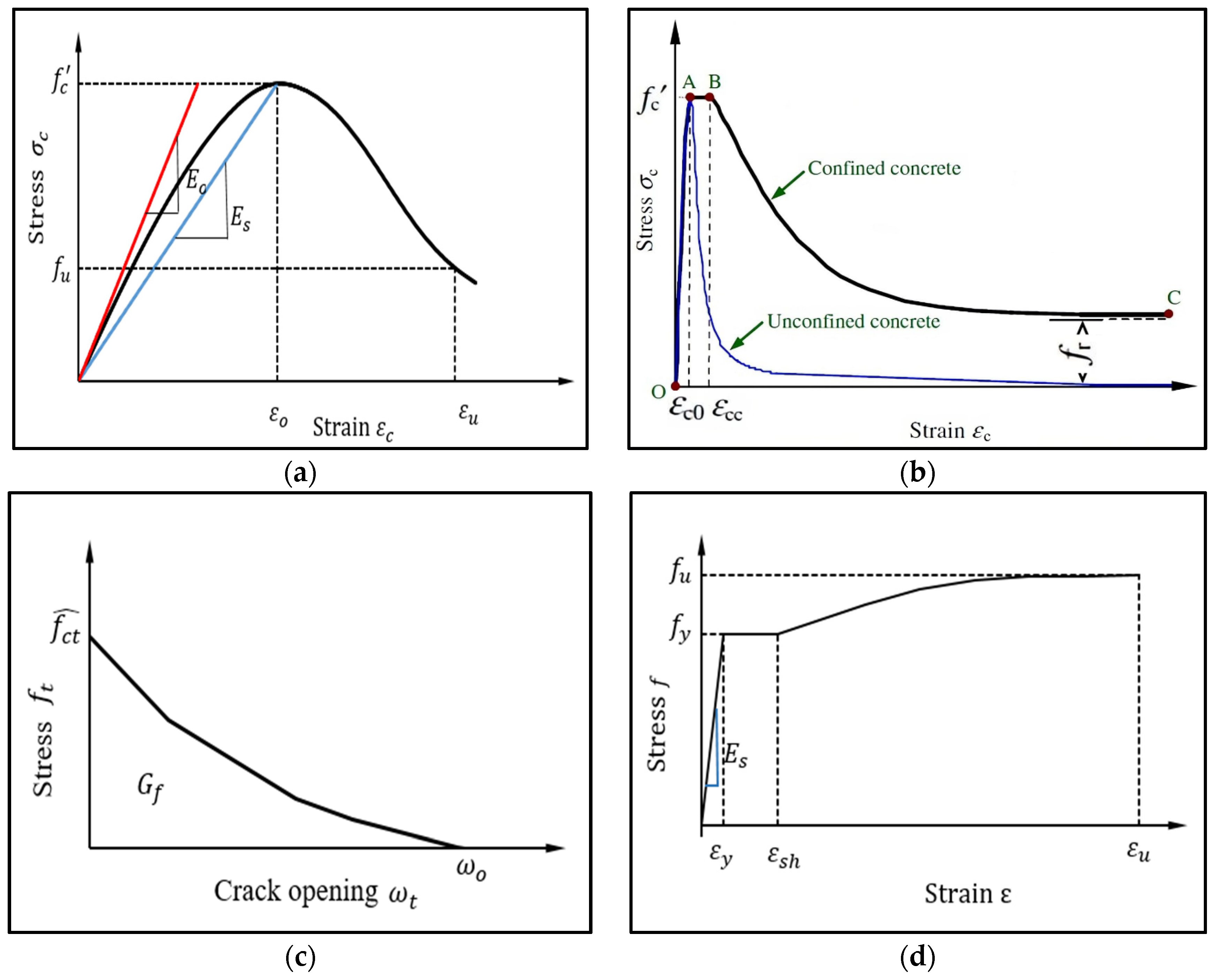
3.2. Modeling of Materials
4. Test Results and Finite Element Validation
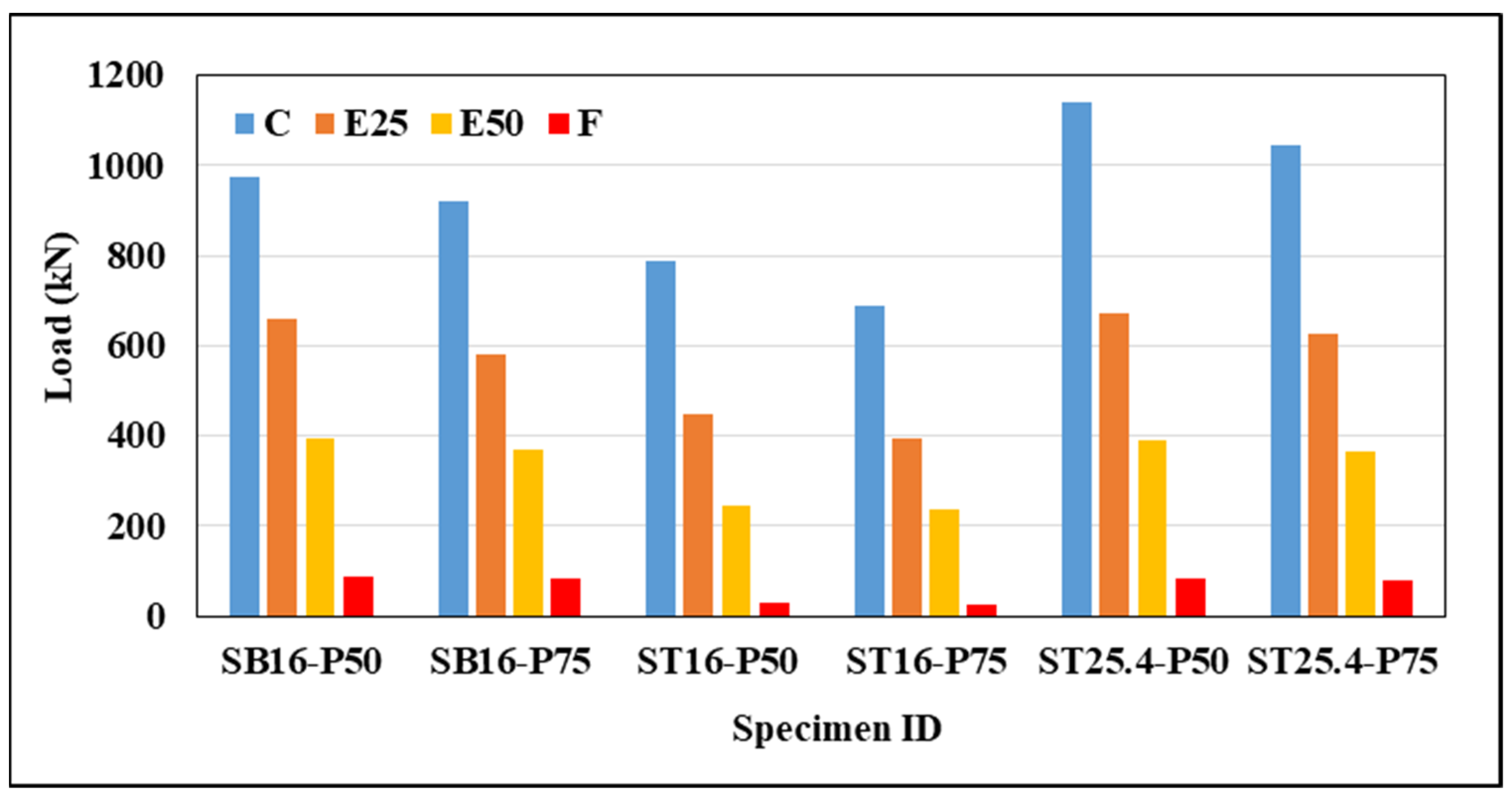
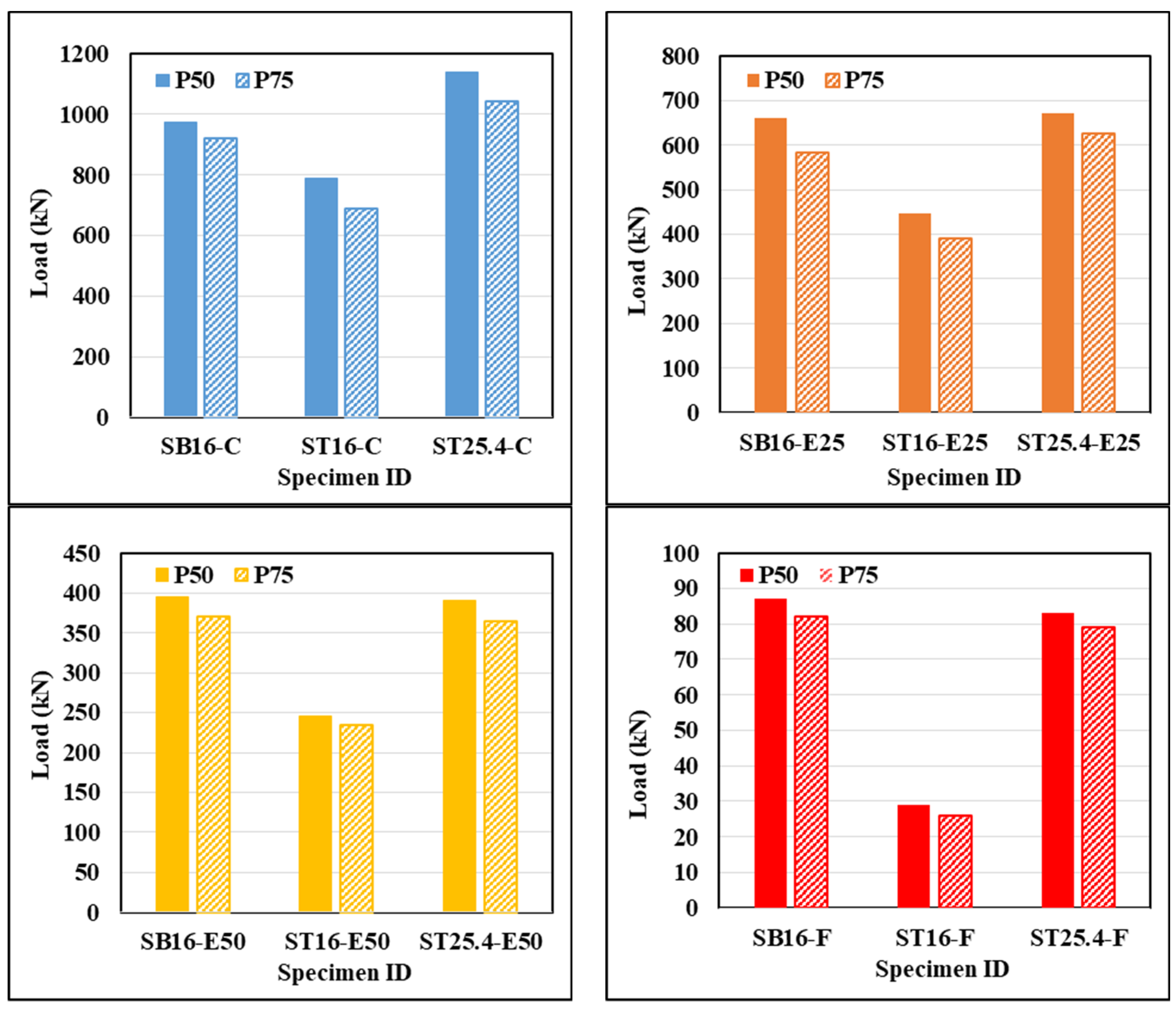
4.1. Load Capacity of CE-GFSTs Columns
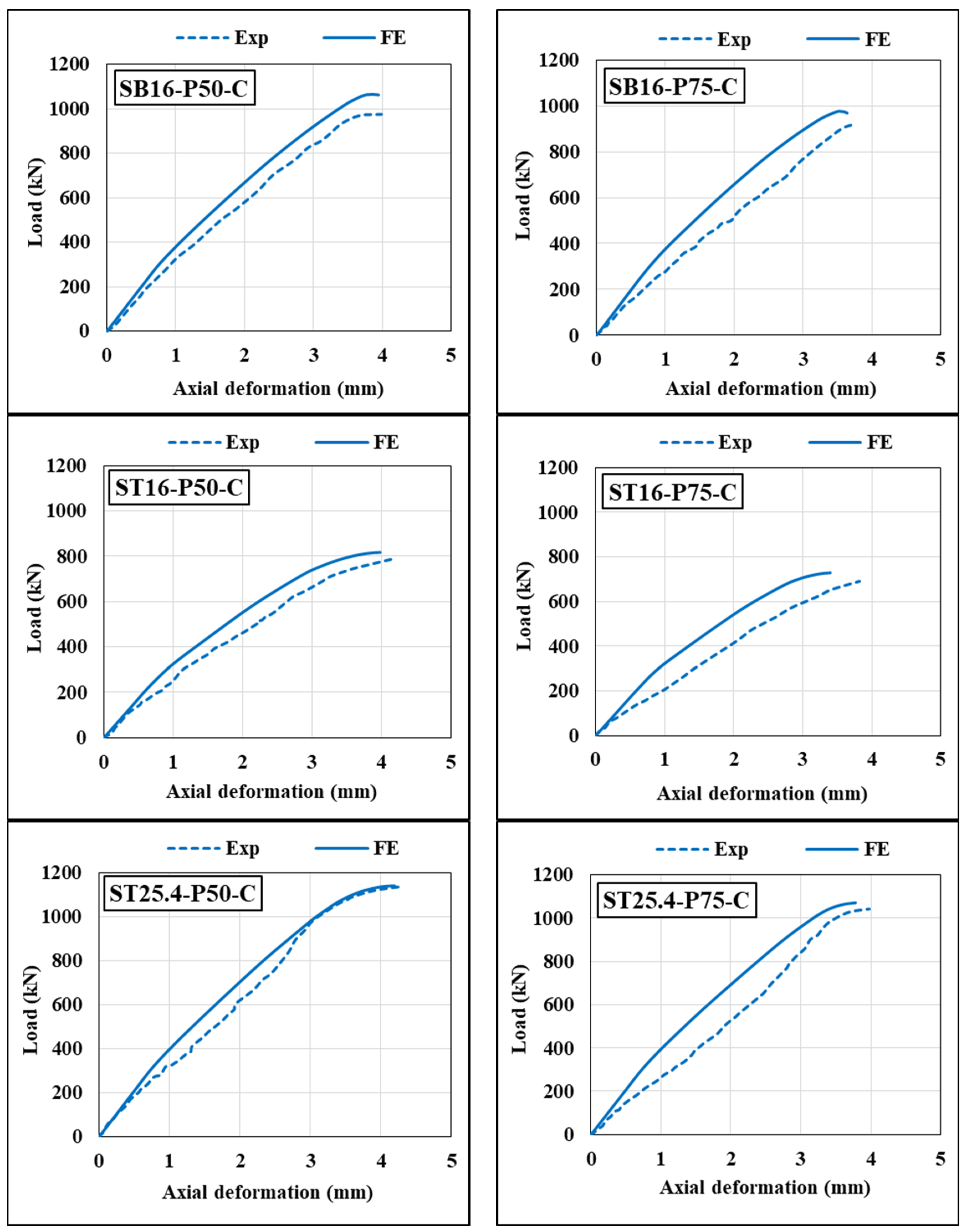
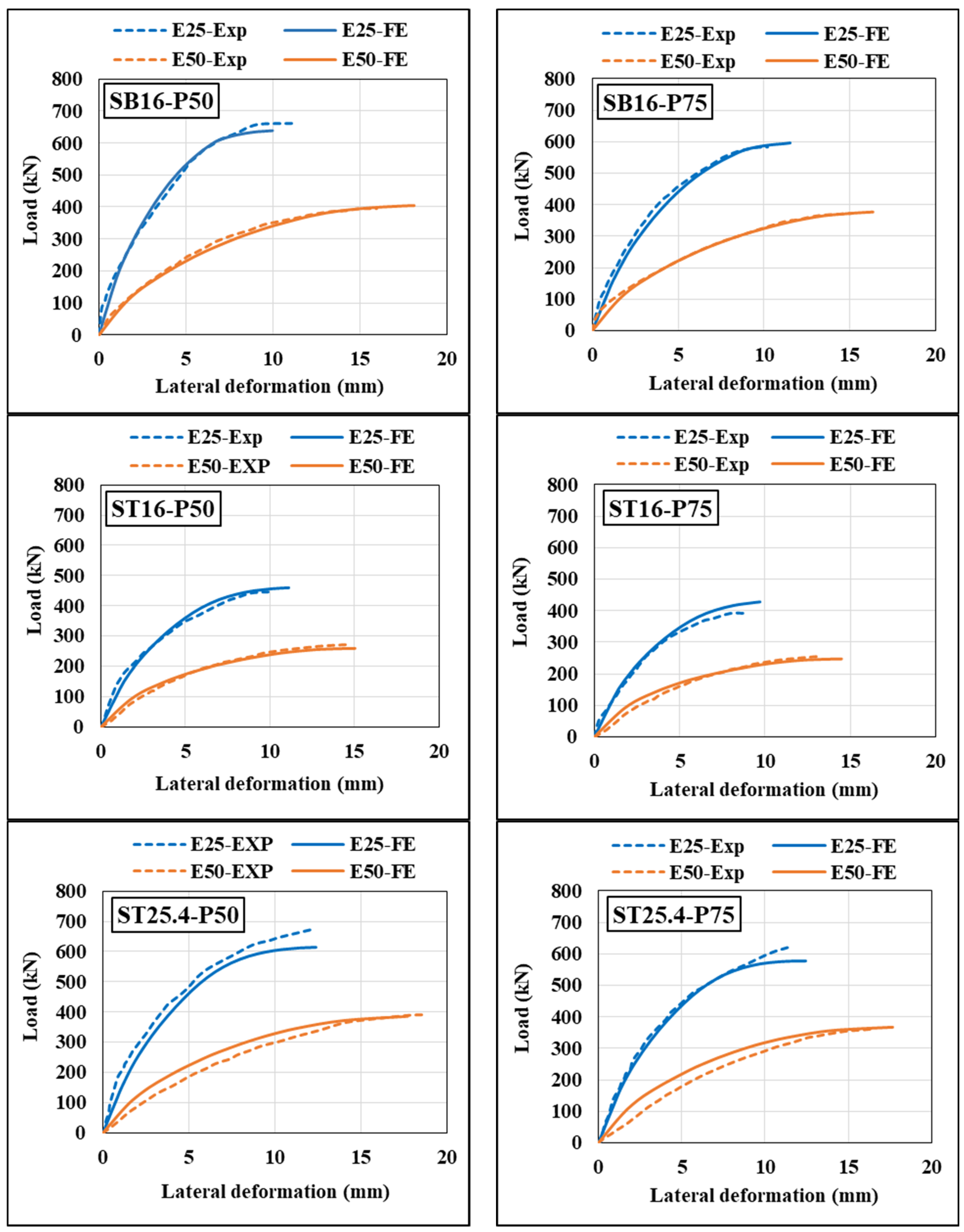
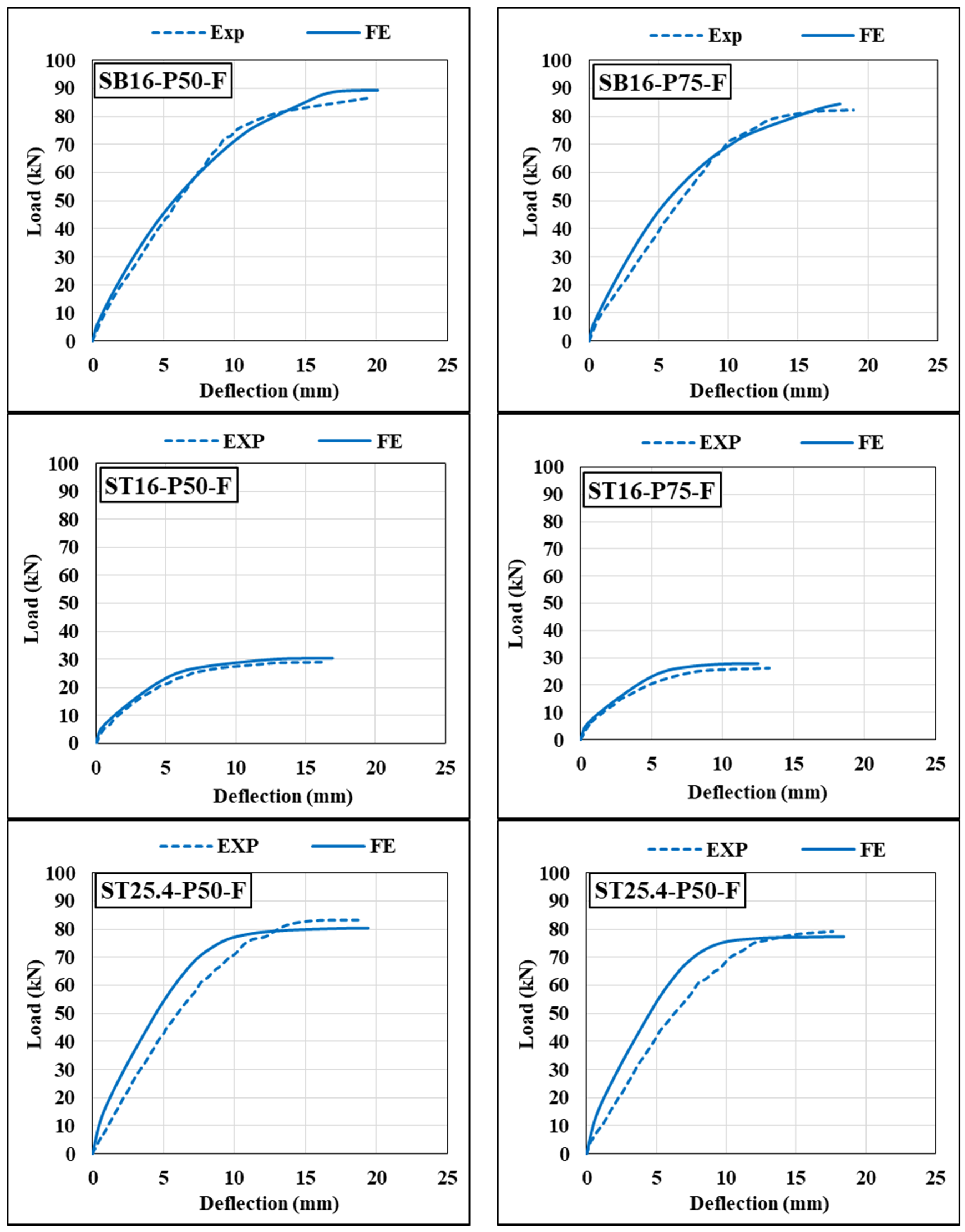
4.2. Load–Deformation Curve of CE-GFSTs Columns
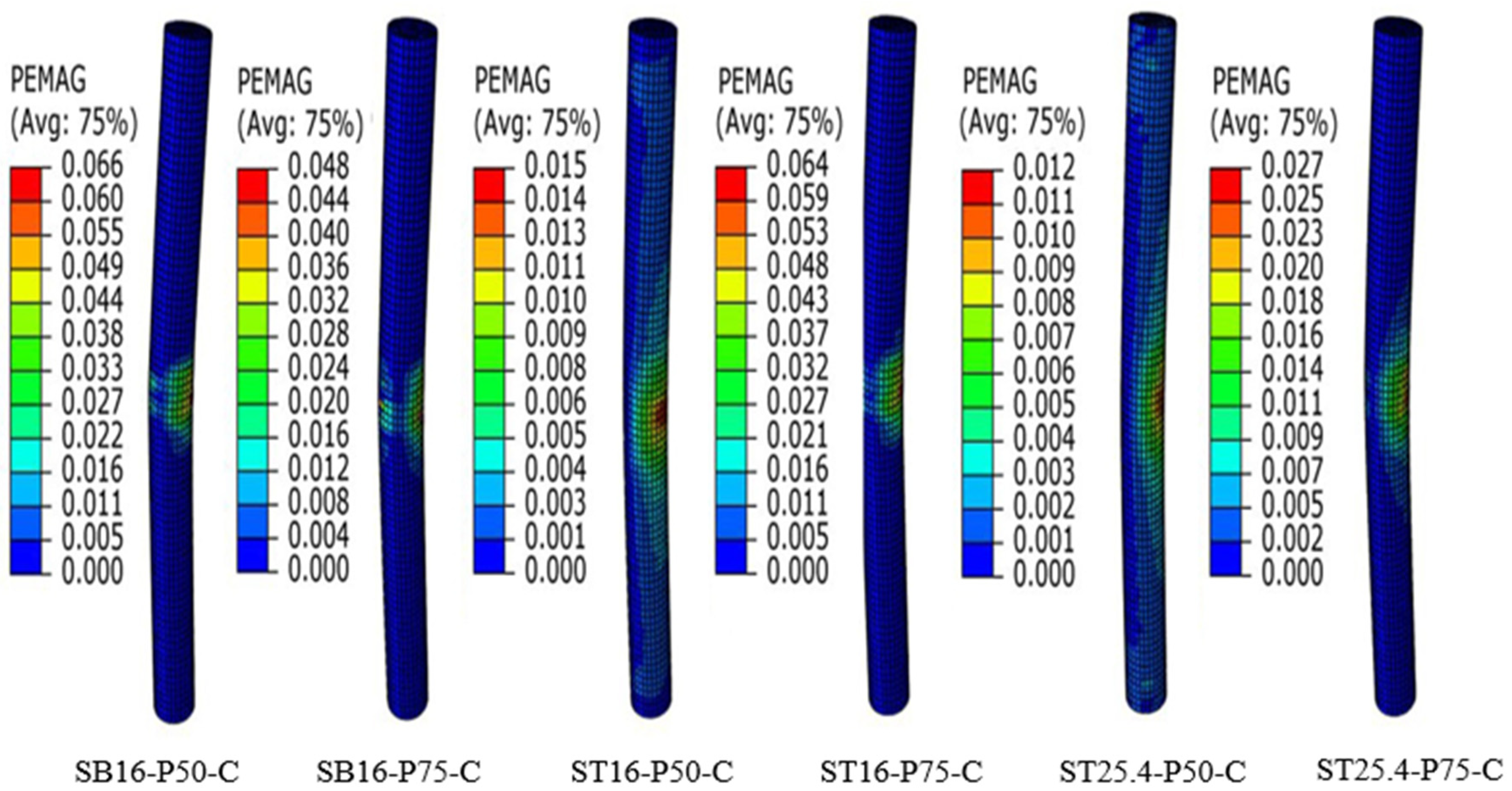
4.3. Crack Pattern and Mode of Failure
4.4. Column Interaction Diagrams
5. Conclusions
- Replacing longitudinal steel bars with small circular steel tubes can increase the ultimate strength of columns under concentric load by 17% and 13%, respectively. The use of small circular steel tubes with a 30% reinforcement ratio resulted in an ultimate strength of 81% of the reference specimen’s strength, but this percentage decreased under eccentric or flexural loading;
- The applied load’s eccentricity significantly impacts the ultimate strength and lateral deformation of columns, causing a decrease in specimen capacity and an increase in lateral deformation;
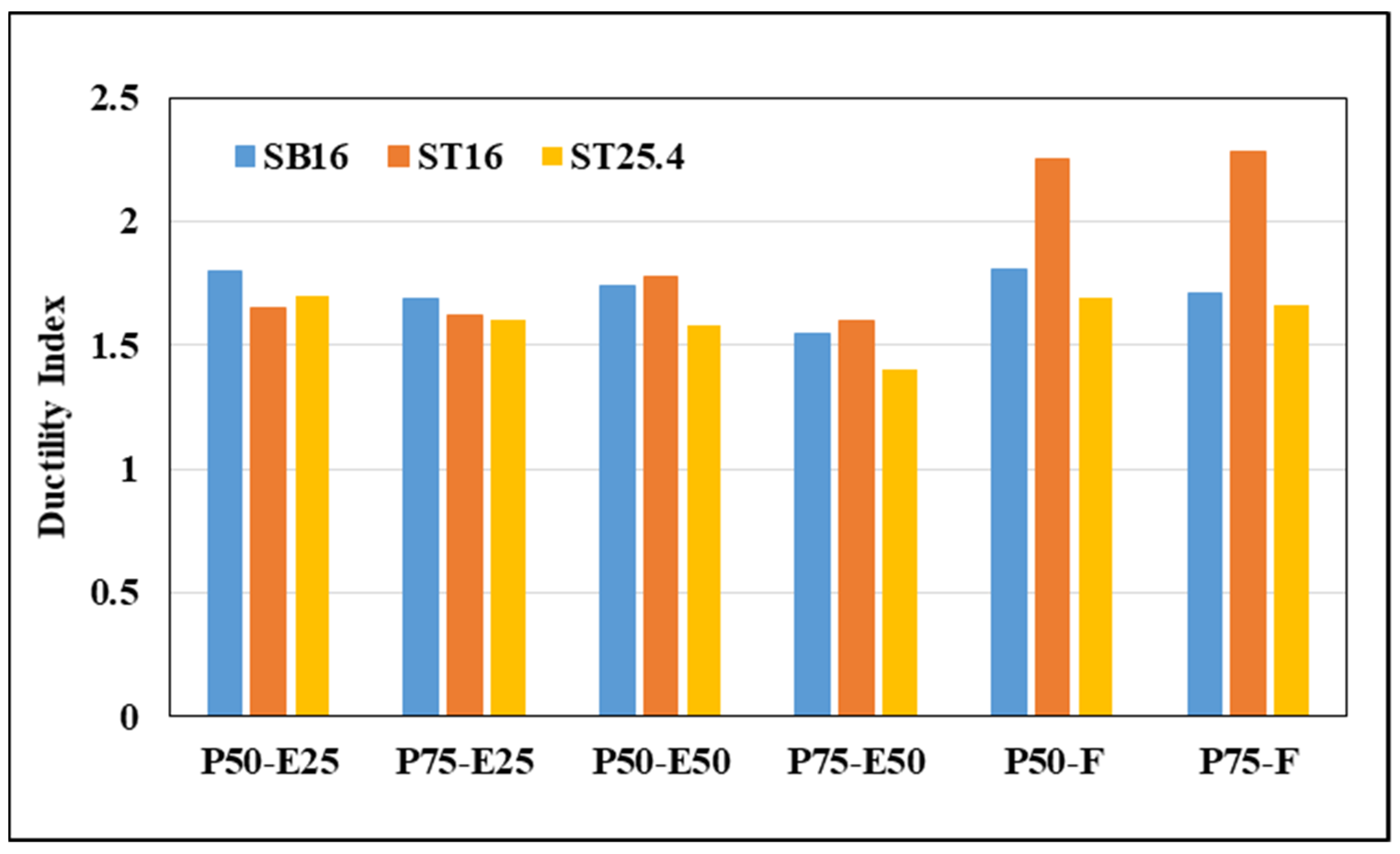
- The tested specimens with the same design parameters exhibited a decrease in ultimate strength when the spiral spacing increased from 50 to 75 mm;
- Three experimental failure modes of concrete-encased GFSTs columns were observed: compression failure mode for concentrically tested columns, flexural–compression failure mode for columns under 25 mm eccentric load, and tensile failure mode for columns under high eccentricity or flexural load;
- Finite element models (FEA) were developed to simulate CE-GFST columns’ behavior under different loading conditions. Experimental results validated the models, showing high concordance with test outcomes for ultimate strength, deformation, and failure modes;
- According to the outcomes of the present study, the first type of reinforcement—conventional steel bars—is 25% more expensive than the second type, which consists of concrete-filled steel tubes with a 30% steel bar reinforcement ratio. On the other hand, the third type—concrete-filled steel tubes with the same reinforcement ratio as steel bars—outperforms traditional steel bars in terms of failure load at the same cost. Nevertheless, the current study has several limitations, including sample size and testing circumstances within the evaluated specimens. Therefore, in order to construct steel tubes filled with cementitious grouting material that is used to reinforce columns, future research should optimize the design parameters by looking at different slenderness ratios, grades of steel tubes, compressive strength of grouting materials, etc.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, D.Y.; Han, L.H.; Ji, X.; Yang, W.B. Behaviour of hexagonal concrete-encased CFST columns subjected to cyclic bending. J. Const. Steel Res. 2018, 144, 283–294. [Google Scholar] [CrossRef]
- Zhou, J.; Li, P.; Guo, N. Seismic performance assessment of a precast concrete-encased CFST composite wall with twin steel tube connections. Eng. Struct. 2020, 207, 110240. [Google Scholar] [CrossRef]
- Alshimmeri, A.J.H. Structural Behavior of Confined Concrete Filled Aluminum Tubular (CFT) Columns under Concentric Load. J. Eng. 2016, 22, 125–139. [Google Scholar] [CrossRef]
- Hassooni, A.N.; Al-Zaidee, S.R. Rehabilitation of Composite Column Subjected to Axial Load. Civil Eng. J. 2022, 8, 595–611. [Google Scholar] [CrossRef]
- Hassooni, A.N.; Al Zaidee, S.R. Behavior and Strength of Composite Columns under the Impact of Uniaxial Compression Loading. Eng. Tech. Appl. Sci. Res. 2022, 12, 8843–8849. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Tan, J.; Vandevyvere, B.; Xiaopeng, L. Nonlinear analysis of ECC-encased CFST columns under axial compression. J. Build. Eng. 2020, 31, 101401. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.C.; Chen, C.C.; Lin, T.K.; Tullini, N. Compressive column load identification in steel space frames using second-order deflection-based methods. Inter. J. Struct. Stab. Dyna. 2018, 18, 1850092. [Google Scholar] [CrossRef]
- Niyirora, R.; Niyonyungu, F.; Hakuzweyezu, T.; Masengesho, E.; Nyirandayisabye, R.; Munyaneza, J. Behavior of concrete-encased concrete-filled steel tube columns under diverse loading conditions: A review of current trends and future prospects. Cog. Eng. 2023, 10, 2156056. [Google Scholar] [CrossRef]
- Morino, S. Design and construction of concrete-filled steel tube column system in Japan. Earthq. Eng. Eng. Seismol. 2003, 4, 51–73. [Google Scholar]
- Nguyen, D.H.; Kee Hong, W.; Hyo Jin, K.; Kyum Kim, S. Finite element model for the interface between steel and concrete of CFST (concrete-filled steel tube). Eng. Struct. 2019, 185, 141–158. [Google Scholar] [CrossRef]
- Guo, X.H.; Jiao, J.F.; Wu, Z.A.; Zhang, J.L. Research on the reinforcement mechanism and safety monitoring of heavy-duty concrete-encased CFST columns. Adva. Civil Eng. 2020, 2020, 7372345. [Google Scholar] [CrossRef]
- An, Y.F.; Han, L.H.; Zhao, X.L. Experimental behaviour of box concrete-encased CFST eccentrically loaded column. Mag. Conc. Res. 2013, 65, 1219–1235. [Google Scholar] [CrossRef]
- An, Y.F.; Han, L.H.; Zhao, X.L. Analytical behaviour of eccentrically loaded concrete-encased CFST box columns. Mag. Conc. Res. 2014, 66, 789–808. [Google Scholar] [CrossRef]
- Han, L.H.; An, Y.F. Performance of concrete-encased CFST stub columns under axial compression. J. Const. Steel Res. 2014, 93, 62–76. [Google Scholar] [CrossRef]
- Li, Y.J.; Han, L.H.; Xu, W.; Tao, Z. Circular concrete-encased concrete-filled steel tube (CFST) stub columns subjected to axial compression. Mag. Conc. Res. 2016, 68, 995–1010. [Google Scholar] [CrossRef]
- Hadi, M.N.; Alhussainy, F.; Sheikh, M.N. Behavior of self-compacting concrete columns reinforced longitudinally with steel tubes. J. Struct. Eng. 2017, 143, 04017024. [Google Scholar] [CrossRef]
- Alhussainy, F.; Sheikh, M.N.; Hadi, M.N. Axial load-axial deformation behaviour of SCC columns reinforced with steel tubes. Structures 2018, 15, 259–269. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Lu, C. Mechanical behavior of ECC-encased CFST columns subjected to eccentric loading. Eng. Struct. 2018, 162, 22–28. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Su, H.; Lu, C. Experimental study on the hysteretic behavior of ECC-encased CFST columns. Eng. Struct. 2018, 173, 107–121. [Google Scholar] [CrossRef]
- Chen, J.Y.; Li, W.; Han, L.H.; Wang, F.C.; Mu, T.M. Structural behaviour of concrete-encased CFST box stub columns under axial compression. J. Const. Steel Res. 2019, 158, 248–262. [Google Scholar] [CrossRef]
- Manjusha, K.T.; Anila, S. Finite Element Investigation of ECC Encased CFST Columns Under Eccentric Loading. Int. J. Eng. Res. Techn. 2019, 8, 274–279. [Google Scholar]
- Lee, H.J.; Park, H.G.; Choi, I.R. Eccentric compression behavior of concrete-encased-and-filled steel tube columns with high-strength circular steel tube. Thin-Walled Struct. 2019, 144, 106339. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Tan, J.; Vandevyvere, B.; Li, X. Behavior of ECC-encased CFST columns under eccentric loading. J. Buil. Eng. 2020, 30, 101188. [Google Scholar] [CrossRef]
- Hameed, M.H.; Al-Ahmed, A.H.A.; Abbas, Z.K. Enhancing the strength of reinforced concrete columns using steel embedded tubes. Mech. Adva. Mater. Struct. 2022, 29, 2008–2023. [Google Scholar] [CrossRef]
- ACI. Committee 318 Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- ASTM C39-18; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: Conshohocken, PA, USA, 2018.
- ASTM C496-17; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: Conshohocken, PA, USA, 2017; pp. 1–4.
- ASTM C78/C78M-22; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading). ASTM International: Conshohocken, PA, USA, 2022; pp. 1–3.
- ASTM-C469/C469M-14; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2014; pp. 1–9.
- ASTM A615; Standard Specifications for Testing Methods and Definition for Mechanical Testing Steel Products. Annual Book of ASTM Standards American Society for Testing and Materials: Philadelphia, PA, USA, 2020; Section 1.01. pp. 248–287.
- ASTM A370; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM International: Conshohocken, PA, USA, 2018.
- ABAQUS, version 6.14; [Computer software]; Assault Systems: Waltham, MA, USA, 2019.
- ABAQUS, Analysis User’s Manual, version 2019; SIMULIA/ABAQUC INC.: Dearborn, MI, USA, 2019.
- Elwi, A.A.; Murray, D.W. A 3D hypoelastic concrete constitutive relationship. J. Eng. Mech. Div. 1979, 105, 623–641. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Z.B.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar] [CrossRef]
- Hordijk, D.A. Tensile and tensile fatigue behaviour of concrete; experiments, modelling and analyses. Heron 1992, 37, 1–79. [Google Scholar]
- Yun, X.; Gardner, L. Stress-strain curves for hot-rolled steels. J. Constr. Steel Res. 2017, 133, 36–46. [Google Scholar] [CrossRef]
- Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing. Bull. N. Z. Soc. Earth Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
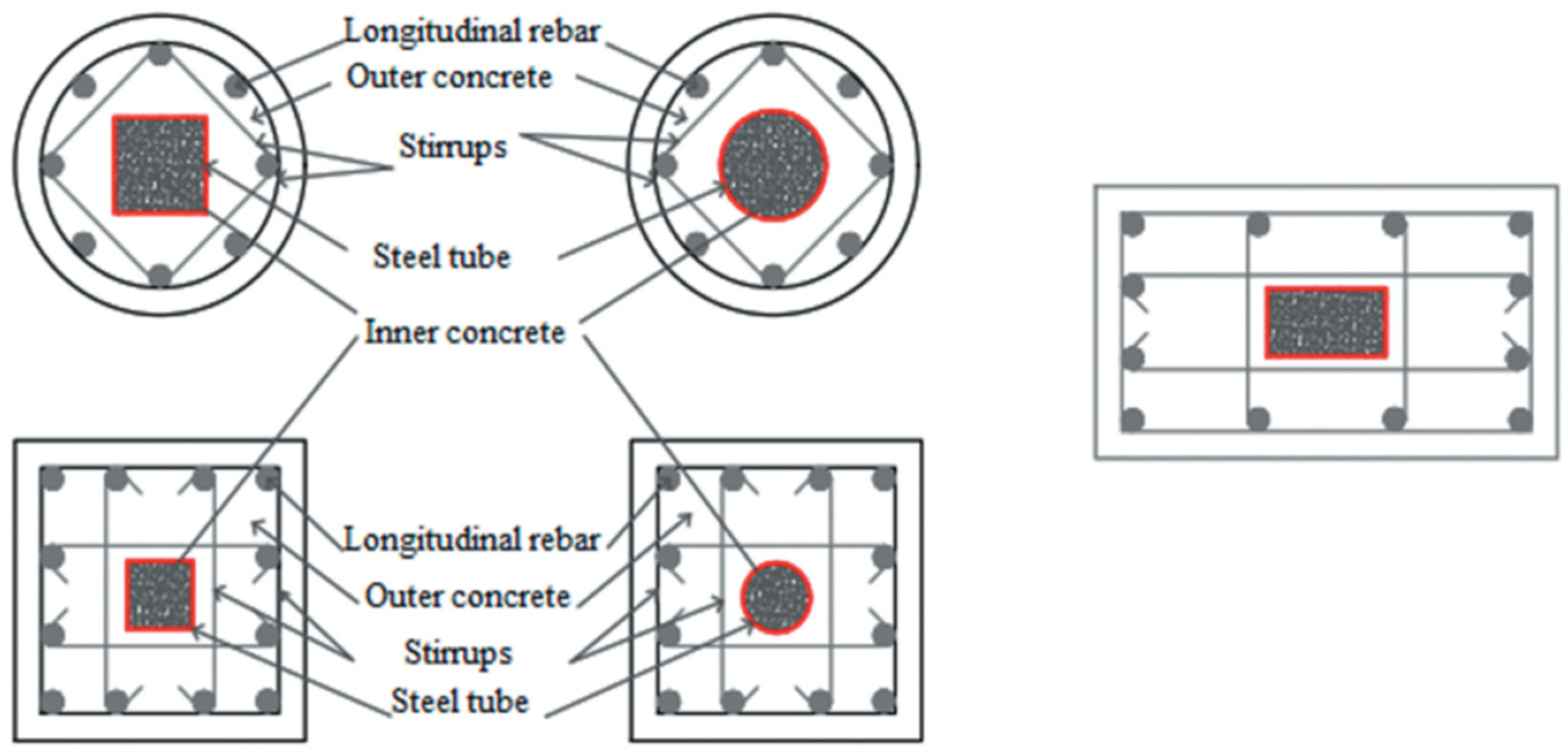
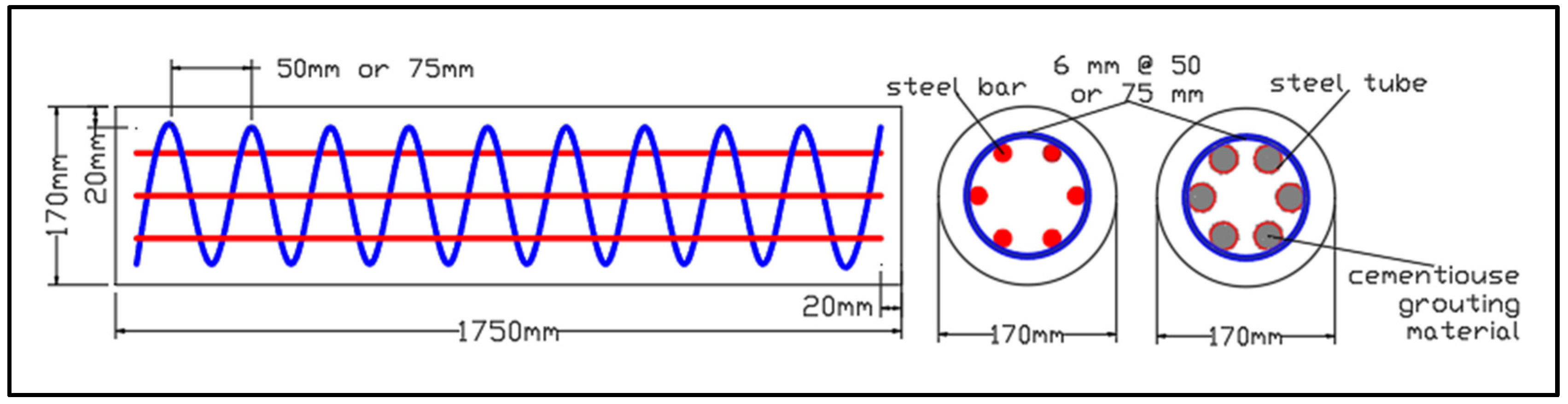





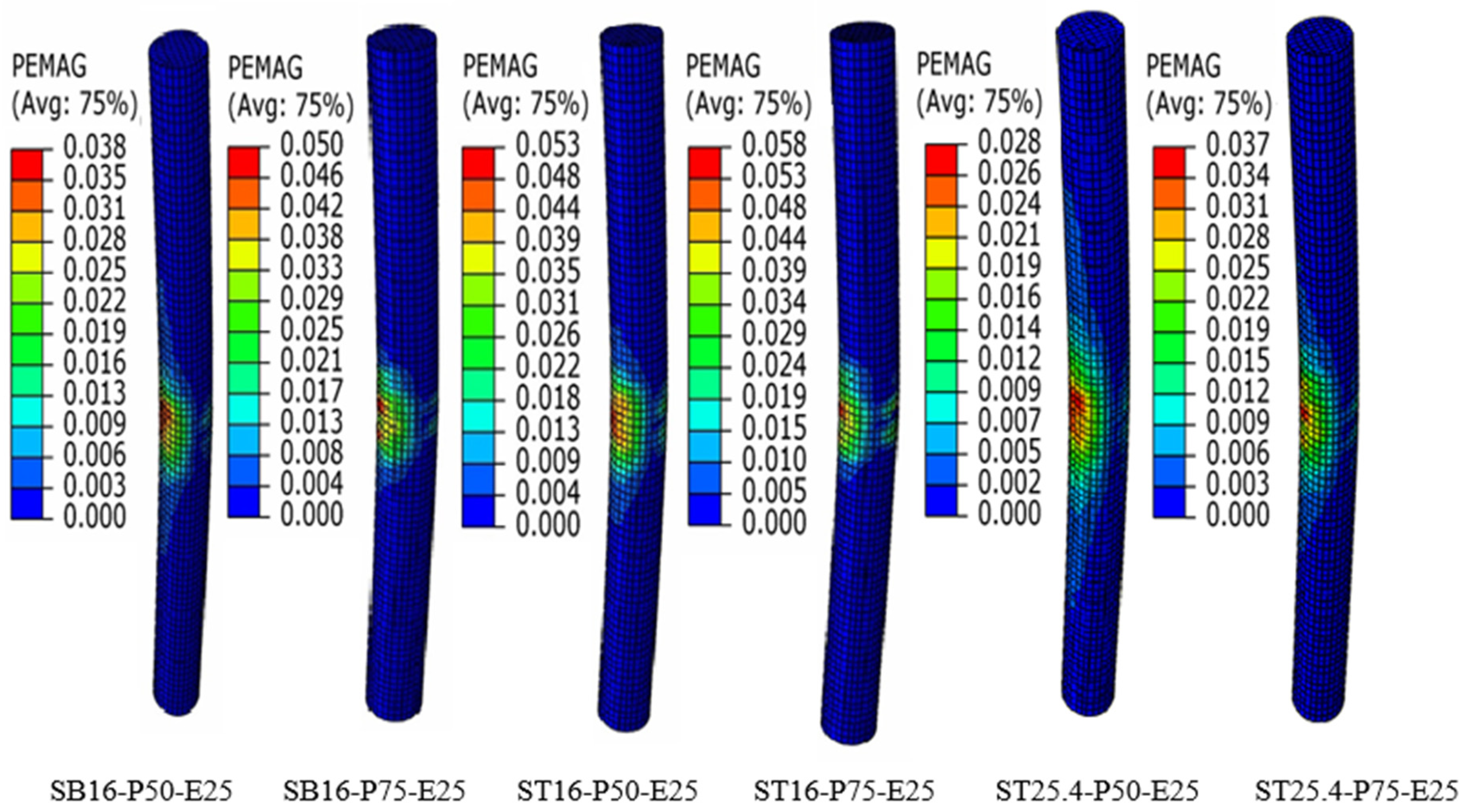

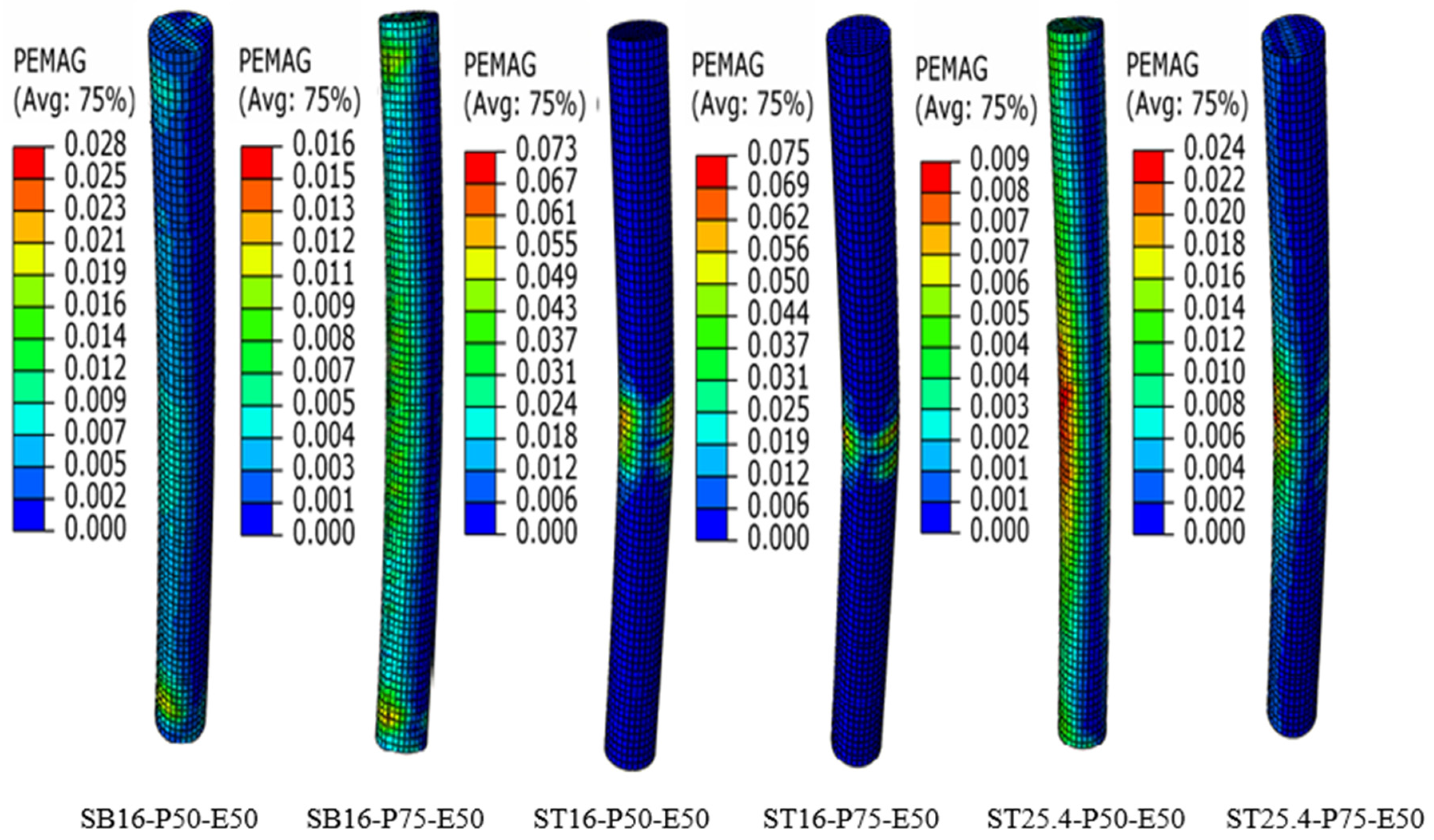


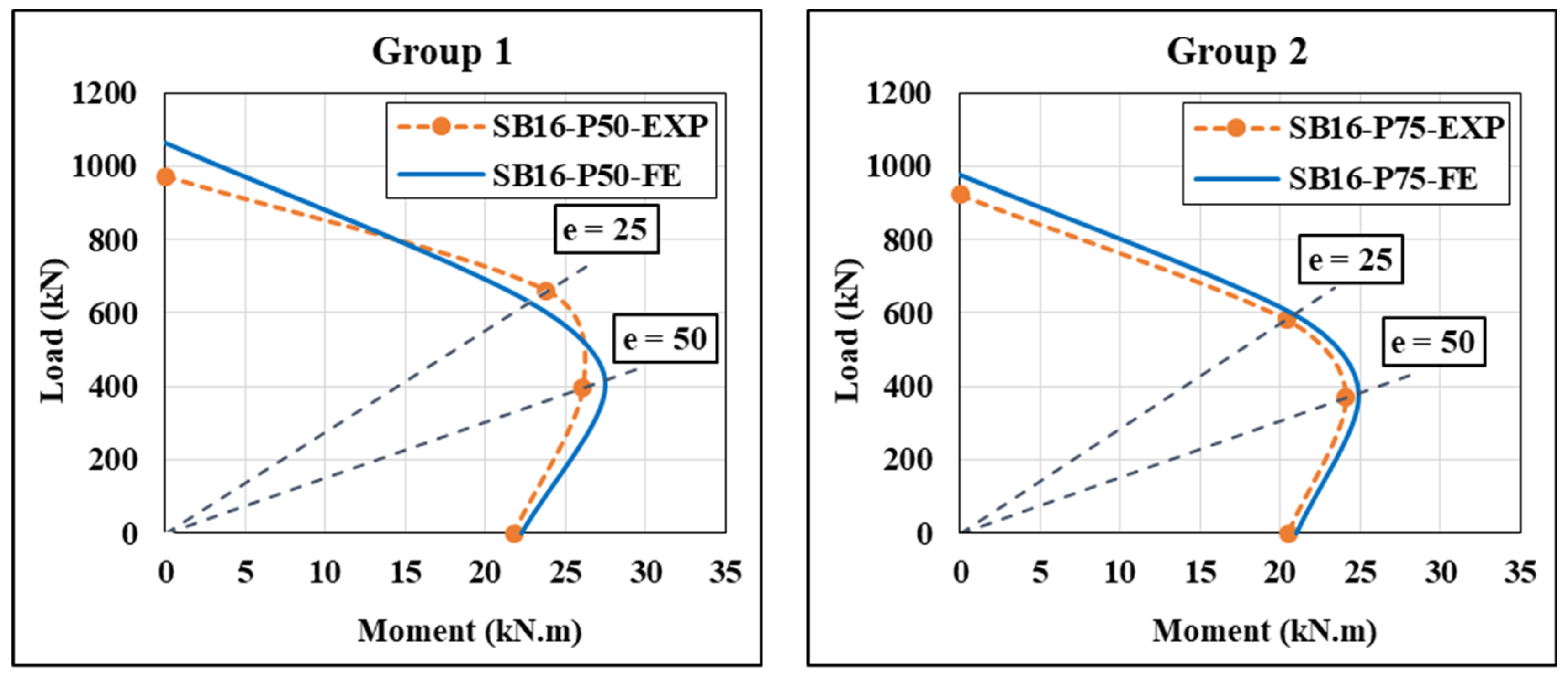
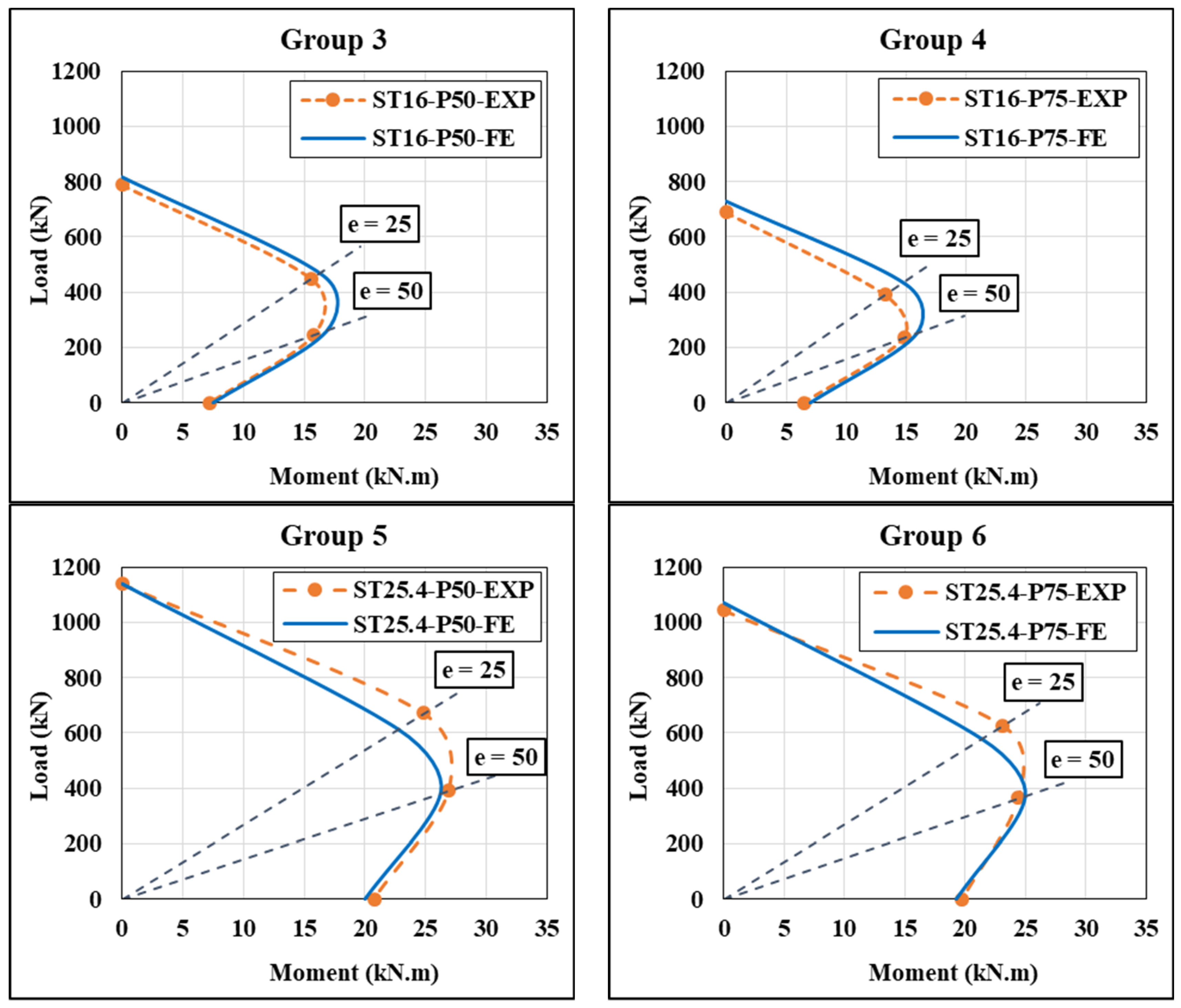
| Group No. | Specimen ID * | Main Reinforcement | Transverse Reinforcement | Type of Applied Load | ||||
|---|---|---|---|---|---|---|---|---|
| Diameter of Steel Bar or Tube (mm) | Wall Thickness of Steel Tube (mm) | Total Area (mm2) | Reinforcement Ratio (%) | Spiral Pitch (mm) | Reinforcement Ratio (%) | |||
| 1 | SB16-P50-C | 16 | - | 1206 | 5.31 | 50 | 1.74 | Concentric |
| SB16-P50-E25 | Eccentric (25 mm) | |||||||
| SB16-P50-E50 | Eccentric (50 mm) | |||||||
| SB16-P50-F | Flexural | |||||||
| 2 | SB16-P75-C | 16 | - | 1206 | 5.31 | 75 | 1.16 | Concentric |
| SB16-P75-E25 | Eccentric (25 mm) | |||||||
| SB16-P75-E50 | Eccentric (50 mm) | |||||||
| SB16-P50-F | Flexural | |||||||
| 3 | ST16-P50-C | 16 | 1.3 | 360 | 1.59 | 50 | 1.74 | Concentric |
| ST16-P50-E25 | Eccentric (25 mm) | |||||||
| ST16-P50-E50 | Eccentric (50 mm) | |||||||
| ST16-P50-F | Flexural | |||||||
| 4 | ST16-P75-C | 16 | 1.3 | 360 | 1.59 | 75 | 1.16 | Concentric |
| ST16-P75-E25 | Eccentric (25 mm) | |||||||
| ST16-P75-E50 | Eccentric (50 mm) | |||||||
| ST16-P50-F | Flexural | |||||||
| 5 | ST25.4-P50-C | 25.4 | 2.8 | 1193 | 5.31 | 50 | 1.74 | Concentric |
| ST25.4-P50-E25 | Eccentric (25 mm) | |||||||
| ST25.4-P50-E50 | Eccentric (50 mm) | |||||||
| ST25.4-P50-F | Flexural | |||||||
| 6 | ST25.4-P75-C | 25.4 | 2.8 | 1193 | 5.31 | 75 | 1.16 | Concentric |
| ST25.4-P75-E25 | Eccentric (25 mm) | |||||||
| ST25.4-P75-E50 | Eccentric (50 mm) | |||||||
| ST25.4-P75-F | Flexural | |||||||
| Type of Material | Compressive Strength (MPa) | Splitting Tensile Strength (MPa) | Modulus of Rupture (MPa) | Modulus of Elasticity (MPa) |
|---|---|---|---|---|
| Concrete | 34 | 3.06 | 3.96 | 27,405 |
| Cementitious grouting material | 62.9 | 4.1 | 5.14 | 37,275 |
| Type of Steel | Nominal Outer Diameter (mm) | Actual Area (mm2) | Yield Strength (MPa) | Ultimate Strength (MPa) |
|---|---|---|---|---|
| Steel bars | 6 | 26.42 | 489 | 624 |
| 16 | 197 | 428 | 542 | |
| Steel tubes | 25.4 | 198.8 | 316 | 413 |
| 16 | 60.03 | 322 | 414 |
| Groups No. | Specimens ID | Ultimate Load (kN) | Ultimate Deformation (mm) | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | SB16-P50-C | 974 | 1064 | Ref. | 1.09 | 3.99 | 3.86 | 0.97 |
| SB16-P50-E25 | 661 | 639 | Ref. | 0.96 | 11.07 | 9.97 | 0.9 | |
| SB16-P50-E50 | 395 | 404 | Ref. | 1.02 | 15.97 | 18.11 | 1.13 | |
| SB16-P50-F | 87 | 89 | Ref. | 1.02 | 19.37 | 20.09 | 1.04 | |
| 2 | SB16-P75-C | 922 | 977 | Ref. | 1.06 | 3.76 | 3.52 | 0.94 |
| SB16-P75-E25 | 582 | 596 | Ref. | 1.02 | 10.21 | 11.52 | 1.13 | |
| SB16-P75-E50 | 371 | 377 | Ref. | 1.01 | 15.11 | 16.34 | 1.08 | |
| SB16-P75-F | 82 | 84 | Ref. | 1.02 | 18.95 | 18 | 0.95 | |
| 3 | ST16-P50-C | 789 | 817 | 0.81 | 1.03 | 4.16 | 3.98 | 0.96 |
| ST16-P50-E25 | 448 | 460 | 0.78 | 1.02 | 9.89 | 11.11 | 1.12 | |
| ST16-P50-E50 | 245 | 259 | 0.62 | 1.06 | 14.46 | 15.03 | 1.04 | |
| ST16-P50-F | 29 | 30 | 0.33 | 1.03 | 16.21 | 16.92 | 1.04 | |
| 4 | ST16-P75-C | 690 | 729 | 0.75 | 1.05 | 3.82 | 3.4 | 0.89 |
| ST16-P75-E25 | 392 | 428 | 0.67 | 1.09 | 8.74 | 9.7 | 1.11 | |
| ST16-P75-E50 | 235 | 247 | 0.63 | 1.05 | 13.13 | 14.48 | 1.1 | |
| ST16-P75-F | 26 | 28 | 0.32 | 1.07 | 13.3 | 13.00 | 0.98 | |
| 5 | ST25.4-P50-C | 1138 | 1140 | 1.17 | 1 | 4.28 | 4.2 | 0.98 |
| ST25.4-P50-E25 | 671 | 614 | 1.02 | 0.91 | 12.12 | 12.38 | 1.02 | |
| ST25.4-P50-E50 | 390 | 386 | 0.99 | 0.99 | 18.59 | 17.71 | 0.95 | |
| ST25.4-P50-F | 83 | 80 | 0.95 | 0.96 | 18.9 | 19.42 | 1.03 | |
| 6 | ST25.4-P75-C | 1043 | 1071 | 1.13 | 1.02 | 3.98 | 3.78 | 0.95 |
| ST25.4-P75-E25 | 625 | 587 | 1.07 | 0.94 | 11.6 | 12.43 | 1.07 | |
| ST25.4-P75-E50 | 364 | 367 | 0.98 | 1.01 | 16.55 | 17.66 | 1.07 | |
| ST25.4-P75-F | 79 | 77 | 0.96 | 0.97 | 17.64 | 18.4 | 1.04 | |
| Average | 1.01 | 1.02 | ||||||
| Standard of deviation () | 0.018 | 0.011 | ||||||
| Coefficient of variation (COV) | 0.017 | 0.01 | ||||||
| Loading Mode | Specimens ID | Ultimate Steel Strain at Tension Zone × 10−6 | Ultimate Steel Strain at Compression Zone × 10−6 | Experimental Results | ||
|---|---|---|---|---|---|---|
| (mm) | (mm) | DI | ||||
| Eccentricity 25 mm | SB16-P50-E25 | 977 | 3497 | 6.15 | 11.07 | 1.80 |
| SB16-P75-E25 | 623 | 3122 | 6.05 | 10.21 | 1.69 | |
| ST16-P50-E25 | 1233 | 3668 | 6.00 | 9.89 | 1.65 | |
| ST16-P75-E25 | 1058 | 3201 | 5.40 | 8.74 | 1.62 | |
| ST25.4-P50-E25 | 852 | 3259 | 7.10 | 12.10 | 1.70 | |
| ST25.4-P75-E25 | 799 | 2915 | 7.25 | 11.60 | 1.60 | |
| Eccentricity 50 mm | SB16-P50-E50 | 2222 | 3022 | 9.20 | 15.97 | 1.74 |
| SB16-P75-E50 | 1834 | 2948 | 9.75 | 15.11 | 1.55 | |
| ST16-P50-E50 | 2744 | 2449 | 8.10 | 13.20 | 1.78 | |
| ST16-P75-E50 | 2365 | 2776 | 8.20 | 11.50 | 1.60 | |
| ST25.4-P50-E50 | 4631 | 4141 | 11.75 | 18.59 | 1.58 | |
| ST25.4-P75-E50 | 3479 | 3735 | 11.85 | 16.55 | 1.40 | |
| Flexural | SB16-P50-F | 6230 | 4530 | 10.70 | 19.37 | 1.81 |
| SB16-P75-F | 5958 | 3132 | 11.10 | 18.95 | 1.71 | |
| ST16-P50-F | 13971 | 1071 | 7.90 | 14.10 | 2.25 | |
| ST16-P75-F | 12116 | 1745 | 7.10 | 12.02 | 2.18 | |
| ST25.4-P50-F | 10282 | 3341 | 11.21 | 18.90 | 1.69 | |
| ST25.4-P75-F | 11948 | 4207 | 10.60 | 17.60 | 1.66 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbood, A.A.; Oukaili, N.; Allawi, A.A.; Wardeh, G. Strength and Deformation of Concrete-Encased Grouting-Filled Steel Tubes Columns Exposed to Monotonic Quasi-Static Loading Conditions. Infrastructures 2024, 9, 26. https://doi.org/10.3390/infrastructures9020026
Abbood AA, Oukaili N, Allawi AA, Wardeh G. Strength and Deformation of Concrete-Encased Grouting-Filled Steel Tubes Columns Exposed to Monotonic Quasi-Static Loading Conditions. Infrastructures. 2024; 9(2):26. https://doi.org/10.3390/infrastructures9020026
Chicago/Turabian StyleAbbood, Ahlam A., Nazar Oukaili, Abbas A. Allawi, and George Wardeh. 2024. "Strength and Deformation of Concrete-Encased Grouting-Filled Steel Tubes Columns Exposed to Monotonic Quasi-Static Loading Conditions" Infrastructures 9, no. 2: 26. https://doi.org/10.3390/infrastructures9020026
APA StyleAbbood, A. A., Oukaili, N., Allawi, A. A., & Wardeh, G. (2024). Strength and Deformation of Concrete-Encased Grouting-Filled Steel Tubes Columns Exposed to Monotonic Quasi-Static Loading Conditions. Infrastructures, 9(2), 26. https://doi.org/10.3390/infrastructures9020026










