Dynamic Amplification of Railway Bridges under Varying Wagon Pass Frequencies
Abstract
1. Introduction
1.1. Railway Bridge Dynamic Amplification Factor
1.2. Modelling Railway Bridge Dynamic Response
1.3. Studies on Railway Bridge Dynamic Amplification
1.4. Train–Bridge Interaction (TBI) Models
1.5. The Need for Further Work and Simplified Models
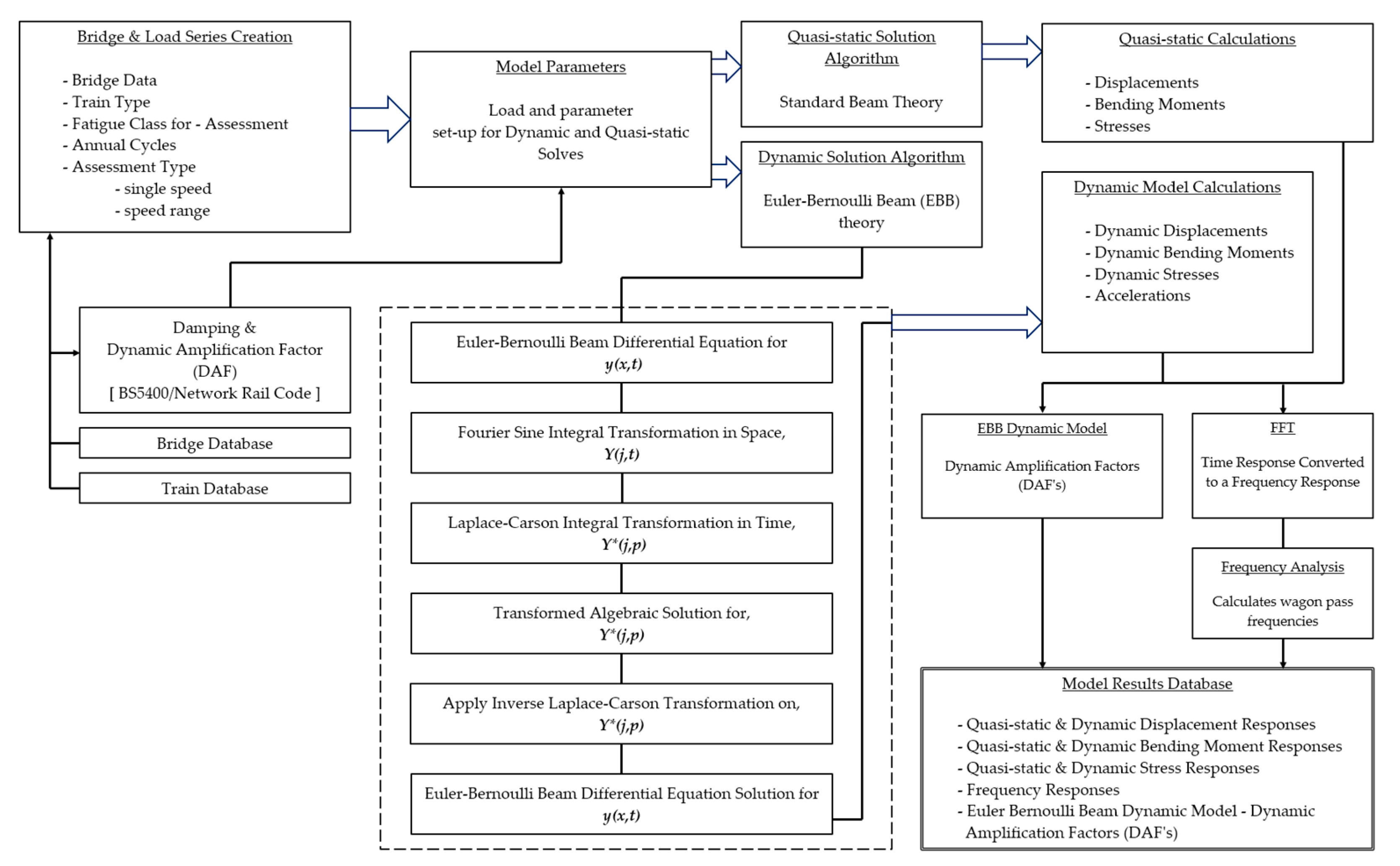
2. Bridge Moving Load Models
2.1. Euler–Bernoulli Beam (EBB) Model
| Flexural rigidity of the beam with a constant moment of inertia, | |
| Linear combination of normal modes, | |
| Generalised coordinate of the nth mode, | |
| Length coordinate from origin—right hand of the beam, | |
| Elapsed time from the instant at which the moving concentrated load P enters the beam, | |
| Mass per unit length of the beam, | |
| Equivalent coefficient of viscous damping of the beam, | |
| Dirac delta function which describes moving concentrated load, | |
| Load travelling speed, | |
| Moving concentrated load. |
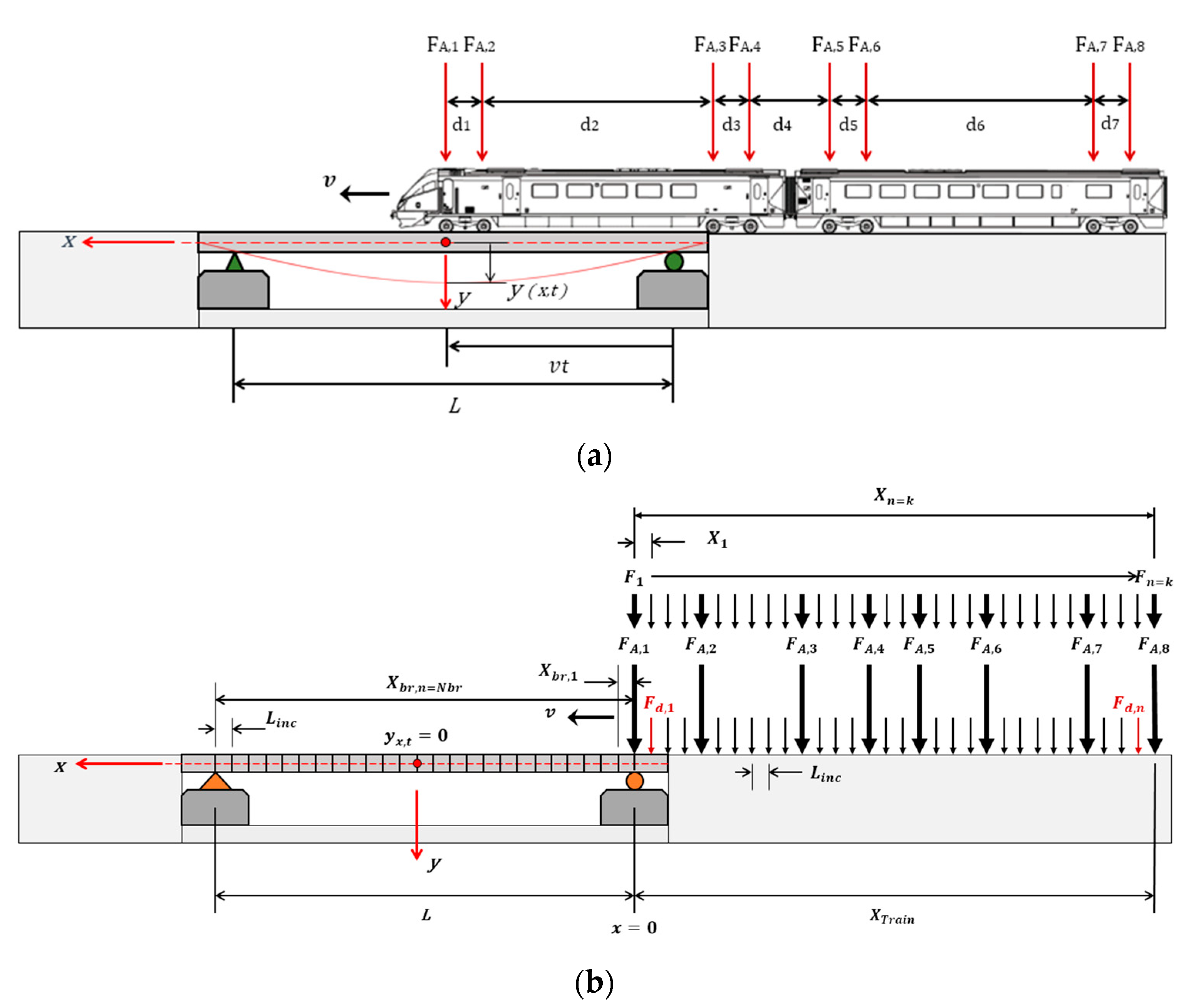
| Vertical deflection of the bridge at position x and time t, | |
| Circular damped frequency of the bridge, | |
| Describes the Heaviside unit step function for the arrival (turning on) and departure (turning off) of the nth axle force, Fn, | |
| Constant magnitude concentrated axle force, | |
| Position of the nth axle force, Fn, from the first axle, | |
| Train constant speed, | |
| Position of the nth axle force, Fn, from the bridge origin. |
| Unit load deflection, | |
| Bridge span, | |
| jth Modal frequency (j = 1 for first vertical bending mode), | |
| Forcing frequency, | |
| Circular natural frequency of vibration of the bridge (1st vertical bending mode). |
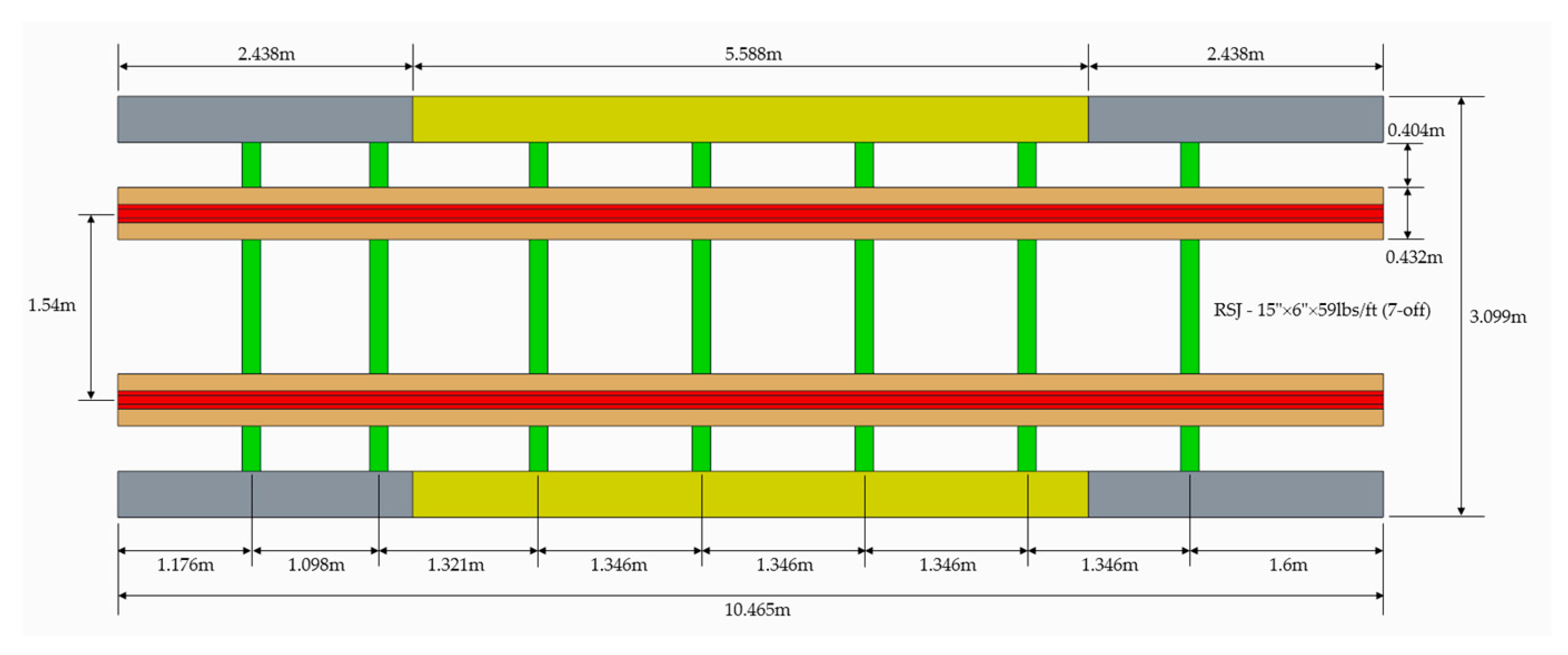
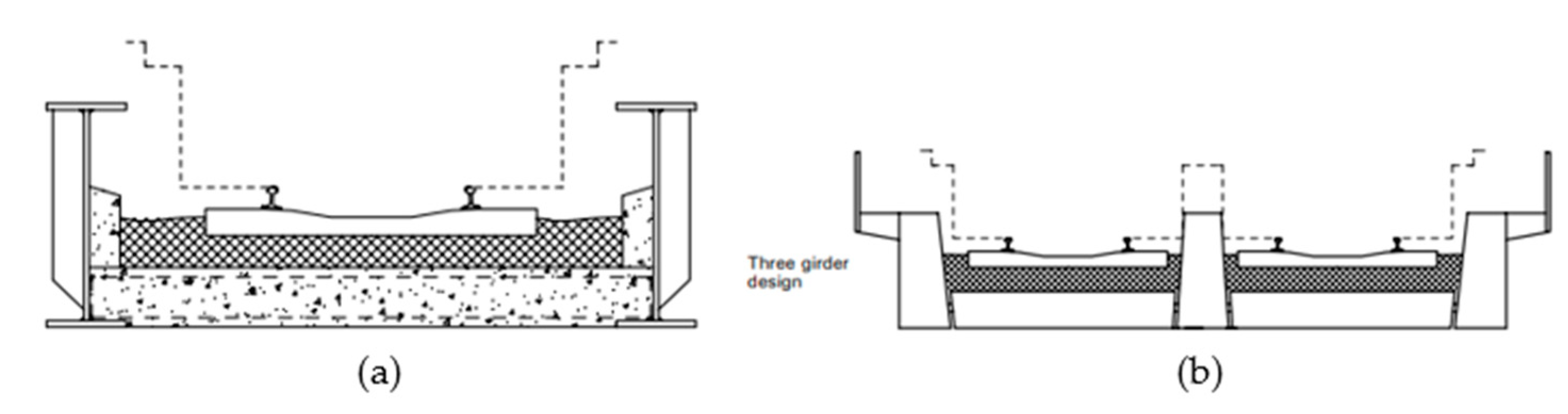
2.2. Case Study Plate Girder Bridges
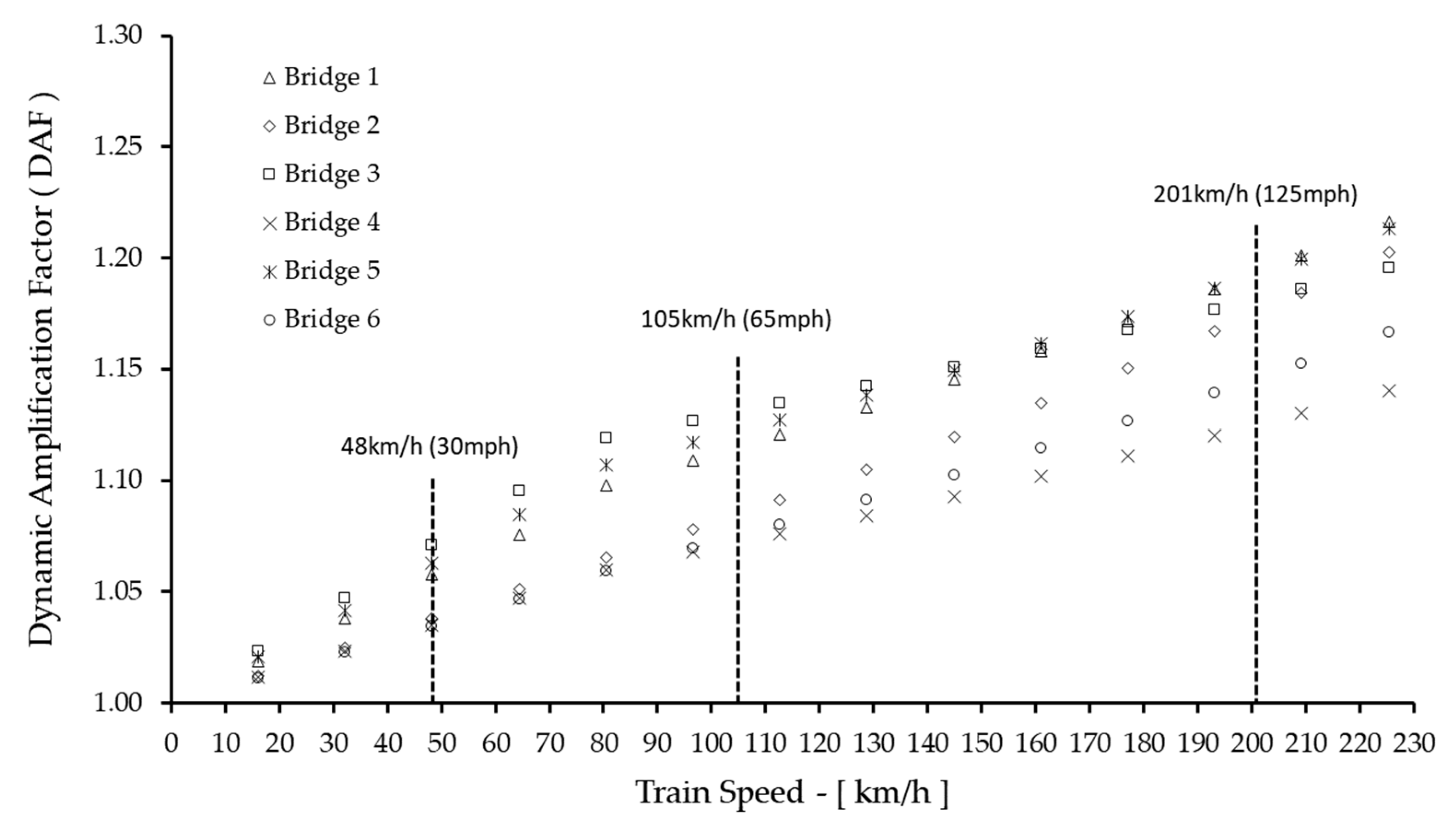
2.3. Dynamic Amplification Factor (DAF)
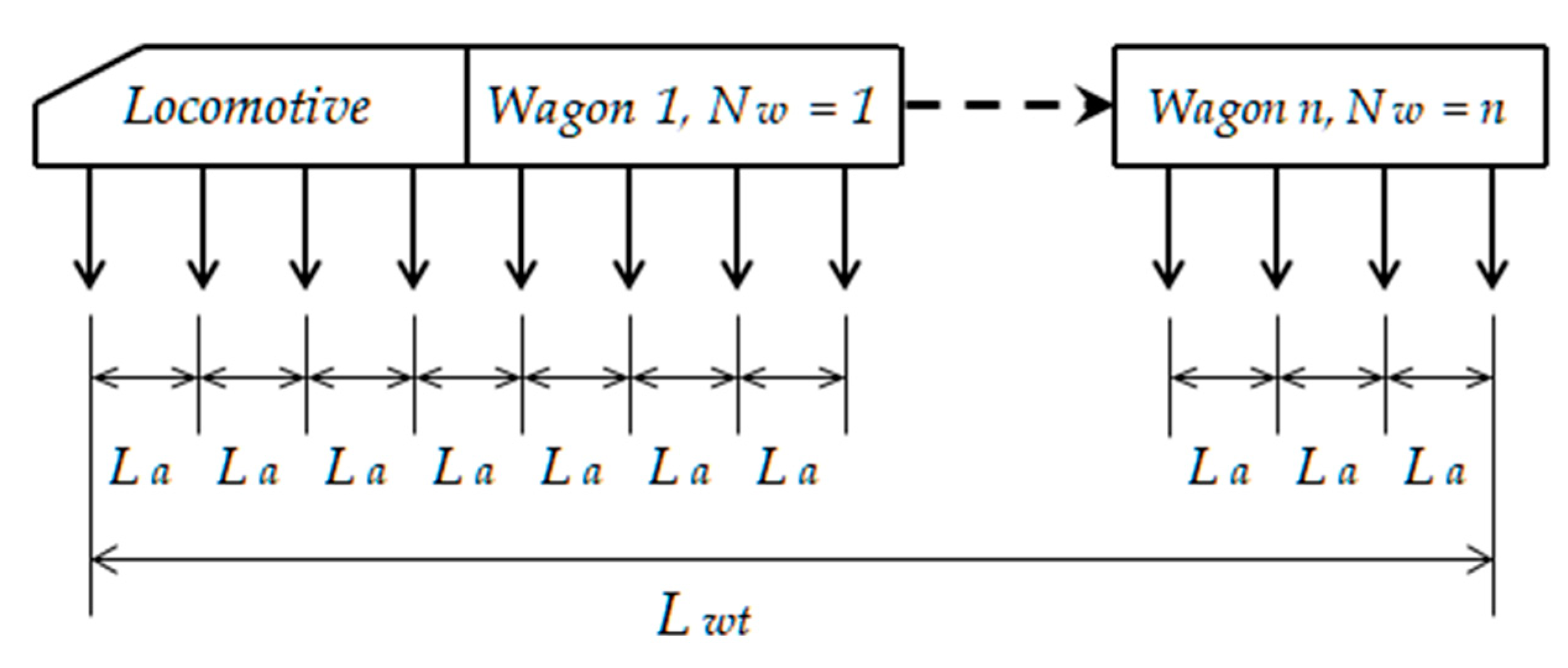
2.4. BS 5400 Train Configurations
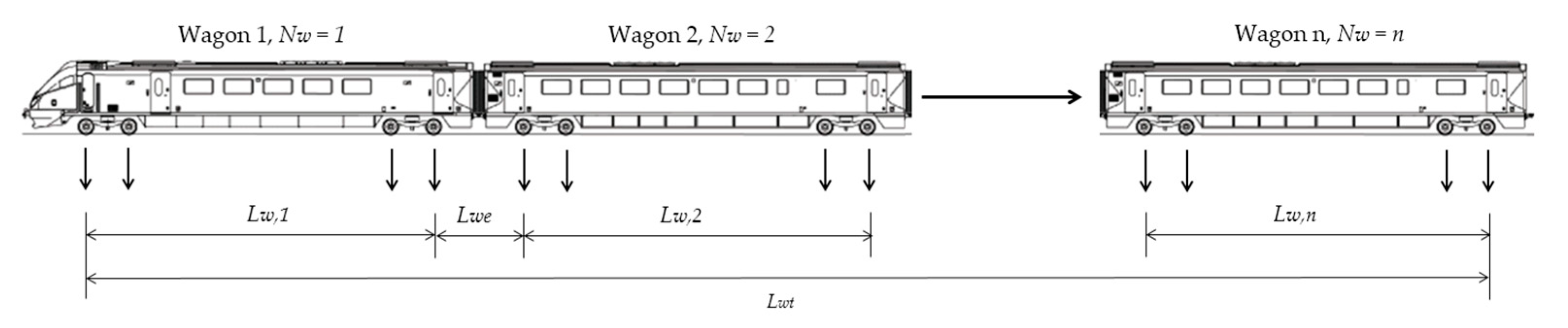
2.5. Wagon Pass Frequency
| V | Train speed in km/h, |
| Wagon spacing of two outer axles according to Figure 4, | |
| Wagon end coupling distance, | |
| Number of wagons. | |
| j | Integer multiples, j = 1,2,3 …n. |
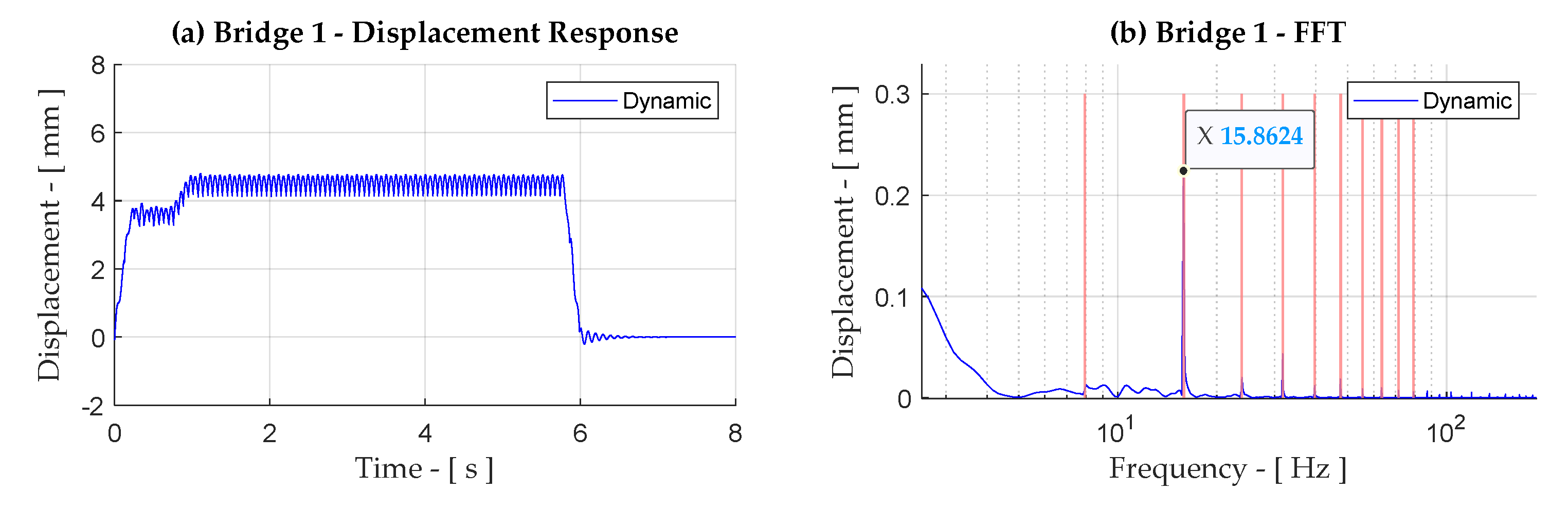
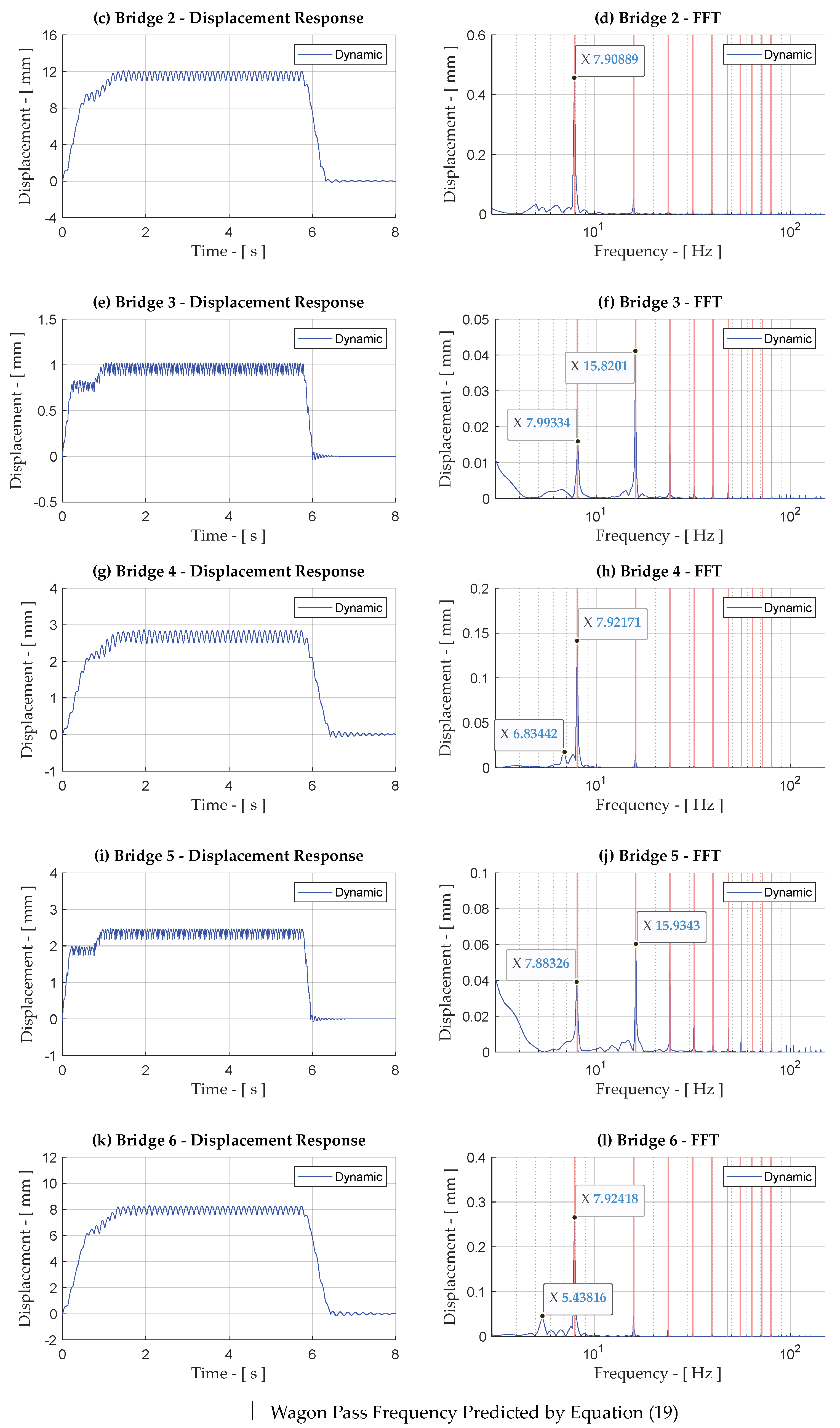
3. EBB Dynamic Model Validation
- -
- Verification based on standard beam theory.
- -
- A comparison of modal response and displacement influence curves obtained from a 3D FE model of the case study bridge that was developed (Figure A1) with those obtained from the EBB dynamic model.
- -
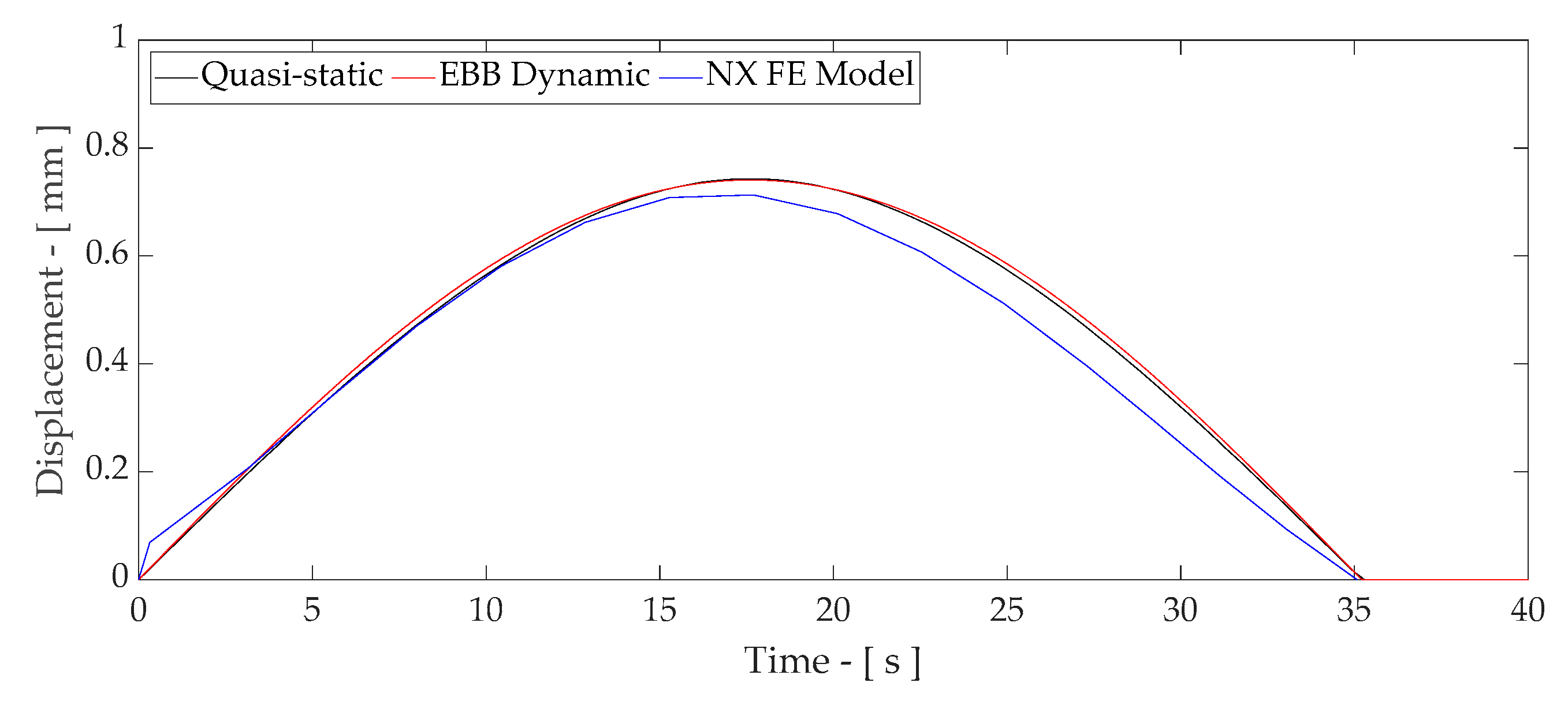
- Correlation of the displacement time history of the EBB dynamic model with measured response data.
- -
- Correlation of the measured acceleration frequency response and the primary wagon pass frequency with those predicted by the model.
4. Results and Discussion for Case Study Bridges 1–6
4.1. Bridge Dynamic Response at 100 km/h—Train S-T1
4.2. Bridge Dynamic Response at 100 km/h—Train DHP-T5
4.3. Bridge Dynamic Response at 100 km/h—Train HF-T7
4.4. Bridge Dynamic Response at 100 km/h—Train HF-T8
- -
- Have an optimum blanket train speed limit for all train types for a given bridge;
- -
- Have individual train speeds for different train types for given bridges;
- -
- For new bridge designs, ensure that the vertical natural frequency vibration is not a factor of the primary wagon pass frequency for the different train types on the route.
4.5. Train Dominant Frequencies at 100 km/h
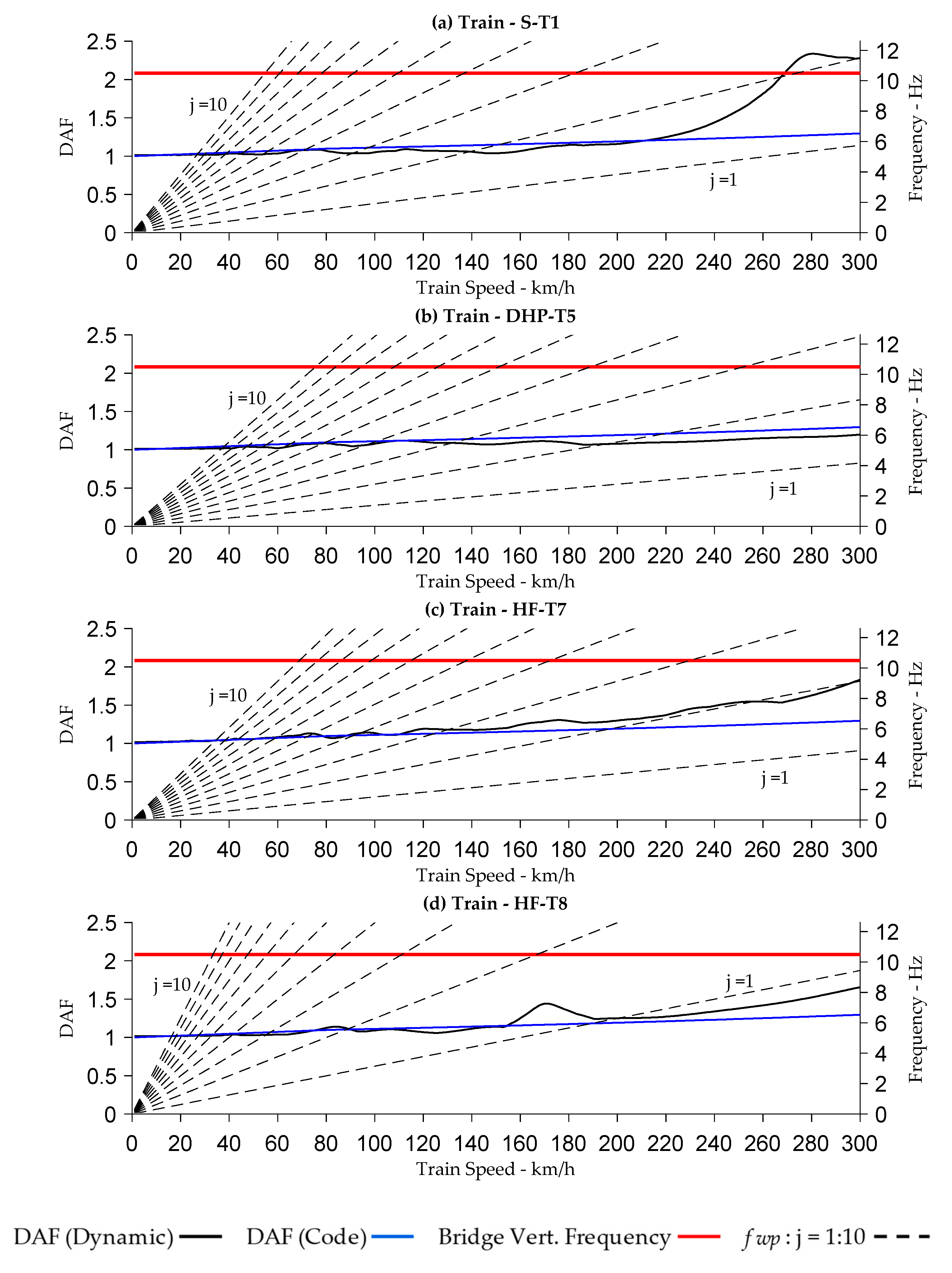
4.6. Dynamic Amplification and Critical Speeds
4.7. Bridge Dynamic Response for Trains with Equal Axle Spacing
5. Conclusions
- o
- The primary wagon pass frequencies and its integer multiples can cause a significant increase in the dynamic amplification factor when the frequency coincides with the bridge’s natural frequency. This condition is more crucial if the primary wagon pass frequency is a factor of the bridge resonant frequency. These effects are not captured in bridge assessment codes when estimating the DAF.
- o
- The results show that for longer wagon lengths, the dominant frequency is the primary wagon pass frequency but it is the higher integer multiples which are responsible for dynamic amplification. As the wagon lengths shorten, such as for trains ST-1 and HF-T8, the first, second and third (j = 1, 2, 3) integer multiple of the wagon pass frequency become dominant, but it is the higher integer multiples which are responsible for dynamic amplification. The shorter the wagon, the more higher integer multiples start affecting dynamic amplification.
- o
- For Bridges 2, 4 and 6, it was found that train HF-T8 had the highest dynamic amplification at the second integer multiple j = 2 of the wagon pass frequency, where this coincided with the bridge natural frequency.
- o
- Generally, where no resonance conditions prevail, the DAF under dynamic conditions are comparable to those calculated by the design/assessment codes. This was demonstrated using the Campbell diagram for each analysed bridge and train type.
- o
- The results obtained in this study show that the fatigue damage accumulating on the bridge could potentially be overestimated, or underestimated, if using DAF values based on bridge assessment codes. Where resonance conditions prevail, it is more likely that fatigue damage will be underestimated at train speeds which excite the bridge’s resonant frequency.
- o
- The DAFs obtained from the dynamic analysis for each train type can provide an indication of optimum speed ranges which will minimise the DAF. This can give train operators and bridge asset owners important information which can be used to help prolong bridge fatigue life by specifying operating train speeds for a given train/bridge configuration. Moreover, this work showed that when the train axle spacings and coupling distances become more uniform (equal) the displacement ranges reduce significantly with the frequency content showing distinct narrow peaks. This would also result in reduced stress ranges which is beneficial for fatigue. The design of new trains, where axle and coupling distances are made shorter, can therefore have significant fatigue benefits for bridges.
Limitiations of the Euler–Bernoulli Beam (EBB) Model and Scope for Further Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. EBB Dynamic Model Validation
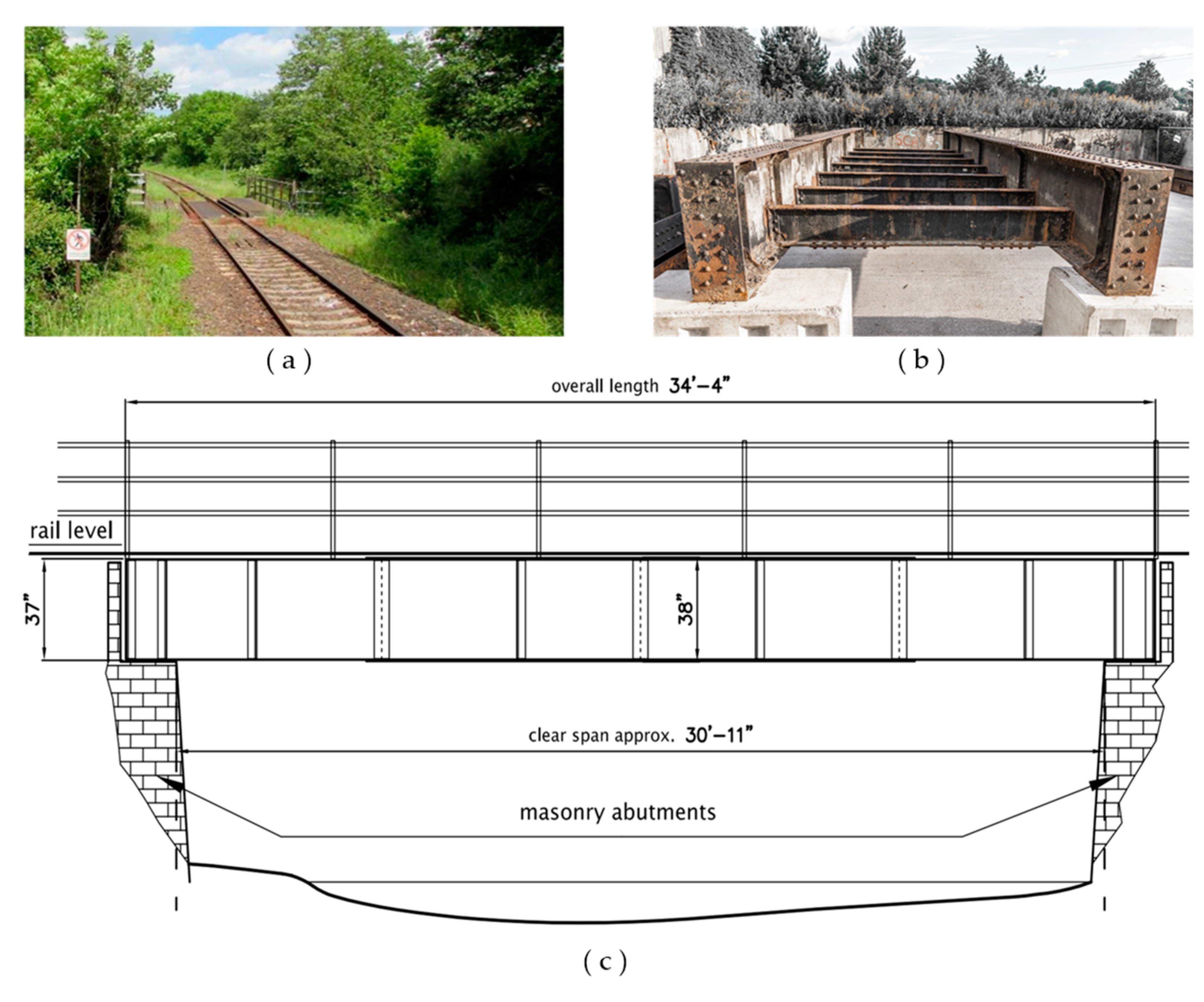
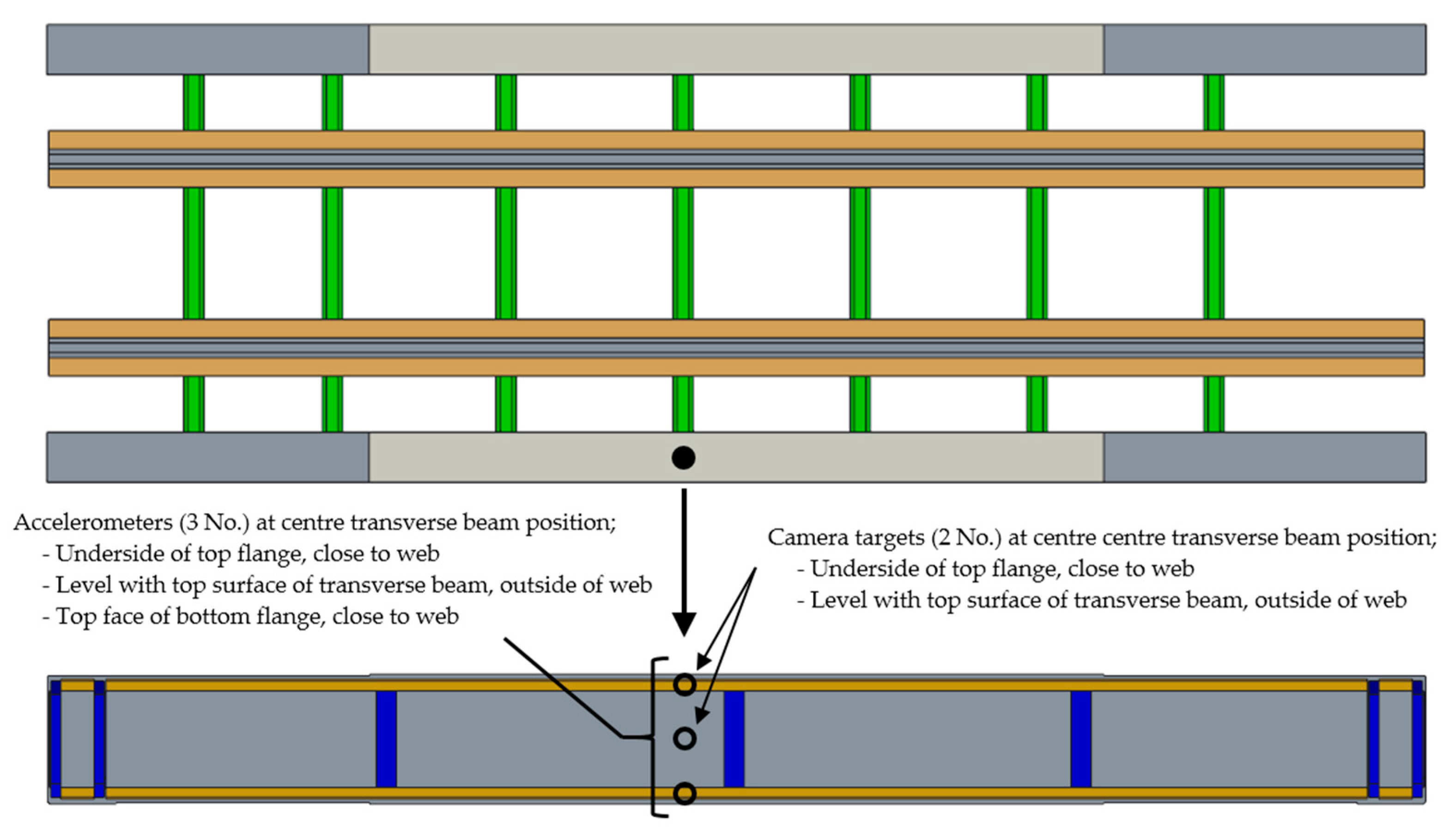
Appendix A.1. Field Measurement Instrumentation
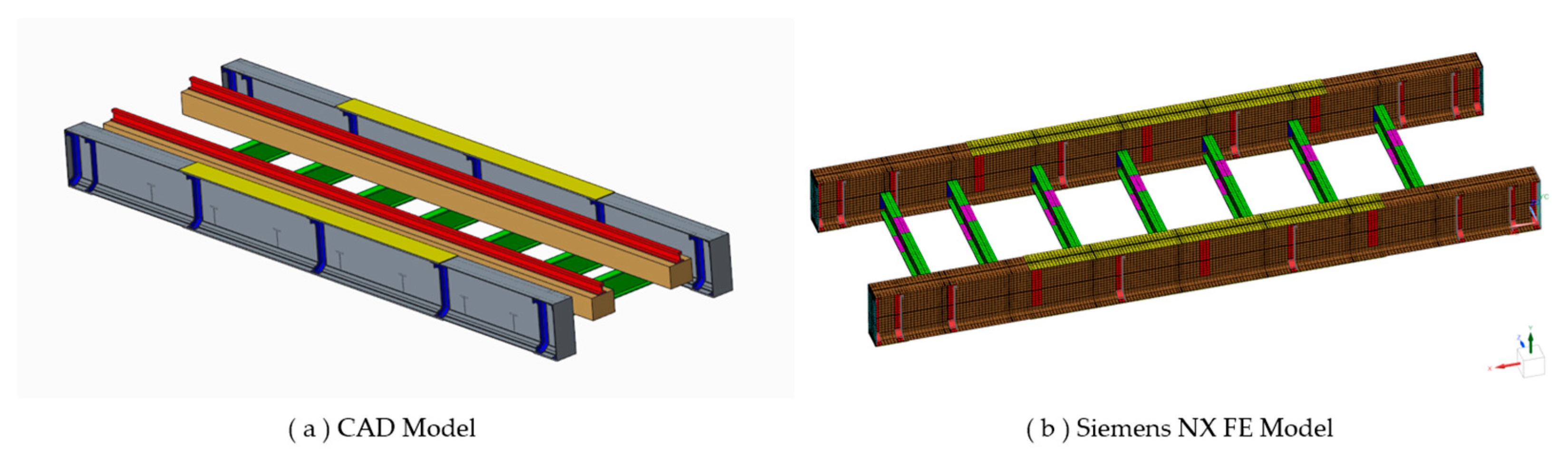
Appendix A.2. Finite Element Analysis
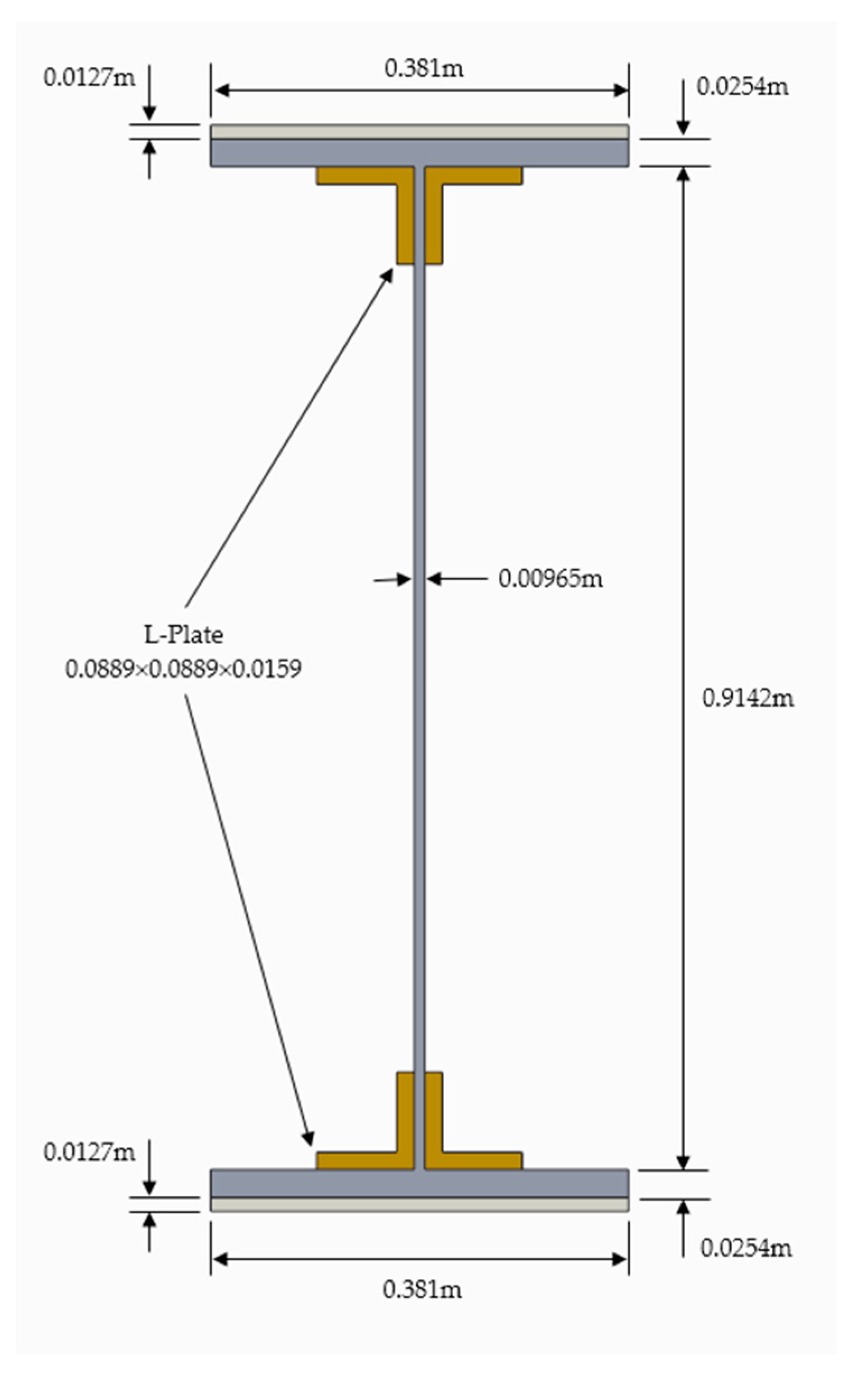
| Parameter | ||
|---|---|---|
| Bridge main and transverse girders density | 7853 | kg/m3 |
| Rail density | 7800 | kg/m3 |
| Wheel timbers and floors density | 2541 | kg/m3 |
| Young’s Modulus, Esteel | 190 | GPa |
| Young’s Modulus, Ewood | 14 | GPa |
| Poisson Ratio, νsteel | 0.3 | |
| Poisson Ratio, νwood | 0.45 | |
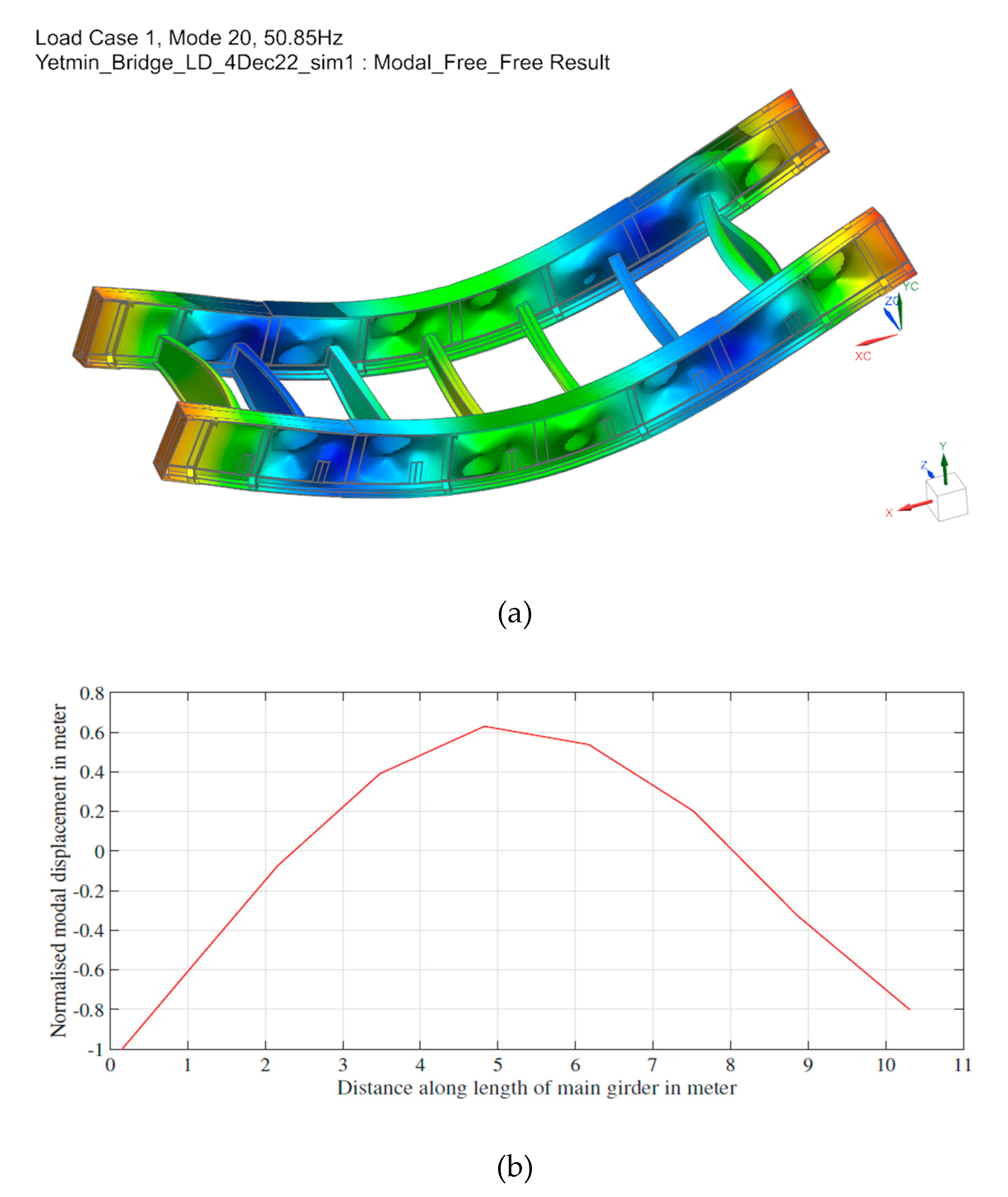

Appendix A.3. Measured Bridge Response Correlation with EBB Dynamic Model
| EBB Model Input Data | ||
|---|---|---|
| Span, L (between supports) | 9.78 | m |
| Uniformly Distributed Mass (UDM), μ | 1748 | kg/m |
| Young’s Modulus, E | 190 | GPa |
| Second Moment of Area, I (at mid-section) | 0.01358 | m4 |
| First Vertical Bending Frequency, fn | 20 | Hz |
| British Rail Class 158—Diesel Multiple Unit (DMU) | 38 | tons |
| British Rail Class 168—Diesel Multiple Unit (DMU) | 37 | tons |
| British Rail Class 166—Diesel Multiple Unit (DMU) | 37 | tons |

| Train | Train Speed | Train Configuration | Wagon Pass Frequency, fwp—[Hz] | ||
|---|---|---|---|---|---|
| [km/h] | Measured Response FFT | EBB Dynamic Model FFT | Calculated [Equation (9)] | ||
| 13:48 to Gloucester (Figure A10) | 30 | 1 Locomotive 2 Wagons | 0.388 | 0.369 (−4.9%) | 0.397 (2.3%) |
| 15:37 to Gloucester (Figure A11) | 26.5 | 1 Locomotive 2 Wagons | 0.349 | 0.326 (−6.9%) | 0.351 (0.6%) |
| 13:20 to Weymouth (Figure A12) | 27 | 1 Locomotive 2 Wagons | 0.345 | 0.332 (−3.8%) | 0.357 (3.5%) |
| 16:26 to Weymouth (Figure A13) | 29.5 | 1 Locomotive 1 Wagons | 0.419 | 0.422 (0.7%) | 0.442 (5.5%) |
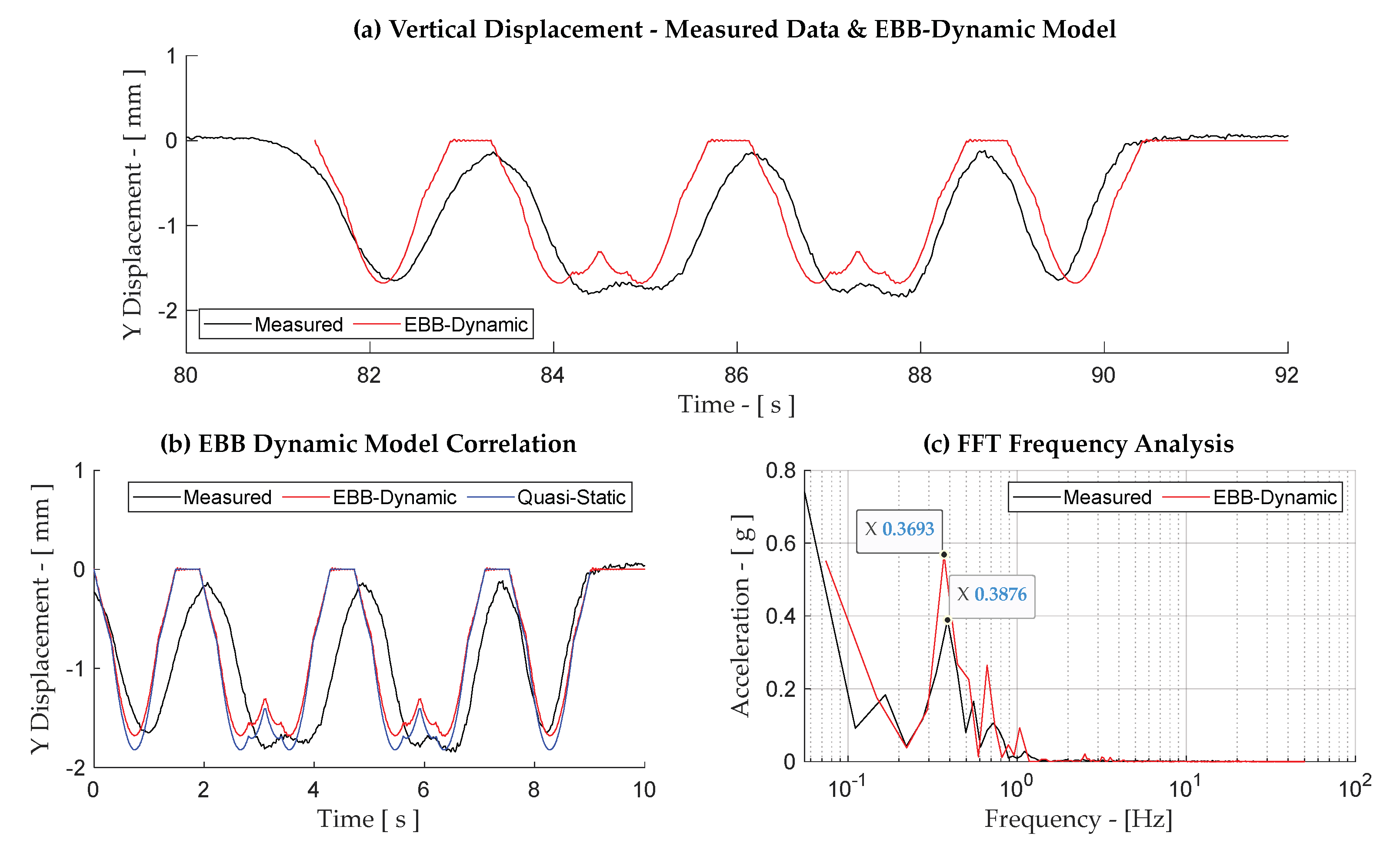
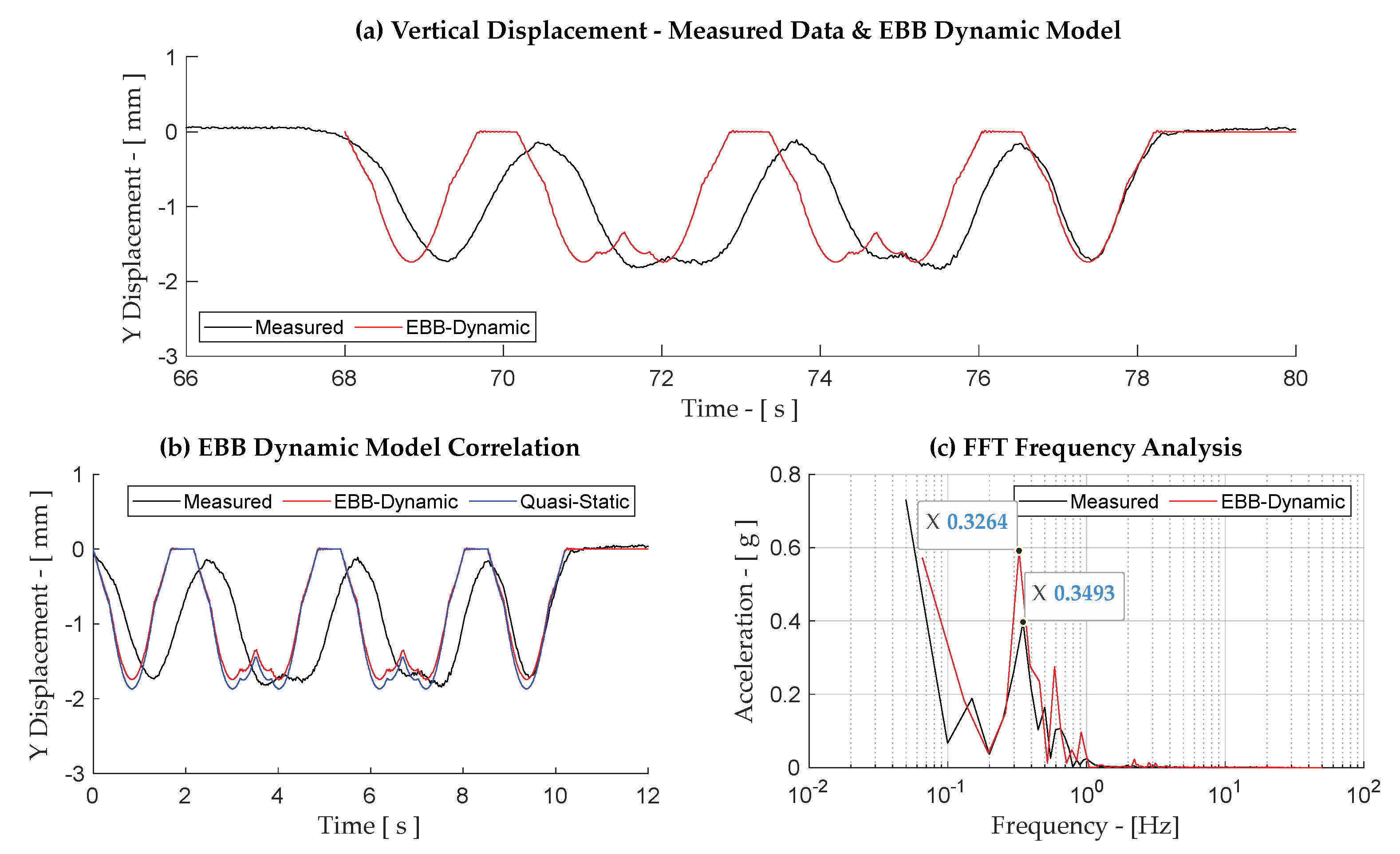
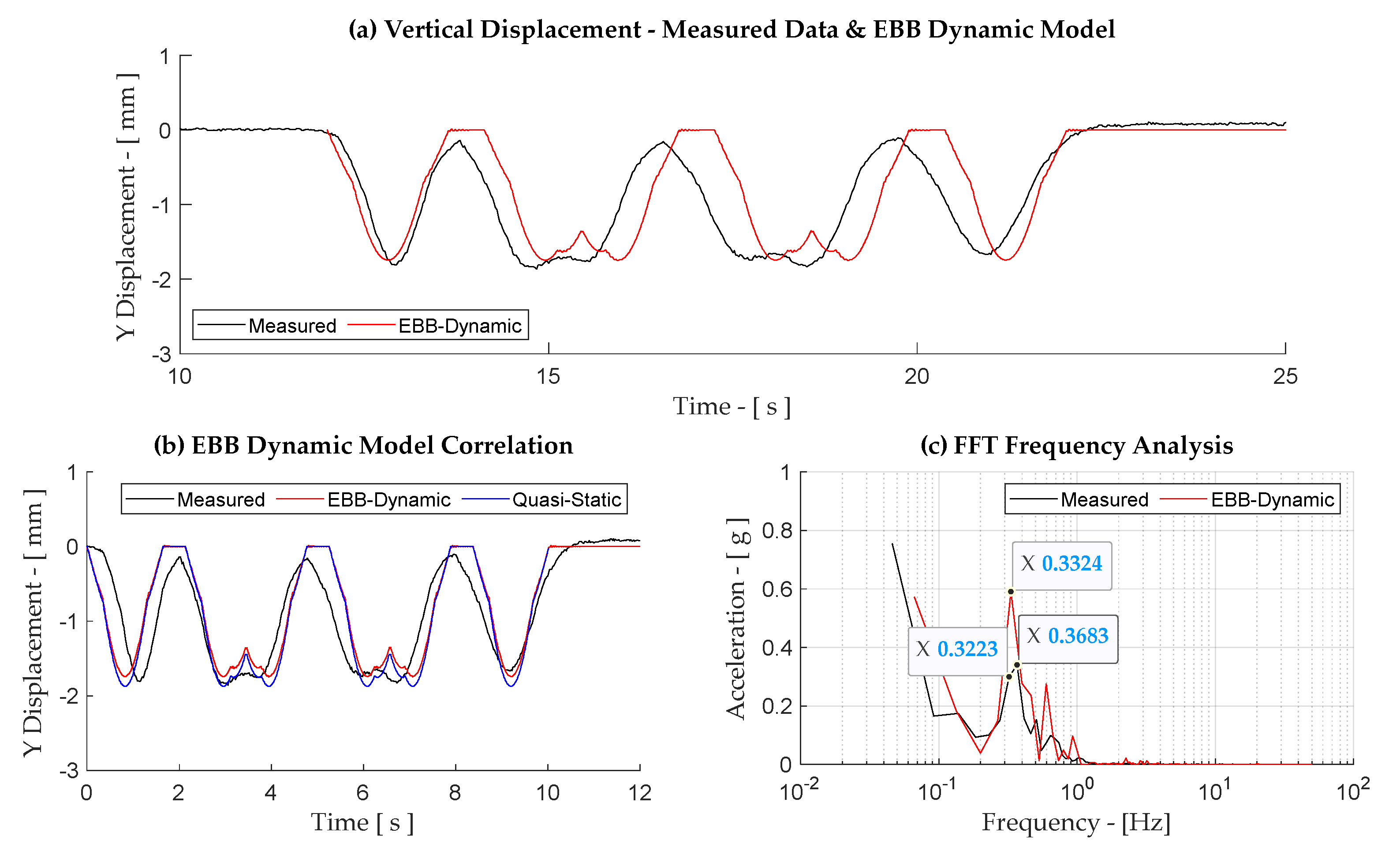
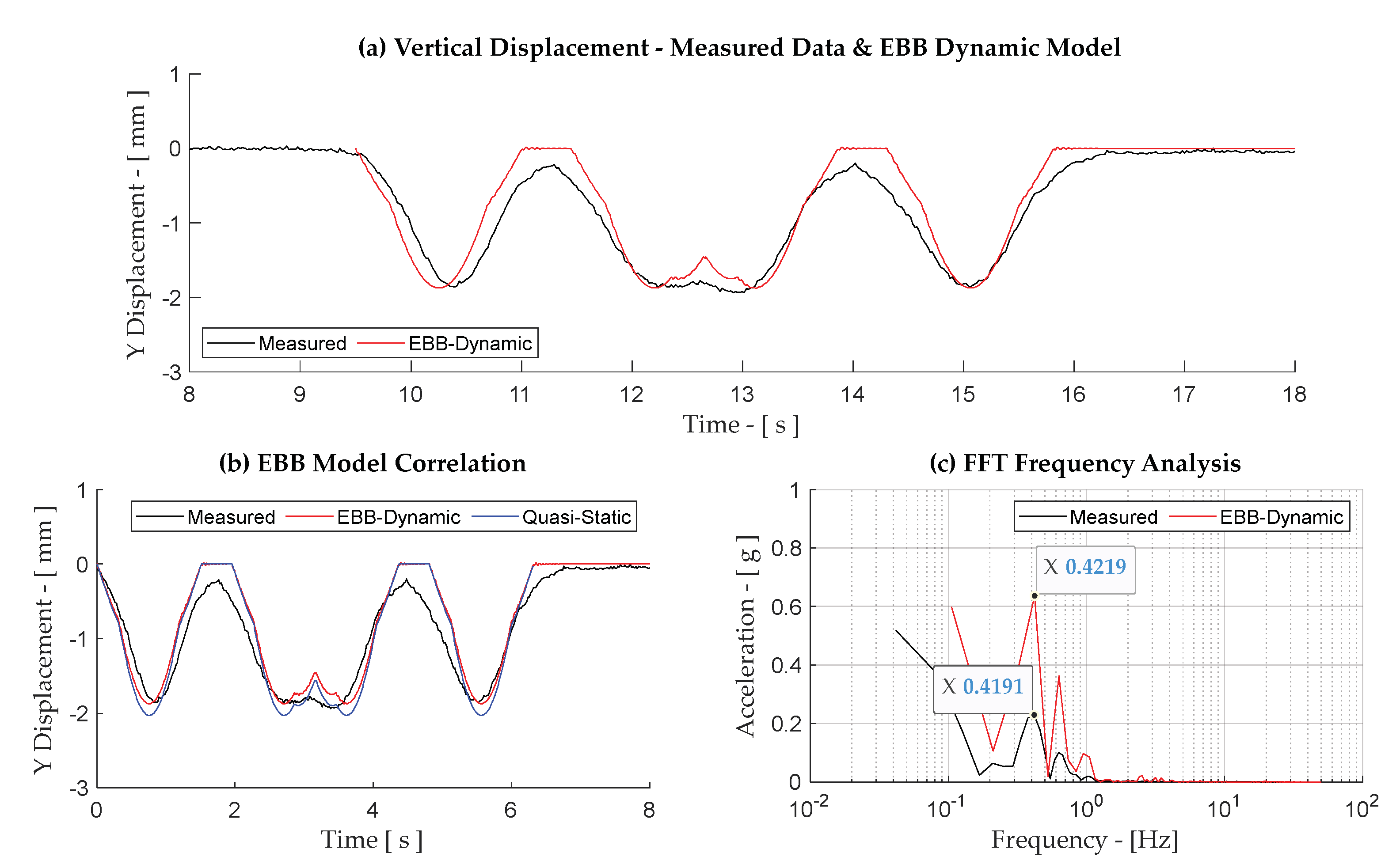
Appendix B. Results for Case Study—Trains S-T1, DHP-T5, HF-T7 and HF-T8
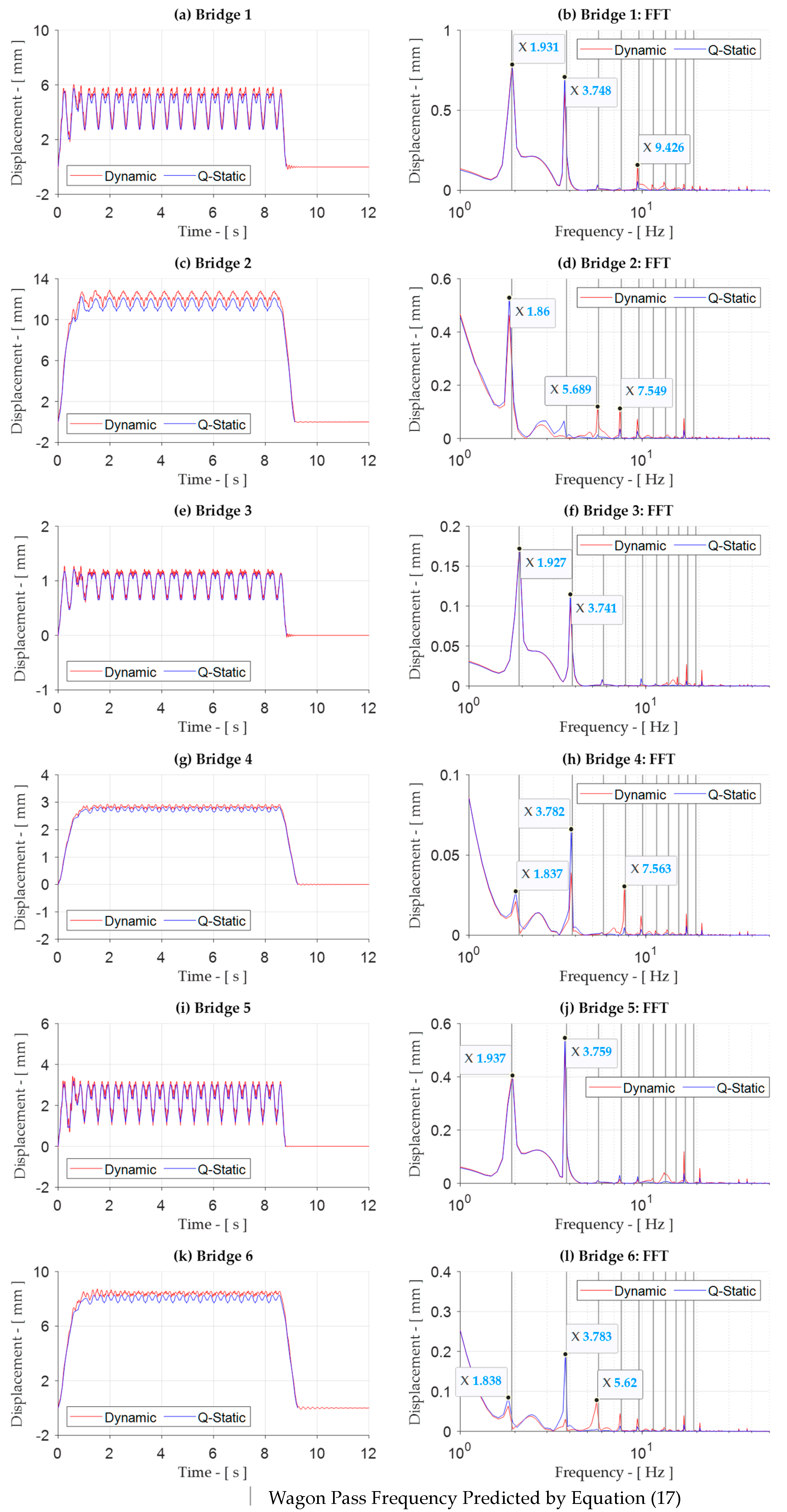
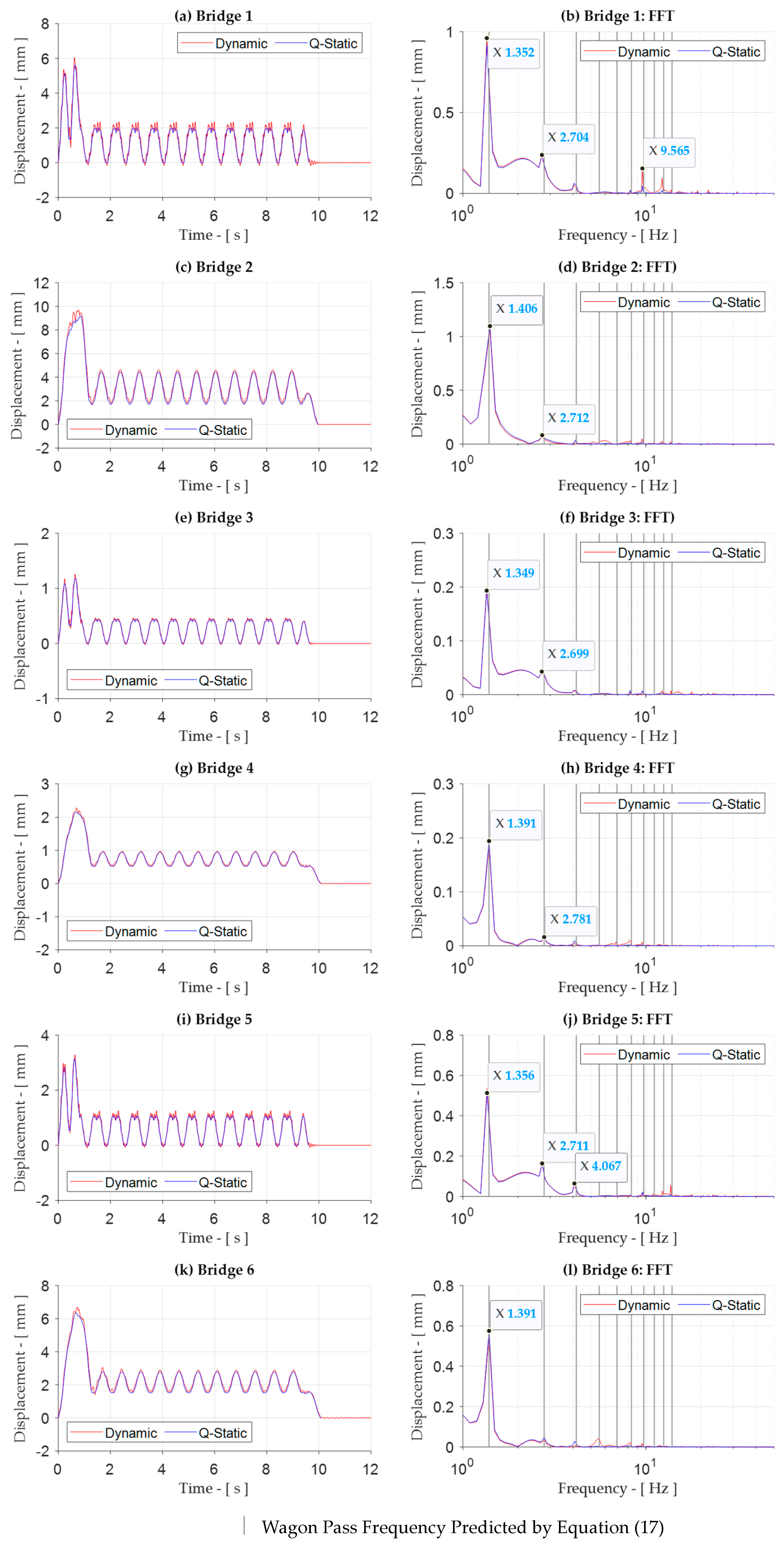

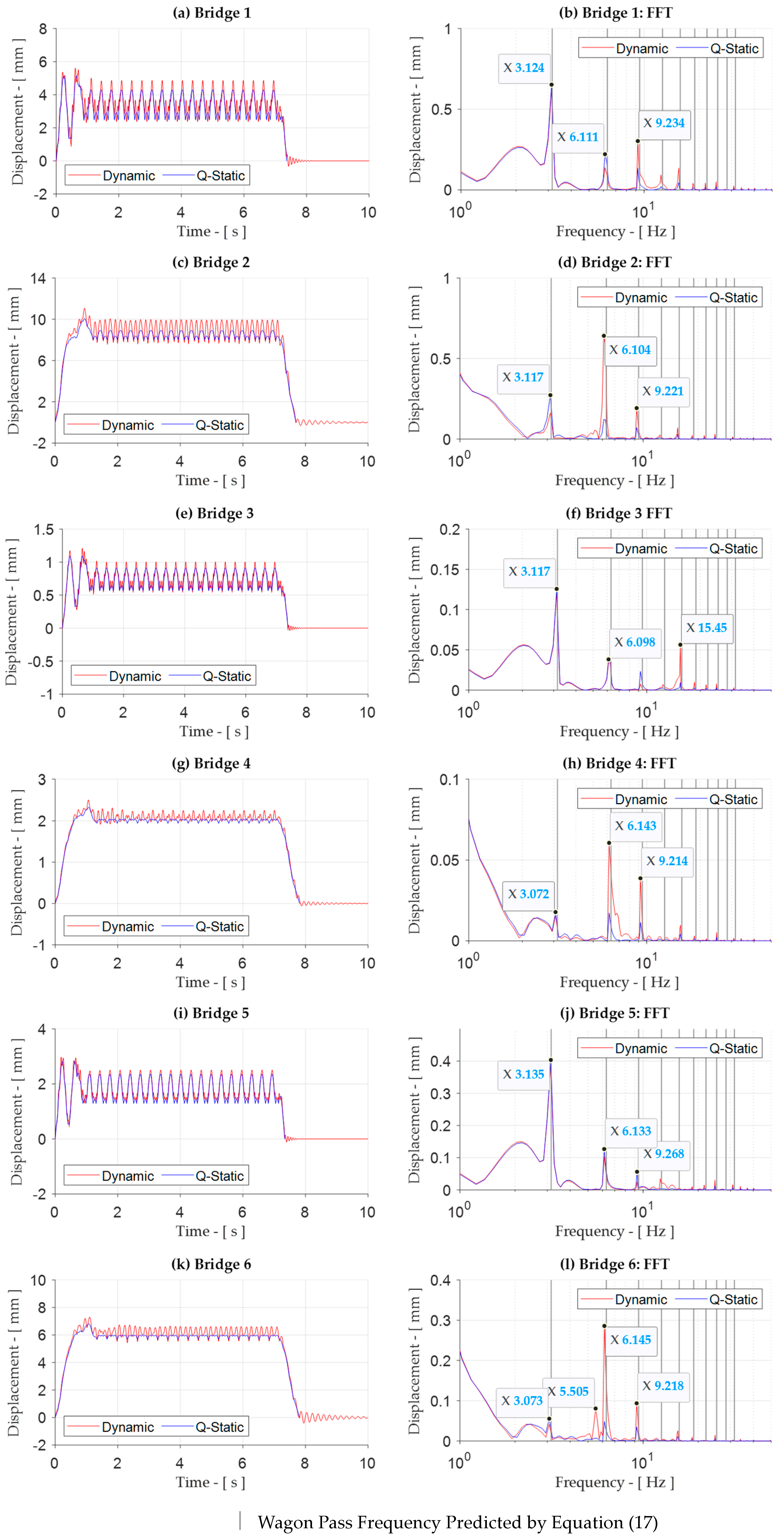

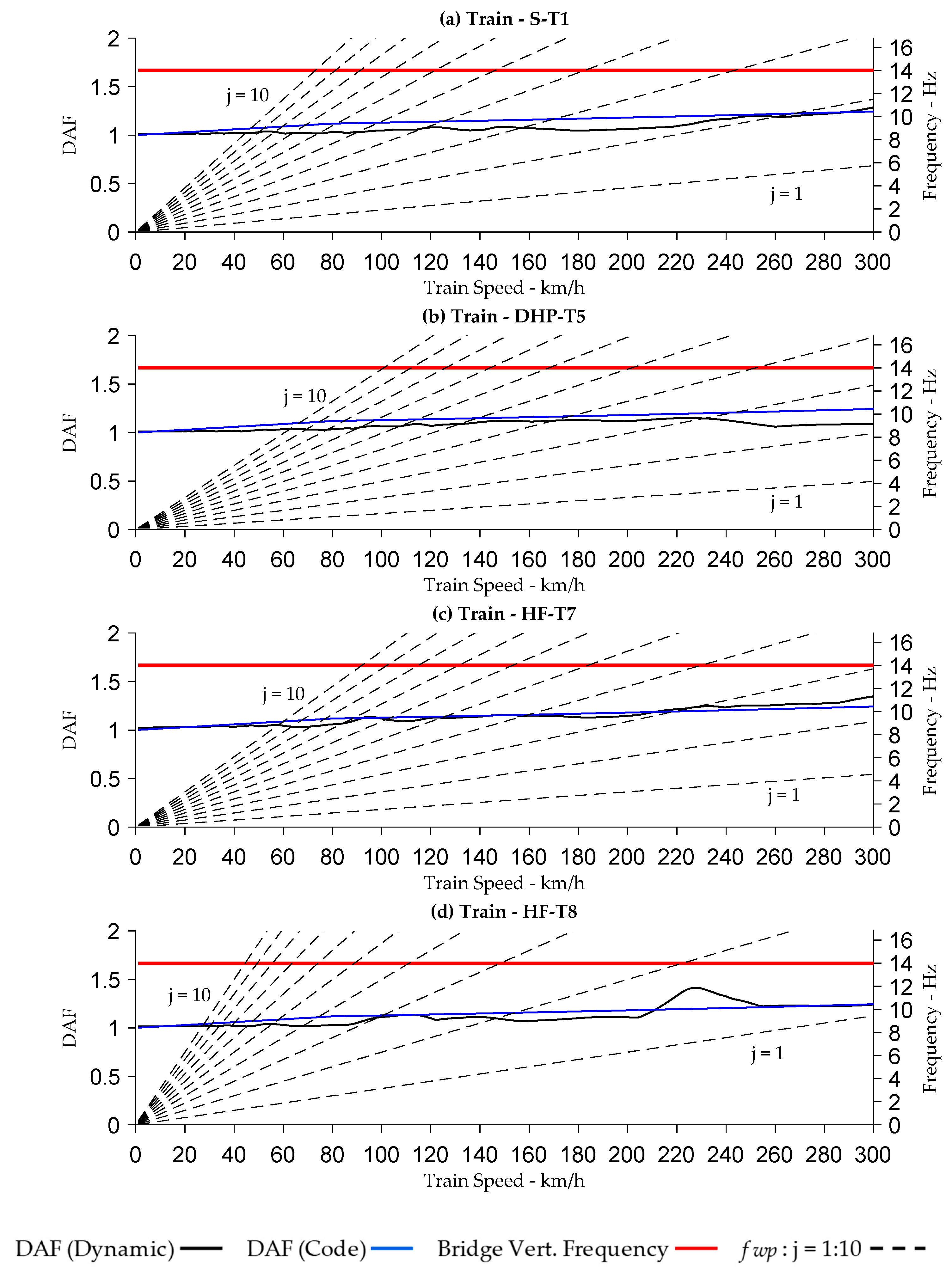
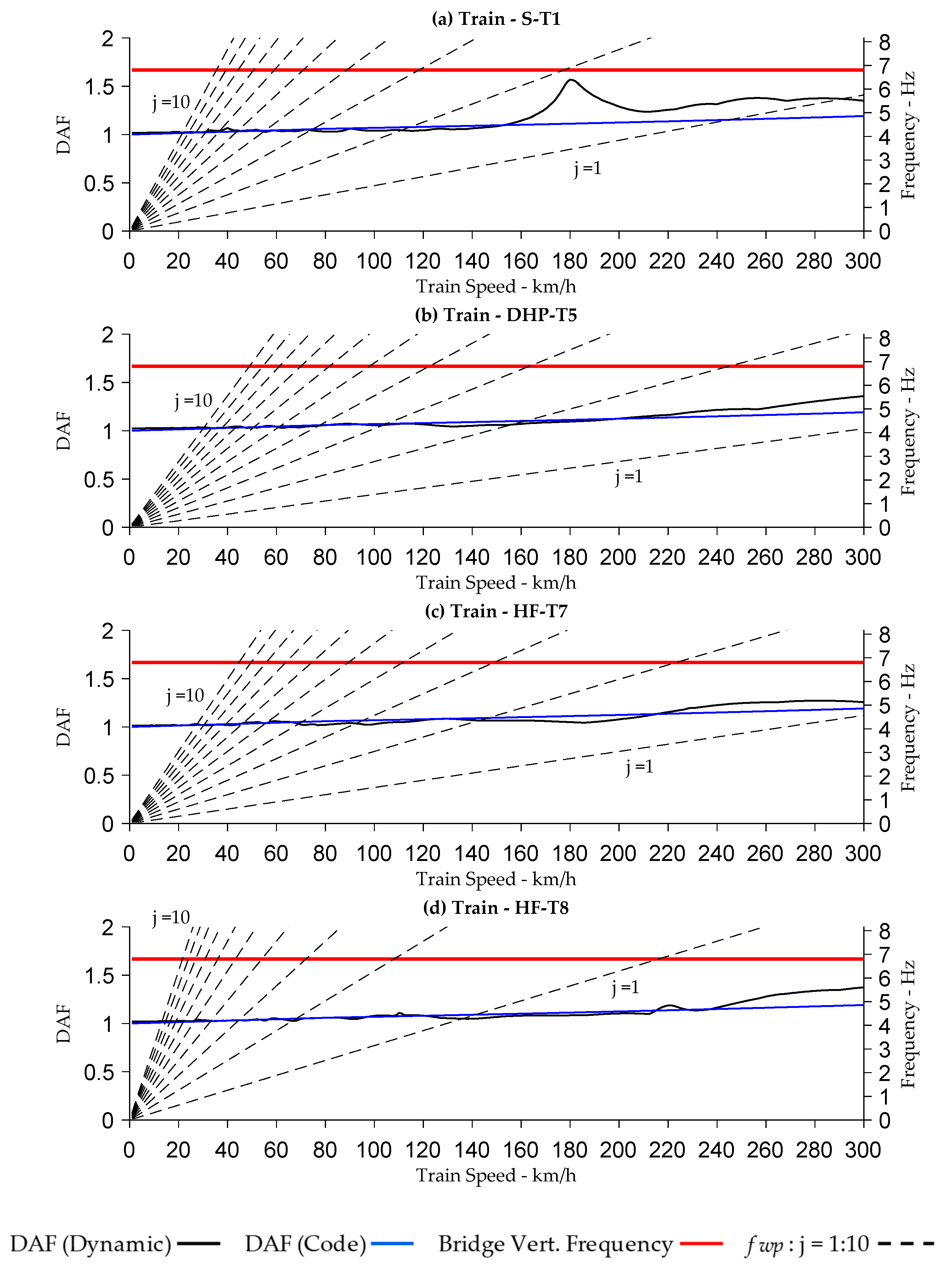
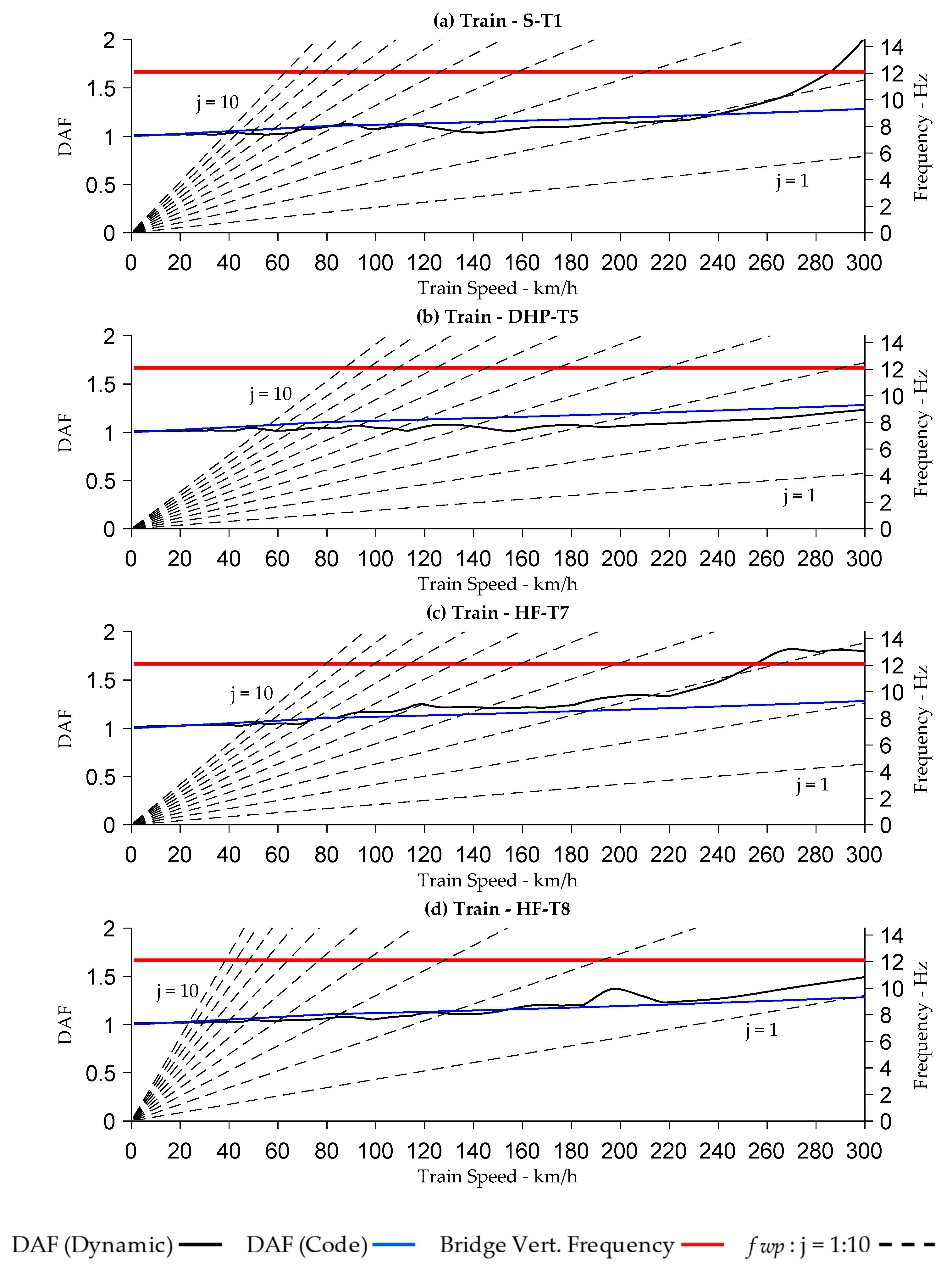
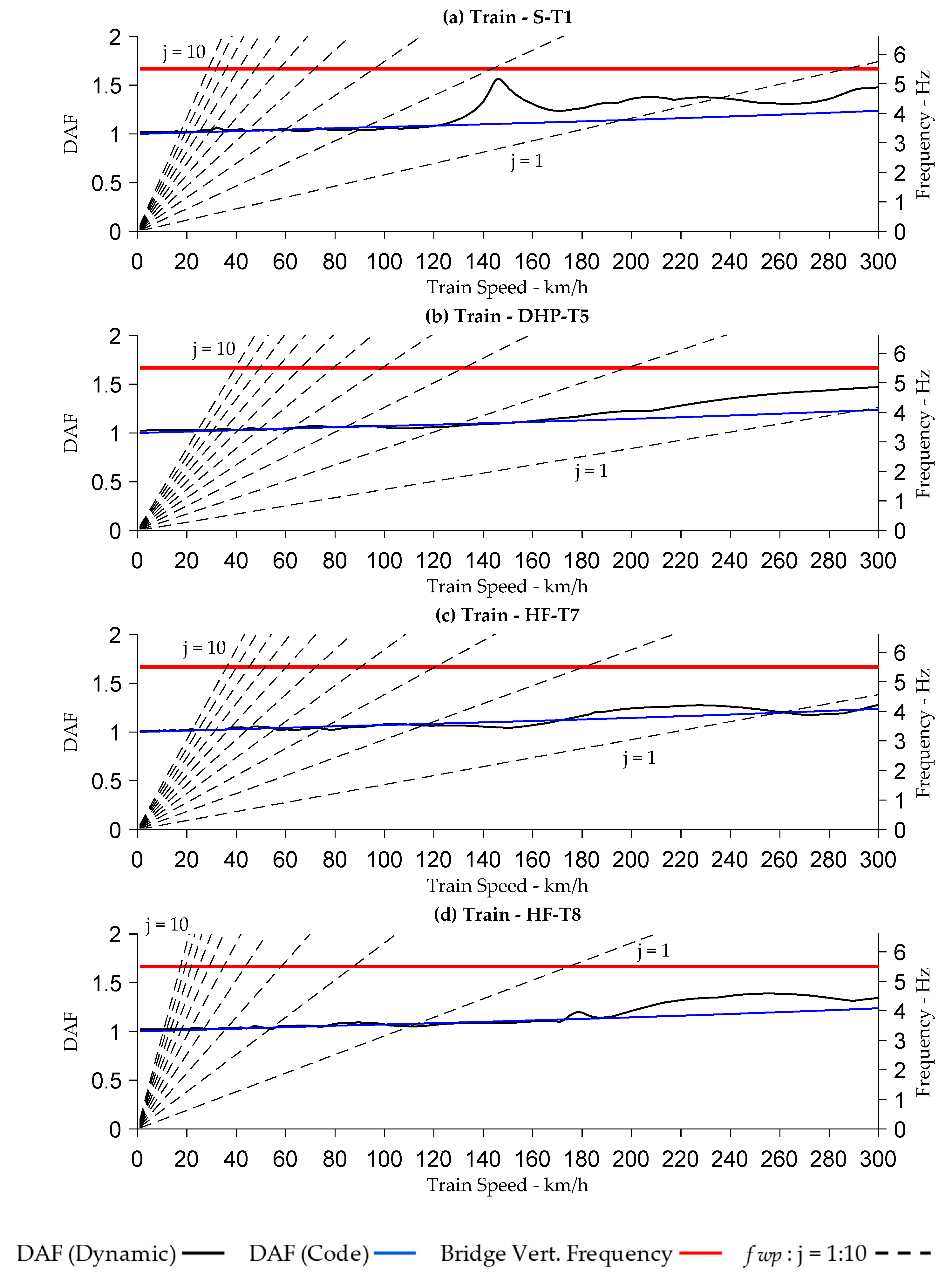
References
- Binns, D. High Speed Rail ‘For Whole UK’. METRO, 29 May 2018.
- Department of Transport (DOT). High Speed Rail: Investing in Britain’s Future—Decisions and Next Steps; The Stationary Office Ltd.: London, UK, 2012; ISBN 9780101824729. [Google Scholar]
- Imam, B. Fatigue Analysis of Riveted Railway Bridges. Ph.D. Thesis, School of Engineering, Civil Engineering, University of Surrey, Surrey, UK, 2006. [Google Scholar]
- Bozigit, B.; Acikgoz, S. Dynamic amplification in masonry arch railway bridges. J. Struct. 2022, 45, 1717–1728. [Google Scholar] [CrossRef]
- Lu, Y.; Mao, L.; Woodward, P. Frequency characteristic of railway bridge response to moving trains with consideration of train mass. Eng. Struct. 2012, 42, 9–22. [Google Scholar] [CrossRef]
- BS-5400; Steel, Concrete and Composite Bridges—Part 10: Code of Practice for Fatigue. British Standards Institution: London, UK, 1980.
- Milne, D.R.M.; LePen, L.M.; Thompson, D.J. Properties of train load frequencies and their application. J. Sound Vib. 2017, 397, 123–140. [Google Scholar] [CrossRef]
- Connolly, D.P.; Kouroussis, G. Benchmarking railway vibrations—Track, vehicle, ground and building effects. Constr. Build. Mater. 2015, 92, 64–81. [Google Scholar] [CrossRef]
- Hunley, J.B. Impact in steel railway bridges of simple span. Am. Railw. Eng. Assoc. Proc. 1936, 37, 747. [Google Scholar]
- Looney, C.T.G. Hi-speed computer applied to bridge impact. In Proceedings of the American Society of Civil Engineers, Chicago IL, USA, 27 August 1958; Volume 84. [Google Scholar]
- Turneaure, F.E.; Crandall, C.L.; Cartlidge, C.H.; Schneider, C.C. Report of Committee on Impact. In Proceedings of the Annual Convention: American Railway Engineering Association (AREA) Proc, Chicago, IL, USA, 21–23 March 1911. Volume 12, Part 3. [Google Scholar]
- Britain, G.; Ewing, J.A.; Dalby, W.E.; Gribble, C.; Moullin, E.B.; Inglis, C.E.; Gough, G.S. Report of the Bridge Stress Committee; H.M. Stationery Off.: London UK, 1928. [Google Scholar]
- BS EN 1991-2:2003; Eurocode-1: Actions on Structures—Part 2: Traffic Loads on Bridges. British Standard: Chiswick, London, UK, 2003.
- NR/GN/CIV/025; The Structural Assessment of Underbridges. Network Rail: London, UK, 2006.
- Garg, V.K.; Dukkipati, R.V. Dynamics of Railway Vehicle Systems, 1st ed.; Academic Press: Toronto, ON, Canada, 2004; pp. 1–400. [Google Scholar]
- Willis, R. Appendix to the Report of the Commissioners Appointed to Inquire into the Application of Iron to Railway Structures; H.M. Stationary Office: London, UK, 1849. [Google Scholar]
- Stokes, G.G. Discussion of a differential equation related to the breaking of railway bridges. Trans. Camb. Phil. Soc. 1867, 8, 12–16. [Google Scholar]
- Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering, 3rd ed.; D. Van Nostrand: New York, NY, USA, 1956. [Google Scholar]
- Jeffcott, H.H. On the vibrations of beams under the action of moving loads. Phil. Mag. 1929, 8, 66–97. [Google Scholar] [CrossRef]
- Inglis, C.E. A Mathematical Treatise on Vibration in Railway Bridges, 1st ed; The University Press: Cambridge, UK, 1934; pp. 1–203. [Google Scholar]
- Arvidsson, T.; Karoumi, R. Train-interaction—A review and discussion of key model parameters. Int. J. Rail Transp. 2014, 2, 147–186. [Google Scholar] [CrossRef]
- Perelmuter, A.V.; Slivker, V. Handbook of Mechanical Stability in Engineering; World Scientific Publishing: Munich, Germany, 2013; Volume 1, ISBN 978-981-4383-75-2. [Google Scholar]
- Fryba, L. Vibration of Solid Structures under Moving Loads, 3rd ed.; Thomas Telford: London, UK, 1999. [Google Scholar]
- Yang, Y.B.; Yau, J.D.; Wu, Y.S. Vehicle-Bridge Interaction Dynamics—With Applications to High-Speed Railways, 1st ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2004; pp. 1–530. [Google Scholar]
- Kargarnovin, M.H.; Younesian, D.; Thompson, D.; Jones, C. Ride Comfort of High-speed Trains Travelling over Railway Bridges. Veh. Sys. Dyn. 2005, 43, 173–199. [Google Scholar] [CrossRef]
- Karoumi, R.; Wiberg, J.; Liljencrantz, A. Monitoring traffic loads and dynamic effects using instrumented railway bridge. Eng. Struct. 2005, 27, 1813–1819. [Google Scholar] [CrossRef]
- Kwark, J.W.; Choi, E.S.; Kim, Y.J.; Kim, B.S.; Kim, S.I. Dynamic behavior of two-span continuous concrete bridges under moving high-speed train. Comp. Struct. 2004, 82, 463–474. [Google Scholar] [CrossRef]
- Wiberg, J. Railway Bridge Response to Passing Trains—Measurements and FE Model Updating. Ph.D. Thesis, KTH Architecture and the Built Environment, Stockholm, Sweden, 2009. [Google Scholar]
- Hamidi, S.A.; Danshjoo, F. Determination of impact factor for steel railway bridges considering simultaneous effects of vehicle speed and axle distance to span length ratio. Eng. Struct. 2010, 32, 1369–1376. [Google Scholar] [CrossRef]
- Imam, B.; Yahya, N.F. Dynamic amplification factors for existing truss bridges for the purposes of fatigue damage. In Proceedings of the 9th International Conference on Structural Dynamics (EURODYN), Porto, Portugal, 30 June–2 July 2014; ISBN 978-972-752-165-4, ISSN 2311-9020. [Google Scholar]
- Bisadi, M.; Ma, Q.T.; Beskhyroun, S. Evaluation of the Dynamic Amplification Factor for Railway Bridges Subjected to a Series of Moving Mass. In Proceedings of the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015. [Google Scholar]
- Mensinger, M.; Fard, R.R.; Hacker, A.; Nable, A. Validation of the dynamic amplification factor in case of historic railway steel bridges with short and medium spans. Procedia Eng. 2016, 156, 233–240. [Google Scholar] [CrossRef]
- Mao, L.; Lu, Y. Critical Speed and Resonance Criteria of Railway Bridge Response to Moving Trains. ASCE J. Bridge Eng. 2013, 18, 131–141. [Google Scholar] [CrossRef]
- Esmailzadeh, E.; Ghorashi, M. Vibration analysis of beams traversed by uniform partially distributed moving masses. J. Sound Vibr. 1995, 184, 9–17. [Google Scholar] [CrossRef]
- Dehestani, M.; Mofid, M.; Vafai, A. Investigation of critical influential speed for moving mass problems on beams. Appl. Math. Model. 2009, 33, 3885–3895. [Google Scholar] [CrossRef]
- Li, J.Z.; Su, M.B. The resonant vibration for a simply supported girder bridge under high speed trains. J. Sound Vib. 1999, 224, 897–915. [Google Scholar] [CrossRef]
- Li, J.Z.; Su, M.B.; Fan, L.C. Natural frequency of railway girder bridges under vehicle loads. J. Bridge Eng. 2003, 8, 199–203. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chang, K.C. Extracting modal parameters of high-speed railway bridge using the TDD technique. Mech. Syst. Signal Proc. 2009, 24, 707–720. [Google Scholar]
- Auersch, L. The excitation of ground vibration by rail traffic: Theory of vehicle–track–soil interaction and measurements on high-speed lines. J. Sound Vib. 2005, 284, 103–132. [Google Scholar] [CrossRef]
- Ju, S.H.; Lin, H.T.; Huang, J.Y. Dominant frequencies of train-induced vibrations. J. Sound Vib. 2009, 319, 247–259. [Google Scholar] [CrossRef]
- Gatti, G.; Brennan, M.J.; Tehrani, M.G.; Thompson, D.J. Harvesting energy from the vibration of a passing train using a single-degree-of-freedom oscillator. Mech. Syst. Signal Process. 2016, 66–67, 785–792. [Google Scholar] [CrossRef]
- Delgado, R.; Calçada, R.; Ribeiro, D.; Pinto, J.R.; Figueiredo, H.; Faria, I. Assessment of the dynamic response of high-speed railway bridges in interoperable lines. In Dynamics of High-Speed Railway Bridges; CRC Press: London, UK, 2008. [Google Scholar] [CrossRef]
- Koç, M.A.; Esen, I. Analysis of Vehicle Bridge Dynamics Interaction using Quarter Car Model. In Proceedings of the 1st International Conference on Engineering Technology and Applied Science, Afyon Kocatepe University, Afyonkarahisar, Turkey, 21–22 April 2016. [Google Scholar]
- Koç, M.A.; Esen, I. Influence of Train Mass on Vertical Vibration Behaviour of Railway Vehicle and Bridge Structure. In Proceedings of the 3rd International Symposium on Railway Systems Engineering (ISERSE’16), Karabuk, Turkey, 13–15 October 2021. [Google Scholar]
- Koç, M.A. Finite element and numerical vibration analysis of a Timoshenko and Euler-Bernoulli beams traversed by a moving high-speed train. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 165. [Google Scholar] [CrossRef]
- Koç, M.A.; Esen, I.; Eroğlu, M.; Çay, Y. A new numerical method for analysing the interaction of a bridge structure and travelling cars due to multiple high-speed trains. Int. J. Heavy Veh. Syst. 2021, 28, 79–109. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhu, D.; Li, C. A moving load amplitude spectrum for analysing the resonance and vibration cancellation of simply supported bridges under moving loads. Eur. J. Mech. A/Solids. 2022, 92, 104428. [Google Scholar] [CrossRef]
- Salama, A.; Eraky, A.; Yahya, M.; Samir, R. Dynamic Analysis of High-speed Railway Bridges Applying Bridge-Vehicle Interaction. Jordan J. Civ. Eng. 2022, 16, 402–416. [Google Scholar]
- Erduran, E.; Gonen, S.; Alkanany, A. Parametric analysis of the dynamic response of railway bridges due to vibrations induced by heavy-haul trains. Struct. Infrastruct. Eng. 2022, 20, 326–339. [Google Scholar] [CrossRef]
- Majka, M.; Hartnett, M. Dynamic response of bridges to moving trains: A study on effects of random track irregularities and bridge skewness. Comput. Struct. 2009, 87, 1233–1252. [Google Scholar] [CrossRef]
- Bin, Y.Y.; Wu, Y.S. A versatile element for analyzing vehicle-bridge interaction Response. Eng. Struct. 2001, 23, 452–469. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, C.S. Reliability-Based Dynamic Amplification Factor on Stress Ranges for Fatigue Design of Existing Bridges. J. Bridge Eng. 2001, 18, 538–552. [Google Scholar] [CrossRef]
- Warburton, G.B. Assessment of errors in the newmark method in structural dynamics. Earthq. Engng. Struct. Dyn. 1990, 19, 457–467. [Google Scholar] [CrossRef]
- Pesterev, A.V.; Bergman, L.A.; Tan, C.A.; Tsao, T.C.; Yang, B. On asymptotics of the solution of the moving oscillator problem. J. Sound Vib. 2003, 260, 519–536. [Google Scholar] [CrossRef]
- Johansson, C.; Ní Nualláin, N.A.; Pacoste, C.; Andersson, A. A methodology for the preliminary assessment of existing railway bridges for high-speed traffic. Eng. Struct. 2014, 58, 25–35. [Google Scholar] [CrossRef]
- Svedholm, C. Efficient Modelling Techniques for Vibration Analysis of Railway Bridges. Ph.D. Thesis, Structural Engineering and Bridges, Stockholm, Sweden, 2017. [Google Scholar]
- Bracewell, R. The Impulse Symbol. The Fourier Transform and Its Applications; McGraw Hill: New York, NY, USA, 2000; pp. 74–104, Chapter 5. [Google Scholar]
- Gaillard, C.S. Dynamic effects on structures of Freight Trains: Project Report. Project Reference T174. Rails Safety and Standards Board. 2003. Available online: https://www.rssb.co.uk/en/research-catalogue/CatalogueItem/rp000122. (accessed on 9 March 2024).
- Gu, G.; Kapoor, A.; Lilley, D.M. Calculation of Dynamic Impact Loads for Railway Bridges Using a Direct Integration Method. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2008, 222, 385–398. [Google Scholar] [CrossRef]
- Iles, D.C. Design Guide for Steel Railway Bridges; The Steel Construction Institute: London, UK, 2004; pp. 36–42. [Google Scholar]
- Chan, T.H.; O’Connor, C. Vehicle Model for Highway Bridge Impact. J. Struct. Eng. 1990, 116, 1772–1793. [Google Scholar] [CrossRef]
- Ichikawa, M.; Miyakawa, Y.; Matsuda, A. Vibration Analysis of the Continuous Beam Subjected to a Moving Mass. J. Sound Vib. 2000, 230, 493–506. [Google Scholar] [CrossRef]
- Brady, S.P.; OBrien, E.J.; Žnidaric, A. The effect of vehicle velocity on the dynamic amplification of a vehicle crossing a simply supported bridge. ASCE J. Bridge Eng. 2006, 11, 241–249. [Google Scholar] [CrossRef]
- Mohamed, O.; Cantero, D.; Gonzalez, A.; Al-Sabah, S. Dynamic Amplification Factor of Continuous verses Simply Supported Bridges due to the Action of a Moving Load. In Proceedings of the Civil Engineering Research in Ireland (CERI 2014), Queen’s University, Belfast, Ireland, 28–29 August 2014; Available online: https://hdl.handle.net/10197/6582 (accessed on 9 March 2024).
- Cantieni, R. Dynamic Load Testing of Highway Bridges; Proceedings P-75/84; International Association for Bridge and Highway Engineering (IABSE): Zurich, Switzerland, 1984; Volume 3, pp. 57–72. [Google Scholar]
- Green, M.F.; Cebon, D.; Cole, D.J. Effects of Vehicle Suspension Design on Dynamics of Highway Bridges. J. Struct. Eng. 1995, 121, 272–282. [Google Scholar] [CrossRef]
- Yang, Y.B.; Liao, S.S.; Lin, B.H. Impact Formulas for Vehicles Moving Over Simple and Continuous Beams. J. Struct. Eng. 1995, 121, 1644–1650. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, W.; Shamsabadi, A.; Shi, L.; Taciroglu, E. A Vehicle–Bridge Interaction Element: Implementation in ABAQUS and Verification. Appl. Sci. 2023, 13, 8812. [Google Scholar] [CrossRef]
- Monitoring Factual Report Job No: PN45829 Client: Network Rail Yetminster Bridge Deflection Test JFTS Document No: PN45829-REP-01-R2. Internal Report, 2020.
- Biswal, S.; Imam, B.; Wang, Y.; Chryssanthopoulos, M.K. Modal Testing of a Riveted Metallic Bridge under Different End Conditions. In Proceedings of the 11th International Conference on Bridge Maintenance, Safety and Management (IABMAS’22), Barcelona, Spain, 11–15 July 2022. [Google Scholar]
- Biswal, S.; Imam, B.; Chryssanthopoulos, M.K. Deliverable D4: Report on numerical modelling procedure. University of Surrey Report submitted to Network Rail UK. 2021; pp. 1–82. Internal Document. [Google Scholar]
| Bridge No. | Bridge Type | Bridge Span, L | Bridge Mass, M | Vertical Bending Frequency, fn | Second Moment of Area, I |
|---|---|---|---|---|---|
| [m] | [kg] | [Hz] | [m4] | ||
| 1 | Half-through | 8.84 | 42,400 | 10.5 | 0.0062 |
| 2 | Half-through | 18.1 | 133,200 | 5.3 | 0.0428 |
| 3 | Western Box and Half-through deck | 9.3 | 115,000 | 14 | 0.0350 |
| 4 | Western Box and Half-through deck | 21.33 | 400,600 | 6.8 | 0.3468 |
| 5 | Half-through | 8.1 | 55,527 | 12.1 | 0.0083 |
| 6 * | Half-through | 21.26 | 207,832 | 5.5 | 0.1166 |
| Train No. | BS-5400 Train Type | No. Axles & Weights [t] | No Wagons | Locomotive-Wagon (Train) Configuration | |||
|---|---|---|---|---|---|---|---|
| Locomotive | Wagons | ||||||
| 1 | Steel | S-T1 | 6 × 21.5 t | 6 × 18.5 t | 15 | W | L—15 × W |
| 2 | Electric Multiple Unit | EMU-T2 | 4 × 16.5 t | 4 × 10 t 4 × 16.5 t (Loc) 4 × 10 t | 3 1 3 | W1 L W2 | L—3 × W1—L—3 × W2 |
| 3 | Southern Regional Suburban | SRS-T3 | 2 × 13 t + 2 × 11 t | 4 × 9.5 t 2 × 11 t + 2 × 13 t 2 × 13 t + 2 × 11 t 4 × 9.5 t 2 × 11 t + 2 × 13 t | 2 1 1 2 1 | W1 W2 W3 W1 W2 | L—2 × W1—W2—W3—2 × W1—W2 |
| 4 | Southern Regional Suburban | SRS-T4 | 2×13 t + 2×11 t | 4 × 9.5 t 2 × 11 t + 2 × 13 t | 2 1 | W1 W2 | L—2 × W1—W2 |
| 5 | Diesel Hauled Passenger | DHP-T5 | 6 × 20 t | 4 × 10 t | 12 | W | L—12 × W |
| 6 | Electric Hauled Passenger | EHP-T6 | 4 × 23 t | 4 × 10 t | 12 | W | L—12 × W |
| 7 | Heavy Freight | HF-T7 | 6 × 20 t | 4 × 25 t | 10 | W | L—10 × W |
| 8 | Heavy Freight | HF-T8 | 6 × 20 t | 2 × 25 t | 20 | W | L—20 × W |
| 9 | Mixed Freight | MF-T9 | 6 × 20 t | 2 × 7 t 4 × 20 t 6 × 20 t | 18 3 2 | W1 W2 W3 | L—2 × W1—W2—10 × W1—W3—W2 —2 × W1—W2—4 × W1—W3 |
| Train Parameters | S-T1 | DHP-T5 | HF-T7 | HF-T8 | |
|---|---|---|---|---|---|
| Wagon Length, Lw | [m] | 11.2 | 16.7 | 15.7 | 5.5 |
| Wagon Coupling Distance, Lwe | [m] | 3.5 | 3.6 | 3.6 | 3.5 |
| Number of Wagons, Nw | 15 | 12 | 10 | 20 |
| (a) Train S-T1 | ||||
|---|---|---|---|---|
| Bridge No. | Vertical Bending Frequency | Wagon Pass Frequency, fwp | Dominant Frequencies | Frequencies Affecting DAF |
| [Hz] | [Hz] | j × fwp | j × fwp | |
| 1 | 10.5 | 1.92 | j = 1 and 2 | j = 5 |
| 2 | 5.3 | j = 1 | j = 3, 4, 5 and 9 | |
| 3 | 14 | j = 1 and 2 | j = 8 and 9 | |
| 4 | 6.8 | j=2 | j = 4, 5 and 9 | |
| 5 | 12.1 | j = 1 and 2 | j = 7 and 8 | |
| 6 | 5.5 | j = 2 | j = 3, 4, 5 and 9 | |
| (b) Train DHP-T5 | ||||
| Bridge No. | Vertical Bending Frequency | Wagon Pass Frequency, fwp | Dominant Frequencies | Frequencies Affecting DAF |
| [Hz] | [Hz] | j × fwp | j × fwp | |
| 1 | 10.5 | 1.41 | j = 1 | j = 5 |
| 2 | 5.3 | j = 1 | - | |
| 3 | 14 | j = 1 | - | |
| 4 | 6.8 | j = 1 | - | |
| 5 | 12.1 | j = 1 | j = 10 | |
| 6 | 5.5 | j = 1 | j = 4 | |
| (c) Train HF-T7 | ||||
| Bridge No. | Vertical Bending Frequency | Wagon Pass Frequency, fwp | Dominant Frequencies | Frequencies Affecting DAF |
| [Hz] | [Hz] | j × fwp | j × fwp | |
| 1 | 10.5 | 1.52 | j = 1 | j = 7 |
| 2 | 5.3 | j = 1 | j = 4 | |
| 3 | 14 | j = 1 | j = 10 | |
| 4 | 6.8 | j = 1 | - | |
| 5 | 12.1 | j = 1 | j = 9 | |
| 6 | 5.5 | j = 1 | - | |
| (d) Train HF-T8 | ||||
| Bridge No. | Vertical Bending Frequency | Wagon Pass Frequency, fwp | Dominant Frequencies | Frequencies Affecting DAF |
| [Hz] | [Hz] | j × fwp | j × fwp | |
| 1 | 10.5 | 3.15 | j = 1, 2 and 3 | j = 3, 4 and 5 |
| 2 | 5.3 | j = 1, 2 and 3 | j = 2, 3 and 5 | |
| 3 | 14 | j = 1 | j = 4 | |
| 4 | 6.8 | j = 2 and 3 | j = 2 and 3 | |
| 5 | 12.1 | j = 1 | j = 4 | |
| 6 | 5.5 | j = 2 | j = 2 and 3 | |
| Bridge No. Span and Frequency | BS5400 Train | Wagon Pass Frequency fwp—[Hz] | Dynamic Amplification Factor (DAF) at Dominant Train Load Frequencies | |||||
|---|---|---|---|---|---|---|---|---|
| Calculated | EBB Model FFT | j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | ||
| 1 L = 8.84 m, fn = 10.5 Hz | S-T1 | 1.92 | 1.93 | 1.03 | 0.87 | - | - | 2.79 |
| DHP-T5 | 1.41 | 1.35 | 1.04 | 0.98 | - | - | - | |
| HF-T7 | 1.52 | 1.45 | 1.03 | 0.96 | - | - | - | |
| HF-T8 | 3.15 | 3.12 | 0.95 | 0.61 | 2.22 | 4.40 | 2.99 | |
| 2 L = 18.1 m, fn = 5.3 Hz | S-T1 | 1.92 | 1.86 | 0.87 | 0.13 | 8.50 | 3.08 | 2.64 |
| DHP-T5 | 1.41 | 1.41 | 0.98 | 0.79 | - | - | - | |
| HF-T7 | 1.52 | 1.52 | 0.95 | 0.68 | 1.52 | 6.02 | - | |
| HF-T8 | 3.15 | 3.12 | 0.59 | 5.26 | 2.67 | - | 2.27 | |
| 3 L = 9.3 m, fn = 14 Hz | S-T1 | 1.92 | 1.93 | 1.02 | 0.90 | - | - | - |
| DHP-T5 | 1.41 | 1.35 | 1.02 | 0.98 | - | - | - | |
| HF-T7 | 1.52 | 1.45 | 1.02 | 0.97 | - | - | - | |
| HF-T8 | 3.15 | 3.12 | 0.96 | 0.87 | 0.32 | - | 5.94 | |
| 4 L = 21.33 m, fn = 6.8 Hz | S-T1 | 1.92 | 1.84 | 0.77 | 0.59 | - | 6.31 | 3.20 |
| DHP-T5 | 1.41 | 1.39 | 0.96 | 0.91 | - | - | - | |
| HF-T7 | 1.52 | 1.50 | 0.94 | 0.88 | - | - | - | |
| HF-T8 | 3.15 | 3.07 | 0.86 | 3.51 | 3.37 | 2.38 | ||
| 5 L = 8.1 m, fn = 12.1 Hz | S-T1 | 1.92 | 1.94 | 1.03 | 0.92 | - | - | - |
| DHP-T5 | 1.41 | 1.36 | 1.04 | 1.00 | 0.89 | - | - | |
| HF-T7 | 1.52 | 1.46 | 1.04 | 0.99 | 0.81 | - | - | |
| HF-T8 | 3.15 | 3.14 | 0.97 | 0.82 | 0.45 | 7.77 | - | |
| 6 L = 21.26 m, fn = 5.5 Hz | S-T1 | 1.92 | 1.84 | 0.75 | 0.16 | 14.58 | 3.28 | 2.66 |
| DHP-T5 | 1.41 | 1.39 | 0.95 | 0.76 | 0.20 | 17.17 | - | |
| HF-T7 | 1.52 | 1.50 | 0.93 | 0.68 | - | - | - | |
| HF-T8 | 3.15 | 3.07 | 0.75 | 5.87 | 2.67 | - | 2.89 | |
| Bridge No. Span and Frequency | BS5400 Train | Train Critical Speeds, Vcritical—[km/h] | ||||
|---|---|---|---|---|---|---|
| j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | ||
| 1 L = 8.84 m, fn = 10.5 Hz | S-T1 | 547 | 273 | 182 | 137 | 109 |
| DHP-T5 | 756 | 378 | 252 | 189 | 151 | |
| HF-T7 | 716 | 358 | 239 | 179 | 143 | |
| HF-T8 | 334 | 167 | 111 | 83 | 67 | |
| 2 L = 18.1 m, fn = 5.3 Hz | S-T1 | 276 | 138 | 92 | 69 | 55 |
| DHP-T5 | 382 | 191 | 127 | 95 | 76 | |
| HF-T7 | 361 | 181 | 120 | 90 | 72 | |
| HF-T8 | 168 | 84 | 56 | 42 | 34 | |
| 3 L = 9.3 m, fn = 14 Hz | S-T1 | 729 | 365 | 243 | 182 | 146 |
| DHP-T5 | 1008 | 504 | 336 | 252 | 202 | |
| HF-T7 | 955 | 477 | 318 | 239 | 191 | |
| HF-T8 | 445 | 222 | 148 | 111 | 89 | |
| 4 L = 21.33 m, fn = 6.8 Hz | S-T1 | 354 | 177 | 118 | 89 | 71 |
| DHP-T5 | 490 | 245 | 163 | 122 | 98 | |
| HF-T7 | 464 | 232 | 155 | 116 | 93 | |
| HF-T8 | 216 | 108 | 72 | 54 | 43 | |
| 5 L = 8.1 m, fn = 12.1 Hz | S-T1 | 630 | 315 | 210 | 158 | 126 |
| DHP-T5 | 871 | 436 | 290 | 218 | 174 | |
| HF-T7 | 825 | 413 | 275 | 206 | 165 | |
| HF-T8 | 384 | 192 | 128 | 96 | 77 | |
| 6 L = 21.26 m, fn = 5.5 Hz | S-T1 | 286 | 143 | 95 | 72 | 57 |
| DHP-T5 | 396 | 198 | 132 | 99 | 79 | |
| HF-T7 | 375 | 188 | 125 | 94 | 75 | |
| HF-T8 | 175 | 87 | 58 | 44 | 35 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.K.; Imam, B.; Hajializadeh, D. Dynamic Amplification of Railway Bridges under Varying Wagon Pass Frequencies. Infrastructures 2024, 9, 62. https://doi.org/10.3390/infrastructures9030062
Rahman AK, Imam B, Hajializadeh D. Dynamic Amplification of Railway Bridges under Varying Wagon Pass Frequencies. Infrastructures. 2024; 9(3):62. https://doi.org/10.3390/infrastructures9030062
Chicago/Turabian StyleRahman, Aminur K., Boulent Imam, and Donya Hajializadeh. 2024. "Dynamic Amplification of Railway Bridges under Varying Wagon Pass Frequencies" Infrastructures 9, no. 3: 62. https://doi.org/10.3390/infrastructures9030062
APA StyleRahman, A. K., Imam, B., & Hajializadeh, D. (2024). Dynamic Amplification of Railway Bridges under Varying Wagon Pass Frequencies. Infrastructures, 9(3), 62. https://doi.org/10.3390/infrastructures9030062







