Ensemble Learning Approach for Developing Performance Models of Flexible Pavement
Abstract
:1. Introduction
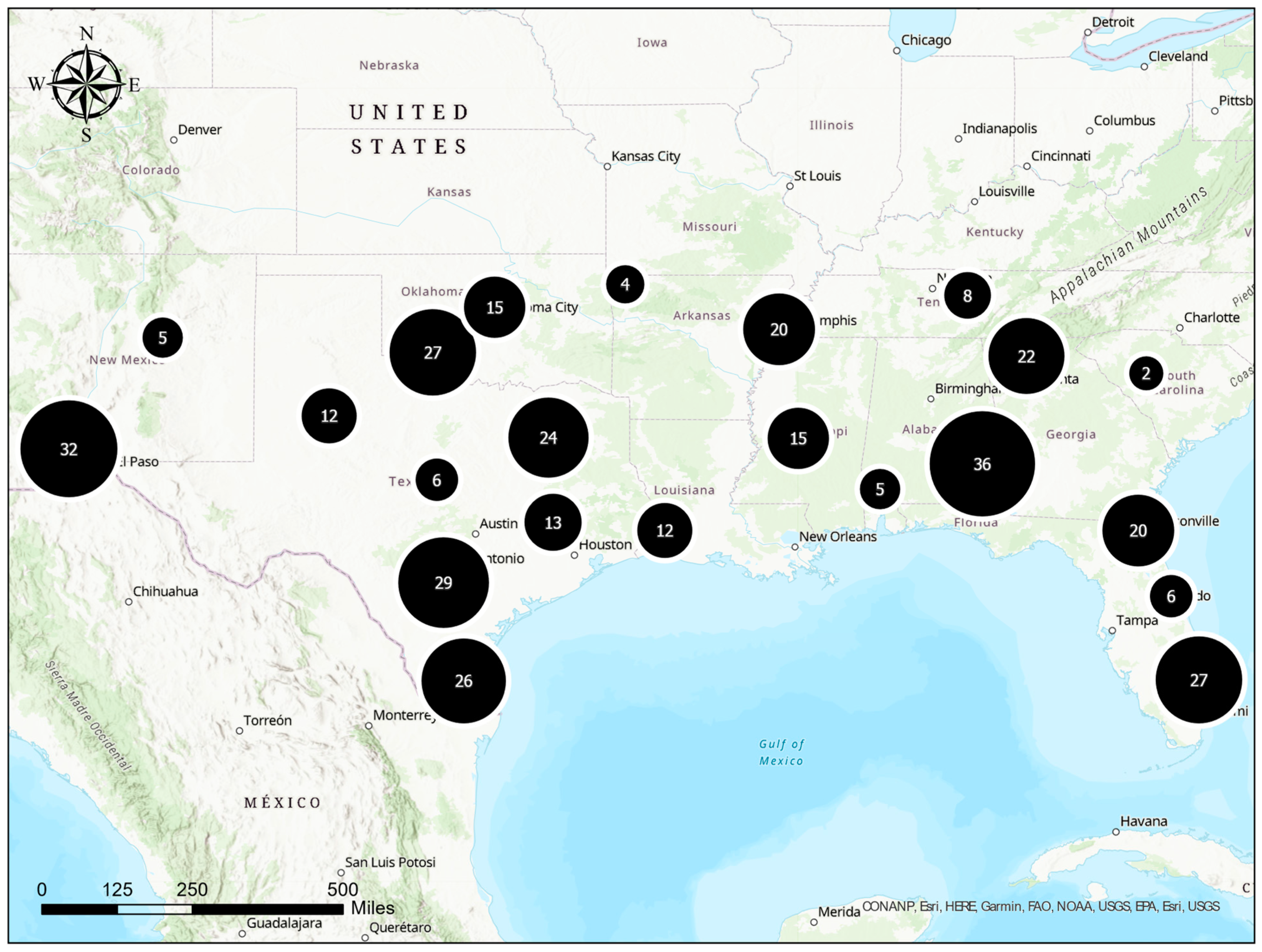
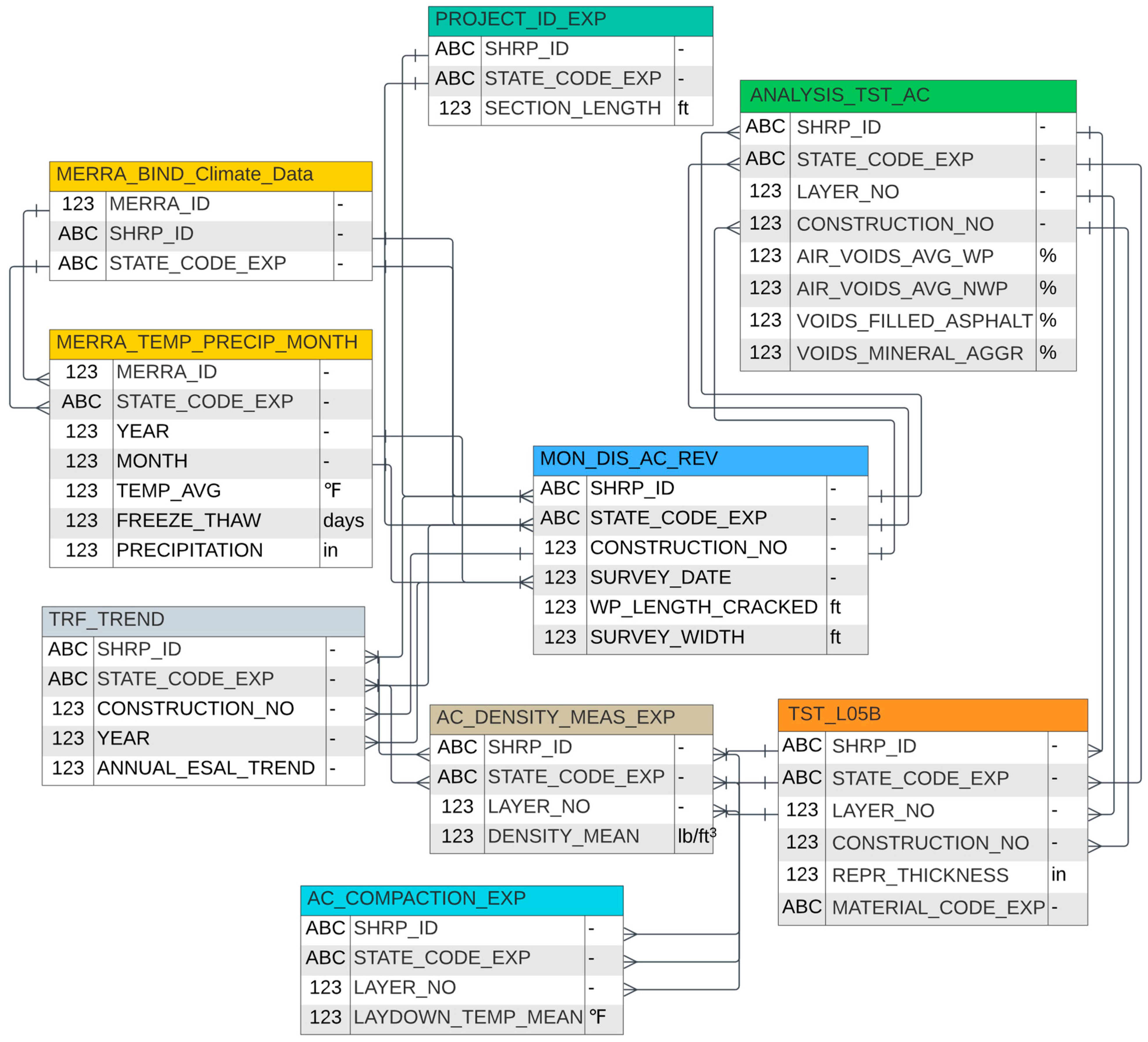
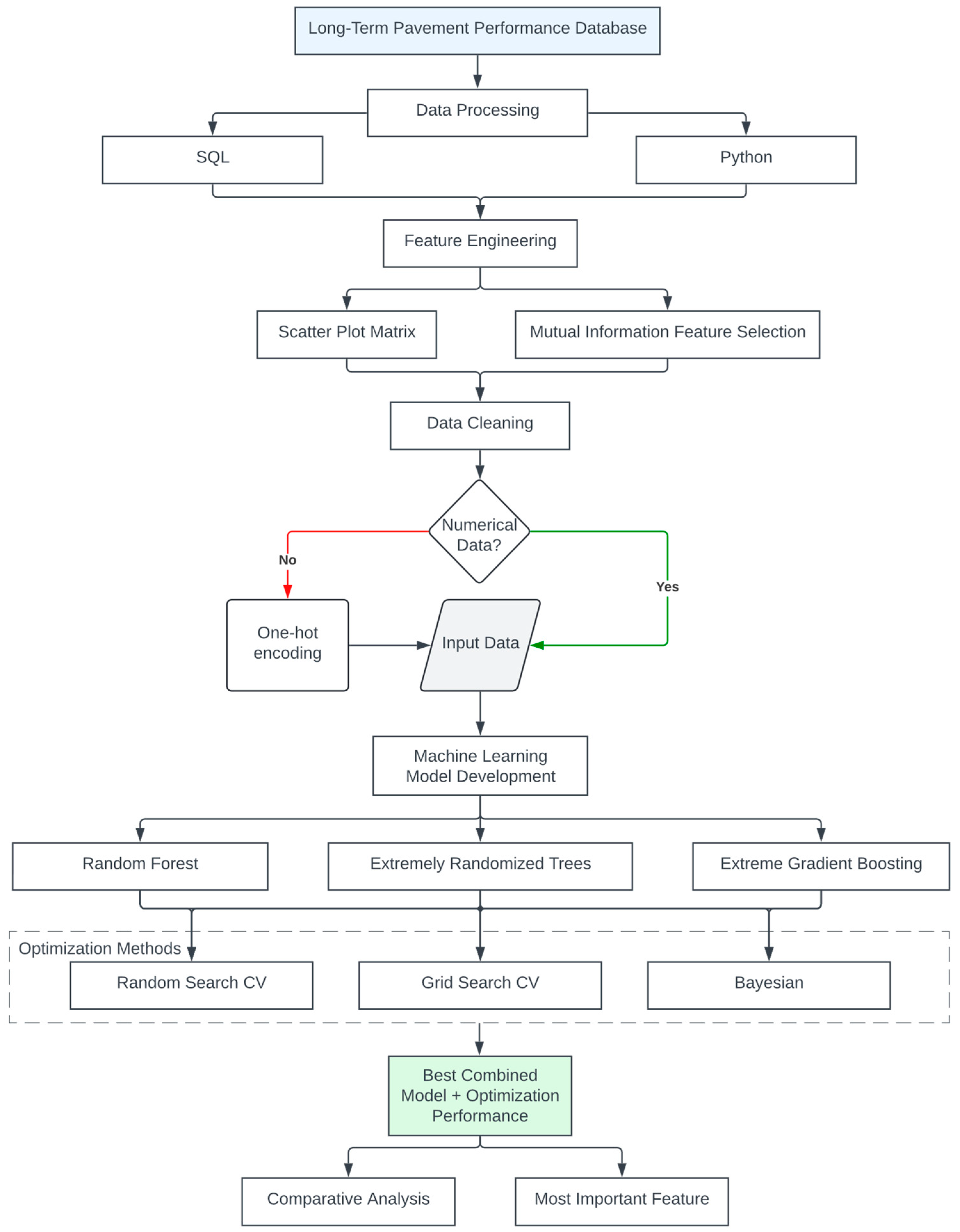
2. Data Processing
3. Methodology
3.1. Machine Learning Models
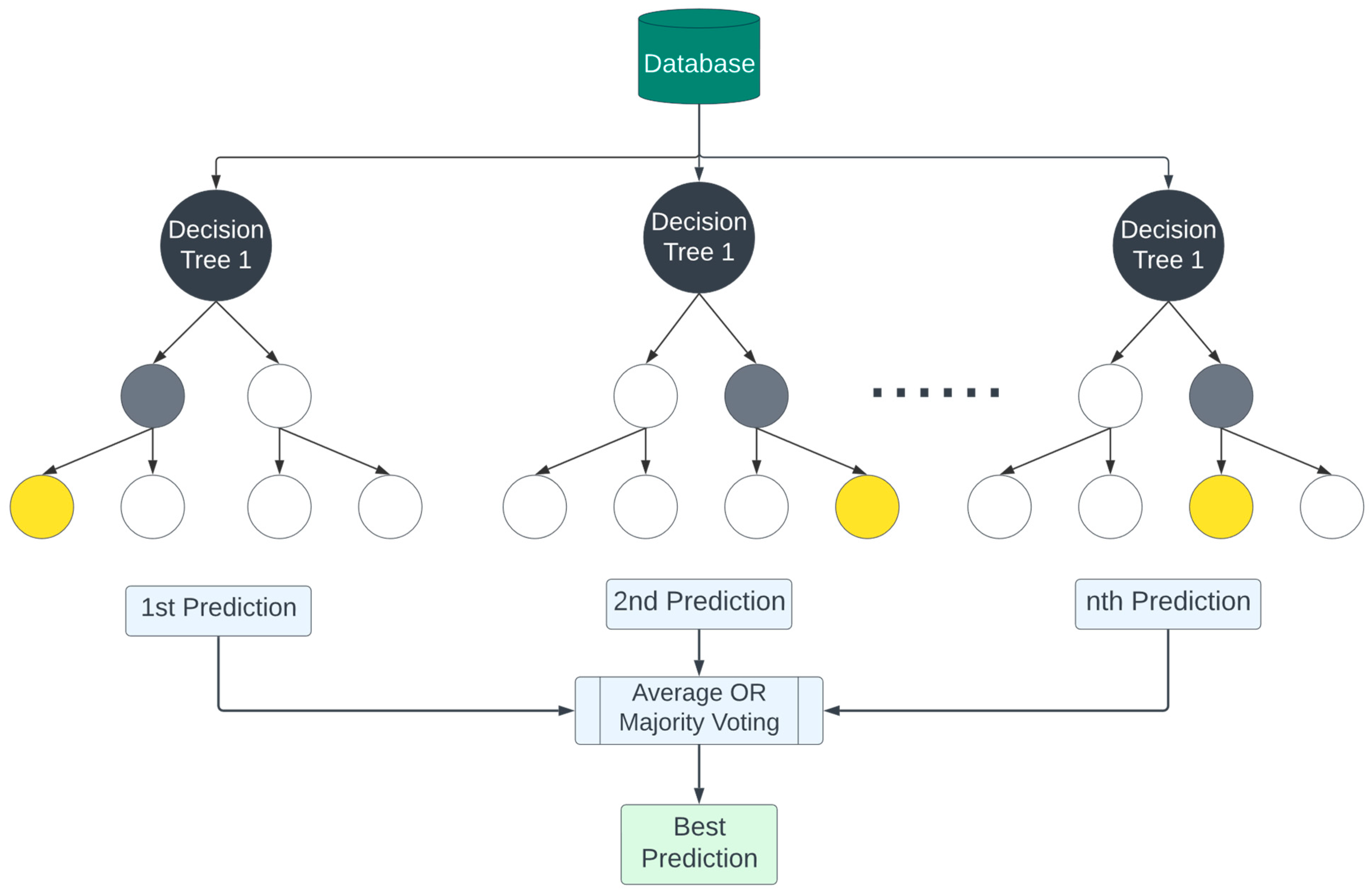
3.1.1. Random Forest
| Algorithm 1 Pseudocode algorithm for random forest |
| Precondition: A training set S:= (X_train, y_train), features F, and number of trees in forest B. 1 function RandomForestRegression(S, F, B) 2 H ← empty list//This will store all the individual trees 3 for i ∈ 1, …, B do 4 S(i) ← BootstrapSample(S)//Generate a bootstrap sample from the original dataset 5 tree ← BuildDecisionTree(S(i), F) 6 Append tree to H 7 end for 8 return H//Return the ensemble of trees 9 end function 10 function BootstrapSample(S) 11 sample ← empty list 12 for i ∈ 1, …, length(S) do 13 s ← Randomly select an instance from S with replacement 14 Append s to sample 15 end for 16 return sample 17 end function 18 function BuildDecisionTree(S, F) 19 if StoppingCriteriaMet(S) then 20 return a leaf node with the mean of y-values in S 21 end if 22 23 best_split ← FindBestSplit(S, F) 24 left_subtree ← BuildDecisionTree(S where instances match left side of best_split, F) 25 right_subtree ← BuildDecisionTree(S where instances match right side of best_split, F) 26 27 return a node representing best_split with left_subtree and right_subtree as children 28 end function 29 function FindBestSplit(S, F) 30 best_score ← infinity//Initialize with a very high value since we’re looking to minimize error for regression 31 best_feature ← null 32 best_threshold ← null 33 34 for each feature f in F do 35 for each value v in f do 36 left_subset, right_subset ← SplitData(S, f, v) 37 current_score ← CalculateMSE(left_subset) + CalculateMSE(right_subset) 38 39 if current_score < best_score then 40 best_score ← current_score 41 best_feature ← f 42 best_threshold ← v 43 end if 44 end for 45 end for 46 47 return best_feature and best_threshold as the best split 48 end function 49 function CalculateMSE(subset) 50 mean_value ← Calculate mean of y-values in subset 51 mse ← Mean of (y_i - mean_value)^2 for each instance in subset 52 return mse 53 end function |
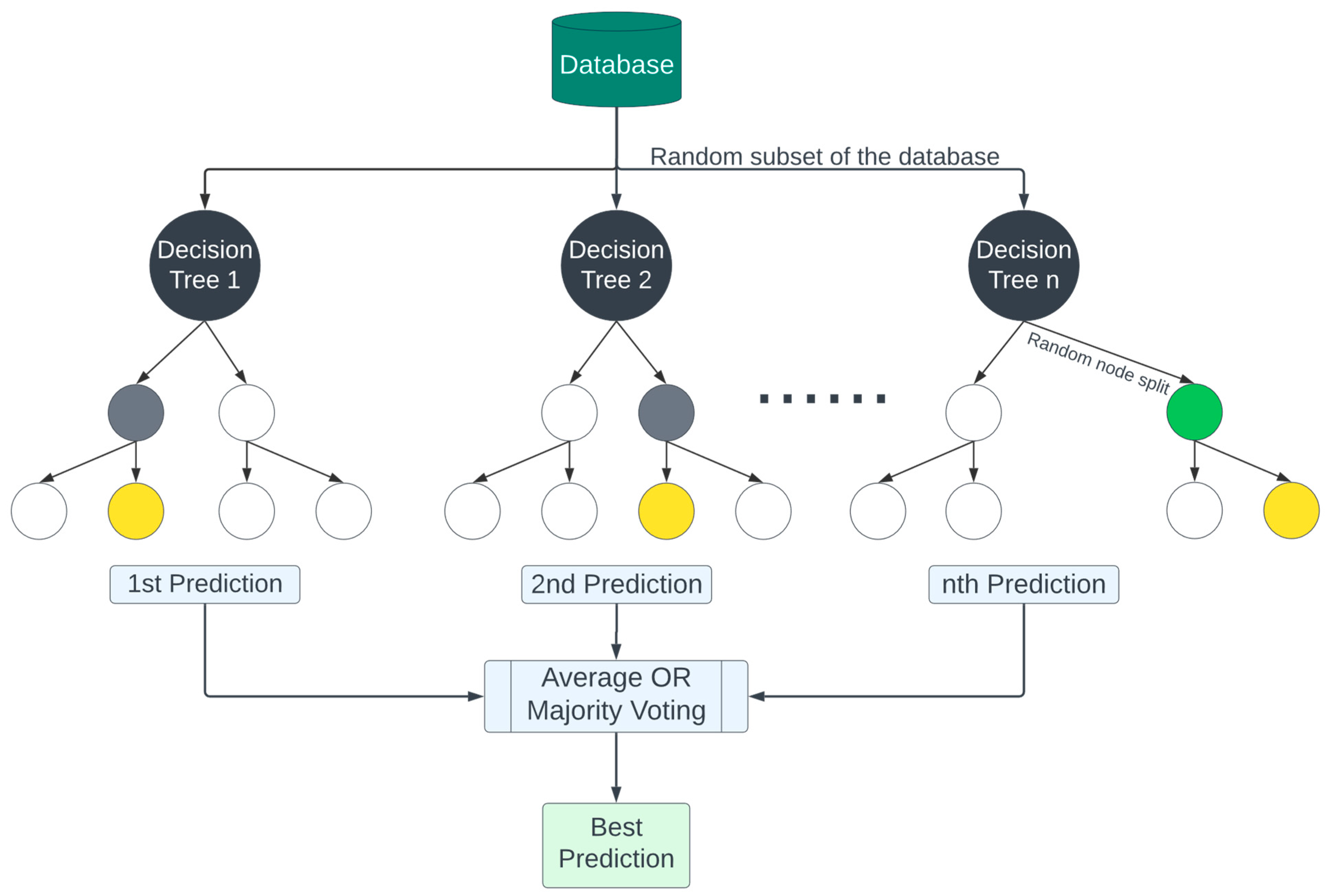
3.1.2. Extremely Randomized Trees (Extra Trees)
| Algorithm 2 Pseudocode algorithm for extra trees |
| Precondition: A training set S:= (X_train, y_train), features F, and number of trees in forest B. 1 function Extra TreesRegression(S, F, B) 2 H ← empty list // This will store all the individual trees 3 for i ∈ 1, …, B do 4 S(i) ← BootstrapSample(S)//Generate a bootstrap sample from the original dataset 5 tree ← BuildDecisionTree(S(i), F) 6 Append tree to H 7 end for 8 return H//Return the ensemble of trees 9 end function 10 function BootstrapSample(S) 11 sample ← empty list 12 for i ∈ 1, …, length(S) do 13 s ← Randomly select an instance from S with replacement 14 Append s to sample 15 end for 16 return sample 17 end function 18 function BuildDecisionTree(S, F) 19 if StoppingCriteriaMet(S) then 20 return a leaf node with the mean of y-values in S 21 end if 22 23 random_split ← FindRandomSplit(S, F) 24 left_subtree ← BuildDecisionTree(S where instances match left side of random_split, F) 25 right_subtree ← BuildDecisionTree(S where instances match right side of random_split, F) 26 27 return a node representing random_split with left_subtree and right_subtree as children 28 end function 29 function FindRandomSplit(S, F) 30 random_feature ← Randomly select a feature from F 31 random_threshold ← Randomly select a value from random_feature’s values in S 32 33 return random_feature and random_threshold as the random split 34 end function 35 function CalculateMSE(subset) 36 mean_value ← Calculate mean of y-values in subset 37 mse ← Mean of (y_i-mean_value)^2 for each instance in subset 38 return mse 39 end function |
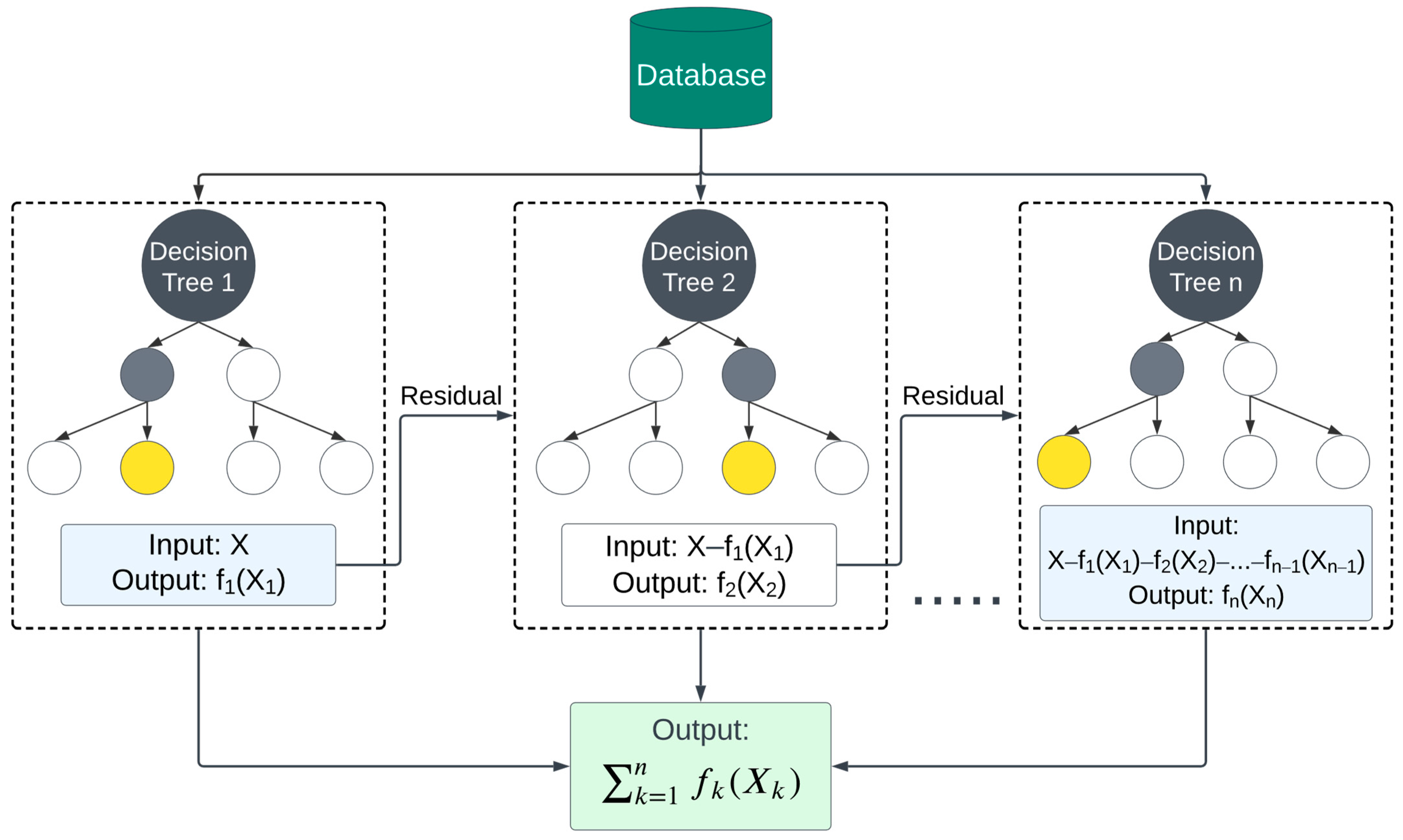
3.1.3. Extreme Gradient Boosting (XGBoost)
- Loss Function: This part measures the difference between the predicted value () and the actual value () across all n training samples. The loss function () can be any differentiable function that quantifies the error of the model’s predictions.
| Algorithm 3 Pseudocode algorithm for extreme gradient boosting |
| Precondition: A training set S:= (X_train,y_train), features F, and number of boosting rounds R. 1 function XGBoostRegression(S, F, R) 2 Initialize predictions P for all instances in S to a constant value (often the mean of y in S) 3 for r ∈ 1, …, R do 4 Compute the negative gradients (residuals) D based on the current predictions P and true y-values 5 tree ← BuildDecisionTree(S, F, D) 6 Update predictions P using the tree’s output values and a learning rate 7 end for 8 return Final model with R trees 9 end function 10 function BuildDecisionTree(S, F, D) 11 if Depth reaches maximum or other stopping criteria are met then 12 return a leaf node with the value that minimizes the objective (loss) function over D 13 end if 14 15 best_split ← FindBestSplit(S, F, D) 16 left_subtree ← BuildDecisionTree(S where instances match left side of best_split, F, D) 17 right_subtree ← BuildDecisionTree(S where instances match right side of best_split, F, D) 18 19 return a node representing best_split with left_subtree and right_subtree as children 20 end function 21 function FindBestSplit(S, F, D) 22 best_gain ← -infinity 23 best_feature ← null 24 best_threshold ← null 25 26 for each feature f in F do 27 for each value v in f do 28 Compute the gain (reduction in loss) if we split on feature f at value v over D 29 if computed_gain > best_gain then 30 best_gain ← computed_gain 31 best_feature ← f 32 best_threshold ← v 33 end if 34 end for 35 end for 36 37 return best_feature and best_threshold as the best split 38 end function |
3.2. Model Comparison
3.3. Optimization Methods
- is the mean function estimating the expected performance metric for hyperparameters;
- represents the model’s uncertainty about the objective function’s value at hyperparameters , derived from the GP’s overall covariance structure, as determined by the kernel function .
- and are two points in the hyperparameter space;
- is the Euclidean norm (or L2 norm) of a vector between and ;
- is the length scale parameter, which determines how quickly the correlation between points decreases with distance. This parameter plays a crucial role in controlling the GP’s flexibility. A small makes the GP sensitive to small changes in the input space, leading to a wigglier function. Conversely, a large results in a smoother function.
- is the predictive mean of given by the GP;
- is the predictive standard deviation of given by the GP;
- is the cumulative distribution function (CDF) of the standard normal distribution, contributing to the expectation calculation by integrating over all possible improvements;
- is the probability density function (PDF) of the standard normal distribution, contributing to the expectation of improvement by weighing the magnitude of the potential improvement;
- is a standardized measure that allows the EI formula to balance the potential for improvement (exploitation) against the uncertainty of that improvement (exploration), given as follows:
3.4. Evaluation Criteria
- Data cleaning and preparation: The initial dataset may contain missing values, outliers, or other errors that can affect the model’s performance. Data cleaning involves identifying and correcting these issues to ensure that the data is consistent and accurate.
- Feature input selection: machine learning models rely on input features to make predictions. Feature input selection involves selecting the most relevant features that have the highest impact on the model’s performance. The authors performed MIFS and correlation matrix analysis for the feature selection purpose.
- Hyperparameter tuning: Three different approaches, including randomized search, grid search, and Bayesian, were conducted to select the optimal combination of parameters for each model.
- Fitting: Once the optimal hyperparameters and algorithm have been constructed, the model can be fitted to the data. Also, 80% of the data was used for training, and the remaining 20% was utilized for testing. The training and testing sets were consistently maintained across all models fitting and evaluations processes to ensure uniformity and comparability between different models.
- Validation: To ensure that the model is accurate and reliable, it is essential to validate the results by introducing testing subsets of the dataset to check its performance.
- Performance Evaluation: MAE and R2 were evaluated to choose the best-performing models in terms of prediction accuracy for both training and testing datasets.
4. Results
4.1. Random Forest
4.2. Extremely Randomized Trees (Extra Trees)
4.3. Extreme Gradient Boosting (XGBoost)
5. Discussion
6. Conclusions
- To create a unified database, a unique SQL script was created that links various tables extracted from the original LTPP dataset.
- The mutual information feature selection was applied to narrow down the dimension of input by removing variables that did not contribute to model improvement. The scatterplot matrix revealed no significant correlations among the variables, underscoring the complexity and varied nature of the factors influencing pavement performance.
- The ensemble learning techniques instantly outperformed linear regression methods, demonstrating the capabilities of advanced machine learning technologies.
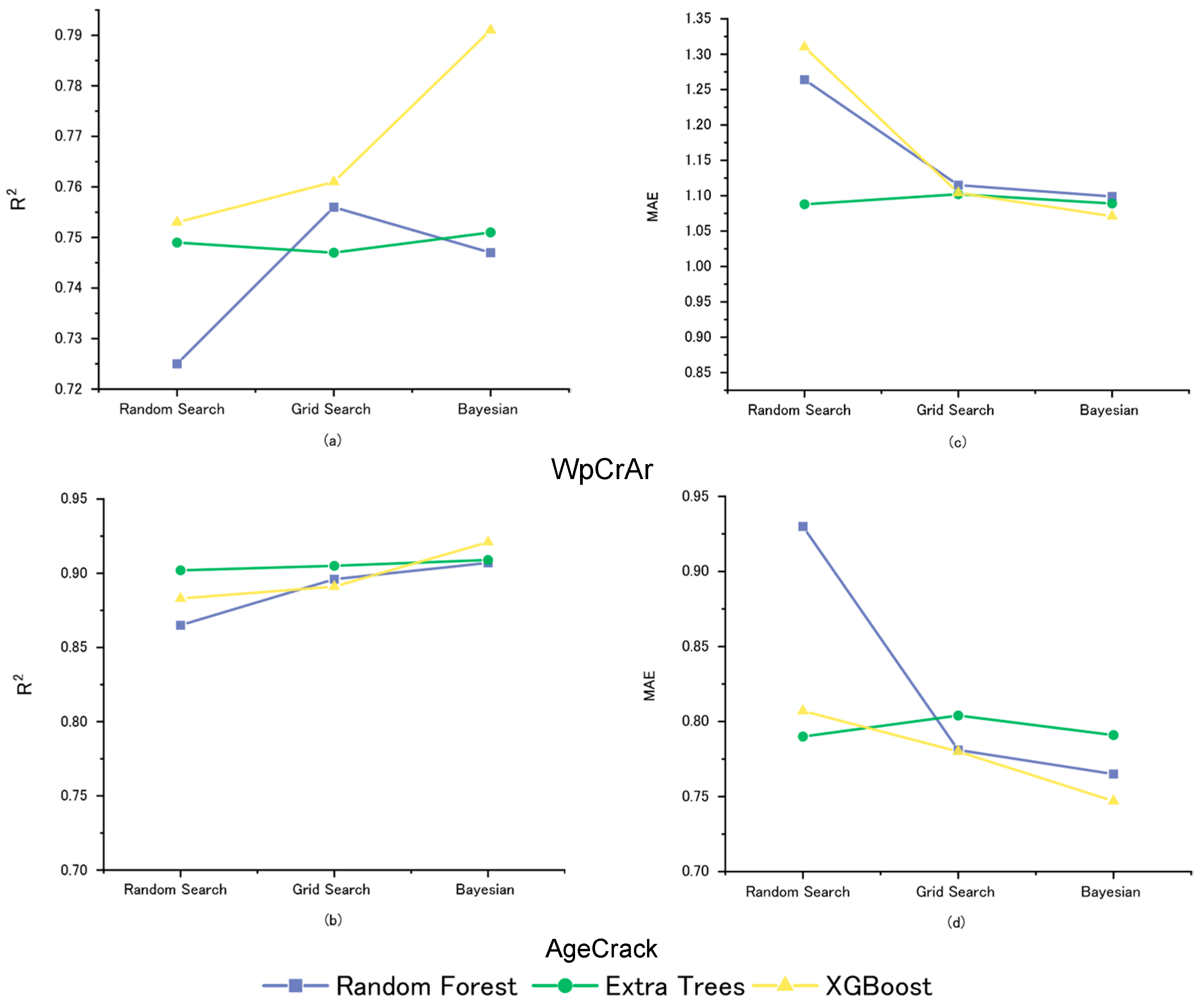
- To achieve an even better prediction performance, three different optimization algorithms, namely, random search, grid search, and Bayesian, were evaluated, resulting in a total of nine models with various hyperparameter settings. The Bayesian optimization approach offers the best balance between training and testing in terms of prediction accuracy, as well as computational efficiency.
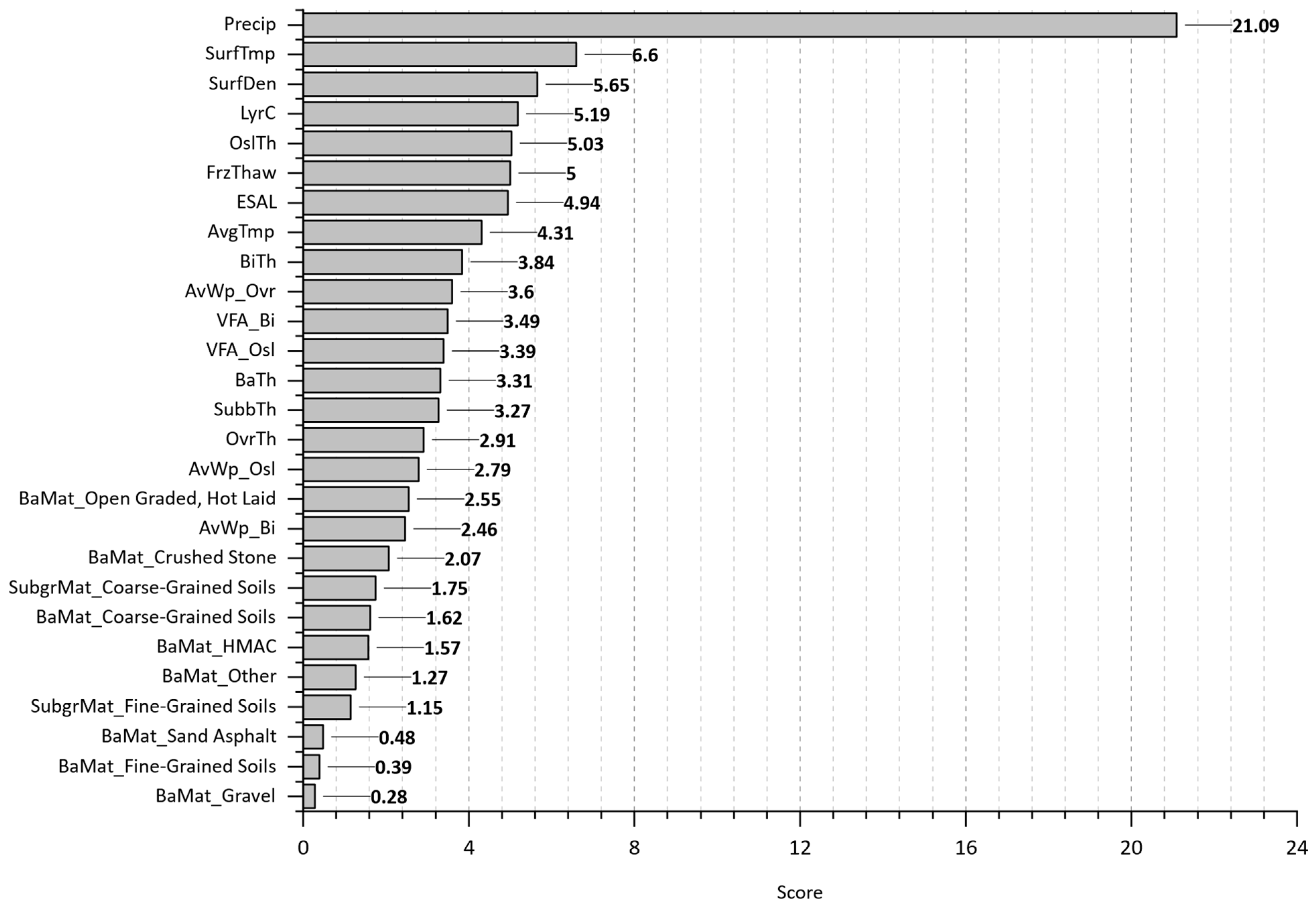
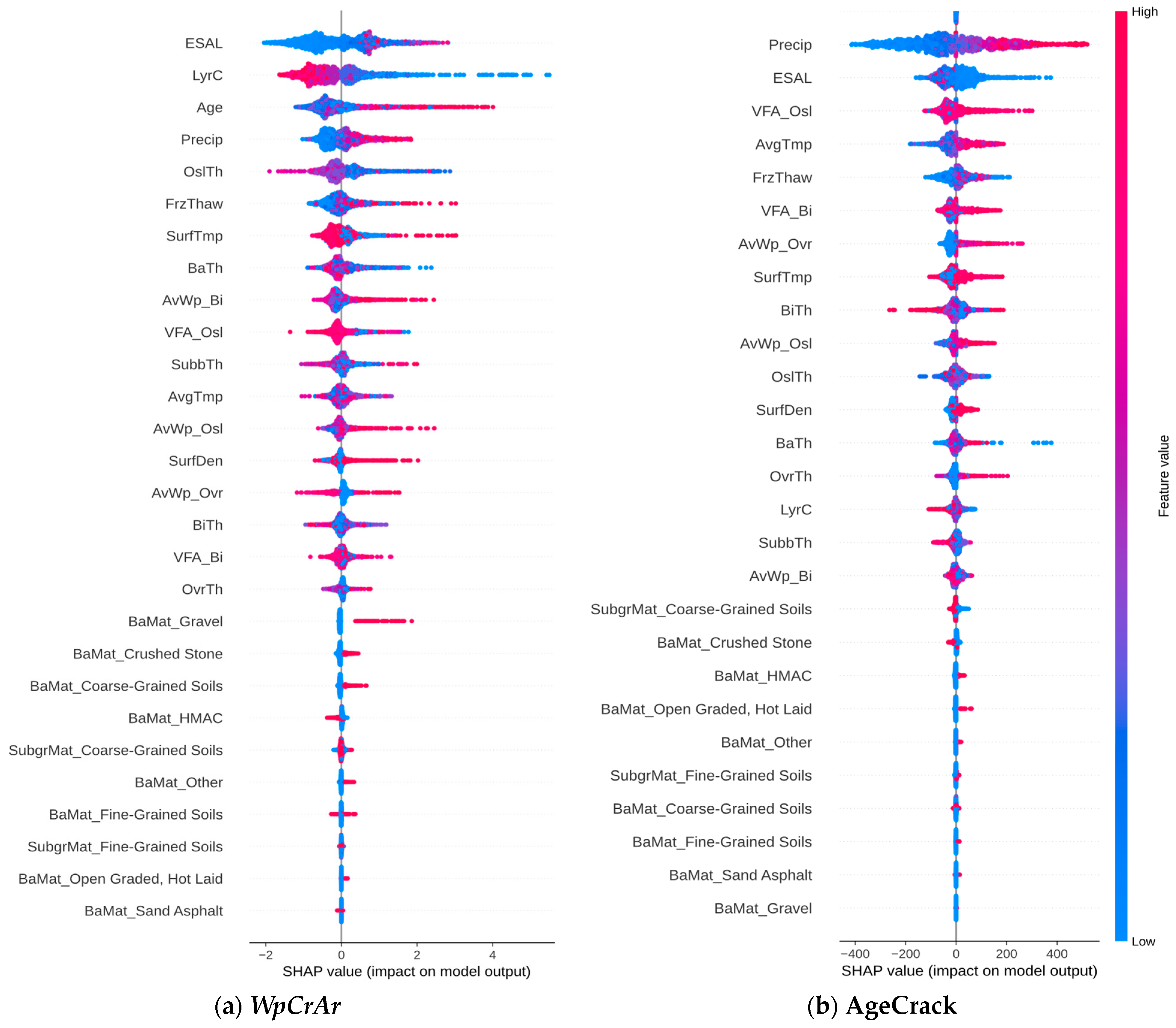
- The most significant features that substantially affect the initiation and progression of cracking over time were identified.
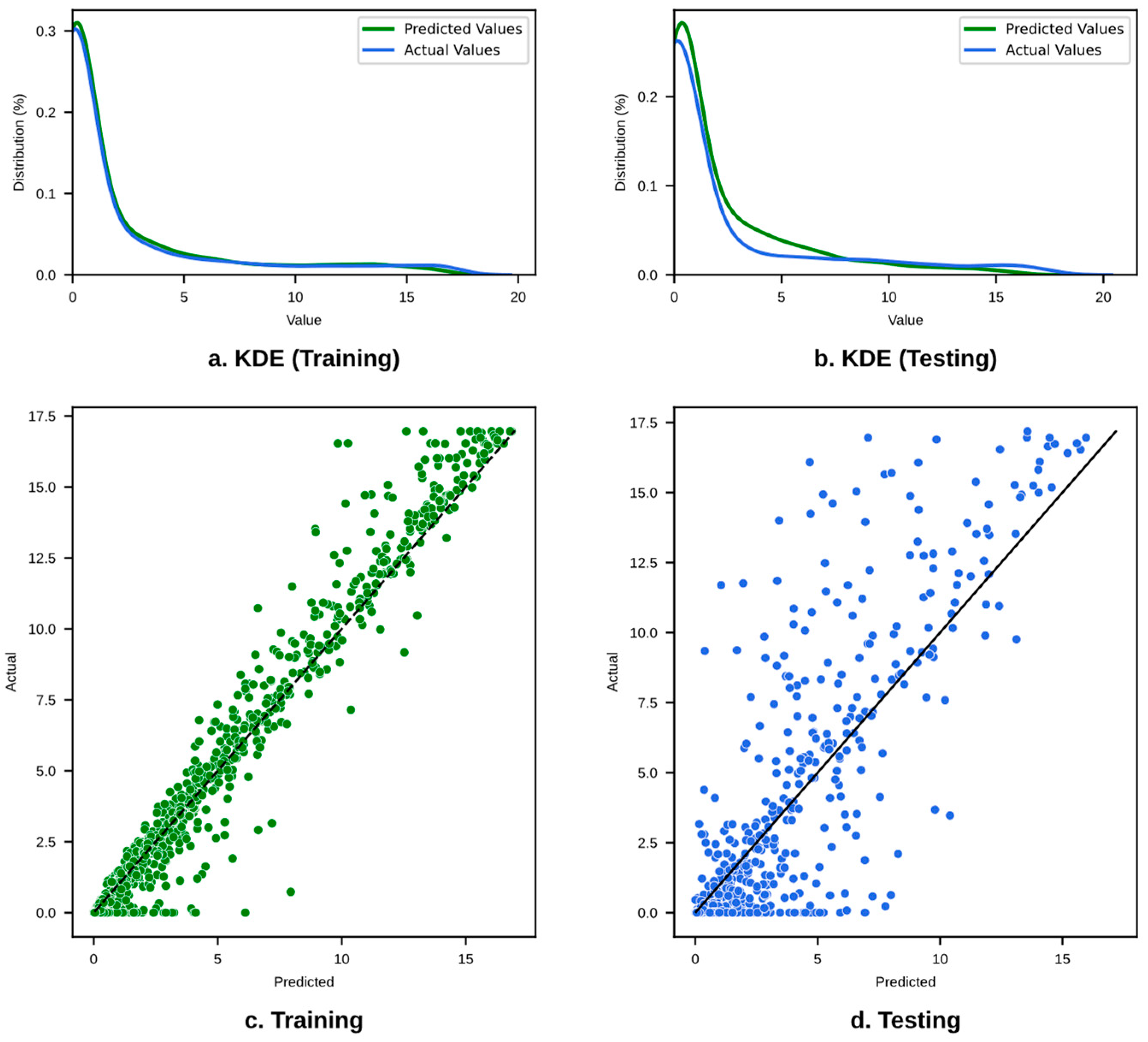
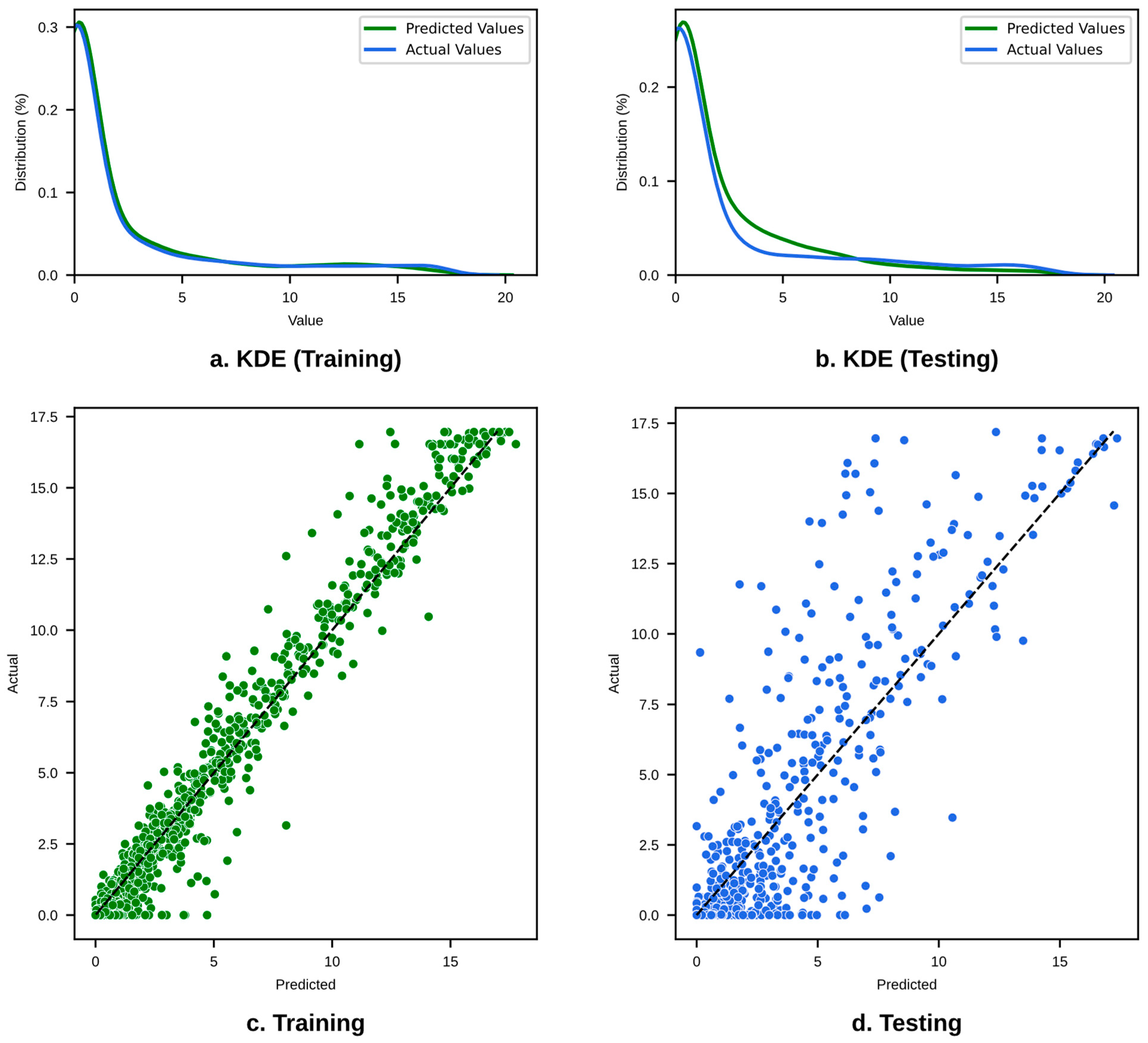
- For WpCrAr, the XGBoost model optimized using the Bayesian method appears to be the superior option, with the lowest errors (MSE = 3.862, MAE = 1.071) and the highest R2 scores in both training (0.983) and testing (0.791).
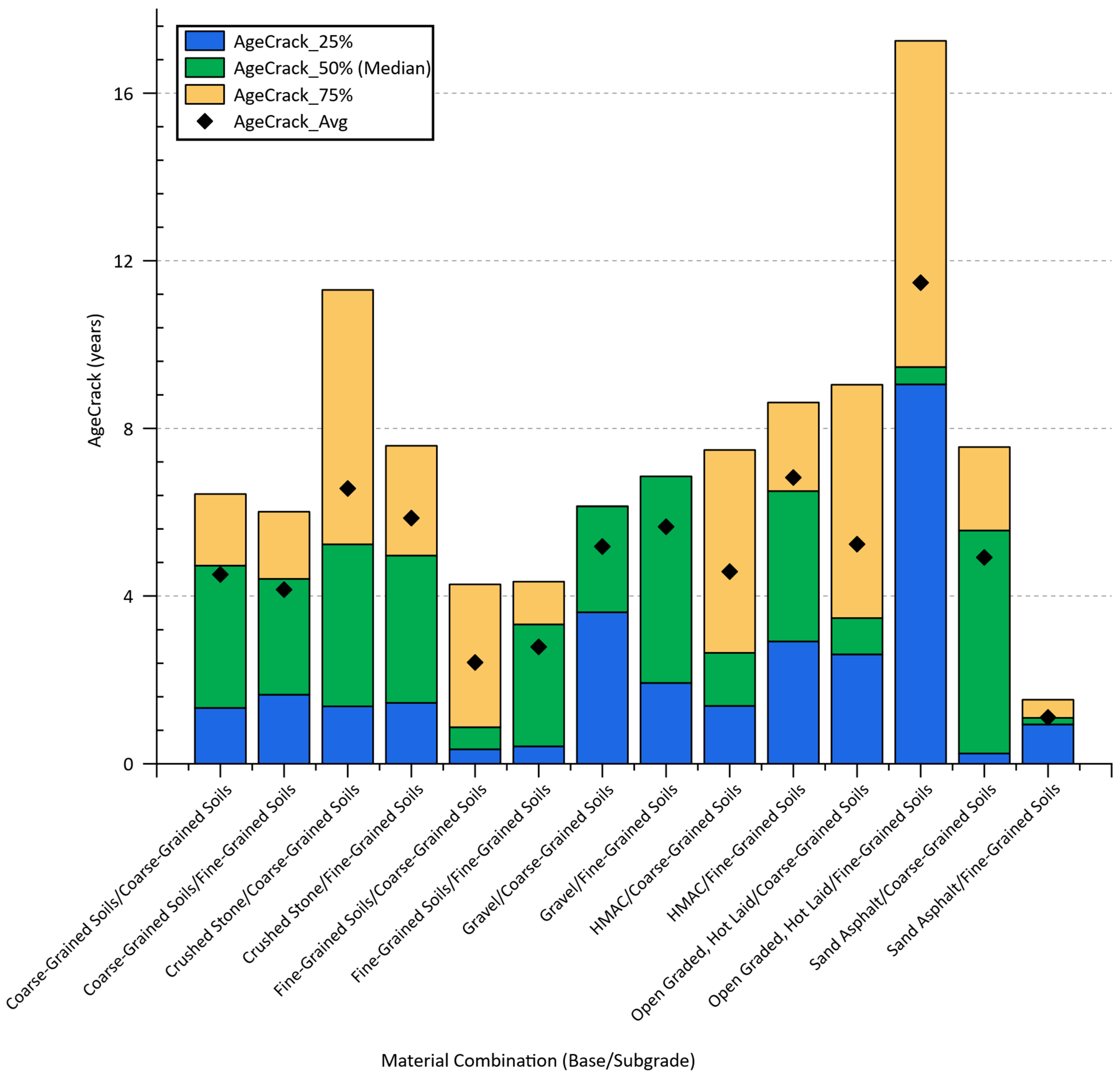
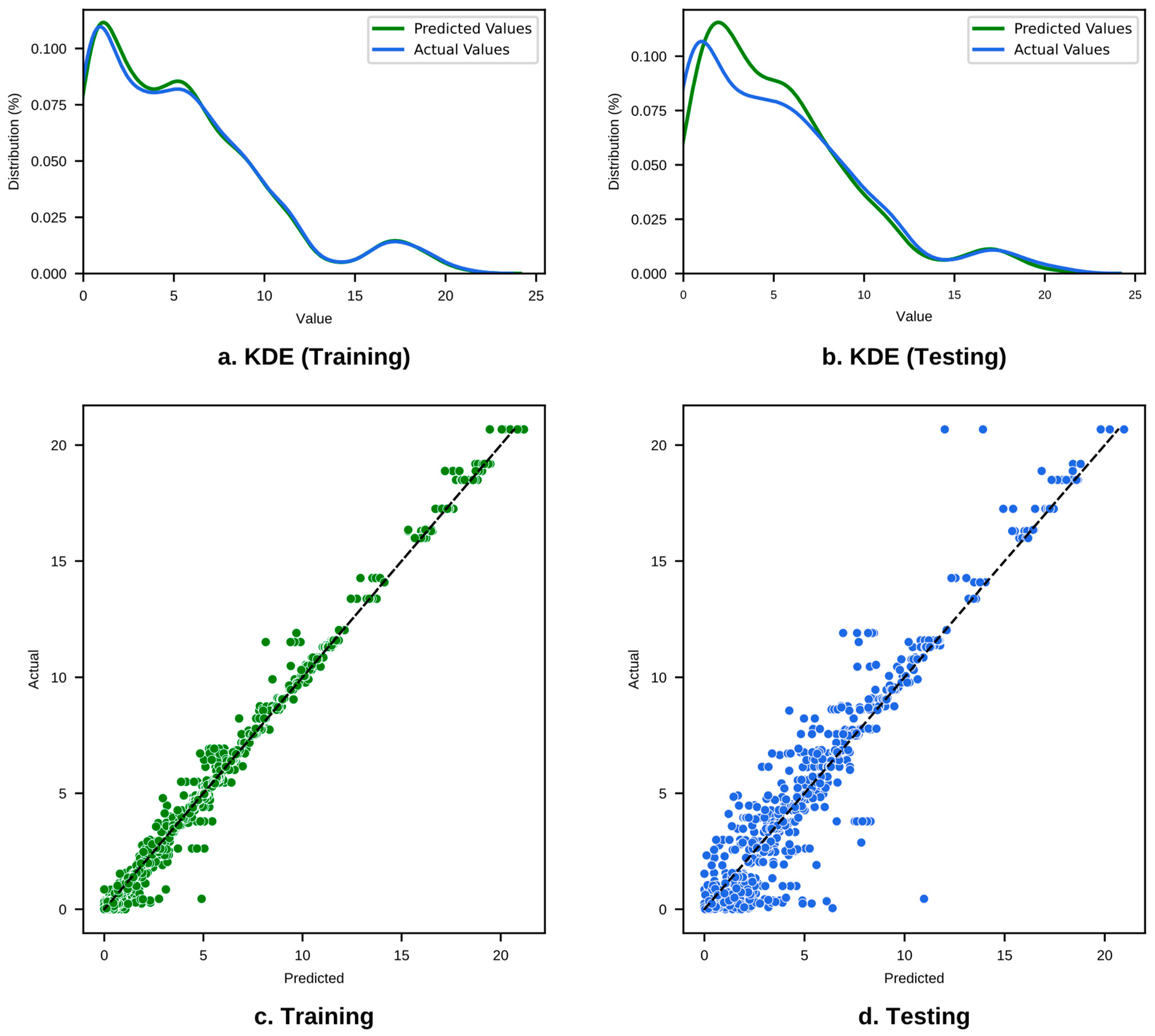
- For AgeCrack, the XGBoost model also achieved the highest prediction accuracy, with an R2 value of 0.921 and the lowest error metrics (MSE = 1.603, MAE = 0.747, RMSE = 1.266), proving its reliability and consistency.
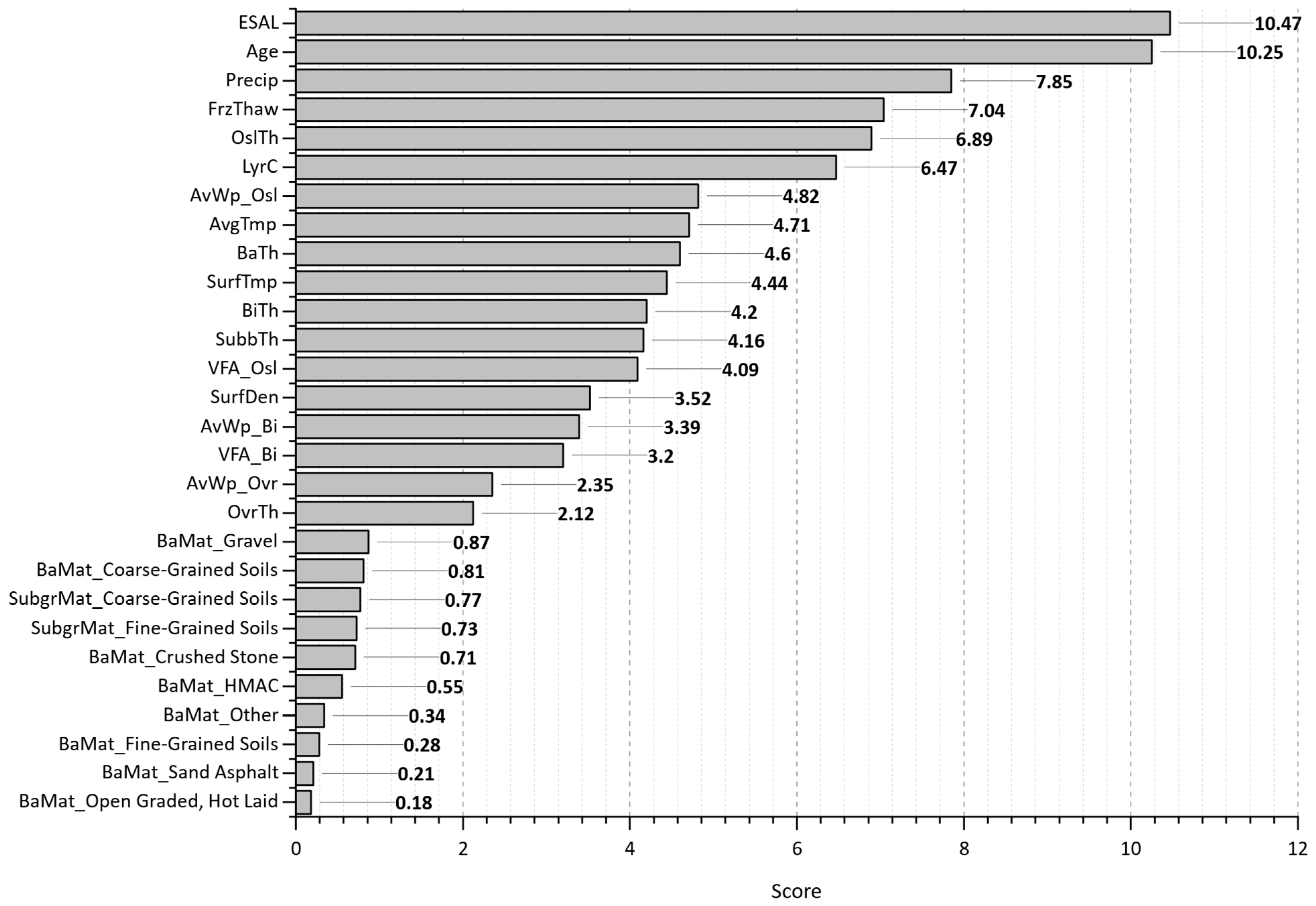
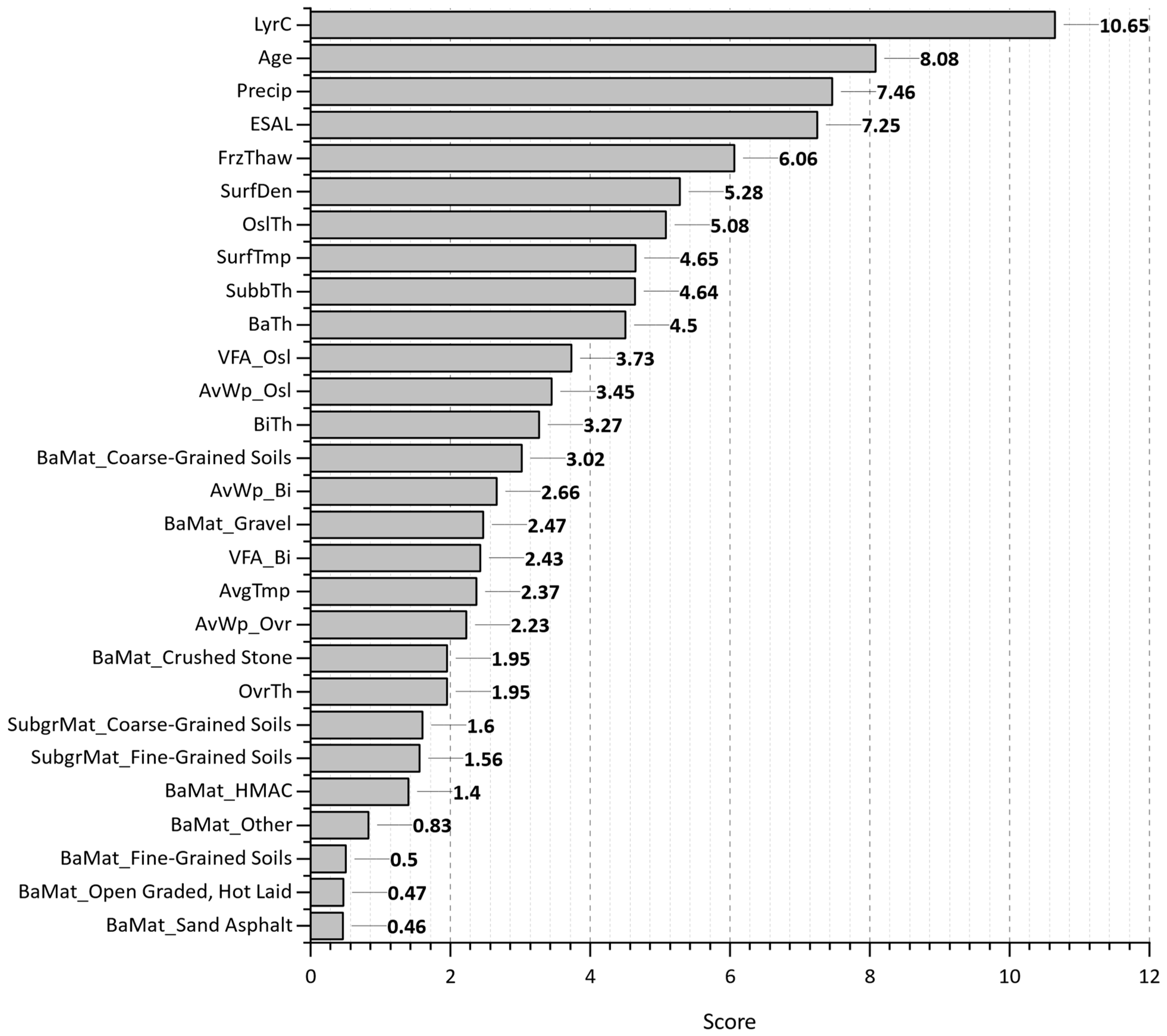
- Evaluating the best-trained models on WpCrAr (III, VI, VIII) revealed that ESALs have been proven to be of the highest importance, despite displaying a surprising negative Pearson correlation in the scatterplot matrix. In contrast to the correlation analysis, the finding from the machine learning models output aligns significantly better with the expected reality that traffic loads cause pavement deterioration. The XGBoost model also revealed that pavement sections with a higher number of layers and deeper original surface layers experienced lower crack propagation.
- Future studies could focus on developing models that include more material data such as stress–strain relationships or mean asphalt content in the pavement surface layer. This would involve incorporating the principles of material science and the mechanics of cracking to better understand the conditions leading to cracking and employing neural network models, especially physics-informed models that are specifically trained not only on data but also on the underlying physical laws governing pavement deterioration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghasemi, P. Application of Optimization and Machine Learning Techniques in Predicting Pavement Performance and Performance-Based Pavement Design. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2019. [Google Scholar]
- Cano-Ortiz, S.; Pascual-Muñoz, P.; Castro-Fresno, D. Machine learning algorithms for monitoring pavement performance. Autom. Constr. 2022, 139, 104309. [Google Scholar] [CrossRef]
- Kang, J. Pavement Performance Prediction Using Machine Learning and Instrumentation in Smart Pavement. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2022. [Google Scholar]
- Sholevar, N.; Golroo, A.; Esfahani, S.R. Machine learning techniques for pavement condition evaluation. Autom. Constr. 2022, 136, 104190. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.I.; Leung, A.A.; Walker, R.L.; Sikdar, K.C.; O’Beirne, M.; Quan, H.; Turin, T.C. A comparison of machine learning algorithms and traditional regression-based statistical modeling for predicting hypertension incidence in a Canadian population. Sci. Rep. 2023, 13, 13. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Fan, J.; Han, F.; Liu, H. Challenges of Big Data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef]
- Dong, J.; Meng, W.; Liu, Y.; Ti, J. A Framework of Pavement Management System Based on IoT and Big Data. Adv. Eng. Inform. 2021, 47, 101226. [Google Scholar] [CrossRef]
- Asghari, V.; Kazemi, M.H.; Shahrokhishahraki, M.; Tang, P.; Alvanchi, A.; Hsu, S.-C. Process-oriented guidelines for systematic improvement of supervised learning research in construction engineering. Adv. Eng. Inform. 2023, 58, 102215. [Google Scholar] [CrossRef]
- Mohmd Sarireh, D. Causes of Cracks and Deterioration of Pavement on Highways in Jordan from Contractors’ Perspective. 2013, 3. Available online: www.iiste.org (accessed on 10 November 2023).
- Gurule, A.; Ahire, T.; Ghodke, A.; Mujumdar, N.P.; Ahire, G.D. Investigation on Causes of Pavement Failure and Its Remedial Measures. 2022. Available online: www.ijraset.com (accessed on 25 March 2023).
- Milling, A.; Martin, H.; Mwasha, A. Design, Construction, and In-Service Causes of Premature Pavement Deterioration: A Fuzzy Delphi Application. J. Transp. Eng. Part B Pavements 2023, 149, 05022004. [Google Scholar] [CrossRef]
- Rulian, B.; Hakan, Y.; Salma, S.; Yacoub, N. Pavement Performance Modeling Considering Maintenance and Rehabilitation for Composite Pavements in the LTPP Wet Non-Freeze Region Using Neural Networks. In International Conference on Transportation and Development; Pavements: Middleton, MA, USA, 2022. [Google Scholar]
- Qiao, Y.; Dawson, A.R.; Parry, T.; Flintsch, G.; Wang, W. Flexible pavements and climate change: A comprehensive review and implication. Sustainability 2020, 12, 1057. [Google Scholar] [CrossRef]
- Yu-Shan, A.; Shakiba, M. Flooded Pavement: Numerical Investigation of Saturation Effects on Asphalt Pavement Structures. J. Transp. Eng. Part B Pavements 2021, 147, 04021025. [Google Scholar] [CrossRef]
- Degu, D.; Fayissa, B.; Geremew, A.; Chala, G. Investigating Causes of Flexible Pavement Failure: A Case Study of the Bako to Nekemte Road, Oromia, Ethiopia. J. Civ. Eng. Sci. Technol. 2022, 13, 112–135. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Z. LTPP data-based investigation on asphalt pavement performance using geospatial hot spot analysis and decision tree models. Int. J. Transp. Sci. Technol. 2022, 12, 606–627. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic Road Crack Detection Using Random Structured Forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Fan, L.; Wang, D.; Wang, J.; Li, Y.; Cao, Y.; Liu, Y.; Chen, X.; Wang, Y. Pavement Defect Detection with Deep Learning: A Comprehensive Survey. IEEE Trans. Intell. Veh. 2024, 1–21. [Google Scholar] [CrossRef]
- Tamagusko, T.; Ferreira, A. Machine Learning for Prediction of the International Roughness Index on Flexible Pavements: A Review, Challenges, and Future Directions. Infrastructures 2023, 8, 170. [Google Scholar] [CrossRef]
- Luo, X.; Wang, F.; Bhandari, S.; Wang, N.; Qiu, X. Effectiveness evaluation and influencing factor analysis of pavement seal coat treatments using random forests. Constr. Build. Mater. 2021, 282, 122688. [Google Scholar] [CrossRef]
- Alnaqbi, A.J.; Zeiada, W.; Al-Khateeb, G.G.; Hamad, K.; Barakat, S. Creating Rutting Prediction Models through Machine Learning Techniques Utilizing the Long-Term Pavement Performance Database. Sustainability 2023, 15, 13653. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Hu, W.; Polaczyk, P.A.; Huang, B. Investigating impacts of asphalt mixture properties on pavement performance using LTPP data through random forests. Constr. Build. Mater. 2019, 204, 203–212. [Google Scholar] [CrossRef]
- Li, M.; Dai, Q.; Su, P.; You, Z.; Ma, Y. Surface layer modulus prediction of asphalt pavement based on LTPP database and machine learning for Mechanical-Empirical rehabilitation design applications. Constr. Build. Mater. 2022, 344, 128303. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Tran, V.Q. Data-driven approach for investigating and predicting rutting depth of asphalt concrete containing reclaimed asphalt pavement. Constr. Build. Mater. 2023, 377, 131116. [Google Scholar] [CrossRef]
- Zhang, M.; Gong, H.; Jia, X.; Xiao, R.; Jiang, X.; Ma, Y.; Huang, B. Analysis of critical factors to asphalt overlay performance using gradient boosted models. Constr. Build. Mater. 2020, 262, 120083. [Google Scholar] [CrossRef]
- Leong, P. Using LTPP Data to Develop Spring Load Restrictions: A Pilot Study; AISIM: Waterloo, ON, Canada, 2005. [Google Scholar]
- Inkoom, S.; Sobanjo, J.O.; Chicken, E.; Sinha, D.; Niu, X. Assessment of Deterioration of Highway Pavement using Bayesian Survival Model. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 310–325. [Google Scholar] [CrossRef]
- Meng, S.; Bai, Q.; Chen, L.; Hu, A. Multiobjective Optimization Method for Pavement Segment Grouping in Multiyear Network-Level Planning of Maintenance and Rehabilitation. J. Infrastruct. Syst. 2023, 29, 04022047. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, X.; Cheng, J.; Yang, S.; Ma, Y. Establishment of probabilistic prediction models for pavement deterioration based on Bayesian neural network. Int. J. Pavement Eng. 2023, 24, 2076854. [Google Scholar] [CrossRef]
- Aldabbas, L.J. Empirical Models Investigation of Pavement Management for Advancing the Road’s Planning Using Predictive Maintenance. Civ. Eng. Archit. 2023, 11, 1346–1354. [Google Scholar] [CrossRef]
- Mers, M.; Yang, Z.; Hsieh, Y.A.; Tsai, Y. Recurrent Neural Networks for Pavement Performance Forecasting: Review and Model Performance Comparison. Transp. Res. Rec. J. Transp. Res. Board 2023, 2677, 610–624. [Google Scholar] [CrossRef]
- Perkins, R.; Couto, C.D.; Costin, A. Data Integration and Innovation: The Future of the Construction, Infrastructure, and Transportation Industries. Future Inf. Exch. Interoperability 2019, 85, 85–94. [Google Scholar]
- Costin, A.; Adibfar, A.; Hu, H.; Chen, S.S. Building Information Modeling (BIM) for Transportation Infrastructure—Literature Review, Applications, Challenges, and Recommendations. Autom. Constr. 2018, 94, 257–281. [Google Scholar] [CrossRef]
- Wasiq, S.; Golroo, A. Smartphone-Based Cost-Effective Pavement Performance Model Development Using a Machine Learning Technique with Limited Data. Infrastructures 2024, 9, 9. [Google Scholar] [CrossRef]
- Sujon, M.A. Weigh-in-Motion Data-Driven Pavement Performance Prediction Models. Ph.D. Thesis, West Virginia University Libraries, Morgantown, WV, USA, 2023. [Google Scholar] [CrossRef]
- Guan, J.; Yang, X.; Liu, P.; Oeser, M.; Hong, H.; Li, Y.; Dong, S. Multi-scale asphalt pavement deformation detection and measurement based on machine learning of full field-of-view digital surface data. Transp. Res. Part C Emerg. Technol. 2023, 152, 104177. [Google Scholar] [CrossRef]
- Guo, X.; Wang, N.; Li, Y. Enhancing pavement maintenance: A deep learning model for accurate prediction and early detection of pavement structural damage. Constr. Build Mater. 2023, 409, 133970. [Google Scholar] [CrossRef]
- Ker, H.W.; Lee, Y.H.; Wu, P.H. Development of Fatigue Cracking Performance Prediction Models for Flexible Pavements Using LTPP Database. In Proceedings of the Transportation Research Board 86th Annual Meeting Compendium of Papers (CD-ROM), Transportation Research Board, Washington, DC, USA, 21–25 January 2007. [Google Scholar]
- Radwan, M.; Abo-Hashema, M.; Hashem, M. Modeling Pavement Performance Based on LTPP Database for Flexible Pavements. Teknik. Dergi. 2020, 31, 10127–10146. [Google Scholar] [CrossRef]
- Alnaqbi, A.J.; Zeiada, W.; Al-Khateeb, G.; Abttan, A.; Abuzwidah, M. Predictive models for flexible pavement fatigue cracking based on machine learning. Transp. Eng. 2024, 16, 100243. [Google Scholar] [CrossRef]
- Marasteanu, M.; Zofka, A.; Turos, M.; Li, X.; Velasquez, R.; Li, X.; Buttlar, W.; Paulino, G.; Braham, A.; Dave, E.; et al. Investigation of Low Temperature Cracking in Asphalt Pavements, Minnesota Department of Transportation. 2007. Available online: http://www.lrrb.org/PDF/200743.pdf (accessed on 15 February 2022).
- Luo, S.; Bai, T.; Guo, M.; Wei, Y.; Ma, W. Impact of Freeze–Thaw Cycles on the Long-Term Performance of Concrete Pavement and Related Improvement Measures: A Review. Materials 2022, 15, 4568. [Google Scholar] [CrossRef] [PubMed]
- Amarasiri, S.; Muhunthan, B. Evaluating Performance Jumps for Pavement Preventive Maintenance Treatments in Wet Freeze Climates Using Artificial Neural Network. J. Transp. Eng. Part B Pavements 2022, 148, 04022008. [Google Scholar] [CrossRef]
- Cary, C.E.; Zapata, C.E. Resilient Modulus for Unsaturated Unbound Materials. Road Mater. Pavement Des. 2011, 12, 615–638. [Google Scholar] [CrossRef]
- Kandhal, P.S.; Cooley, L.A., Jr. Loaded Wheel Testers in the United States: State of the Practice. Transp. Res. Rec. 2000. Available online: https://www.eng.auburn.edu/research/centers/ncat/files/technical-reports/rep00-04.pdf (accessed on 30 June 2023).
- Nodes, J. Impact of Incentives on In-Place Air Voids, Transportation Research Board. 2006. Available online: www.TRB.org (accessed on 12 December 2022).
- Brown, E.R.; Brunton, J.M. An Introduction to the Analytical Design of Bituminous Pavements, Transportation Research Board 1980. Available online: https://trid.trb.org/View/164432 (accessed on 15 April 2023).
- Kandhal, P.S.; Mallick, R.B. Open Graded Asphalt Friction Course: State of the Practice; National Center for Asphalt Technology: Auburn, AL, USA, 1988. [Google Scholar]
- Roberts, F.L.; Kandhal, P.S.; Brown, E.R.; Lee, D.Y.; Kennedy, T.W. Hot Mix Asphalt Materials, Mixture Design and Construction; NAPA Research and Education Foundation: Lanham, MD, USA, 1996. [Google Scholar]
- Dong, S.; Zhong, J.; Hao, P.; Zhang, W.; Chen, J.; Lei, Y.; Schneider, A. Mining multiple association rules in LTPP database: An analysis of asphalt pavement thermal cracking distress. Constr. Build. Mater. 2018, 191, 837–852. [Google Scholar] [CrossRef]
- Battiti, R. Using Mutual Information for Selecting Features in Supervised Neural Net Learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning: Adaptive Computation and Machine Learning Series; The MIT Press: Cambridge, MA, USA, 2016; Available online: https://mitpress.mit.edu/9780262337373/deep-learning/ (accessed on 2 March 2023).
- Bhandari, S.; Luo, X.; Wang, F. Understanding the effects of structural factors and traffic loading on flexible pavement performance. Int. J. Transp. Sci. Technol. 2022, 12, 258–272. [Google Scholar] [CrossRef]
- Bergstra, J.; Ca, J.B.; Ca, Y.B. Random Search for Hyper-Parameter Optimization Yoshua Bengio. 2012. Available online: http://scikit-learn.sourceforge.net (accessed on 17 January 2022).
- Kohavi, R.; John, G.H. Automatic Parameter Selection by Minimizing Estimated Error. In Machine Learning Proceedings 1995; Elsevier: Amsterdam, The Netherlands, 1995; pp. 304–312. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]






| Models | Considered Factors | Accuracy | Year | References | ||
|---|---|---|---|---|---|---|
| 1 | Poisson loglinear model | 1. Viscosity of the AC layer. 2. Min and Max mean annual temperature. 3. Average Annual Precipitation. | R2 = 0.47 | 2007 | Ker, H. et al. [39] | |
| 2 | Generalized additive mode | 1. Age. 2. ESAL. 3. Average Annual Precipitation. 4. Average Annual Temperature. 5. Critical tensile strain. 6. Annual freeze–thaw cycle. | R2 = 0.49 | 2007 | Ker, H. et al. [39] | |
| 3 | Multiple regression | 1. Pavement age since overlay. 2. Moisture content of subgrade soil. 3. Climate data. | R2 = 0.88 | 2020 | Radwan et al. [40] | |
| 4 | Machine Learning | 1. Age. 2. ESAL. 3. Average annual precipitation. 4. Average annual temperature. 5. Average annual daily traffic. 6. Average annual Daily Truck Traffic. 7. Annual freeze index. 8. International roughness index. | 9. Total Thickness. 10. Moisture Content. 11. Annual Average Wind Velocity. 12. Climate Zone. 13. Resilient Modulus. 14. Annual Average Humidity. 15. Air Voids. 16. Min and Max Humidity. 17. Marshal stability. | R2 = 0.71 | 2024 | Alnaqbi et al. [41] |
| Category | Acronym | Feature | Description | Range|Unit | |
|---|---|---|---|---|---|
| 1 | Pavement Structure and Construction | CN | Construction Number | Changes in pavement structure. | 1–3|- |
| 2 | LyrC | Layer Count | The overall number of layers in a section throughout a construction number. | 3–11|- | |
| 3 | OvrTh | Overlay thickness | The thickness of the overlay layer. | 0–8|Inches | |
| 4 | OslTh | Original surface layer thickness | The thickness of the original surface layer. | 0–7.6|Inches | |
| 5 | BiTh | Binder layer thickness | The thickness of the AC layer below the surface (Binder Course). | 0–13.4|Inches | |
| 6 | BaTh | Base layer thickness | The thickness of the base layer. | 2.5–17|Inches | |
| 7 | SubbTh | Subbase layer thickness | The thickness of the subbase layer. | 0–37.8|Inches | |
| 8 | BaMat | Base layer Material | The type of material used for the base layer. | - | |
| 9 | SubgrMat | Subgrade layer Material | The type of material used for the subgrade layer. | - | |
| 10 | Construction Quality | AvWp | Wheel path air void | Average calculated air voids in the wheel path in the binder, original surface, and overlay layers. | 0–16|% |
| 11 | Den | Density | The density of the top surface layer, e.g., original surface or overlay layers. | 127–149|lb/ft3 | |
| 12 | VFA | Voids Filled Asphalt | The percentage of the total volume of the voids in the compacted aggregate that is filled with asphalt for the binder, original surface, and overlay layers. | 0–94|% | |
| 13 | VMA | Voids Mineral Aggregate | The percentage of the total volume of the voids between the mineral aggregate particles of a compacted asphalt mixture that includes the air voids and the volume of the asphalt binder not absorbed into the aggregate for the binder, original surface, and overlay layers. | 0–30|% | |
| 14 | SurfTmp | Surface Laydown Temperature | Average temperature of the asphalt concrete at lay down for original surface or overlay layers. | 200–340|℉ | |
| 15 | Climate | AvgTmp | Average Ambient Temperature | Average of the daily air temperatures 2 m above the MERRA centroid in between survey dates. | 29–86|℉ |
| 16 | Precip | Precipitation | The cumulative water equivalent of total surface precipitation over a month for each construction number. | 0–344|Inches | |
| 17 | FrzThaw | Freezing Thaw | The cumulative number of days in the month when the maximum air temperature is greater than 0 and minimum air temperature is less than 0 degrees Celsius on the same day. | 0–480|days | |
| 18 | Traffic | ESAL | Equivalent Single Axle Load | Estimated annual equivalent single axle load (ESAL) for vehicle classes 4–13 on LTPP lanes. ESAL values are cumulative traffic loading summary statistics. | 0–12e+6|- |
| 19 | In-service | Service Age | Age | The service age of a given section during one construction number period. | 0–32|Years |
| 20 | WpCrAr | Wheel path Crack per area | The wheel path cracking length divided by the area of the given section. | 0–0.2|ft/ft2 | |
| 21 | AgeCrack | Crack initiation age | Age at which the initial wheel path cracking was observed. | 0.25–20/years |
| Parameters | Resource |
|---|---|
| CPU | Intel Xeon (R) E5 2670 @ 2.60 GHz, 32 Cores |
| RAM | 32 GB DDR4 2600 MT/s |
| GPU | NVIDIA GeForce GTX 1080 Ti, with 11 GB GDDR5X Memory |
| Disk | Panasas Parallel Storage, Up to 156 TB usable in a RAID-6 configuration |
| NCU/year | 35.50 USD |
| Attributes | Random Forest | Extremely Randomized Trees | Extreme Gradient Boosting |
|---|---|---|---|
| Learning Method | Ensemble learning | Ensemble learning | Ensemble learning–Gradient boosting algorithm |
| Complexity | Low to medium | Low to medium | Medium to high |
| Interpretability | Medium | Low to medium | Low to medium |
| Scalability | High | High | Medium to high |
| Robust-ness | Medium | Medium | Medium to high |
| Versatility | High | High | High |
| Regression | Uses multiple trees; Average results for Regression | Builds trees using the whole dataset; Randomized thresholds for splits | Sequentially adds trees; Each new tree corrects predecessor errors |
| Optimization Technique | Reducing variance through averaging predictions | Reducing variance through averaging predictions | Gradient boosting with regularization terms |
| Base Learner | Decision Trees | Decision Trees | Decision Trees or Linear Models |
| Handling Missing Data | Imputation or surrogate splits | Internally | Sparsity-aware split finding |
| Features | Bayesian | Grid Search | Randomized Search |
|---|---|---|---|
| Search Type | Probabilistic | Deterministic | Stochastic |
| Accuracy | High | Medium to High | Medium |
| Computation | Fast | Slow | Medium to Fast |
| Strategy | Surrogate model-based (e.g., Gaussian process) | User-defined (applicable to various functions) | User-defined (applicable to various functions) |
| Objective function | Sequential model-based optimization | Full factorial search over specified parameter ranges | Random sampling of parameters from specified distributions |
| Advantages | Can handle noisy data | Systematic exploration of parameter space | Less computationally intensive |
| Disadvantages | Challenging to set priors | Computationally intensive, not scalable with dimensionality | May miss optimal parameters |
| Random Forest | Extra Trees | XGBoost | |||
|---|---|---|---|---|---|
| Most Important Features | WpCrAr | 1 | ESAL | LyrC | ESAL |
| 2 | Age | Age | LyrC | ||
| 3 | Precip | Precip | Age | ||
| 4 | FrzThaw | ESAL | Precip | ||
| 5 | OslTh | FrzThaw | OslTh | ||
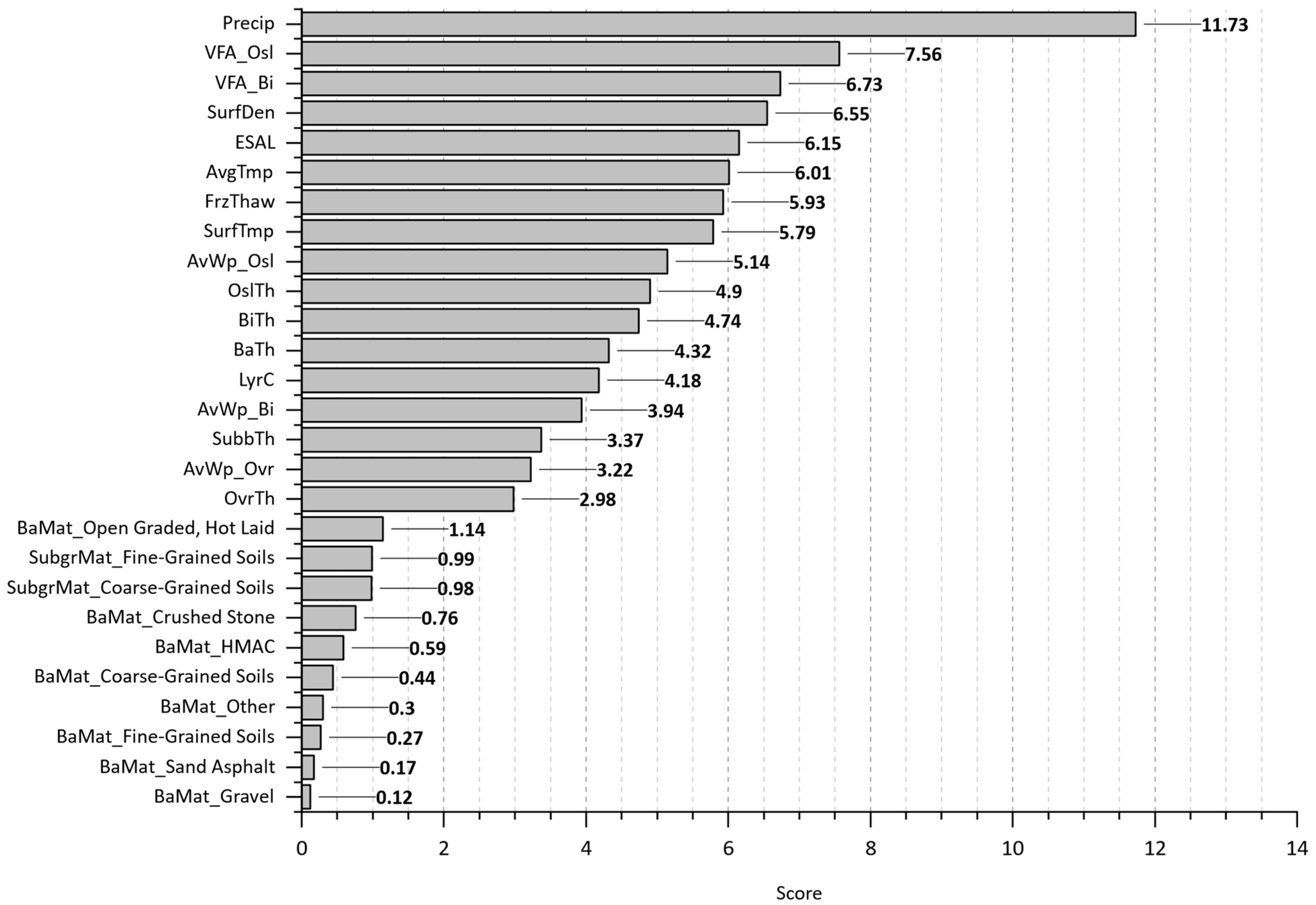
| AgeCrack | 1 | Precip | Precip | Precip | |
| 2 | VFA_Osl | SurfTmp | ESAL | ||
| 3 | VFA_Bi | SurfDen | VFA_Osl | ||
| 4 | SurfDen | LyrC | AvgTmp | ||
| 5 | ESAL | OslTh | FrzThaw |
| Random Forest | Extra Trees | XGBoost | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameters | RS * | GS ** | B *** | RS | GS | B | RS | GS | B |
| bootstrap | False | False | False | False | False | False | - | - | - |
| max_depth | 30 | 29 | 45 | 26 | 25 | 46 | 17 | 13 | 23 |
| max_features | sqrt | sqrt | log2 | log2 | log2 | sqrt | - | - | - |
| max_leaf_node | None | None | None | None | None | None | - | - | |
| min_samples_leaf | 1 | 1 | 1 | 1 | 1 | 1 | - | - | - |
| min_samples_split | 2 | 3 | 3 | 5 | 4 | 3 | - | - | - |
| n_estimators | 1200 | 1100 | 2000 | 2000 | 1900 | 2000 | 2300 | 1850 | 2700 |
| subsample | - | - | - | - | - | - | 0.8 | 0.7 | 0.75 |
| min_child_weight | - | - | - | - | - | - | 8 | 7 | 7 |
| learning_rate | - | - | - | - | - | - | 0.01 | 0.009 | 0.01 |
| gamma | - | - | - | - | - | - | 1.2 | 0.95 | 0.93 |
| colsample_bytree | - | - | - | - | - | - | 0.85 | 0.8 | 0.85 |
| cross-validation | 5 | 5 | 10 | 5 | 5 | 10 | 5 | 5 | 10 |
| n_iter | 500 | - | 38 | 500 | - | 28 | 500 | - | 30 |
| total fits | 2500 | 400 | 380 | 2500 | 675 | 280 | 2500 | 1500 | 300 |
| time | 7.5 min | 14 min | 18 min | 4.5 min | 10 min | 12 min | 12 min | 35 min | 15 min |
| XGBoost | Extra Trees | Random Forest | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimization | Random Search | Grid Search | Bayesian | Random Search | Grid Search | Bayesian | Random Search | Grid Search | Bayesian | ||
| Model | I | II | III | IV | V | VI | VII | VIII | IX | ||
| WpCrAr | Training | R2 | 0.948 | 0.957 | 0.983 | 0.973 | 0.970 | 0.972 | 0.939 | 0.965 | 0.970 |
| MSE | 0.888 | 0.725 | 0.453 | 0.464 | 0.528 | 0.470 | 1.046 | 0.995 | 0.513 | ||
| MAE | 0.472 | 0.427 | 0.352 | 0.296 | 0.319 | 0.296 | 0.587 | 0.456 | 0.315 | ||
| RMSE | 0.942 | 0.851 | 0.673 | 0.681 | 0.727 | 0.686 | 1.022 | 0.997 | 0.716 | ||
| Testing | R2 | 0.753 | 0.761 | 0.791 | 0.749 | 0.747 | 0.751 | 0.725 | 0.756 | 0.747 | |
| MSE | 4.250 | 4.131 | 3.862 | 4.302 | 4.442 | 4.302 | 4.820 | 4.177 | 4.345 | ||
| MAE | 1.131 | 1.104 | 1.071 | 1.088 | 1.102 | 1.089 | 1.264 | 1.115 | 1.099 | ||
| RMSE | 2.061 | 2.032 | 1.965 | 2.074 | 2.107 | 2.074 | 2.195 | 2.044 | 2.084 | ||
| AgeCrack | Training | R2 | 0.952 | 0.961 | 0.987 | 0.993 | 0.990 | 0.992 | 0.968 | 0.994 | 0.999 |
| MSE | 0.373 | 0.270 | 0.117 | 0.152 | 0.190 | 0.156 | 0.535 | 0.484 | 0.002 | ||
| MAE | 0.293 | 0.248 | 0.173 | 0.195 | 0.218 | 0.195 | 0.291 | 0.200 | 0.019 | ||
| RMSE | 0.611 | 0.520 | 0.342 | 0.390 | 0.436 | 0.395 | 0.360 | 0.335 | 0.054 | ||
| Testing | R2 | 0.883 | 0.891 | 0.921 | 0.902 | 0.905 | 0.909 | 0.865 | 0.896 | 0.907 | |
| MSE | 1.855 | 1.777 | 1.603 | 1.839 | 1.979 | 1.839 | 2.190 | 1.766 | 1.874 | ||
| MAE | 0.807 | 0.780 | 0.747 | 0.790 | 0.804 | 0.791 | 0.930 | 0.781 | 0.765 | ||
| RMSE | 1.362 | 1.333 | 1.266 | 1.356 | 1.389 | 1.356 | 1.480 | 1.329 | 1.369 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taheri, A.; Sobanjo, J. Ensemble Learning Approach for Developing Performance Models of Flexible Pavement. Infrastructures 2024, 9, 78. https://doi.org/10.3390/infrastructures9050078
Taheri A, Sobanjo J. Ensemble Learning Approach for Developing Performance Models of Flexible Pavement. Infrastructures. 2024; 9(5):78. https://doi.org/10.3390/infrastructures9050078
Chicago/Turabian StyleTaheri, Ali, and John Sobanjo. 2024. "Ensemble Learning Approach for Developing Performance Models of Flexible Pavement" Infrastructures 9, no. 5: 78. https://doi.org/10.3390/infrastructures9050078
APA StyleTaheri, A., & Sobanjo, J. (2024). Ensemble Learning Approach for Developing Performance Models of Flexible Pavement. Infrastructures, 9(5), 78. https://doi.org/10.3390/infrastructures9050078







