X-Ray Diffraction under Extreme Conditions at the Advanced Light Source
Abstract
:1. Introduction
2. Synchrotron Facilities
3. Beamline Design and Capabilities at the Advanced Light Source
3.1. Beamline 12.2.2
3.1.1. Instrumentation
3.1.2. Powder Diffraction under Non-Ambient Conditions
3.1.3. In-Situ Laser Heating
3.1.4. Resistive and Lamp Heating
3.1.5. High Pressure Single Crystal Diffraction
3.2. Beamline 12.3.2
3.3. Beamline 11.3.1 and 12.2.1
4. High Pressure Experiments at the Advanced Light Source
4.1. Materials Science
4.2. Chemistry
4.3. Geoscience
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. X-ray Diffraction

Appendix B. The Diamond Anvil Cell
Appendix B.1. DAC Assembly

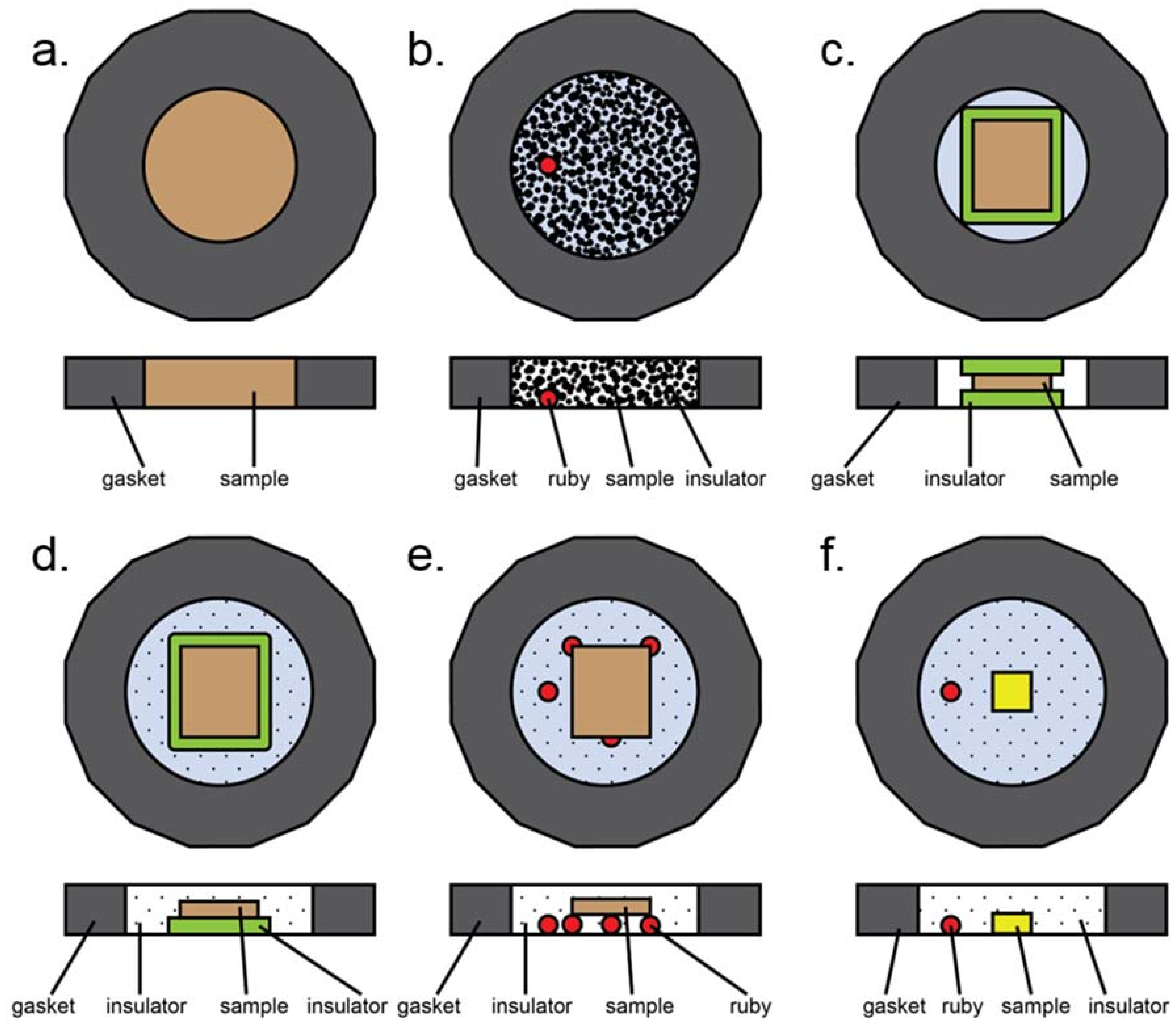
Appendix B.2. Pressure Determination
| Synchrotron | Location | Beamlines | Technique | HPD | Energy |
|---|---|---|---|---|---|
| ALBA | Cerdanyola del Vallès, Barcelona, Spain | BL04 (MSPD) | Powder XRD | DAC | 8 – 50 keV |
| ALS [2] | Berkeley, CA, USA | 11.3.1 | Single crystal XRD | DAC | 6 – 18 keV |
| 12.2.2 | Single crystal XRD Powder XRD | DAC | 6 – 40 keV | ||
| 12.3.2 | Laue XRD Powder XRD XRF | DAC | 6 – 22 keV | ||
| APS [3] | Argonne, IL, USA | 3-ID-B,C,D | Nuclear resonant inelastic X-Ray scattering High energy resonant inelastic X-Ray scattering Synchrotron Mossbauer spectroscopy | DAC | 7 – 27 keV |
| 13-BM-C | Powder XRD Single crystal XRD | DAC | 28.6 keV | ||
| 13-BM-D | Powder XRD Single crystal XRD Brillouin Spectroscopy | DAC LVP | 4.5 – 80 keV | ||
| 13-ID-C,D | Powder XRD Single crystal XRD Raman Spectroscopy | DAC LVP | 4.9 – 75 keV | ||
| 16-BM-B | Laue XRD Radiography Viscometry | PEP DAC | 10 – 120 keV | ||
| 16-BM-D | Powder XRD Single crystal XRD X-ray absorption | DAC | 6 – 70 keV | ||
| 16-ID-B | Powder XRD Single crystal XRD | DAC | 18 – 60 keV | ||
| 16-ID-D | X-ray emission spectroscopy Nuclear resonant inelastic X-Ray scattering Synchrotron Mossbauer spectroscopy | DAC | 5 – 37 keV | ||
| Diamond [4] | Didcot, Oxfordshire, UK | I15 | Single crystal XRD Powder XRD | DAC | 20 – 80 keV |
| I19 | Single crystal XRD | DAC | 5 – 25 keV | ||
| ESRF [5] | Grenoble, France | ID06 | Powder XRD | LVP | 33 keV, 55 keV |
| ID15B | Powder XRD Single crystal XRD Diffuse X-ray scattering | DAC | 30 keV | ||
| ID18 | Nuclear resonance techniques | DAC | 7 – 80 keV | ||
| BM23 | X-ray absorption spectroscopy Powder XRD XRF | PEP | 5 – 75 keV | ||
| ID24 | X-ray absorption spectroscopy FTIR | DAC | 5 – 27 keV | ||
| ID27 | Powder XRD Single crystal XRD XRF | DAC PEP | 20 – 90 keV | ||
| NSLS-II [6] | Brookhaven, NY, USA | 28-ID-2 (XPD)a | Powder XRD | DAC | 40 – 70 keV |
| NSRRC [7] | Hsinchu, Taiwan | BL01C2 | Powder XRD | DAC | 12 – 33 keV |
| Petra-III [8] | DESY, Hamburg, Germany | P02.2 | Powder XRD Single crystal XRD XRF | DAC | 25.7 keV, 42.8 keV, 60 keV |
| Soleil [9] | Saint-Aubin, France | PSICHÉ | Laue XRD Powder XRD X-ray tomography | DAC LVP PEP | 15 – 100 keV |
| SPring-8 [10,11] | Harima Science Park City, Japan | BL04B1 | Laue XRD Radiography | LVP | 20-150 keV |
| BL10XU | Powder XRD Raman Spectroscopy Brillouin Spectroscopy | DAC | 14-61 keV |
References
- Beamline Information—en. Available online: https://www.cells.es/en/beamlines/bl04-mspd (accessed on 12 December 2017).
- Advanced Light Source Beamline Detail Archive. Available online: https://als.lbl.gov/beamlines/ (accessed on 24 October 2017).
- Beamlines Directory | Advanced Photon Source. Available online: https://www1.aps.anl.gov/Beamlines/Directory (accessed on 24 October 2017).
- Beamlines—Diamond Light Source. Available online: http://www.diamond.ac.uk/Beamlines.html (accessed on 24 October 2017).
- Matter at Extremes—ESRF. Available online: http://www.esrf.eu/UsersAndScience/Experiments/MEx (accessed on 24 October 2017).
- Photon Sciences | Beamlines | XPD: X-ray Powder Diffraction. Available online: https://www.bnl.gov/ps/beamlines/beamline.php?b=XPD (accessed on 24 October 2017).
- NSRRC Powder and Fiber X-ray Diffraction. Available online: http://efd.nsrrc.org.tw/EFD.php?num=237 (accessed on 24 October 2017).
- Extreme Conditions Beamline (ECB) P02.2. Available online: http://photon-science.desy.de/facilities/petra_iii/beamlines/p02_hard_x_ray_diffraction_beamline/ecb/index_eng.html (accessed on 24 October 2017).
- Welcome to Centre de Rayonnement Synchrotron Français | French National Synchrotron Facility. Available online: https://www.synchrotron-soleil.fr/en (accessed on 12 December 2017).
- BL04B1. Available online: http://www.spring8.or.jp/wkg/BL04B1/instrument/lang-en/INS-0000000317/instrument_summary_view (accessed on 24 October 2017).
- BL10XU. Available online: http://www.spring8.or.jp/wkg/BL10XU/instrument/lang-en/INS-0000000352/instrument_summary_view (accessed on 24 October 2017).
- Kunz, M.; MacDowell, A.A.; Caldwell, W.A.; Cambie, D.; Celestre, R.S.; Domning, E.E.; Duarte, R.M.; Gleason, A.E.; Glossinger, J.M.; Kelez, N.; et al. A beamline for high-pressure studies at the Advanced Light Source with a superconducting bending magnet as the source. J. Synchrotron Radiat. 2005, 12, 650–658. [Google Scholar] [CrossRef] [PubMed]
- Kunz, M.; Tamura, N.; Chen, K.; MacDowell, A.A.; Celestre, R.S.; Church, M.M.; Fakra, S.; Domning, E.E.; Glossinger, J.M.; Kirschman, J.L.; et al. A dedicated superbend X-ray microdiffraction beamline for materials, geo-, and environmental sciences at the advanced light source. Rev. Sci. Instrum. 2009, 80, 035108. [Google Scholar] [CrossRef] [PubMed]
- Robin, D.; Benjegerdes, R.; Biocca, A.; Bish, P.; Brown, W.; Byrne, W.; Calais, D.; Chin, M.; Corradi, C.; Coulomb, D.; et al. Successful completion of the ALS superbend project. In Proceedings of the EPAC 2002, Paris, France, 4 June 2002; pp. 215–217. [Google Scholar]
- MacDowell, A.A.; Celestre, R.S.; Howells, M.; McKinney, W.; Krupnick, J.; Cambie, D.; Domning, E.E.; Duarte, R.M.; Kelez, N.; Plate, D.W.; et al. Suite of three protein crystallography beamlines with single superconducting bend magnet as the source. J. Synchrotron Radiat. 2004, 11, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Arndt, U.W.; Creagh, D.C.; Deslattes, R.D.; Hubbell, J.H.; Indelicato, P.; Kessler, E.G., Jr.; Lindroth, E.; Coolidge, X. X-rays. In International Tables for Crystallography Volume C: Mathematical, Physical and Chemical Tables; International Union of Crystallography: Chester, UK, 2006; Volume C, pp. 191–258. ISBN 978-1-4020-1900-5. [Google Scholar]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Fiquet, G.; Andrault, D.; Dewaele, A.; Charpin, T.; Kunz, M.; Haüsermann, D. P-V-T equation of state of MgSiO3 perovskite. Phys. Earth Planet Inter. 1998, 105, 21–31. [Google Scholar] [CrossRef]
- Shen, G.; Prakapenka, V.B.; Rivers, M.L.; Sutton, S.R. Structure of liquid iron at pressures up to 58 GPa. Phys. Rev. Lett. 2004, 92, 185701. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Shen, G.; Mao, H.K. Double-sided laser heating system at HPCAT for in situ X-Ray diffraction at high pressures and high temperatures. J. Phys. Condens. Matter 2006, 18, S1097. [Google Scholar] [CrossRef] [PubMed]
- Watanuki, T.; Shimomura, O.; Yagi, T.; Kondo, T.; Isshiki, M. Construction of laser-heated diamond anvil cell system for in situ X-Ray diffraction study at SPring-8. Rev. Sci. Instrum. 2001, 72, 1289–1292. [Google Scholar] [CrossRef]
- Liermann, H.-P.; Morgenroth, W.; Ehnes, A.; Berghäuser, A.; Winkler, B.; Franz, H.; Weckert, E. The Extreme Conditions Beamline at PETRA III, DESY: Possibilities to conduct time resolved monochromatic diffraction experiments in dynamic and laser heated DAC. J. Phys. Conf. Ser. 2010, 215, 012029. [Google Scholar] [CrossRef]
- Caldwell, W.A.; Kunz, M.; Celestre, R.S.; Domning, E.E.; Walter, M.J.; Walker, D.; Glossinger, J.; MacDowell, A.A.; Padmore, H.A.; Jeanloz, R.; et al. Laser-heated diamond anvil cell at the advanced light source beamline 12.2.2. Nucl. Instrum. Methods Phys. Res. Sect. A 2007, 582, 221–225. [Google Scholar] [CrossRef]
- Kaner, R.B.; Gilman, J.J.; Tolbert, S.H. Designing Superhard Materials. Science 2005, 308, 1268–1269. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.-Y.; Weinberger, M.B.; Levine, J.B.; Kavner, A.; Yang, J.-M.; Tolbert, S.H.; Kaner, R.B. Synthesis of ultra-incompressible superhard rhenium diboride at ambient pressure. Science 2007, 316, 436–439. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, R.; Lech, A.T.; Xie, M.; Weaver, B.E.; Yeung, M.T.; Tolbert, S.H.; Kaner, R.B. Tungsten tetraboride, an inexpensive superhard material. Proc. Natl. Acad. Sci. USA 2011, 108, 10958–10962. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, A.; Winkler, B.; Bayarjargal, L.; Morgenroth, W.; Juarez-Arellano, E.A.; Milman, V.; Refson, K.; Kunz, M.; Chen, K. Novel Rhenium Nitrides. Phys. Rev. Lett. 2010, 105, 085504. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, A.; Winkler, B.; Juarez-Arellano, E.A.; Bayarjargal, L. Synthesis of Binary Transition Metal Nitrides, Carbides and Borides from the Elements in the Laser-Heated Diamond Anvil Cell and Their Structure-Property Relations. Materials 2011, 4, 1648–1692. [Google Scholar] [CrossRef] [PubMed]
- Santamaría-Pérez, D.; McGuire, C.; Makhluf, A.; Kavner, A.; Chuliá-Jordán, R.; Pellicer-Porres, J.; Martinez-García, D.; Doran, A.; Kunz, M.; Rodríguez-Hernández, P.; et al. Exploring the Chemical Reactivity between Carbon Dioxide and Three Transition Metals (Au, Pt, and Re) at High-Pressure, High-Temperature Conditions. Inorg. Chem. 2016, 55, 10793–10799. [Google Scholar] [CrossRef] [PubMed]
- Armentrout, M.M.; Kavner, A. Incompressibility of osmium metal at ultrahigh pressures and temperatures. J. Appl. Phys. 2010, 107, 093528. [Google Scholar] [CrossRef]
- Nisr, C.; Meng, Y.; MacDowell, A.A.; Yan, J.; Prakapenka, V.; Shim, S.-H. Thermal expansion of SiC at high pressure-temperature and implications for thermal convection in the deep interiors of carbide exoplanets. J. Geophys. Res. Planets 2017, 122, 124–133. [Google Scholar] [CrossRef]
- Gleason, A.E.; Mao, W.L. Strength of iron at core pressures and evidence for a weak Earth’s inner core. Nat. Geosci. 2013, 6, 571–574. [Google Scholar] [CrossRef]
- Miyagi, L.; Kanitpanyacharoen, W.; Kaercher, P.; Lee, K.K.M.; Wenk, H.-R. Slip Systems in MgSiO3 Post-Perovskite: Implications for D” Anisotropy. Science 2010, 329, 1639–1641. [Google Scholar] [CrossRef] [PubMed]
- Miyagi, L.; Kanitpanyacharoen, W.; Stackhouse, S.; Militzer, B.; Wenk, H.-R. The enigma of post-perovskite anisotropy: Deformation versus transformation textures. Phys. Chem. Miner. 2011, 38, 665–678. [Google Scholar] [CrossRef]
- Miyagi, L.; Wenk, H.-R. Texture development and slip systems in bridgmanite and bridgmanite + ferropericlase aggregates. Phys. Chem. Miner. 2016, 43, 597–613. [Google Scholar] [CrossRef]
- Wenk, H.-R.; Lutterotti, L.; Kaercher, P.; Kanitpanyacharoen, W.; Miyagi, L.; Vasin, R. Rietveld texture analysis from synchrotron diffraction images. II. Complex multiphase materials and diamond anvil cell experiments. Powder Diffr. 2014, 29, 220–232. [Google Scholar] [CrossRef]
- Chen, B.; Lutker, K.; Raju, S.V.; Yan, J.; Kanitpanyacharoen, W.; Lei, J.; Yang, S.; Wenk, H.-R.; Mao, H.; Williams, Q. Texture of Nanocrystalline Nickel: Probing the Lower Size Limit of Dislocation Activity. Science 2012, 338, 1448–1451. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Mohammadi, R.; Turner, C.L.; Kaner, R.B.; Kavner, A.; Tolbert, S.H. Lattice stress states of superhard tungsten tetraboride from radial X-Ray diffraction under nonhydrostatic compression. Phys. Rev. B 2014, 90, 104104. [Google Scholar] [CrossRef]
- Xie, M.; Mohammadi, R.; Turner, C.L.; Kaner, R.B.; Kavner, A.; Tolbert, S.H. Exploring hardness enhancement in superhard tungsten tetraboride-based solid solutions using radial X-ray diffraction. Appl. Phys. Lett. 2015, 107, 041903. [Google Scholar] [CrossRef]
- Walter, M.J.; Koga, K.T. The effects of chromatic dispersion on temperature measurement in the laser-heated diamond anvil cell. Phys. Earth Planet Inter. 2004, 143–144, 541–558. [Google Scholar] [CrossRef]
- Rainey, E.S.G.; Kavner, A. Peak scaling method to measure temperatures in the laser-heated diamond anvil cell and application to the thermal conductivity of MgO. J. Geophys. Res. Solid Earth 2014, 119, 8154–8170. [Google Scholar] [CrossRef]
- Miyagi, L.; Kanitpanyacharoen, W.; Raju, S.V.; Kaercher, P.; Knight, J.; MacDowell, A.; Wenk, H.-R.; Williams, Q.; Alarcon, E.Z. Combined resistive and laser heating technique for in situ radial X-ray diffraction in the diamond anvil cell at high pressure and temperature. Rev. Sci. Instrum. 2013, 84, 025118. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Knight, J.; Kunz, M.; Vennila Raju, S.; Chen, B.; Gleason, A.E.; Godwal, B.K.; Geballe, Z.; Jeanloz, R.; Clark, S.M. The resistive-heating characterization of laser heating system and LaB6 characterization of X-ray diffraction of beamline 12.2.2 at advanced light source. J. Phys. Chem. Solids 2010, 71, 1179–1182. [Google Scholar] [CrossRef]
- Grocholski, B.; Speziale, S.; Jeanloz, R. Equation of state, phase stability, and amorphization of SnI4 at high pressure and temperature. Phys. Rev. B 2010, 81, 094101. [Google Scholar] [CrossRef]
- Geballe, Z.M.; Raju, S.V.; Godwal, B.K.; Jeanloz, R. Clapeyron slope reversal in the melting curve of AuGa 2 at 5.5 GPa. J. Phys. Condens. Matter 2013, 25, 415401. [Google Scholar] [CrossRef] [PubMed]
- Raju, S.V.; Geballe, Z.M.; Godwal, B.K.; Kalkan, B.; Williams, Q.; Jeanloz, R. High pressure and temperature structure of liquid and solid Cd: Implications for the melting curve of Cd. Mater. Res. Express 2014, 1, 046502. [Google Scholar] [CrossRef]
- Doran, A.; Schlicker, L.; Beavers, C.; Bhat, S.; Bekheet, M.; Gurlo, A. Compact low power infrared tube furnace for in situ X-ray powder diffraction. Rev. Sci. Instrum. 2017, 88, 013903. [Google Scholar] [CrossRef] [PubMed]
- Mattox, T.M.; Groome, C.; Doran, A.; Beavers, C.M.; Urban, J.J. Anion-mediated negative thermal expansion in lanthanum hexaboride. Solid State Commun. 2017, 265, 47–51. [Google Scholar] [CrossRef]
- Köck, E.-M.; Kogler, M.; Zhuo, C.; Schlicker, L.; Bekheet, M.F.; Doran, A.; Gurlo, A.; Penner, S. Surface chemistry and stability of metastable corundum-type In2O3. Phys. Chem. Chem. Phys. 2017, 19, 19407–19419. [Google Scholar] [CrossRef] [PubMed]
- Beavers, C.M.; O’Bannon, E.F.; Doran, A.; Kunz, M.; Williams, Q. MS18-P2 Single Crystal High Pressure Diffraction at the Advanced Light Source. Found. Crystallogr. 2016, 72, s279. [Google Scholar] [CrossRef]
- O’Bannon, E.; Beavers, C.M.; Kunz, M.; Williams, Q. The high-pressure phase of lawsonite: A single crystal study of a key mantle hydrous phase. J. Geophys. Res. Solid Earth 2017, 122, 6294–6305. [Google Scholar] [CrossRef]
- Jaffe, A.; Lin, Y.; Beavers, C.M.; Voss, J.; Mao, W.L.; Karunadasa, H.I. High-Pressure Single-Crystal Structures of 3D Lead-Halide Hybrid Perovskites and Pressure Effects on their Electronic and Optical Properties. ACS Cent Sci. 2016, 2, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Kapustin, E.A.; Lee, S.; Alshammari, A.S.; Yaghi, O.M. Molecular Retrofitting Adapts a Metal–Organic Framework to Extreme Pressure. ACS Cent. Sci. 2017, 3, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Kantor, I.; Prakapenka, V.; Kantor, A.; Dera, P.; Kurnosov, A.; Sinogeikin, S.; Dubrovinskaia, N.; Dubrovinsky, L. BX90: A new diamond anvil cell design for X-ray diffraction and optical measurements. Rev. Sci. Instrum. 2012, 83, 125102. [Google Scholar] [CrossRef] [PubMed]
- Merrill, L.; Bassett, W.A. Miniature diamond anvil pressure cell for single crystal X-Ray diffraction studies. Rev. Sci. Instrum. 1974, 45, 290–294. [Google Scholar] [CrossRef]
- Parsons, S. ECLIPSE—Program for Masking High Pressure Diffraction Images and Conversion between CCD Image Formats. Department of Chemistry, University of Edinburg: Edinburgh, UK, 2010. [Google Scholar]
- Tamura, N.; Kunz, M.; Chen, K.; Celestre, R.S.; MacDowell, A.A.; Warwick, T. A superbend X-ray microdiffraction beamline at the advanced light source. Mater. Sci. Eng. A 2009, 524, 28–32. [Google Scholar] [CrossRef]
- Dejoie, C.; McCusker, L.B.; Baerlocher, C.; Kunz, M.; Tamura, N. Can Laue microdiffraction be used to solve and refine complex inorganic structures? J. Appl. Cryst. 2013, 46, 1805–1816. [Google Scholar] [CrossRef]
- Tamura, N. XMAS: A Versatile Tool for Analyzing Synchrotron X-ray Microdiffraction Data. In Strain and Dislocation Gradients from Diffraction; Imperial College Press: London, UK, 2014; pp. 125–155. ISBN 978-1-908979-62-9. [Google Scholar]
- Thompson, A.C.; Padmore, H.A.; Oliver, A.G.; Teat, S.J.; Celestre, R.S.; Clark, S.M.; Domning, E.E.; Franck, K.D.; Morrison, G.Y. A Simple High Performance Beamline for Small Molecule Chemical Crystallography. AIP Conf. Proc. 2004, 705, 482–485. [Google Scholar] [CrossRef]
- Moggach, S.A.; Allan, D.R.; Parsons, S.; Warren, J.E. Incorporation of a new design of backing seat and anvil in a Merrill–Bassett diamond anvil cell. J. Appl. Cryst. 2008, 41, 249–251. [Google Scholar] [CrossRef]
- Boehler, R.; Hantsetters, K.D. New anvil designs in diamond-cells. High Press. Res. 2004, 24, 391–396. [Google Scholar] [CrossRef]
- Rodríguez-Velamazán, J.A.; Fabelo, O.; Beavers, C.M.; Natividad, E.; Evangelisti, M.; Roubeau, O. A Multifunctional Magnetic Material under Pressure. Chem. Eur. J. 2014, 20, 7956–7961. [Google Scholar] [CrossRef] [PubMed]
- Woodall, C.H.; Beavers, C.M.; Christensen, J.; Hatcher, L.E.; Intissar, M.; Parlett, A.; Teat, S.J.; Reber, C.; Raithby, P.R. Hingeless Negative Linear Compression in the Mechanochromic Gold Complex [(C6F5Au)2(μ-1,4-diisocyanobenzene)]. Angew. Chem. Int. Ed. 2013, 52, 9691–9694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gagnon, K.J.; Beavers, C.M.; Clearfield, A. MOFs Under Pressure: The Reversible Compression of a Single Crystal. J. Am. Chem. Soc. 2013, 135, 1252–1255. [Google Scholar] [CrossRef] [PubMed]
- Shan, Z.; Stach, E.A.; Wiezorek, J.M.K.; Knapp, J.A.; Follstaedt, D.M.; Mao, S.X. Grain Boundary-Mediated Plasticity in Nanocrystalline Nickel. Science 2004, 305, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Tamura, N.; Mi, Z.; Lei, J.; Yan, J.; Zhang, L.; Deng, W.; Ke, F.; Yue, B.; Chen, B. Reversal in the Size Dependence of Grain Rotation. Phys. Rev. Lett. 2017, 118, 096101. [Google Scholar] [CrossRef] [PubMed]
- Woodall, C.H.; Fuertes, S.; Beavers, C.M.; Hatcher, L.E.; Parlett, A.; Shepherd, H.J.; Christensen, J.; Teat, S.J.; Intissar, M.; Rodrigue-Witchel, A.; et al. Tunable Trimers: Using Temperature and Pressure to Control Luminescent Emission in Gold(I) Pyrazolate-Based Trimers. Chem. Eur. J. 2014, 20, 16933–16942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, H.-C.; Long, J.R.; Yaghi, O.M. Introduction to Metal–Organic Frameworks. Chem. Rev. 2012, 112, 673–674. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kapustin, E.A.; Yaghi, O.M. Coordinative alignment of molecules in chiral metal-organic frameworks. Science 2016, 353, 808–811. [Google Scholar] [CrossRef] [PubMed]
- Gándara, F.; Furukawa, H.; Lee, S.; Yaghi, O.M. High Methane Storage Capacity in Aluminum Metal–Organic Frameworks. J. Am. Chem. Soc. 2014, 136, 5271–5274. [Google Scholar] [CrossRef] [PubMed]
- Graham, A.J.; Allan, D.R.; Muszkiewicz, A.; Morrison, C.A.; Moggach, S.A. The Effect of High Pressure on MOF-5: Guest-Induced Modification of Pore Size and Content at High Pressure. Angew. Chem. Int. Ed. 2011, 50, 11138–11141. [Google Scholar] [CrossRef]
- Spek, A.L. PLATON SQUEEZE: A tool for the calculation of the disordered solvent contribution to the calculated structure factors. Acta Cryst. C 2015, 71, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Macrae, C. F.; Bruno, I. J.; Chisholm, J. A.; Edgington, P. R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0 – new features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 1952, 57, 227–286. [Google Scholar] [CrossRef]
- Song, X. Anisotropy of the Earth’s inner core. Rev. Geophys. 1997, 35, 297–313. [Google Scholar] [CrossRef]
- Deuss, A. Heterogeneity and Anisotropy of Earth’s Inner Core. Annu. Rev. Earth Planet. Sci. 2014, 42, 103–126. [Google Scholar] [CrossRef]
- Jeanloz, R.; Wenk, H.-R. Convection and anisotropy of the inner core. Geophys. Res. Lett. 1988, 15, 72–75. [Google Scholar] [CrossRef]
- Hemley, R.J.; Mao, H.; Shen, G.; Badro, J.; Gillet, P.; Hanfland, M.; Häusermann, D. X-ray Imaging of Stress and Strain of Diamond, Iron, and Tungsten at Megabar Pressures. Science 1997, 276, 1242–1245. [Google Scholar] [CrossRef]
- Hammond, C. The Basics of Crystallography and Diffraction: Fourth Edition; International Union of Crystallography Texts on Crystallography, 4th ed.; Oxford University Press: Oxford, NY, USA, 2015; ISBN 978-0-19-873868-8. [Google Scholar]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Milanesio, M.; Gilli, G.; Gilli, P.; Zanotti, G.; Ferraris, G.; Catti, M. Fundamentals of Crystallography, 3rd ed.; Giacovazzo, C., Ed.; International Union of Crystallography Monographs on Crystallography; Oxford University Press: Oxford, NY, USA, 2011; ISBN 978-0-19-957366-0. [Google Scholar]
- He, B.B. Two-Dimensional X-ray Diffraction, 1st ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Shmueli, U. Theories and Techniques of Crystal Structure Determination; International Union of Crystallography Monographs on Crystallography; Oxford University Press: Oxford, NY, USA, 2007; ISBN 978-0-19-921966-7. [Google Scholar]
- Massa, W. Crystal Structure Determination, 2nd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-662-06431-3. [Google Scholar]
- Pecharsky, V.; Zavalij, P. Fundamentals of Powder Diffraction and Structural; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-09579-0. [Google Scholar]
- Pickworth Glusker, J.; Trueblood, K.N. Crystal Structure Analysis: A Primer, 3rd ed.; Oxford University Press: Oxford, NY, USA, 2010; ISBN 978-0-19-957635-7. [Google Scholar]
- Structure Determination from Powder Diffraction Data, 1st ed.; David, W.I.F.; Shankland, K.; McCusker, L.B.; Baerlocher, C. (Eds.) Oxford University Press: Oxford, NY, USA, 2002; ISBN 978-0-19-850091-9. [Google Scholar]
- Mueller, P.; Herbst-Irmer, R.; Spek, A.L.; Schneider, T.; Sawaya, M. Crystal Structure Refinement: A Crystallographer’s Guide to SHELXL; International Union of Crystallography Texts on Crystallography; Oxford University Press: Oxford, NY, USA, 2006; ISBN 978-0-19-857076-9. [Google Scholar]
- Abboud, A.; Kirchlechner, C.; Keckes, J.; Conka Nurdan, T.; Send, S.; Micha, J.S.; Ulrich, O.; Hartmann, R.; Strüder, L.; Pietsch, U. Single-shot full strain tensor determination with microbeam X-ray Laue diffraction and a two-dimensional energy-dispersive detector. J. Appl. Crystallogr. 2017, 50, 901–908. [Google Scholar] [CrossRef] [PubMed]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Marín, C.; Diéguez, E. A method of complete generation of back-reflection Laue patterns of any single crystal. J. Appl. Cryst. 1995, 28, 839–842. [Google Scholar] [CrossRef]
- Krahl-Urban, B.; Butz, R.; Preuss, E. A simplified procedure for orientation of single crystals of any structure. Acta Cryst. A 1973, 29, 86–88. [Google Scholar] [CrossRef]
- Barabash, R.I.; Ice, G.E.; Larson, B.C.; Yang, W. Application of white X-Ray microbeams for the analysis of dislocation structures. Rev. Sci. Instrum. 2002, 73, 1652–1654. [Google Scholar] [CrossRef]
- Weir, C.E.; Lippincott, E.R.; Van Valkenburg, A.; Bunting, E.N. Infrared studies in the 1- to 15-micron region to 30,000 atmospheres. J. Res. NBS A Phys. Ch. 1959, 63, 55–62. [Google Scholar] [CrossRef]
- Bassett, W.A. Diamond anvil cell, 50th birthday. High Press. Res. 2009, 29, 163–186. [Google Scholar] [CrossRef]
- Giriat, G.; Wang, W.; Attfield, J.P.; Huxley, A.D.; Kamenev, K.V. Turnbuckle diamond anvil cell for high-pressure measurements in a superconducting quantum interference device magnetometer. Rev. Sci. Instrum. 2010, 81, 073905. [Google Scholar] [CrossRef] [PubMed]
- Andrault, D.; Fiquet, G. Synchrotron radiation and laser heating in a diamond anvil cell. Rev. Sci. Instrum. 2001, 72, 1283–1288. [Google Scholar] [CrossRef]
- Boffa Ballaran, T.; Kurnosov, A.; Trots, D. Single-crystal X-ray diffraction at extreme conditions: A review. High Press. Res. 2013, 33, 453–465. [Google Scholar] [CrossRef]
- Jayaraman, A. Diamond anvil cell and high-pressure physical investigations. Rev. Mod. Phys. 1983, 55, 65–108. [Google Scholar] [CrossRef]
- Chapman, K.W.; Chupas, P.J.; Halder, G.J.; Hriljac, J.A.; Kurtz, C.; Greve, B.K.; Ruschman, C.J.; Wilkinson, A.P. Optimizing high-pressure pair distribution function measurements in diamond anvil cells. J. Appl. Cryst. 2010, 43, 297–307. [Google Scholar] [CrossRef]
- Xu, J.; Mao, H.; Hemley, R.J.; Hines, E. The moissanite anvil cell: A new tool for high-pressure research. J. Phys. Condens. Matter 2002, 14, 11543. [Google Scholar] [CrossRef]
- Siqueira, M.; (Almax easyLab, Cambridge, MA, USA); Stan, C.V.; (Advanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, CA, USA). Personal communication, 2017.
- Klotz, S.; Chervin, J.-C.; Munsch, P.; Le Marchand, G. Hydrostatic limits of 11 pressure transmitting media. J. Phys. D Appl. Phys. 2009, 42, 075413. [Google Scholar] [CrossRef]
- Kaercher, P.; Speziale, S.; Miyagi, L.; Kanitpanyacharoen, W.; Wenk, H.-R. Crystallographic preferred orientation in wüstite (FeO) through the cubic-to-rhombohedral phase transition. Phys. Chem. Miner. 2012, 39, 613–626. [Google Scholar] [CrossRef]
- Stan, C.V.; Dutta, R.; White, C.E.; Prakapenka, V.; Duffy, T.S. High-pressure polymorphism of PbF2 to 75 GPa. Phys. Rev. B 2016, 94, 024104. [Google Scholar] [CrossRef]
- Fei, Y.; Ricolleau, A.; Frank, M.; Mibe, K.; Shen, G.; Prakapenka, V. Toward an internally consistent pressure scale. Proc. Natl. Acad. Sci. USA 2007, 104, 9182–9186. [Google Scholar] [CrossRef] [PubMed]
- Hanfland, M.; Syassen, K. A Raman study of diamond anvils under stress. J. Appl. Phys. 1985, 57, 2752–2756. [Google Scholar] [CrossRef]
- Akahama, Y.; Kawamura, H. Pressure calibration of diamond anvil Raman gauge to 310 GPa. J. Appl. Phys. 2006, 100, 043516. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Datchi, F.; Dewaele, A.; Loubeyre, P.; Letoullec, R.; Godec, Y.L.; Canny, B. Optical pressure sensors for high-pressure–high-temperature studies in a diamond anvil cell. High Press. Res. 2007, 27, 447–463. [Google Scholar] [CrossRef]
- Tange, Y.; Takahashi, E.; Nishihara, Y.; Funakoshi, K.; Sata, N. Phase relations in the system MgO-FeO-SiO2 to 50 GPa and 2000 °C: An application of experimental techniques using multianvil apparatus with sintered diamond anvils. J. Geophys. Res. 2009, 114, B02214. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Prakapenka, V.B.; Meng, Y.; Duffy, T.S. Intercomparison of pressure standards (Au, Pt, Mo, MgO, NaCl and Ne) to 2.5 Mbar. J. Geophys. Res. 2012, 117, B08210. [Google Scholar] [CrossRef]
- Dorogokupets, P.I.; Dewaele, A. Equations of state of MgO, Au, Pt, NaCl-B1, and NaCl-B2: Internally consistent high-temperature pressure scales. High Press. Res. 2007, 27, 431–446. [Google Scholar] [CrossRef]
- Takemura, K.; Dewaele, A. Isothermal equation of state for gold with a He-pressure medium. Phys. Rev. B 2008, 78, 104119. [Google Scholar] [CrossRef]
- Nellis, W.J. Adiabat-reduced isotherms at 100 GPa pressures. High Press. Res. 2007, 27, 393–407. [Google Scholar] [CrossRef]
- Nellis, W. Ultracondensed Matter by Dynamic Compression; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-108-22853-4. [Google Scholar]
- Zha, C.-S.; Mao, H.; Hemley, R.J. Elasticity of MgO and a primary pressure scale to 55 GPa. Proc. Natl. Acad. Sci. USA 2000, 97, 13494–13499. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.K.; Bell, P.M.; Shaner, J.W.; Steinberg, D.J. Specific volume measurements of Cu, Mo, Pd, and Ag and calibration of the ruby R1 fluorescence pressure gauge from 0.06 to 1 Mbar. J. Appl. Phys. 1978, 49, 3276–3283. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Mezouar, M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar] [CrossRef]
- Dewaele, A.; Torrent, M.; Loubeyre, P.; Mezouar, M. Compression curves of transition metals in the Mbar range: Experiments and projector augmented-wave calculations. Phys. Rev. B 2008, 78, 104102. [Google Scholar] [CrossRef]
- Lin, J.-F.; Degtyareva, O.; Prewitt, C.T.; Dera, P.; Sata, N.; Gregoryanz, E.; Mao, H.; Hemley, R.J. Crystal structure of a high-pressure/high-temperature phase of alumina by in situ X-ray diffraction. Nat Mater. 2004, 3, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Oganov, A.R.; Koyama, T.; Shimizu, H. Stability and compressibility of the high-pressure phases of Al2O3 up to 200 GPa: Implications for the electrical conductivity of the base of the lower mantle. Earth Planet. Sci. Lett. 2006, 246, 326–335. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Angel, R.J. Equations of State. Rev. Mineral. Geochem. 2000, 41, 35–59. [Google Scholar] [CrossRef]
- Besson, J.M.; Nelmes, R.J.; Hamel, G.; Loveday, J.S.; Weill, G.; Hull, S. Neutron powder diffraction above 10 GPa. Phys. B Condens. Matter 1992, 180–181, 907–910. [Google Scholar] [CrossRef]
















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stan, C.V.; Beavers, C.M.; Kunz, M.; Tamura, N. X-Ray Diffraction under Extreme Conditions at the Advanced Light Source. Quantum Beam Sci. 2018, 2, 4. https://doi.org/10.3390/qubs2010004
Stan CV, Beavers CM, Kunz M, Tamura N. X-Ray Diffraction under Extreme Conditions at the Advanced Light Source. Quantum Beam Science. 2018; 2(1):4. https://doi.org/10.3390/qubs2010004
Chicago/Turabian StyleStan, Camelia V., Christine M. Beavers, Martin Kunz, and Nobumichi Tamura. 2018. "X-Ray Diffraction under Extreme Conditions at the Advanced Light Source" Quantum Beam Science 2, no. 1: 4. https://doi.org/10.3390/qubs2010004
APA StyleStan, C. V., Beavers, C. M., Kunz, M., & Tamura, N. (2018). X-Ray Diffraction under Extreme Conditions at the Advanced Light Source. Quantum Beam Science, 2(1), 4. https://doi.org/10.3390/qubs2010004






