Modification of SiO₂, ZnO, Fe₂O₃ and TiN Films by Electronic Excitation under High Energy Ion Impact

Abstract

It has been known that the modification of non-metallic solid materials (oxides, nitrides, etc.), e.g., the formation of tracks, sputtering representing atomic displacement near the surface and lattice disordering are induced by electronic excitation under high-energy ion impact. We have investigated lattice disordering by the X-ray diffraction (XRD) of SiO₂, ZnO, Fe₂O₃ and TiN films and have also measured the sputtering yields of TiN for a comparison of lattice disordering with sputtering. We find that both the degradation of the XRD intensity per unit ion fluence and the sputtering yields follow the power-law of the electronic stopping power and that these exponents are larger than unity. The exponents for the XRD degradation and sputtering are found to be comparable. These results imply that similar mechanisms are responsible for the lattice disordering and electronic sputtering. A mechanism of electron–lattice coupling, i.e., the energy transfer from the electronic system into the lattice, is discussed based on a crude estimation of atomic displacement due to Coulomb repulsion during the short neutralization time (~fs) in the ionized region. The bandgap scheme or exciton model is examined.

1. Introduction

Material modification induced by electronic excitation under high-energy (> 0.1 MeV/u) ion impact has been observed for many non-metallic solids since the late 1950’s; for example, the formation of tracks (each track is characterized by a long cylindrical disordered region or amorphous phase in crystalline solids) in LiF crystal (photographic observation after chemical etching) by Young [1], in mica (a direct observation using transmission electron microscopy, TEM, without chemical etching, and often called a latent track) by Silk et al. [2], in SiO₂-quartz, crystalline mica, amorphous P-doped V₂O₅, etc. (TEM) by Fleischer et al. [3,4], in oxides (SiO₂-quartz, Al₂O₃, ZrSi₂O₄, Y₃Fe₅O₁₂, high-Tc superconducting copper oxides, etc.) (TEM) by Meftah et al. [5] and Toulemonde et al. [6], in Al₂O₃ crystal (atomic force microscopy, AFM) by Ramos et al. [7], in Al₂O₃ and MgO crystals (TEM and AFM) by Skuratov et al. [8], in Al₂O₃ crystal (AFM) by Khalfaoui et al. [9], in Al₂O₃ crystal (high resolution TEM) by O’Connell et al. [10], in amorphous SiO₂ (small angle X-ray scattering (SAXS)) by Kluth et al. [11], in amorphous SiO₂ (TEM) by Benyagoub et al. [12], in polycrystalline Si₃N₄ (TEM) by Zinkle et al. [13] and by Vuuren et al. [14], in amorphous Si_3.55N₄ (TEM) by Kitayama et al. [15], in amorphous SiN_0.95:H and SiO_1.85:H (SAXS) by Mota-Santiago et al. [16], in epilayer GaN (TEM) by Kucheyev et al. [17], in epilayer GaN (AFM) by Mansouri et al. [18], in epilayer GaN and InP (TEM) by Sall et al. [19], in epilayer GaN (TEM) by Moisy et al. [20], in InN single crystal (TEM) by Kamarou et al. [21], in SiC crystal (AFM) by Ochedowski et al. [22] and in crystalline mica (AFM) by Alencar et al. [23]. Amorphization has been observed for crystalline SiO₂ [5] and the Al₂O₃ surface at a high ion fluence (though the XRD peak remains) by Ohkubo et al. [24] and Grygiel et al. [25]. The counter process, i.e., the recrystallization of the amorphous or disordered regions, has been reported for SiO₂ by Dhar et al. [26], Al₂O₃ by Rymzhanov [27] and InP, etc., by Williams [28]. Density modification, i.e., a lower density in the track core surrounded by a shell with a higher density, has been observed for Al₂O₃ [10], amorphous SiO₂ [11], Si₃N₄ [14] and amorphous SiN_0.95:H and SiO_1.85:H [16]. Interestingly, an electrically conducting track formation in tetrahedral-amorphous carbon (sp³ into sp² bond transformation) has been observed by Gupta et al. [29]. The track radius, hillock height and diameter characterizing the surface morphology modification associated with the track are well described in terms of the electronic stopping power S_e (defined as the energy loss due to electronic excitation and ionization per unit path length), and the velocity effect has been noticed [12]. The threshold of S_e for the track formation has been reported [3,6,8,9,12,13,30] and the data appear to scatter, and it seems that the threshold S_e depends on the observation method of the track [12]. No track formation by monatomic ions has been observed in AlN [19].

Moreover, electronic sputtering (the erosion of solid materials caused by electronic energy deposition) has been observed for various compound solids: UO₂ by thermal-neutron-induced ²³⁵U fission fragments by Rogers [31,32] and by Nilsson [33], UO₂ by energetic ions by Meins et al. [34], Bouffard et al. [35] and Schlutig [36], H₂O ice by Brown et al. [37,38], Bottiger et al. [39], Baragiola et al. [40], Dartois et al. [41] and Galli et al. [42], frozen gas films of Xe, CO₂ and SF₆ [39], those of CO, Ar and N₂ by Brown et al. [43], CO₂ ice by Mejia et al. [44], SiO₂ by Qui et al. [45], Sugden et. al. [46], Matsunami et al. [47,48], Arnoldbik et al. [49] and Toulemonde et al. [50,51], MgAl₂O₄ [48], UF₄ ([34], by Griffith et al. [52] and Toulemonde et al. [53]), LiNbO₃ [45], Al₂O₃ ([45] and by Matsunami et al. [54]), various oxides by Matsunami et al. (SrTiO₃ and SrCeO₃ [47,54], CeO₂, MgO, TiO₂ and ZnO [54], Y₂O₃ and ZrO₂ [55], Cu₂O [56,57], WO₃ [58], CuO [59], Fe₂O₃ [60]), Si₃N₄ [45], Si₃N₄ and AlN by Matsunami et al. [55], Cu₃N by Matsunami et al. [56,61], LiF ([50], by Assmann et al. [62] and Toulemonde et al. [63]), KBr [56], NaCl [63], CaF₂ [53] and SiC [56]. The sputtering of frozen Xe films has been observed for low energy electron impact, against the anticipation of no atomic displacement [39], and the result confirms that the sputtering is caused by electronic excitation. Mechanisms of electronic excitation leading to atomic displacement will be discussed in Section 4.

As mentioned above, electronic sputtering has been observed for a variety of non-metallic materials, indicating that it seems to be a general phenomenon for non-metallic solids by high-energy ion impact. In many cases, ions with an equilibrium charge have been employed, which is usually attained by inserting thin foils, such as carbon, metals, etc., before impact on samples, and sputtered atoms are collected in carbon, metals, etc., followed by neutron activation and ion beam analysis to obtain sputtering yields. This article concerns the equilibrium charge incidence, though charge-state effects for non-equilibrium charge incidence have been observed and discussed ([23,29,34,49,52,58,62,64]). The electronic energy deposition or electronic stopping power (S_e) at the equilibrium charge can be calculated using a TRIM or SRIM code by Ziegler et al. [65,66], a CasP code by Grande et al. [67] and the nuclear stopping power (S_n, defined as the energy loss due to elastic collisions per unit path length) [65,66]. Characteristic features of the electronic sputtering by high-energy ions are as follows:

(a).

Electronic sputtering yields (Y_SP) are found to be larger by 10–10³ than nuclear sputtering yields due to elastic collision cascades, which can be estimated assuming linear dependence on S_n;

(b).

Y_SP super linearly depends on S_e and is approximated by the power-law fit: Y_SP = (B_SPS_e)^Nsp with 1 ≦ N_SP ≦ 4 for most cases, with B_SP being a material dependent constant.

Stoichiometric sputtering has been observed for many materials, whereas a considerable deviation from the stoichiometric sputtering has been reported for YBa₂Cu₃O₇ [68], Gd₃Ga₅O₁₂ and Y₃Fe₅O₁₂ [69] and CaF₂ and UF₄ [53]. Only the heavy element of U [31,32,33,34,35,36] and the light element of O [49] have been detected.

Besides track formation and electronic sputtering, lattice disordering (the degradation of X-ray diffraction (XRD) intensity) with lattice expansion (an increase in the lattice parameter) by high-energy ions has been observed for the polycrystalline films of SiO₂ [70] and WO₃ [58], and lattice disordering with lattice compaction for those of Cu₂O [57], CuO [59], Fe₂O₃ [60], Cu₃N [61] and Mn-doped ZnO [71]. Only lattice disordering has been observed for the ultra-thin films of WO₃ [72]. It should be noted that a comparison between high-energy and low-energy ion impact effects is important. Lattice expansion has been observed for a few keV D ion irradiation on Fe₂O₃ [73], and this can be understood by the incorporation of D into non-substitutional sites (incorporation or implantation effect). Thus, lattice expansion by medium-energy ions (100 keV Ne) on Fe₂O₃ [60] could be understood by Ne incorporation and/or interstitial-type defects generated by ion impact, with a possible stabilization by incorporating Ne in the film, whereas lattice compaction has been observed for a 100 MeV Xe ion impact on Fe₂O₃ [60]. It should be noted that the incorporation of ions in thin films does not take place for high-energy ions, since the projected range of ions (R_p) is much larger than the film thickness (e.g., R_p of 14 μm for 100 MeV Xe in SiO₂), unless the thickness is too large. The lattice expansion due to the incorporation effect has been observed for a few keV H and D irradiation at a low fluence on WNO_x with x ≈ 0.4, whereas lattice compaction has been observed at a high fluence of D [74]. Peculiarly, lattice expansion at a low ion fluence and compaction at a high fluence, as well as disordering, have been reported for medium-energy (100 keV Ne and N) and high-energy (100 MeV Xe and 90 MeV Ni) ion impact on WNO_x [75,76]. One speculation is that the lattice compaction is due to vacancy-type defects generated by ion impact, which is to be investigated. Furthermore, a drastic increase in electrical conductivity has been observed for Cu₃N [61], Mn-doped ZnO [71] and WNO_x with x ≈ 0.4 [75,76]. The conductivity increase is ascribed to the increase in the carrier concentration and mobility.

There are a few reports on the S_e dependence of the XRD intensity degradation per unit fluence (Y_XD) for SiC and KBr [56] and WO₃ [72]. Y_XD is found to follow the power-law fit: Y_XD = (B_XDS_e)^N_XD, B_XD being a material-dependent constant and the exponent N_XD being comparable with the Nsp of the electronic sputtering. The results imply that similar mechanisms operate for lattice disordering and electronic sputtering. It is of interest to compare the S_e dependence of lattice disordering with that of electronic sputtering for materials other than those mentioned above. In this paper, we have measured the lattice disordering of SiO₂, ZnO, Fe₂O₃ and TiN films, and the sputtering of TiN. The XRD results are compared with the sputtering. The exciton model is examined and scaling parameters are explored for representing electronic excitation effects.

2. Materials and Methods

XRD has been measured using Cu-k_α radiation. Accuracy of the XRD intensity is estimated to be approximately 10%, based on the variation of repeated measurements. Rutherford backscattering (RBS) has been performed with MeV He ions for evaluation of film thickness and composition. Similarly, accuracy of the RBS is estimated considering the variation of the repeated measurements. High-energy ion irradiation has been performed at room temperature and normal incidence. Irradiation of high-energy ion with lower incident charge than the equilibrium charge without carbon foil is often employed for the samples of XRD measurement; however, the effect of non-equilibrium charge incidence does not come into play because the length for attaining the equilibrium charge is much smaller than the film thickness, as described for each material in Section 3.

SiO₂ films have been grown by thermal oxidation of Si(001) at 1300 °C for 5 hr. According to XRD, the films are polycrystalline with diffraction peaks at ~21°, 22°, 31°, 33°, 36° and 69°, with very weak peak at 44° and 47°. The peaks at ~21°, 22°, 44° and 47° have been assigned to (100), (002), (004) and (202) diffraction of hexagonal-tridymite structure [70]. The strong peak at 69° is Si(004) and peak at 33° is possibly Si(002). Film thickness is ~1.5 μm and the composition is stoichiometric (O/Si = 2.0 ± 5%) by RBS of 1.8 MeV He. Film density is taken to be the same as that of amorphous-SiO₂ (a-SiO₂), since it has been derived to be 2.26 gcm⁻³ from XRD results, which is close to that of a-SiO₂ (2.2 gcm⁻³)

Pure ZnO films have been prepared on MgO (001) substrate by using a radio frequency magnetron sputtering (RFMS) deposition method with ZnO target, and it has been reported that the dominant growth orientation is (001) and (100) of hexagonal-wurtzite structure depending on the substrate temperature of 350 °C and 500 °C during the film growth, respectively [71,77,78]. The composition is stoichiometric, i.e., O/Zn = 1.0 ± 0.05, and film thickness is ~100 nm by He RBS. Here, the density is taken to be 4.2 × 10²² Zn cm⁻³ (5.67 gcm⁻³).

Preparation and characterization methods of Fe₂O₃ films are described in [60]. Briefly, Fe₂O₃ films have been prepared by deposition of Fe layers on SiO₂-glass and C-plane cut Al₂O₃ (C-Al₂O₃) substrates using a RFMS deposition method with Fe target (99.99%) and Ar gas, followed by oxidation at 500 °C for 2–5 hr in air. According to RBS of 1.4–1.8 MeV He ions, the composition is stoichiometric (O/Fe = 1.5 ± 0.1) and film thickness used in this study is ~100 nm. Here, the density of 3.96 × 10²² Fe cm⁻³ (5.25 gcm⁻³) is employed. Diffraction peaks have been observed at ~33° and 36°, and crystalline structure has been identified as hexagonal Fe₂O₃ (hematite or α-Fe₂O₃). These correspond to (104) and (110) diffraction planes.

TiN films have been prepared on SiO₂-glass, C-plane cut Al₂O₃ (C-Al₂O₃) and R-plane cut Al₂O₃ (R-Al₂O₃) substrates at 600°C using a RFMS deposition method with Ti target (99.5%) and high purity N₂ gas. RBS of 1.4–1.8 MeV He ions shows that the composition is stoichiometric (N/Ti = 1.0 ± 0.05) and that the film thickness used in this study is ~170 nm (deposition time of 1 hr). Here, the density of 5.25x10²² Ti cm⁻³ (5.4 gcm⁻³) is employed. Diffraction peaks have been observed at 36.6°, 42.6° and ~77° on SiO₂ glass and C-Al₂O₃. Crystalline structure has been identified as a cubic structure and these correspond to (111), (200) and (222) diffractions [79]. Diffraction intensity of (111) is larger than that of (200) on SiO₂ glass, and diffraction of (111) on C-Al₂O₃ is very intensive. TiN on R-Al₂O₃ has preferential growth orientation of (220) of a cubic structure (diffraction angle at ~61°). Sputtered atoms are collected in the carbon foil (100 nm) and the sputtered atoms are analyzed by RBS to obtain the sputtering yields [54] (carbon collector method).

3. Results and Discussion

3.1. SiO₂

The XRD intensity at the diffraction angle of ~22° (the most intensive (002) diffraction of hexagonal-trydimite) normalized to that of as-grown SiO₂ films on Si(001) is shown in Figure 1 as a function of the ion fluence for 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴ ion impact. The XRD intensity of the irradiated sample normalized to that of the unirradiated sample is proportional to the ion fluence to a certain fluence. Deviation from the linear dependence for the high fluence could be due to the overlapping effect. As observed in latent track formation (e.g., [5,6]), electronic excitation effects extend to a region (approximately cylindrical) with a radius of several nm and a length of the projected range or film thickness, and thus ions may hit the ion-irradiated part for a high ion fluence (called the overlapping effect). As described below, the XRD degradation yield per unit ion fluence (Y_XD) is reduced at a high fluence, and this could be understood as thermal annealing and/or a reduction in the disordered regions via ion-induced defects (recrystallization [26]). The damage cross-sections (A_D obtained by RBS-channeling (RBS-C) technique and TEM [5]) are compared with Y_XD in Figure 2, and it appears that both agree well for S_e > 10 keV. A discrepancy between A_D and Y_XD is seen for S_e < 10 keV, and the reason for this is not understood. In addition, sputtering yields are often reduced, and this is unlikely to be explained by the annealing effect. Therefore, the reasons for the sputtering suppression at a high fluence remain in question. The XRD degradation yields (Y_XD) per unit ion fluence are obtained and given in

Table 1. XRD data of SiO₂ films. Ion, incident energy (E in MeV), XRD intensity degradation (Y_XD), appropriate E* (MeV) considering the energy loss in the film and electronic stopping power in keV/nm (S_e*) appropriate for Y_XD (see text). S_e from SRIM2013. The deviation ∆S_e* = (S_e*/S_e(E) − 1) × 100 is also given.

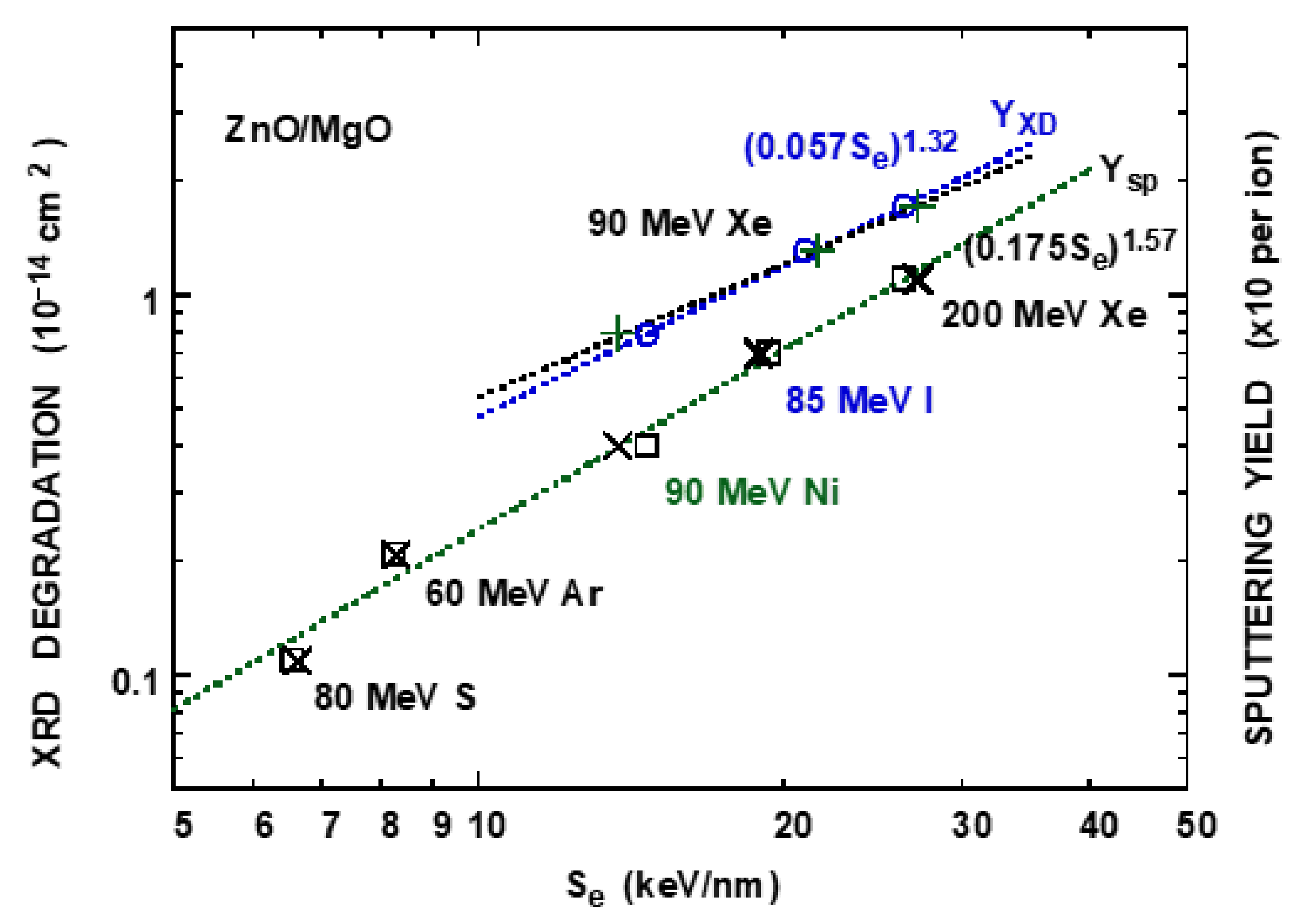
Ion	Energy	YXD	E*	Se*	∆Se*
	(MeV)	(10−12 cm2)	(MeV)	(keV/nm)	(%)
58Ni	90	0.066	84.5	7.246	−0.32
136Xe	100	0.27	91.0	11.56	−3.2
136Xe	200	0.475	189	14.22	−1.3

. The film thickness has been obtained to be ~1.5 μm, using 1.8 MeV He RBS. The attenuation length (L_XA) of Cu-k_α (8.0 keV) is obtained to be 128 μm [80] and the attenuation depth (L_XA·sin(22°/2)) = 24.3 μm. The film thickness (~1.5 μm) is much smaller than the attenuation depth and thus no correction is necessary for the XRD intensity. The lattice expansion or increase in the lattice parameter of 0.5% with an estimated error of 0.2% at 1 × 10¹² cm⁻² is found to be nearly independent of the electronic stopping power.

The electronic stopping power (S_e*) appropriate for XRD intensity degradation is calculated using SRIM 2013, using a half-way approximation that the ion loses its energy for half of the film thickness (~0.75 μm), i.e., S_e* = S_e(E*) with E* = E(incidence) − S_e(E) × 0.75 μm (Table 1). The correction for the film thickness on S_e appears to be a few percent. It is noticed that the incident charge (Ni⁺¹⁰, Xe⁺¹⁴) differs from the equilibrium charge (+19, +25 and +30 for 90 MeV Ni, 100 MeV Xe and 200 MeV Xe, respectively (Shima et al.) [81], and +18.2, +23.9 and +29.3 (Schiwietz et al.) [82]), both being in good agreement. Following [64], the characteristic length (L_EQ = 1/(electron loss cross-section times N)) for attaining the equilibrium charge is estimated to be 8.7, 8.3 and 7.9 nm for 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴, respectively, from the empirical formula of the single-electron loss cross-section σ_1L (10⁻¹⁶ cm²) of 0.52 (90 MeV Ni⁺¹⁰), 0.55 (100 MeV Xe⁺¹⁴) and 0.57 (200 MeV Xe⁺¹⁴) [83,84], N (2.2 × 10²² Si cm⁻³) being the density, and (target atomic number)^2/3 dependence being included. Here, σ_1L = σ_1L(Si) + 2σ_1L(O), ionization potential I_P = 321 eV [85,86] with the number of removable electrons N_eff = 8 and I_P = 343 eV with N_eff = 12 are employed for Ni⁺¹⁰ and Xe⁺¹⁴. L_EQ is much smaller than the film thickness and hence the charge-state effect is insignificant.

The sputtering yields Y_sp of SiO₂ (normal incidence) are summarized in

Table 2. Sputtering data of SiO₂ (normal incidence). Ion, incident energy (E in MeV), energy (E* in MeV) corrected for the energy loss in carbon foils (see footnote), electronic stopping power (S_e), nuclear stopping power (S_n), projected range (R_p) and sputtering yield (Y_SP). S_e, S_n and R_p are calculated using SRIM2013. (S_e(E*)/S_e(E) − 1), (S_n(E*)/S_n(E) − 1) and (R_p(E*)/R_p(E) − 1) in % are given in the parentheses after S_e(E*), S_n(E*) and R_p(E*), respectively. Y_SP in the parenthesis is for SiO₂ films. S_e(E) by CasP is also listed. Y_EC is the calculated sputtering yield due to elastic collisions.

Ion	E(E*)	Se(E*)	Sn(E*)	Rp(E*)	YSP	Se(CasP)	YEC
	(MeV)	(keV/nm)	(keV/nm)	(μm)		(keV/nm)
Qiu et al. [45]
35Cl	5 (4.6)	2.59 (−4.26)	0.0426 (6.8)	3.0 (−4.6)	5.1 (4.4)	1.87	0.12
35Cl	20 (19.4)	4.15 (−0.35)	0.0134 (2.7)	7.0 (−2.0)	8.77 (8.22)	3.83	0.036
Sugden et al. [46]
35Cl	30 (29.9)	4.24 (−2.4 × 10−3)	9.3 × 10−3 (0.3)	9.5 (−0.25)	11	3.99	0.025
Matsunami et al. [47,48]
58Ni	90 (89)	7.265 (−0.055)	0.0145 (0.84)	18.3 (−0.60)	120	7.66	0.039
136Xe	100 (99)	11.88 (−0.49)	0.091 (1.2)	14.4 (−0.83)	362	14.0	0.246
136Xe	200 (198)	14.37 (−0.19)	0.051 (0.73)	21.9 (−0.51)	404	16.0	0.138
40Ar	60 (60)	4.40	6.5 × 10−3	16.3	32	4.19	0.018
32S	80 (80)	3.49	3.3 × 10−3	23	9.7	3.23	0.0089
Arnoldbik et al. [49]
63Cu	50 (50)	7.17	0.027	11.6	80	7.55	0.073
Toulemonde et al. [51]
197Au	190 (190)	16.9	0.143	20.5	1425	20.9	0.39
197Au	190 (190)				1320
197Au	197 (197)	17.1	0.14	20.9	1110	21.2	0.38
197Au	210 (210)	17.4	0.13	21.7	1230	21.7	0.36
127I	148 (148)	12.9	0.06	20	525	15.3	0.16
58Ni	69 (69)	7.15	0.018	15.5	135	7.75	0.049

Equilibrium charge has been obtained by using carbon foils of 120 nm [45], 25 nm [46], 100 nm [47,48], 20 nm [49] and 50 nm [51].

for the comparison of the S_e dependence of the XRD degradation yields Y_XD. There are various versions of TRIM/SRIM starting in 1985, and in this occasion, the results used the latest version of SRIM2013 are compared with those earlier versions. Firstly, the correction on the stopping power and projected range for carbon foils (20–120 nm), which have been used to achieve the equilibrium charge incidence, is less than a few %, except for low-energy Cl ions (several %). Secondly, S_e by CasP (version 5.2) differs ~30% from that by SRIM 2013. Figure 2 shows the S_e dependence of the XRD degradation yields Y_XD and Y_sp. Both Y_XD and Y_sp fit to the power-law of S_e, and the exponents of XRD degradation N_XD = 2.9 and N_sp = 3 (sputtering) are almost identical, indicating that the same mechanism is responsible for lattice disordering and sputtering. Further plotted is the sputtering yields vs. S_e calculated using earlier versions of TRIM/SRIM (TRIM1985 to SRIM2010) [45,46,47,48,49,51], and the plot using earlier versions give the same exponent (N_sp = 3) with a 6% smaller constant B_sp in the power-law fit (20% smaller in the sputtering yields). This means that the plot and discussion using SRIM2013 do not significantly differ from those using the earlier versions of TRIM/SRIM. One notices that no appreciable difference in sputtering yields is observed among a-SiO₂, films and single-crystal-SiO₂ (c-SiO₂) [45,46,47,48], even though the density of c-SiO₂ is larger by 20% than that of a-SiO₂, whereas much smaller yields (by a factor of three) have been observed for c-SiO₂ [51]. The discrepancy remains in question. Sputtering yields Y_EC, which are due to elastic collision cascades, is estimated assuming Y_EC is proportional to the nuclear stopping power, discarding the variation of the α-factor (order of unity) depending on the ratio of target mass over ion mass (Sigmund) [87]. The proportional constant is obtained to be 2.7 nm/keV using the sputtering yields by low-energy ions (Ar and Kr) (Betz et al.) [88]. Y_EC is given in Table 2 and it is shown that Ysp/Y_EC ranges from 44 (5 MeV Cl) to 3450 (210 MeV Au).

In order to obtain the stopping powers (S) for the non-metallic compounds, such as SiO₂, described above, we apply the Bragg’s additive rule, e.g., S(SiO₂) = S(Si) + 2S(O) and S of the constituting elements is calculated using TRIM/SRIM and CasP codes. Before moving to the discussion of the Bragg’s deviation, the accuracy of S is briefly mentioned. It is estimated to be 8% (Be through U ions in Ag) near the maximum of S (~0.8 MeV/u) [66], 17% (K to U ions in Au) (Paul) [89]. Besenbacher et al. have reported no difference between solid and gas phases for 0.5–3 MeV He ion stopping in Ar with an experimental accuracy of 3% [90], and this could be understood by the fact that the binding energy (cohesive energy) of solid Ar is too small (0.08 eV (Kittel) [91]), compared with the ionization potential (I_Bethe) of 188 eV [92], to affect the stopping. On the other hand, Arnau et al. have reported a large deviation (~50% near the stopping power maximum at ~50 keV) for proton stopping between solid and gas phases of Zn, and the deviation reduces ~10% at ~1 MeV [93]. The cohesive energy of 1.35 eV [91] is much smaller than the mean ionization potential I_Bethe of 330 eV [92], and hence the small increase in I_Bethe cannot explain the Bragg’s deviation of Zn. They have argued that the difference in the 4s into 4p transition probability and screening effect between solid and gas phases are responsible. Both TRIM/SRIM and CasP codes are based on the experiments of conveniently available solid targets and molecular gas (e.g., N₂, O₂), and thus it is anticipated that the binding effect is included to some or large extent and that the Bragg’s deviation is not serious for nitrides and oxides, and is roughly 10% or less at around 1 MeV/u.

3.2. ZnO

The XRD intensity at a diffraction angle of ~34° ((001) diffraction) and 32° ((100) diffraction) normalized to those of unirradiated ZnO films on the MgO substrate is shown in Figure 3 as a function of the ion fluence for 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴ ion impact. It appears that the XRD intensity degradation is nearly independent of the diffraction planes. The XRD intensity degradation per unit fluence Y_XD is given in

Table 3. XRD data of ZnO films. Ion, incident energy (E in MeV), XRD intensity degradation (Y_XD), E* = E − ∆E (energy loss in carbon foil of 100 nm) (MeV) and electronic (S_e*) and nuclear (S_n*) stopping powers in keV/nm and projected range R_p* (μm) at E* calculated using SRIM2013. Sputtering yield Y_sp from [54]. Sputtering yield by 100 keV Ne ion is also given.

Ion	Energy	YXD	E*	Se*	Sn*	Rp*	Ysp
	(MeV)	(10−14 cm2)	(MeV)	(keV/nm)	(keV/nm)	(μm)
32S	80		80	6.62	0.007	13	1.09
40Ar	60		60	8.3	0.014	9.5	2.08
58Ni	90	0.788	89	13.72	0.031	11	4.0
127I	85		84	18.92	0.205	8.8	7.0
136Xe	100	1.3	99	21.60	0.20	8.8
136Xe	200	1.7	198	27.14	0.112	13	11
20Ne	0.10	0.10		0.29	0.24	0.12	0.9

, together with sputtering yields [54], stopping powers and projected ranges (SRIM2013). The X-ray (Cu-kα) attenuation length L_XA is obtained to be 36.6 μm [80] and the attenuation depth is 11 and 10 μm for the diffraction angle of ~34° and 32°, respectively; thus, the X-ray attenuation correction is unnecessary. It appears that the appropriate energy for the Y_XD vs. S_e plot, E − S_eℓ/2, where ℓ = a film thickness of ~100 nm, is nearly the same as E* for sputtering, in which the energy loss of a carbon foil of 100 nm is considered. Similarly to the case of SiO₂, the characteristic length (L_EQ) is estimated to be 4.6, 4.4 and 4.2 nm for 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴, respectively, from the empirical formula of the single-electron loss cross-section σ_1L(10⁻¹⁶ cm²) of 0.52 (90 MeV Ni⁺¹⁰), 0.54 (100 MeV Xe⁺¹⁴) and 0.57 (200 MeV Xe⁺¹⁴) [83,84]. Here, σ_1L = σ_1L(Zn) + σ_1L(O), and the ionization potential I_P and N_eff are described in Section 3.1. Again, L_EQ is much smaller than the film thickness and the charge-state effect is insignificant.

Figure 4 shows the XRD intensity degradation Y_XD vs. electronic stopping power (S_e) (SRIM2013 and TRIM1997) together with the sputtering yields Y_sp vs. S_e. Both Y_XD and Y_sp follow the power-law fit and the exponent for Y_XD using TRIM1997 gives a slightly larger value than that using SRIM2013. The exponent of lattice disordering is nearly the same as that of sputtering. The change in the lattice parameter ∆ℓc appears to scatter, and roughly −0.2% and −0.1% with an estimated error of 0.1% are obtained for (100) and (002) diffractions by 100 MeV Xe at 10 × 10¹² cm⁻², assuming that ∆ℓc is proportional to the ion fluence. ∆ℓc is obtained at −0.3% for (002) diffraction by 200 MeV Xe at 5 × 10¹² cm⁻², and no appreciable change in the lattice parameter is observed by 90 MeV Ni ions at 40 × 10¹² cm⁻²; more data are desired.

3.3. Fe₂O₃

The XRD intensity at a diffraction angle of ~33° and 36° (corresponding to diffraction planes of (104) and (110)) normalized to those of unirradiated Fe₂O₃ films on C-Al₂O₃ and SiO₂ glass substrates as a function of the ion fluence is shown in Figure 5 for 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴ ion impact. It appears that the XRD intensity degradation is nearly independent of the diffraction planes and substrates. The XRD intensity degradation per unit fluence Y_XD is given in

Table 4. XRD data of Fe₂O₃ films. Ion, energy (E in MeV), XRD intensity degradation (Y_XD), E* = E-∆E (energy loss in carbon foil of 100 nm) (MeV) and electronic (S_e*) and nuclear (S_n*) stopping powers in keV/nm and projected range R_p* (μm) calculated using SRIM2013. Sputtering yield Y_sp from [60]. Results by low energy (100 keV Ne) ion are also given.

Ion	Energy	YXD	E*	Se*	Sn*	Rp*	Ysp
	(MeV)	(10−12 cm2)	(MeV)	(keV/nm)	(keV/nm)	(μm)
58Ni	90	0.12	89	14.28	0.030	9.8	38.3
136Xe	100	0.38	99	23.25	0.19	7.9	57.9
136Xe	200	0.60	198	28.27	0.11	11.7	81.7
20Ne	0.10		0.10	0.354	0.258	0.12	2.3

, together with the sputtering yields [60] and stopping powers (SRIM2013). The X-ray (Cu-kα) attenuation length L_XA is obtained to be 8.8 μm [80] and the attenuation depth is 2.5 and 2.7 μm for the diffraction angle of ~33° and 36°, respectively, which are much larger the film thickness of ~100 nm and thus the X-ray attenuation correction is unnecessary. The appropriate energy for the XRD vs. S_e plot, using half-way approximation (E − S_eℓ/2) with the film thickness ℓ of ~100 nm, again gives nearly the same as E* for sputtering, in which the energy loss of the carbon foil of 100 nm is taken into account.

Similarly to SiO₂ and ZnO, the characteristic length (L_EQ) is estimated to be 4.5, 4.3 and 4.1 nm for 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴, respectively, from the empirical formula of the single-electron loss cross-section σ_1L(10⁻¹⁶ cm²) of 0.56 (90 MeV Ni⁺¹⁰), 0.59 (100 MeV Xe⁺¹⁴) and 0.61 (200 MeV Xe⁺¹⁴) [83,84]. Here, σ_1L = σ_1L(Fe) + 1.5σ_1L(O). L_EQ is much smaller than the film thickness and the charge-state effect does not come into play.

Figure 6 shows XRD intensity degradation Y_XD vs. electronic stopping power (S_e) (SRIM2013 and TRIM1997) together with the sputtering yields Y_sp vs. S_e. Both Y_XD and Y_sp follow the power-law fit and the exponent using TRIM1997 gives a slightly larger fit than those using SRIM2013. The exponent of lattice disordering is two times larger than that of sputtering (N_sp is exceptionally close to unity, in contrast to the SiO₂ and ZnO cases). The change in the lattice parameter appears to scatter depending on the substrate and diffraction planes, and is not proportional to the ion fluence. The average of the lattice parameter change in the (104) and (110) diffractions of Fe₂O₃ on C-Al₂O₃ is −0.2, −0.3% (an estimated error of 0.1%) and nearly zero at ~1 × 10¹² cm⁻² for 200 MeV Xe, 100 MeV Xe and 90 MeV Ni ion impact. The dependence of the lattice parameter change on the ion fluence and S_e is complicated, and is to be investigated.

3.4. TiN

The XRD patterns are shown in Figure 7 for unirradiated and irradiated TiN films on the SiO₂ glass substrate. As already mentioned in Section 2, (111) and (200) diffraction peaks are observed and the XRD intensity decreases due to ion impact. Figure 8 shows XRD intensities normalized to those of unirradiated TiN films on SiO₂ glass, C-Al₂O₃ and R-Al₂O₃ substrates as a function of the ion fluence. It is seen that the XRD intensity degradation is nearly the same for the diffraction planes of (111) and (200) on SiO₂, and for (111) on C-Al₂O₃. The XRD intensity degradation is less sensitive to the ion impact for the diffraction plane (220) on the R-Al₂O₃ substrate (~30% smaller than that for (111) and (200) on SiO₂, and for (111) on C-Al₂O₃). The XRD intensity degradation per unit fluence Y_XD for (111) and (200) diffractions is given in

Table 5. XRD data of TiN films. Ion, energy (E in MeV), XRD intensity degradation (Y_XD) for (111) and (200) diffraction on SiO₂ and C-Al₂O₃, substrates, Y_XD for (220) diffraction on R-Al₂O₃ in the parenthesis, E* = E − ∆E (energy loss in carbon foil of 100 nm) (MeV) and electronic (S_e*) and nuclear (S_n*) stopping powers in keV/nm and projected range R_p* (μm) calculated using SRIM2013 and sputtering yield Y_sp of Ti. S_e* (TRIM1997) is given in parenthesis.

Ion	Energy	YXD	E*	Se*	Sn*	Rp*	Ysp(Ti)
	(MeV)	(10−12 cm2)	(MeV)	(keV/nm)	(keV/nm)	(μm)
40Ar	60	0.14	60	9.41 (9.33)	0.0135	7.6	51.8
58Ni	90	0.27 (0.2)	89	15.5 (16.5)	0.0305	8.6	147
136Xe	100	0.50 (0.35)	99	26.7 (25.5)	0.19	6.9	380
136Xe	200	0.60	198	30.85 (30.25)	0.11	10	529

, together with sputtering yields and stopping powers (TRIM1997 and SRIM2013). No appreciable change in the lattice parameter is observed, as shown in Figure 7. Similarly to the SiO₂, ZnO and Fe₂O₃ cases, the appropriate energy, E − S_eℓ/2, ℓ = film thickness of ~170 nm is taken into account, and the energy is close to that for sputtering, in which the energy loss of the carbon foil of 100 nm is considered. The X-ray (Cu-kα) attenuation length L_XA is obtained to be 11.8 μm [80], and the attenuation depth is 3.7, 4.3 and 6.0 μm for diffraction angles of 36.6°, ~43° and 61°, respectively; thus, the X-ray attenuation correction is insignificant.

The characteristic length (L_EQ) is estimated to be 4.5, 4.4, 4.2 and 4.0 nm for 60 MeV Ar⁺⁷, 90 MeV Ni⁺¹⁰, 100 MeV Xe⁺¹⁴ and 200 MeV Xe⁺¹⁴, respectively, from the empirical formula of the single-electron loss cross-section σ_1L(10⁻¹⁶ cm²) of 0.43 (60 MeV Ar⁺⁷), 0.44 (90 MeV Ni⁺¹⁰), 0.46 (100 MeV Xe⁺¹⁴) and 0.48 (200 MeV Xe⁺¹⁴) [83,84]. Here, σ_1L = σ_1L(Ti) + σ_1L(N), and the ionization potential I_P and N_eff are (I_P = 143 eV and N_eff = 1) for Ar⁺⁷, with those described in Section 3.1 for Ni⁺¹⁰ and Xe⁺¹⁴. L_EQ is much smaller than the film thickness, and hence the charge-state effect is insignificant.

It is found that sputtered Ti collected in the carbon foil is proportional to the ion fluence, as shown in Figure 9 for 60 MeV Ar, 90 MeV Ni, 100 MeV Xe and 200 MeV Xe ions. The sputtering yield of Ti is obtained using the collection efficiency of 0.34 in the carbon foil collector [47] and the results are given in Table 5. Sputtered N collected in the carbon foil is obtained to be 0.4 × 10¹⁴ and 0.44 × 10¹⁴ cm⁻² with an estimated error of 20% for 200 MeV Xe at 0.22 × 10¹² cm⁻² and 60 MeV Ar at 2.8 × 10¹² cm⁻², respectively, and this is comparable with the Ti areal density of 0.4 × 10¹⁴ cm⁻² (200 MeV Xe) and 0.475 × 10¹⁴ cm⁻² (60 MeV Ar). The results imply stoichiometric sputtering, due to the collection efficiency of N in the carbon foil collector of 0.35 [55], which is close to that of Ti. Thus, the total sputtering yield (Ti + N) is obtained by doubling Y_sp (Ti) in Table 5. The sputtering yields of TiN (Y_EC) due to elastic collisions can be estimated assuming that Y_EC is proportional to the nuclear stopping power. Here, the proportional constant is obtained to be ~1.6 nm/keV using the experimental yields of 0.527 (0.6 keV Ar) and 0.427 (0.6 keV N) [94] and 0.7 (0.5 keV Cd) [88]. Y_sp(TiN)/Y_EC ranges from 2.5 × 10³ to 6 × 10³. The XRD intensity degradations Y_XD and Y_sp(Ti + N) are plotted as a function of the electronic stopping power S_e in Figure 10. It appears that both fit to the power-law: Y_XD = (0.0224S_e)^1.26 and Y_sp = (1.17S_e)^1.95. The exponents are comparable for XRD intensity degradation and sputtering.

4. Discussion

4.1. Comparison of Lattice Disordering with Sputtering

The electronic stopping power (S_e) dependence of lattice disordering Y_XD, together with electronic sputtering, is summarized in

Table 6. Summary of electronic stopping power (S_e in keV/nm) dependence of lattice disordering Y_XD = (B_XDS_e)^NXD for the present results of SiO₂, ZnO, Fe₂O₃ and TiN films, and sputtering yields Y_sp = (B_spS_e)^Nsp of the present result for TiN. Lattice disordering and sputtering yields of WO₃ film from [58,72], those of KBr and SiC from [56] and sputtering yields of SiO₂, ZnO and Fe₂O₃ (see Section 3). Constant B_XD and B_sp and the exponent N_XD and N_sp are obtained using TRIM1997 and those using SRIM2013 are in parentheses. Y_XD at S_e = 10 keV and Y_XD/Y_sp (10⁻¹⁵ cm²) are given.

Sample	BXD	NXD	Bsp	Nsp	YXD	YXD/Ysp
	(nm/keV)		(nm/keV)		(10−12 cm2)	(10−15 cm2)
					(Se = 10 keV/nm)
SiO2	0.055 (0.0545)	3.4 (2.9)	0.58 (0.62)	3.0 (3.0)	0.13	0.67
ZnO	0.057 (0.0585)	1.32 (1.16)	0.175	1.57	0.476	198
Fe2O3	0.029 (0.028)	2.54 (2.28)	1.16 (2.2)	1.25 (1.05)	0.043	2.0
TiN	0.0224	1.26	1.17	1.95	0.15	1.26
WO3	0.07355	2.65	0.65	3.6	0.44	0.53
KBr	0.127	2.4	0.77	3.0	1.78	3.9
SiC	0.0377	1.97	1.86	1.53	0.15	1.7

, recognizing that most of the data have used TRIM1997. Results using SRIM2013 and TRIM1997 are compared in Section 3. Both exponents of the power-law fits are similar for SiO₂, ZnO, Fe₂O₃, TiN and WO₃ films, as well as for KBr and SiC. As mentioned in Section 3, it can be seen that the exponent of the lattice disordering N_XD is comparable with that of sputtering N_sp, except for Fe₂O₃, in which N_sp is exceptionally close to unity, as in the case of Cu₂O (N_sp = 1.0) [56] and CuO (N_sp = 1.08) [59]. The similarity of the exponent of lattice disordering and sputtering for SiO₂, ZnO, Fe₂O₃, TiN, WO₃, KBr and SiC imply that both phenomena originate from similar mechanisms, despite the fact that small displacements and annealing and/or the reduction in disordering via ion-induced defects are involved in the lattice disordering, whereas large displacements are involved in sputtering. The result of Fe₂O₃ indicates that the electronic excitation is more effective for lattice disordering. In the case of CuO, N_XD is nearly zero [59]. In Table 6, Y_XD (10⁻¹² cm²) at S_e = 10 keV/nm and Y_XD/Y_sp (×10⁻¹⁵ cm²) are listed. It is found that the ratio Y_XD/Y_sp is an order of 10⁻¹⁵ cm², except for ZnO, where the sputtering yields are exceptionally small. More data of lattice disordering would be desired for further discussion.

4.2. Electron–Lattice Coupling

Three models have been suggested for atomic displacement induced by electronic excitation: Coulomb explosion (CE) [3,4], thermal spike (TS) [50] and exciton model [30,95,96,97]. The neutralization time of the ionized region along the ion path is generally too short, and the fraction of the charged sputtered ions is small, e.g., 100 MeV Xe ions on SiO₂ glass [48]. Hence, the CE model is unsound. However, a small atomic separation during the short time might be enough for electron–lattice coupling (a key for electronic excitation effects), which will be discussed later. A crude estimation of the evaporation yield for SiO₂ based on the TS model appears to be far smaller than the experimental sputtering yield [55] and thus the TS model is also unsound. Moreover, the electron–lattice coupling or transfer mechanism of electronic energy into the lattice is not clear in the model. In the exciton model, the non-radiative decay of self-trapped excitons (STX, i.e., localized excited-state of electronic system coupled with lattice) leads to atomic displacement. According to the exciton model (or bandgap scheme), it is anticipated that the energy of the atoms in motion from the non-radiative decay of STX is comparable with the bandgap, leading to a larger sputtering yield with a larger bandgap, discarding the argument for the efficiency of STX generation from the electron–hole pairs, which is inversely proportional to the bandgap. This bandgap scheme is examined below. The effective depth contributing to the electronic sputtering of WO₃ has been obtained to be 40 nm, which is nearly independent of S_e [98], which would shed light on understanding the electronic sputtering; therefore, more data are desired.

The electronic sputtering yield Y_sp super-linearly depends on the electronic stopping power (S_e), and Y_sp at S_e = 10 keV/nm is taken to be a representative value, which is plotted as a function of the bandgap (E_g) in Figure 11 from [56], including the present TiN result. The optical absorbance (defined as log₁₀(I_o/I), I_o and I being the incident and transmitted photon intensities) of TiN films are measured, and the direct bandgap E_g is obtained to be 4.5 eV for a film thickness of 25–50 nm, which decreases to 2.8 eV for a film thickness of ~180 nm by using the relation: (absorbance ● photon energy)² is proportional to photon energy—E_g. The thickness dependence of E_g is under investigation by considering the influence of the reflectivity, film growth conditions and experimental problems, such as stray light, etc. A large variation has been reported for E_g, 4.0 eV (film thickness of 260 nm on Si substrate) (Popovic et al.) [99], 3.4 eV (thickness of ~100 nm on glass substrate) (Solovan et al.) [100] and 2.8–3.2 eV (film thickness of 460 nm on glass substrate) (Kavitha et al.) [101]. In this study, E_g is taken to be 4 eV and this choice is tolerable in the following discussion. It has been reported that the bandgap is reduced by 0.06 eV under a 400 KeV Xe ion implantation at 10¹⁶ cm⁻² [99]. High-energy ion impact effects on optical properties are under way. It can be observed that the bandgap scheme seems to work for E_g > 3 eV [56]. A large deviation (two orders of magnitude) from the upper limit (dashed line indicated in Figure 11) is observed for ZrO₂, MgO, MgAl₂O₄ and Al₂O₃. The existence of STX is known for limited materials, rare gas solids, SiO₂ and alkali halides [30,95,96]. The STX does not exist for MgO and probably does not exist for Al₂O₃ [102]. The deviation for MgO and Al₂O₃ could be explained by the non-existence of STX. The numbers of electron–hole pairs leading to STX are inversely proportional to E_g, which could be a reason for the dependence of the sputtering yields for E_g < 3 eV. In any case, the single parameter of the band gap is insufficient for the explanation of the bandgap dependence of the sputtering yields.

Martin et al. [102] argued that STX exists for materials with small elastic constants. Following this suggestion, sputtering yields are plotted as a function of the elastic constant (C₁₁) in Figure 12. Here, C₁₁ (GPa) is taken to be 87 (SiO₂), 348 (SrTiO₃), 497 (Al₂O₃), 294 (MgO), 270 (TiO₂), 210 (ZnO), 299 (MgAl₂O₄), 242 (Fe₂O₃), 35 (KBr) and 114 (LiF) [85], and, for other materials, 403 (CeO₂) [103], 224 (Y₂O₃) [104], 400 (ZrO₂) [105], 13 (WO₃) [106], 126 (Cu₂O) [107], 135 (CuO) [108], 388 (Si₃N₄) as an average of the values [109,110], 345 (polycrystalline-AlN) [111], which is smaller by 16% than 410 (AlN single crystal) [112], 234 (Cu₃N) [113], 500 (SiC) [114] and 625 (TiN) [115]. It can be observed for oxides (the most abundant data are available at present) that Y_sp decreases exponentially with an increase in the elastic constant for C₁₁ < 300 GPa, except for MgO and ZrO₂. Y_sp for nitrides and SiC is larger than that for oxides at a given C₁₁, and these are to be separately treated. It can be understood that the elastic constant represent the resistance of lattice deformation by electronic energy deposition. However, a single parameter, either the bandgap or elastic constant, is not adequate, and at least one more parameter is necessary. Furthermore, parameters other than those mentioned above are to be explored. More data for nitrides, alkali halides and especially carbides are desired.

Finally, a mechanism for the electron–lattice coupling is discussed. In an ionized region along the ion path, Coulomb repulsion leads to atomic motion, which is not adequate to cause sputtering because of its short neutralization time. Nevertheless, displacement comparable with the lattice vibration amplitude (one tenth of the average atomic separation, d_av of ~0.25 nm for a-SiO₂) is highly achievable during the neutralization time. As a first step, the time required for the Si⁺–O⁺ displacement of 0.025 nm (one tenth of d_av) from d_av is estimated to be ~15 fs using a formula [116]. Also, the time is estimated to be ~ 15 fs and ~ 12 fs for the Zn⁺–O⁺ displacement of 0.02 nm from d_av of 0.2 nm in ZnO and for the Ti⁺–N⁺ displacement of 0.02 nm from d_av of 0.2 nm in TiN, respectively. A similar situation has been reported for the Fe⁺–O⁺ displacement of 0.01 nm in Fe₂O₃ (~7 fs) [60], the K⁺–Br⁺ displacement of 0.01 nm in KBr (~9 fs) and the Si⁺–C⁺ displacement of 0.01 nm in SiC (~6 fs). These suggest a possibility that a small displacement comparable with the lattice vibration amplitude caused by Coulomb repulsion during the short neutralization time leads to the generation of a highly excited-state coupled with the lattice (h-ESCL), and h-ESCL is considered to be equivalent to STX or multi STX. The non-radiative decay of h-ESCL leads to atomic displacement (a larger displacement results in sputtering and smaller displacement results in phonon generation or lattice distortion).

5. Conclusions

We have measured the lattice disordering of polycrystalline SiO₂, ZnO, Fe₂O₃ and TiN films, as well as the sputtering yield of TiN, by high-energy ion impact. It is found that lattice disordering is caused by electronic excitation and the degradation of the XRD intensity fits to the power-law on the electronic stopping power. The exponent in the fit of the XRD degradation is comparable with that of the electronic sputtering yield for these films, as well as the published results of WO₃, KBr and SiC, implying that both lattice disordering and sputtering originate from similar mechanisms. In the case of Fe₂O₃, on the other hand, the exponent of the lattice disordering is larger by twice than that of the sputtering (the exponent for the sputtering is close to unity). The exciton mechanism seems to work for Eg > 3 eV, with some exceptions, and the elastic constant is examined as another scaling parameter for the electronic sputtering yields. A possibility of electron–lattice coupling is discussed based on a crude estimation that an atomic displacement comparable with the vibration amplitude due to Coulomb repulsion during the short neutralization time in the ionized region along the ion path can be attainable and, thus, the generation of a highly excited state coupled with the lattice is highly achievable, resulting in atomic displacement.