Simulation Dosimetry Studies for FLASH Radiation Therapy (RT) with Ultra-High Dose Rate (UHDR) Electron Beam
Abstract
:1. Introduction
2. Materials and Methods
2.1. FLASH-RT Conditions
- Irradiation time ti < 100 ms;
- Average dose rate > 100 Gy/s;
- In-peak dose rate > 106 Gy/s;
- Pulse repetition frequency PRF > 100 Hz;
- Dose per pulse > 1 Gy.
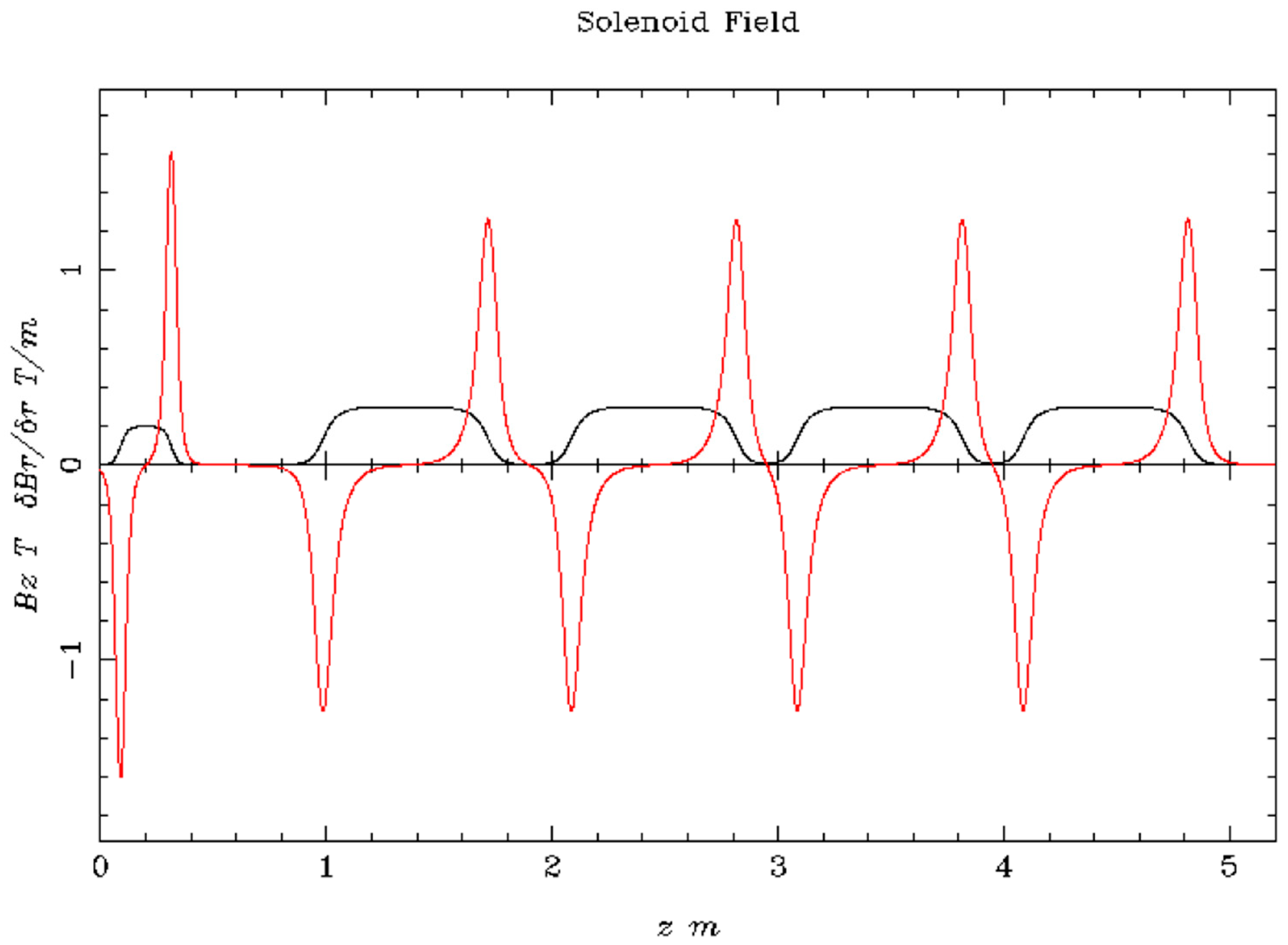
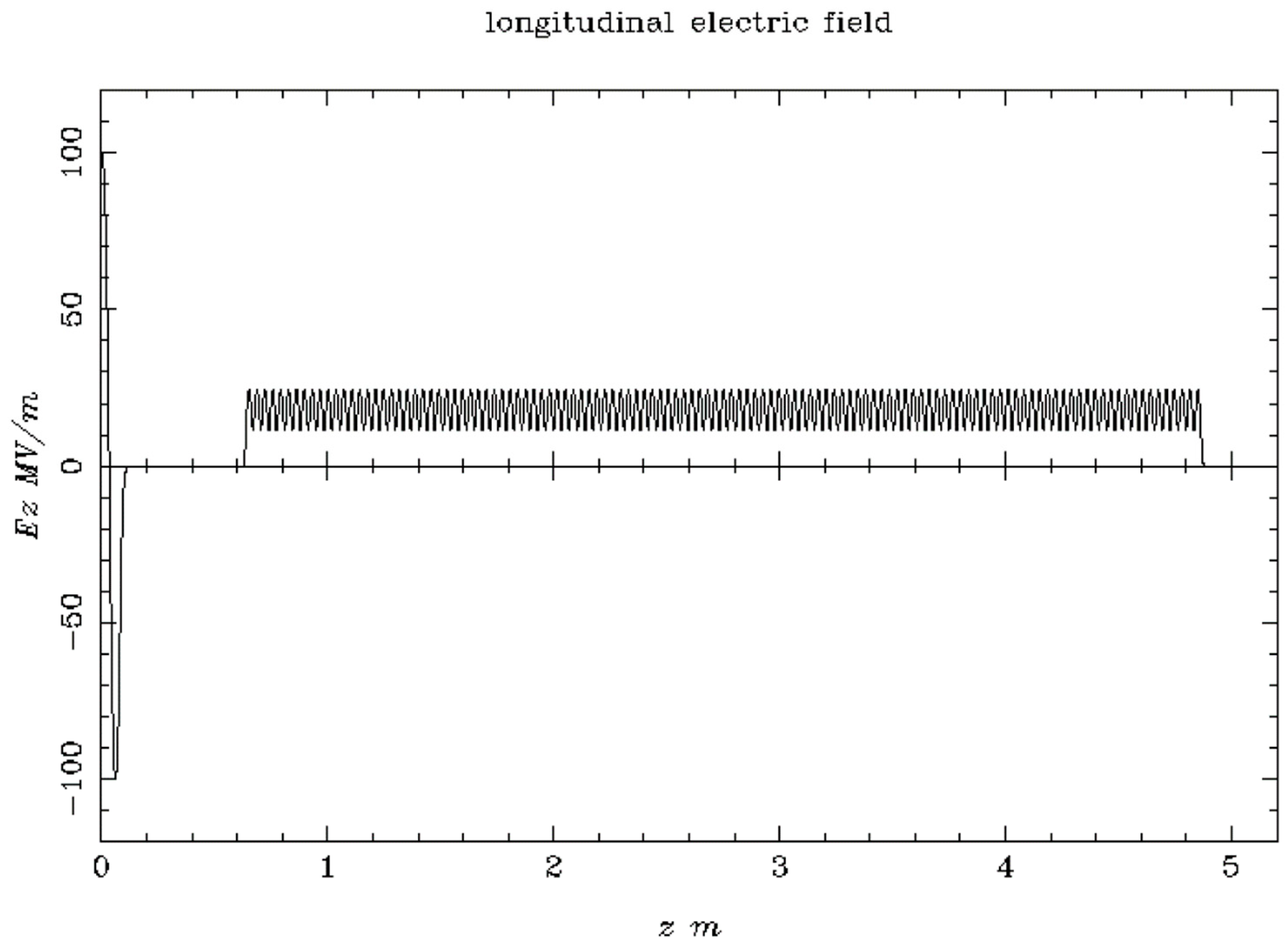
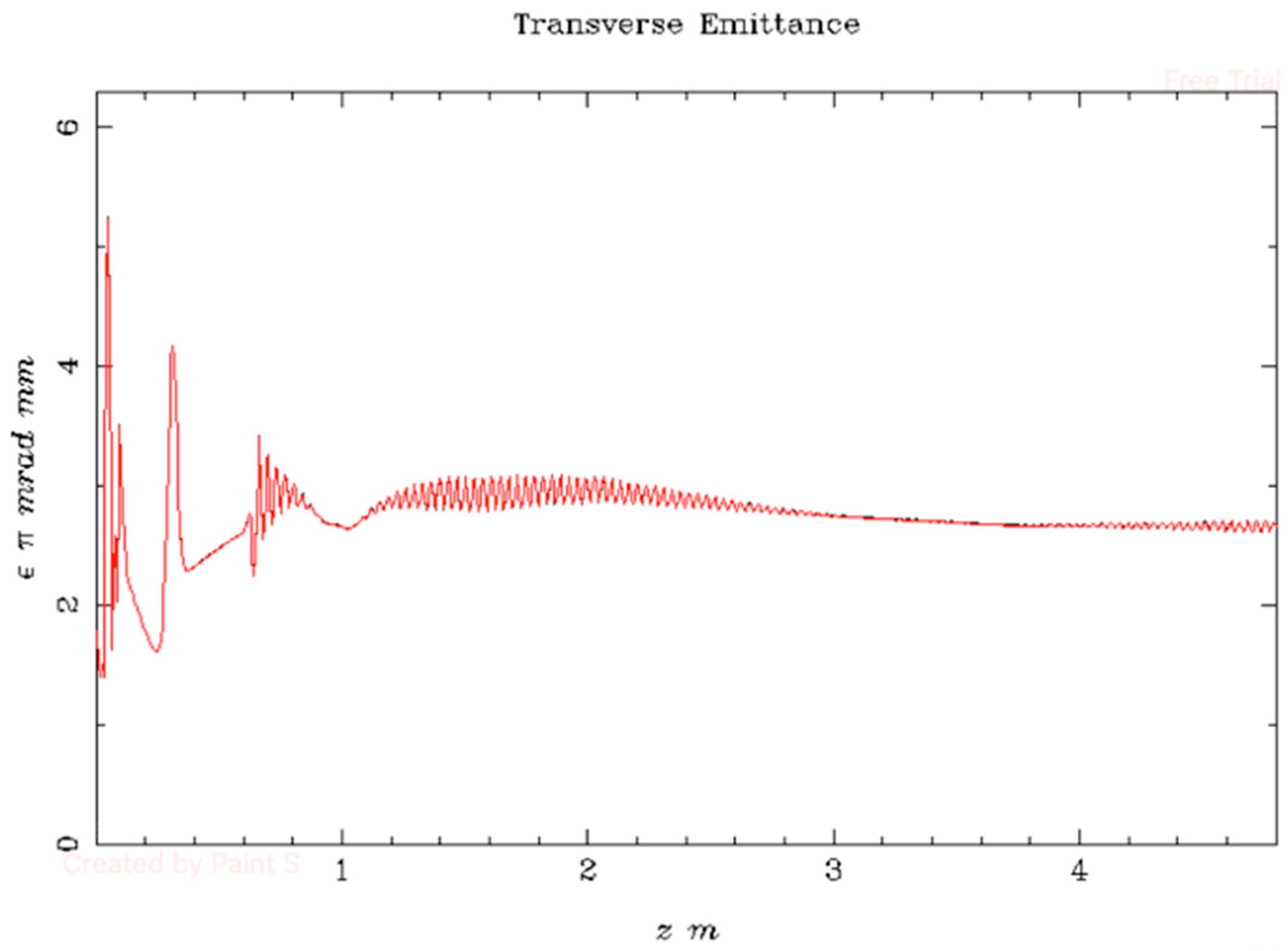
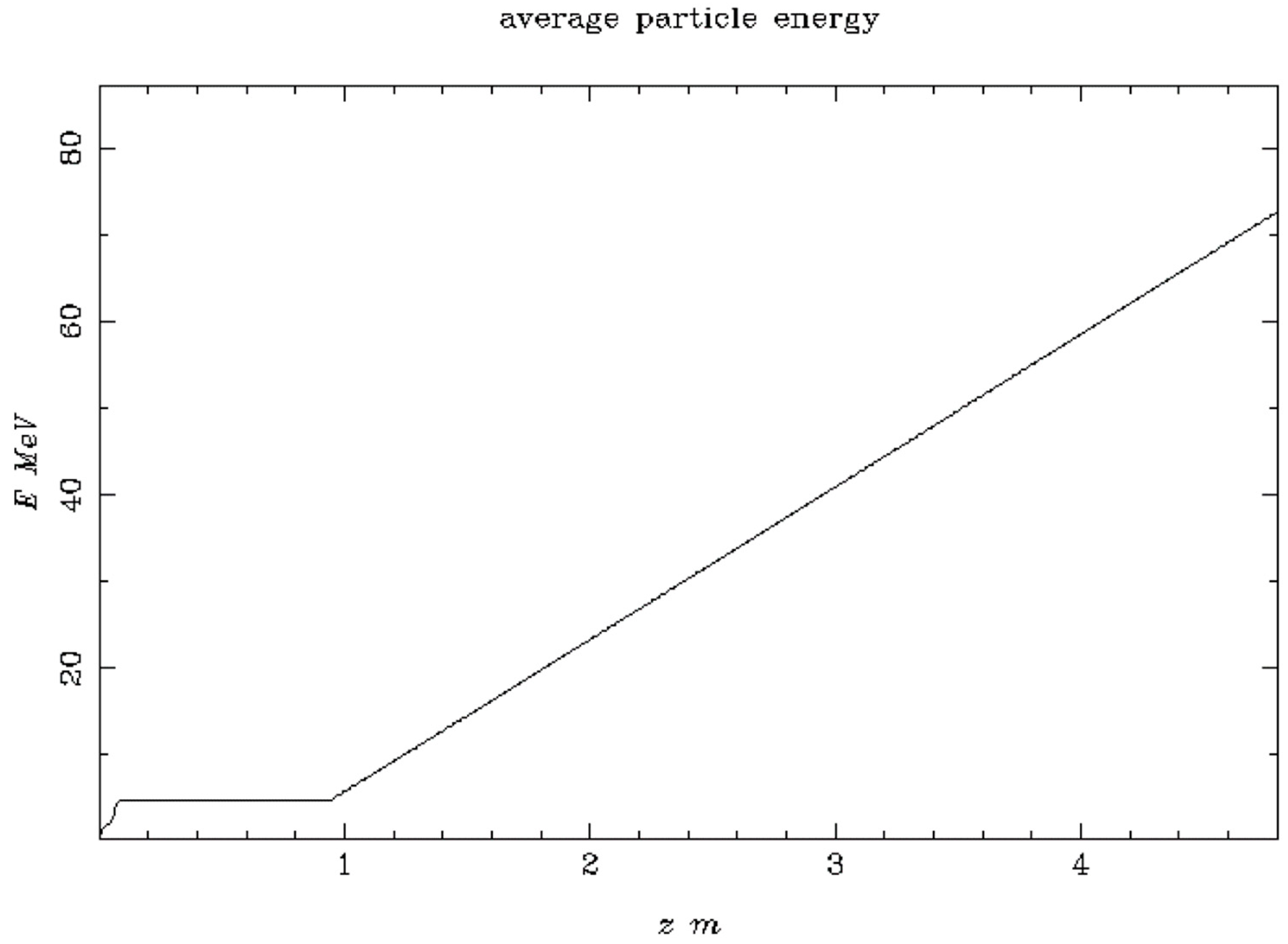
2.2. FLASH-RT Injector Design
2.3. Phantoms in Medical and Health Physics
2.4. Electron Dosimetry
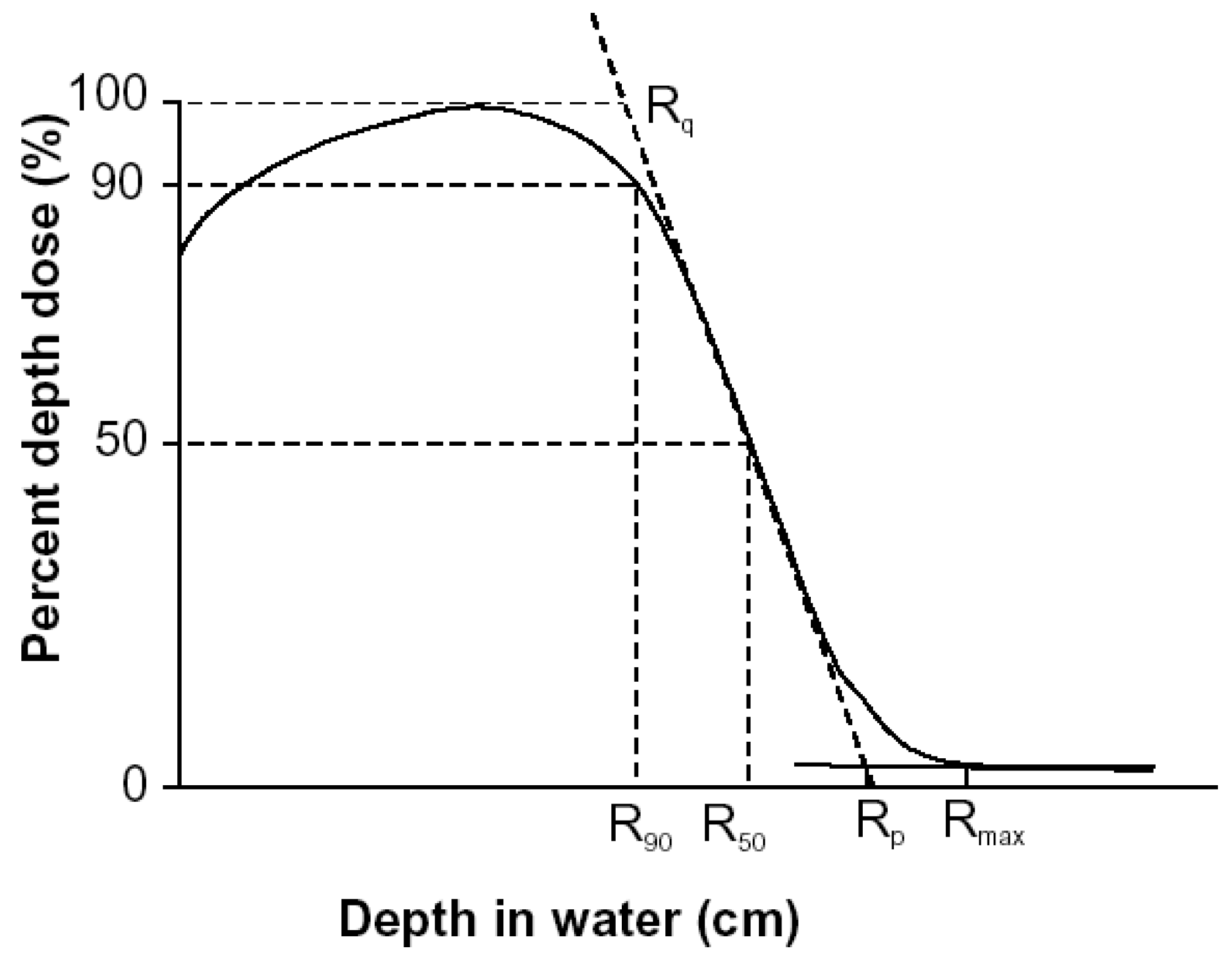
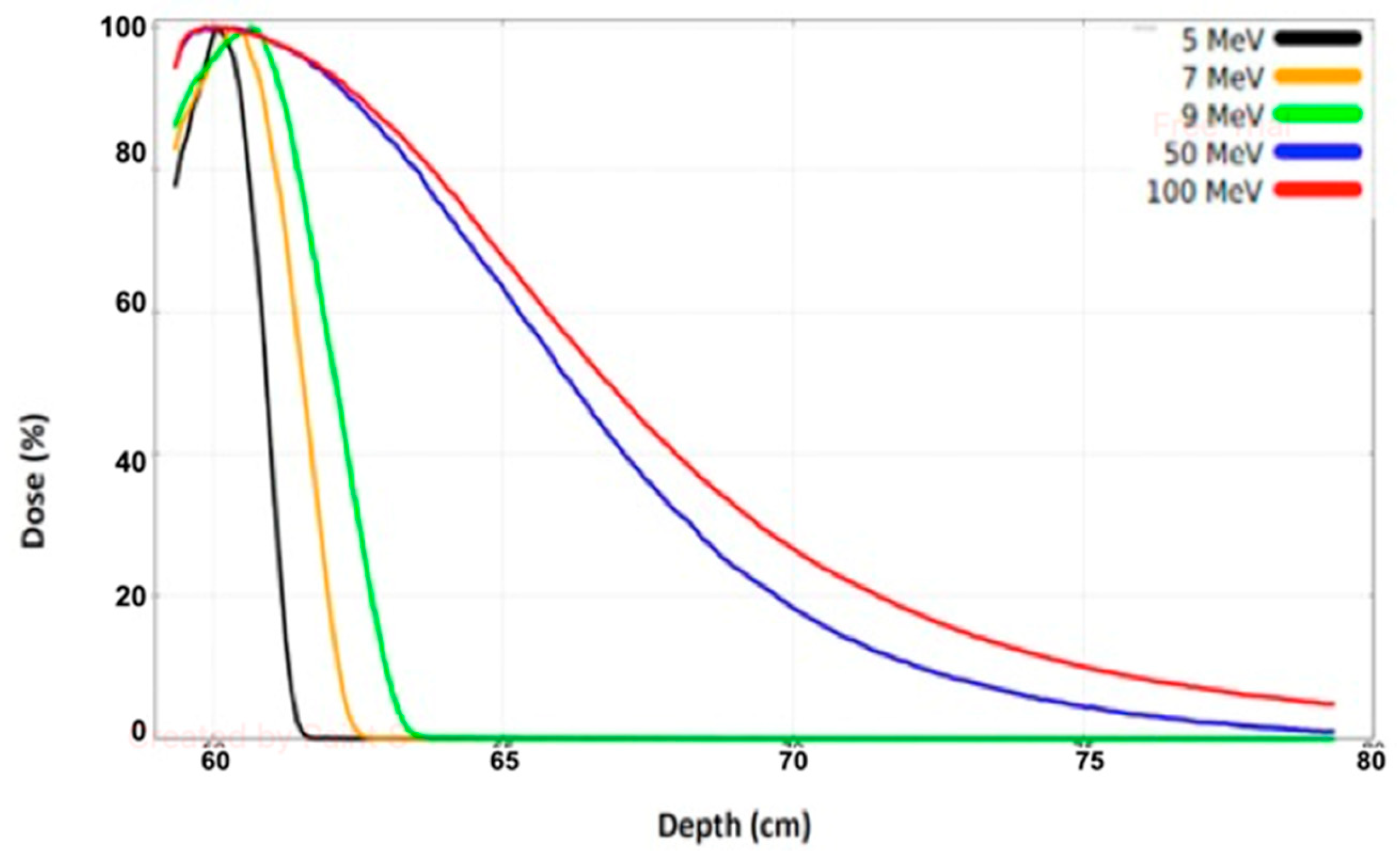
2.4.1. Percentage Depth Dose (PDD) of Electron Beam
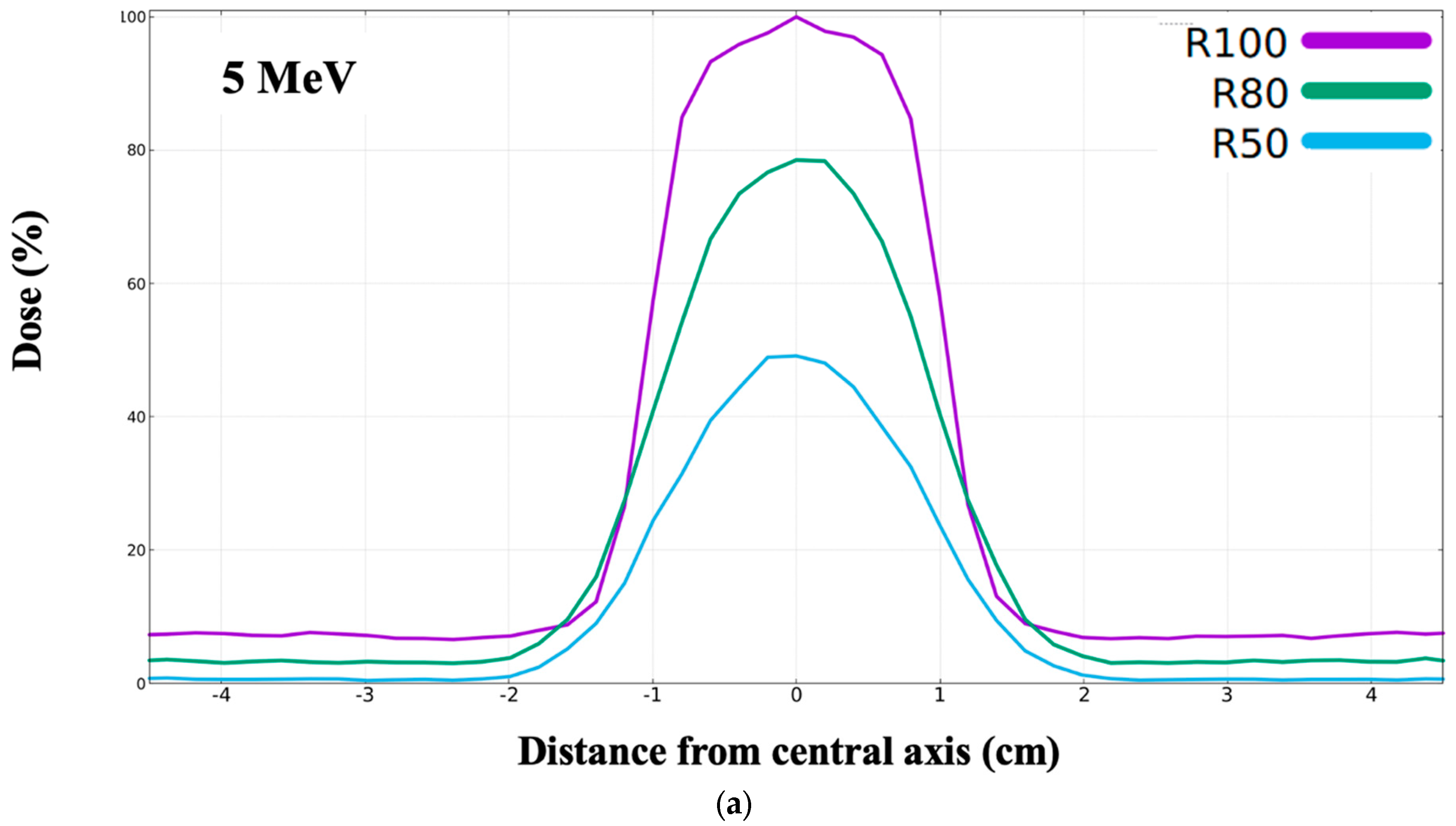
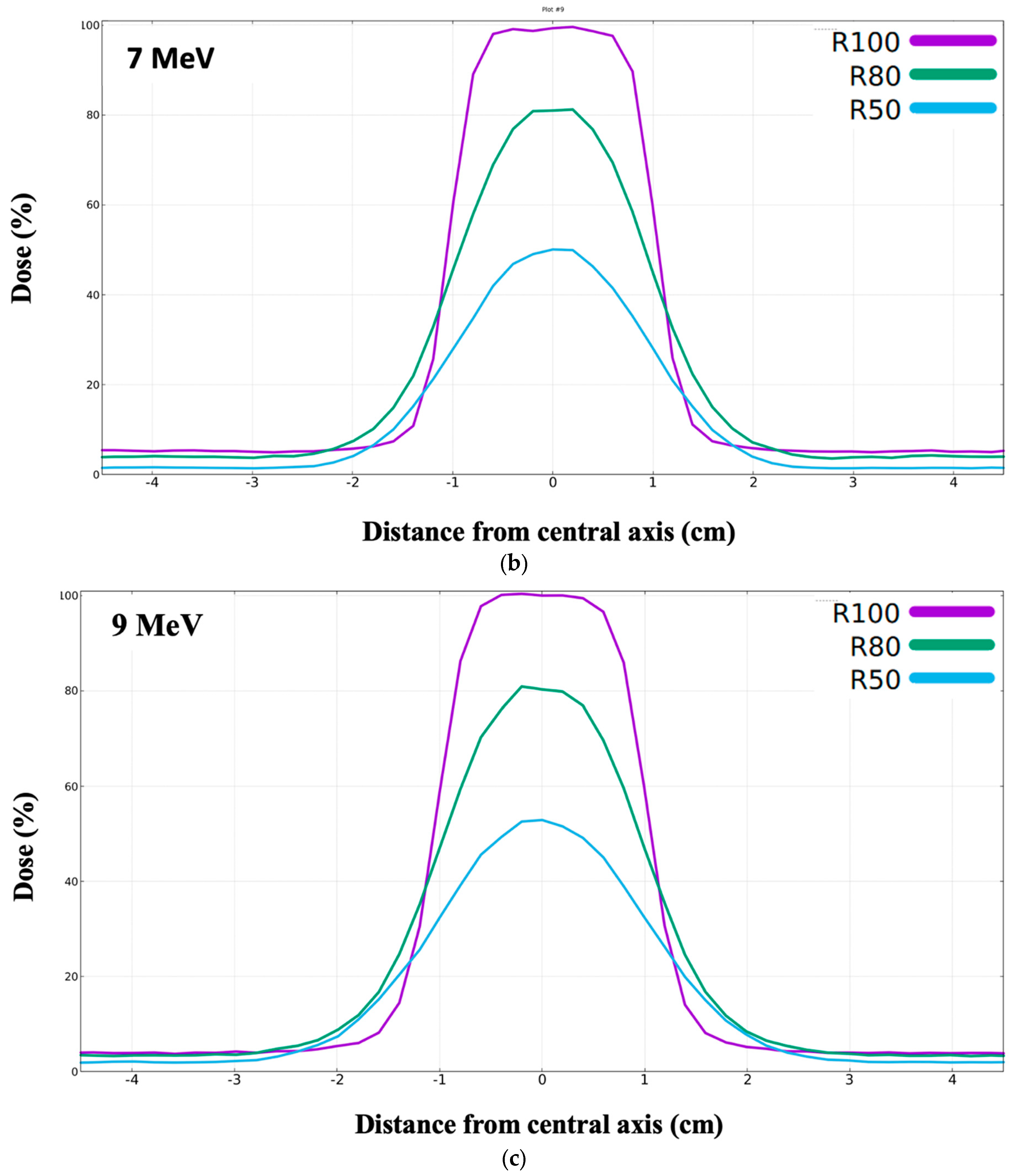
2.4.2. Transverse Dose Profile
2.5. Electron Beam to Phantom Simulation Studies
2.6. Simulations for FLASH-RT
3. Dosimetry Results and Discussion
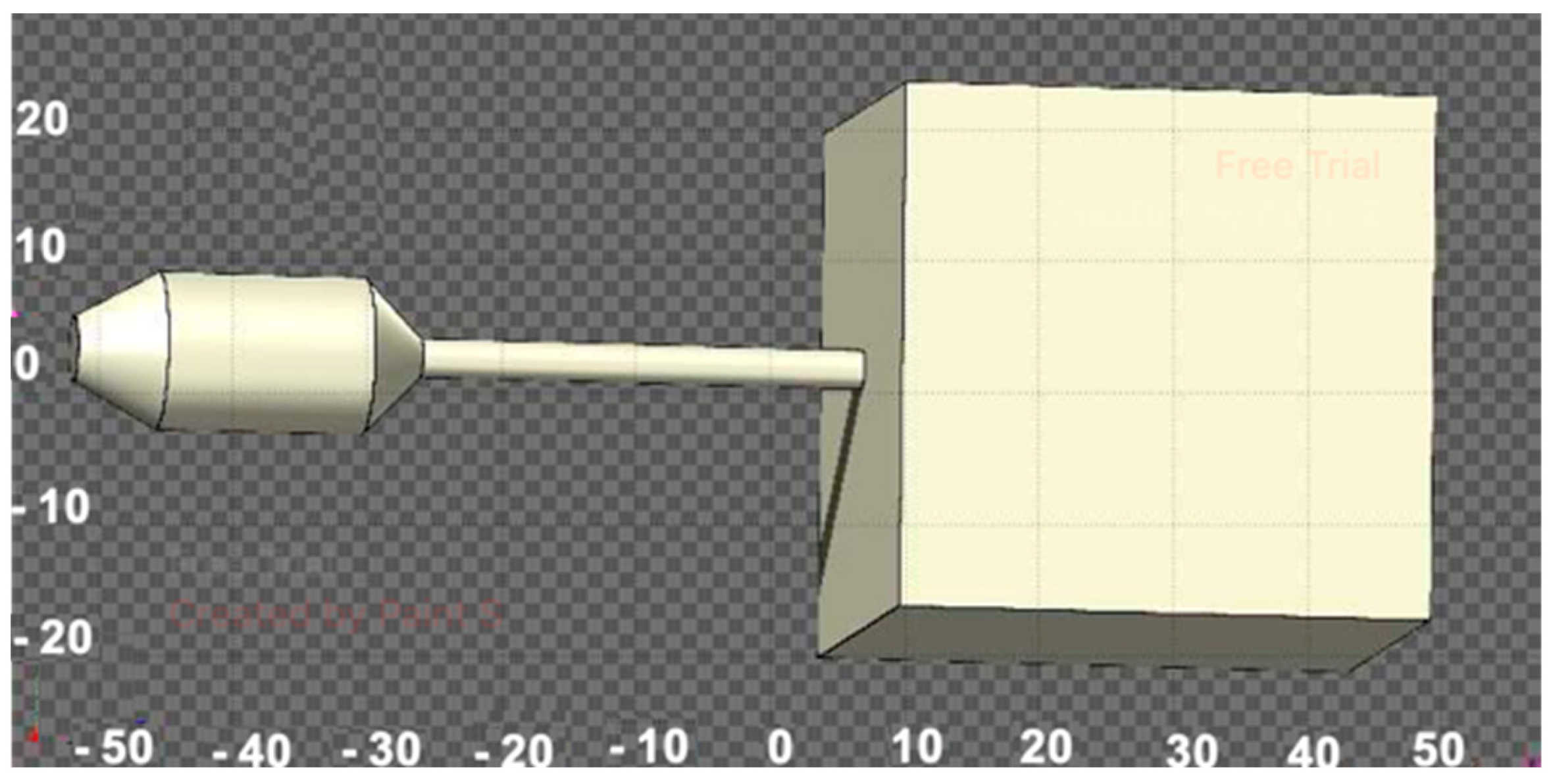
3.1. PMMA Applicator with PMMA Phantom
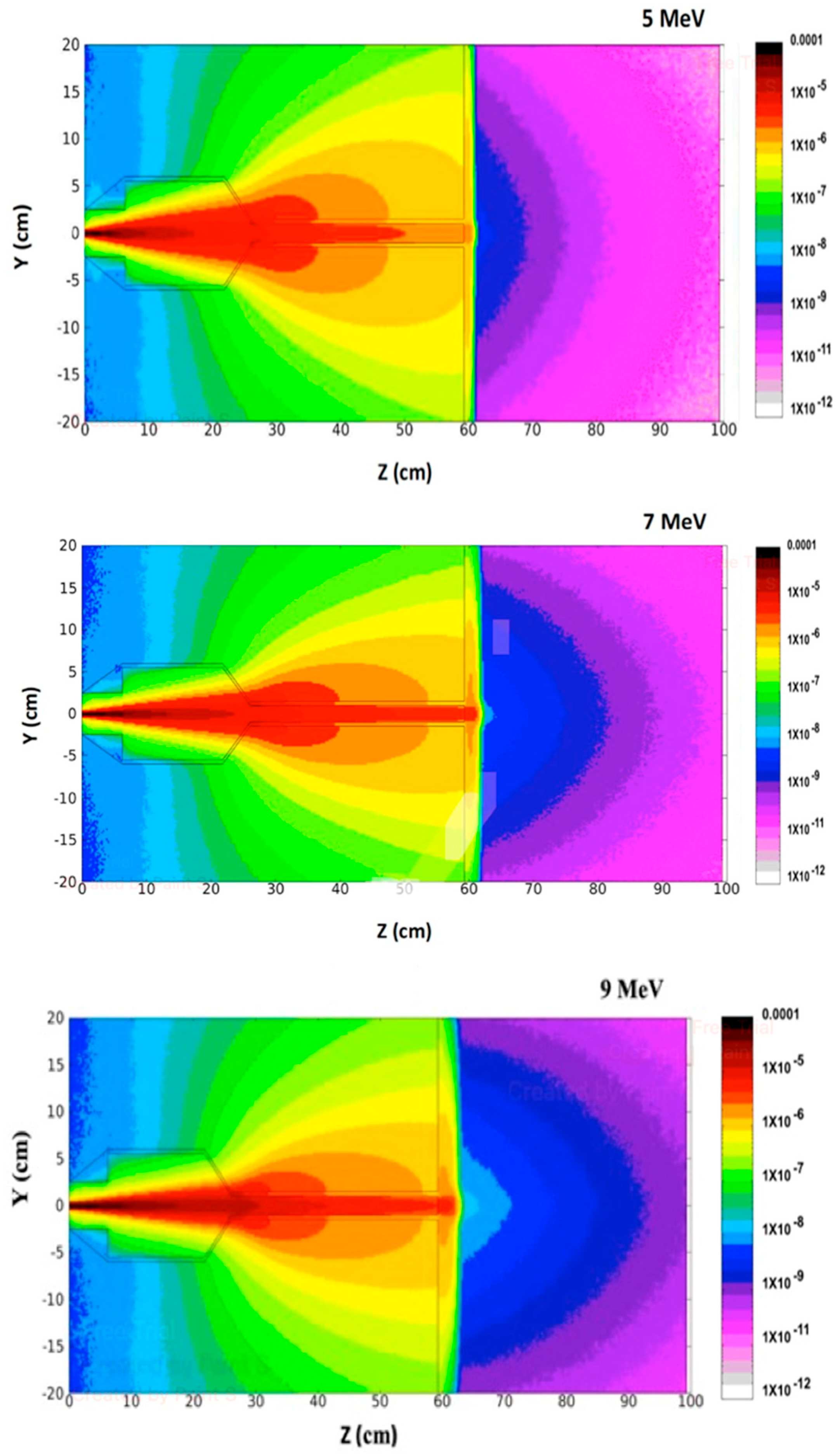
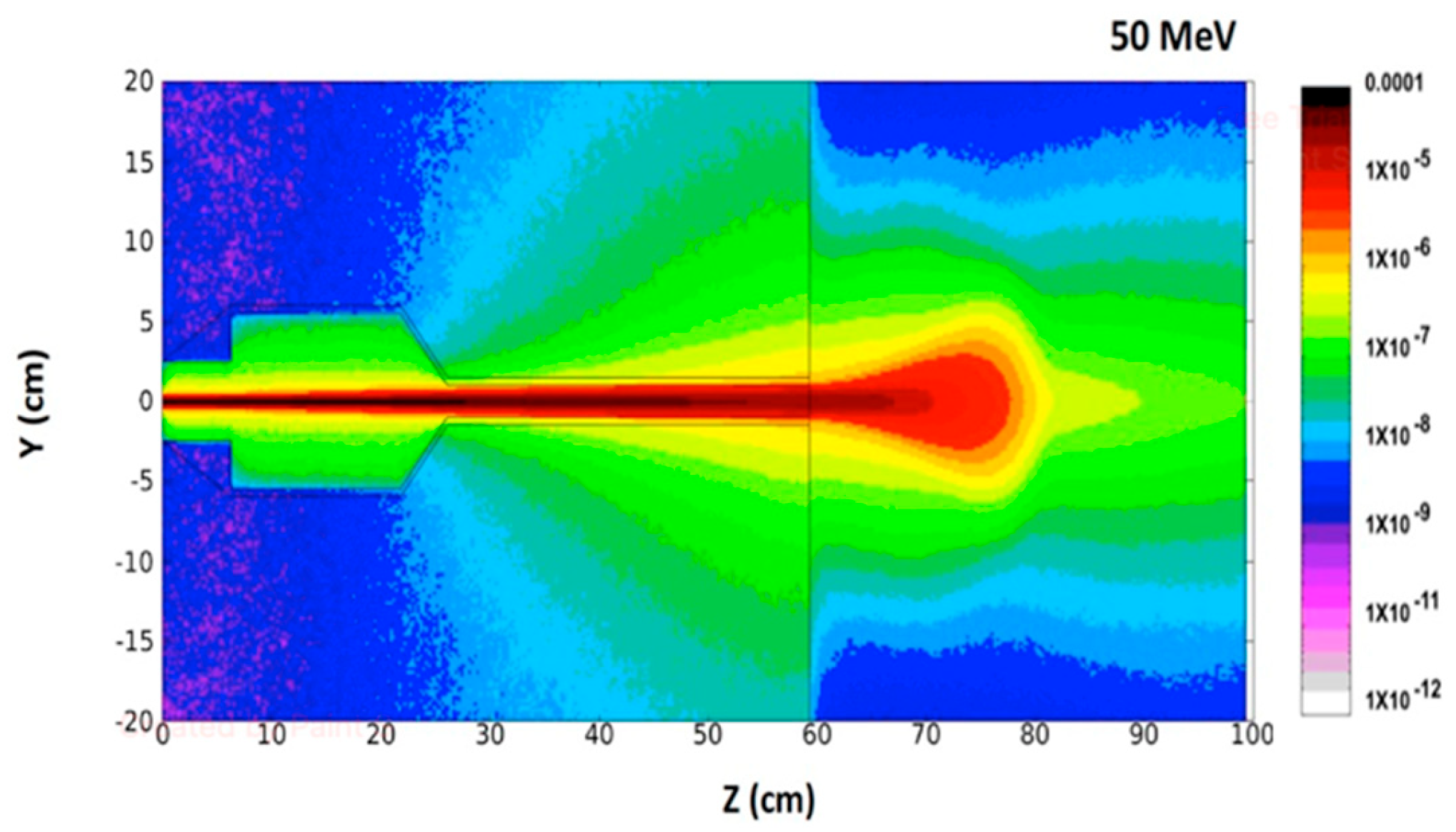
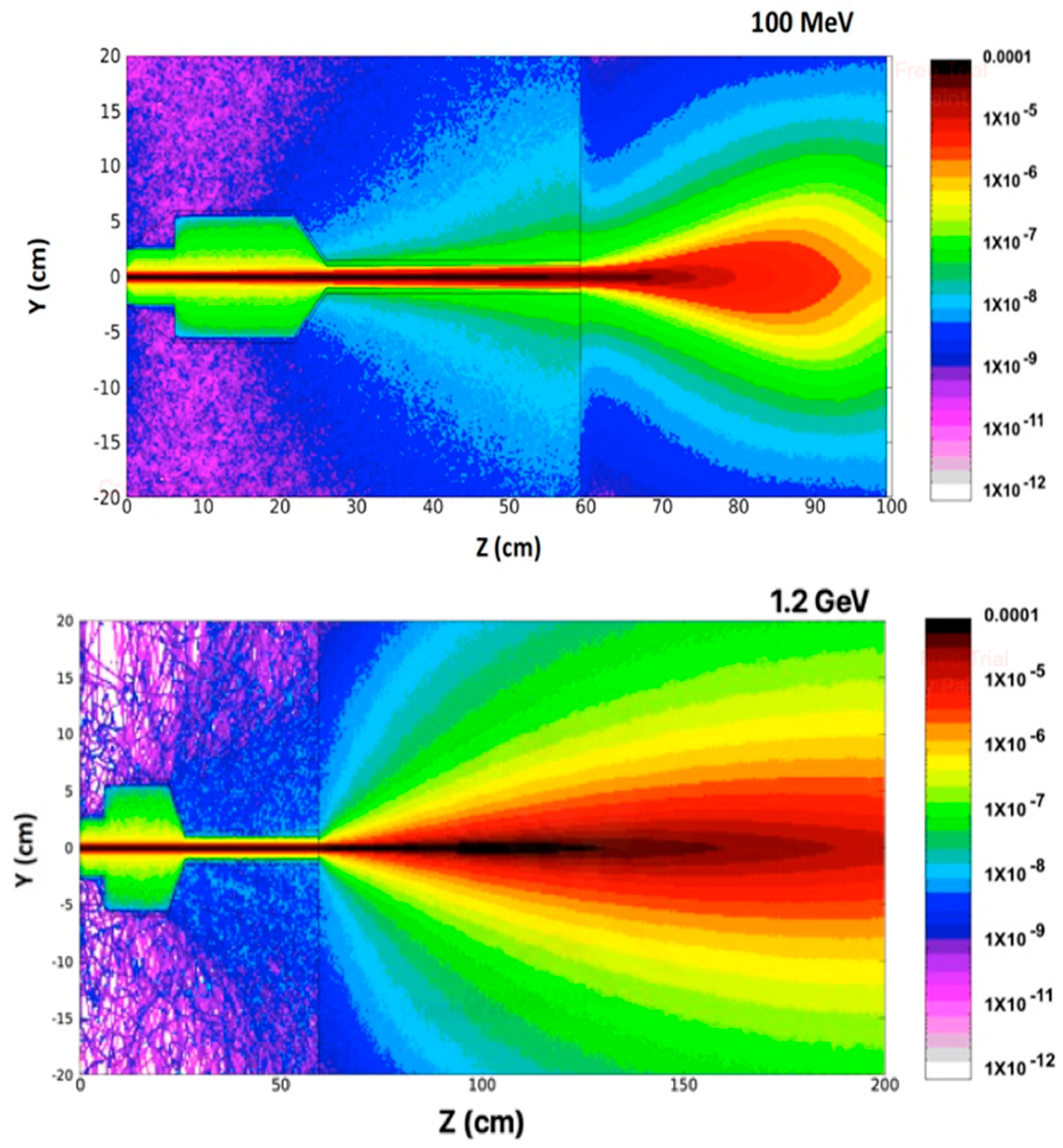
3.2. Dose–Depth Distribution
3.3. The Percentage Depth Dose (PDD) Curves (Gy vs. cm)
3.4. Dose Profile vs. Phantom Depth
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gianfaldoni, S.; Gianfaldoni, R.; Wollina, U.; Lotti, J.; Tchernev, G.; Lotti, T. An Overview on Radiotherapy: From Its History to Its Current Applications in Dermatology. Open Access Mac. J. Med. Sci. 2017, 5, 521. [Google Scholar] [CrossRef] [PubMed]
- Tsujii, H. Overview of Carbon-ion Radiotherapy. IOP Conf. Ser. J. Phys. Conf. Ser. 2017, 777, 012032. [Google Scholar] [CrossRef]
- Tian, X.; Liu, K.; Hou, Y.; Cheng, J.; Zhang, J. The evolution of proton beam therapy: Current and future status (Review). Mol. Clin. Oncol. 2017, 8, 15–21. [Google Scholar] [CrossRef]
- Gagnebin, S.; Twerenbold, D.; Pedroni, E.; Meer, D.; Zenklusen, S.; Bula, C. Experimental determination of the absorbed dose to water in a scanned proton beam using a water calorimeter and an ionization chamber. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 524–528. [Google Scholar] [CrossRef]
- Bourhis, J.; Sozzi, W.J.; Jorge, P.G.; Gaide, O.; Bailat, C.; Duclos, F.; Patin, D.; Ozsahin, M.; Bochud, F.; Germond, J.F.; et al. Clinical translation of FLASH radio- therapy: Why and how? Radiother. Oncol. 2019, 139, 11–17. [Google Scholar] [CrossRef]
- Pratx, G.; Kapp, D.S. A computational model of radiolytic oxygen depletion during FLASH irradiation and its effect on the oxygen enhancement ratio. Phys. Med. Biol. 2019, 64, 185005. [Google Scholar] [CrossRef] [PubMed]
- Favaudon, V.; Caplier, L.; Monceau, V.; Pouzoulet, F.; Sayarath, M.; Fouillade, C.; Poupon, M.F.; Brito, I.; Hupe, P.; Bourhis, J.; et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci. Transl. Med. 2020, 12, 1671. [Google Scholar] [CrossRef] [PubMed]
- Varnava, M.; Jun-ichi Saitoh Tashiro, M.; Kubo, N.; Okano, N.; Kawamura, H.; Ohno, T. Dose–volume constraints for head-and-neck cancer in carbon ion radiotherapy: A literature review. Cancer Med. 2023, 12, 8267–8277. [Google Scholar] [CrossRef] [PubMed]
- Mohamad, O.; Sishc, B.J.; Saha, J.; Pompos, A.; Rahimi, A.; Story, M.D.; Davis, A.J.; Kim, D.W.N. Carbon Ion Radiotherapy: A Review of Clinical Experiences and Preclinical Research, with an Emphasis on DNA Damage/Repair. Cancers 2017, 9, 66. [Google Scholar] [CrossRef] [PubMed]
- Debowski, M.; Murphy, A.; Jones, J. Electron Therapy. Reference Article. Radiopaedia.org. Available online: https://radiopaedia.org/articles/67623 (accessed on 23 June 2023).
- Kokurewicz, K.; Brunetti, E.; Welsh, G.H.; Wiggins, S.M.; Boyd, M.; Sorensen, A.; Chalmers, A.J.; Schettino, G.; Subiel, A.; DesRosiers, C.; et al. Focused very high-energy electron beams as a novel radiotherapy modality for producing high-dose volumetric elements. Sci. Rep. 2019, 9, 10837. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, A.; Eley, J.G.; Onyeuku, N.E.; Rice, S.R.; Wright, C.C.; McGovern, N.E.; Sank, M.; Zhu, M.; Vujaskovic, Z.; Simone, C.B.; et al. Proton Therapy Delivery and Its Clinical Application in Select Solid Tumor Malignancies. J. Vis. Exp. 2019, 144, e58372. [Google Scholar] [CrossRef] [PubMed]
- Giuliano, L.; Franciosini, G.; Palumbo, L.; Aggar, L.; Dutreix, M.; Faillace, L.; Favaudon, V.; Felici, G.; Galante, F.; Mostacci, A.; et al. Characterization of Ultra-High-Dose Rate Electron Beams with ElectronFlash Linac. Appl. Sci. 2023, 13, 631. [Google Scholar] [CrossRef]
- Montay-Gruel, P.; Petersson, K.; Jaccard, M.; Boivin, G.; Germond, J.-F.; Petit, B.; Doenlen, R.; Favaudon, V.; Bochud, F.; Bailat, C.; et al. Irradiation in a flash: Unique sparing of memory in mice after whole brain irradiation with dose rates above 100 Gy/s. Radiother. Oncol. 2017, 124, 365–369. [Google Scholar] [CrossRef] [PubMed]
- Floettmann, K. ASTRA, A Space Charge Tracking Algorithm, Version 3.2; DESY: Hamburg, Germany, 2017. [Google Scholar]
- Gazis, N.; Tanke, E.; Trachanas, E.; Apostolopoulos, T.; Karagiannaki, A.; Pramatari, K.; Telali, I.; Tzanetou, K.; Gazis, E. Photocathode study of the CompactLight Collaboration for a novel XFEL development. In International Journal of Modern Physics: Conference Series 2020 50—International Conference on Applications of Nuclear Techniques (“CRETE19”) Crete, Greece, 5–15 June 2019; World Scientific Publishing Company: Singapore, 2020. [Google Scholar] [CrossRef]
- Chevallay, E.; Csatari, M.; Dabrowski, A.; Doebert, S.; Egger, D.; Fedosseev, V.; Mete, O.; Olvegaar, M.; Petrarca, M. PHIN photo-injector as the CLIC drive beam source. In Journal of Physics, Conference Series, 2nd International Conference on Particle Physics in Memoriam Engin Arık and Her Colleagues, Istanbul, Turkey, 20–25 June 2011; Doğuş University: Istanbul, Turkey, 2012; Volume 347. [Google Scholar]
- Mete, O. Study and Experimental Characterization of a Novel Photo Injector for the CLIC Drive Beam. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2011. [Google Scholar]
- Alves, M.; Arnault, C.; Auguste, D.; Babigeon, J.L.; Blot, F.; Brossard, J.; Bruni, C.; Cavalier, S.; Cayla, J.N.; Chaumat, V.; et al. PHIL photoinjector test line. J. Instrum. 2012, 8, T01001. [Google Scholar] [CrossRef]
- Li, J.; Asova, G.; Isaev, I.V.; Groß, M.; Hakobyan, L.; Ivanisenko, Y.; Khojoyan, M.; Klemz, G.; Kourkafas, G.; Krasilnikov, M.; et al. Emission Studies of Photocathode RF Gun at PITZ. In Proceedings of the ICAP2012, Rostock-Warnemünde, Germany, 19–24 August 2012. [Google Scholar]
- Halloran, A. Dosimetric Advantages of Personalized Phantoms for Quality Assurance and Research in Radiation Dose Measurements. Master’s Thesis, Louisiana State University: Baton Rouge, LA, USA, 2015. Available online: https://repository.lsu.edu/gradschool_theses/1227/ (accessed on 23 June 2023).
- Yadav, N.; Singh, M.; Mishra, S.P. Tissue-equivalent materials used to develop phantoms in radiation dosimetry: A review. Mater. Today Proc. 2021, 47, 7170–7173. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Absorbed Dose Determination in External Beam Radiotherapy An International Code of Practice for Dosimetry Based on Standards of Absorbed Dose to Water. Vienna. 2000. Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/TRS398_scr.pdf (accessed on 23 June 2023).
- Strydom, W.; Parker, W.; Olivares, M. Chapter 8 Electron Beams: Physical and Clinical Aspects. Available online: http://www-naweb.iaea.org/nahu/DMRP/documents/Chapter8.pdf (accessed on 23 June 2023).
- Raychaudhuri, S. Introduction to Monte Carlo Simulation. Available online: https://www.informs-sim.org/wsc08papers/012.pdf (accessed on 23 June 2023).
- fluka.cern. About FLUKA|The Official CERN FLUKA Website. Available online: https://fluka.cern/about (accessed on 23 June 2023).
- fluka.cern. The Flair Graphical User Interface|The Official CERN FLUKA Website. Available online: https://fluka.cern/documentation/running/flair-gui (accessed on 25 August 2023).

| Beam Characteristics | Conventional RT | FLASH RT |
|---|---|---|
| Dose Per Pulse | ~0.4 mGy | ~1 Gy |
| Dose Rate | ~102 Gy/s | ~105 Gy/s |
| Mean Dose Rate | ~0.1 Gy/s | ~100 Gy/s |
| Total Treatment Time | ~days/minutes | <500 ms |
| Parameter | Unit | Value |
|---|---|---|
| Photocathode material | - | Cs2Te |
| RMS laser spot size (XY) | mm | 0.9 |
| Laser pulse duration | ps | 10 |
| Laser rise/fall time | ps | 7 |
| Laser wavelength | nm | 262 (UVC) |
| Laser photon energy | eV | 4.73 |
| Initial kinetic energy | eV | 1.609 |
| Beam charge | nC | 1 |
| Electric field at cathode | MV/m | 99 |
| Energy distribution | Isotropic | |
| Longitudinal distribution | Uniform ellipsoid | |
| Transverse distribution | Radial |
| Energy (MeV) | Maximum Peak Beam Current (mA) | Dose per Pulse (Gy) | Instantaneous Dose Rate (Gy/s) × 106 | Average Dose Rate (Gy/s) ×103 |
|---|---|---|---|---|
| 5 | 108 | 9.5 | 2.38 | 2.38 |
| 7 | 120 | 20.7 | 5.18 | 5.18 |
| 9 | 120 | 30.8 | 7.70 | 7.70 |
| 50 | 120 | 48.0 | 12.00 | 12.00 |
| 100 | 120 | 67.0 | 16.75 | 16.75 |
| 1200 | 120 | 99.0 | 24.75 | 24.75 |
 | ||||
| FLASH effect conditions | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gazis, N.; Bignami, A.; Trachanas, E.; Moniaki, M.; Gazis, E.; Bandekas, D.; Vordos, N. Simulation Dosimetry Studies for FLASH Radiation Therapy (RT) with Ultra-High Dose Rate (UHDR) Electron Beam. Quantum Beam Sci. 2024, 8, 13. https://doi.org/10.3390/qubs8020013
Gazis N, Bignami A, Trachanas E, Moniaki M, Gazis E, Bandekas D, Vordos N. Simulation Dosimetry Studies for FLASH Radiation Therapy (RT) with Ultra-High Dose Rate (UHDR) Electron Beam. Quantum Beam Science. 2024; 8(2):13. https://doi.org/10.3390/qubs8020013
Chicago/Turabian StyleGazis, Nick, Andrea Bignami, Emmanouil Trachanas, Melina Moniaki, Evangelos Gazis, Dimitrios Bandekas, and Nikolaos Vordos. 2024. "Simulation Dosimetry Studies for FLASH Radiation Therapy (RT) with Ultra-High Dose Rate (UHDR) Electron Beam" Quantum Beam Science 8, no. 2: 13. https://doi.org/10.3390/qubs8020013
APA StyleGazis, N., Bignami, A., Trachanas, E., Moniaki, M., Gazis, E., Bandekas, D., & Vordos, N. (2024). Simulation Dosimetry Studies for FLASH Radiation Therapy (RT) with Ultra-High Dose Rate (UHDR) Electron Beam. Quantum Beam Science, 8(2), 13. https://doi.org/10.3390/qubs8020013






