Comparative Evaluation of Two Analytical Functions for the Microdosimetry of Ions from 1H to 238U
Abstract
1. Introduction
2. Methodology
2.1. RBE
2.2. Experimental RBE Data
2.3. Computer Simulations
2.4. RBE Modeling
2.5. Structure of the Study
3. Results and Discussion
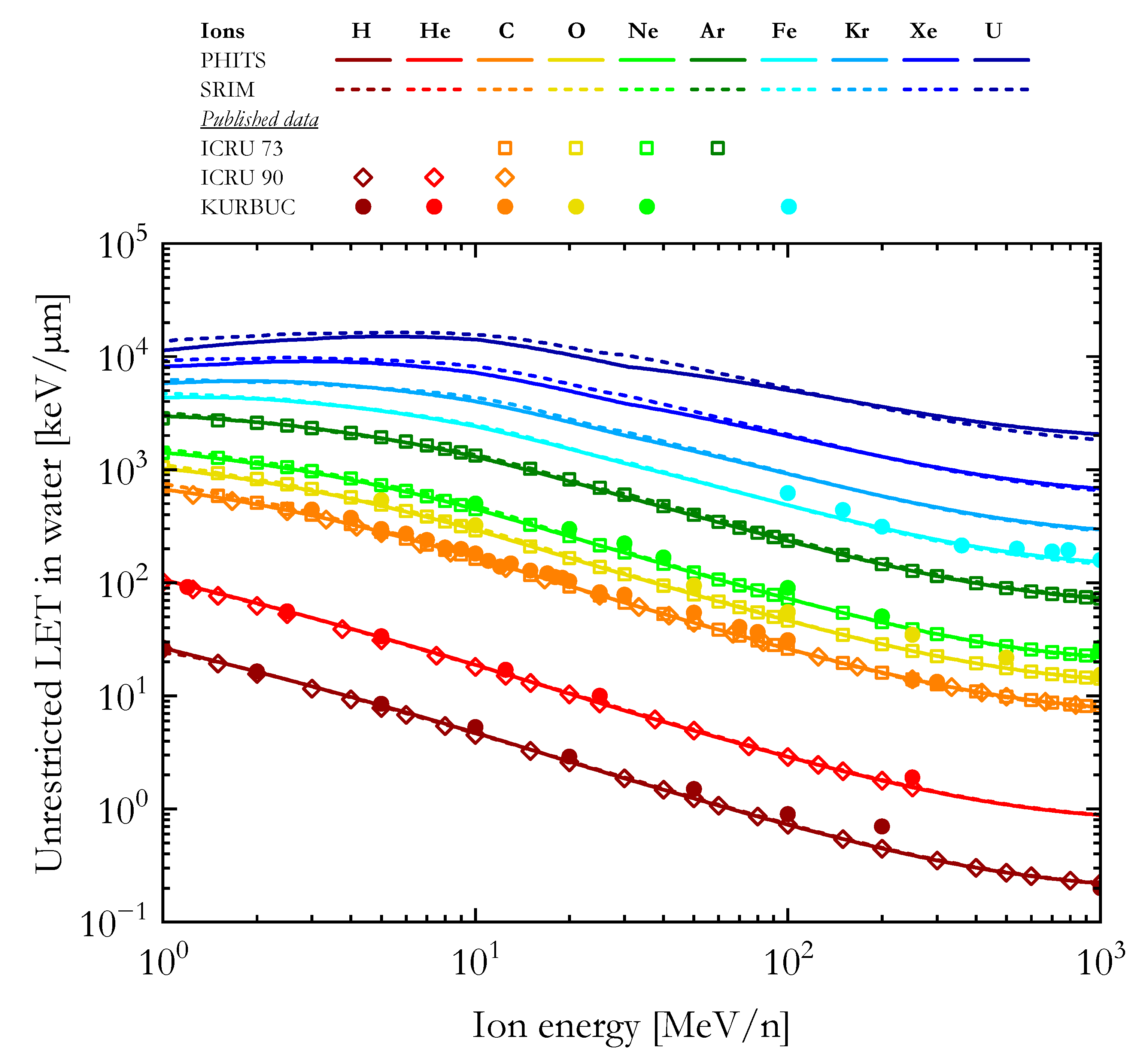
3.1. LET
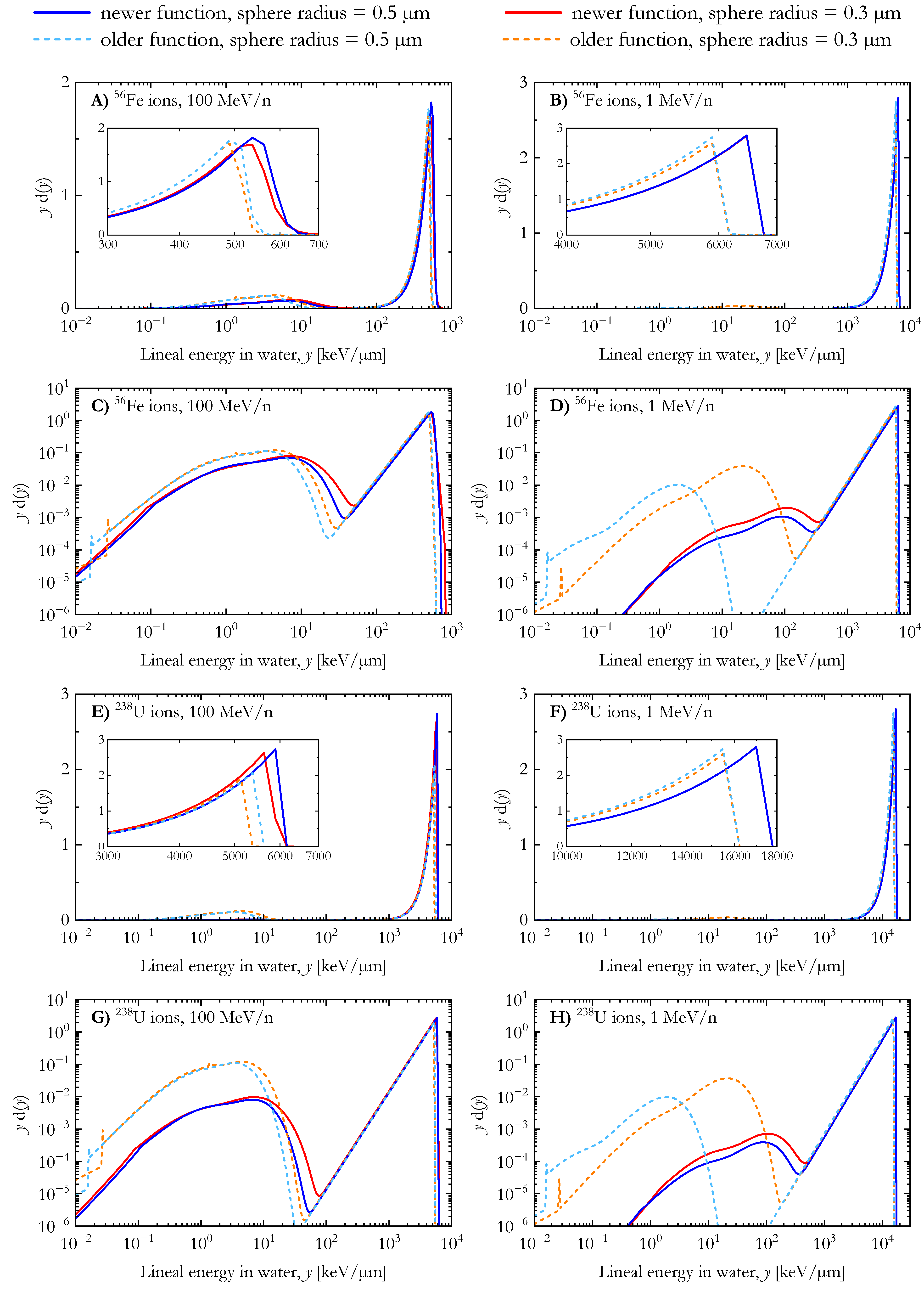
3.2. Lineal Energy Distributions

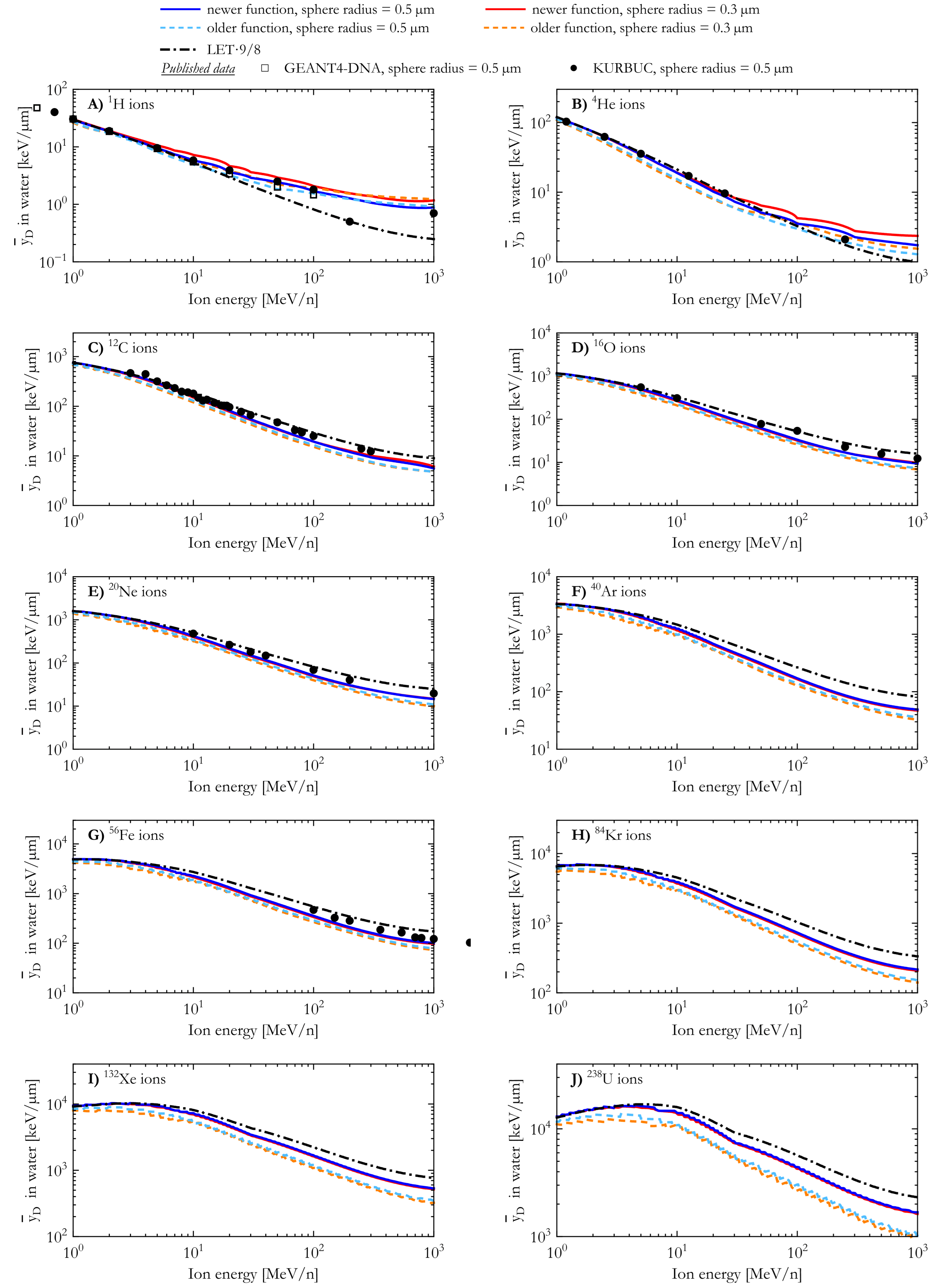
3.3. Dose-Mean Lineal Energy
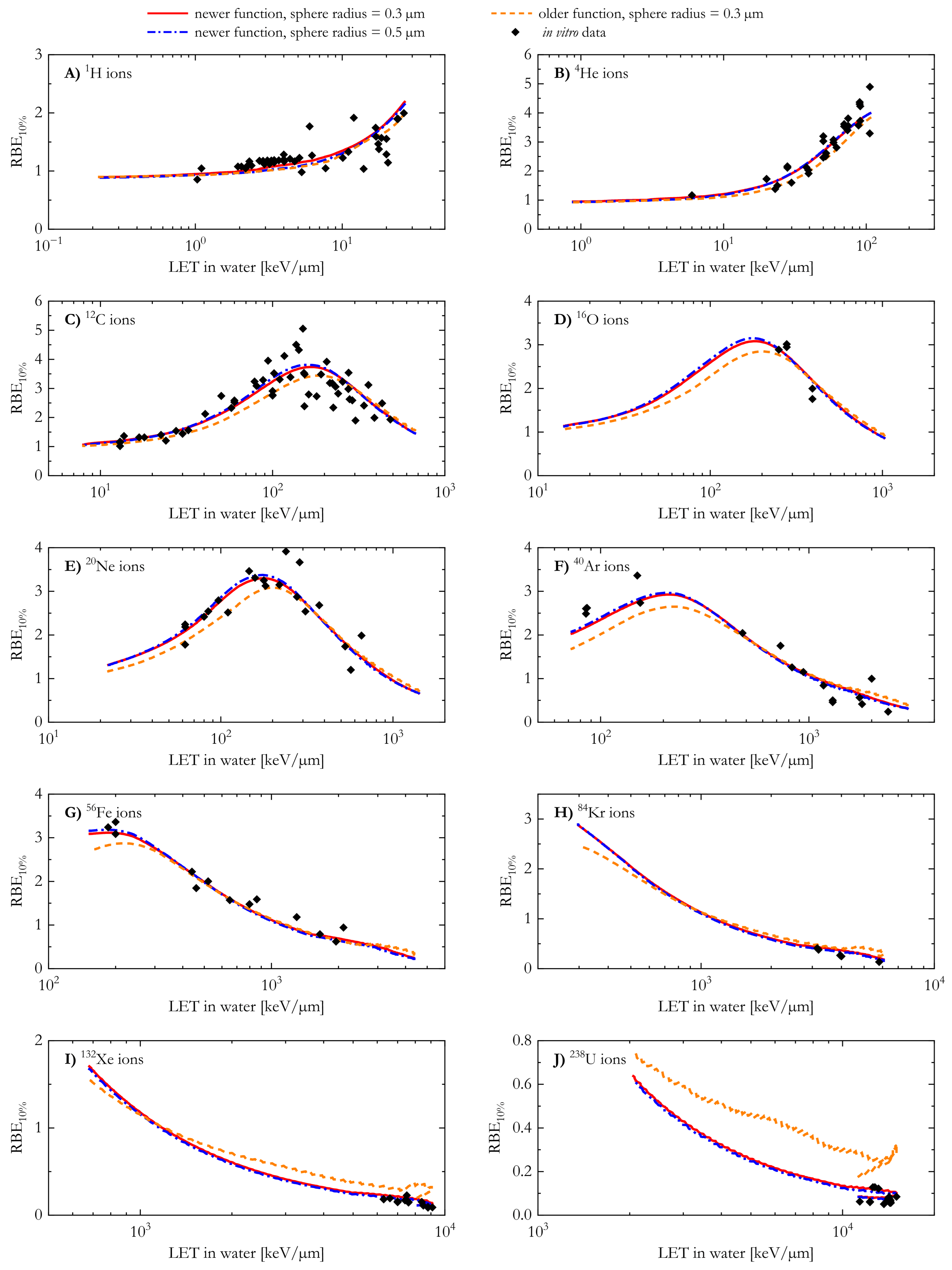
3.4. RBE

4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scholz, M. Effects of Ion Radiation on Cells and Tissues. In Radiation Effects on Polymers for Biological Use; Springer: Berlin/Heidelberg, Germany, 2003; Volume 162, pp. 95–155. [Google Scholar]
- Friedrich, T.; Scholz, U.; Elsasser, T.; Durante, M.; Scholz, M. Systematic analysis of RBE and related quantities using a database of cell survival experiments with ion beam irradiation. J. Radiat. Res. 2013, 54, 494–514. [Google Scholar] [CrossRef] [PubMed]
- ICRU. ICRU Report 85: Fundamental Quantities and Units for Ionizing Radiation; Technical Report for International Commission on Radiation Units & Measurements: Bethesda, MD, USA, 2011. [Google Scholar]
- Furusawa, Y.; Fukutsu, K.; Aoki, M.; Itsukaichi, H.; Eguchi-Kasai, K.; Ohara, H.; Yatagai, F.; Kanai, T.; Ando, K. Inactivation of Aerobic and Hypoxic Cells from Three Different Cell Lines by Accelerated3He-,12C- and20Ne-Ion Beams. Radiat. Res. 2000, 154, 485–496. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T.; Durante, M.; Scholz, M. Particle species dependence of cell survival RBE: Evident and not negligible. Acta Oncol. 2013, 52, 589–603. [Google Scholar] [CrossRef] [PubMed]
- ICRU. ICRU Report 36: Microdosimetry; Technical Report for International Commission on Radiation Units & Measurements: Bethesda, MD, USA, 1983. [Google Scholar]
- Rossi, H.H.; Zaider, M. Microdosimetry and Its Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- ICRU. ICRU Report 98: Stochastic Nature of Radiation Interactions: Microdosimetry. J. ICRU 2023, 23, 1–168. [Google Scholar] [CrossRef]
- Olko, P.; Booz, J. Energy deposition by protons and alpha particles in spherical sites of nanometer to micrometer diameter. Radiat. Environ. Biophys. 1990, 29, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Olko, P.; Swakon, J.; Horwacik, T.; Jablonski, H.; Malinowski, L.; Nowak, T.; Struelens, L.; Vanhavere, F. Microdosimetric characterization of a clinical proton therapy beam: Comparison between simulated lineal energy distributions in spherical water targets and experimental measurements with a silicon detector. Phys. Med. Biol. 2022, 67, 015006. [Google Scholar] [CrossRef]
- IAEA. TRS 461: Relative Biological Effectiveness in Ion Beam Therapy; Technical Report Series; IAEA: Vienna, Austria, 2008. [Google Scholar]
- Kanai, T.; Endo, M.; Minohara, S.; Miyahara, N.; Koyama-ito, H.; Tomura, H.; Matsufuji, N.; Futami, Y.; Fukumura, A.; Hiraoka, T.; et al. Biophysical characteristics of HIMAC clinical irradiation system for heavy-ion radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 1999, 44, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.; Scholz, M. Rapid calculation of biological effects in ion radiotherapy. Phys. Med. Biol. 2006, 51, 1959–1970. [Google Scholar] [CrossRef] [PubMed]
- Inaniwa, T.; Kanematsu, N.; Matsufuji, N.; Kanai, T.; Shirai, T.; Noda, K.; Tsuji, H.; Kamada, T.; Tsujii, H. Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the National Institute of Radiological Sciences, Japan. Phys. Med. Biol. 2015, 60, 3271–3286. [Google Scholar] [CrossRef] [PubMed]
- ICRP. ICRP, 123: Assessment of radiation exposure of astronauts in space. ICRP Publication 123. Ann. ICRP 2013, 42, 1–339. [Google Scholar] [CrossRef] [PubMed]
- Bellinzona, V.E.; Cordoni, F.; Missiaggia, M.; Tommasino, F.; Scifoni, E.; La Tessa, C.; Attili, A. Linking Microdosimetric Measurements to Biological Effectiveness in Ion Beam Therapy: A Review of Theoretical Aspects of MKM and Other Models. Front. Phys. 2021, 8, 578492. [Google Scholar] [CrossRef]
- Parisi, A.; Furutani, K.M.; Beltran, C.J. On the calculation of the relative biological effectiveness of ion radiation therapy using a biological weighting function, the microdosimetric kinetic model (MKM) and subsequent corrections (non-Poisson MKM and modified MKM). Phys. Med. Biol. 2022, 67, 095014. [Google Scholar] [CrossRef] [PubMed]
- Friedland, W.; Dingfelder, M.; Kundrat, P.; Jacob, P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat. Res. 2011, 711, 28–40. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; Emfietzoglou, D.; Liamsuwan, T.; Taleei, R.; Liljequist, D.; Uehara, S. Radiation track, DNA damage and response-a review. Rep. Prog. Phys. 2016, 79, 116601. [Google Scholar] [CrossRef] [PubMed]
- Incerti, S.; Kyriakou, I.; Bernal, M.A.; Bordage, M.C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739. [Google Scholar] [CrossRef] [PubMed]
- Schuemann, J.; McNamara, A.L.; Ramos-Mendez, J.; Perl, J.; Held, K.D.; Paganetti, H.; Incerti, S.; Faddegon, B. TOPAS-nBio: An Extension to the TOPAS Simulation Toolkit for Cellular and Sub-cellular Radiobiology. Radiat. Res. 2019, 191, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Plante, I.; Poignant, F.; Slaba, T. Track Structure Components: Characterizing Energy Deposited in Spherical Cells from Direct and Peripheral HZE Ion Hits. Life 2021, 11, 1112. [Google Scholar] [CrossRef]
- Ogawa, T.; Hirata, Y.; Matsuya, Y.; Kai, T. Development and validation of proton track-structure model applicable to arbitrary materials. Sci. Rep. 2021, 11, 24401. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Iwamoto, Y.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Abe, S.-I.; Kai, T.; Matsuya, Y.; Matsuda, N.; Hirata, Y.; et al. Recent improvements of the particle and heavy ion transport code system—PHITS version 3.33. J. Nucl. Sci. Technol. 2023, 61, 127–135. [Google Scholar] [CrossRef]
- Sato, T.; Watanabe, R.; Niita, K. Development of a calculation method for estimating specific energy distribution in complex radiation fields. Radiat. Prot. Dosim. 2006, 122, 41–45. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Watanabe, R.; Sihver, L.; Niita, K. Applications of the microdosimetric function implemented in the macroscopic particle transport simulation code PHITS. Int. J. Radiat. Biol. 2012, 88, 143–150. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Van Hoey, O.; Mégret, P.; Vanhavere, F. Microdosimetric specific energy probability distribution in nanometric targets and its correlation with the efficiency of thermoluminescent detectors exposed to charged particles. Radiat. Meas. 2019, 123, 1–12. [Google Scholar] [CrossRef]
- Parisi, A.; Dabin, J.; Schoonjans, W.; Van Hoey, O.; Mégret, P.; Vanhavere, F. Photon energy response of LiF:Mg,Ti (MTS) and LiF:Mg,Cu,P (MCP) thermoluminescent detectors: Experimental measurements and microdosimetric modeling. Radiat. Phys. Chem. 2019, 163, 67–73. [Google Scholar] [CrossRef]
- Parisi, A.; Struelens, L.; Vanhavere, F. Nanoscale calculation of the relative efficiency of 7LiF: Mg, Ti (MTS-7) and 7LiF: Mg, Cu, P (MCP-7) thermoluminescent detectors for measuring electrons and positrons. J. Phys. Conf. Ser. 2020, 1662, 012025. [Google Scholar] [CrossRef]
- Parisi, A.; Olko, P.; Swakon, J.; Horwacik, T.; Jablonski, H.; Malinowski, L.; Nowak, T.; Struelens, L.; Vanhavere, F. Modeling the radiation-induced cell death in a therapeutic proton beam using thermoluminescent detectors and radiation transport simulations. Phys. Med. Biol. 2020, 65, 015008. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Sawakuchi, G.; Granville, D.; Yukihara, E.G. Microdosimetric modeling of the relative efficiency of Al2O3:C (Luxel, blue emission) optically stimulated luminescent detectors exposed to ions from 1H to 132Xe. Radiat. Meas. 2022, 150, 106678. [Google Scholar] [CrossRef]
- Hirata, Y.; Sato, T.; Watanabe, K.; Ogawa, T.; Parisi, A.; Uritani, A. Theoretical and experimental estimation of the relative optically stimulated luminescence efficiency of an optical-fiber-based BaFBr:Eu detector for swift ions. J. Nucl. Sci. Technol. 2022, 59, 915–924. [Google Scholar] [CrossRef]
- Sato, T.; Watanabe, R.; Kase, Y.; Tsuruoka, C.; Suzuki, M.; Furusawa, Y.; Niita, K. Analysis of cell-survival fractions for heavy-ion irradiations based on microdosimetric kinetic model implemented in the particle and heavy ion transport code system. Radiat. Prot. Dosim. 2011, 143, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Furusawa, Y. Cell survival fraction estimation based on the probability densities of domain and cell nucleus specific energies using improved microdosimetric kinetic models. Radiat. Res. 2012, 178, 341–356. [Google Scholar] [CrossRef] [PubMed]
- Matsuya, Y.; Sasaki, K.; Yoshii, Y.; Okuyama, G.; Date, H. Integrated Modelling of Cell Responses after Irradiation for DNA-Targeted Effects and Non-Targeted Effects. Sci. Rep. 2018, 8, 4849. [Google Scholar] [CrossRef]
- Matsuya, Y.; McMahon, S.J.; Ghita, M.; Yoshii, Y.; Sato, T.; Date, H.; Prise, K.M. Intensity Modulated Radiation Fields Induce Protective Effects and Reduce Importance of Dose-Rate Effects. Sci. Rep. 2019, 9, 9483. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Sato, T.; Matsuya, Y.; Kase, Y.; Magrin, G.; Verona, C.; Tran, L.; Rosenfeld, A.; Bianchi, A.; Olko, P.; et al. Development of a new microdosimetric biological weighting function for the RBE(10) assessment in case of the V79 cell line exposed to ions from (1)H to (238)U. Phys. Med. Biol. 2020, 65, 235010. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Beltran, C.J.; Furutani, K.M. The Mayo Clinic Florida microdosimetric kinetic model of clonogenic survival: Formalism and first benchmark against in vitro and in silico data. Phys. Med. Biol. 2022, 67, 185013. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Beltran, C.J.; Furutani, K.M. The Mayo Clinic Florida Microdosimetric Kinetic Model of Clonogenic Survival: Application to Various Repair-Competent Rodent and Human Cell Lines. Int. J. Mol. Sci. 2022, 23, 2491. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Matsuya, Y.; Hamada, N. Microdosimetric Modeling of Relative Biological Effectiveness for Skin Reactions: Possible Linkage Between In Vitro and In Vivo Data. Int. J. Radiat. Oncol. Biol. Phys. 2022, 114, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Matsuya, Y.; Ogawa, T.; Kai, T.; Hirata, Y.; Tsuda, S.; Parisi, A. Improvement of the hybrid approach between Monte Carlo simulation and analytical function for calculating microdosimetric probability densities in macroscopic matter. Phys. Med. Biol. 2023, 68, 155005. [Google Scholar] [CrossRef]
- Fowler, J.F. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol. 1989, 62, 679–694. [Google Scholar] [CrossRef]
- McMahon, S.J. The linear quadratic model: Usage, interpretation and challenges. Phys. Med. Biol. 2018, 64, 01TR01. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T.; Pfuhl, T.; Scholz, M. Update of the particle irradiation data ensemble (PIDE) for cell survival. J. Radiat. Res. 2021, 62, 645–655. [Google Scholar] [CrossRef] [PubMed]
- Grun, R.; Friedrich, T.; Traneus, E.; Scholz, M. Is the dose-averaged LET a reliable predictor for the relative biological effectiveness? Med. Phys. 2019, 46, 1064–1074. [Google Scholar] [CrossRef] [PubMed]
- Parisi, A.; Beltran, C.J.; Furutani, K.M. Variable RBE in proton radiotherapy: A comparative study with the predictive Mayo Clinic Florida microdosimetric kinetic model and phenomenological models of cell survival. Phys. Med. Biol. 2023, 68, 185020. [Google Scholar] [CrossRef] [PubMed]
- ICRU. ICRU Report 90: Key Data For Ionizing-Radiation Dosimetry; Technical Report for International Commission on Radiation Units & Measurements: Bethesda, MD, USA, 2016. [Google Scholar]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Hawkins, R.B. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat. Res. 1994, 140, 366–374. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.B. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET. Med. Phys. 1998, 25, 1157–1170. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, R.B. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET. Radiat. Res. 2003, 160, 61–69. [Google Scholar] [CrossRef] [PubMed]
- Kellerer, A.M.; Rossi, H.H. The theory of dual radiation action. Curr. Top. Radiat. Res. Quart. 1972, 8, 85–158. [Google Scholar]
- Yokota, H.; Vandenengh, G.; Hearst, J.E.; Sachs, R.K.; Trask, B.J. Evidence for the Organization of Chromatin in Megabase Pair-Sized Loops Arranged Along a Random-Walk Path in the Human G0/G1 Interphase Nucleus. J. Cell Biol. 1995, 130, 1239–1249. [Google Scholar] [CrossRef] [PubMed]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA double-stranded breaks induce histone H2AX phosphorylation on serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T.; Durante, M.; Scholz, M. Modeling cell survival after photon irradiation based on double-strand break clustering in megabase pair chromatin loops. Radiat. Res. 2012, 178, 385–394. [Google Scholar] [CrossRef]
- Sigmund, P.; Schinner, A.; Paul, H. Errata and Addenda for ICRU Report 73. J. ICRU 2009, 5, 1–10. [Google Scholar]
- Parisi, A.; Struelens, L.; Vanhavere, F. Comparison between the results of a recently-developed biological weighting function (V79-RBE(10)BWF) and thein vitroclonogenic survival RBE(10) of other repair-competent asynchronized normoxic mammalian cell lines and ions not used for the development of the model. Phys. Med. Biol. 2021, 66, 235006. [Google Scholar] [CrossRef]
- Chatterjee, A.; Schaefer, H.J. Microdosimetric structure of heavy ion tracks in tissue. Radiat. Environ. Biophys. 1976, 13, 215–227. [Google Scholar] [CrossRef] [PubMed]
- Butts, J.J.; Katz, R. Theory of RBE for heavy ion bombardment of dry enzymes and viruses. Radiat. Res. 1967, 30, 855–871. [Google Scholar] [CrossRef] [PubMed]
- Vassiliev, O.N.; Peterson, C.B.; Cao, W.; Grosshans, D.R.; Mohan, R. Systematic microdosimetric data for protons of therapeutic energies calculated with Geant4-DNA. Phys. Med. Biol. 2019, 64, 215018. [Google Scholar] [CrossRef] [PubMed]
- ICRU. ICRU Report 40: The Quality Factor in Radiation Protection; Technical Report for International Commission on Radiation Units & Measurements: Bethesda, MD, USA, 1986. [Google Scholar]
- Magrin, G. A method to convert spectra from slab microdosimeters in therapeutic ion-beams to the spectra referring to microdosimeters of different shapes and material. Phys. Med. Biol. 2018, 63, 215021. [Google Scholar] [CrossRef]
- Wulf, H.; Kraft-Weyrather, W.; Miltenburger, H.G.; Blakely, E.A.; Tobias, C.A.; Kraft, G. Heavy-ion effects on mammalian cells: Inactivation measurements with different cell lines. Radiat. Res. Suppl. 1985, 8, S122–S134. [Google Scholar] [CrossRef] [PubMed]
| Ion | Number of Ion- Irradiated Survival Curves | [Gy−1] | [Gy] |
|---|---|---|---|
| 1–2H | 42 | 0.113 | 4.58 |
| 3–4He | 31 | 0.176 | 9.70 |
| 12C | 54 | 0.179 | 10.0 |
| 16O | 5 | 0.250 | 17.2 |
| 20Ne | 20 | 0.211 | 12.4 |
| 40Ar | 16 | 0.237 | 17.0 |
| 56Fe | 13 | 0.199 | 11.4 |
| 84Kr | 5 | 0.240 | 17.2 |
| 132Xe | 14 | 0.244 | 17.2 |
| 238U | 19 | 0.233 | 16.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parisi, A.; Furutani, K.M.; Sato, T.; Beltran, C.J. Comparative Evaluation of Two Analytical Functions for the Microdosimetry of Ions from 1H to 238U. Quantum Beam Sci. 2024, 8, 18. https://doi.org/10.3390/qubs8030018
Parisi A, Furutani KM, Sato T, Beltran CJ. Comparative Evaluation of Two Analytical Functions for the Microdosimetry of Ions from 1H to 238U. Quantum Beam Science. 2024; 8(3):18. https://doi.org/10.3390/qubs8030018
Chicago/Turabian StyleParisi, Alessio, Keith M. Furutani, Tatsuhiko Sato, and Chris J. Beltran. 2024. "Comparative Evaluation of Two Analytical Functions for the Microdosimetry of Ions from 1H to 238U" Quantum Beam Science 8, no. 3: 18. https://doi.org/10.3390/qubs8030018
APA StyleParisi, A., Furutani, K. M., Sato, T., & Beltran, C. J. (2024). Comparative Evaluation of Two Analytical Functions for the Microdosimetry of Ions from 1H to 238U. Quantum Beam Science, 8(3), 18. https://doi.org/10.3390/qubs8030018








