Aromaticity Concepts Derived from Experiments
Abstract
:1. Introduction
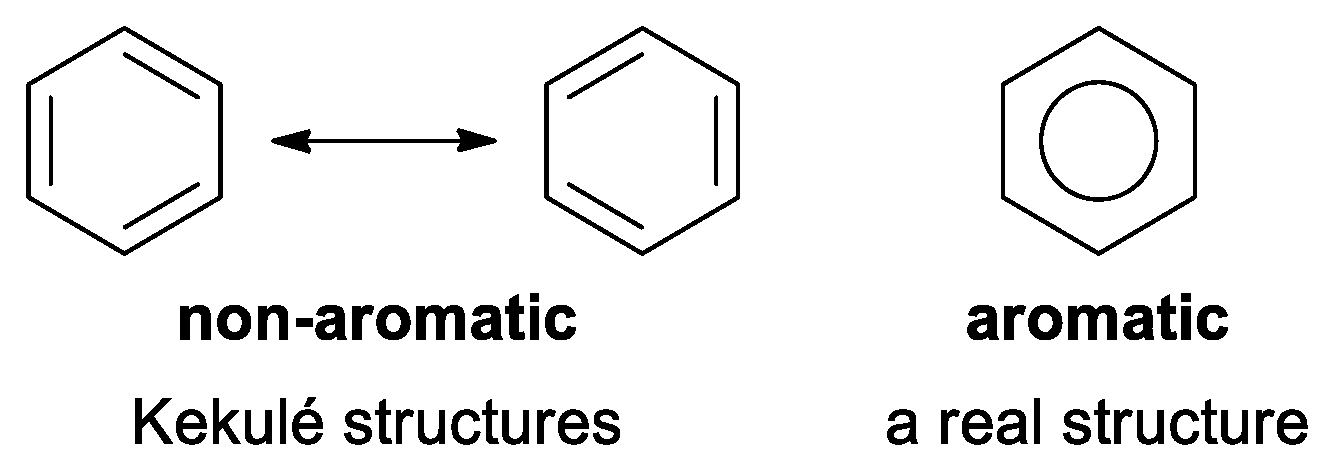
- they are more stable than their olefinic analogs by energy named ‘resonance energy’,
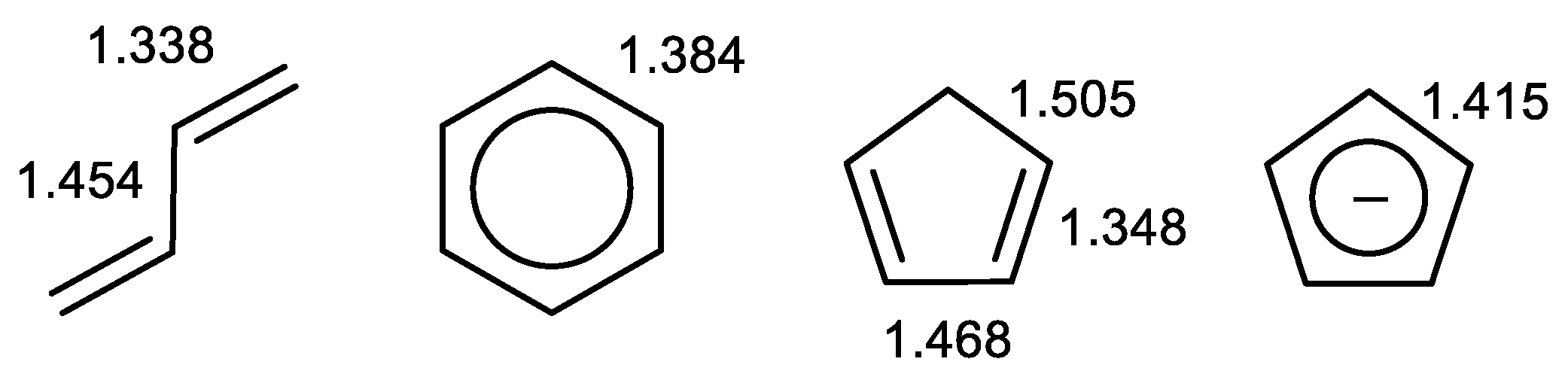
- they have bond lengths intermediate between those for typical single and double bonds,
- a π-electron ring current induced in aromatic molecules by an external magnetic field leads to increased diamagnetic susceptibility and typical diatropic (low field) chemical shifts of exocyclic protons in 1H NMR spectra,
- aromatic compounds generally undergo substitution reactions more easily than addition.”
- ribbon delocalization of either π- or σ-electrons (i.e., electrons occupying respectively π- and σ-orbitals);
- surface delocalization of σ-electrons occurring through an overlap of radially oriented σ-orbitals of a cyclic molecule as is the case of cyclopropane and
- volume delocalization of σ-electrons through an overlap of σ-orbitals directed inside a molecular polyhedron.”
2. Aromaticity Concepts Based on Experiments
2.1. Energy-Based Approaches
2.2. Geometry-Based Approaches
2.3. Magnetism-Based Aromaticity Descriptors
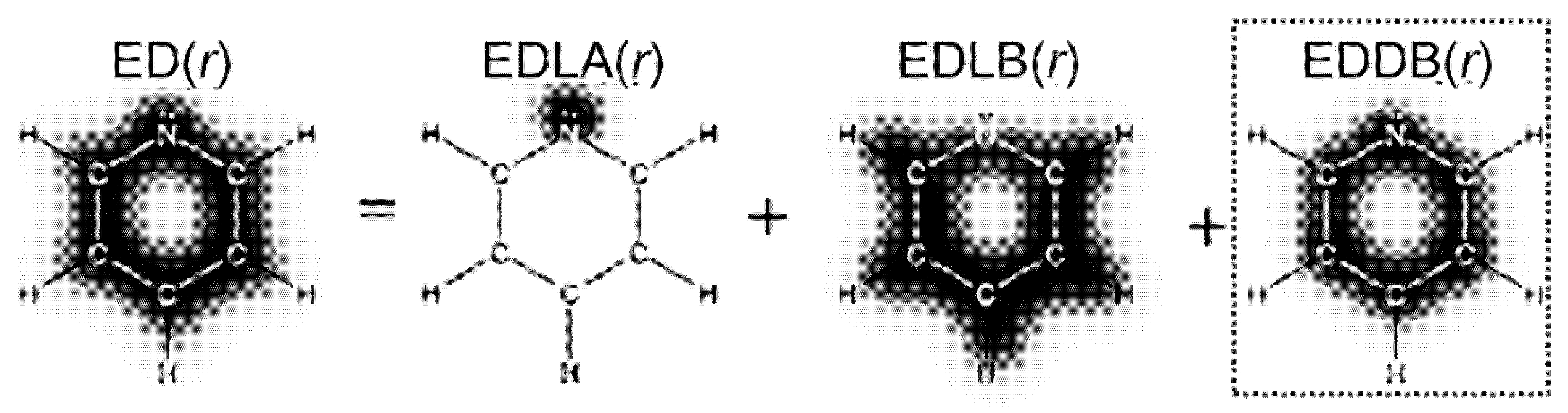
2.4. Electron Delocalization Indices
3. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coulson, C.A.; McWeeny, R. Coulson’s Valence, 3rd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 1979. [Google Scholar]
- Iczkowski, R.P.; Margrave, J.L. Electronegativity. J. Am. Chem. Soc. 1961, 83, 3547–3551. [Google Scholar] [CrossRef]
- Kekule, A. Über die Constitution der aromatischen Substanzen. Bull. Soc. Chim. Fr. 1865, 3, 98–110. [Google Scholar]
- Lonsdale, K. The structure of the benzene ring in C6(CH3)6. Proc. R. Soc. A Math. Phys. Eng. Sci. 1929, 123, 494–515. [Google Scholar]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Z. Physik 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Erlenmayer, E. Studien über die s. g. aromatischen Säuren. Ann. Chem. Pharm. 1866, 137, 327–359. [Google Scholar]
- Childs, R.F. The Homotropylium Ion and Homo-aromaticity. Acc. Chem. Res. 1984, 17, 347–352. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Wang, L.-S. All-metal aromaticity and antiaromaticity. Chem. Rev. 2005, 105, 3716–3757. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Bankiewicz, B.; Czarnecki, Z.; Palusiak, M. Quasi-aromaticity—What does it mean? Tetrahedron 2015, 71, 4895. [Google Scholar] [CrossRef]
- Rzepa, H.S. Möbius aromaticity and delocalization. Chem. Rev. 2005, 105, 3697–3715. [Google Scholar] [CrossRef]
- Chen, Z.; King, R.B. Spherical aromaticity: Recent work in fullerenes, polyhedral boranes, and related structures. Chem. Rev. 2005, 105, 3613–3642. [Google Scholar] [CrossRef]
- Solà, M. Why Aromaticity Is a Suspicious Concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Cyrański, M.K.; Czarnocki, Z.; Haefelinger, G.; Katritzky, A.R. Aromaticity: A theoretical concept of immense practical importance. Tetrahedron 2000, 56, 1783–1796. [Google Scholar] [CrossRef]
- Minkin, V.I. Glossary of Terms Used in Theoretical Organic Chemistry. Pure Appl. Chem. 1999, 71, 1919–1981. [Google Scholar] [CrossRef]
- Alonso, M.; Fernández, I. Quantifying Aromaticity According to the Energetic Criterion. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 6; pp. 195–235. [Google Scholar]
- SDBSWeb (National Institute of Advanced Industrial Science and Technology). Available online: https://sdbs.db.aist.go.jp (accessed on 20 April 2022).
- Guo, Y.-B.; Liu, Z.-Z.; Liu, H.-X.; Zhang, F.-Y.; Yin, J.-Q. A new aromatic probe—The ring stretching vibration Raman spectroscopy frequency. Spectrochim. Acta A 2016, 164, 84–88. [Google Scholar] [CrossRef]
- De Oteyza, D.G.; Gorman, P.; Chen, Y.-C.; Wickenburg, S.; Riss, A.; Mowbray, D.J.; Etkin, G.; Pedramrazi, Z.; Tsai, H.-Z.; Rubio, A.; et al. Direct Imaging of Covalent Bond Structure in Single-Molecule Chemical Reactions. Science 2013, 340, 1434–1437. [Google Scholar] [CrossRef] [PubMed]
- Gross, L.; Mohn, F.; Moll, N.; Schuler, B.; Criado, A.; Guitián, E.; Peña, D.; Gourdon, A.; Meyer, G. Bond-Order Discrimination by Atomic Force Microscopy. Science 2012, 337, 1326–1329. [Google Scholar] [CrossRef] [PubMed]
- Pigot, C.; Dumur, F. Molecular engineering in 2D surface covalent organic frameworks: Towards next generation of molecular tectons—A mini review. Synth. Met. 2020, 260, 116265. [Google Scholar] [CrossRef]
- Pauling, L.; Sherman, J. The Nature of the Chemical Bond. VI. The Calculation from Thermochemical Data of the Energy of Resonance of Molecules Among Several Electronic Structures. J. Chem. Phys. 1933, 1, 606–617. [Google Scholar] [CrossRef]
- Kistiakowsky, G.B.; Ruhoff, J.R.; Smith, H.A.; Vaughan, W.E. Heats of Organic Reactions. IV. Hydrogenation of Some Dienes and of Benzene. J. Am. Chem. Soc. 1936, 58, 146–153. [Google Scholar] [CrossRef]
- Cyranski, M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Radom, L.; Pople, J.A. Molecular orbital theory of the electronic structure of organic compounds. V. Molecular theory of bond separation. J. Am. Chem. Soc. 1970, 92, 4796–4801. [Google Scholar] [CrossRef]
- George, P.; Trachtman, M.; Bock, C.W.; Brett, A.M. Homodesmotic reactions for the assessment of stabilization energies in benzenoid and other conjugated cyclic hydrocarbons. J. Chem. Soc. Perkin Trans. 2 1976, 11, 1222–1227. [Google Scholar] [CrossRef]
- Pross, A.; Radom, L.; Taft, R.W. Theoretical Approach to Substituent Effects. Phenols and Phenoxide Ions. J. Org. Chem. 1980, 45, 818–826. [Google Scholar] [CrossRef]
- Wheeler, S.E. Homodesmotic reactions for thermochemistry. WIREs Comput. Mol. Sci. 2012, 2, 204–220. [Google Scholar] [CrossRef]
- George, P.; Bock, C.W.; Trachtman, M.J. The evaluation of empirical resonance energies as reaction enthalpies with particular reference to benzene. J. Chem. Educ. 1984, 61, 225. [Google Scholar] [CrossRef]
- Afeely, H.Y.; Liebman, J.F.; Stein, S.E. Neutral Thermochemical Data. In NIST Chemistry WebBook; NIST Standard Reference Database No. 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [Google Scholar]
- George, P. A Critique of the Resonance Energy Concept with Particular Reference to Nitrogen Heterocycles, Especially Porphyrins. Chem. Rev. 1975, 75, 85–111. [Google Scholar] [CrossRef]
- Pedley, J.B.; Naylor, R.D.; Kirby, S.P. Thermodynamical Data of Organic Compounds; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Schleyer, P.v.R.; Puhlhofer, F. Recommendations for the Evaluation of Aromatic Stabilization Energies. Org. Lett. 2002, 4, 2873–2876. [Google Scholar] [CrossRef]
- Fishtik, I.; Datta, R. Aromaticity vs Stoichiometry. J. Phys. Chem. A 2003, 107, 10471–10476. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Jiao, H.; van Eikema Hommes, N.J.R.; Malkin, V.G.; Malkina, O.L. An Evaluation of the Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. [Google Scholar] [CrossRef]
- Schrier, J. Introduction to Computational Physical Chemistry; University Science Books: Mill Valley, CA, USA, 2017. [Google Scholar]
- Aihara, J. Graph Theory of Aromatic Stabilization. BCSJ 2016, 89, 1425–1454. [Google Scholar] [CrossRef]
- Allen, F.H.; Kennard, O.; Watson, D.G.; Brammer, L.; Orpen, A.G.; Taylor, R. Tables of bond lengths determined by x-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc. Perkin Trans. 2 1987, 12, S1–S19. [Google Scholar] [CrossRef]
- Hückel, E. Theoretische Grundlagen der Organischen Chemie, 1 Band; Akademische Verlagsgesellschaft: Leipzig, Germany, 1956. [Google Scholar]
- Julg, A.; François, P. Recherches sur la geometrie de quelques hydrocarbures non-altenants—Son influence sur les energies de transition une nouvelle definition de l’aromaticite. Theor. Chim. Acta 1967, 7, 249–256. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intra- molecular Interactions Reflected in Aromatic Character of π-electron Systems. J. Chem. Inf. Comp. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Szatylowicz, H.; Stasyuk, O.A.; Dominikowska, J.; Palusiak, M. Aromaticity from the Viewpoint of Molecular Geometry: Application to Planar Systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef] [PubMed]
- Zborowski, K.K.; Alkorta, I.; Elguero, J.; Proniewicz, L.M. HOMA parameters for the boron-boron bond: How the interpretation of the BB bond influences the aromaticity of selected hydrocarbons. Struct. Chem. 2013, 24, 543–548. [Google Scholar]
- Zborowski, K.K.; Alkorta, I.; Elguero, J.; Proniewicz, L.M. Calculation of the HOMA model parameters for the carbon-boron bond. Struct. Chem. 2012, 23, 595–600. [Google Scholar]
- Madura, I.D.; Krygowski, T.M.; Cyrański, M.K. Structural Aspects of the Aromaticity of Cyclic π-electron Systems with BN Bonds. Tetrahedron 1998, 54, 14913–14918. [Google Scholar] [CrossRef]
- Zborowski, K.K.; Proniewicz, L.M. HOMA Model Extension for the Compounds Containing the Carbon–Selenium Bond. Pol. J. Chem. 2009, 83, 477–484. [Google Scholar]
- Raczyńska, E.D.; Hallman, M.; Kolczyńska, K.; Stępniewski, T. On the Harmonic Oscillator Model of Electron Delocalization (HOMED) Index and its Application to Heteroatomic π-Electron Systems. Symmetry 2010, 2, 1485–1509. [Google Scholar] [CrossRef]
- Frizzo, C.P.; Martins, M.A.P. Aromaticity in heterocycles: New HOMA index parametrization. Struct. Chem. 2012, 23, 375–380. [Google Scholar] [CrossRef]
- Raczyńska, E. Application of the Extended HOMED (Harmonic Oscillator Model of Aromaticity) Index to Simple and Tautomeric Five-Membered Heteroaromatic Cycles with C, N, O, P, and S Atoms. Symmetry 2019, 11, 146. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Description of Aromaticity with the Help of Vibrational Spectroscopy: Anthracene and Phenanthrene. J. Phys. Chem. A 2014, 118, 223–237. [Google Scholar] [CrossRef] [PubMed]
- Setiawan, D.; Kraka, E.; Cremer, D. Quantitative Assessment of Aromaticity and Antiaromaticity Utilizing Vibrational Spectroscopy. J. Org. Chem. 2016, 81, 9669–9686. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.M.; Sinclair, V.C.; Trotter, J. The Crystal and Molecular Structure of Tetracene. Acta Cryst. 1961, 14, 697–704. [Google Scholar] [CrossRef]
- Campbell, R.B.; Robertson, J.M. The crystal structure of hexacene, and a revision of the crystallographic data for tetracene and pentacene. Acta Cryst. 1962, 15, 289–290. [Google Scholar] [CrossRef]
- Berionni, G.; Wu, J.I.-C.; Schleyer, P.v.R. Aromaticity Evaluations of Planar (6)Radialenes. Org. Lett. 2014, 16, 6116–6119. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Cyrański, M.K.; Nakata, K.; Fujio, M.; Tsuno, Y. Separation of the Energetic and Geometric Contributions to Aromaticity. Part VI. Changes of the Aromatic Character of the Rings in Naphthalene, Anthracene, Phenanthrene and Pyrene Derivatives Induced by the Charged Substituent CH2+. Tetrahedron 1997, 53, 11383–11398. [Google Scholar] [CrossRef]
- Haags, A.; Reichmann, A.; Fan, Q.; Egger, L.; Kirschner, H.; Naumann, T.; Werner, S.; Vollgraff, T.; Sundermeyer, J.; Eschmann, L.; et al. Kekulene: On-Surface Synthesis, Orbital Structure, and Aromatic Stabilization. ACS Nano 2020, 14, 15766–15775. [Google Scholar] [CrossRef] [PubMed]
- Bird, C.W. A new aromaticity index and its application to five membered ring heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to six-membered ring heterocycles. Tetrahedron 1986, 42, 89–92. [Google Scholar] [CrossRef]
- Bird, C.W. Hetero-aromaticity, 8, the influence of N-oxide formation on heterocyclic aromaticity. Tetrahedron 1993, 49, 8441–8448. [Google Scholar] [CrossRef]
- Gordy, W.J. A Relation between Bond Force Constants, Bond Orders, Bond Lengths, and the Electronegativities of the Bonded Atoms. J. Chem. Phys. 1947, 14, 305–310. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 4 The status of phosphorus and arsenic heteroatoms. Tetrahedron 1990, 46, 5697–5702. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to some bicyclic heterocycles. Tetrahedron 1987, 43, 4725–4730. [Google Scholar] [CrossRef]
- Kertesz, M.; Choi, C.H.; Yang, S. Conjugated Polymers and Aromaticity. Chem. Rev. 2005, 105, 3448–3481. [Google Scholar] [CrossRef] [PubMed]
- Casademont-Reig, I.; Woller, T.; Contreras-Garcıa, J.; Alonso, M.; Torrent-Sucarrat, M.; Matito, E. New electron delocalization tools to describe the aromaticity in porphyrinoids. Phys. Chem. Chem. Phys. 2018, 20, 2787–2796. [Google Scholar] [CrossRef] [PubMed]
- Kurach, E.; Djurado, D.; Rimarcik, J.; Kornet, A.; Wlostowski, M.; Lukes, V.; Pecaut, J.; Zagorska, M.; Pron, A. Effect of substituents on redox, spectroscopic and structural properties of conjugated diaryltetrazines—A combined experimental and theoretical study. Phys. Chem. Chem. Phys. 2011, 13, 2690–2700. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility exaltation in hydrocarbons. J. Am. Chem. Soc. 1969, 91, 1991–1998. [Google Scholar] [CrossRef]
- Minkin, V.I.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity. Electronic and Structural Aspects; Wiley: New York, NY, USA, 1994; pp. 63–103. [Google Scholar]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility exaltation as a criterion of aromaticity. J. Am. Chem. Soc. 1968, 90, 811–813. [Google Scholar] [CrossRef]
- Benson, R.C.; Flygare, W.H. Molecular Zeeman Effect of Cyclopentadiene and Isoprene and Comparison of the Magnetic Susceptibility Anisotropies. J. Am. Chem. Soc. 1970, 92, 7523–7529. [Google Scholar]
- Flygare, W.H. Magnetic interactions in molecules and an analysis of molecular electronic charge distribution from magnetic parameters. Chem. Rev. 1974, 74, 653–687. [Google Scholar] [CrossRef]
- Mitchell, R.H. Measuring Aromaticity by NMR. Chem. Rev. 2001, 101, 1301–1315. [Google Scholar] [CrossRef] [PubMed]
- Rickhaus, M.; Jirasek, M.; Tejerina, L.; Gotfredsen, H.; Peeks, M.D.; Haver, R.; Jiang, H.-W.; Claridge, T.D.W.; Anderson, H.L. Global aromaticity at the nanoscale. Nat. Chem. 2020, 12, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Jirásek, M.; Anderson, H.L.; Peeks, M.D. From Macrocycles to Quantum Rings: Does Aromaticity Have a Size Limit? Acc. Chem. Res. 2021, 54, 3241–3251. [Google Scholar] [CrossRef] [PubMed]
- Herges, R.; Geuenich, D. Delocalization of Electrons in Molecules. J. Phys. Chem. A 2001, 105, 3214–3220. [Google Scholar] [CrossRef]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef] [PubMed]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The Gauge Including Magnetically Induced Current Method. Phys. Chem. Chem. Phys. 2011, 13, 20500. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Zanasi, R. AACID: Anisotropy of the Asymmetric Magnetically Induced Current Density Tensor. J. Phys. Chem. A 2018, 122, 4681–4686. [Google Scholar] [CrossRef]
- Monaco, G.; Zanasi, R. Delocalization Energy Retrieved from the Current Density Tensor. Phys. Chem. Chem. Phys. 2019, 21, 11564–11568. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Cyrański, M.K.; Krygowski, T.M.; Wisiorowski, M.; van Eikema Hommes, N.J.R.; Schleyer, P.v.R. Global and Local Aromaticity in Porphyrins: An Analysis Based on Molecular Geometriesand Nucleus-Independent Chemical Shifts. Angew. Chem. Int. Ed. 1998, 37, 177–180. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Carminboef, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Lazzeretti, P. Ring currents. Progr. Nucl. Magn. Res. Spectr. 2000, 36, 1–88. [Google Scholar] [CrossRef]
- Lazzeretti, P. Assessment of aromaticity via molecular response properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
- Corminboeuf, C.; Heine, T.; Seifert, G.; Schleyer, P.v.R.; Weber, J. Induced magnetic fields in aromatic [n]-annulenes—Interpretation of NICS tensor components. Phys. Chem. Chem. Phys. 2004, 6, 273–276. [Google Scholar] [CrossRef]
- Paenurk, E.; Gershoni-Poranne, R. Simple and efficient visualization of aromaticity: Bond currents calculated from NICS values. Phys. Chem. Chem. Phys. 2022, 24, 8631–8644. [Google Scholar] [CrossRef]
- Gajda, L.; Kupka, T.; Broda, M.A.; Leszczyńska, M.; Ejsmont, K. Method and basis set dependence of the NICS indexes of aromaticity for benzene. Magn. Reson. Chem. 2018, 56, 265–275. [Google Scholar] [CrossRef] [PubMed]
- London, F. Théorie quantique des courants interatomiques dans les combinaisons aromatiques. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- Fowler, P.W.; Havenith, R.W.A.; Jenneskens, L.W.; Soncini, A.; Steiner, E. Survival and extinction of delocalised ring currents in clamped benzenes. Chem. Commun. 2001, 22, 2386–2387. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R.; Stanger, A. The NICS-XY-Scan: Identification of Local and Global Ring Currents in Multi-Ring Systems. Chem. Eur. J. 2014, 20, 5673–5688. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R. Piecing it together: An additivity scheme for aromaticity using NICS-XY scans. Chem. Eur. J. 2018, 24, 4165–4172. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, P.; Gershoni-Poranne, R. An additivity scheme for aromaticity: The heteroatom case. ChemPhysChem 2019, 20, 1508. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Stanger, A. NICS—Nucleus-Independent Chemical Shift. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 4; pp. 99–154. [Google Scholar]
- Báez-Grez, R.; Ruiz, L.; Pino-Rios, R.; Tiznado, W. Which NICS Method Is Most Consistent with Ring Current Analysis? Assessment in Simple Monocycles. RSC Adv. 2018, 8, 13446–13453. [Google Scholar] [CrossRef]
- Stanger, A.; Monaco, G.; Zanasi, R. NICS- XY -Scan Predictions of Local, Semi-Global, and Global Ring Currents in Annulated Pentalene and S-Indacene Cores Compared to First-Principles Current Density Maps. ChemPhysChem 2020, 21, 65–82. [Google Scholar] [CrossRef]
- Amnon Stanger, the Aroma Package. Available online: https://chemistry.technion.ac.il/en/team/amnon-stanger/ (accessed on 20 April 2022).
- Gershoni-Poranne, R.; Stanger, A. Magnetic criteria of aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W.; Soncini, A.; Jenneskens, L.W. Current-Density Maps as Probes of Aromaticity: Global and Clar π Ring Currents in Totally Resonant Polycyclic Aromatic Hydrocarbons. Faraday Discuss. 2007, 135, 309–323. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Solà, M.; Krygowski, T.M.; Szatylowicz, H.; Andrzejak, M.; Pawełek, B.; Dominikowska, J.; Kukułka, M.; Dyduch, K. Aromaticity of Acenes: The Model of Migrating π-Circuits. Phys. Chem. Chem. Phys. 2018, 20, 13430–13436. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Żak, E.; Dyduch, K.; Mrozek, J. Electron Delocalization Index Based on Bond Order Orbitals. Chem. Phys. Lett. 2014, 593, 154–159. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Andrzejak, M.; Dyduch, K.; Żak, E.; Makowski, M.; Mazur, G.; Mrozek, J. A Uniform Approach to the Description of Multicenter Bonding. Phys. Chem. Chem. Phys. 2014, 16, 20514–20523. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W.; Solà, M. The Electron Density of Delocalized Bonds (EDDBs) as a Measure of Local and Global Aromaticity. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 8; pp. 259–284. [Google Scholar]
- Homepage: D.W. Szczepanik—EDDB. Available online: http://www.eddb.pl/runeddb/gallery/ (accessed on 20 April 2022).
- Casati, N.; Kleppe, A.; Jephcoat, A.P.; Macchi, P. Putting Pressure on Aromaticity along with in Situ Experimental Electron Density of a Molecular Crystal. Nat. Commun. 2016, 7, 10901. [Google Scholar] [CrossRef] [PubMed]
- Genoni, A.; Macchi, P. Quantum Crystallography in the Last Decade: Developments and Outlooks. Crystals 2020, 10, 473. [Google Scholar] [CrossRef]
- Bader, R.F.W. A Quantum Theory of Molecular Structure and Its Applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; The International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Matta, C.F.; Hernández-Trujillo, J. Bonding in Polycyclic Aromatic Hydrocarbons in Terms of the Electron Density and of Electron Delocalization. J. Phys. Chem. A 2003, 107, 7496–7504. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solà, M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef]
- Matito, E.; Duran, M.; Solà, M. The Aromatic Fluctuation Index (FLU): A New Aromaticity Index Based on Electron Delocalization. J. Chem. Phys. 2005, 122, 014109. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; van Damme, S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Matito, E. An Electronic Aromaticity Index for Large Rings. Phys. Chem. Chem. Phys. 2016, 18, 11839–11846. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Gatti, C. A Green’s Function for the Density. Chem. Phys. Lett. 1998, 287, 233–238. [Google Scholar] [CrossRef]
- Gatti, C.; Saleh, G.; Lo Presti, L. Source Function Applied to Experimental Densities Reveals Subtle Electron-Delocalization Effects and Appraises Their Transferability Properties in Crystals. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 180–193. [Google Scholar] [CrossRef] [PubMed]
- Monza, E.; Gatti, C.; Lo Presti, L.; Ortoleva, E. Revealing Electron Delocalization through the Source Function. J. Phys. Chem. A 2011, 115, 12864–12878. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Andrzejak, M.; Dominikowska, J.; Pawełek, B.; Krygowski, T.M.; Szatylowicz, H.; Solà, M. The Electron Density of Delocalized Bonds (EDDB) Applied for Quantifying Aromaticity. Phys. Chem. Chem. Phys. 2017, 19, 28970–28981. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W. RunEDDB, Version 26-Jun-2021. Available online: http://www.eddb.pl/runeddb/ (accessed on 20 April 2022).
- Gross, L.; Mohn, F.; Moll, N.; Liljeroth, P.; Meyer, G. The Chemical Structure of a Molecule Resolved by Atomic Force Microscopy. Science 2009, 325, 1110–1114. [Google Scholar] [CrossRef]
- Casademont-Reig, I.; Ramos-Cordoba, E.; Torrent-Sucarrat, M.; Matito, E. Aromaticity Descriptors Based on Electron Delocalization. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 7; pp. 235–259. [Google Scholar]
- Curutchet, C.; Poater, J.; Sola, M.; Elguero, J. Analysis of the effects of n-substituents on some aspects of the aromaticity of imidazoles and pyrazoles. J. Phys. Chem. A 2011, 115, 8571–8577. [Google Scholar] [CrossRef] [PubMed]
- Stanger, A. Reexamination of NICS π,zz: Height Dependence, Off-Center Values, and Integration. J. Phys. Chem. A 2019, 123, 3922–3927. [Google Scholar] [CrossRef]
- Alonso, M.; Miranda, C.; Martin, N.; Herradon, B. Chemical applications of neural networks: Aromaticity of pyrimidine derivatives. Phys. Chem. Chem. Phys. 2011, 13, 20564–20574. [Google Scholar] [CrossRef]
- Wieczorkiewicz, P.A.; Szatylowicz, H.; Krygowski, T.M. Energetic and Geometric Characteristics of Substituents, Part 3: The Case of NO2 and NH2 Groups in Their Mono-Substituted Derivatives of Six-Membered Heterocycles. Symmetry 2022, 14, 145. [Google Scholar] [CrossRef]
- Matito, E.; Salvador, P.; Duran, M.; Solà, M. Aromaticity Measures from Fuzzy-Atom Bond Orders (FBO). The Aromatic Fluctuation (FLU) and the Para-Delocalization (PDI) Indexes. J. Phys. Chem. A 2006, 110, 5108–5113. [Google Scholar] [CrossRef]
- Szatylowicz, H.; Wieczorkiewicz, P.A.; Krygowski, T.M. Molecular Geometry as a Source of Electronic Structure of π-Electron Systems and Their Physicochemical Properties. In Aromaticity; Fernández, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 3; pp. 71–99. [Google Scholar]
- Szatylowicz, H.; Stasyuk, O.A.; Solà, M.; Krygowski, T.M. Aromaticity of Nucleic Acid Bases. WIREs Comput. Mol. Sci. 2021, 11, e1509. [Google Scholar] [CrossRef]
- Jezuita, A.; Szatylowicz, H.; Marek, P.H.; Krygowski, T.M. Aromaticity of the Most Stable Adenine and Purine Tautomers in Terms of Hückel’s 4N+2 Principle. Tetrahedron 2019, 75, 130474. [Google Scholar] [CrossRef]
- Mohajeri, A.; Shahamirian, M. Pi-electron delocalization in aza derivatives of naphthalene and indole. Comput. Theor. Chem. 2011, 976, 19–29. [Google Scholar] [CrossRef]
- Rakhi, R.; Suresh, C.H. A DFT study on dihydropyrazine annulated linear polyacenes: Aromaticity, stability and HOMO–LUMO energy modulation. Phys. Chem. Chem. Phys. 2016, 18, 24631–24641. [Google Scholar] [CrossRef] [PubMed]










| No | Reaction Scheme | ASE /kcal/mol | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) |  | + | 6 | CH4 | → | 3 | CH3−CH3 | + | 3 | CH2=CH2 | 61.1 [24] |
| 64.2 [28] | |||||||||||
| 64.7 [29] | |||||||||||
| 66.9 | |||||||||||
| (2) | 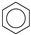 | + | 3 | CH3−CH3 | → |  | + | 3 | CH2=CH2 | 48.7 [30] | |
| 48.5 [29] | |||||||||||
| 55.3 | |||||||||||
| (3) | 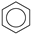 | + | 2 | 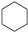 | → | 3 |  | 35.6 [31,32] | |||
| 35.9 [29,32] | |||||||||||
| 37.5 | |||||||||||
| (4) | 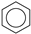 | + | 3 |  | → | 3 |  | + | 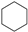 | 32.4 | |
| 31.3 [33] | |||||||||||
| 30.5 [31] | |||||||||||
| (5) | 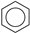 | + | 3 | CH2=CH2 | → | 3 |  | 21.6 [28] | |||
| 20.6 [29] | |||||||||||
| 23.2 | |||||||||||
| (6) | 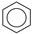 | + | 3 | CH2=CH2 | → | 3 | 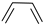 | 34.1 * [34] | |||
| 33.6 | |||||||||||
| (7) | 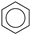 | + | 3 |  | → | 3 |  | 22.5 [29] | |||
| 19.3 | |||||||||||
| Type of Bond | Ropt/Å | α | Reference |
|---|---|---|---|
| BB | 1.5665 | 244.147 | [43] |
| BBw | 1.5693 | 250.544 | [43] |
| BCexp | 1.4235 | 104.507 | [44] |
| BCtheo | 1.4378 | 118.009 | [44] |
| BCtheo/w | 1.4386 | 118.618 | [44] |
| BN | 1.402 | 72.03 | [45] |
| CC | 1.388 | 257.7 | [41] |
| CN | 1.334 | 93.52 | [41] |
| CO | 1.265 | 157.38 | [41] |
| CP | 1.698 | 118.91 | [41] |
| CS | 1.677 | 94.09 | [41] |
| CSe | 1.8217 | 84.9144 | [46] |
| NN | 1.309 | 130.33 | [41] |
| NO | 1.248 | 57.21 | [41] |
| Compound | Aromatic Character | HOMA | FLU | NICS(1)zz | EDDB |
|---|---|---|---|---|---|
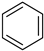 Benzene a | + | 1.000 | 0.000 | −30.6 | 5.54 |
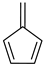 Fulvene a | 0 | −0.363 | 0.049 | −5.5 | 0.47 |
 Cyclobutadiene d | − | − | − | 50.25 | − |
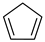 Cyclopentadiene a | 0 | −0.878 | 0.058 | −13.0 | 0.34 |
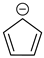 Cyclopentadienyl anion a | + | 0.753 | 0.000 | −34.8 | 4.35 |
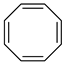 Cyclooctatetraene (COT) | 0 | −0.21 i | − | 94.09 d | − |
| COT2− | + | 0.800 i | − | −41.65 d | − |
| COT2+ | + | − | −27.16 d | − | |
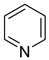 Pyridine | + | 1.000 b | 0.005 b | −31.63 j | 5.249 b |
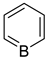 borabenzene | + | 0.908 f | − | − | 5.044 g |
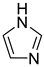 Imidazole c | + | 0.880 | 0.0118 | −31.68 | − |
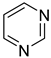 pyrimidine | + | 0.999 e | 0.0045 h | −29.74 j | 5.181 a |
| Ring 1 | Ring 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Compound | HOMA | FLU | NICS(1)zz | EDDB | HOMA | FLU | NICS(1)zz | EDDB |
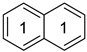 Naphthalene a | 0.743 | 0.0096 | −29.9 m | 3.29 | - | - | - | - |
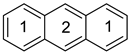 Anthracene a | 0.557 | 0.0175 | −26.32 n | 2.30 | 0.714 | 0.0080 | −34.11 n | 3.68 |
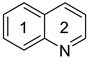 Quinoline | 0.793 m | 0.0154 h | −29.5 m | 0.821m | 0.0173 h | −28.4 m | ||
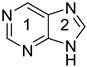 purine 9 H k | 0.976 | 0.009 l | −26.2 | 0.834 | 0.036 l | −29.9 | ||
 purine 1H k | 0.665 | 0.032 l | −23.7 | 0.667 | 0.021 l | −31.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szatylowicz, H.; Wieczorkiewicz, P.A.; Krygowski, T.M. Aromaticity Concepts Derived from Experiments. Sci 2022, 4, 24. https://doi.org/10.3390/sci4020024
Szatylowicz H, Wieczorkiewicz PA, Krygowski TM. Aromaticity Concepts Derived from Experiments. Sci. 2022; 4(2):24. https://doi.org/10.3390/sci4020024
Chicago/Turabian StyleSzatylowicz, Halina, Paweł A. Wieczorkiewicz, and Tadeusz M. Krygowski. 2022. "Aromaticity Concepts Derived from Experiments" Sci 4, no. 2: 24. https://doi.org/10.3390/sci4020024
APA StyleSzatylowicz, H., Wieczorkiewicz, P. A., & Krygowski, T. M. (2022). Aromaticity Concepts Derived from Experiments. Sci, 4(2), 24. https://doi.org/10.3390/sci4020024






