A System Dynamics Model to Facilitate the Development of Policy for Urban Heat Island Mitigation
Abstract
:1. Introduction
Article Organization
- Section 2. Materials and Methods provides: an overview description of the UHIMPT model (incl., its components, required data inputs and data outputs), and a thorough review of its mathematical parameterization (incl., the presentation of each equation);
- Section 3. Results provides an illustrative demonstration of how the UHIMPT model may be customized and used to facilitate an improved understanding of the public health threat of heat within the urban heat island and, therewith, the informed development of policy for its mitigation within a given location;
- Section 4. Discussion reviews: the results of the illustrative demonstration of the UHIMPT model, and the demonstrated utility of the UHIMPT model;
- Section 5. Model Validation applies common structural and behavioral validation tests to the UHIMPT model in order to verify that: the model structure represents actual conditions accurately and in sufficient detail, and simulated behavior reasonably mimics observed behavior to a degree that is sufficient to instill confidence;
- Section 6. Model Limitations provides a discussion of the various limitations of the UHIMPT model and, where relevant, identifies potential means to overcome same;
- Section 7. Proper Model Use explores, in consideration of model structure and limitations, how the UHIMPT model should, and should not, be used;
- Section 8. Conclusion summarizes the utility of the UHIMPT model.
2. Materials and Methods
2.1. Model Description
2.1.1. Components
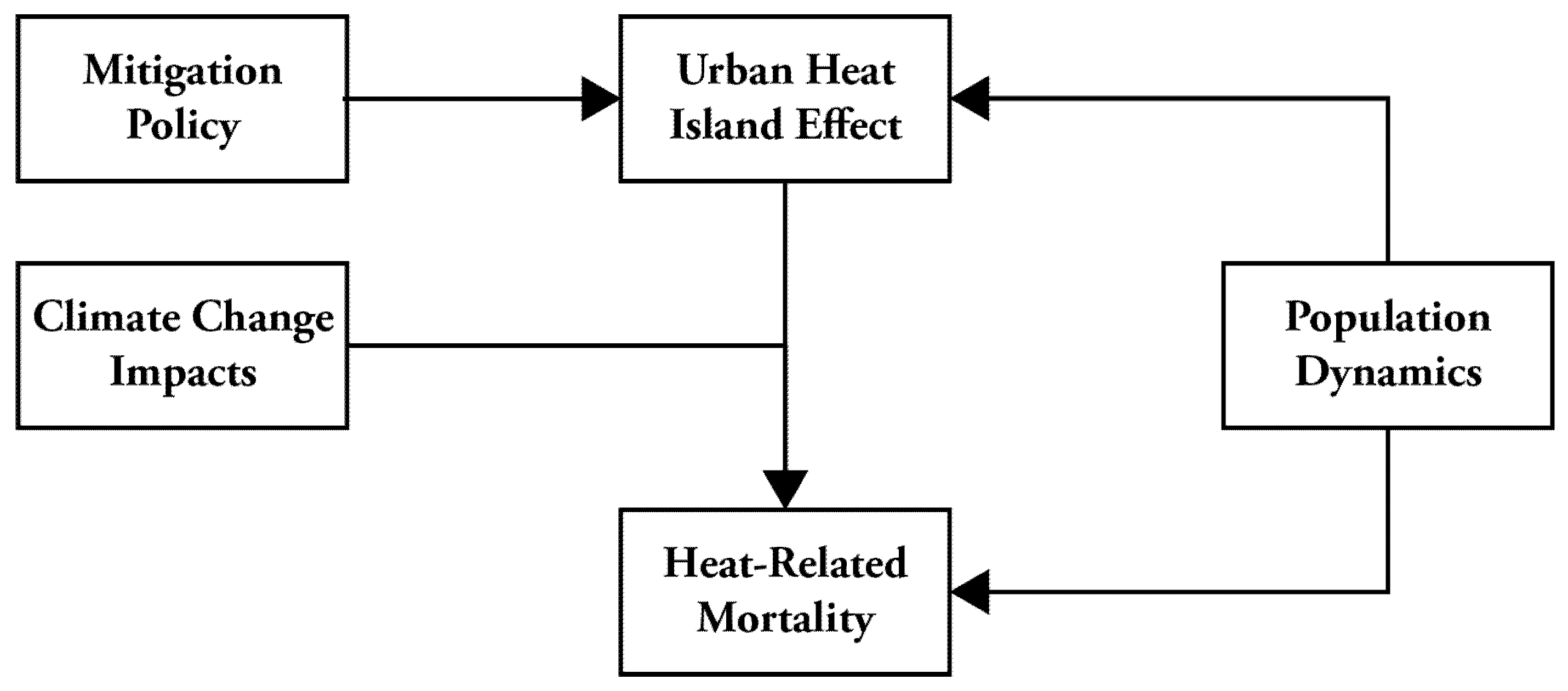
Urban Heat Island
- Normal mean warmest month urban heat island amplitude;
- Normal mean maximum warmest month urban heat island amplitude;
- Development of the urban heat island effect, as determined by an adapted population size–urban heat island amplitude function for North American settlements;
- Impact of sundry hypothetical policies for urban heat island mitigation.
Climate Change Impacts
- Normal mean warmest month air temperature;
- Normal mean maximum warmest month air temperature;
- Projected mean warmest month air temperature;
- Projected mean maximum warmest month air temperature;
- Impact of projected temperatures on urban heat island amplitude.
Population Dynamics
- Fertility;
- All-cause mortality;
- Net migration.
Heat-Related Mortality
- Impact of mean warmest month air temperature on mortality (i.e., heat-related mortality);
- Impact of mean maximum warmest month air temperature on mortality (i.e., heat-related mortality);
- Impact of acclimatization to higher temperatures resulting from future climate change on heat-related mortality.
Summary of Relationships between Model Components
2.1.2. Data Inputs
Urban Heat Island
Climate Change Impacts
Population Dynamics
Heat-Related Mortality
Other Data Requirements
2.1.3. Model Outputs
- Future urban heat island amplitude, as measured by urban–rural differences in mean warmest month and mean maximum warmest month temperatures and impacted by climate change and the dynamic nature of urban heat island amplitude, but not hypothetical policies for urban heat island mitigation;
- Future urban heat island amplitude, as measured by urban–rural differences in mean warmest month and mean maximum warmest month temperatures and impacted by climate change and the dynamic nature of urban heat island amplitude, as well as hypothetical policies for urban heat island mitigation;
- The impacts of heat-related mortality in the urban area, as expressed as the number of deaths that can be expected to result from one day of exposure to the mean warmest month and mean maximum warmest month temperatures for both a no-mitigation and urban heat island mitigation scenarios, but not accounting for the impacts of the human capacity for acclimatization to higher temperatures;
- The impacts of heat-related mortality in the urban area, as expressed as the number of deaths that can be expected to result from one day of exposure to mean warmest month temperature and mean maximum warmest month temperature for both no-mitigation and urban heat island mitigation scenarios with accounting for the impacts of the human capacity for acclimatization to higher temperatures.
2.2. Model Parameterization
2.2.1. Urban Heat Island
2.2.2. Climate Change Impacts
2.2.3. Population Dynamics
2.2.4. Heat-Related Mortality
3. Results
3.1. Illustrative Model Demonstration
3.1.1. Preparation of Customized Multiple Linear Regression Model
3.1.2. Outline of Data Inputs Used in Illustrative Model Demonstration
3.1.3. Simulation of Hypothetical Intervention Scenarios
- Increasing mean surface albedo, but making no changes to the mean proportions of vegetation or impervious surface cover;
- Increasing the mean proportion of vegetation, but making no changes to mean surface albedo or the mean proportion of impervious surface cover;
- Decreasing the mean proportion of impervious surface cover, but making no changes to mean surface albedo or the mean proportion of vegetation;
- Increasing mean surface albedo and the mean proportion of vegetation in equal amounts, while decreasing the mean proportion of impervious surface cover in an amount that is equal to the additive inverse of said increases.
Increasing the Mean Surface Albedo
Increasing the Mean Proportion of Vegetation
Decreasing the Mean Proportion of Impervious Surface
Simultaneously Increasing Mean Surface Albedo and the Mean Proportion of Vegetation, and Decreasing the Mean Proportion of Impervious Surface
Mortality Impacts of all Hypothetical Scenarios
4. Discussion
4.1. Results of Illustrative Model Demonstration
4.2. UHIMPT Model Potential
5. Model Validation
5.1. Structural Validation
5.1.1. Boundary Adequacy
- Urban heat island amplitude, as affected by population size, which is used as a proxy for development intensity, and the application of hypothetical urban heat island mitigation measures;
- Climate change impacts, and specifically the annualized projections of mean and mean maximum warmest month temperatures;
- A cohort–component population projection, which impacts urban heat island amplitude with its projection of total population and is also used in the estimation of future heat-related mortality;
- Future heat-related mortality, which is driven by: the mortality calculations of the cohort–component population projection, and temperature–mortality functions and an acclimatization factor, all of which have been developed by Nordio et al. [50].
5.1.2. Structure Verification
Structure of Actual System
Structure of UHIMPT Model
Result of Structure Verification Test
5.1.3. Parameter Verification
5.2. Behavioral Validation
6. Model Limitations
6.1. Total Impact of Multi-Day Extreme Events
6.2. Accidental Mortality
6.3. Assumption of Constant Growth or Stagnant Conditions in the Built Environment
6.4. Assumption of Constant Mortality, Fertility and Net Migration Rates
6.5. Unforseen Circumstances
6.6. Limitations of Population Size–Urban Heat Island Amplitude Function
6.7. Conversion of Land Surface Temperature to Air Temperature
6.8. Selection of Appropriate Temperature–Mortality Function
7. Proper Model Use
8. Conclusions
9. Notes
- Please note that although data on normal extreme maximum temperature exists (e.g., the dataset that is presented in Wang et al. [56] includes data for extreme maximum temperature over thirty years), the UHIMPT model uses normal mean maximum warmest month temperature in its accounting for the urban heat island effect. Both indicators represent extremes with: normal mean maximum warmest month temperature able to be considered as the mean extreme; and the normal extreme maximum temperature able to be considered as the extreme of extremes. The UHIMPT model, however, includes normal mean maximum warmest month temperature in its accounting for the urban heat island effect because addressing the mean extreme is, generally, more attainable than addressing the extreme of extremes. Moreover, addressing the mean extreme, as opposed to the extreme of extremes, may often be considered to be a more efficient use of resources. Indeed, it may be better to plan for the mean extreme, which represents conditions that are more likely to happen on an annual basis, than conditions that are less likely to occur at a given time (n.b., to borrow from the example of flood hazard mitigation, it is noted that the United States Federal Emergency Management Agency [FEMA] requires that levees be designed to provide protection for floods that have a 1.0 percent chance of occurring on an annual basis [i.e., a 100-year flood], as opposed to a more extreme flood that has a 0.2 percent chance of occurring on an annual basis [i.e., a 500-year flood]). Please note, however, that this approach of planning for the mean extreme and not the extreme of extremes may not be universally applicable within the realm of hazard mitigation and climate change adaptation; it should not be applied without careful consideration outside of the context of application of the UHIMPT model.
- As noted, the canopy layer urban heat island generally exhibits its highest amplitude during the nighttime hours. Although the data used to calculate the baseline measurements of urban heat island amplitude are not specifically representative of nighttime, the UHIMPT model, as explained in Section 2.2.2, uses urban heat island amplitude to develop estimates of mean warmest month and mean maximum warmest month air temperature within the urban heat island. Thus, the overall focus of the UHIMPT model is not on the mere amplitude, but on the total temperature to which the urban heat island amplitude contributes. Nonetheless, we note that while the canopy layer urban heat island generally exhibits its highest amplitude at nighttime, nighttime does not correspond to the highest air temperatures. This distinction is important given the UHIMPT model’s incorporation of heat-related mortality. By developing an estimate of mean maximum warmest month air temperature within the urban heat island, however the basis for analysis of the maximum impacts of the urban heat island on heat-related mortality is provided.
- Although the UHIMPT model makes use of a population size–urban heat island amplitude function for North American settlements, it can be easily adapted to incorporate similar functions for other regions.
- Despite its age, the population size–urban heat island amplitude function for North American settlements of Oke [34] remains the most comprehensive analysis of the relationship between population size and urban heat island amplitude of North American cities available to date. Moreover, it relies on a methodology that has been proven to be highly reliable in several subsequent studies (see: [39,40,41]).
- In the event that population should decline between two consecutive time steps, the factor of change in urban heat island amplitude is assumed to be zero. This assumes that no significant changes in urban geometry that would alter urban heat island amplitude accompany such a decline in population.
- A key explanation why the UHIMPT model uses an adaptation of Oke’s [34] population size–urban heat island amplitude function is to keep the model as simple as possible. Adding sky view factor measurements would result in the need to include their measurement, which would result in a significant increase in data input requirements for the user. However, as is indicated in Section 2.1.1, the UHIMPT model already includes a cohort-component population projection. By using an adaptation of Oke’s [34] population size–urban heat island amplitude function, the numbers of individual components and required inputs is reduced, which, thereby, simplifies the model and makes it more user-friendly and easier to run.
- Although sky view factor, which is directly representative of urban geometry, may, upon first consideration, seem to have a more direct relationship with the formation of the urban heat island effect than population size, population size is a reliable indicator of urban heat island amplitude when its relationship with temperature is determined at the regional level (see: [34,39,40]). By doing so, the influence of regional practices in land use and the construction and operation of the built environment, which impact urban heat island formation, are captured.
- Although long-term climate projections are generally reported as averages over multiple-year periods in order to reduce associated variability, the user-input projections are annualized in the UHIMPT model through the application of linear interpolation. This is done in order to make the projections of mean and mean maximum air temperatures compatible with the annual time step of the UHIMPT model.
- Please note that although the cohort-component population projection is used in, and impacts, the heat-related mortality calculations that are discussed in Section 2.1.1, it is not impacted by said calculations. The reason for this is associated with the fact that the UHIMPT model operates on an annual time step to simulate conditions in the warmest month. For the impacts of air temperature on population development to be isolated and reliably estimated on a continuous basis, the model would need to operate on a daily time step. However, given the presence of seasonal variability and the impacts of climate change, development of such a model that would simulate change over a continuous period (i.e., a period represented by a daily time step over multiple years) is impractical.
- It is important to note that mean summer and winter air temperatures, not mean maximum summer and mean minimum winter air temperatures (i.e., not extremes), are used to determine the appropriate relative risk factor for a given location. The reason for this is that the human capacity for acclimatization to higher temperatures is linked to climate as a whole, not just its extremes (see: [50,72]). Moreover, the temperature–mortality and temperature increase–acclimatization functions of Nordio et al. [50] have been developed with data that represents mean air temperatures. Nonetheless, as is described in Section 2.2, the impact of heat-related mortality on population dynamics is estimated using mean maximum warmest month air temperatures. This allows the user to understand the impacts of extreme heat, as represented by projected mean maximum warmest month air temperatures.
- Please note that Equations (3) and (4) include a modification of the population size–urban heat island amplitude function for North American settlements of Oke [34]. The original function was expressed by Oke [34] as: , where represents maximum urban heat island amplitude and represents total population. The coefficient of determination of this function , as calculated by Oke [34], was 0.96 (i.e., ).
- The constant (i.e., intercept) of the customized multiple linear regression model is excluded from Equations (5) and (6), and replaced with the mean and mean maximum urban heat island amplitude of the warmest month in a given time step (i.e., and , respectively). This is explained by the fact that the customized multiple linear regression model is used for no other purpose than to simulate the impacts of changes in surface albedo, impervious surface cover and the proportion of vegetation on urban heat island amplitude. While the constant (i.e., intercept) could be used, the UHIMPT model already includes a more-accurate simulation of urban heat island amplitude with and . The acceptability of this adaptation is confirmed by the fact that the relative impacts of the independent variables remain unmodified.
- The linear regression model of Gallo et al. [30] is based on a comparison of air temperature and land surface temperature data, which was collected at a total of 14 United States Climate Reference Network meteorological observation stations located throughout the continental United States. Their model indicates that air temperature is a significant factor in explaining variation of land surface temperature (). Their model, the coefficient of determination of which is 0.88, expresses the relationship between land surface temperature and air temperature as , where represents land surface temperature and represents air temperature. For use in Equations (5) and (6) of the UHIMPT model, which pertain to the modification of mean and mean maximum warmest month urban heat island amplitude, the linear regression model of Gallo et al. [30] has been algebraically restated as: . As restated, however, even a null value for will result in a value for that is not zero, but . This is problematic because the linear regression model is only used to convert the simulated impacts of alterations of surface albedo, impervious surface cover and the proportion of vegetation on land surface temperature to air temperature and lack of alteration would not result in change. Thus, application of a correction factor of is necessary to cause a null value for to result in a value of zero for .
- Please note that change in is measured from negative one (i.e., ) to one with one being the highest possible value. Negative values represent decreases in the proportion of impervious surface cover, which serves to mitigate the urban heat island effect. Positive values represent increases to the proportion of impervious surface cover, which increases the intensity of the urban heat island effect and is, therefore, undesirable in this instance. The value of change applied must be no more than the greatest possible positive or negative value less (i.e., minus) the initial (i.e., baseline) value.
- Please note that change in is measured from zero to one with one being the highest possible value. The value of change applied must be no more than the highest possible value less (i.e., minus) the initial (i.e., baseline) value.
- Please note that change in is measured from zero to one with one being the highest possible value. The value of change applied must be no more than the highest possible value less (i.e., minus) the initial (i.e., baseline) value.
- It is noted that this methodology results in the realization of projected temperatures at the midpoint of the projected period. This is supported by the fact that climate projections are typically reported as average values for multi-year periods (n.b., the aforementioned projections of Wang et al. [56] are reported as average values for 30-year periods). The realization of projected temperatures at the midpoint of the projected period facilitates an accurate portrayal of same because the midpoint is equivalent to the average between two or more points (e.g., starting point, ending point).
- Equations (26)–(33) have been obtained through analysis of Figure 2, Part A of Nordio et al. [50] with the open-source graph digitizing software package known as Engauge Digitizer (Release 10.3) by Mark Mitchell of Torrance, California. Because of the method through which these equations have been obtained, they may differ slightly from those represented by the data used by Nordio et al. [50] to create aforesaid Figure 2, Part A. Analysis with Engauge Digitizer was necessary because Nordio et al. [50] report neither the data used to prepare the aforementioned figure, nor provide equations for the curves it represents. In Equations (26)–(33), curves are represented with sextic polynomial equations. This type of equation was chosen because it most accurately reflects all of the data represented in Figure 2, Part A of Nordio et al. [50]. The coefficient of determination for these equations ranges from 0.99970 in Equation (28) to 0.99995 in Equation (30).
- As has been previously indicated, the parameterization of this component is based on the analysis of Nordio et al. [50], which indicates that every 5 °C increase in mean air temperature results in a 1.78 percent reduction in heat-related mortality. The UHIMPT model, however, applies this function continuously, such that every fractional degree increase in mean air temperature results in a corresponding percent reduction in heat-related mortality. In addition, as may be seen in Equation (37) this function is also applied bi-directionally, such that a decrease in mean temperature would result in a corresponding increase in the factor of relative risk of mortality. This results from the fact that subtracting a negative number results in adding a positive (e.g.: ). Nevertheless, it is noted that, as may be seen in Equation (36), the acclimatization factor can only be negative if there is a decline in mean temperature between the current time step and the next time step. Given the general trend to higher mean temperatures as a result of global warming, a negative acclimatization factor is unlikely and only possible in the UHIMPT model if a decrease in mean temperature is indicated by the user-input mean temperature projections that have been described in Section 2.1.2.
- Data representing areas that were at least partially located within a water feature were not entered into the multiple linear regression model. It is noted that the surface albedo and surface temperature of water features is generally low. However, low surface albedo over land is generally associated with high surface temperature. Data representing areas that were at least partially within a water feature were, therefore, excluded in order to prevent surface albedo over water from skewing the multiple linear regression model’s depiction of the correlation between land surface temperature and surface albedo.
- Had a modified cohort-component projection been applied in the UHIMPT model, a buildout analysis would have been required in order to estimate remaining development capacity. This would have dramatically increased user-input data requirements and model complexity, thereby potentially rendering the model less useful.
- Despite its age, Oke’s [34] population size–urban heat island amplitude function was used in the UHIMPT model because of its comprehensiveness, very high coefficient of determination (n.b., the coefficient of determination [] was 0.96 [i.e., ]), and the fact that no suitable alternative currently exists for the entirety of North America.
- When calculating the sum of absolute differences between user-input mean summer and winter air temperatures and those of the climate clusters as provided by Nordio et al. [50] in accordance with Equation (34), the difference between the climate cluster associated with the temperature–mortality function identified by the UHIMPT model’s approach and the climate cluster provided by Nordio et al. [50] was between 0.03 and 0.73, with a mean difference of 0.49, in eight of 48 cases.
- It is noted that the raw data used by Nordio et al. [50] were unavailable in these tests. Had the mean summer and winter temperatures used by Nordio et al. [50] been available, it is likely that the accuracy of the UHIMPT model’s approach to selection of the appropriate temperature–mortality function would have been shown to be higher than demonstrated here. This is suggested by the fact that, when calculating the sum of absolute differences between user-input mean summer and winter air temperatures and those of the climate clusters as provided by Nordio et al. [50] in accordance with Equation (34), the difference between the climate cluster associated with the temperature–mortality function identified by the UHIMPT model’s approach and the climate cluster provided by Nordio et al. [50] was 0.73 or less in eight of 48 cases.
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Kalkstein, L.; Greene, S.; Mills, D.; Samenow, J. An evaluation of the progress in reducing heat-related human mortality in major US cities. Nat. Hazards 2011, 56, 113–129. [Google Scholar] [CrossRef]
- Cheng, C.; Campbell, M.; Li, Q.; Li, G.; Auld, H.; Day, N.; Pengelly, D.; Gingrich, S.; Klaasen, J.; MacIver, D.; et al. Differential and combined impacts of extreme temperatures and air pollution on human mortality in South-Central Canada. Part II: Future estimates. Air Qual. Atmos. Health 2009, 1, 223–235. [Google Scholar] [CrossRef] [Green Version]
- Guest, C.; Wilson, K.; Woodward, A.; Henessy, K.; Kalkstein, L.; Skinner, C.; McMichael, A. Climate and mortality in Australia: Retrospective study, 1979–1990, and predicted impacts in five major cities in 2030. Clim. Res. 1999, 13, 1–15. [Google Scholar] [CrossRef]
- Changnon, S.; Kunkel, K.; Reinke, B. Impacts and responses to the 1995 heatwave: A call to action. Bull. Am. Meteorol. Soc. 1996, 77, 1497–1506. [Google Scholar] [CrossRef] [Green Version]
- Robine, J.-M.; Cheung, S.L.K.; Le Roy, S.; Van Oyen, H.; Griffiths, C.; Michel, J.-P.; Herrmann, F.R. Death toll exceeded 70,000 in Europe during the summer of 2003. Comptes Rendus Biol. 2008, 331, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Barriopedro, D.; Fischer, E.; Luterbacher, J.; Trigo, R.; Garcia-Herrera, R. The hot summer of 2010: Redrawing the temperature record map of Europe. Science 2011, 332, 220–224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Armstrong, B. Estimated Number of Premature Deaths Attributable to Heat in England, 6–14 July 2013; London School of Hygiene and Tropical Medicine: London, UK, 2013. [Google Scholar]
- Shaposhnikov, D.; Revich, B.; Bellander, T.; Bedada, G.B.; Bottai, M.; Kharkova, T.; Kvasha, E.; Lezina, E.; Lind, T.; Semutnikova, E.; et al. Mortality related to air pollution with the Moscow heatwave and wildfire of 2010. Epidemiology 2014, 25, 359–364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- IPCC. Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the 5th Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013.
- He, W.; Goodkind, D.; Kowal, P. An Aging World: 2015; United States Government Publishing Office: Washington, DC, USA, 2016.
- Frumkin, H. Urban sprawl and public health. Public Health Rep. 2002, 117, 201–217. [Google Scholar] [CrossRef]
- Naughton, M.; Henderson, A.; Mirabelli, M.; Kaiser, R.; Wilhelm, J.; Kieszak, S.; Rubin, C.; McGeehin, M. Heat-related mortality during a 1999 heat wave in Chicago. Am. J. Prev. Med. 2002, 22, 221–227. [Google Scholar] [CrossRef]
- Lugo-Amador, N.; Rothenhaus, T.; Moyer, P. Heat-related illness. Emerg. Med. Clin. N. Am. 2004, 22, 315–327. [Google Scholar] [CrossRef]
- Harlan, S.; Brazel, A.; Prashad, L.; Stefanov, W.; Larsen, L. Neighborhood microclimates and vulnerability to heat stress. Soc. Sci. Med. 2006, 63, 2847–2863. [Google Scholar] [CrossRef] [PubMed]
- Bouchama, A.; Dehbi, M.; Mohamed, G.; Mattheis, F.; Shoukri, M.; Menne, B. Prognostic factors in heat wave-related deaths: A meta-analysis. Arch. Intern. Med. 2007, 167, 2170–2176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harlan, S.; Decket-Barreto, J.; Stefanov, W.; Petitti, D. Neighborhood effects on heat deaths: Social and environmental predictors of vulnerability in Maricopa County, Arizona. Environ. Health Perspect. 2013, 121, 197–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keller, R. Fatal Isolation: The Devastating Paris Heat Wave of 2003; University of Chicago Press: Chicago, IL, USA, 2015. [Google Scholar]
- Kalkstein, L.; Greene, J.S. An evaluation of climate/mortality relationships in large US cities and the possible impacts of a climate change. Environ. Health Perspect. 1997, 105, 84–93. [Google Scholar] [CrossRef] [PubMed]
- Doyon, B.; Bélanger, D.; Gosselin, P. The potential impact of climate change on annual and seasonal mortality for three cities in Québec, Canada. Int. J. Health Geogr. 2008, 7, 23–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hayhoe, K.; Sheridan, S.; Kalkstein, L.; Greene, S. Climate change, heatwaves, and mortality projections for Chicago. J. Great Lakes Res. 2010, 36, 65–73. [Google Scholar] [CrossRef]
- Hajat, S.; Vardoulakis, S.; Heaviside, C.; Eggen, B. Climate change effects on human health: Projections of temperature-related mortality for the United Kingdom during the 2020s, 2050s and 2080s. J. Epidemiol. Community Health 2014, 68, 641–648. [Google Scholar] [CrossRef] [Green Version]
- Kingsley, S.; Eliot, M.; Gold, J.; Vandersclice, R.; Wellenius, G. Current and projected heat-related morbidity and mortality in Rhode Island. Environ. Health Perspect. 2016, 124, 460–467. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Horton, R.; Bader, D.; Zhou, M.; Liang, X.; Ban, J.; Sun, Q.; Kinney, P. Aging will amplify the heat-related mortality risk under a changing climate: Projection for the elderly in Beijing, China. Sci. Rep. 2016, 6, 28161. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Barnett, A.; Wang, X.; Vaneckova, P.; Fitzgerald, G.; Tong, S. Projecting future heat-related mortality under climate change scenarios: A systematic review. Environ. Health Perspect. 2011, 119, 1681–1690. [Google Scholar] [CrossRef] [Green Version]
- Hémon, D.; Jougla, E. Surmortalité liée à la canicule d’août 2003; Institut national de la santé et de la recherche médicale: Paris, France, 2003. [Google Scholar]
- Stone, B. The City and the Coming Climate: Climate Change in the Places We Live; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Roth, M. Urban heat islands. In Handbook of Environmental Fluid Dynamics: Systems, Pollution, Modeling and Measurements; Fernando, H., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 143–159. [Google Scholar]
- Saaroni, H.; Ben-Dor, E.; Bitan, A.; Potchter, O. Spatial distribution and microscale characteristics of the urban heat island in Tel-Aviv, Israel. Landsc. Urban Plan. 2000, 48, 1–18. [Google Scholar] [CrossRef]
- Martin, P.; Baudouin, Y.; Gachon, P. An alternative method to characterize the surface urban heat island. Int. J. Biometeorol. 2015, 59, 849–861. [Google Scholar] [CrossRef] [PubMed]
- Gallo, K.; Hale, R.; Tarpley, D.; Yu, Y. Evaluation of the relationship between air and land surface temperature under clear and cloudy sky conditions. J. Appl. Meteorol. Climatol. 2011, 50, 767–775. [Google Scholar] [CrossRef]
- Klok, L.; Zwart, S.; Verhagen, H.; Mauri, E. The surface heat island of Rotterdam and its relationship with urban surface characteristics. Resour. Conserv. Recycl. 2012, 64, 23–29. [Google Scholar] [CrossRef]
- Dare, R. A review of local-level land use planning and design policy for urban heat island mitigation. J. Extrem. Events 2020, 6, 1–27. [Google Scholar] [CrossRef]
- Bonan, G. Ecological Climatology: Concepts and Applications; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Oke, T. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Landsberg, H. The Urban Climate; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Gaffin, S.; Rosenzweig, C.; Khanbilvardi, R.; Parshall, L.; Mahani, S.; Glickman, H.; Goldberg, R.; Blake, R.; Slosberg, R.; Hillel, D. Variations in New York City’s urban heat island strength over time and space. Theor. Appl. Climatol. 2008, 94, 1–11. [Google Scholar] [CrossRef]
- Miller, J. Urban and regional temperature trends in Las Vegas and southern Nevada. J. Ariz. Nev. Acad. Sci. 2011, 43, 27–39. [Google Scholar] [CrossRef]
- László, E.; Bottyán, Z.; Szegedi, S. Long-term changes of meteorological conditions of urban heat island development in the region of Debrecen, Hungary. Theor. Appl. Climatol. 2016, 124, 365–373. [Google Scholar] [CrossRef]
- Sakakibara, Y.; Matsui, E. Relation between heat island intensity and city size indices/urban canopy characteristics in settlements of Nagano Basin, Japan. Geogr. Rev. Jpn. 2005, 78, 812–824. [Google Scholar] [CrossRef] [Green Version]
- Saaroni, H.; Ziv, B. Estimating the urban heat island contribution to urban and rural air temperature differences over complex terrain: Application to an arid city. J. Appl. Meteorol. Climatol. 2010, 49, 2159–2166. [Google Scholar] [CrossRef]
- Huang, Q.; Lu, Y. The effect of urban heat island on climate warming in the Yangtze River delta urban agglomeration in China. Int. J. Environ. Res. Public Health 2015, 12, 8773–8789. [Google Scholar] [CrossRef] [Green Version]
- Oke, T. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Svensson, M. Sky view factor analysis: Implications for urban air temperature differences. Meteorol. Appl. 2004, 11, 201–211. [Google Scholar] [CrossRef]
- Blankenstein, S.; Kuttler, W. Impact of street geometry on downward longwave radiation and air temperature in an urban environment. Meteorol. Z. 2004, 13, 373–379. [Google Scholar] [CrossRef]
- Shryock, H.; Siegel, J.; Larmon, E.; Bayo, F.; Davidson, M.; Demeny, P.; Glick, P.; Grabill, W.; Grove, R.; Israel, R.; et al. The Methods and Materials of Demography; United States Census Bureau: Washington, DC, USA, 1975.
- Klosterman, R. Community Analysis and Planning Techniques; Rowman and Littlefield Publishers: Lanham, MD, USA, 1990. [Google Scholar]
- Smith, S.; Tayman, J.; Swanson, D. State and Local Population Projections: Methodology and Analysis; Kluwer Academic Publishers: New York, NY, USA, 2002. [Google Scholar]
- Berke, P.; Godschalk, D.; Kaiser, E.; Rodriguez, D. Urban Land Use Planning; University of Illinois Press: Urbana, IL, USA, 2006. [Google Scholar]
- Swanson, D.; Tayman, J. Subnational Population Estimates; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Nordio, F.; Zanobetti, A.; Colicino, E.; Kloog, I.; Schwartz, J. Changing patterns of the temperature–mortality association by time and location in the United States, and implications for climate change. Environ. Int. 2015, 81, 80–86. [Google Scholar] [CrossRef] [Green Version]
- Day, J. Population Projections of the United States by Age, Sex, Race, and Hispanic Origin: 1995 to 2050; United States Census Bureau: Washington, DC, USA, 1996. [Google Scholar]
- Treadway, R. Population Projections for the State and Counties of Illinois; Springfield: Geneseo, IL, USA, 1997. [Google Scholar]
- Curriero, F.; Heiner, K.; Samet, J.; Zeger, S.; Strug, L.; Patz, J. Temperature and mortality in 11 cities of the eastern United States. Am. J. Epidemiol. 2002, 156, 80–87. [Google Scholar] [CrossRef]
- Bai, L.; Ding, D.; Gu, S.; Bi, P.; Su, B.; Qin, D.; Xu, G.; Liu, Q. The effects of summer temperature and heat waves on heat-related illness in a coastal city of China, 2011–2013. Environ. Res. 2014, 132, 212–219. [Google Scholar] [CrossRef] [Green Version]
- Bobb, J.; Peng, R.; Bell, M.; Dominici, F. Heat-related mortality and adaptation to heat in the United States. Environ. Health Perspect. 2014, 122, 811–816. [Google Scholar] [CrossRef]
- Wang, T.; Hamann, A.; Spittlehouse, D.; Carroll, C. Locally downscaled and spatially customizable climate data for historical and future periods for North America. PLoS ONE 2016, 11, e0156720. [Google Scholar] [CrossRef]
- Forrester, J.; Senge, P. Tests for building confidence in system dynamics models. In TIMS Studies in the Management Sciences; Legasto, A., Forrester, J., Lyneis, J., Eds.; North Holland Publishing Company: Amsterdam, The Netherlands, 1980; Volume 14, pp. 209–228. [Google Scholar]
- Barlas, Y. Multiple tests for validation of system dynamics type of simulation models. Eur. J. Oper. Res. 1989, 42, 59–87. [Google Scholar] [CrossRef]
- Qudrat-Ullah, H. On the validation of system dynamics type simulation models. In Proceedings of the International Conference on Information Science and Applications, Seoul, Korea, 21–23 April 2010. [Google Scholar]
- Oke, T. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Potter, S.; Zutter, H.; Souch, C. Rapid methods to estimate sky-view factors applied to urban areas. Int. J. Climatol. 2001, 21, 903–913. [Google Scholar] [CrossRef]
- Guo, Y.; Gasparrini, A.; Armstrong, B.G.; Tawatsupa, B.; Tobias, A.; Lavigne, E.; De Sousa-Zanotti-Stagliorio-Coelho, M.; Pan, E.; Kim, H.; Hashizume, M.; et al. Heat wave and mortality: A multicounty, multicommunity study. Environ. Health Perspect. 2017, 125, 087006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, B.; Bell, M. Heat waves in the United States: Mortality risk during heat waves and effect modification by heat wave characteristics in 43 United States communities. Environ. Health Perspect. 2011, 119, 210–218. [Google Scholar] [CrossRef] [Green Version]
- Basagaña, X.; Sartini, C.; Barrera-Gómez, J.; Dadvand, P.; Cunillera, J.; Ostro, B.; Sunyer, J.; Medina-Ramón, M. Heat waves and cause-specific mortality at all ages. Epidemiology 2011, 22, 765–772. [Google Scholar] [CrossRef] [PubMed]
- Schuman, S. Patterns of urban heat-wave deaths and implications for prevention: Data from New York and St. Louis during July 1966. Environ. Res. 1972, 5, 59–75. [Google Scholar] [CrossRef] [Green Version]
- Hajat, S.; Kovats, R.; Atkinson, R.; Haines, A. Impact of hot temperatures on death in London: A time series approach. J. Epidemiol. Community Health 2002, 56, 367–372. [Google Scholar] [CrossRef] [Green Version]
- Joe, L.; Hoshiko, S.; Dobraca, D.; Jackson, R.; Smorodinsky, S.; Smith, D.; Harnly, M. Mortality during a large-scale heat wave by place, demographic group, internal and external causes of death, and building climate zone. Int. J. Environ. Res. Public Health 2016, 13, 299–315. [Google Scholar] [CrossRef] [Green Version]
- Schilling, J.; Logan, J. Greening the rust belt: A green infrastructure model for right sizing America’s shrinking cities. J. Am. Plan. Assoc. 2008, 74, 451–466. [Google Scholar] [CrossRef]
- Bontje, M. Facing the challenge of shrinking cities in East Germany: The case of Leipzig. GeoJournal 2004, 61, 13–21. [Google Scholar] [CrossRef]
- Fuhrich, M. Renaturierung als Vorwärtsstrategie nachhaltiger Stadtentwicklung. Infor. Raumentwick. 2009, 7, 503–514. [Google Scholar]
- Bonham, B.; Smith, P. Transformation through greening. In Growing Greener Cities: Urban Sustainability in the Twenty-First Century; Birch, E., Wachter, S., Eds.; University of Pennsylvania Press: Philadelphia, PA, USA, 2008; pp. 227–243. [Google Scholar]
- Honda, Y.; Ono, M.; Ebi, K.L. Adaptation to the heat-related health impact of climate change in Japan. In Climate Change Adaptation in Developed Nations: From Theory to Practice; Ford, J.D., Berrang-Ford, L., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 189–203. [Google Scholar]
- Hamman, A. ClimateEU: Historical and Projected Climate Data for Europe. Available online: https://sites.ualberta.ca/~ahamann/data/climateeu.html (accessed on 6 October 2017).
- Hamman, A. ClimateSA: Historical and projected climate data for Mexico, Central and South America. Available online: https://sites.ualberta.ca/~ahamann/data/climatesa.html (accessed on 6 October 2017).
- Rouse, J.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite Symposium, Washington, DC, USA, 10–14 December 1973. [Google Scholar]
- Jiménez-Muñoz, J.; Sobrino, J.; Gillespie, A.; Sabol, D.; Gustafson, W. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sens. Environ. 2006, 103, 474–487. [Google Scholar] [CrossRef]
- Avdan, U.; Jovanovska, G. Algorithm for automated mapping of land surface temperature using Landsat 8 satellite data. J. Sens. 2016, 2016, 1480307. [Google Scholar] [CrossRef] [Green Version]
- United States Geological Survey (2017). Using the USGS Landsat 8 Product. Available online: https://landsat.usgs.gov/using-usgs-landsat-8-product (accessed on 14 November 2017).
- Sobrino, J.; Jiménez-Muñoz, J.; Paolini, L. Land surface temperature retrieval from Landsat TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Wu, Z. Land surface temperature retrieval from Landsat 8 TIRS—Comparison between radiative transfer equation-based method, split window algorithm and single channel method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Seo, M.; Lee, K.-S.; Choi, S.; Sung, N.-H.; Kim, H.; Jin, D.; Kwon, C.; Huh, M.; Han, K.-S. Landsat 8-based high resolution surface broadband albedo retrieval. Korean J. Remote Sens. 2016, 32, 741–746. [Google Scholar] [CrossRef] [Green Version]
- Xu, H. Modification of normalized difference water index (MNDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
| Temperature–Mortality Function | Summer Air Temperature | Winter Air Temperature | ||
|---|---|---|---|---|
| Mean (°C) | Standard Deviation (SD) | Mean (°C) | Standard Deviation (SD) | |
| Temperature–Mortality Function 1 (TM1) | 22.79 | 3.78 | 0.78 | 5.42 |
| Temperature–Mortality Function 2 (TM2) | 21.31 | 3.81 | −3.19 | 6.57 |
| Temperature–Mortality Function 3 (TM3) | 23.90 | 3.54 | 0.40 | 6.58 |
| Temperature–Mortality Function 4 (TM4) | 25.90 | 2.85 | 6.53 | 5.82 |
| Temperature–Mortality Function 5 (TM5) | 19.67 | 3.79 | 9.54 | 4.57 |
| Temperature–Mortality Function 6 (TM6) | 27.35 | 1.92 | 12.03 | 5.40 |
| Temperature–Mortality Function 7 (TM7) | 27.74 | 1.57 | 17.59 | 4.87 |
| Temperature–Mortality Function 8 (TM8) | 29.17 | 4.29 | 10.18 | 3.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dare, R. A System Dynamics Model to Facilitate the Development of Policy for Urban Heat Island Mitigation. Urban Sci. 2021, 5, 19. https://doi.org/10.3390/urbansci5010019
Dare R. A System Dynamics Model to Facilitate the Development of Policy for Urban Heat Island Mitigation. Urban Science. 2021; 5(1):19. https://doi.org/10.3390/urbansci5010019
Chicago/Turabian StyleDare, Robert. 2021. "A System Dynamics Model to Facilitate the Development of Policy for Urban Heat Island Mitigation" Urban Science 5, no. 1: 19. https://doi.org/10.3390/urbansci5010019
APA StyleDare, R. (2021). A System Dynamics Model to Facilitate the Development of Policy for Urban Heat Island Mitigation. Urban Science, 5(1), 19. https://doi.org/10.3390/urbansci5010019




