Using Spatial Analysis to Design a Solid Waste Collection System
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Context
2.2. Collection of Starting Data
2.2.1. Waste Generation
2.2.2. Current Waste Collection System
2.3. Grouping of Waste Production Areas (Waste Collection Sectors)
2.4. Analysis of Waste Generation Sources
2.5. Analysis of Waste Collection Routes
2.5.1. Location–Allocation of Waste Collection Points
- Maximize coverage: This model chooses the facilities (waste collection points) so that the maximum number of possible demand locations (MSW production sources) are served within a specified impedance value, which can be the distance or service time [42]. This location–allocation problem was developed by Church and Reveille [43], and its objective function is the one presented in Equations (13)–(15).
- Minimize facilities: This location–allocation problem is similar to the problem of maximizing coverage, with the exception that the number of facilities to be located is determined by the solver of the software used, in this case, ArcGis 10.8 [42]. The “Minimize facilities” model has received multiple contributions from researchers who study the location of public and private services [44,45,46]. Its objective function is presented in Equations (19) and (20).
2.5.2. Waste Collection Vehicles Routes
2.5.3. Impedances and Other Aspects Considered in the Analysis
3. Results and Discussion
3.1. Waste Production in the Study Area
3.1.1. Analysis of Waste Collection Sectors and Their Characteristics
3.1.2. Analysis of Waste Production Sources
3.2. Provision of the Current Waste Collection Service
3.3. Proposal for MSW Collection in the Study Area
4. Limitations and Comments
- According to Araiza [12], in Chiapas, Mexico, there are currently several municipalities that lack local laws and regulations regarding MSW management, so the development of such regulatory mechanisms should be promoted.
- Although this work produces information about the urban population served by the waste collection service, about the lengths traveled by each collection truck, and about the service times associated with waste collection, there is still a lack of many other data that do not allow us to analyze aspects related to the efficiency, quality, and costs of waste collection services. For this reason, it will be necessary to promote the development of a greater number of studies to collect more information.
- MSW containers are not currently used in the study area due to costs but also due to the lack of knowledge about the benefits of using these temporary MSW storage methods. For this reason, it will be necessary to create economic instruments such as the payment of fees to allow the purchase and replacement of these implements. Additionally, environmental education talks should be given to both the general population and waste management workers about the efficient use and benefits of these containers.
- The technical principles of this work can be applicable to several municipalities in the state of Chiapas, Mexico, and other states of the Mexican Republic, as well as other Latin countries, not only due to similarities in socioeconomic characteristics but also due to the similarity in the use of the MSW collection infrastructure used. However, certain adaptations must be made to consider variants such as patterns of urban settlements, narrow or unpaved streets, and others.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akhtar, M.; Hannan, M.; Begum, R.; Basri, H.; Scavino, E. Backtracking search algorithm in CVRP models for efficient solid waste collection and route optimization. Waste Manag. 2017, 61, 117–128. [Google Scholar] [CrossRef]
- Jaunich, M.; Levis, J.; DeCarolis, J.; Barlaz, M.; Bartelt-Hunt, S.; Jones, E.; Jaikumar, R. Characterization of municipal solid waste collection operations. Resour. Conserv. Recycl. 2016, 114, 92–102. [Google Scholar] [CrossRef]
- Hoornweg, D.; Bhada-Tata, P. What A Waste: A Global Review of Solid Waste Management; Urban Development Series; World Bank: Washington, DC, USA, 2012; p. 98. [Google Scholar]
- Owolabi, S.; Mmereki, D.; Baldwin, A.; Li, B. A comparative analysis of solid waste management in developed, developing and lesser developed countries. Environ. Technol. Rev. 2016, 5, 120–141. [Google Scholar] [CrossRef]
- Rızvanoğlu, O.; Kaya, S.; Ulukavak, M.; Yeşilnacar, M. Optimization of municipal solid waste collection and transportation routes, through linear programming and geographic information system: A case study from Şanlıurfa, Turkey. Environ. Monit. Assess. 2020, 192, 9. [Google Scholar] [CrossRef]
- Tavares, G.; Zsigraiova, Z.; Semiao, V.; Carvalho, M. Optimisation of MSW collection routes for minimum fuel consumption using 3D GIS modelling. Waste Manag. 2009, 29, 1176–1185. [Google Scholar] [CrossRef] [PubMed]
- Martinho, G.; Gomes, A.; Santos, P.; Ramos, M.; Cardoso, J.; Silveira, A.; Pires, A. A case study of packaging waste collection systems in Portugal—Part I: Performance and operation analysis. Waste Manag. 2017, 61, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Tallentire, C.; Steubing, B. The environmental benefits of improving packaging waste collection in Europe. Waste Manag. 2020, 103, 426–436. [Google Scholar] [CrossRef] [PubMed]
- Bernstad, A.; Jansen, J. Separate collection of household food waste for anaerobic degradation—Comparison of different techniques from a systems perspective. Waste Manag. 2012, 32, 806–815. [Google Scholar] [CrossRef]
- Coffey, M.; Coad, A. Collection of Municipal Solid Waste in Developing Countries; United Nations Human Settlements Programme (UN HABITAT): Nairobi, Kenya, 2010; p. 200. Available online: https://unhabitat.org/collection-of-municipal-solid-waste-in-developing-countries-2 (accessed on 10 June 2023).
- Abarca, L.; Maas, G.; Hogland, W. Solid waste management challenges for cities in developing countries. Waste Manag. 2013, 33, 220–232. [Google Scholar] [CrossRef]
- Araiza-Aguilar, J.A. Spatial Modeling of the Sanitary-Ecological Risk, Derived from the Poor Management of Municipal Solid Waste, in the Municipalities of the Cuenca del Cañon del Sumidero, Chiapas. Ph.D. Thesis, National Autonomous University of México, Mexico City, Mexico, 2019; 136p. Available online: https://repositorio.unam.mx/contenidos/3471779 (accessed on 10 June 2023).
- Hannan, M.; Lipu, M.; Akhtar, M.; Begum, R.; Al Mamun, M.; Hussain, A.; Mia, M.; Basri, H. Solid waste collection optimization objectives, constraints, modeling approaches, and their challenges toward achieving sustainable development goals. J. Clean. Prod. 2020, 277, 123557. [Google Scholar] [CrossRef]
- Carranza, O.; Antón, F. A Continuous Approximation Model for Vehicle Routing in Solid Waste Management Systems. Investig. Oper. 1999, 8, 109–153. [Google Scholar]
- Rodrigues, S.; Martinho, G.; Pires, A. Waste collection systems. Part A: A taxonomy. J. Clean. Prod. 2016, 113, 374–387. [Google Scholar] [CrossRef]
- Araiza, J.; José, M. Mejora del servicio de recolección de residuos sólidos urbanos empleando herramientas SIG: Un caso de estudio. Ingeniería 2015, 19, 118–128. [Google Scholar]
- Lella, J.; Mandla, V.; Zhu, X. Solid waste collection/transport optimization and vegetation land cover estimation using Geographic Information System (GIS): A case study of a proposed smart-city. Sustain. Cities Soc. 2017, 35, 336–349. [Google Scholar] [CrossRef]
- Singh, A. Remote sensing and GIS applications for municipal waste management. J. Environ. Manag. 2019, 242, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Rybova, K.; Burcin, B.; Slavik, J. Spatial and non-spatial analysis of socio-demographic aspects influencing municipal solid waste generation in the Czech Republic. Detritus 2018, 1, 3–7. [Google Scholar] [CrossRef]
- Mahmood, S.; Sharif, F.; Rahman, A. Analysis and forecasting of municipal solid waste in Nankana City using geo-spatial techniques. Environ. Monit. Assess. 2018, 190, 275. [Google Scholar] [CrossRef]
- Khorsandi, H.; Faramarzi, A.; Aghapour, A.; Jafari, S. Landfill site selection via integrating multi-criteria decision techniques with geographic information systems: A case study in Naqadeh, Iran. Environ. Monit. Assess. 2019, 191, 730. [Google Scholar] [CrossRef]
- Damasceno, I.; Ennes, R.; de Almeida, T.; Zandonadi, L.; Contreras, F. Allocation of sanitary landfill in consortium: Strategy for the Brazilian municipalities in the State of Amazonas. Environ. Monit. Assess. 2019, 191, 39. [Google Scholar] [CrossRef]
- Ağacsapan, B.; Cabuk, S. Determination of suitable waste transfer station areas for sustainable territories: Eskisehir case. Sustain. Cities Soc. 2020, 52, 101829. [Google Scholar] [CrossRef]
- Amal, L.; Son, L.; Chabchoub, H.; Lahini, H. Analysis of municipal solid waste collection using GIS and multi-criteria decision aid. Appl. Geomat. 2020, 12, 193–208. [Google Scholar] [CrossRef]
- Fennonato, N.; Preziosi, G.; Gorritty, M.; Guisbert, E.; Torretta, V. Assessment of municipal solid waste selective collection scenarios with geographic information systems in Bolivia. Waste Manag. 2020, 102, 919–931. [Google Scholar] [CrossRef]
- Kinobe, J.; Bosona, T.; Gebresenbet, G.; Niwagaba, C.; Vinnerås, B. Optimization of waste collection and disposal in Kampala city. Habitat. Int. 2015, 49, 126–137. [Google Scholar] [CrossRef]
- INEGI. National Institute of Statistic and Geography. Population and Housing Census 2020: Tabulated. 2020. Available online: https://www.inegi.org.mx/programas/ccpv/2020/#tabulados (accessed on 10 June 2023).
- CEIEG. State Committee of Statistics and Geographical Information. Municipal Profiles—Reforma, Chiapas. 2023. Available online: https://www.ceieg.chiapas.gob.mx/perfiles/Inicio (accessed on 23 January 2023).
- Racero, J.; Eguía, I.; García, J.; Villa, G. Modeling for the design of routes in an urban solid waste collection system. In Proceedings of the II International Conference on Industrial Engineering and Industrial Management, Burgos, Spain, 3–5 September 2008. [Google Scholar]
- Araiza, J.; Chávez, J.; Moreno, J.; Rojas, M. Municipal Solid Waste Management in a Municipality of Chiapas, Mexico. Soc. Sci. 2017, 6, 133–140. [Google Scholar] [CrossRef][Green Version]
- Mexican Standard NMX-AA-015-1985; Environmental Protection—Soil Pollution—Municipal Solid Waste—Sampling—Quartering Method. General Directorate of Standards. SECOFI, Secretariat of Commerce and Industrial Development: Mexico City, Mexico, 1985. (In Spanish)
- Mexican Standard NMX-AA-019-1985; Environmental Protection—Soil Pollution—Municipal Solid Waste—Volumetric Weight “In Situ”. General Directorate of Standards. SECOFI, Secretariat of Commerce and Industrial Development: Mexico City, Mexico, 1985. (In Spanish)
- Mexican Standard NMX-AA-022-1985; Environmental Protection—Soil Pollution—Municipal Solid Waste—Selection and Quantification of Sub-Products. General Directorate of Standards. SECOFI, Secretariat of Commerce and Industrial Development: Mexico City, Mexico, 1985. (In Spanish)
- Araiza, J.; Chávez, J.; Moreno, J. Quantification of municipal solid waste generated in the municipal seat of Berriozabal, Chiapas. Rev. Int. Contam. Ambie 2017, 33, 691–699. [Google Scholar] [CrossRef]
- SEDESOL. Secretariat of Social Development. Handbook for the Design of Municipal Solid Waste Collection Routes; SEDESOL—Undersecretary of Urban Development and Housing: Mexico City, Mexico, 1997; p. 50. [Google Scholar]
- ESRI, Environmental Systems Research Institute. Grouping Analysis. 2023. Available online: https://desktop.arcgis.com/en/arcmap/latest/tools/spatial-statistics-toolbox/grouping-analysis.htm (accessed on 23 January 2023).
- Benitez, R. Global Optimization of the Urban Solid Waste Collection System for the Layout of Robust Routes in the Monterrey Metropolitan Area. Ph.D. Thesis, Autonomous University of Nuevo León—Faculty of Chemical Sciences, Nuevo León, México, 2021; 93p. Available online: http://eprints.uanl.mx/22985/ (accessed on 10 June 2023).
- Silverman, B. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK; New York, NY, USA, 1986; 175p. [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- ESRI, Environmental Systems Research Institute. How Cluster and Outlier Analysis (Anselin Local Moran’s I) Works. 2023. Available online: https://desktop.arcgis.com/es/arcmap/latest/tools/spatial-statistics-toolbox/h-how-cluster-and-outlier-analysis-anselin-local-m.htm (accessed on 23 January 2023).
- INEGI, National Institute of Statistic and Geography. Marco Geoestadístico con Censo de Población y Vivienda 2020. 2023. Available online: https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=889463807469 (accessed on 23 January 2023).
- ESRI, Environmental Systems Research Institute. Location-Allocation Analysis. 2023. Available online: https://desktop.arcgis.com/en/arcmap/10.5/extensions/network-analyst/location-allocation.htm#ESRI_SECTION1_F8182D9F421E4EA4AEE11E7B360E1340 (accessed on 23 January 2023).
- Church, R.; ReVelle, C. The maximal covering location problem. Pap. Reg. Sci. 1974, 32, 101–118. [Google Scholar] [CrossRef]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The location of emergency service facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Marianov, V.; ReVelle, C. The Queuing Probabilistic Location Set Covering Problem and Some Extensions. Socio-Econ. Plan. Sci. 1994, 28, 167–178. [Google Scholar] [CrossRef]
- Rajagopalan, H.; Saydam, C.; Xiao, J. A multiperiod set covering location model for dynamic redeployment of ambulances. Comput. Oper. Res. 2008, 35, 814–826. [Google Scholar] [CrossRef]
- ESRI. Environmental Systems Research Institute. Dijkstra’s Algorithm. 2023. Available online: https://desktop.arcgis.com/es/arcmap/latest/extensions/network-analyst/algorithms-used-by-network-analyst.htm#GUID-D50336EC-7FBA-43FA-AD31-4272AB544393 (accessed on 23 January 2023).
- SEDESOL. Secretariat of Social Development. Technical Handbook on Generation, Collection and Transfer of Municipal Solid Waste; SEDESOL—Undersecretary of Urban Development and Housing: Mexico City, Mexico, 1996; p. 139. [Google Scholar]
- Araiza, J.; Rojas, M.; Nájera, H.; Gutiérrez, R.; García, C. Analysis of a Municipal Solid Waste Disposal Site: Use of Geographic Information Technology Tools for Decision Making. Int. J. Geo-Inf. 2023, 12, 280. [Google Scholar] [CrossRef]
- Araiza, J.; López, C.; Ramírez, N. Municipal solid waste management: Case study in Las Margaritas, Chiapas. AIDIS J. Eng. Environ. Sci. Res. Dev. Pract. 2015, 8, 299–311. [Google Scholar]
- Araiza, J.; Nájera, H.; Gutiérrez, R.; Rojas, M. Emplacement of solid waste management infrastructure for the Frailesca region, Chiapas, México, using GIS tools. Egypt. J. Remote Sens. Space Sci. 2018, 21, 391–399. [Google Scholar] [CrossRef]
- Kamdar, I.; Ali, S.; Bennui, A.; Techato, K.; Jutidamrongphan, W. Municipal solid waste landfill siting using an integrated GIS-AHP approach: A case study from Songkhla, Thailand. Resour. Conserv. Recycl. 2019, 149, 220–235. [Google Scholar] [CrossRef]
- Liu, C.; Wu, X. Factors influencing municipal solid waste generation in China: A multiple statistical analysis study. Waste Manag. Res. 2010, 29, 371–378. [Google Scholar] [CrossRef]
- Araiza, J.; Rojas, M.; Aguilar, R. Forecast generation model of municipal solid waste using multiple linear regression. Glob. J. Environ. Sci. Manag. 2020, 6, 1–14. [Google Scholar] [CrossRef]
- Malakahmad, A.; Bakri, P.; Radin, M.; Mokhtar, M. Solid waste collection routes optimization via GIS techniques in Ipoh city, Malaysia. Procedia Eng. 2014, 77, 20–27. [Google Scholar] [CrossRef]
- Das, W.; Bhattacharyya, B. Optimization of municipal solid waste collection and transportation routes. Waste Manag. 2015, 43, 9–18. [Google Scholar] [CrossRef]
- Singh, N.; Agrawal, A.K. Route Optimization for Municipal Solid Waste Collection using ArcGIS Application in Gwalior City, Madhya Pradesh. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 392–398. [Google Scholar] [CrossRef]
- Vijay, R.; Gupta, A.; Kalamdhad, A.; Devotta, S. Estimation and allocation of solid waste to bin through geographical information systems. Waste Manag. Res. 2005, 23, 479–484. [Google Scholar] [CrossRef]
- López, J.V.; Aguilar, M.; Fernandez, S.; Jimenez, A. Optimizing the collection of used paper from small businesses through GIS techniques: The Legane’s case (Madrid, Spain). Waste Manag. 2008, 28, 282–293. [Google Scholar] [CrossRef] [PubMed]



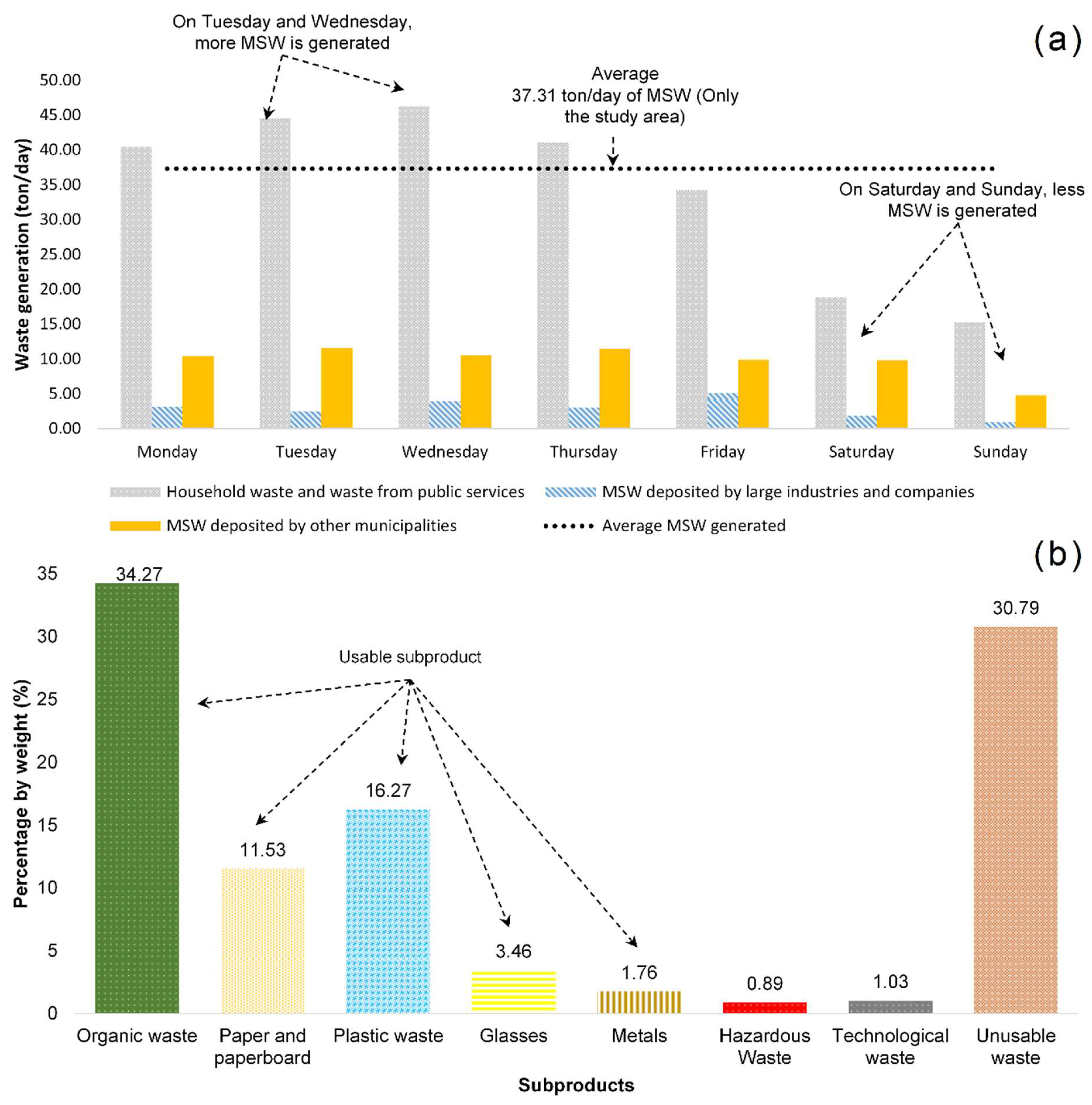

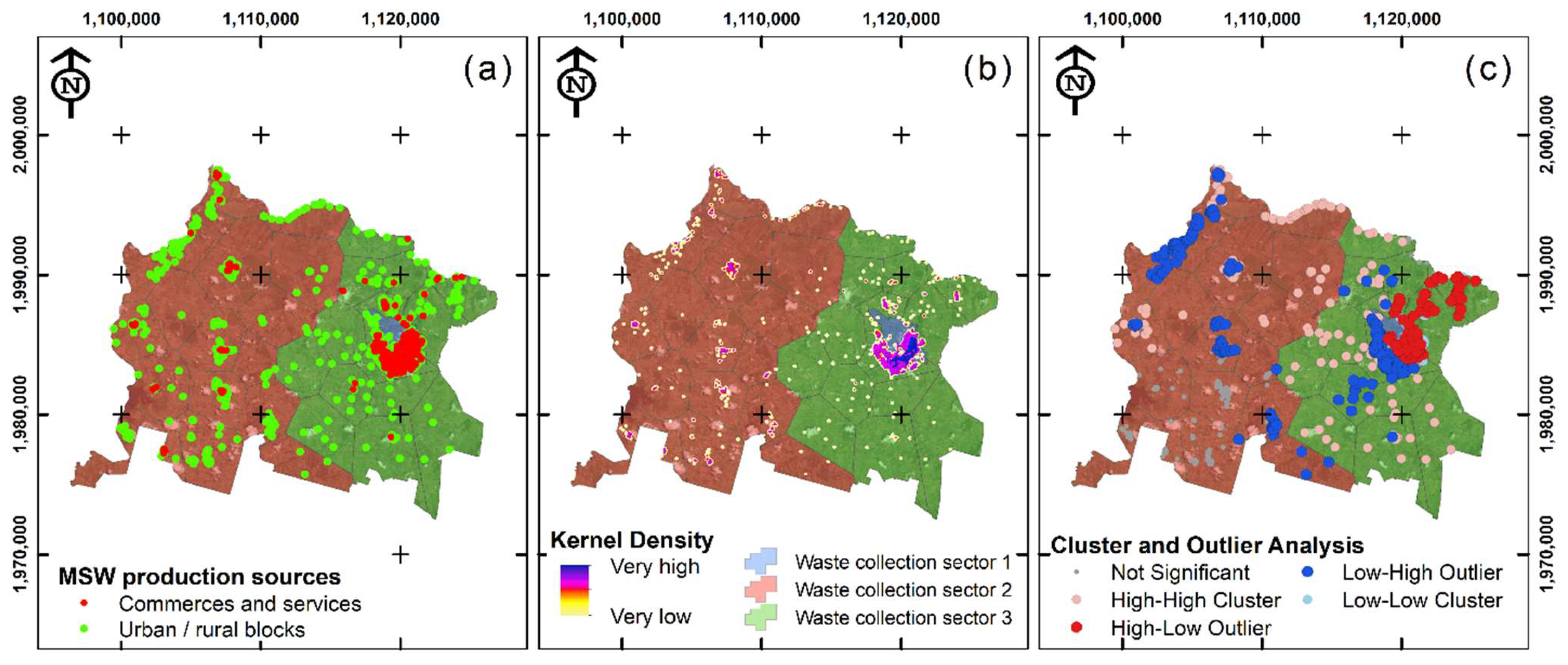
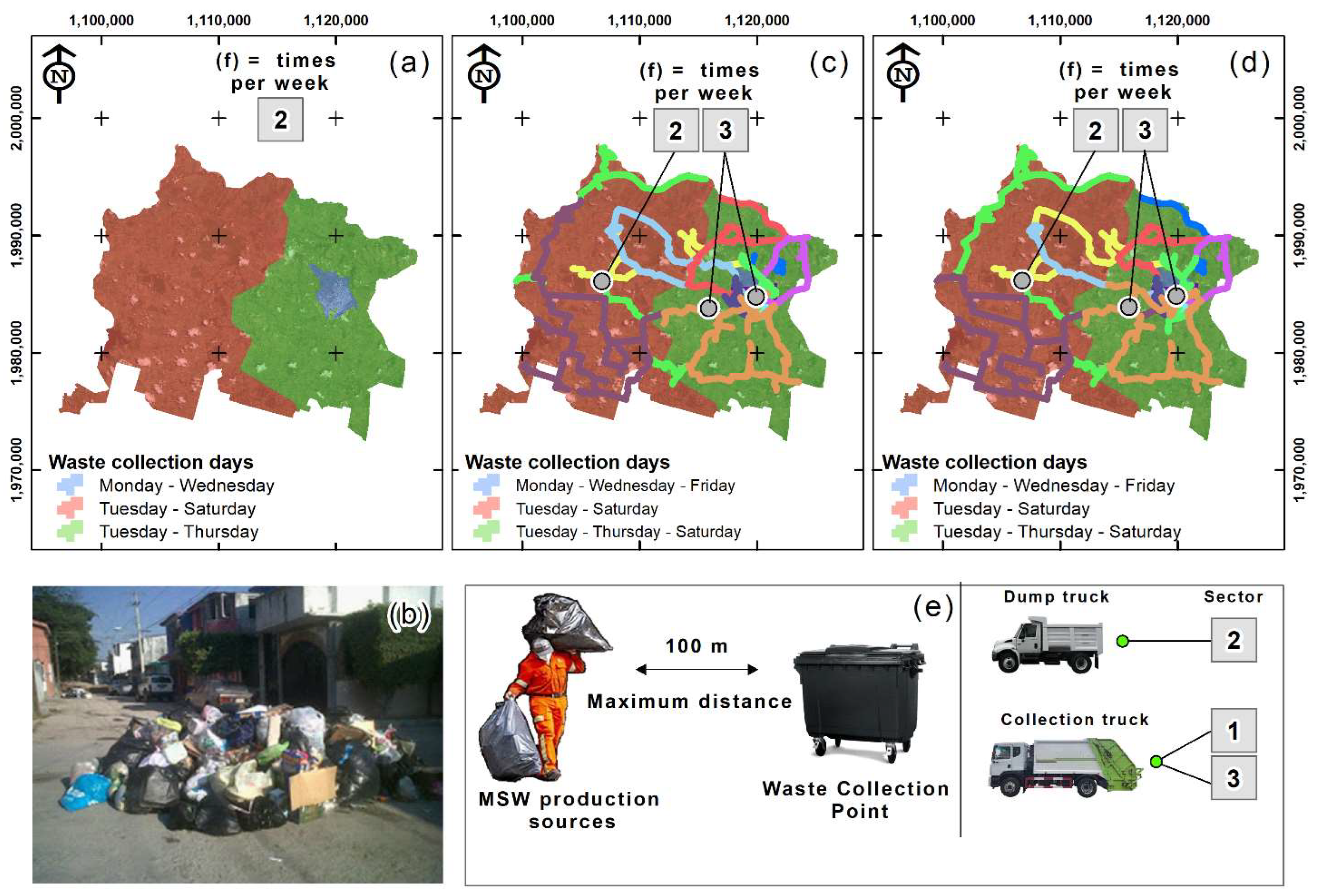
| Frequency (f) | Days of Normal Waste Accumulation | Days of Peak Waste Accumulation | 1 |
|---|---|---|---|
| 6 times per week | 1 | 2 | [1.17 to 2.17] |
| 3 times per week | 2 | 3 | [2.33 to 3.33] |
| 2 times per week | 3 | 4 | [3.50 to 4.50] |
| 1 time per week | 6 | 7 | [7.00 to 8.00] |
| Route Indicators | Scenario 1 | Scenario 2 | Scenario 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sector 1 | Sector 2 | Sector 3 | Sector 1 | Sector 2 | Sector 3 | Sector 1 | Sector 2 | Sector 3 | |
| Waste generation sources | 2382.00 | 483.00 | 516.00 | 2382.00 | 483.00 | 516.00 | 2382.00 | 483.00 | 516.00 |
| Collection trucks in use | 3.00 | 1.00 | 2.00 | 3.00 | 2.00 | 2.00 | 3.00 | 2.00 | 2.00 |
| Operational shifts | 1.00 | 1.00 | 1.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| Micro routes | 3.00 | 2.00 | 3.00 | 3.00 | 2.00 | 3.00 | 3.00 | 2.00 | 3.00 |
| Average collection time on route (h) | 8.00 | 8.00 | 8.00 | 11.95 | 12.41 | 12.8 | 10.65 | 9.65 | 8.69 |
| Distance traveled (km/route) | 27.01 | 81.21 | 72.68 | 39.40 | 174.56 | 215.67 | 33.76 | 162.42 | 103.83 |
| Collection times at waste collection point (min) | 5.00 | 5.00 | 5.00 | 3.00 | 3.00 | 3.00 | 5.00 | 5.00 | 5.00 |
| Waste collection point by sector | 235.00 | 98.00 | 146.00 | 557.00 | 296.00 | 449.00 | 294.00 | 195.00 | 208.00 |
| Number of trips per day (trips/day) | 2.00 | 2.00 | 2.00 | 4.00 | 2.00 | 3.00 | 4.00 | 2.00 | 3.00 |
| Waste collection point per trip | 118.00 | 49.00 | 73.00 | 46.00 | 74.00 | 79.00 | 25.00 | 49.00 | 35.00 |
| MSW collected (tons/day) | 20.08 | 1.94 | 5.831 | 25.10 | 3.88 | 8.33 | 25.1 | 3.88 | 8.33 |
| Improvement of collected waste (%) | - | - | - | 25.00 1 | 100.00 1 | 42.86 1 | 25.00 1 | 100.00 1 | 42.86 1 |
| Improvement of service times (%) | - | - | - | - | - | - | 10.88 2 | 22.24 2 | 32.11 2 |
| Improvement of distances traveled (%) | - | - | - | - | - | - | 14.31 2 | 6.95 2 | 51.86 2 |
| Improvement of waste collection points (%) | - | - | - | - | - | - | 47.22 2 | 34.12 2 | 53.67 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araiza-Aguilar, J.A.; Rojas-Valencia, M.N.; Nájera-Aguilar, H.A.; Gutiérrez-Hernández, R.F.; García-Lara, C.M. Using Spatial Analysis to Design a Solid Waste Collection System. Urban Sci. 2024, 8, 95. https://doi.org/10.3390/urbansci8030095
Araiza-Aguilar JA, Rojas-Valencia MN, Nájera-Aguilar HA, Gutiérrez-Hernández RF, García-Lara CM. Using Spatial Analysis to Design a Solid Waste Collection System. Urban Science. 2024; 8(3):95. https://doi.org/10.3390/urbansci8030095
Chicago/Turabian StyleAraiza-Aguilar, Juan Antonio, María Neftalí Rojas-Valencia, Hugo Alejandro Nájera-Aguilar, Rubén Fernando Gutiérrez-Hernández, and Carlos Manuel García-Lara. 2024. "Using Spatial Analysis to Design a Solid Waste Collection System" Urban Science 8, no. 3: 95. https://doi.org/10.3390/urbansci8030095
APA StyleAraiza-Aguilar, J. A., Rojas-Valencia, M. N., Nájera-Aguilar, H. A., Gutiérrez-Hernández, R. F., & García-Lara, C. M. (2024). Using Spatial Analysis to Design a Solid Waste Collection System. Urban Science, 8(3), 95. https://doi.org/10.3390/urbansci8030095









