Multimodal Approach of Improving Spatial Abilities
Abstract
:1. Introduction
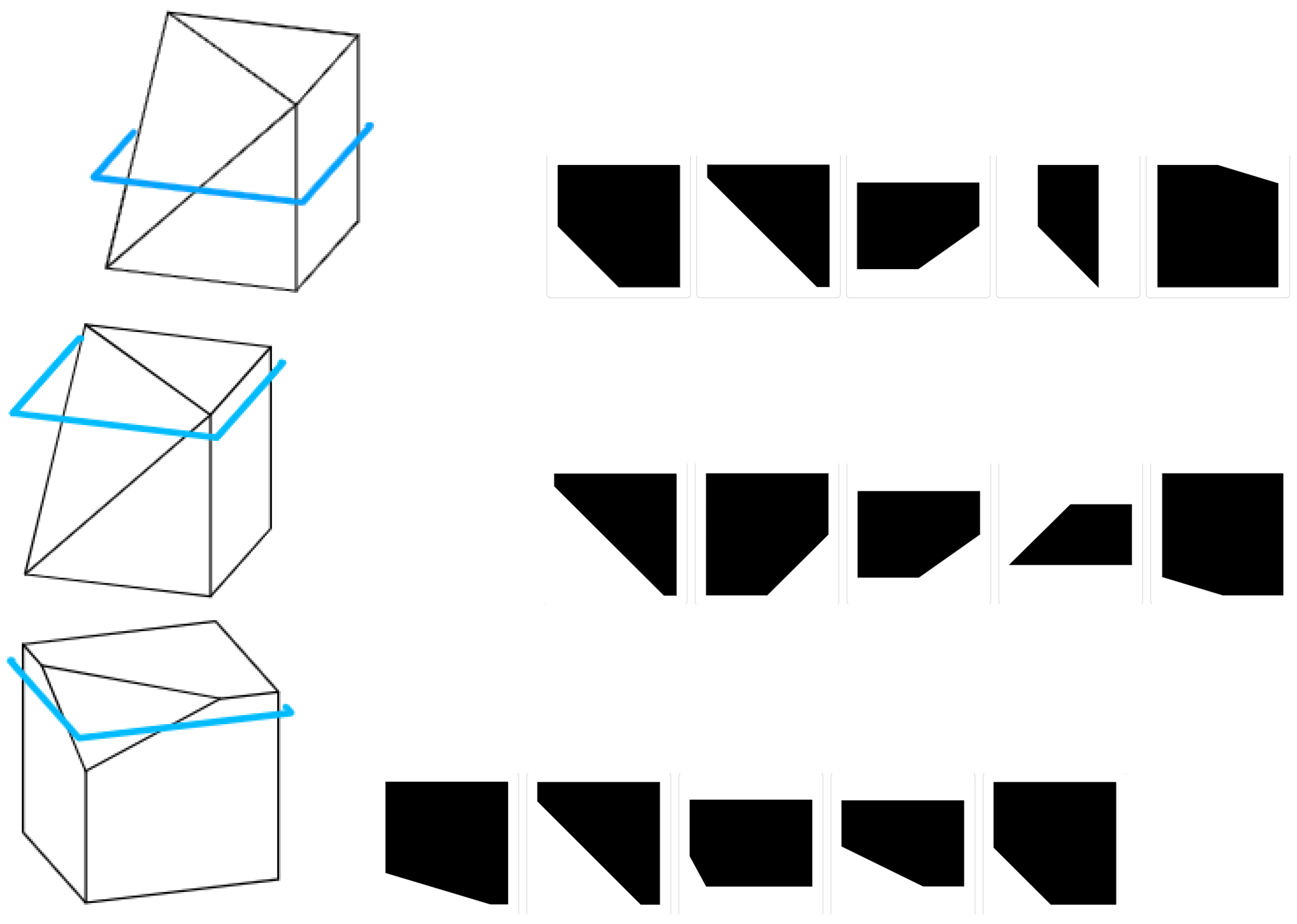
2. Assessing Spatial Skills: The Mental Cutting Test
3. Media and Technology Support of Training and Testing: The Multimodal Approach
4. Methodology
- The test starts with a short explanation of MCT.
- The test consists of 10 exercises (maximum score is 10).
- The 2D viewer is available to all the users, while the 3D viewer is available only to the second group (3D).
5. Results
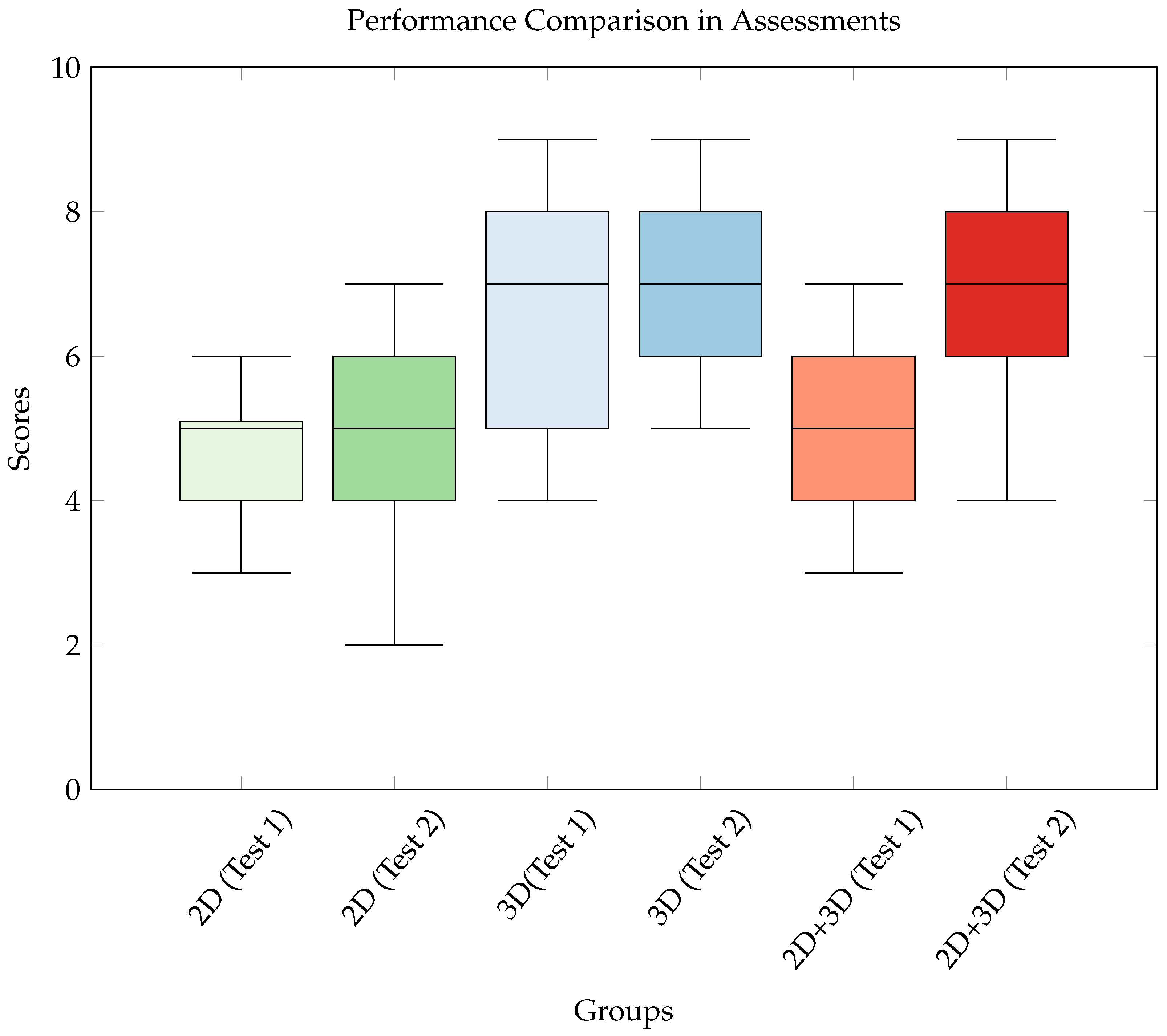
- 2D Group: The increase in the mean score from 3.43 to 3.64 was not statistically significant, with a p-value > 0.05. This suggests that the observed change was likely due to random variation and not the result of any effective intervention.
- 3D Group: The improvement in the mean score from 5.00 to 6.30 was statistically significant (p-value < 0.05), indicating that the use of 3D tools had a meaningful impact on the group’s performance. Additionally, the reduction in standard deviation suggests that the intervention was particularly useful for those who underperformed in the first test, and this method not only improved scores but also led to more uniformity in performance across participants.
- 2D+3D Group: The increase in mean score from 3.86 to 6.00 was also statistically significant (p-value < 0.05). The multimodal combination of 2D and 3D tools appears to be the most effective intervention among the three groups, leading to a substantial improvement in each participant’s overall performance, while the scores’ spread remained similar.
- Small effect: from ;
- Medium effect: from ;
- Large effect: or greater.
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCT | Mental Cutting Test |
| MRT | Mental Rotation Test |
| ULT | Urban Layout Test |
| IPT | Indoor Perspective Test |
| 2D | Planar figure, and test with planar view of the task |
| 3D | Spatial figure, and test with spatial view of the task |
References
- Verdine, B.N.; Golinkoff, R.M.; Hirsh-Pasek, K.; Newcombe, N.S.; Bailey, D.H. Links between spatial and mathematical skills across the preschool years. Monogr. Soc. Res. Child Dev. 2017, 82, 1–149. [Google Scholar]
- Atit, K.; Power, J.R.; Pigott, T.; Lee, J.; Geer, E.A.; Uttal, D.H.; Ganley, C.M.; Sorby, S.A. Examining the relations between spatial skills and mathematical performance: A meta-analysis. Psychon. Bull. Rev. 2022, 29, 699–720. [Google Scholar] [CrossRef] [PubMed]
- Anstey, K.J.; Horswill, M.S.; Wood, J.M.; Hatherly, C. The role of cognitive and visual abilities as predictors in the Multifactorial Model of Driving Safety. Accid. Anal. Prev. 2012, 45, 766–774. [Google Scholar] [CrossRef] [PubMed]
- Langlois, J.; Bellemare, C.; Toulouse, J.; Wells, G.A. Spatial abilities and technical skills performance in health care: A systematic review. Med. Educ. 2015, 49, 1065–1085. [Google Scholar] [CrossRef] [PubMed]
- Lohman, D.F. Spatial abilities as traits, processes, and knowledge. In Advances in the Psychology of Human Intelligence; Psychology Press: London, UK, 2014; pp. 181–248. [Google Scholar]
- Bohlmann, N.; Benölken, R. Complex Tasks: Potentials and Pitfalls. Mathematics 2020, 8, 1780. [Google Scholar] [CrossRef]
- Bishop, A.J. Spatial abilities and mathematics education—A review. Educ. Stud. Math. 1980, 11, 257–269. [Google Scholar] [CrossRef]
- Tosto, M.G.; Hanscombe, K.B.; Haworth, C.M.; Davis, O.S.; Petrill, S.A.; Dale, P.S.; Malykh, S.; Plomin, R.; Kovas, Y. Why do spatial abilities predict mathematical performance? Dev. Sci. 2014, 17, 462–470. [Google Scholar] [CrossRef]
- Cole, M.; Wilhelm, J.; Vaught, B.M.M.; Fish, C.; Fish, H. The Relationship between Spatial Ability and the Conservation of Matter in Middle School. Educ. Sci. 2021, 11, 4. [Google Scholar] [CrossRef]
- Carroll, J.B. Human Cognitive Abilities: A Survey of Factor-Analytic Studies; Number 1; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Hegarty, M. Components of Spatial Intelligence. In The Psychology of Learning and Motivation; Academic Press: Cambridge, MA, USA, 2010; Volume 52, pp. 265–297. [Google Scholar]
- Shepard, R.N.; Metzler, J. Mental rotation of three-dimensional objects. Science 1971, 171, 701–703. [Google Scholar] [CrossRef]
- Porat, R.; Ceobanu, C. Enhancing Spatial Ability among Undergraduate First-Year Engineering and Architecture Students. Educ. Sci. 2024, 14, 400. [Google Scholar] [CrossRef]
- Buckley, J.; Seery, N.; Canty, D. A heuristic framework of spatial ability: A review and synthesis of spatial factor literature to support its translation into STEM education. Educ. Psychol. Rev. 2018, 30, 947–972. [Google Scholar] [CrossRef]
- Guay, R. Purdue Spatial Vizualization Test; Educational Testing Service: Princeton, NJ, USA, 1976. [Google Scholar]
- Bölcskei, A.; Gál-Kállay, S.; Kovács, A.Z.; Sörös, C. Development of Spatial Abilities of Architectural and Civil Engineering Students in the Light of the Mental Cutting Test. J. Geom. Graph. 2012, 16, 103–115. [Google Scholar]
- Šipuš, Ž.M.; Cižmešija, A. Spatial ability of students of mathematics education in Croatia evaluated by the Mental Cutting Test. Ann. Math. Inform. 2012, 40, 203–216. [Google Scholar]
- Hegarty, M.; Waller, D. Individual differences in spatial abilities. In The Cambridge Handbook of Visuospatial Thinking; Cambridge University Press: Cambridge, UK, 2005; pp. 121–169. [Google Scholar]
- Németh, B.; Hoffmann, M. Gender differences in spatial visualization among engineering students. Ann. Math. Inform. 2006, 33, 169–174. [Google Scholar]
- Reilly, D.; Neumann, D.L.; Andrews, G. Gender differences in spatial ability: Implications for STEM education and approaches to reducing the gender gap for parents and educators. In Visual-Spatial Ability in STEM Education: Transforming Research into Practice; Springer: Cham, Switzerland, 2017; pp. 195–224. [Google Scholar]
- Voyer, D.; Voyer, S.; Bryden, M.P. Magnitude of sex differences in spatial abilities: A meta-analysis and consideration of critical variables. Psychol. Bull. 1995, 117, 250. [Google Scholar] [CrossRef]
- Németh, B.; Sörös, C.; Hoffmann, M. Typical mistakes in Mental Cutting Test and their consequences in gender differences. Teach. Math. Comput. Sci. 2007, 5, 385–392. [Google Scholar] [CrossRef]
- Uttal, D.H.; McKee, K.; Simms, N.; Hegarty, M.; Newcombe, N.S. How can we best assess spatial skills? Practical and Conceptual Challenges. J. Intell. 2024, 12, 8. [Google Scholar] [CrossRef]
- Tóth, R.; Hoffmann, M.; Zichar, M. Lossless encoding of mental cutting test scenarios for efficient development of spatial skills. Educ. Sci. 2023, 13, 101. [Google Scholar] [CrossRef]
- Tóth, R.; Tóth, B.; Hoffmann, M.; Zichar, M. viskillz-blender—A Python package to generate assets of Mental Cutting Test exercises using Blender. SoftwareX 2023, 22, 101328. [Google Scholar] [CrossRef]
- Tóth, R.; Zichar, M.; Hoffmann, M. Gamified Mental Cutting Test for enhancing spatial skills. In Proceedings of the 2020 11th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Mariehamn, Finland, 23–25 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 299–304. [Google Scholar]
- Pinkl, J.; Villegas, J.; Cohen, M. Multimodal Drumming Education Tool in Mixed Reality. Multimodal Technol. Interact. 2024, 8, 70. [Google Scholar] [CrossRef]
- Rangarajan, V.; Badr, A.S.; De Amicis, R. Evaluating Virtual Reality in Education: An Analysis of VR through the Instructors’ Lens. Multimodal Technol. Interact. 2024, 8, 72. [Google Scholar] [CrossRef]
- Estapa, A.; Nadolny, L. The effect of an augmented reality enhanced mathematics lesson on student achievement and motivation. J. STEM Educ. 2015, 16, 40–48. [Google Scholar]
- Chen, Y.c. Effect of mobile augmented reality on learning performance, motivation, and math anxiety in a math course. J. Educ. Comput. Res. 2019, 57, 1695–1722. [Google Scholar] [CrossRef]
- del Cerro Velázquez, F.; Morales Méndez, G. Application in Augmented Reality for Learning Mathematical Functions: A Study for the Development of Spatial Intelligence in Secondary Education Students. Mathematics 2021, 9, 369. [Google Scholar] [CrossRef]
- Petrov, P.D.; Atanasova, T.V. The Effect of Augmented Reality on Students’ Learning Performance in Stem Education. Information 2020, 11, 209. [Google Scholar] [CrossRef]
- Flores-Bascuñana, M.; Diago, P.D.; Villena-Taranilla, R.; Yáñez, D.F. On Augmented Reality for the learning of 3D-geometric contents: A preliminary exploratory study with 6-Grade primary students. Educ. Sci. 2020, 10, 4. [Google Scholar] [CrossRef]
- Suselo, T.; Wünsche, B.C.; Luxton-Reilly, A. Using Mobile Augmented Reality for Teaching 3D Transformations. In Proceedings of the 52nd ACM Technical Symposium on Computer Science Education, Virtual, 13–20 March 2021; pp. 872–878. [Google Scholar]
- Velázquez, F.d.C.; Méndez, G.M. Systematic review of the development of spatial intelligence through augmented reality in stem knowledge areas. Mathematics 2021, 9, 3067. [Google Scholar] [CrossRef]
- Lundin, R.M.; Yeap, Y.; Menkes, D.B. Adverse effects of virtual and augmented reality interventions in psychiatry: Systematic review. JMIR Ment. Health 2023, 10, e43240. [Google Scholar] [CrossRef]
- Bartlett, K.A.; Palacios-Ibáñez, A.; Camba, J.D. Design and Validation of a Virtual Reality Mental Rotation Test. ACM Trans. Appl. Percept. 2024, 21, 1–22. [Google Scholar] [CrossRef]
- Krüger, J.M.; Palzer, K.; Bodemer, D. Learning with augmented reality: Impact of dimensionality and spatial abilities. Comput. Educ. Open 2022, 3, 100065. [Google Scholar] [CrossRef]
- Lampropoulos, G.; Keramopoulos, E.; Diamantaras, K.; Evangelidis, G. Augmented reality and gamification in education: A systematic literature review of research, applications, and empirical studies. Appl. Sci. 2022, 12, 6809. [Google Scholar] [CrossRef]
- Cronbach, L. Coefficient alpha and the internal structure of tests. Psychometirka 1951, 16, 297–334. [Google Scholar] [CrossRef]
- Hegarty, M.; Waller, D. A dissociation between mental rotation and perspective-taking spatial abilities. Intelligence 2004, 32, 175–191. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 66–70. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: London, UK, 2013. [Google Scholar]
- Gómez-Tone, H.C.; Martin-Gutierrez, J.; Valencia Anci, L.; Mora Luis, C.E. International comparative pilot study of spatial skill development in engineering students through autonomous augmented reality-based training. Symmetry 2020, 12, 1401. [Google Scholar] [CrossRef]
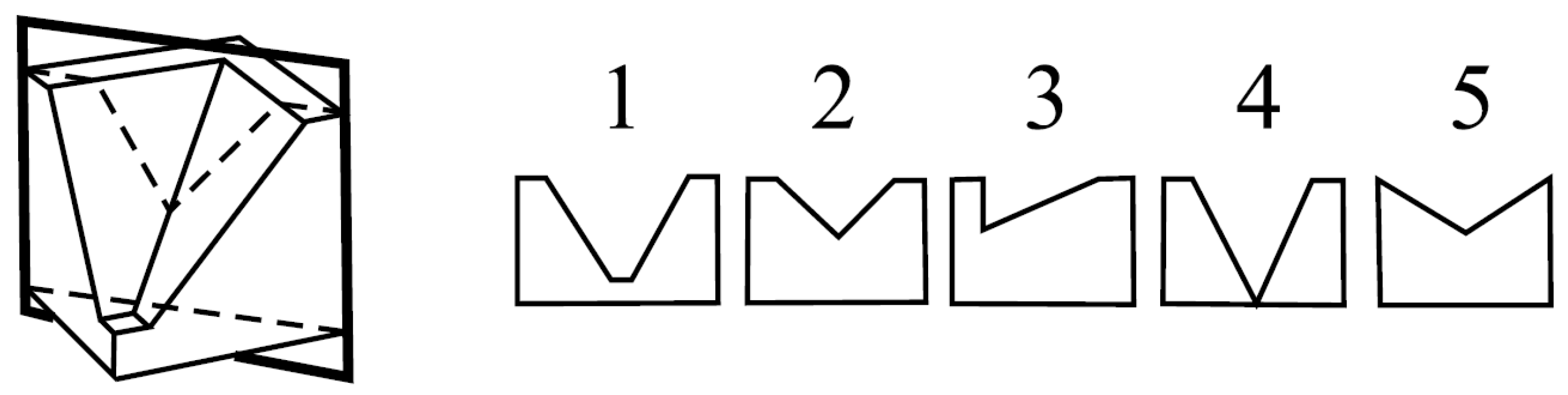


| Group | Test 1 | Test 2 | ||||
|---|---|---|---|---|---|---|
| Median | Mean | Std. Dev. | Median | Mean | Std. Dev. | |
| 2D | 5 | 3.43 | 1.24 | 5 | 3.64 | 1.34 |
| 3D | 7 | 5.00 | 1.96 | 7 | 6.30 | 1.49 |
| 2D+3D | 5 | 3.86 | 2.04 | 7 | 6.00 | 2.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balla, T.; Tóth, R.; Zichar, M.; Hoffmann, M. Multimodal Approach of Improving Spatial Abilities. Multimodal Technol. Interact. 2024, 8, 99. https://doi.org/10.3390/mti8110099
Balla T, Tóth R, Zichar M, Hoffmann M. Multimodal Approach of Improving Spatial Abilities. Multimodal Technologies and Interaction. 2024; 8(11):99. https://doi.org/10.3390/mti8110099
Chicago/Turabian StyleBalla, Tamás, Róbert Tóth, Marianna Zichar, and Miklós Hoffmann. 2024. "Multimodal Approach of Improving Spatial Abilities" Multimodal Technologies and Interaction 8, no. 11: 99. https://doi.org/10.3390/mti8110099
APA StyleBalla, T., Tóth, R., Zichar, M., & Hoffmann, M. (2024). Multimodal Approach of Improving Spatial Abilities. Multimodal Technologies and Interaction, 8(11), 99. https://doi.org/10.3390/mti8110099








