On a Data-Driven Optimization Approach to the PID-Based Algorithmic Trading
Abstract
:1. Introduction and Motivation
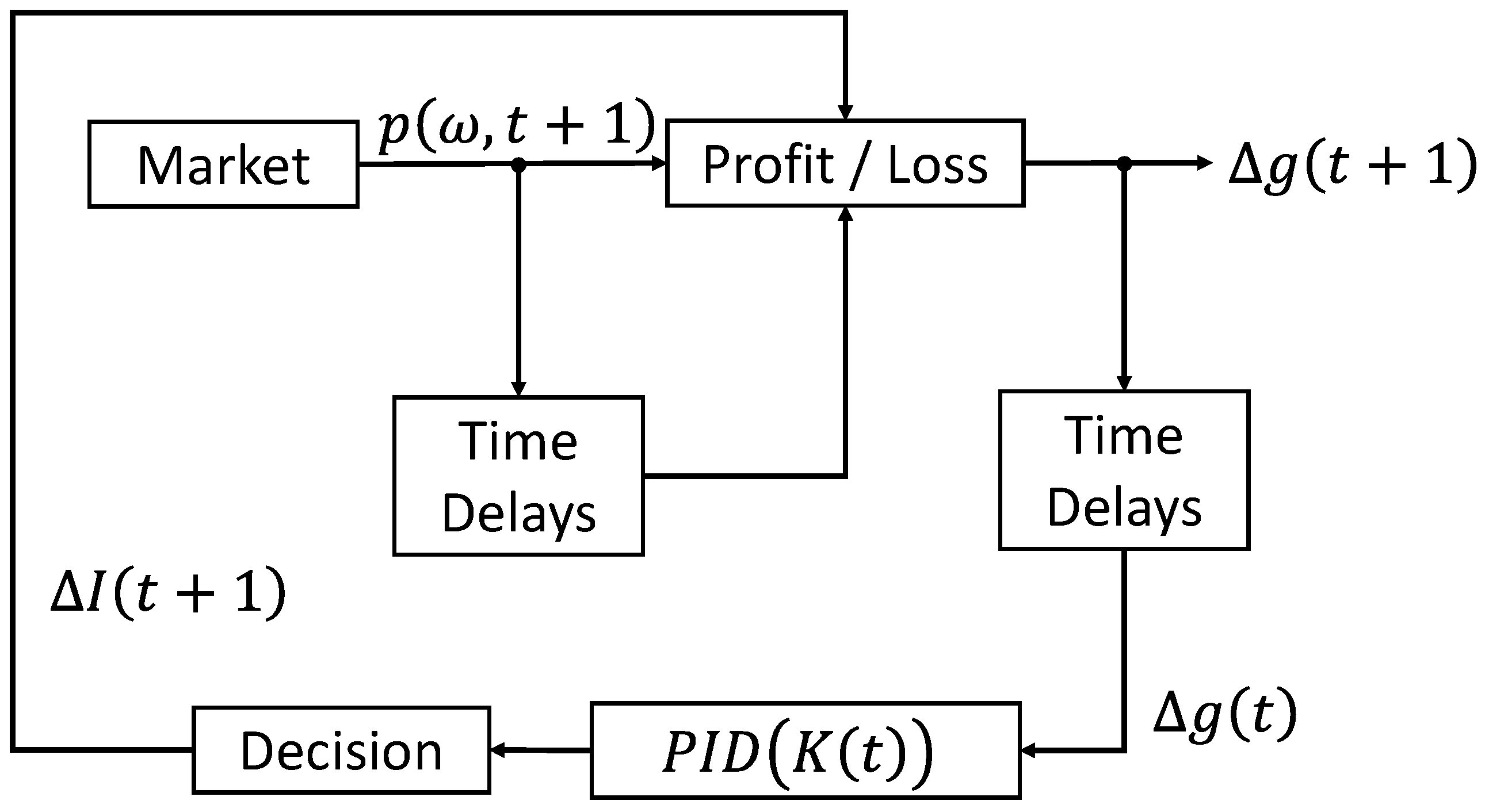
2. Model-Free PID-Based Trading Algorithm
3. Statistical Assumptions on the Stock Market
4. Data-Driven Optimization Approaches to the PID Gains Tuning
4.1. Regression Involved Gains Optimization
4.2. On the Stochastic Optimal Gains Tuning
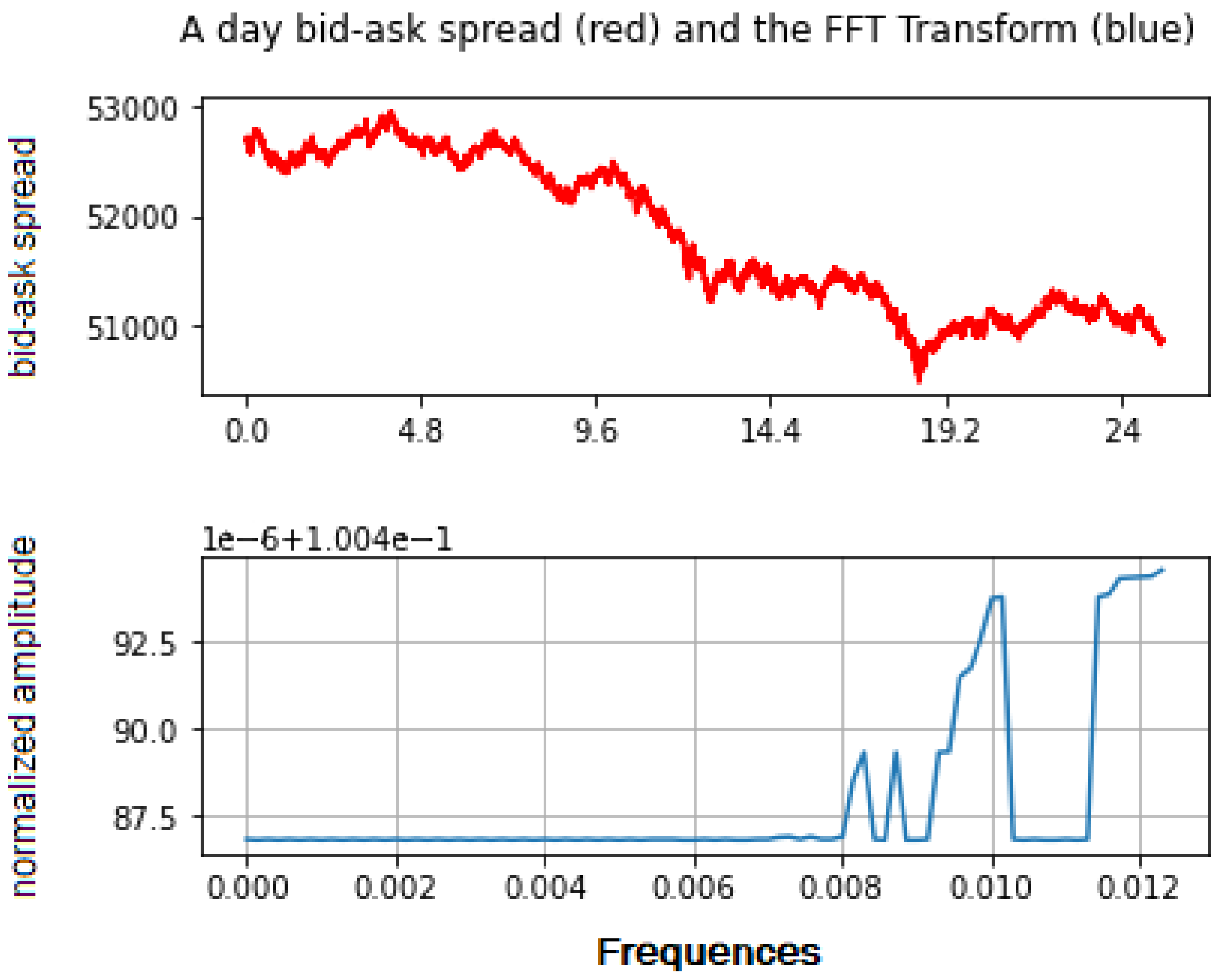
5. Frequency Domain Representation of the PID Trading Algorithm
6. On the Implementation of the Optimal PID Trading Algorithm
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Antoniou, Ioannis E., Vi V. Ivanov, Va V. Ivanov, and Petr V. Zrelov. 2004. On the log-normal distribution of stock market data. Physica A 331: 617–38. [Google Scholar] [CrossRef]
- Azhmyakov, Vadim. 2019. A Relaxation Based Approach to Optimal Control of Switched Systems. Oxford: Elsevier. [Google Scholar]
- Azhmyakov, Vadim, Ilya Shirokov, and Luz Adriana Guzman Trujillo. 2022a. Application of a switched PIDD control strategy to the model-free algorithmic trading. IFAC PapersOnline 55: 145–50. [Google Scholar] [CrossRef]
- Azhmyakov, Vadim, Ilya Shirokov, Yuri Dernov, and Luz Adriana Guzman Trujillo. 2022b. On the Proportional-Integral-Derivative based trading algorithm under the condition of the log-normal distribution of stock market data. Paper presented at the Sixteenth International Conference on Advanced Engineering Computing and Applications in Sciences (ADVCOMP 2022), Valencia, Spain, November 13–17; pp. 17–21. [Google Scholar]
- Azhmyakov, Vadim, Jose Perea Arango, Moises Bonilla, Raymundo Juarez del Toro, and Stefan Pickl. 2021. Robust state Estimations in Controlled ARMA Processes with the Non-Gaussian Noises: Applications to the Delayed Dynamics. IFAC PapersOnline 54: 334–39. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, and Ford Brown. 2004. Kalman Filter approach to estimate the demand for international reserves. Applied Economics 36: 1655–68. [Google Scholar] [CrossRef]
- Barmish, B. Ross. 2008. On trading of equities: A robust control paradigm. IFAC Proceedings Volumes 41: 1621–26. [Google Scholar] [CrossRef]
- Barmish, B. Ross, and James A. Primbs. 2012. On market-neutral stock trading arbitrage via linear feedback. Paper presented at the American Control Conference, Montreal, QC, Canada, June 27–29; pp. 3693–98. [Google Scholar]
- Barmish, B. Ross, and James A. Primbs. 2016. On a new paradigm for stock trading via a model-free feedback controller. IEEE Transactions on Automatic Control 61: 662–76. [Google Scholar] [CrossRef]
- Baumann, Michael Heinrich. 2017. On stock trading via feedback control when underlying stock returns are discontinuous. IEEE Transactions on Automatic Control 62: 2987–92. [Google Scholar] [CrossRef]
- Bemporad, Alberto, Tommaso Gabbriellini, Laura Puglia, and Leonardo Bellucci. 2010. Scenario-based stochastic model predictive control for dynamic option hedging. Paper presented at the IEEE Conference on Decision and Control, Atlanta, GA, USA, December 15–17; pp. 3216–21. [Google Scholar]
- Bertsekas, Dimitri. 2019. Reinforcement Learning and Optimal Control. Nashua: Athena Scientific. [Google Scholar]
- Bertsimas, Dimitris, and Andrew W. Lo. 1998. Optimal control of execution costs. Journal of Financial Markets 1: 1–50. [Google Scholar] [CrossRef]
- Birge, John R., and Francois Louveaux. 2011. Introduction to Stochastic Programming. New York: Springer. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–59. [Google Scholar] [CrossRef]
- Brooks, Chris. 2015. Introductory Econometcs for Finance. Glasgow: Cambridge University Press. [Google Scholar]
- Cornuejols, Gérard, Pena Javier, and Tutuncu Reha. 2018. Optimization Methods in Finance. Cambridge: Cambridge University Press. [Google Scholar]
- Crow, Edwin L., and Kunio Shimizu, eds. 1988. Lognormal Distributions, Theory and Applications. New York: Marcel Dekker, Inc. [Google Scholar]
- Formentin, Simone, Fabio Previdi, Gabriele Maroni, and Claudio Cantaro. 2018. Stock trading via feedback control: An extremum seeking approach. Paper presented at the Mediterranean Conference on Control and Automation, Zadar, Croatia, June 19–22; pp. 523–28. [Google Scholar]
- Gallager, Robert G. 2013. Stochastic Processes. New York: Cambridge University Press. [Google Scholar]
- Gill, Philip E., Walter Murray, and Margaret H. Wright. 1981. Practical Optimization. New York: Academic Press. [Google Scholar]
- Hammel, C., and Wolfgang B. Paul. 2002. Monte Carlo simulations of a trader-based market model. Physica A 313: 640–50. [Google Scholar] [CrossRef]
- Hens, Thorsten, and Marc Oliver Rieger. 2010. Financial Economics. Berlin: Springer. [Google Scholar]
- Huang, Shian-Chang. 2008. Online option price forecasting by using unscented Kalman filters and support vector machines. Journal of Expert Systems with Applications 34: 2819–25. [Google Scholar] [CrossRef]
- Huber, P. J., and Elvezio Ronchetti. 2005. Robust Statistics. New York: Wiley. [Google Scholar]
- Isidori, Alberto. 1995. Nonlinear Control Systems. London: Springer. [Google Scholar]
- Jansen, Stefan. 2020. Machine Learning for Algorithmic Trading. Birmingham: Packt Publishing Ltd. [Google Scholar]
- Khalil, Hassan. 2015. Nonlinear Control. Boston: Pearson. [Google Scholar]
- Lewis, Frank L. 1986. Optimal Estimation. New York: Wiley. [Google Scholar]
- Liu, Ji, and Stephen J. Wright. 2015. Asynchronous stochastic coordinate descent: Parallelism and convergence properties. SIAM Journal on Optimization 25: 351–76. [Google Scholar] [CrossRef]
- Malekpour, Shirzad, James A. Primbs, and B. Ross Barmish. 2013. On stock trading using a PI controller in an idealized market: The robust positive expectation property. Paper presented at the IEEE Conference on Decision and Control, Florence, Italy, December 10–13; pp. 1210–16. [Google Scholar]
- Michaud, Richard O., and Robert O. Michaud. 2008. Efficient Asset Management. Oxford: Oxford University Press. [Google Scholar]
- Nemirovski, Arkadi, Anatoli Juditsky, Guanghui Lan, and Alexander Shapiro. 2009. Robust stochastic approximation approach to stochastic programming. SIAM Journal on Optimization 19: 1574–609. [Google Scholar] [CrossRef]
- Poznyak, Alexander S. 2008. Advanced Mathematical Tools for Automatic Control Engineers: Deterministic Technique. New York: Elsevier. [Google Scholar]
- Poznyak, Alexander S. 2009. Advanced Mathematical Tools for Automatic Control Engineers: Stochastic Tools. New York: Elsevier. [Google Scholar]
- Prakash, Jagadeesan, and K. Srinivasan. 2009. Design of nonlinear PID controller and nonlinear model predictive controller for a continuous stirred tank reactor. ISA Transactions 48: 273–82. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, Reuven Y., and Dirk P. Kroese. 1981. Simulation and the Monte Carlo Method. New York: John Wiley Inc. [Google Scholar]
- Rudoy, Melanie B., and Charles E. Rohrs. 2008. A dynamic programming approach to two-stage mean-variance portfolio selection in cointegrated vector autoregressive systems. Paper presented at the IEEE Conference on Decision and Control, Cancun, Mexico, December 9–11; pp. 4280–85. [Google Scholar]
- Shapiro, Alexander, and Tito Homem-de-Mello. 2000. On the rate of convergence of optimal solutions of Monte Carlo approximations of stochastic programs. SIAM Journal on Optimization 11: 70–86. [Google Scholar] [CrossRef]
- Taylor, Stephen J. 1986. Modeling Financial Time Series. Chichester: Wiley. [Google Scholar]
- Vo, Nguyen, and Robert Ślepaczuk. 2022. Applying hybrid ARIMA-SGARCH in algorithmic investment strategies on S&P500 index. Entropy 24: 158. [Google Scholar] [CrossRef] [PubMed]
- Wets, Roger J.-B. 1990. Stochastic programming. In Optimization, Handbooks in Operations Research and Management Science. Edited by Nemhauser George L., Rinnooy Kan A. H. G. and Todd Michael J. New York: Elsevier, vol. 1. [Google Scholar]
- Zenios, Stavros A., ed. 1993. Financial Optimization. Cambridge: Cambridge University Press. [Google Scholar]
- Ziembaand, William T., and Raymond G. Vickson. 1975. Stochastic Optimization Models in Finance. New York: Academic Press. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azhmyakov, V.; Shirokov, I.; Dernov, Y.; Guzman Trujillo, L.A. On a Data-Driven Optimization Approach to the PID-Based Algorithmic Trading. J. Risk Financial Manag. 2023, 16, 387. https://doi.org/10.3390/jrfm16090387
Azhmyakov V, Shirokov I, Dernov Y, Guzman Trujillo LA. On a Data-Driven Optimization Approach to the PID-Based Algorithmic Trading. Journal of Risk and Financial Management. 2023; 16(9):387. https://doi.org/10.3390/jrfm16090387
Chicago/Turabian StyleAzhmyakov, Vadim, Ilya Shirokov, Yuri Dernov, and Luz Adriana Guzman Trujillo. 2023. "On a Data-Driven Optimization Approach to the PID-Based Algorithmic Trading" Journal of Risk and Financial Management 16, no. 9: 387. https://doi.org/10.3390/jrfm16090387
APA StyleAzhmyakov, V., Shirokov, I., Dernov, Y., & Guzman Trujillo, L. A. (2023). On a Data-Driven Optimization Approach to the PID-Based Algorithmic Trading. Journal of Risk and Financial Management, 16(9), 387. https://doi.org/10.3390/jrfm16090387





