Comb Model with Non-Static Stochastic Resetting and Anomalous Diffusion
Abstract
:1. Introduction
2. The Model
3. The Model with Memory Kernels Effects: Crossover between Anomalous Diffusion Regimes
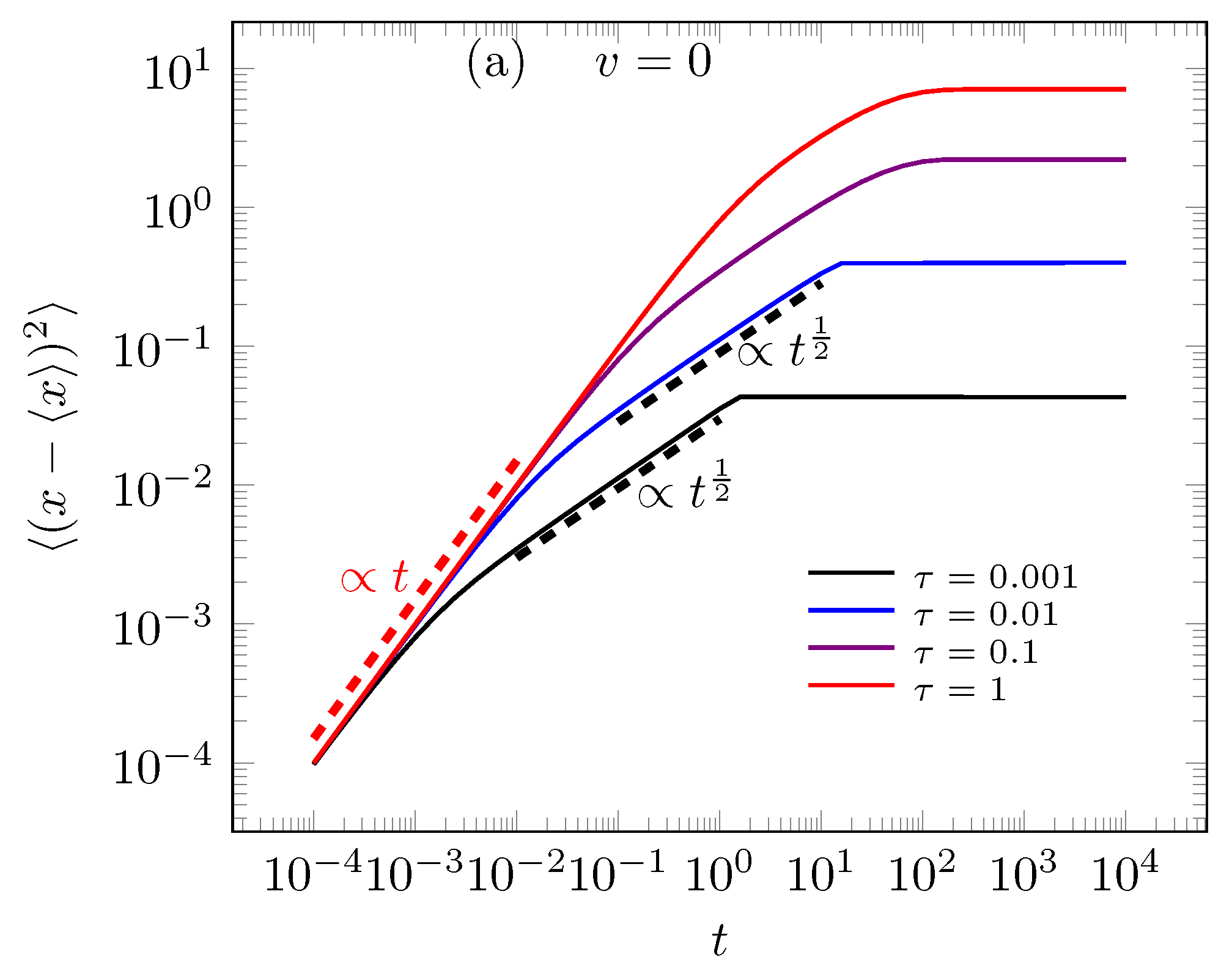
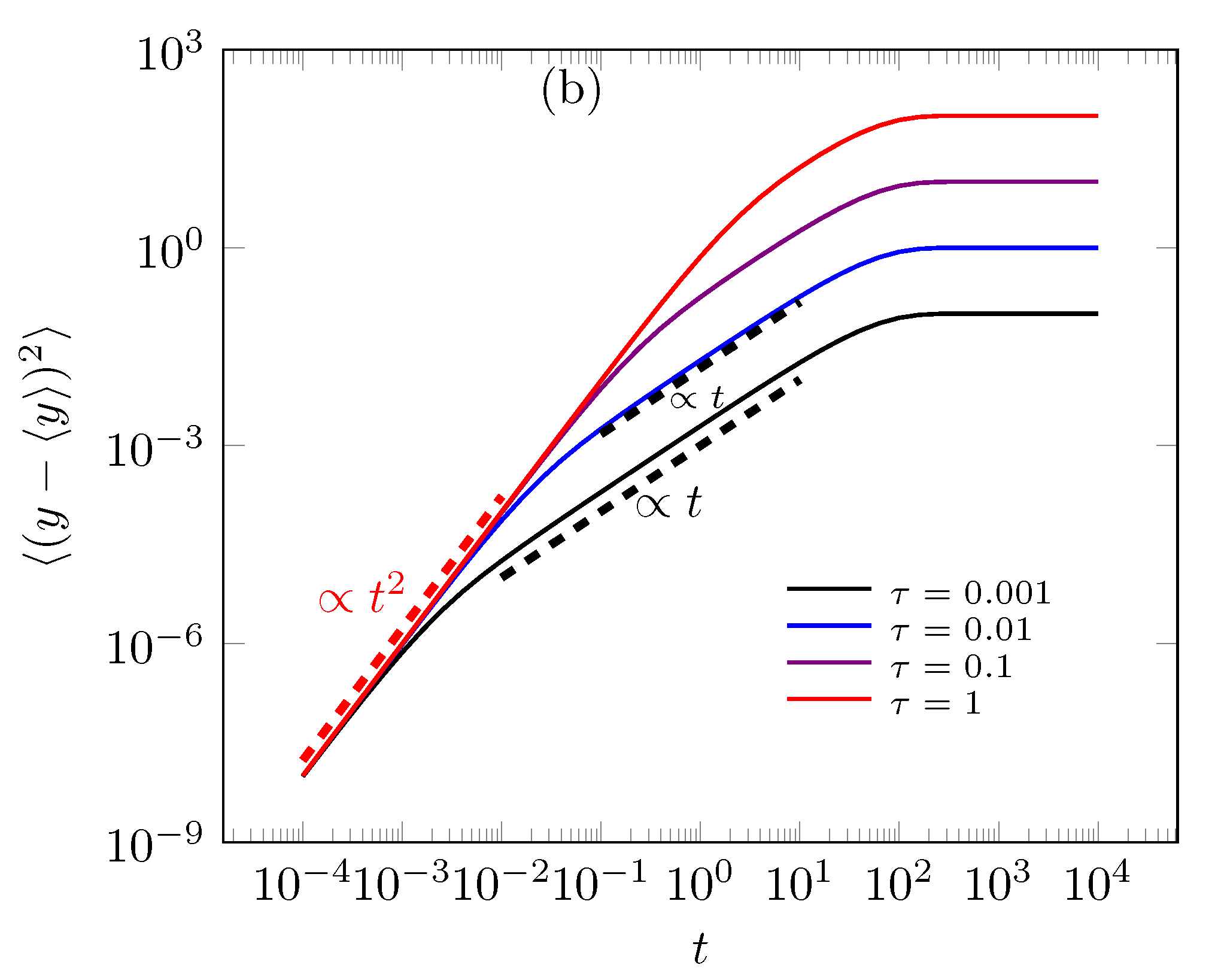
3.1. First Case: Exponential Memory in Diffusion Terms
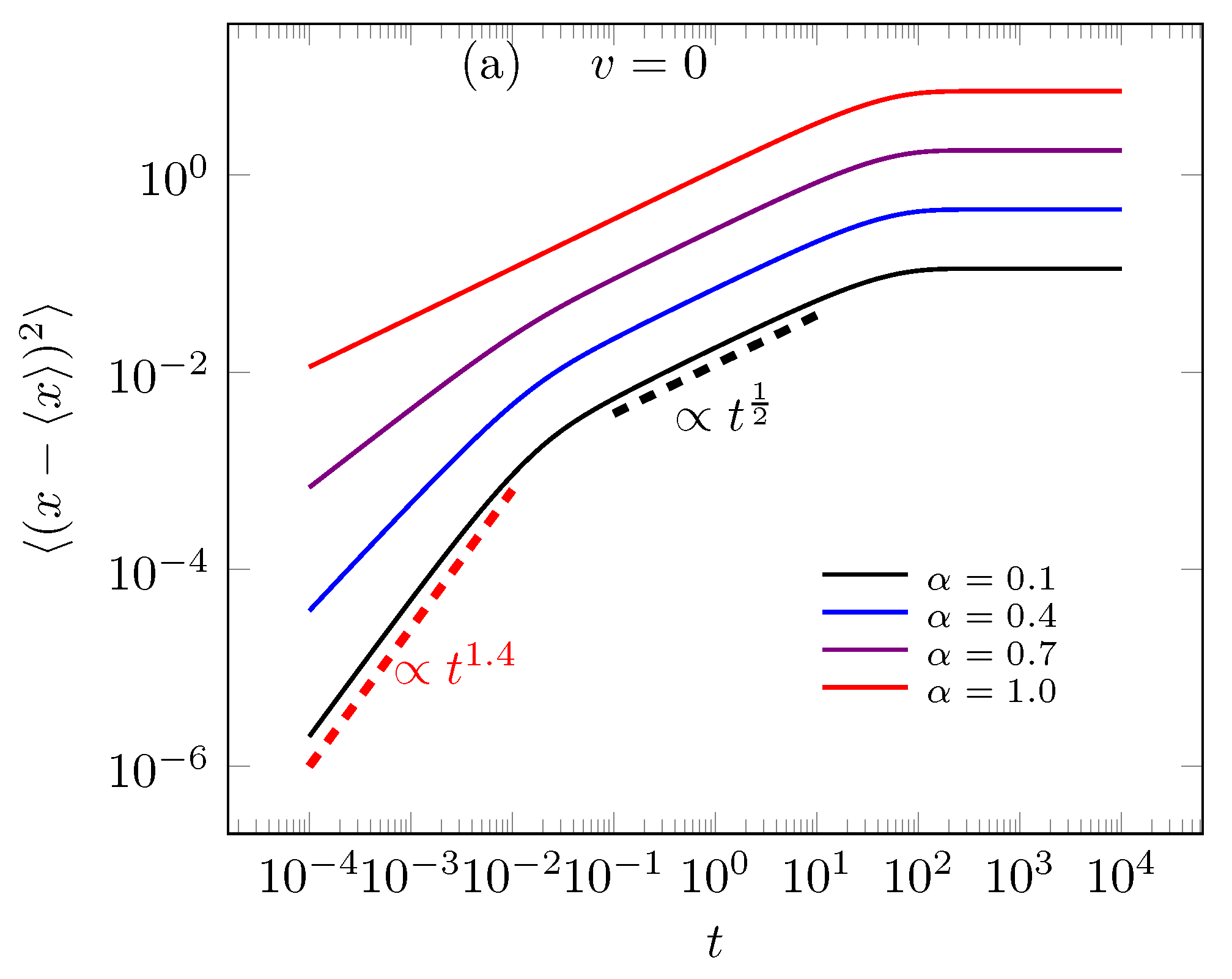
3.2. Second Case: Tempered Power-Law Memory in Diffusion Terms
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Roldán, É.; Lisica, A.; Sánchez-Taltavull, D.; Grill, S.W. Stochastic resetting in backtrack recovery by RNA polymerases. Phys. Rev. E 2016, 93, 062411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eule, S.; Metzger, J.J. Non-equilibrium steady states of stochastic processes with intermittent resetting. New J. Phys. 2016, 18, 033006. [Google Scholar] [CrossRef]
- Campos, D.; Méndez, V. Phase transitions in optimal search times: How random walkers should combine resetting and flight scales. Phys. Rev. E 2015, 92, 062115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pal, A.; Prasad, V.V. First passage under stochastic resetting in an interval. Phys. Rev. E 2019, 99, 032123. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, J.; Goldt, S.; Seifert, U. Stochastic thermodynamics of resetting. EPL 2016, 113, 60009. [Google Scholar] [CrossRef] [Green Version]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A 2020, 53, 193001. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [Green Version]
- Chechkin, A.; Sokolov, I.M. Random search with resetting: A unified renewal approach. Phys. Rev. Lett. 2018, 121, 050601. [Google Scholar] [CrossRef]
- Mejía-Monasterio, C.; Oshanin, G.; Schehr, G. First passages for a search by a swarm of independent random searchers. J. Stat. Mech. Theory Exp. 2011, 2011, P06022. [Google Scholar] [CrossRef] [Green Version]
- Durang, X.; Henkel, M.; Park, H. The statistical mechanics of the coagulation–diffusion process with a stochastic reset. J. Phys. A 2014, 47, 045002. [Google Scholar] [CrossRef] [Green Version]
- Masoliver, J.; Montero, M. Anomalous diffusion under stochastic resettings: A general approach. Phys. Rev. E 2019, 100, 042103. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, M.A.F. Fractional prabhakar derivative in diffusion equation with non-static stochastic resetting. Physics 2019, 1, 5. [Google Scholar] [CrossRef] [Green Version]
- Kuśmierz, Ł.; Gudowska-Nowak, E. Optimal first-arrival times in Lévy flights with resetting. Phys. Rev. E 2015, 92, 052127. [Google Scholar]
- Dos Santos, M.A.F. Non-Gaussian distributions to random walk in the context of memory kernels. Fractal Fract. 2018, 2, 20. [Google Scholar] [CrossRef] [Green Version]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Barkai, E. Fractional Fokker-Planck equation, solution, and application. Phys. Rev. E 2001, 63, 046118. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, M.A.F. Analytic approaches of the anomalous diffusion: A review. Chaos Solitons Fractals 2019, 124, 86–96. [Google Scholar] [CrossRef] [Green Version]
- Hristov, J. Diffusion models of heat and momentum with weakly singular kernels in the fading memories: How the integral-balance method can be applied? Therm. Sci. 2015, 19, 947–957. [Google Scholar] [CrossRef]
- Hristov, J. On the Atangana–Baleanu derivative and its relation to the fading memory concept: The diffusion equation formulation. In Fractional Derivatives with Mittag–Leffler Kernel; Springer International Publishing: Cham, Switzerland, 2019; pp. 175–193. [Google Scholar]
- Sene, N. Analytical solutions and numerical schemes of certain generalized fractional diffusion models. Eur. Phys. J. Plus 2019, 134, 199. [Google Scholar] [CrossRef]
- Sene, N. Analytical solutions of Hristov diffusion equations with non-singular fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023112. [Google Scholar] [CrossRef]
- Dos Santos, M.A.F. Mittag–leffler memory kernel in lévy flights. Mathematics 2019, 7, 766. [Google Scholar] [CrossRef] [Green Version]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Oliveira, F.A.; Ferreira, R.; Lapas, L.C.; Vainstein, M.H. Anomalous diffusion: A basic mechanism for the evolution of inhomogeneous systems. Front. Phys. 2019, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman New York: New York, NY, USA, 1983; Volume 173. [Google Scholar]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; Mandelbrot, B.B., Ed.; WH Freeman & Co.: San Francisco, CA, USA, 1979; 365p. [Google Scholar]
- Gefen, Y.; Aharony, A.; Alexander, S. Anomalous diffusion on percolating clusters. Phys. Rev. Lett. 1983, 50, 77. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Havlin, S. Diffusion on percolation clusters at criticality. J. Phys. A 1982, 15, L691. [Google Scholar] [CrossRef] [Green Version]
- Pandey, R.; Stauffer, D. Confirmation of dynamical scaling at the percolation threshold. Phys. Rev. Lett. 1983, 51, 527. [Google Scholar] [CrossRef]
- White, S.R.; Barma, M. Field-induced drift and trapping in percolation networks. J. Phys. A 1984, 17, 2995. [Google Scholar] [CrossRef]
- Arkhincheev, V.; Baskin, E. Anomalous diffusion and drift in a comb model of percolation clusters. Sov. Phys. JETP 1991, 73, 161–300. [Google Scholar]
- Méndez, V.; Iomin, A. Comb-like models for transport along spiny dendrites. Chaos Solitons Fractals 2013, 53, 46–51. [Google Scholar] [CrossRef] [Green Version]
- Iomin, A. Subdiffusion on a fractal comb. Phys. Rev. E 2011, 83, 052106. [Google Scholar] [CrossRef] [Green Version]
- Sandev, T.; Schulz, A.; Kantz, H.; Iomin, A. Heterogeneous diffusion in comb and fractal grid structures. Chaos Solitons Fractals 2018, 114, 551–555. [Google Scholar] [CrossRef] [Green Version]
- Tateishi, A.A.; Michels, F.S.; Dos Santos, M.A.F.; Lenzi, E.K.; Ribeiro, H.V. First passage time for a diffusive process under a geometric constraint. J. Stat. Mech. Theory Exp. 2013, 2013, P09017. [Google Scholar] [CrossRef]
- Sandev, T.; Iomin, A.; Kocarev, L. Random search on comb. J. Phys. A 2019, 52, 465001. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Zhang, X. Fractional anomalous diffusion with Cattaneo–Christov flux effects in a comb-like structure. Appl. Math. Model. 2016, 40, 6663–6675. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Sandev, T.; Petreska, I.; Lenzi, E.K. Quenched and annealed disorder mechanisms in comb models with fractional operators. Phys. Rev. E 2020, 101, 022135. [Google Scholar] [CrossRef] [Green Version]
- Sandev, T.; Iomin, A. Finite-velocity diffusion on a comb. EPL 2018, 124, 20005. [Google Scholar] [CrossRef] [Green Version]
- Prudnikov, A.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 4, Direct Laplace Transforms; Gordon and Breach: New York, NY, USA, 1992; Volume 4. [Google Scholar]
- Domazetoski, V.; Masó-Puigdellosas, A.; Sandev, T.; Méndez, V.; Iomin, A.; Kocarev, L. Stochastic resetting on comb-like structures. arXiv 2020, arXiv:2005.11575. [Google Scholar]
- Dos Santos, M.A.F. From continuous-time random walks to controlled-diffusion reaction. J. Stat. Mech. Theory Exp. 2019, 2019, 033214. [Google Scholar] [CrossRef] [Green Version]
- Sokolov, I.M. Solutions of a class of non-Markovian Fokker-Planck equations. Phys. Rev. E 2002, 66, 041101. [Google Scholar] [CrossRef] [Green Version]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A 1997, 30, 7277. [Google Scholar] [CrossRef]
- Sandev, T.; Deng, W.; Xu, P. Models for characterizing the transition among anomalous diffusions with different diffusion exponents. J. Phys. A 2018, 51, 405002. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Zheng, L.; Fan, Y.; Chen, Y.; Liu, F. Comb model for the anomalous diffusion with dual-phase-lag constitutive relation. Commun. Nonlinear Sci. Numer. Simul. 2018, 63, 135–144. [Google Scholar] [CrossRef] [Green Version]
- Liemert, A.; Sandev, T.; Kantz, H. Generalized Langevin equation with tempered memory kernel. Physica A 2017, 466, 356–369. [Google Scholar] [CrossRef]
- Rosiński, J. Tempering stable processes. Stoch. Process. Their Appl. 2007, 117, 677–707. [Google Scholar] [CrossRef] [Green Version]
- Koponen, I. Analytic approach to the problem of convergence of truncated Lévy flights towards the Gaussian stochastic process. Phys. Rev. E 1995, 52, 1197. [Google Scholar] [CrossRef]
- Sibatov, R.T.; Sun, H.G. Tempered fractional equations for quantum transport in mesoscopic one-dimensional systems with fractal disorder. Fractal Fract. 2019, 3, 47. [Google Scholar] [CrossRef] [Green Version]
- Sandev, T.; Iomin, A.; Kantz, H.; Metzler, R.; Chechkin, A. Comb model with slow and ultraslow diffusion. Math. Model. Nat. Phenom. 2016, 11, 18–33. [Google Scholar] [CrossRef]

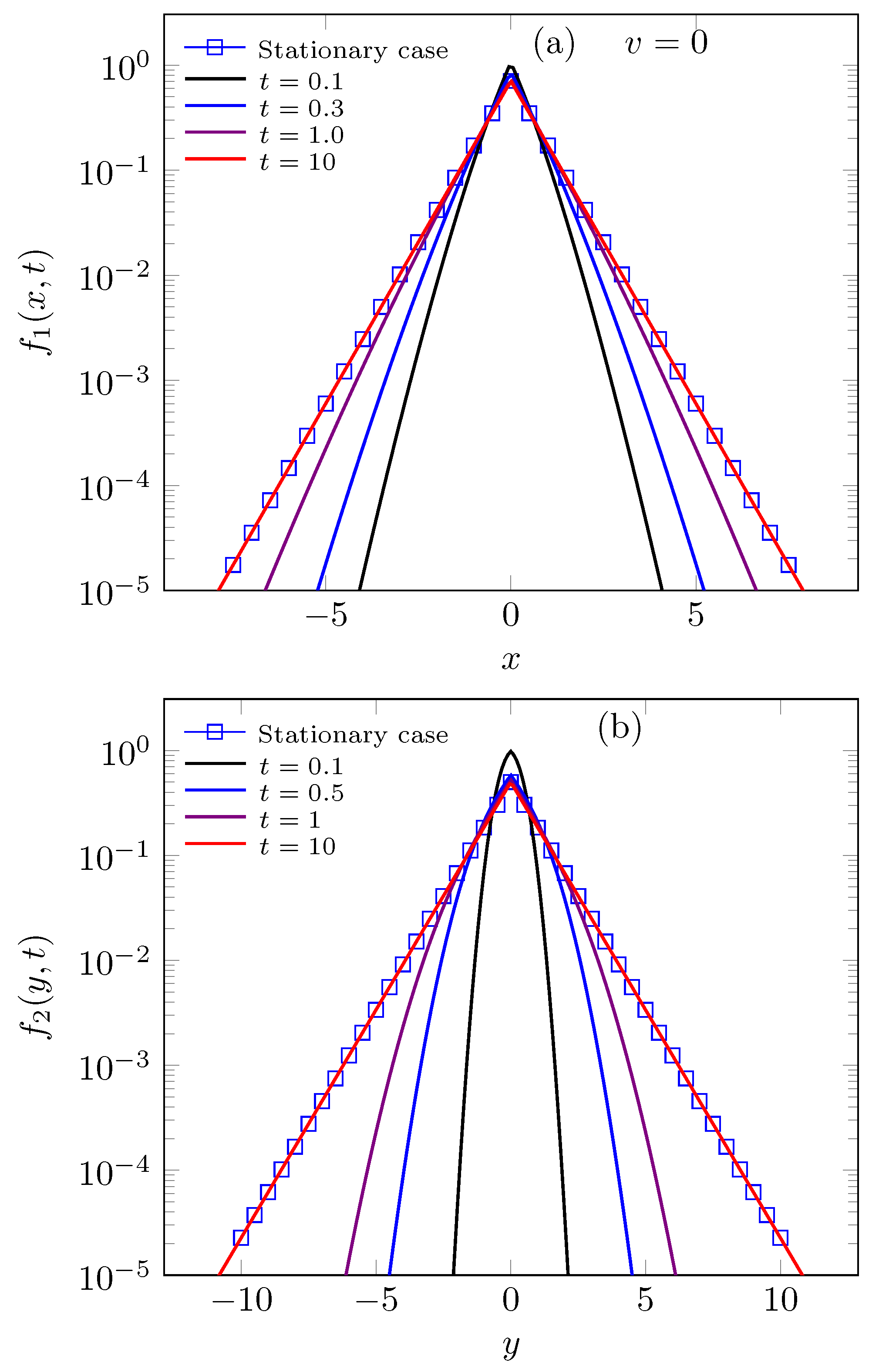
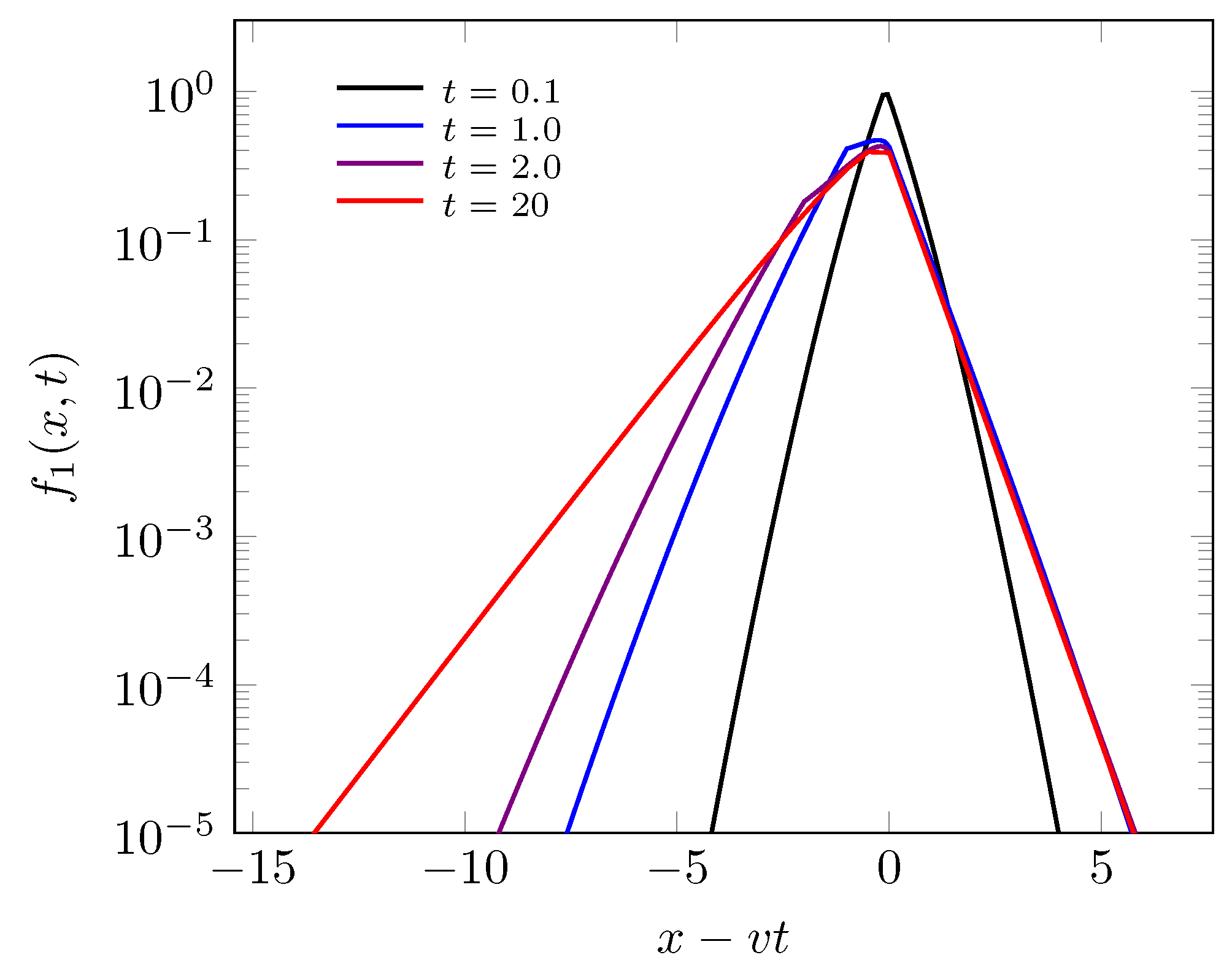
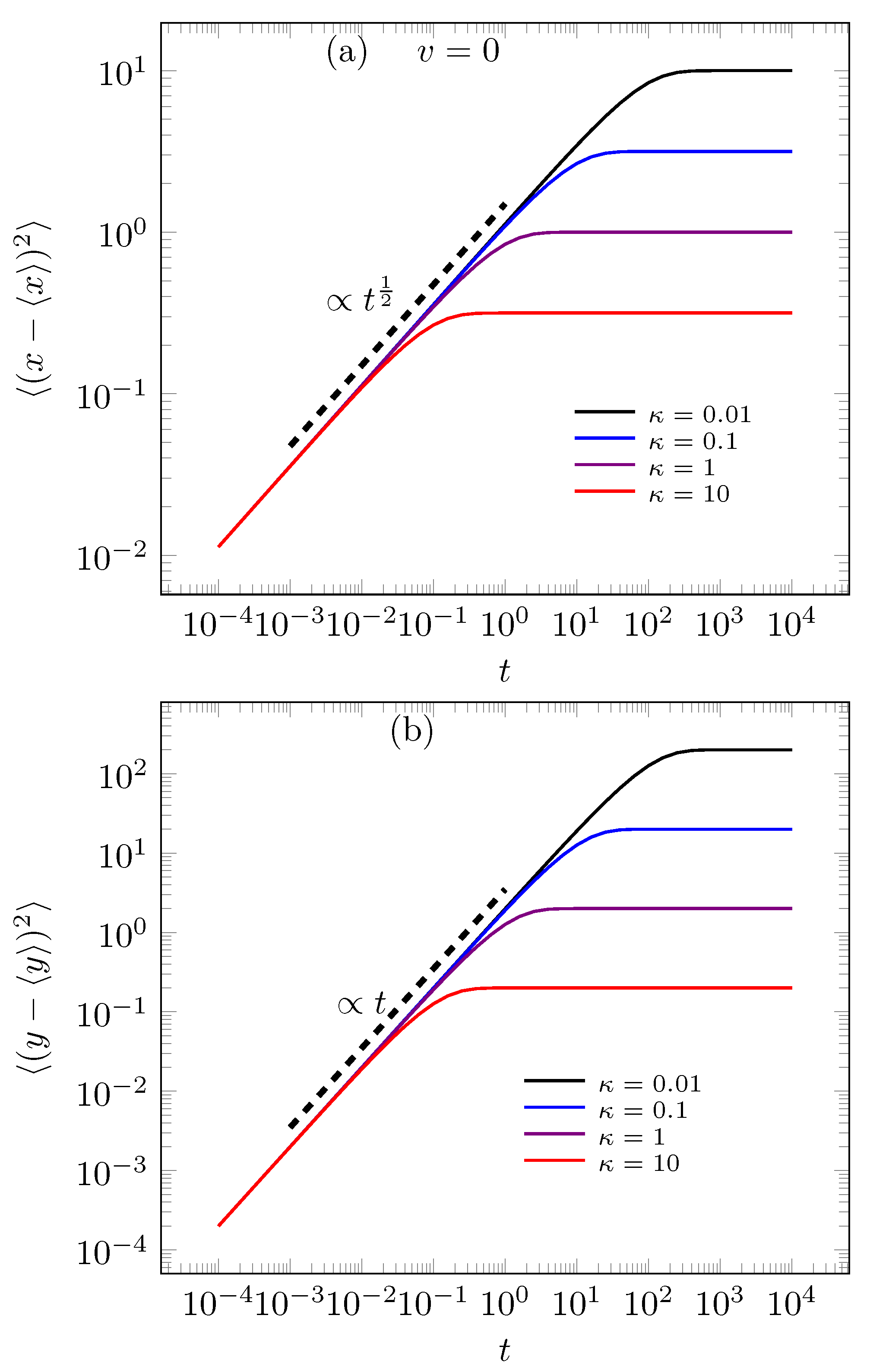
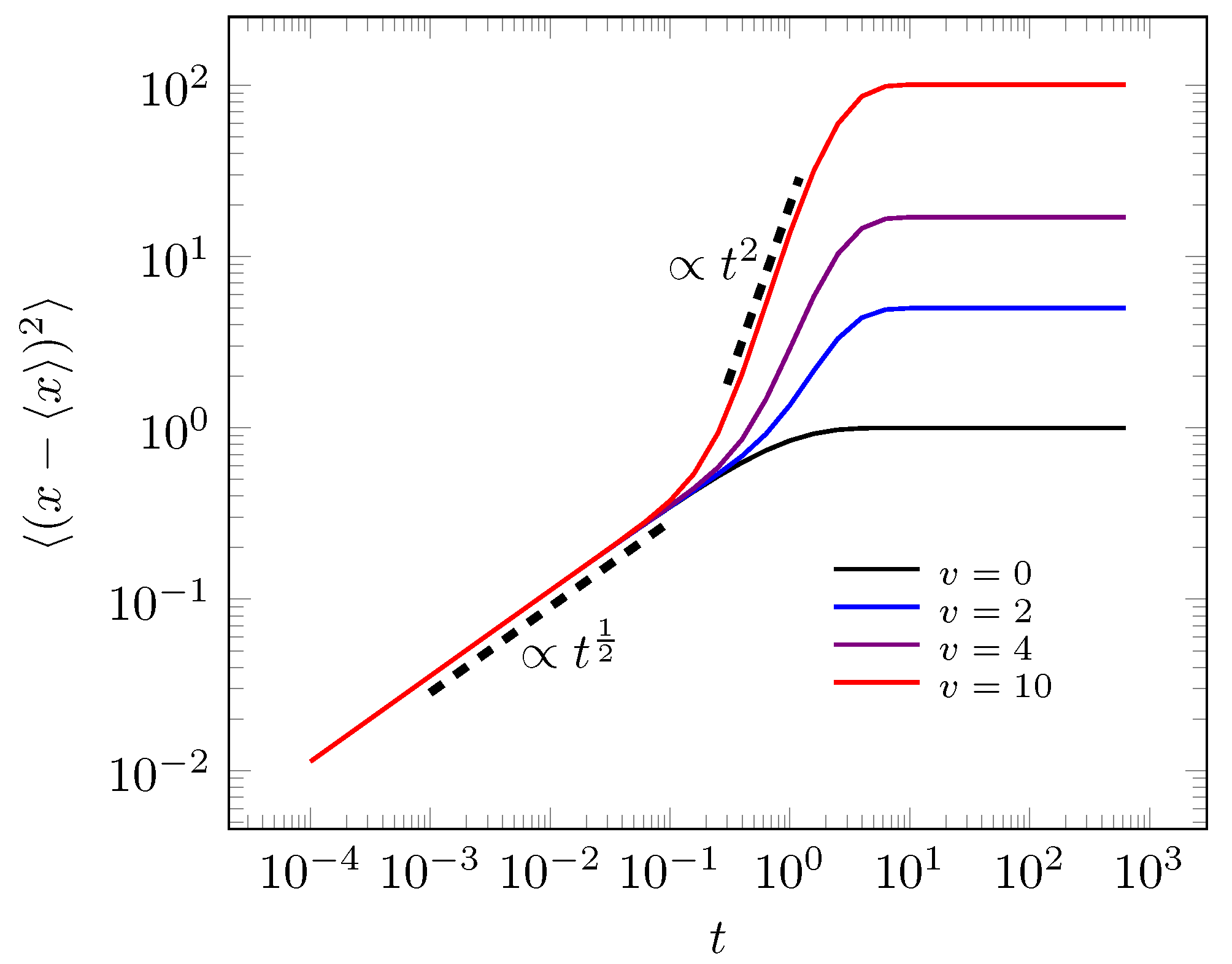



© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonio Faustino dos Santos, M. Comb Model with Non-Static Stochastic Resetting and Anomalous Diffusion. Fractal Fract. 2020, 4, 28. https://doi.org/10.3390/fractalfract4020028
Antonio Faustino dos Santos M. Comb Model with Non-Static Stochastic Resetting and Anomalous Diffusion. Fractal and Fractional. 2020; 4(2):28. https://doi.org/10.3390/fractalfract4020028
Chicago/Turabian StyleAntonio Faustino dos Santos, Maike. 2020. "Comb Model with Non-Static Stochastic Resetting and Anomalous Diffusion" Fractal and Fractional 4, no. 2: 28. https://doi.org/10.3390/fractalfract4020028
APA StyleAntonio Faustino dos Santos, M. (2020). Comb Model with Non-Static Stochastic Resetting and Anomalous Diffusion. Fractal and Fractional, 4(2), 28. https://doi.org/10.3390/fractalfract4020028




