-
 Regarding a Class of Nonlocal BVPs for the General Time-Fractional Diffusion Equation
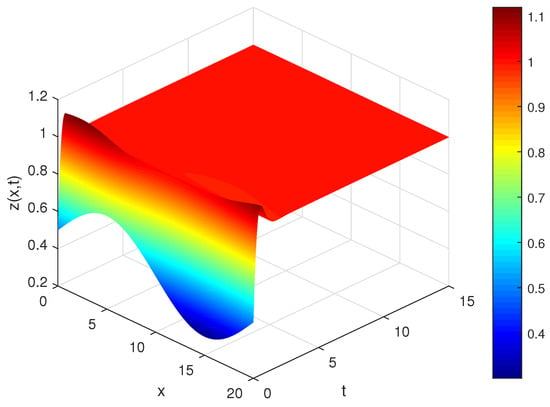
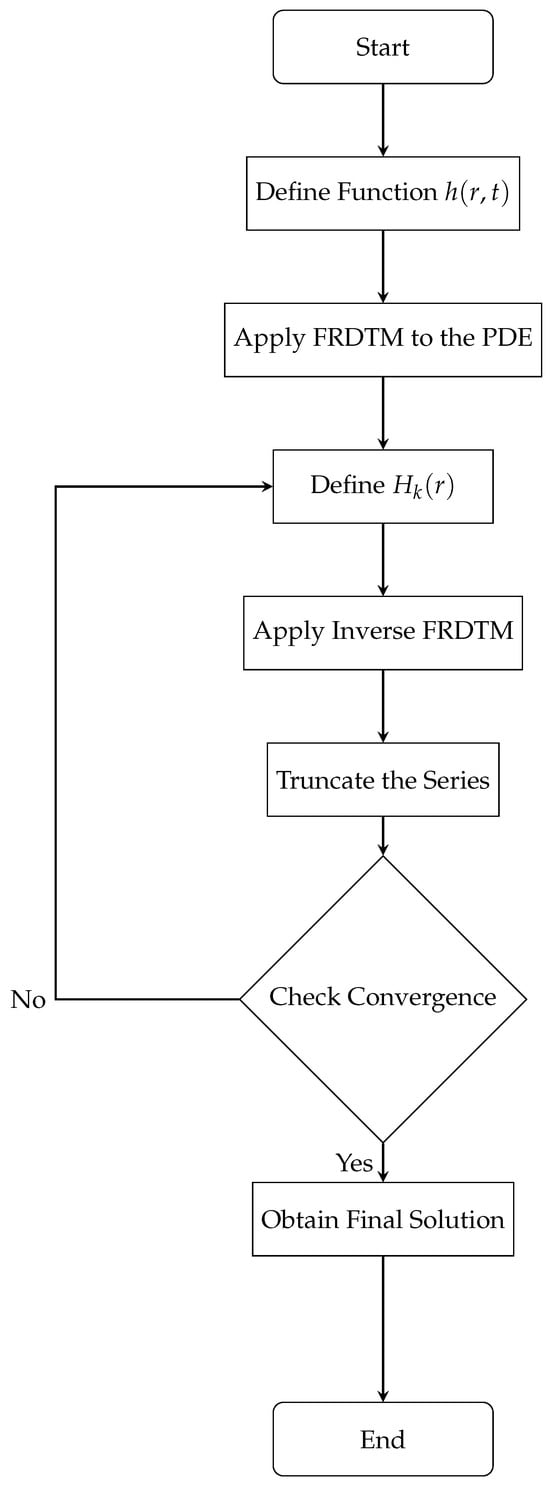
Regarding a Class of Nonlocal BVPs for the General Time-Fractional Diffusion Equation -
 A Sufficient Condition for the Practical Stability of Riemann-Liouville Fractional Nonlinear Systems with Time Delays
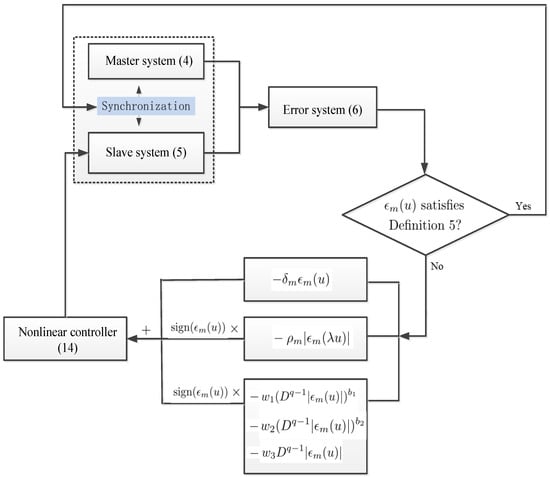
A Sufficient Condition for the Practical Stability of Riemann-Liouville Fractional Nonlinear Systems with Time Delays -
 Existence of Positive Solutions for a Class of Nabla Fractional Difference Equations with Parameter-Dependent Summation Boundary Conditions
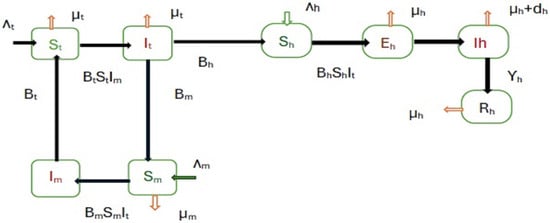
Existence of Positive Solutions for a Class of Nabla Fractional Difference Equations with Parameter-Dependent Summation Boundary Conditions
Journal Description
Fractal and Fractional
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), Inspec, and other databases.
- Journal Rank: JCR - Q1 (Mathematics, Interdisciplinary Applications) / CiteScore - Q1 (Analysis)
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 19.9 days after submission; acceptance to publication is undertaken in 2.7 days (median values for papers published in this journal in the first half of 2025).
- Recognition of Reviewers: reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any MDPI journal, in appreciation of the work done.
- Journal Cluster of Mathematics and Its Applications: AppliedMath, Axioms, Computation, Fractal and Fractional, Geometry, International Journal of Topology, Logics, Mathematics and Symmetry.
Latest Articles
E-Mail Alert
News
MDPI Launches the Michele Parrinello Award for Pioneering Contributions in Computational Physical Science

Topics
Deadline: 31 December 2025
Deadline: 30 May 2026
Deadline: 30 June 2026
Deadline: 31 July 2026
Conferences
Special Issues
Deadline: 10 December 2025
Deadline: 15 December 2025
Deadline: 15 December 2025
Deadline: 20 December 2025