Dispersive Transport Described by the Generalized Fick Law with Different Fractional Operators

Abstract

The approach based on fractional advection–diffusion equations provides an effective and meaningful tool to describe the dispersive transport of charge carriers in disordered semiconductors. A fractional generalization of Fick’s law containing the Riemann–Liouville fractional derivative is related to the well-known fractional Fokker–Planck equation, and it is consistent with the universal characteristics of dispersive transport observed in the time-of-flight experiment (ToF). In the present paper, we consider the generalized Fick laws containing other forms of fractional time operators with singular and non-singular kernels and find out features of ToF transient currents that can indicate the presence of such fractional dynamics. Solutions of the corresponding fractional Fokker–Planck equations are expressed through solutions of integer-order equation in terms of an integral with the subordinating function. This representation is used to calculate the ToF transient current curves. The physical reasons leading to the considered fractional generalizations are elucidated and discussed.

1. Introduction

Fractional advection–diffusion equations provide effective and meaningful approach to description of dispersive charge carrier transport in disordered semiconductors [1,2,3,4,5]. The fractional generalization of the Fokker–Planck (FFP) equation was obtained using the Continuous Time Random Walk (CTRW) model [2,6]. Significantly earlier, in 1975, the CTRW model successfully explained the basic laws of dispersive transport in amorphous semiconductors observed by the ToF method [7]. The FFP equation is related to the fractional generalization of Fick’s law [8]. The mentioned works operate with time fractional derivatives of the Riemann–Liouville and Caputo type. An extended system of fractional equations for dispersive transport was obtained later, and it takes into account recombination, bipolar diffusion for various transport mechanisms, and densities of localized states [4,5,9]. Waiting time distribution for localized carriers plays a central role in the statistical models of dispersive transport [10].

The time-of-flight (ToF) experiment is an important method for studying electron transfer in low-conductivity semiconductors. The statistical theory of dispersive transport was developed precisely from the analysis of ToF experimental data for amorphous semiconductors [7,11]. The ToF method is still widely used. Particularly, it has been recently utilized to study the features of charge transport in perovskite solar cells [12] and organic bulk heterojunction cells [13]. In the ToF method, the photocurrent response is studied after the injection of nonequilibrium charge carriers by a short laser pulse from the side of the transparent electrode. Typically, a strong electric field (>${10}^5$ V/cm) close to the dielectric breakdown conditions is applied to the sample in order to eliminate the effects of space charge and reduce the contribution of carrier diffusion to the observed response. The ToF method is commonly used in sandwich geometry, which may not be suitable for some nanostructured systems. Figure 1 shows schematic of the ToF experiment in coplanar geometry for studying charge carrier transport in thin films. This geometry is more appropriate to measure transient currents in organic nanocomposites, bulk heterojunctions, and perovskite solar cells. The correct interpretation of the ToF measurements in inhomogeneous structures remains relevant. Different physical features influence the observed kinetics. Among them are the density of localized states, morphology of the percolation regions, the presence of defective layers, inhomogeneity of the electric field, recombination, etc. [14,15,16,17].

The transient current curves $I(t)$ measured by ToF method for amorphous semiconductors are often characterized by similarity of the shape in the $logI-logt$ plot [7]. These curves essentially differ from the step-wise plot typical for the normal drift-diffusion. For dispersive transport, current decays as power laws: $I(t)\propto t^{-1+\alpha }$ for $t<t_T$, and $I(t)\propto t^{-1-\alpha }$ for $t>t_T$. The dispersion parameter $\alpha \in (0,1)$ corresponds to the order of fractional time Riemann–Liouville derivative in the FFP equation (see [2]). In Ref. [18], it is shown that the universality of the transient current curves $I(t)$ and the power-law dependence of the transient time $t_T$ on the sample thickness L, observed in the ToF experiment, unambiguously indicate the fractional-differential kinetics of dispersive transport of nonequilibrium charge carriers.

Often the picture differs from both the stepwise one, characteristic of normal transport, and from the universal one, which is characteristic of dispersive transport in amorphous semiconductors. In this paper, we consider how the choice of fractional operator in fractional Fick’s law is related to the observed transient current curves. Additionally, we try to identify the physical reasons leading to the fractional generalizations under consideration. The fractional generalizations that are used in this work were motivated by the studies of anomalous diffusion reported in Refs. [19,20,21,22,23,24]. Tateishi et al. [19] studied fractional diffusion equation with other forms of fractional time operators instead of the Riemann–Liouville derivative. They obtained the expressions for kernels and for waiting time distributions in case of anomalous diffusion described by equation with the Caputo–Fabrizio and Atangana–Baleanu operators. They considered anomalous diffusion without external forces in an unbounded region. Sene and Abdelmalek [23], dos Santos and Gomez [24] considered generalizations of the diffusion equation in terms of a non-singular fractional temporal operator. Note that representations of fractional diffusion equations with the indicated operators in [19] and in [23,24] are different. We study dispersive transport in a sample of finite width, and try to find out features of ToF transient currents that can indicate the generalized fractional dynamics. Solutions of the corresponding FFP equations are presented in terms of an integral with the subordinating function, and used to calculate the ToF characteristics. The physical reasons leading to the considered fractional generalizations are discussed.

2. Fractional Fokker-Planck Equation

Anomalous diffusion in complex media can be caused by different specific mechanisms [25]. The dispersive transport of nonequilibrium charge carriers is observed in many disordered materials differing in their microscopic structure, and can be caused by multiple trapping into the band tail states, by hopping via spatially distributed localized states, or by percolation over cluster with dead ends. The statistical features of anomalous diffusion are often described within the CTRW model. Considering CTRW with space dependent jump probabilities, Barkai et al. [2] derived a time-fractional Fokker–Planck equation for the case, when the mean waiting time diverges. FFP equation describes anomalous diffusion in an external force field; it is derived in the form [6,26],

$$\frac{\partial p(x,t)}{\partial t}={}_0{\mathsf{D}}_t^{1-\alpha }K\frac{\partial }{\partial x}\left[\frac{\partial p(x,t)}{\partial x}+\frac{p(x,t)}{kT}\frac{\partial V}{\partial x}\right],$$

(1)

where $p(x,t)$ is particle concentration, $V(x)$ is an external potential, K is a generalized diffusion coefficient, and $kT$ is the thermal energy.

Here,

$${}_0{\mathsf{D}}_t^{1-\alpha }p(x,t)=\frac{1}{\Gamma (\alpha )}\frac{\partial }{\partial t}{\int }_0^t\frac{p(x,\tau )}{{(t-\tau )}^{1-\alpha }}d\tau ,0<\alpha \le 1,$$

(2)

is the Riemann–Liouville derivative of fractional order $1-\alpha$ [27]. Fundamental solutions to Equation (1) can be found in [26,28,29].

We consider the following generalization of the Fokker–Planck equation

$$\frac{\partial }{\partial t}p(x,t)=\frac{\partial }{\partial t}\underset{0}{\overset{t}{\int }}d{t}^{\prime }K(t-t^{\prime }){\mathcal{L}}_{\mathrm{FP}}p(x,t^{\prime }).$$

(3)

Here, $p(x,t)$ is the concentration of non-equilibrium charge carriers, ${\mathcal{L}}_{\mathrm{FP}}$ denotes the following spatial (time-independent) operator

$${\mathcal{L}}_{\mathrm{FP}}p(x,t)=\frac{\partial }{\partial x}\left[D(x)\frac{\partial p(x,t)}{\partial x}-A(x)p(x,t)\right],$$

(4)

where $D(x)$ and $A(x)$ are the anomalous diffusion and advection coefficients.

Kernel $K(t)$ will be specified below, it will be related to certain types of fractional operators. To represent this generalization in the form similar to the known fractional Fokker–Planck equation [6], we rewrite it, as follows

$$\frac{\partial }{\partial t}p(x,t)={\mathcal{D}}_t^{1-\alpha }{\mathcal{L}}_{\mathrm{FP}}p(x,t),$$

(5)

where integro-differential operator

$${\mathcal{D}}_t^{1-\alpha }p(x,t)=\frac{\partial }{\partial t}{\int }_0^{t}K(t-t^{\prime })p(x,t^{\prime })d{t}^{\prime }$$

(6)

will correspond to a certain type of fractional derivative of order $1-\alpha$ with $\alpha \in (0,1]$. Further, we consider four types of time fractional operators ${\mathcal{D}}_t^{1-\alpha }$ (6). To define ${\mathcal{D}}_t^{1-\alpha }$, we need to choose certain type of integral kernel in (6). The names of these time fractional operators, corresponding memory kernels, and their Laplace transforms are listed below.

• Riemann–Liouville derivative

  $$K(t)=\frac{t^{\alpha -1}}{\Gamma (\alpha )},{\left[\tilde{K}\left(s\right)\right]}^{-1}=s^{\alpha }.$$

  (7)
• Tempered fractional operator

  $$K(t)=e^{-\gamma t}{t}^{\alpha -1}{E}_{\alpha ,\alpha }\left({\left(\gamma t\right)}^{\alpha }\right),{\left[\tilde{K}\left(s\right)\right]}^{-1}={(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }.$$

  (8)
• Caputo–Fabrizio operator

  $$K(t)=b_{\alpha }exp\left(-t(1-\alpha )/\alpha \right),{\left[\tilde{K}\left(s\right)\right]}^{-1}=b_{\alpha }^{-1}\left[s+(1-\alpha )/\alpha \right].$$

  (9)
• Atangana–Baleanu operator

  $$K(t)=b_{\alpha }{E}_{1-\alpha }\left(-t^{1-\alpha }(1-\alpha )/\alpha \right),{\left[\tilde{K}\left(s\right)\right]}^{-1}=b_{\alpha }^{-1}\left[s+s^{\alpha }(1-\alpha )/\alpha \right].$$

  (10)

Here $0<\alpha \le 1$ is a fractional order corresponding to the dispersion parameter, $\gamma$ is a truncation parameter, $b_{\alpha }$ is a normalization constant, $E_{\alpha }(t)$ and $E_{\alpha ,\beta }(t)$ are one-parameter and two-parameter Mittag-Leffler functions, respectively.

When $\alpha =1$, operator ${\mathcal{D}}_t^{1-\alpha }$ becomes the identity operator, and we deal with the standard Fick law and Fokker-Planck equation. Note that, in Ref. [19], the authors use notation ${\mathcal{F}}_t^{\alpha }$, and that operator turns to the identity operator, when $\alpha \to 0$. The authors of [19] do not meet contradictions because the main numerical results in [19] are presented for the case $\alpha =1/2$.

From the continuity equation and Equation (5), one can write the expression for flux

$$j(x,t)=-{\mathcal{D}}_t^{1-\alpha }\left[D\frac{\partial p(x,t)}{\partial x}-A(x)p(x,t)\right].$$

(11)

This is a generalized fractional Fick law (FFL). For indicated cases of fractional operators we distinguish FFL with the Riemann-Liouville operator (RL-FFL, case 1), the truncated operator (T-FFL, case 2), the Caputo–Fabrizio operator (CF-FFL, case 3), and Atangana–Baleanu operator (AB-FFL, case 4).

The solution of the FFP equation with time-independent operator ${\mathcal{L}}_{\mathrm{FP}}$ can be written in terms of an integral with the subordinating function

$$p(x,t)={\int }_0^{\infty }\rho (x,\tau )q(\tau ,t)d\tau .$$

(12)

Here, $\rho (x,t)$ is a solution of the standard Fokker-Planck equation (without operator ${\mathcal{D}}_t^{1-\alpha }$) with the same initial condition. In many cases, $\tau$ can be considered as an operational time that is defined by a certain stochastic process $T_t$. Laplace transform of function $q(\tau ,t)$ is of the form

$$\tilde{q}(\tau ,s)=\frac{1}{s\tilde{K}(s)}exp\left(-\frac{\tau }{\tilde{K}(s)}\right).$$

Let us show that solution (12) satisfies the generalized Fokker–Planck equation. The Laplace image of function (12) is

$$\tilde{p}(x,s)={\int }_0^{\infty }\rho (x,\tau )\tilde{q}(\tau ,s)d\tau ={\int }_0^{\infty }\rho (x,\tau )\frac{e^{-\tau /\tilde{K}(s)}}{s\tilde{K}(s)}d\tau =\frac{1}{s\tilde{K}(s)}\tilde{\rho }\left(x,{\left[\tilde{K}(s)\right]}^{-1}\right).$$

(13)

Substituting it into the Laplace transformation of Equation (5) with time-independent operator ${\mathcal{L}}_{\mathrm{FP}}$,

$$s\tilde{p}(x,s)-p(x,0)=s\tilde{K}(s){\mathcal{L}}_{\mathrm{FP}}p(x,s),$$

(14)

we arrive at the following relation

$${\left[\tilde{K}(s)\right]}^{-1}\tilde{\rho }\left(x,{\left[\tilde{K}(s)\right]}^{-1}\right)-p(x,0)={\mathcal{L}}_{\mathrm{FP}}\tilde{\rho }\left(x,{\left[\tilde{K}(s)\right]}^{-1}\right),$$

which, after change of variable $u=1/\tilde{K}(s)$, represents the Laplace transform of the ordinary Fokker–Planck equation:

$$u\tilde{\rho }(x,u)-\rho (x,0)={\mathcal{L}}_{\mathrm{FP}}\tilde{\rho }(x,u),\rho (x,0)=p(x,0).$$

3. Physical Interpretations with the Multiple Trapping Model

Further, we will use the multiple trapping model [3,11,14] to interpret the resulting fractional equations. Note, however, that the discussed fractional dynamics can be a consequence of the hopping mechanism, diffusion in a percolation cluster, and other mechanisms. The multiple trapping model considers the transport of delocalized charge carriers controlled by trapping-detrapping events in localized states with distributed energy.

Assume that, for delocalized carriers in the absence of traps, the standard Fokker–Planck equation is valid. In the case of the multiple trapping, we have

$$\frac{\partial p_{\mathrm{d}}(x,t)}{\partial t}+\frac{\partial p_{\mathrm{tr}}(x,t)}{\partial t}={\mathcal{L}}_{\mathrm{FP}},\mathrm{d}{p}_{\mathrm{d}}(x,t).$$

(15)

The latter equation should be supplemented by the trapping and release equation

$$\frac{\partial p_{\mathrm{tr}}(x,t)}{\partial t}=\lambda p_{\mathrm{d}}(x,t)-\nu p_{\mathrm{tr}}(x,t),$$

(16)

where $p_{\mathrm{d}}$ is the delocalized carrier density, $p_{\mathrm{tr}}$ is the trapped carrier density, $\lambda$ and $\nu$ are the trapping and delocalization rates. From the latter equation, the relationship follows

$$p_{\mathrm{tr}}(x,t)=\lambda {\int }_0^t{e}^{-\nu (t-\tau )}{p}_{\mathrm{d}}(x,\tau )d\tau .$$

(17)

Delocalization rate $\nu$ is defined by activation energy $\epsilon$ according to the Arrhenius equation

$$\nu ={\nu }_0{e}^{-\epsilon /kT},$$

where ${\nu }_0$ is a constant prefactor, and $kT$ is the Boltzmann temperature. After averaging over random activation energy, the relationship (17) turns into

$$p_{\mathrm{tr}}(x,t)=\lambda {\int }_0^{t}Q(t-\tau )p_{\mathrm{d}}(x,\tau )d\tau ,$$

(18)

where kernel Q is determined via the distribution of localized state energy,

$$Q(t)=\underset{0}{\overset{\infty }{\int }}exp\left(-{\nu }_{0}t{e}^{-\epsilon /kT}\right)\rho (\epsilon )d\epsilon .$$

For exponential distribution of localized state energy

$$\rho (\epsilon )=\frac{1}{{\epsilon }_0}exp\left(-\frac{\epsilon }{{\epsilon }_0}\right),\epsilon >0,$$

(19)

after change of variables $\xi ={\nu }_{0}t{e}^{-\epsilon /kT}$, we obtain the power law kernel

$$Q(t)=\frac{kT}{{\epsilon }_0{({\nu }_{0}t)}^{kT/{\epsilon }_0}}\underset{0}{\overset{{\nu }_{0}t}{\int }}{e}^{-\xi }{\xi }^{kT/{\epsilon }_0-1}d\xi \sim \frac{C_{\alpha }}{\Gamma (1-\alpha )}{t}^{-\alpha },t\to \infty .$$

Here, fractional index and constant $C_{\alpha }$ are defined as

$$\alpha =\frac{kT}{{\epsilon }_0},C_{\alpha }=\frac{\pi \alpha }{sin(\pi \alpha )}{\nu }_0^{-\alpha }.$$

Consequently, we have the following relationship

$$p_{\mathrm{tr}}(x,t)=\frac{\lambda C_{\alpha }}{\Gamma (1-\alpha )}\underset{0}{\overset{t}{\int }}\frac{p_{\mathrm{d}}(x,\tau )}{{(t-\tau )}^{\alpha }}d\tau =\lambda C_{\alpha }{}_0{I}_t^{1-\alpha }{p}_{\mathrm{d}}(x,\tau ).$$

This expression leads to the fractional advection–diffusion equation

$$\frac{\partial p_{\mathrm{d}}(x,t)}{\partial t}+\lambda C_{\alpha }{}_0{D}_t^{\alpha }{p}_{\mathrm{d}}(x,t)={\mathcal{L}}_{\mathrm{FP}},\mathrm{d}{p}_{\mathrm{d}}(x,t),0<\alpha \le 1.$$

(20)

When $\alpha <1$, for $t\gg {(\lambda C_{\alpha })}^{1/(1-\alpha )}$, $p(x,t)\approx p_{\mathrm{tr}}(x,t)$, the term with the first-order derivative can be neglected, and we have,

$$\frac{\partial p(x,t)}{\partial t}={}_0{D}_t^{1-\alpha }{\mathcal{L}}_{\mathrm{FP}}p(x,t)+\delta (t)p(x,0),$$

(21)

or

$${}_0{D}_t^{\alpha }p(x,t)={\mathcal{L}}_{\mathrm{FP}}p(x,t)+\frac{t^{-\alpha }}{\Gamma (1-\alpha )}p(x,0),$$

(22)

where ${\mathcal{L}}_{\mathrm{FP}}={\mathcal{L}}_{\mathrm{FP}},\mathrm{d}/(\lambda C_{\alpha })$. For other (non-exponential) distribution of localized state energy, other forms of kernel $Q(t)$ can be obtained.

Consider FFP equations that correspond to the generalized Fick law with different fractional time derivative operators and discuss the physical meaning of these equations within the multiple trapping model of dispersive transport. Note that names listed in the previous section for fractional derivative operators correspond to ${\mathcal{D}}_t^{1-\alpha }$ that arises in the fractional Fick law (11). Derivatives arising in FFP-equation corresponding to inverse transformation of expression

$${\left[\tilde{K}(s)\right]}^{-1}\left[\tilde{p}(x,s)-\frac{p(x,0)}{s}\right]={\mathcal{L}}_{\mathrm{FP}}\tilde{p}(x,s)$$

(23)

can be of different types.

• For the case of the generalized Fick law containing the Riemann–Liouville derivative (RL-FFL), we have the following FFP-equation,

  $$s^{\alpha }\tilde{p}(x,s)={\mathcal{L}}_{\mathrm{FP}}\tilde{p}(x,s)+s^{\alpha -1}\delta (x)\to {}_0{D}_t^{\alpha }p(x,t)={\mathcal{L}}_{\mathrm{FP}}p(x,t)+\frac{t^{-\alpha }}{\Gamma (1-\alpha )}\delta (x).$$

  (24)
  This case is well known (see [2,4,6,8]). The presence of fractional time derivative is related to localization events that are characterized by waiting times distributed according to fractional exponential law (with ‘heavy’ tails). The random number of delocalization events at time t is described by the fractional Poisson process. Features of physical mechanisms leading to such waiting time distributions are discussed in many works (see references in [4]). Among popular models leading to such kinetics are the multiple trapping into the band tail states, hopping via spatially distributed localized states, and comb model of percolation over cluster with dead ends (see [21,22], and references therein). Equation (24) is equivalent to (22) with $p(x,0)=\delta (x)$ for the ToF method.
• In the second case, the Fick law with tempered fractional operator (T-FFL) leads to the following equation

  $$\left[{(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }\right]\left[\tilde{p}(x,s)-\frac{\delta (x)}{s}\right]={\mathcal{L}}_{\mathrm{FP}}\tilde{p}(x,s)\to {}_0{D}_t^{\alpha ,\gamma }[p(x,t)-\delta (x)]={\mathcal{L}}_{\mathrm{FP}}p(x,t).$$
  Here, ${}_0{D}_t^{\alpha ,\gamma }$ is a tempered fractional derivative defined as

  $${}_0{D}_t^{\alpha ,\gamma }p(x,t)={\mathrm{e}}^{-\gamma t}{}_0{D}_t^{\alpha }{\mathrm{e}}^{\gamma t}p(x,t)-{\gamma }^{\alpha }p(x,t).$$
  This case can be derived from the CTRW model, when tempered fractional exponential function is used for waiting time density (see [21,22,30,31]). In terms of the multiple trapping model, the tempered power law can arise due to special case of localized state energy distribution [20], particularly due to the truncation of exponential density of states $\rho (\epsilon )$.
• For the Fick law with the Caputo–Fabrizio operator (CF-FFL), we arrive at the integer-order Fokker–Planck equation containing recombination and generation terms,

  $$s\tilde{p}(x,s)+\frac{1-\alpha }{\alpha }\tilde{p}(x,s)=b_{\alpha }{\mathcal{L}}_{\mathrm{FP}}\tilde{p}(x,s)+\delta (x)+\frac{1-\alpha }{\alpha }\frac{\delta (x)}{s},$$

  $$\frac{\partial p(x,t)}{\partial t}=b_{\alpha }{\mathcal{L}}_{\mathrm{FP}}p(x,t)-\frac{1-\alpha }{\alpha }p(x,t)+\frac{1-\alpha }{\alpha }\delta (x)+\delta (x)\delta (t).$$

  (25)
  The case of the Caputo–Fabrizio operator is interpreted in [19] in terms of diffusive process with stochastic resetting. Interpreting Equation (25), we see that it is an ordinary Fokker–Planck equation with the first-order time derivative, the recombination and constant generation terms. However, the recombination and generation of charge carriers are balanced in a special way, which really leads to an effect that can be associated with a stochastic resetting. However, such a balance in the ToF experiment requires special tuning. Additionally, it seems to us that there is no need to use to the fractional Fick law with the Caputo–Fabrizio derivative and it is sufficient to use the classical equation with more general generation and recombination terms.
• For the Fick law with the Atangana–Baleanu operator (AB-FFL), we arrive at the simple distributed-order FFP equation. From the Laplace transform of the expression

  $$s\tilde{p}(x,s)+\frac{1-\alpha }{\alpha }{s}^{\alpha }\tilde{p}(x,s)=b_{\alpha }{\mathcal{L}}_{\mathrm{FP}}\tilde{p}(x,s)+\delta (x)+\frac{1-\alpha }{\alpha }{s}^{\alpha -1}\delta (x),$$

  we obtain the following equation

  $$\frac{\partial p(x,t)}{\partial t}+\frac{1-\alpha }{\alpha }{}_0{D}_t^{\alpha }p(x,t)=b_{\alpha }{\mathcal{L}}_{\mathrm{FP}}p(x,t)+\delta (t)\delta (x)+\frac{1-\alpha }{\alpha }\frac{t^{-\alpha }}{\Gamma (1-\alpha )}\delta (x).$$

  (26)
  The equation similar to this is obtained in [9] (see Equation (19) and solution (14) in [9]). It is related to the multiple trapping model with a separation of carriers into trapped and delocalized groups (see Equation (20)). On the other hand, Equation (26) can be considered as a simple example of FFP equation for a mixture of waiting time distributions [4].

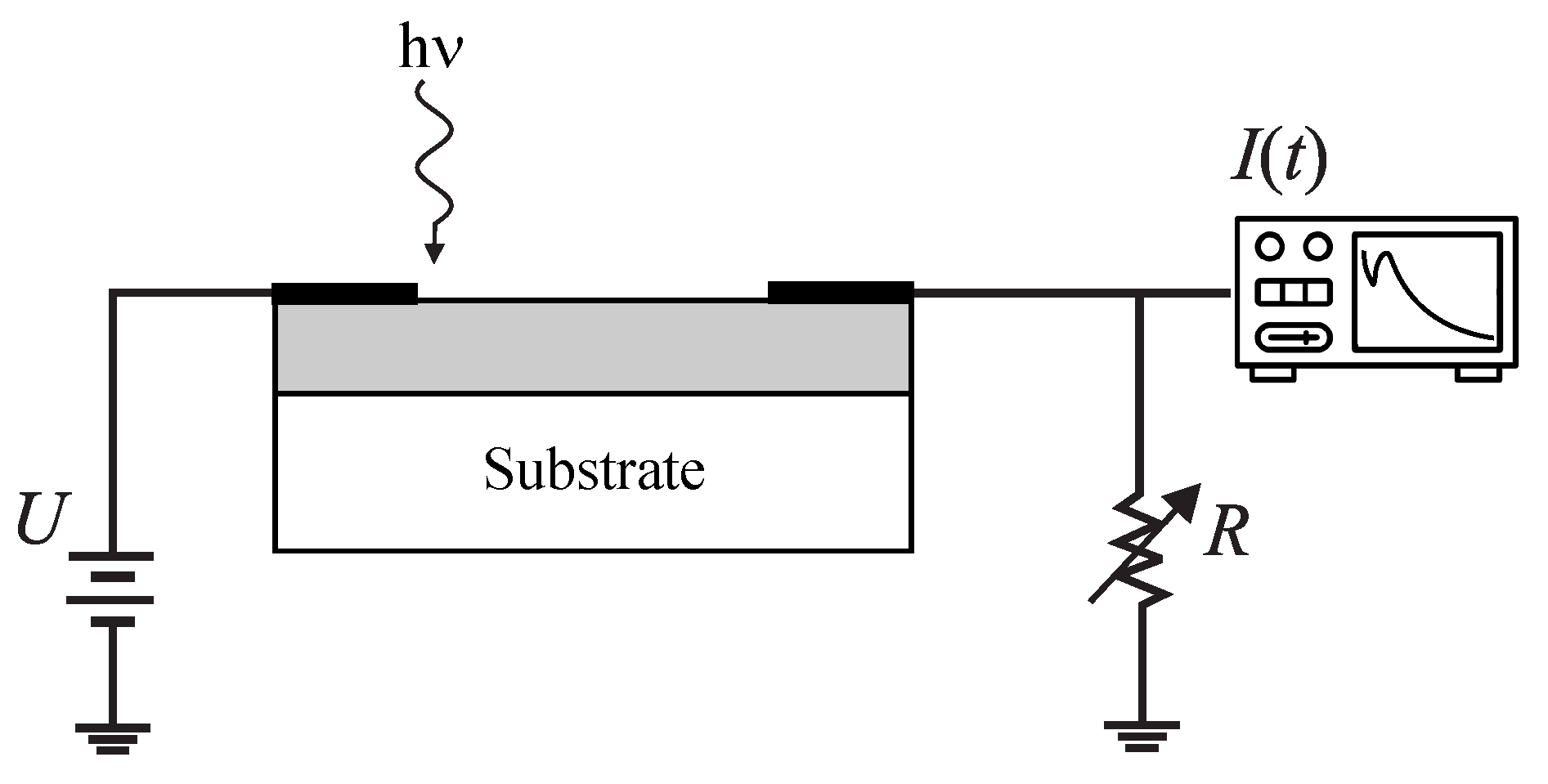
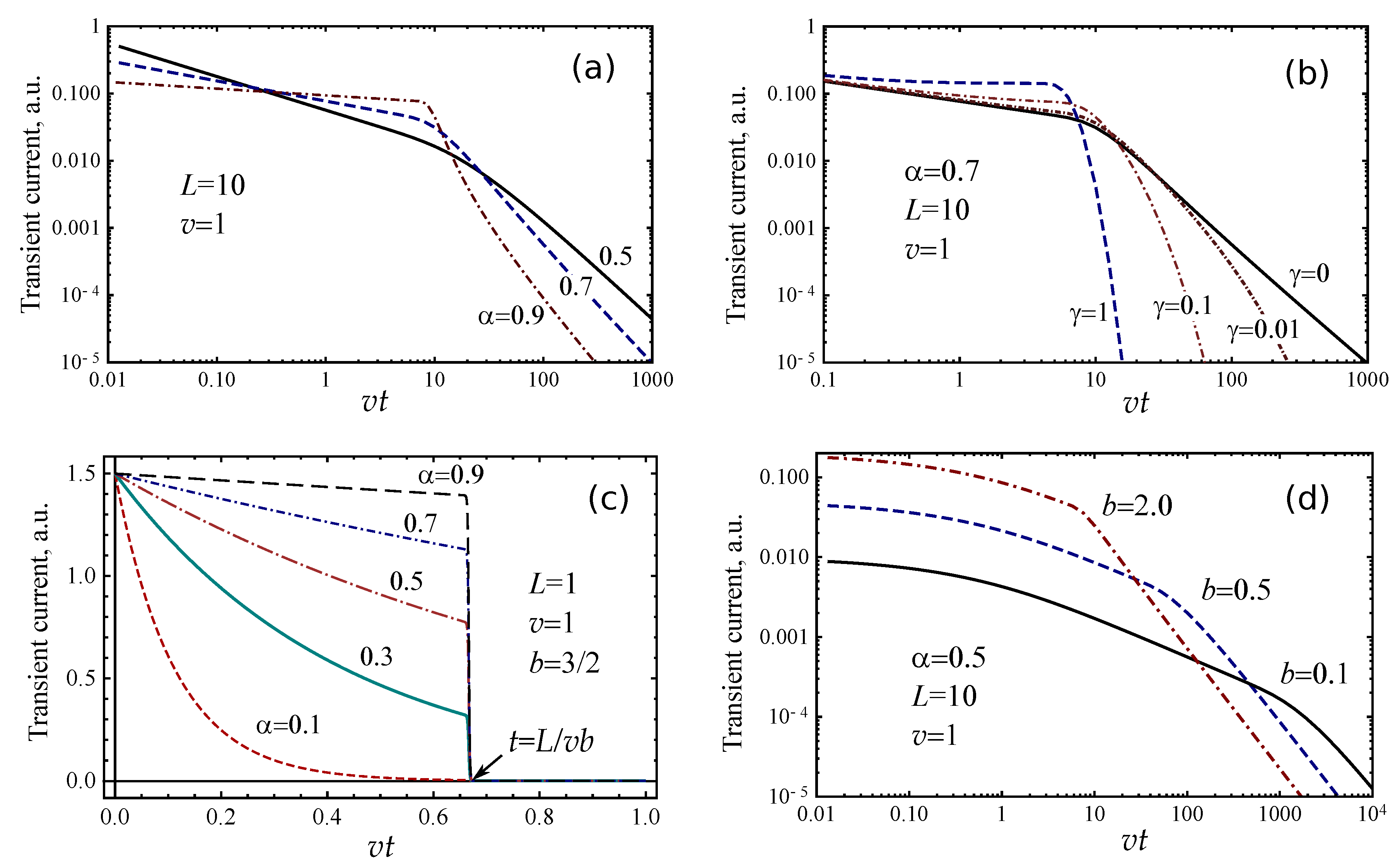
4. Transient Current of the Time-of-Flight Method

Using the presented solutions, it is possible to study different characteristics of anomalous diffusion described by Equation (5). Tateishi et al. [19] calculated mean square displacements and found crossovers between ordinary and confined diffusion, and between usual and subdiffusion. Here, we calculate the transient current in the ToF experiment to find out features indicating the generalized fractional dynamics.

In the ToF method, nonequilibrium charge carriers are generated near the electrode by a short laser pulse. Typically, a strong electric field is applied to the sample in order to eliminate the effects of space charge and reduce the contribution of carrier diffusion to the observed response. The transient current in the ToF method is a displacement current that can be found via the following formula

$$I(t)=\frac{1}{L}{\int }_0^{L}j(x,t)dx=\frac{eN}{L}\frac{d}{dt}{\int }_0^L(x-L)p(x,t)dx,$$

(27)

where L is a distance between electrodes.

Substituting distribution (13) into the Laplace transform of the latter expression

$$\tilde{I}(s)=\frac{eN}{L}s{\int }_0^L(x-L)\tilde{p}(x,s)dx-q_0;q_0=\frac{eN}{L}{\int }_0^L(x-L)p(x,0)dx$$

we arrive at the following

$$\tilde{I}(s)=\frac{eN}{L}s{\int }_0^{L}dx(x-L){\int }_0^{\infty }d\tau \rho (x,\tau )\frac{e^{-\tau /\tilde{K}(s)}}{s\tilde{K}(s)}-q_0$$

$$=\frac{eN}{L}\underset{0}{\overset{L}{\int }}dx(x-L)\left[{\left\{-\rho (x,\tau )e^{-\tau /\tilde{K}(s)}\right\}}_{\tau \to 0}^{\tau \to \infty }+\underset{0}{\overset{\infty }{\int }}\frac{\partial \rho (x,\tau )}{\partial \tau }{e}^{-\tau /\tilde{K}(s)}d\tau \right]-q_0$$

$$=\underset{0}{\overset{\infty }{\int }}d\tau e^{-\tau /\tilde{K}(s)}\left[\frac{eN}{L}\frac{\partial }{\partial \tau }\underset{0}{\overset{L}{\int }}dx(x-L)\rho (x,\tau )\right]=\underset{0}{\overset{\infty }{\int }}d\tau e^{-\tau /\tilde{K}(s)}{I}_{\mathrm{NT}}(\tau )={\tilde{I}}_{\mathrm{NT}}\left[{\left(\tilde{K}(s)\right)}^{-1}\right],$$

(28)

where $I_{\mathrm{NT}}(t)$ is a transient current for normal transport, which can be found by solving the standard Fokker–Planck equation, ${\tilde{I}}_{\mathrm{NT}}(s)$ is its Laplace transform.

The function $w(t,\tau )$ that is defined by its Laplace transform $e^{-\tau /\tilde{K}(s)}$ is related to $q(\tau ,t)$ by the following relation:

$$q(\tau ,t)=-\frac{\partial }{\partial \tau }{\int }_0^{t}w(t,\tau )dt,\tilde{w}(s,\tau )=e^{-\tau /\tilde{K}(s)}.$$

(29)

Further, to identify the main features of transient currents for indicated cases of fractional operators, we only consider one-sided motion. Under conditions of the time-of-flight experiment, assuming homogeneous strong electric field inside the sample ($F=\mathrm{const}$), one can neglect by influence of diffusion term. In this case, for normal drift we have the step-wise current $I_{\mathrm{NT}}(t)=v{L}^{-1}[1-H(t-L/v)]$, and its Laplace image is

$${\tilde{I}}_{\mathrm{NT}}(s)=v{L}^{-1}{s}^{-1}[1-exp(-sL/v)].$$

For the dispersive transient current, we have

$$\tilde{I}\left(s\right)=\frac{v\tilde{K}(s)}{L}\left[1-exp\left(-\frac{L}{v\tilde{K}(s)}\right)\right]=\frac{1}{L}{\int }_0^{L}exp\left(-\frac{x}{v\tilde{K}(s)}\right)dx\Rightarrow$$

$$I(t)=\frac{v}{L}{\int }_0^{L/v}w(t,\tau )d\tau .$$

(30)

Comparing the latter formula with expression (27), we find that $j(x,t)=w(t,x/v)$.

To calculate $p(x,t)$ and $I(t)$, we need to know function $q(\tau ,t)$ or related function $w(t,\tau )$ (see Formula (29)). For the considered cases (7)–(10) of fractional operators, transform $\tilde{w}(s,\tau )=exp\left(-\tau /\tilde{K}(s)\right)$ and its inverse are as follows.

• $\tilde{w}(s,\tau )=exp\left(-\tau s^{\alpha }\right)\Rightarrow w(t,\tau )={\tau }^{-1/\alpha }{g}^{(\alpha )}\left({\tau }^{-1/\alpha }t\right)$;
• $\tilde{w}(s,\tau )=exp\left(-\tau \left[{(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }\right]\right)\Rightarrow w(t,\tau )={\tau }^{-1/\alpha }exp\left(-\gamma t-{\gamma }^{\alpha }\frac{x}{v}\right)g^{(\alpha )}\left({\tau }^{-1/\alpha }t\right)$;
• $\tilde{w}(s,\tau )=exp\left(-\frac{\tau s}{b}\right)exp\left(-\frac{\tau (1-\alpha )}{b\alpha }\right)\Rightarrow w(t,\tau )=exp\left(-\frac{\tau (1-\alpha )}{b\alpha }\right)\delta \left(t-\frac{\tau }{b}\right)$;
• $\tilde{w}(s,\tau )=exp\left(-\frac{\tau s}{b}\right)exp\left(-\frac{\tau (1-\alpha )}{b\alpha }{s}^{\alpha }\right)\Rightarrow w(t,\tau )={\left[\frac{\tau (1-\alpha )}{b\alpha }\right]}^{-\frac{1}{\alpha }}{g}^{(\alpha )}\left({\left[\frac{\tau (1-\alpha )}{b\alpha }\right]}^{-\frac{1}{\alpha }}\left(t-\frac{\tau }{b}\right)\right)$.

Here, $g^{(\alpha )}(t)$ is the one-sided Lévy stable density with characteristic exponent $\alpha \in (0,1]$.

Substituting obtained functions $w(t,\tau )$ into Formula (30), we calculate the transient current for dispersive transport described by drift-diffusion equations with different fractional time-derivative operators defined by kernels (7)–(10). The results of these calculations are presented in Figure 2.

The transient current curves corresponding to RL-FFL are shown in Figure 2a. The current decays as power laws: $I(t)\propto t^{-1+\alpha }$ for $t<t_T$, and $I(t)\propto t^{-1-\alpha }$ for $t>t_T$. This behavior is typical for dispersive transport and it is described in the Introduction. For the second case (T-FFL, Figure 2b), when $\gamma >0$ the tail of $I(t)$ is smoothly truncated. Transition to the normal case can be controlled not only by dispersion parameter $\alpha$, but also by truncation parameter $\gamma$. The statistical explanation of such a transition can be found in [20]. In the third case, CF-FFL, we observe unusual behavior of transient current curves: $I(t)$ decays exponentially, while $t<t_T$, and then goes to zero, in spite of constant generation of charge carriers near the left electrode. To observe such behavior, the carrier generation in the ToF method needs special tuning. This generation is compensated by regular recombination (it is another view on stochastic resetting discussed in [19]). The transient currents (Figure 2d) in the last case (AB-FFL) are characterized by the presence of plateau in the initial range, and this plateau can suppress the power law decay $I(t)\propto t^{-1+\alpha }$ for $t<t_T$. For all cases, we observed transition to the normal transport case, when $\alpha \to 1$. Thus, the considered generalizations obey the correspondence principle.

5. Conclusions

We considered the dispersive transport of charge carriers in disordered semiconductors described by the generalized Fick laws with different fractional time-derivative operators. Solutions of the corresponding FFP equations are expressed through the solution of integer-order Fokker-Planck equation in terms of an integral with the subordinating function. For all cases, we observe transition to the normal transport case, when $\alpha \to 1$. This is confirmed by calculated transient current curves for the ToF-method. We shortly discussed the physical reasons leading to the studied generalizations of dispersive transport equations. We have shown how to calculate the solutions and the transient current for the generalized Fick law with a convolution type integro-differential operator. Note that representations (12), (28), and (30) are quite general and they can be used to solve other fractional generalizations of the diffusion-advection equation. In addition to disordered semiconductors, electrode materials and electrolytes of supercapacitors [32] and lithium-ion batteries [33] can be considered as possible applications of the proposed generalizations of Fick’s law and solutions of FFP equations.