Fractal Frames of Functions on the Rectangle

Abstract

In this paper, we define fractal bases and fractal frames of ${\mathcal{L}}^2(I\times J)$, where I and J are real compact intervals, in order to approximate two-dimensional square-integrable maps whose domain is a rectangle, using the identification of ${\mathcal{L}}^2(I\times J)$ with the tensor product space ${\mathcal{L}}^2\left(I\right)⨂{\mathcal{L}}^2\left(J\right)$. First, we recall the procedure of constructing a fractal perturbation of a continuous or integrable function. Then, we define fractal frames and bases of ${\mathcal{L}}^2(I\times J)$ composed of product of such fractal functions. We also obtain weaker families as Bessel, Riesz and Schauder sequences for the same space. Additionally, we study some properties of the tensor product of the fractal operators associated with the maps corresponding to each variable.

1. Introduction

In a rapidly changing world, with unexpected outcomes, the scientific community has to make particular effort to provide a deeper knowledge and understanding of the reality and natural environment surrounding us. In this way, the adoption of new mathematical tools for a better treatment and study of the social, natural and physical phenomena and processes becomes essential. The framework of fractal interpolation makes it possible to enlarge and improve the classical methods of approximation theory. In previous papers, the author defined fractal functions constructed by means of iterated function systems (see, e.g, [1,2,3]). These maps are fractal perturbations of arbitrary continuous functions defined on compact intervals. The new functions interpolate the original mappings on a set of nodes. This approach can be extended to the space of p-integrable functions, defining the fractal analogues of standard maps in ${\mathcal{L}}^p$. A scale vector provides the necessary flexibility to approximate a highly irregular or discontinuous function. If the scale is chosen properly, one can obtain fractal bases of the most used functional spaces, beginning from any basis of these sets. This is done by means of a suitable bounded operator, ${\mathcal{F}}^{\alpha }$, also known as fractal operator ([1,2,3,4,5]), transforming systems of ordinary spanning families into their fractal perturbations. In the case of multivariate maps, this operator can no longer be applied to get necessary functions, and some additional tools are required. While it is true that fractal approximation is an active field of research currently, and there is an abundant bibliography about multivariate fractal interpolation functions (see, e.g., [6,7,8,9,10,11,12,13,14,15,16,17]), our approach has some specificities. One of them is that the functions proposed are products of perturbations of classical maps, and consequently they can be as close to them as desired. In this way, the current approach has two main advantages regarding other existing results. The first one is that the functional bases proposed are a generalization of any product basis (classical or not). This fact provides a wide spectrum of maps, in order to choose the optimum for a particular application, extending the analytical, geometric and dynamical possibilities. The second advantage is the addition of properties, unfeasible for the standard known functions, such as non-differentiability, providing irregular maps whose geometric complexity can be quantified by means of the fractal dimension of their traces for instance.

Although the results presented are deeply theoretical, the potential applications of this type of functions include, but are not restricted to, all the applications of the approximation theory and analysis. These are, for instance, Fourier analysis (used extensively in signal theory), bivariate interpolation and numerical analysis in general, study of chaotic systems, graphical design, mechanical engineering, etc. In particular, all the applications involving the standard functions as polynomial, trigonometric, etc. have their counterpart in this fractal field.

The mappings presented own all the advantages of the traditional functions because they include them as particular cases (taking the scale vectors equal to zero). They also provide new non-smooth geometric objects to model complex behaviors. We could mention as inconveniences, in non-smooth cases, the implicit character of their definition that hinders (though does not prevent) punctual evaluations, and the computational demands for an accurate graphical representation.

In this paper, we define fractal bases and fractal frames of ${\mathcal{L}}^2(I\times J)$, in order to approximate two-dimensional square-integrable maps whose domain is a rectangle. This is accomplished by means of the identification of ${\mathcal{L}}^2(I\times J)$ with the tensor product space ${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right).$

The paper is organized as follows. Iin Section 2, we introduce the fractal perturbation of a continuous function. In Section 3, we define fractal frames and bases of ${\mathcal{L}}^2(I\times J)$ composed of products of fractal functions. We also obtain weaker families, as Bessel, Riesz and Schauder sequences. Additionally, we study some properties of the tensor product of the fractal operators previously mentioned, corresponding to each variable.

2. $\mathit{\alpha }$-Fractal Functions

In this section, we present the basics of the theory of fractal interpolation, initiated by M. Barnsley [18] and developed further by many authors, for instance, M. A. Navascués [2]. Consider a partition $\mathsf{\Delta }$ of a real compact interval $I=[a,b],\mathsf{\Delta }:=a=x_0<x_1\cdots <x_N=b$, and a set of data $\{(x_n,y_n)\in I\times \mathbf{R},n=0,1,\dots ,N\}$. Define subintervals $I_n=[x_{n-1},x_n]$ for $n=1,2,\dots ,N$, and the following Iterated Function System (IFS): $\{I\times \mathbf{R}:\left(L_n(x,F_n(x,y))\right),n=1,2,\dots ,N\}$, where the mappings $L_n$ are such that

$$L_n\left(x_0\right)=x_{n-1},L_n\left(x_N\right)=x_n$$

(1)

$$|L_n\left(x\right)-L_n\left(x^{\prime }\right)|\le k|x-x^{\prime }|\forall x,x^{\prime }\in I$$

for some $0\le k<1$. The maps $F_n$ are continuous functions satisfying a Lipschitz condition in the second variable:

$$|F_n(x,y)-F_n(x,y^{\prime })|\le r|y-y^{\prime }|$$

for $x\in I,y,y^{\prime }\in \mathbf{R}$ and $0\le r<1$. Additionally, $F_n$ must satisfy some join-up conditions:

$$F_n(x_0,y_0)=y_{n-1},F_n(x_N,y_N)=y_n$$

for $n=1,2,\dots ,N$. According to [18] (Theorem 1) and [19] (Theorem 2 of Section 6.2), the described IFS owns a unique attractor that is the graph of a continuous function $g:I\to \mathbf{R}$ interpolating the given data. By definition, g is the fractal interpolation function (FIF) of the IFS defined and it is unique satisfying the fractional equation

$$g\left(x\right)=F_n(L_n^{-1}\left(x\right),g\circ L_n^{-1}\left(x\right))$$

(2)

for $x\in I_n$ and $n=1,2,\dots ,N$.

In this paper, we consider the following mappings:

$$\left\{\begin{array}{c}{L}_n\left(x\right)=a_{n}x+b_n\hfill \\ F_n(x,y)={\alpha }_{n}y+q_n\left(x\right),\hfill \end{array}\right.$$

(3)

where the scale factor ${\alpha }_n$ is such that $-1<{\alpha }_n<1$. The coefficients of $L_n$ are

$$a_n=\frac{x_n-x_{n-1}}{x_N-x_0}{b}_n=\frac{x_N{x}_{n-1}-x_0{x}_n}{x_N-x_0}.$$

(4)

The functions $q_n$ are defined by means of two continuous functions f and b, $f,b:I\to \mathbf{R}$, as

$$q_n\left(x\right)=f\circ L_n\left(x\right)-{\alpha }_{n}b\left(x\right),$$

(5)

where $f\left(x_0\right)=b\left(x_0\right)$ and $f\left(x_N\right)=b\left(x_N\right)$.

The fractal interpolation function $f^{\alpha }$ of this IFS was called by [2] the $\alpha$-fractal function of f with respect to the partition $\mathsf{\Delta }$, the scale vector $\alpha ={\left({\alpha }_n\right)}_{n=1}^N$, and the map b.

To define an operator ${\mathcal{F}}^{\alpha }:\mathcal{C}\left(I\right)\to \mathcal{C}\left(I\right)$ given by ${\mathcal{F}}^{\alpha }\left(f\right)=f^{\alpha }$, the first author considered in [2] another operator L such that

$$b=Lf.$$

(6)

If $L:\mathcal{C}\left(I\right)\to \mathcal{C}\left(I\right)$ is linear and bounded, with respect to the supremum norm

$${\parallel f\parallel }_{\infty }=max\left\{\right|f\left(x\right)|;x\in I\}$$

or with respect to ${\mathcal{L}}^2$-norm

$${\parallel f\parallel }_{{\mathcal{L}}^2}=({\int }_a^b{\left|f\right|}^2{dx)}^{1/2},$$

(7)

and $Lf\left(x_0\right)=f\left(x_0\right)$, $Lf\left(x_N\right)=f\left(x_N\right)$, then ${\mathcal{F}}^{\alpha }$ is also linear and bounded regarding the respective norms.

The functional Equation (2) satisfied by $f^{\alpha }$ is:

$$f^{\alpha }\left(x\right)=f\left(x\right)+{\alpha }_n(f^{\alpha }-Lf)\circ L_n^{-1}\left(x\right)$$

(8)

for $x\in I_n.$ A consequence of this expression provides a bound of the distance between f and $f^{\alpha }$

$$\parallel f^{\alpha }{-f\parallel }_{\infty }\le \frac{{\left|\alpha \right|}_{\infty }}{1-{\left|\alpha \right|}_{\infty }}{\parallel f-Lf\parallel }_{\infty },$$

(9)

where ${\left|\alpha \right|}_{\infty }$ is defined as ${\left|\alpha \right|}_{\infty }=max\left\{\right|{\alpha }_n|:n=1,2,\dots ,N\}$.

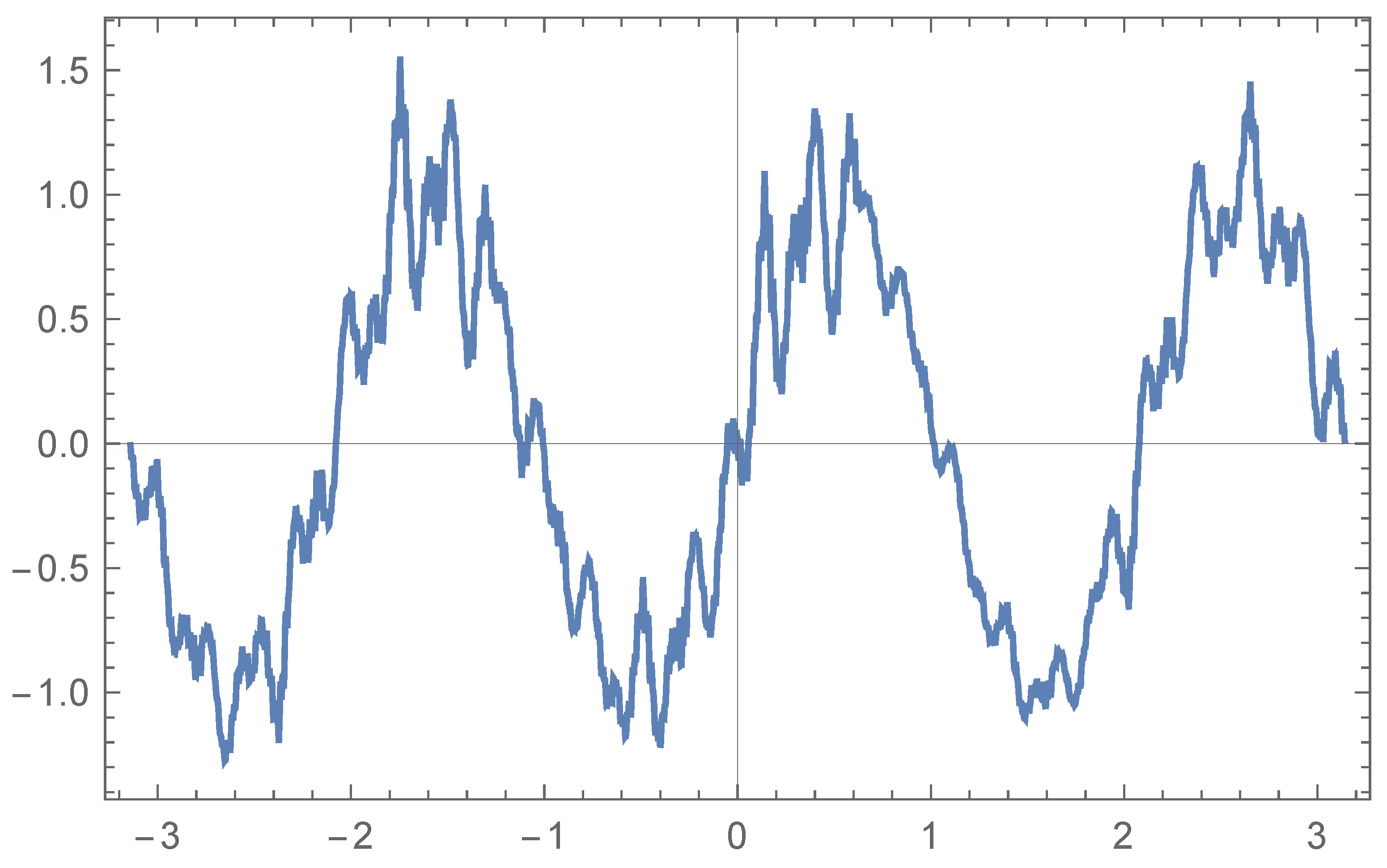
Figure 1 represents the graph of an $\alpha$-fractal function $f^{\alpha }$ with respect to the operator $Lf=f\circ c$, where $f\left(x\right)=sin\left(3x\right)$ and $c\left(x\right)=\pi sin\left(\frac{x}{2}\right)$. The interval is $I=[-\pi ,\pi ]$, $N=10$, the sampling is uniform and $\alpha =(0.15,-0.2,0.3,-0.15,0.2,0.3,-0.1,0.1,-0.2,0.2)$.

Figure 1. Fractal function $f^{\alpha }$ associated with $f\left(x\right)=sin\left(3x\right).$

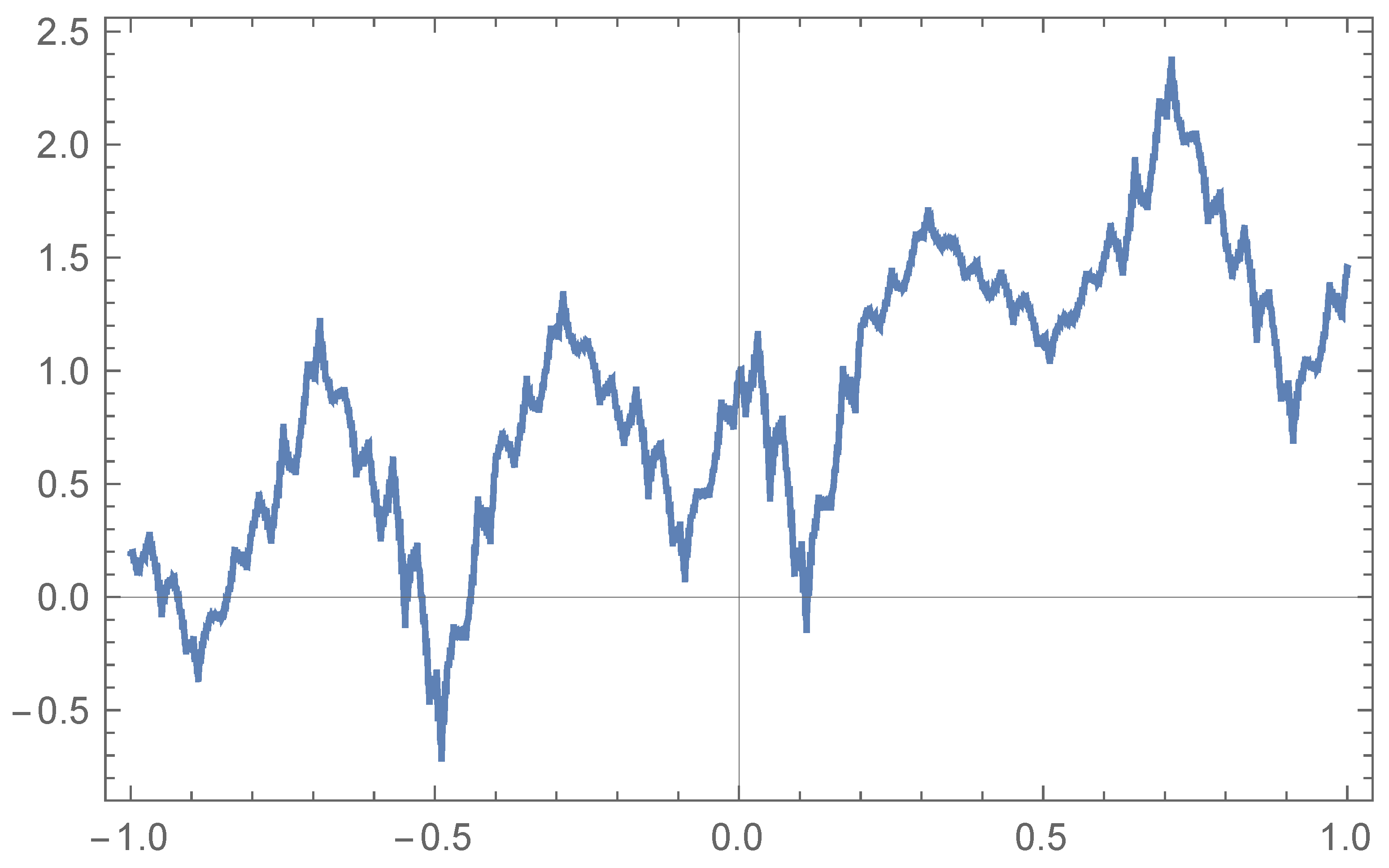
Figure 2 shows the graph of $f^{\alpha }$ for the operator $Lf=vf$, the maps $f\left(x\right)=e^{x}cos\left(x\right)$ and $v\left(x\right)=4-3\left|x\right|$. The interval is $I=[-1,1]$, $N=10,$ the sampling is uniform and $\alpha =(0.15,-0.2,0.3,-0.15,0.2,0.3,-0.1,0.1,-0.2,0.2)$.

Figure 2. Fractal function associated $f^{\alpha }$ with $f\left(x\right)=e^{x}cos\left(x\right).$

${\mathcal{F}}^{\alpha }$ can be extended to ${\mathcal{L}}^p\left(I\right)$, and in this way we obtain fractal perturbations of p-integrable functions ([1]). For convenience, in this paper, we denote as ${\mathcal{F}}^{\alpha }$ the operator extended to ${\mathcal{L}}^2\left(I\right)$ and $f^{\alpha }$ represents the image of $f\in {\mathcal{L}}^2\left(I\right).$

$\parallel {\mathcal{F}}^{\alpha }\parallel$ represents the norm of the operator with respect to the mean square norm in ${\mathcal{L}}^2\left(I\right).$

The operator ${\mathcal{F}}^{\alpha }:{\mathcal{L}}^2\left(I\right)\to {\mathcal{L}}^2\left(I\right)$ enjoys many important properties ([1]). For instance, the following inequality holds:

$$\parallel I-{\mathcal{F}}^{\alpha }\parallel \le \frac{{\left|\alpha \right|}_{\infty }}{1-{\left|\alpha \right|}_{\infty }}\parallel I-L\parallel ,$$

(10)

where I is the identity and L is the extension to ${\mathcal{L}}^2\left(I\right)$ of the corresponding operator of $\mathcal{C}\left(I\right).$

Moreover ([1]),

• If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$, then ${\mathcal{F}}^{\alpha }$ is injective and has a closed range.
• If ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$, then ${\mathcal{F}}^{\alpha }$ is an isomorphism.
• If $\alpha =0$, ${\mathcal{F}}^{\alpha }=I.$

Due to the last item, we can consider that the fractal maps $f^{\alpha }$ are generalizations of any function.

3. Fractal Frames on the Rectangle

In this section, we analyze the spanning properties of the fractal functions on the rectangle $I\times J,$ where I and J are compact real intervals. For this purpose, we use the identification ${\mathcal{L}}^2(I\times J)$ with the tensor product space ${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right).$

Let us recall the definition and properties of the tensor product of two Hilbert spaces $H_1$ and $H_2$. One way of introducing the tensorial product is approached by means of linear operators ([20,21]). We consider spaces on the field R since we deal in general with spaces of real functions (although the extension to complex functions is straightforward). Thus,

Definition 1.

Let $H_1$, $H_2$ be separable real Hilbert spaces. Their tensor product is defined as

$$H_1\otimes H_2=\{A:H_2\to H_1:Alinear,bounded,\sum _{j=1}^{\infty }\parallel A{g}_j{\parallel }^2<\infty \},$$

where $\left\{g_j\right\}$ is an orthonormal basis of $H_2.$

Remark 1.

If $\left\{f_i\right\}$ is an orthonormal basis of $H_1,$ then

$$\sum _{j=1}^{\infty }\parallel A{g}_j{\parallel }^2=\sum _{j=1}^{\infty }\sum _{i=1}^{\infty }|<A{g}_j,f_i{>|}^2=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }|<A^{*}{f}_i,g_j{>|}^2=\sum _{i=1}^{\infty }{\parallel A^{*}{f}_i\parallel }^2.$$

The sum is independent of the basis chosen in every space $H_i$. The operator $A^{*}$ is the adjoint of $A.$

The space $H_1\otimes H_2$ is Hilbert with respect to the inner product:

$$<A,B>=\sum _{j=1}^{\infty }<A{g}_j,B{g}_j>=\sum _{i=1}^{\infty }<A^{*}{f}_i,B^{*}{f}_i>,$$

(11)

that induces the norm

$$\left|\right|\left|A\right|\left|\right|=(\sum _{j=1}^{\infty }\parallel A{g}_j{\parallel }^2{)}^{1/2}=(\sum _{i=1}^{\infty }\parallel A^{*}{f}_i{{\parallel }^2)}^{1/2}.$$

(12)

Remark 2.

The notation $\parallel A\parallel$ is reserved for the norm of A as linear and bounded operator.

Let us define now the tensor product of two vectors $f\in H_1$ and $g\in H_2$ as the operator $f\otimes g:H_2\to H_1$

$$f\otimes g\left(h\right)=<g,h>f\in H_1,$$

where $h\in H_2$. The main properties of this product are summarized as:

• $(f_1+f_2)\otimes g=f_1\otimes g+f_2\otimes g.$
• $\left(\lambda f\right)\otimes g=\lambda (f\otimes g)$.
• $f\otimes (g_1+g_2)=f\otimes g_1+f\otimes g_2$.
• $f\otimes \left(\lambda g\right)=\lambda (f\otimes g)$.
• $f\otimes g\in H_1\otimes H_2$.
• $\parallel f\otimes g\parallel \le \left|\right||f\otimes g|\left|\right|=\parallel f\parallel \parallel g\parallel .$
• $<f\otimes g,f^{\prime }\otimes g^{\prime }>=<f,f^{\prime }><g,g^{\prime }>.$
• If $\left\{f_i\right\}$ is an orthonormal basis of $H_1$ and $\left\{g_j\right\}$ is an orthonormal basis of $H_2$, then $\{f_i\otimes g_j\}$ is an orthonormal basis of $H_1\otimes H_2.$
• ${(f\otimes g)}^{*}=g\otimes f.$

Let $rank\left(A\right)$ denote the dimension of the range of the operator $A.$ Let us define

$$\mathcal{P}=\{f\otimes g:f\in H_1,g\in H_2\},$$

and

$$\mathcal{F}=\{A:H_2\to H_1:Alinear,bounded,rank\left(A\right)<\infty \},$$

then

$$span\left(\mathcal{P}\right)=\mathcal{F}$$

and

$$\overline{span}\left(\mathcal{P}\right)=\overline{\mathcal{F}}=H_1\otimes H_2.$$

The identification of ${\mathcal{L}}^2(I\times J)$ with ${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)$ comes from the equality:

$$(f\otimes g)\left(h\right)=<g,h>f={\int }_{J}f(·)g\left(y\right)h\left(y\right)dy,$$

where $f\in {\mathcal{L}}^2\left(I\right)$ and $g\in {\mathcal{L}}^2\left(J\right).$ Thus, $f\otimes g$ is an integral operator whose kernel is $f\left(x\right)g\left(y\right)$. Similarly, ${\sum }_{k=1}^n{f}_k\otimes g_k$ has as kernel the sum ${\sum }_{k=1}^n{f}_k\left(x\right)g_k\left(y\right).$ The following result can be read in ([20], Th. 7.16)

Theorem 1.

The identification of $f\otimes g$ with the function $f\left(x\right)g\left(y\right)$ extends uniquely to an isometric isomorphism of ${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)$ with ${\mathcal{L}}^2(I\times J)$ whose inverse identifies $F\in {\mathcal{L}}^2(I\times J)$ with the operator $h\to {\int }_{J}F(·,y)h\left(y\right)dy.$

Let $\mathcal{P}=\{f\otimes g:f\in {\mathcal{L}}^2\left(I\right),g\in {\mathcal{L}}^2\left(J\right)\}.$ The definition of the tensor product of ${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)$ implies that:

$$\overline{span}\left(\mathcal{P}\right)={\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right).$$

Definition 2.

A Riesz basis $\left\{x_m\right\}$ of a Hilbert space H is a system equivalent to an orthonormal basis $\left\{p_m\right\}$, that is to say, there is an isomorphism $T:H\to H$ such that $T{p}_m=x_m$ for any m.

Definition 3.

A Riesz sequence $\left\{x_m\right\}$ of a Hilbert space H is a Riesz basis for its closed span $\left[x_m\right]:=\overline{span}\left(x_m\right)$. If $\left[x_m\right]=H$, then it is a Riesz basis.

In [3], the following result is proved:

Theorem 2.

If $\left\{p_m\right\}$ is an orthonormal basis of ${\mathcal{L}}^2\left(I\right)$ and α is a scale factor such that ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$, then $\left\{p_m^{\alpha }\right\}$ is a Riesz basis of ${\mathcal{L}}^2\left(I\right)$.

Remark 3.

This result is also true for a non-orthonormal basis $\left\{f_m\right\}$ since there is a topological isomorphism such that $T{f}_m=p_m$. With these hypotheses, ${\mathcal{F}}^{\alpha }$ is also an isomorphism and $\left\{p_m\right\}$ and $\left\{f_m^{\alpha }\right\}$ are equivalent bases.

Let us recall now the tensor product of two linear operators.

Definition 4.

If S is a linear and bounded operator of $H_1$ and T is a linear and bounded operator of $H_2,$ then

$$S\otimes T:H_1\otimes H_2\to H_1\otimes H_2$$

is defined as:

$$(S\otimes T)A=SA{T}^{*},$$

where $A:H_2\to H_1$ is linear, bounded and satisfying ${\sum }_{i=1}^{\infty }{\parallel A{g}_i\parallel }^2<\infty$.

The main properties of this tensor product are:

• $(S\otimes T)(f\otimes g)=S\left(f\right)\otimes T\left(g\right).$
• $S\otimes T$ is linear and bounded as operator of $H_1\otimes H_2$.
• $\parallel S\otimes T\parallel =\parallel S\parallel \parallel T\parallel$.
• $(S\otimes T)(S^{\prime }\otimes T^{\prime })=\left(S{S}^{\prime }\right)\otimes \left(T{T}^{\prime }\right)$.
• ${(S\otimes T)}^{*}=S^{*}\otimes T^{*}$.
• $I\otimes I=I$.

Remark 4.

The notation $\parallel S\otimes T\parallel$ represents the norm as operator of $H_1\otimes H_2$ (with respect to $\left|\right||·|\left|\right|$ in $H_1\otimes H_2$).

Let us define

$${\tau }^{\alpha \beta }={\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }.$$

Remark 5.

${\mathcal{G}}^{\beta }$ is the operator that maps a function $g\in {\mathcal{L}}^2\left(J\right)$ into $g^{\beta }$ $\left(g^{\beta }={\mathcal{G}}^{\beta }\left(g\right)\right)$. $L^{\prime }$ is the operator defined in (6) for the second variable and β is the scale vector in the y-direction.

Theorem 3.

Let $\left\{U_m\right\}$ and $\left\{V_n\right\}$ be Riesz bases of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right),$ respectively, and let us consider scale vectors α and β satisfying ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$ and ${\left|\beta \right|}_{\infty }<(1+\parallel I-L^{\prime }{\parallel )}^{-1}$, then $\mathcal{B}=\{U_m^{\alpha }\otimes V_n^{\beta }\}$ is a Riesz basis of ${\mathcal{L}}^2(I\times J)$.

Proof. 

The tensor product $\{U_m\otimes V_n\}$ is a Riesz basis. In this case, ${\mathcal{F}}^{\alpha }$ and ${\mathcal{G}}^{\beta }$ are topological isomorphisms due to Theorem 2. Taking $S^{\prime }={\left({\mathcal{F}}^{\alpha }\right)}^{-1}$ and $T^{\prime }={\left({\mathcal{G}}^{\beta }\right)}^{-1}$ in the properties 4 and 6 before Remark 4, we have that ${\tau }^{\alpha \beta }={\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$ is an isomorphism. Then, $\{U_m^{\alpha }\otimes V_n^{\beta }\}$ is a basis equivalent to $\{U_m\otimes V_n\}.$  □

According to Property $\left(3\right)$ of the tensor product of operators:

$$\parallel {\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }\parallel =\parallel {\mathcal{F}}^{\alpha }\parallel \parallel {\mathcal{G}}^{\beta }\parallel .$$

Moreover (Theorem 3.3 of [1]),

$$\parallel {\mathcal{F}}^{\alpha }\parallel \le 1+\frac{{\left|\alpha \right|}_{\infty }}{1-{\left|\alpha \right|}_{\infty }}\parallel I-L\parallel =\left(\frac{1+{\left|\alpha \right|}_{\infty }(\parallel I-L\parallel -1)}{1-{\left|\alpha \right|}_{\infty }}\right)$$

(13)

and

$$\parallel {\mathcal{G}}^{\beta }\parallel \le 1+\frac{{\left|\beta \right|}_{\infty }}{1-{\left|\beta \right|}_{\infty }}\parallel I-L^{\prime }\parallel =\left(\frac{1+{\left|\beta \right|}_{\infty }(\parallel I-L^{\prime }\parallel -1)}{1-{\left|\beta \right|}_{\infty }}\right).$$

(14)

Lemma 1.

If ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$ then

$$\parallel {\left({\mathcal{F}}^{\alpha }\right)}^{-1}\parallel \le \frac{1-{\left|\alpha \right|}_{\infty }}{1-{\left|\alpha \right|}_{\infty }(\parallel I-L\parallel +1)}.$$

Proof. 

If ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$, the inequality (9) and the condition on $\alpha$ imply that

$$\parallel I-{\mathcal{F}}^{\alpha }\parallel \le \frac{{\left|\alpha \right|}_{\infty }}{1-{\left|\alpha \right|}_{\infty }}\parallel I-L\parallel <1.$$

(15)

Thus,

$${\left({\mathcal{F}}^{\alpha }\right)}^{-1}=\sum _{k=0}^{\infty }{(I-{\mathcal{F}}^{\alpha })}^k$$

and

$$\parallel {\left({\mathcal{F}}^{\alpha }\right)}^{-1}\parallel \le \frac{1}{1-\parallel I-{\mathcal{F}}^{\alpha }\parallel }.$$

(16)

Moreover, by Equation (15),

$$1-\parallel I-{\mathcal{F}}^{\alpha }\parallel \ge \frac{1-{\left|\alpha \right|}_{\infty }(1+\parallel I-L\parallel )}{1-{\left|\alpha \right|}_{\infty }}$$

hence (16)

$$\parallel {\left({\mathcal{F}}^{\alpha }\right)}^{-1}\parallel \le \frac{1-{\left|\alpha \right|}_{\infty }}{1-{\left|\alpha \right|}_{\infty }(\parallel I-L\parallel +1)}.$$

 □

Remark 6.

If $\alpha =0$ or $L=I$, the norm reaches the bound given in the previous Lemma since ${\mathcal{F}}^{\alpha }=I$, improving the limit provided in Theorem 3.7 of the reference [1].

Definition 5.

The constant C of a basis $\left\{x_m\right\}$ of a Banach space H is

$$C=su{p}_N\parallel S_N\parallel ,$$

where $S_N$ is the Nth partial sum operator of the expansion

$$x=\sum _{m=1}^{\infty }{c}_m{x}_m,$$

for any $x\in H,$ that is to say, defined by $S_N\left(x\right)={\sum }_{m=1}^N{c}_m{x}_m.$

Proposition 1.

In the conditions of Theorem 3, the constant $C^{\alpha \beta }$ of the basis $\{U_m^{\alpha }\otimes V_n^{\beta }\}$ satisfies the inequality:

$$C^{\alpha \beta }\le \left(\frac{1+{\left|\alpha \right|}_{\infty }(\parallel I-L\parallel -1)}{1-{\left|\alpha \right|}_{\infty }(\parallel I-L\parallel +1)}\right)\left(\frac{1+{\left|\beta \right|}_{\infty }(\parallel I-L^{\prime }\parallel -1)}{1-{\left|\beta \right|}_{\infty }(\parallel I-L^{\prime }\parallel +1)}\right)C,$$

where C is the constant of the basis $U_m\otimes V_n.$

Proof. 

Let us consider $T\in {\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)$ and the expansion of the element $T^{\prime }$ defined as

$$T^{\prime }=({\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1})\left(T\right)=\sum _{m,n=1}^{\infty }{c}_{mn}({\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1}\left(T\right))(U_m\otimes V_n),$$

where $c_{mn}\left(U\right)$ represent the coefficient of U with respect to the basis $U_m\otimes V_n.$ Then,

$$T={\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }\left(T^{\prime }\right)=\sum _{m,n=1}^{\infty }{c}_{mn}({\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1}\left(T\right))(U_m^{\alpha }\otimes V_n^{\beta }).$$

If $S_N^{\alpha \beta }$ is the Nth partial sum of this expansion, then

$$\parallel S_N^{\alpha \beta }\parallel \le \parallel {\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }\parallel \parallel S_N\parallel \parallel {\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1}\parallel ,$$

where $S_N$ is the Nth projection with respect to the basis $U_m\otimes V_n.$ The result follows from the properties of the tensor product of operators, the previous lemma and the inequalities (13) and (14).  □

Definition 6.

A sequence $\left\{x_m\right\}\subseteq H$, where H is a Hilbert space, is a frame if there exist constants $A,B>0$ such that for all $x\in H$

$${A\parallel x\parallel }^2\le \sum _{m=0}^{\infty }|<x,x_m{>|}^2\le B{\parallel x\parallel }^2.$$

(17)

For the next results, we need additional properties of the fractal families in ${\mathcal{L}}^2\left(I\right)$.

Proposition 2.

If $\left\{f_m\right\}$ is a frame and ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$, then $\left\{{\left({\mathcal{F}}^{\alpha }\right)}^{*}{f}_m\right\}$ is a frame of ${\mathcal{L}}^2\left(I\right)$.

Proof. 

For the right inequality of (17), let us think that for $f\in {\mathcal{L}}^2\left(I\right)$,

$$\sum _{m=1}^{\infty }|<f,{\left({\mathcal{F}}^{\alpha }\right)}^{*}\left(f_m\right){>|}^2=\sum _{m=1}^{\infty }|<{\mathcal{F}}^{\alpha }\left(f\right),f_m{>|}^2\le k\parallel {\mathcal{F}}^{\alpha }\left(f\right){\parallel }^2\le k\parallel {\mathcal{F}}^{\alpha }{\parallel }^2{\parallel f\parallel }^2,$$

where k is the right bound of the frame $\left\{f_m\right\}$ (B in the expression (17)). For the left inequality, according to Proposition 4.8 and Theorem 4.18 of [1], ${\mathcal{F}}^{\alpha }$ is injective with closed range and ${\left({\mathcal{F}}^{\alpha }\right)}^{-1}$ is defined on the range of ${\mathcal{F}}^{\alpha }$. For $f\in {\mathcal{L}}^2\left(I\right)$, $f={\left({\mathcal{F}}^{\alpha }\right)}^{-1}\circ {\mathcal{F}}^{\alpha }\left(f\right)$ and

$${,\parallel f\parallel }^2\le K{\parallel {\mathcal{F}}^{\alpha }\left(f\right)\parallel }^2.$$

(18)

Moreover, since $\left\{f_m\right\}$ is a frame,

$$\parallel {\mathcal{F}}^{\alpha }{\left(f\right)\parallel }^2\le k^{\prime }\sum _{m=1}^{\infty }|<{\mathcal{F}}^{\alpha }\left(f\right),f_m{>|}^2=k^{\prime }\sum _{m=1}^{\infty }{|<f,{\left({\mathcal{F}}^{\alpha }\right)}^{*}{f}_m>|}^2,$$

where $1/k^{\prime }$ is is the left bound of the frame $\left\{f_m\right\}$ (A in the expression (17)). Using the inequality (18), the result is proved.  □

Proposition 3.

If $\left\{f_m\right\},\left\{g_n\right\}$ are frames and ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$, ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }^{-1}$ then $\left\{{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}(f_m\otimes g_n)\right\}$ is a frame of ${\mathcal{L}}^2(I\times J)$.

Proof. 

In this case, $\left\{{\left({\mathcal{F}}^{\alpha }\right)}^{*}\left(f_m\right)\right\}$ and $\left\{{\left({\mathcal{G}}^{\beta }\right)}^{*}\left(g_n\right)\right\}$ are frames according to the previous proposition. The tensor product of frames is a frame (Theorem 2.3, [22]) and consequently by Property $\left(5\right)$ of Definition 4

$$\{{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}(f_m\otimes g_n)={\left({\mathcal{F}}^{\alpha }\right)}^{*}\left(f_m\right)\otimes {\left({\mathcal{G}}^{\beta }\right)}^{*}\left(g_n\right)$$

is a frame.  □

Definition 7.

A sequence $\left\{x_m\right\}$ of a Hilbert space H is a Bessel sequence if there exists a constant $B>0$ such that for any $x\in H$

$$\sum _{m=1}^{\infty }|<x,x_m{>|}^2\le B{\parallel x\parallel }^2.$$

Theorem 4.

If $\left\{f_m\right\}$, $\left\{g_n\right\}$ are frames of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right)$, then $\{f_m^{\alpha }\otimes g_n^{\beta }\}$ is a Bessel sequence for any scale vectors α, β.

Proof. 

Let us consider any $A\in {\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right),$ then

$$\begin{array}{ccc}\hfill \sum _{m,n=1}^{\infty }{|<A,f_m^{\alpha }\otimes g_n^{\beta }>|}^2& =& \sum _{m,n=1}^{\infty }{|<{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\left(A\right),f_m\otimes g_n>|}^2\hfill \\ & \le & K\left|\right||{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\left(A\right){\left|\right||}^2\hfill \\ & \le & K\parallel {\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }{\parallel }^2{\left|\right|\left|A\right|\left|\right|}^2\hfill \\ & =& K\parallel {\mathcal{F}}^{\alpha }{\parallel }^2\parallel {\mathcal{G}}^{\beta }{\parallel }^2{\left|\right|\left|A\right|\left|\right|}^2.\hfill \end{array}$$

The first inequality is due to the fact that $f_m\otimes g_m$ is a frame, and the last equality comes from Property (3) of Definition 4.  □

In the following lemma, $A^{*}$ represents the adjoint of A, and the same notation is used for all the operators concerned.

Lemma 2.

If $A\in {\mathcal{L}}^2(I\times J)$ then $A{\mathcal{G}}^{\beta },A\left({\left({\mathcal{G}}^{\beta }\right)}^{*}\right),A^{*}\left({\mathcal{F}}^{\alpha }\right),A^{*}\left({\left({\mathcal{F}}^{\alpha }\right)}^{*}\right)\in {\mathcal{L}}^2(I\times J)$, and

$$max\left\{\right|\left|\right|A{\mathcal{G}}^{\beta }\left|\right||,|\left|\right|A\left({\left({\mathcal{G}}^{\beta }\right)}^{*}\right)\left|\right|\left|\right\}\le \parallel {\mathcal{G}}^{\beta }\parallel \left|\right|\left|A\right|\left|\right|,$$

$$max\left\{\right|\left|\right|A^{*}\left({\mathcal{F}}^{\alpha }\right)\left|\right||,|\left|\right|A^{*}\left({\left({\mathcal{F}}^{\alpha }\right)}^{*}\right)\left|\right|\left|\right\}\le \parallel {\mathcal{F}}^{\alpha }\parallel \left|\right|\left|A\right|\left|\right|,$$

Moreover, if ${\left({\mathcal{G}}^{\beta }\right)}^{*}$ is bounded below, there exists a constant $k>0$ such that

$$\left|\right||A{\mathcal{G}}^{\beta }\left|\right||\ge k\left|\right|\left|A\right|\left|\right|,$$

and, if ${\left({\mathcal{F}}^{\alpha }\right)}^{*}$ is bounded below, there exists a constant $k^{\prime }>0$ such that

$$\left|\right||A^{*}\left({\mathcal{F}}^{\alpha }\right)\left|\right||\ge k^{\prime }\left|\right|\left|A\right|\left|\right|.$$

Proof. 

Let us take, for instance, the first element $A{\mathcal{G}}^{\beta }$. It is linear and bounded operator from ${\mathcal{L}}^2\left(J\right)$ to ${\mathcal{L}}^2\left(I\right)$ and

$$\left|\right||A{\mathcal{G}}^{\beta }{\left|\right||}^2=\sum _{n=1}^{\infty }\parallel A{\mathcal{G}}^{\beta }{V}_n{\parallel }^2=\sum _{m=1}^{\infty }\parallel {\left({\mathcal{G}}^{\beta }\right)}^{*}{A}^{*}{U}_m{\parallel }^2\le \parallel {\mathcal{G}}^{\beta }{\parallel }^2\sum _{m=1}^{\infty }{\parallel A^{*}{U}_m\parallel }^2,$$

and

$$\left|\right||A{\mathcal{G}}^{\beta }{\left|\right||}^2\le \parallel {\mathcal{G}}^{\beta }{\parallel }^2{\left|\right|\left|A\right|\left|\right|}^2,$$

where $\left\{U_m\right\}$ and $\left\{V_n\right\}$ are orthonormal bases of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right)$, respectively. The proof of the rest of the inequalities is similar.  □

Theorem 5.

Let $\left\{U_m\right\}$ and $\left\{V_n\right\}$ be orthonormal bases of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right)$, respectively. If $\left\{V_n^{\beta }\right\}$ is a frame and ${\left({\mathcal{F}}^{\alpha }\right)}^{*}$ is bounded below, then $\{U_m^{\alpha }\otimes V_n^{\beta }\}$ is a frame of ${\mathcal{L}}^2(I\times J).$

The upper frame constant is $\parallel {\mathcal{F}}^{\alpha }{\parallel }^2{\parallel {\mathcal{G}}^{\beta }\parallel }^2$ and the lower is $M{k}^{\prime 2}$, where M is the lower frame constant of $\left\{V_n^{\beta }\right\}$ and $k^{\prime }$ is such that

$$\parallel {\left({\mathcal{F}}^{\alpha }\right)}^{*}f\parallel \ge k^{\prime }\parallel f\parallel ,$$

for any $f\in {\mathcal{L}}^2\left(I\right).$

Proof. 

The right inequality of (17) is proved in the previous theorem. The tensor product of orthonormal bases is an orthonormal basis and the constant K of the previous theorem is equal to one.

For the left one, let us consider any $A\in {\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right),$ then

$$<A,U_m^{\alpha }\otimes V_n^{\beta }>=\sum _{j=1}^{\infty }<A{V}_j,(U_m^{\alpha }\otimes V_n^{\beta })\left(V_j\right)>=\sum _{j=1}^{\infty }<A{V}_j,<V_n^{\beta },V_j>U_m^{\alpha }>=$$

$$\sum _{j=1}^{\infty }<V_n^{\beta },V_j><A{V}_j,U_m^{\alpha }>=<A(\sum _{j=1}^{\infty }<V_n^{\beta },V_j>V_j),U_m^{\alpha }>=<A{V}_n^{\beta },U_m^{\alpha }>,$$

and

$$<A,U_m^{\alpha }\otimes V_n^{\beta }>=<V_n^{\beta },A^{*}{U}_m^{\alpha }>.$$

Consequently,

$$\sum _{m,n=1}^{\infty }|<A,U_m^{\alpha }\otimes V_n^{\beta }{>|}^2=\sum _{m,n=1}^{\infty }|<V_n^{\beta },A^{*}{U}_m^{\alpha }{>|}^2\ge M\sum _{m=1}^{\infty }{\parallel A^{*}{\mathcal{F}}^{\alpha }\left(U_m\right)\parallel }^2.$$

The previous inequality is due to the fact that $\left\{V_n^{\beta }\right\}$ is a frame. Since ${\left({\mathcal{F}}^{\alpha }\right)}^{*}$ is bounded below,

$$\sum _{m,n=1}^{\infty }|<A,U_m^{\alpha }\otimes V_n^{\beta }{>|}^2\ge K\left|\right||A^{*}{\mathcal{F}}^{\alpha }{\left|\right||}^2\ge K{k}^{\prime 2}{\left|\right|\left|A\right|\left|\right|}^2,$$

applying the previous lemma.  □

Proposition 4.

Let $\left\{U_m\right\}$ and $\left\{V_n\right\}$ be orthonormal bases. If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$ and ${\left|\beta \right|}_{\infty }<(1+\parallel I-L^{\prime }{\parallel )}^{-1},$ then $\left({\left({\mathcal{F}}^{\alpha }\right)}^{*}{U}_m\right)\otimes V_n^{\beta }$ is a frame.

Proof. 

It is a consequence of Theorem 2 ($\left\{V_n^{\beta }\right\}$ is a Riesz basis) and Proposition 2 ($\left\{{\left({\mathcal{F}}^{\alpha }\right)}^{*}\left(U_m\right)\right\}$ is a frame).  □

Corollary 1.

Let $\left\{U_m\right\}$ and $\left\{V_n\right\}$ be orthonormal bases. If $\left\{V_n^{\beta }\right\}$ is a frame, then $\{U_m\otimes V_n^{\beta }\}$ is a frame.

Proof. 

In this case, ${\mathcal{F}}^{\alpha }=I$ ($\alpha =0$) and ${\left({\mathcal{F}}^{\alpha }\right)}^{*}=I$ is bounded below. Applying Theorem 5, one obtains the result. In addition, note that the tensor product of frames is a frame.  □

The following lemma can be read in [22], Theorem 2.6.

Lemma 3.

If Q is a linear and bounded invertible operator of H and $\left\{A_n\right\}$ is a frame of $H\otimes K$, then the sequence $\left\{Q{A}_n\right\}$ is also a frame of $H\otimes K.$

Theorem 6.

If ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$ and $\left\{f_m\right\},$ $\left\{g_n\right\}$ are frames of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right)$, respectively, then $\{f_m^{\alpha }\otimes g_n\}$ is a frame.

Proof. 

Let us consider the former lemma for $A_n=f_m\otimes g_n$ and $Q={\mathcal{F}}^{\alpha }$. With the hypothesis on $\alpha$, ${\mathcal{F}}^{\alpha }$ is invertible and consequently ${\mathcal{F}}^{\alpha }\circ (f_m\otimes g_n)$ is a frame. Let us see that ${\mathcal{F}}^{\alpha }\circ (f_m\otimes g_n)=f_m^{\alpha }\otimes g_n$.

$$\left({\mathcal{F}}^{\alpha }\circ (f_m\otimes g_n)\right)\left(g\right)={\mathcal{F}}^{\alpha }\left(<g_n,g>f_m\right)=<g_n,g>f_m^{\alpha }=\left(f_m^{\alpha }\otimes g_n\right)\left(g\right)$$

for every $g\in {\mathcal{L}}^2\left(J\right)$. This completes the proof.  □

Lemma 4.

If Q is an invertible, linear and bounded operator of K and $\left\{T_n\right\}$ is a frame of $H\otimes K$, then $\left\{T_{n}Q\right\}$ is also a frame.

Proof. 

It can be read in [22], Corollary 2.11.  □

Theorem 7.

If ${\left|\beta \right|}_{\infty }<(1+\parallel I-L^{\prime }{\parallel )}^{-1}$ and $\left\{f_m\right\},$ $\left\{g_n\right\}$ are frames of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right)$, respectively, then $\{f_m\otimes g_n^{\beta }\}$ is a frame.

Proof. 

With the hypothesis on the scale vector $\beta$, ${\mathcal{G}}^{\beta }$ is invertible. Consequently, ${\left({\mathcal{G}}^{\beta }\right)}^{*}$ is as well. Since $f_m\otimes g_n$ is a frame, applying the previous lemma, $\left(f_m\otimes g_n\right)\circ {\left({\mathcal{G}}^{\beta }\right)}^{*}$ is a frame.

Let us prove now that

$$\left(f_m\otimes g_n\right)\circ {\left({\mathcal{G}}^{\beta }\right)}^{*}=f_m\otimes g_n^{\beta }.$$

For any $g\in {\mathcal{L}}^2\left(J\right)$,

$$\begin{array}{c}\left(\left(f_m\otimes g_n\right)\circ {\left({\mathcal{G}}^{\beta }\right)}^{*}\right)\left(g\right)=<g_n,{\left({\mathcal{G}}^{\beta }\right)}^{*}\left(g\right)>f_m\hfill \\ \hfill =<{\mathcal{G}}^{\beta }\left(g_n\right),g>f_m=<g_n^{\beta },g>f_m=(f_m\otimes g_n^{\beta })\left(g\right).\end{array}$$

This equality completes the proof.  □

Theorem 8.

If ${\left|\alpha \right|}_{\infty }<{(1+\parallel I-L\parallel )}^{-1}$, ${\left|\beta \right|}_{\infty }<(1+\parallel I-L^{\prime }{\parallel )}^{-1}$ and $\left\{f_m\right\},$ $\left\{g_n\right\}$ are frames, then $\{f_m^{\alpha }\otimes g_n^{\beta }\}$ is a frame.

Proof. 

By definition of the tensor product of operators,

$$f_m^{\alpha }\otimes g_n^{\beta }=\left({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }\right)(f_m\otimes g_n)={\mathcal{F}}^{\alpha }\circ (f_m\otimes g_n)\circ {\left({\mathcal{G}}^{\beta }\right)}^{*}.$$

Let us consider now that, according to the previous theorem,

$$(f_m\otimes g_n)\circ {\left({\mathcal{G}}^{\beta }\right)}^{*}=f_m\otimes g_n^{\beta }.$$

Since ${\left({\mathcal{G}}^{\beta }\right)}^{*}$ is invertible, $f_m\otimes g_n^{\beta }$ is a frame. Then,

$$f_m^{\alpha }\otimes g_n^{\beta }={\mathcal{F}}^{\alpha }\circ (f_m\otimes g_n^{\beta })$$

is a frame, using Theorem 6.  □

Proposition 5.

If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$ and ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }^{-1}$ then ${\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$ is injective and

$$ran\left({\mathcal{F}}^{\alpha }\right)\otimes ran\left({\mathcal{G}}^{\beta }\right)=ran({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }).$$

(19)

Proof. 

With the hypotheses on $\alpha$ and $\beta$, ${\mathcal{F}}^{\alpha }$ and ${\mathcal{G}}^{\beta }$ are injective with closed range (Proposition 4.8 and Theorem 4.18 of [1]). Let us denote ${\tau }^{\alpha \beta }={\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }.$ Then, if $B\in ran\left({\mathcal{F}}^{\alpha }\right)\otimes ran\left({\mathcal{G}}^{\beta }\right)$, due to the properties of the tensor product of vectors:

$$B=\underset{k}{lim}\sum _{i,j=1}^k(f_i^{\alpha }\otimes g_j^{\beta })=\underset{k}{lim}\sum _{i,j=1}^k{\tau }^{\alpha \beta }(f_i\otimes g_j).$$

On the other side,

$$\underset{k}{lim}\sum _{i,j=1}^k(f_i\otimes g_j)=\underset{k}{lim}({\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1})(f_i^{\alpha }\otimes g_j^{\beta })\in {\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right).$$

(The inverse operators are defined on the range of ${\mathcal{F}}^{\alpha }$ and ${\mathcal{G}}^{\beta },$ respectively). The continuity and linearity of ${\tau }^{\alpha \beta }$ imply that

$$B={\tau }^{\alpha \beta }\left(\underset{k}{lim}\sum _{i,j=1}^k(f_i\otimes g_j)\right)\in ran({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }).$$

For the other content, if $B\in ran({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })$, then there exists $A\in {\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)$ such that $B={\tau }^{\alpha \beta }\left(A\right).$ Since

$$A=\underset{k}{lim}\sum _{i,j=1}^k(u_i\otimes v_j),$$

$$B={\tau }^{\alpha \beta }\left(A\right)=\underset{k}{lim}\sum _{i,j=1}^k(u_i^{\alpha }\otimes v_j^{\beta })\in ran\left({\mathcal{F}}^{\alpha }\right)\otimes ran\left({\mathcal{G}}^{\beta }\right).$$

The equality of ranges (19) implies that $ran\left({\tau }^{\alpha \beta }\right)$ is a Hilbert space and then closed. To prove the injectivity of ${\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$, let us consider that, if

$$({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })\left(A\right)=0,$$

then

$$A=({\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1})({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })\left(A\right)=0$$

according to Properties $\left(4\right)$ and $\left(6\right)$ of the tensor product of operators.  □

Corollary 2.

If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$ and ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }^{-1}$ then ${\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$ is bounded below.

Proof. 

In these hypotheses, ${\mathcal{F}}^{\alpha }$ and ${\mathcal{G}}^{\beta }$ are injective and ${\left({\mathcal{F}}^{\alpha }\right)}^{-1}$ and ${\left({\mathcal{G}}^{\beta }\right)}^{-1}$ are isomorphisms on $ran\left({\mathcal{F}}^{\alpha }\right)$ and $ran\left({\mathcal{G}}^{\beta }\right)$, respectively.

$${({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{-1}={\left({\mathcal{F}}^{\alpha }\right)}^{-1}\otimes {\left({\mathcal{G}}^{\beta }\right)}^{-1}$$

is bounded on $ran({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })$ and thus

$$\left|\right|\left|A\right|\left|\right|\le K\left|\right||{\tau }^{\alpha \beta }\left(A\right)\left|\right||,$$

for any $A\in {\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right).$  □

Corollary 3.

If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$ and ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }^{-1}$ then ${({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}$ is surjective.

Proof. 

In general,

$${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)=\overline{ran\left({({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\right)}\oplus ker({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }).$$

However, ${\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$ is injective and $ran({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })$ is closed, thus $ran\left({({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\right)$ is also closed ([23]). Consequently, the operator quoted is surjective.  □

Definition 8.

A sequence $\left\{x_m\right\}\subseteq H$, where H is a Hilbert space, is a frame sequence if it is a frame for its closed span $\left[x_m\right]=\overline{span}\left(x_m\right)$.

Proposition 6.

If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$ and ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }^{-1}$ and $f_m$ and $g_n$ are frames, then $f_m^{\alpha }\otimes g_n^{\beta }$ is a frame sequence.

Proof. 

According to the definition of frame sequence, we need to prove that there exist constants $K^{\prime },k>0$ such that, for all $B\in \overline{span}(f_m^{\alpha }\otimes g_n^{\beta })$,

$${k\left|\right|\left|B\right|\left|\right|}^2\le \sum _{m,n=1}^{\infty }|<B,f_m^{\alpha }\otimes g_n^{\beta }{>|}^2\le K^{\prime }{\left|\right|\left|B\right|\left|\right|}^2.$$

The right inequality is already proved in Theorem 4. According to Proposition 5, ${({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{-1}$ is bounded on the range of ${\tau }^{\alpha \beta }.$

If $B\in \overline{span}\{f_m^{\alpha }\otimes g_n^{\beta }\}$, since $({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })\circ {({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{-1}=Id,$

$$B={\left({({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{-1}\right)}^{*}\circ {({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\left(B\right),$$

then

$${\left|\right|\left|B\right|\left|\right|}^2\le \parallel {({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{-1}{\parallel }^2\left|\right||{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\left(B\right){\left|\right||}^2.$$

(20)

As $f_m\otimes g_n$ is a frame,

$$\left|\right||{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\left(B\right){\left|\right||}^2\le K\sum _{m,n=1}^{\infty }|<{({\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta })}^{*}\left(B\right),f_m\otimes f_n{>|}^2=K\sum _{m=1}^{\infty }{|<B,f_m^{\alpha }\otimes f_n^{\beta }>|}^2.$$

(21)

Hence (Equations (20) and (21)), there exists a constant $k>0$ such that

$${k\left|\right|\left|B\right|\left|\right|}^2\le \sum _{m=1}^{\infty }{|<B,f_m^{\alpha }\otimes g_n^{\beta }>|}^2,$$

and the left inequality is proved.  □

Definition 9.

A sequence $\left\{x_m\right\}$ of a Hilbert space H is a Riesz sequence if there exist $k_1,k_2>0$ such that for any $\left\{x_m\right\}\in l^2$

$$k_1\sum |c_m{|}^2\le \parallel \sum c_m{x}_m{\parallel }^2\le k_2\sum {\left|c_m\right|}^2.$$

Theorem 9.

Let $\left\{f_m\right\}$ and $\left\{g_n\right\}$ be Riesz bases of ${\mathcal{L}}^2\left(I\right)$ and ${\mathcal{L}}^2\left(J\right)$, respectively. If ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }_{\infty }^{-1}$ and ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }_{\infty }^{-1},$ $\{f_m^{\alpha }\otimes g_n^{\beta }\}$ is a Riesz sequence of ${\mathcal{L}}^2(I\times J).$

Proof. 

In these hypotheses, ${\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$ is a topological isomorphism on its range, and thus it preserves the bases.  □

Definition 10.

A sequence $\left\{x_m\right\}\subseteq H$ of a Banach space is a Schauder sequence if it is a Schauder basis ([24]) for $\left[x_m\right]=\overline{span}\left(x_m\right)$.

Theorem 10.

If $\left\{f_m\right\},$ $\left\{g_n\right\}$ are Riesz bases of ${\mathcal{L}}^2\left(I\right)$, ${\mathcal{L}}^2\left(J\right)$ and ${\left|\alpha \right|}_{\infty }<{\parallel L\parallel }^{-1}$, ${\left|\beta \right|}_{\infty }<{\parallel L^{\prime }\parallel }^{-1}$ then $f_m^{\alpha }\otimes g_n^{\beta }$ is a Schauder sequence of ${\mathcal{L}}^2(I\times J)$.

Proof. 

With the hypotheses given ${\tau }^{\alpha \beta }={\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }$ is a topological isomorphism from ${\mathcal{L}}^2\left(I\right)\otimes {\mathcal{L}}^2\left(J\right)$ on $range\left({\tau }^{\alpha \beta }\right)=\overline{span}\{f_m^{\alpha }\otimes g_n^{\beta }\}$ and the isomorphisms preserve the bases.  □

Proposition 7.

If the operators $L,L^{\prime }$ are defined as $Lf=f\circ c$, $L^{\prime }g=g\circ c^{\prime },$ where $c,c^{\prime }:I\to I$ are fixed mappings strictly increasing, continuous and such that $c\left(a\right)=c^{\prime }\left(a\right)=a$ and $c\left(b\right)=c^{\prime }\left(b\right)=b$, then 1 belongs to the point spectrum of ${\mathcal{F}}^{\alpha }\otimes {\mathcal{G}}^{\beta }.$

Proof. 

In this case, 1 belongs to the point spectrum of ${\mathcal{F}}^{\alpha }$ and ${\mathcal{G}}^{\beta }$ (Proposition 2 of [2]) and the product of eigenvalues is an eigenvalue of the tensor product.  □

4. Conclusions

In this article, we define Riesz bases of the Hilbert space ${\mathcal{L}}^2(I\times J),$ composed of products of single variable fractal functions. The factors are of type $\alpha$-fractal functions, which constitute a generalization (or perturbation) of any map defined on a compact real interval. An operator ${\mathcal{F}}^{\alpha }$ maps any (classical) function into its counterpart ($\alpha$-fractal). This operator is generalized in the paper to a two-dimensional operator via tensor product.

We also obtain weaker spanning systems of square integrable functions on the rectangle $I\times J,$ as Bessel, Riesz, Schauder and frame sequences and frames. All of them are composed of products of fractal functions. The frames own a greater flexibility in order to choose good approximations of mappings. We deduce also frame and Bessel constants, in terms of the bounds of the unperturbed (non-fractal) functions. We construct functions defined on the rectangle in order to simplify the formalism, but the definition and properties are straightforwardly generalizable to higher dimensions, considering products of three factors (functions on a parallelepiped) and more. The advantages and inconveniences are similar to the two-variable case. Of course, the higher dimensionality complicates the computational work, cost and graphical performances.