Numerical Simulation for the Treatment of Nonlinear Predator–Prey Equations by Using the Finite Element Optimization Method
Abstract
:1. Introduction
- 1.
- FEM allows for easier modeling of complex geometrical and irregular shapes.
- 2.
- FEM can be adapted to obtain the solution of the problem with a high degree of accuracy to decrease the need for physical prototypes in the design process.
- 3.
- FEM is remarkably useful for certain time-dependent simulations, such as crash simulations in which deformations in one area depend upon deformations in another area.
2. The Model of the Lotka–Volterra System (with Two Predators and One Prey)
3. Procedure of Solution by the Finite Element Method (FEM)
- 1.
- Finite-element discretization:The whole domain is divided into a finite number of sub-domains, which is called the discretization of the domain. Each sub-domain is called an element. The collection of elements is called the finite-element mesh.
- 2.
- Generation of the element equations:
- From the mesh, a typical element is isolated and the variational formulation of the given problem over the typical element is then constructed.
- An approximate solution of the variational problem is assumed and the element equations are formulated by substituting this solution into the above system.
- The element matrix, which is called the stiffness matrix, is constructed by using the element interpolation functions.
- 3.
- Assembly of the element equations:The algebraic equations so obtained are assembled by imposing the inter-element continuity conditions. This yields a large number of algebraic equations known as the global finite element model, which governs the whole domain.
- 4.
- Imposition of the boundary conditions:The essential and natural boundary conditions are imposed on the assembled equations.
- 5.
- Solution a system of algebraic equations:The obtained system of algebraic equations can be solved by any one of the appropriate numerical techniques.
3.1. Variational Formulation of the System
3.2. Finite Element Formulation of the Model
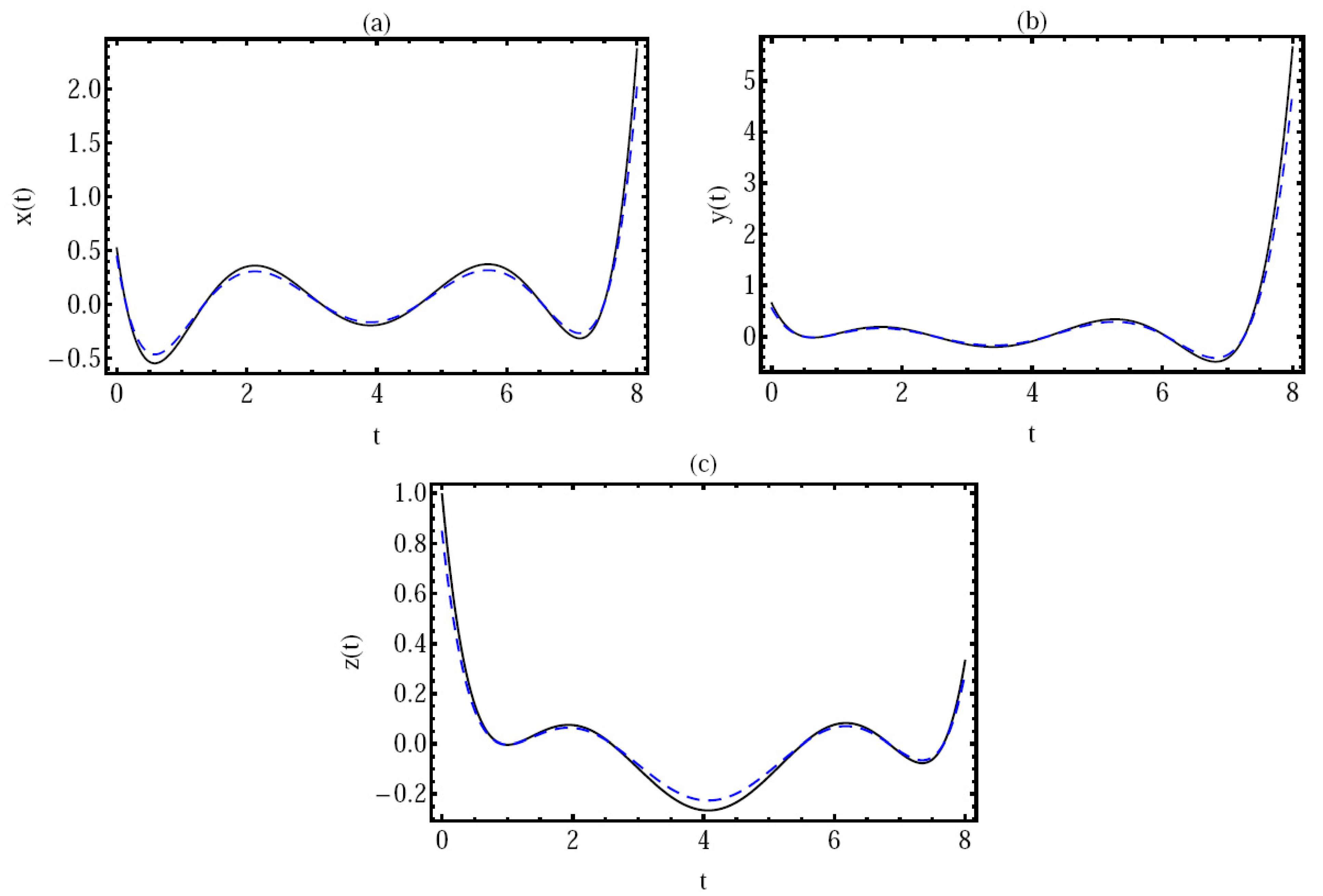
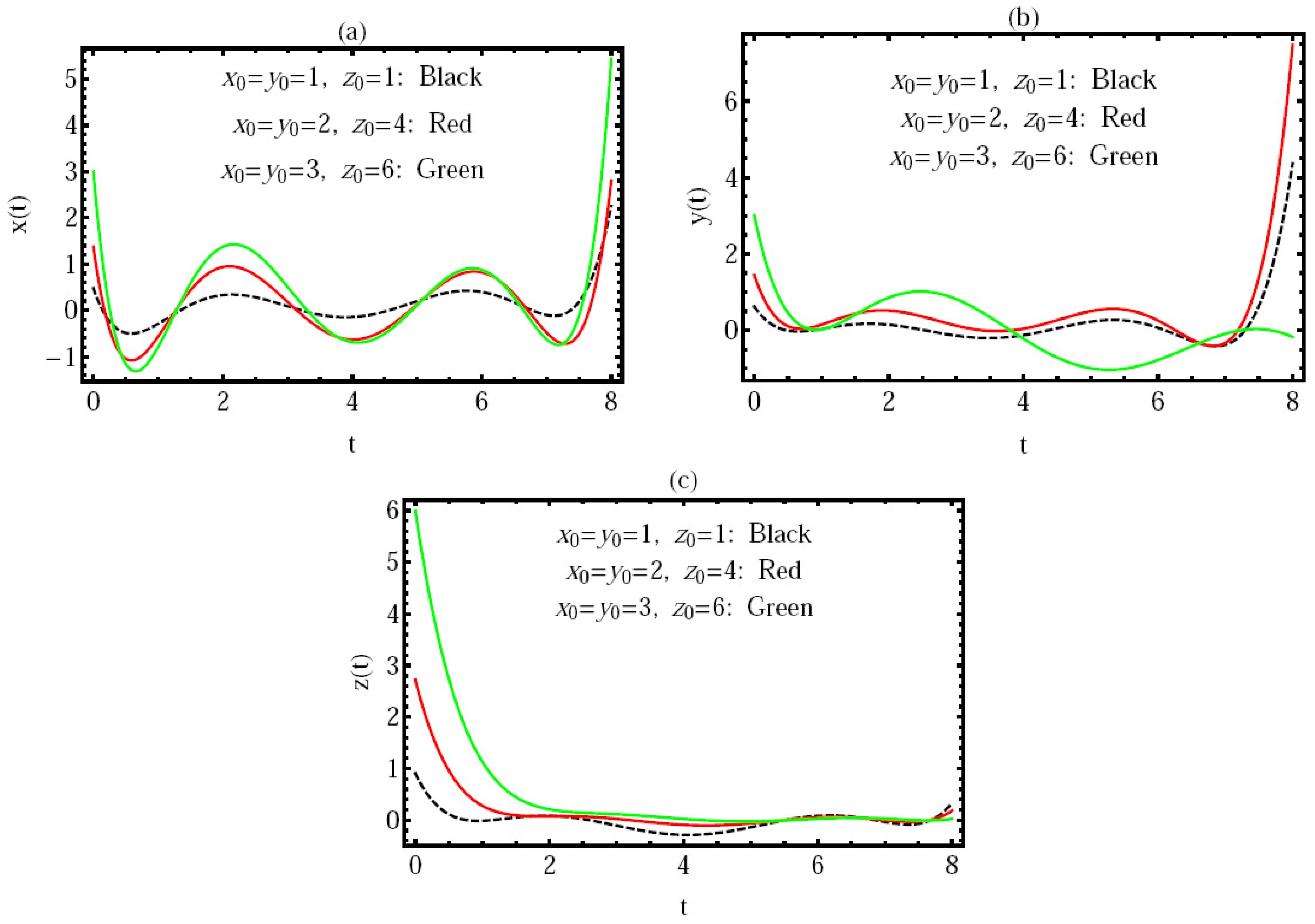
4. Numerical Simulation
- i.
- ; (a) for the solution ;
- ii.
- ; (b) for the solution ;
- iii.
- ; (c) for the solution .
- i.
- (a);
- ii.
- (b);
- iii.
- (c).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, M.R.; Hadhoud, A.R.; Srivastava, H. Solution of fractional Volterra-Fredholm integro-differential equations under mixed boundary conditions by using the HOBW method. Adv. Differ. Equ. 2019, 2019, 115. [Google Scholar] [CrossRef] [Green Version]
- Homeier, H.H.; Srivastava, H.M.; Masjed-Jamei, M.; Moalemi, Z. Some weighted quadrature methods based upon the mean value theorems. Math. Methods Appl. Sci. 2021, 44, 3840–3856. [Google Scholar] [CrossRef]
- Khader, M.M.; Sharma, R.P. Evaluating the unsteady MHD micropolar fluid flow past stretching/shirking sheet with heat source and thermal radiation: Implementing fourth order predictor-corrector FDM. Math. Comput. Simulat. 2021, 181, 333–350. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Iqbal, J.; Arif, M.; Khan, A.; Gasimov, Y.S.; Chinram, R. A new application of Gauss quadrature method for solving systems of nonlinear equations. Symmetry 2021, 13, 432. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Khader, M.M. An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals 2020, 140, 110174. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Garvie, M.R.; Burkardt, J.; Morgan, J. Simple finite element methods for approximating predator-prey dynamics in two dimensions using Matlab. Bull. Math. Biol. 2015, 77, 548–578. [Google Scholar] [CrossRef] [PubMed]
- Khader, M.M.; Abualnaja, K.M. Galerkin-FEM for obtaining the numerical solution of the linear fractional Klein-Gordon equation. J. Appl. Anal. Comput. 2019, 9, 261–270. [Google Scholar] [CrossRef]
- Bougoffa, L.; Khanfer, A. On the solutions of the generalized Lotka-Volterra system. In Proceedings of the ITM Web of Conferences, Moscow, Russia, 28–29 November 2019; pp. 1–6. [Google Scholar]
- Atangana, A.; Gómez-Aguilar, J.F. A new derivative with normal distribution kernel: Theory, methods and applications. Phys. A Statist. Mech. Appl. 2017, 476, 1–14. [Google Scholar] [CrossRef]
- Ghanbari, B.; Günerhan, H.; Srivastava, H.M. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fractals 2020, 138, 109919. [Google Scholar] [CrossRef]
- Bhargava, R.; Sharma, S.; Takhar, H.S.; Beg, O.A.; Bhargava, P. Numerical solutions for micropolar transport phenomena over a nonlinear stretching sheet. Nonlinear Anal. Model. Cont. 2007, 12, 45–63. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall, Pearson Education Incorporated: New York, NY, USA, 2006. [Google Scholar]
- Lin, Y.-Y.; Lo, S.-P. Finite element modeling for chemical mechanical polishing process under different back pressures. J. Mater. Process. Technol. 2003, 140, 646–652. [Google Scholar] [CrossRef]
- Hansbo, A.; Hansbo, P. A finite element method for the simulation of strong and weak discontinuities in solid mechanics. Comput. Methods Appl. Mech. Eng. 2004, 139, 3523–3540. [Google Scholar] [CrossRef]
- Rana, P.; Bhargava, R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 212–226. [Google Scholar] [CrossRef]


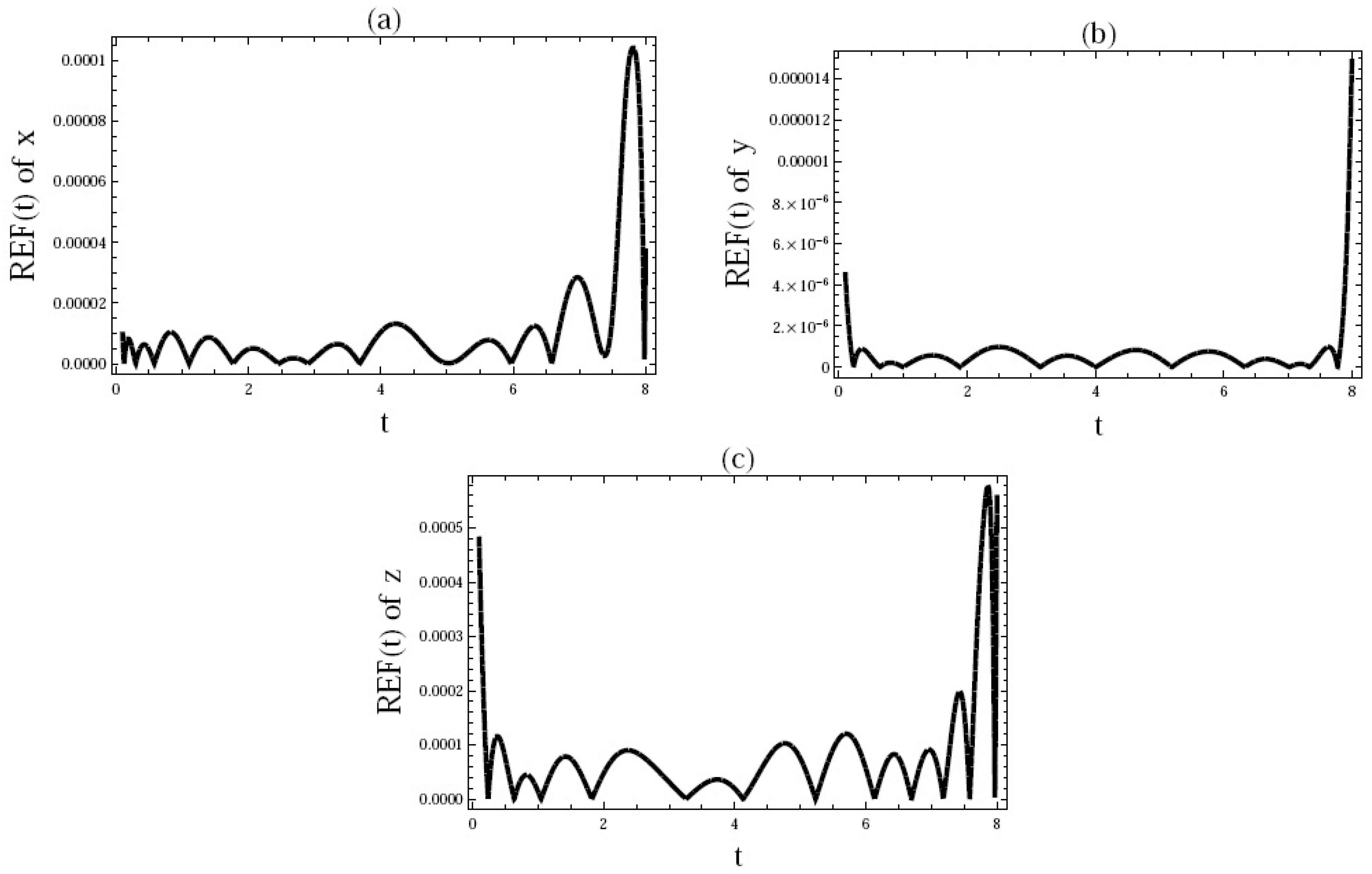
| Relative Error—Present FEOM: | Relative Error—RK4: | |||||
|---|---|---|---|---|---|---|
| 0 | 3.15972 | 4.85231 | 5.98745 | 3.12345 | 1.65482 | 2.35479 |
| 1 | 3.75361 | 4.98765 | 1.85317 | 0.96325 | 2.74123 | 1.85213 |
| 2 | 2.85264 | 0.05217 | 1.85214 | 6.36547 | 2.96542 | 9.85471 |
| 3 | 2.12358 | 4.98541 | 3.65412 | 9.75612 | 2.95423 | 1.95423 |
| 4 | 4.32546 | 6.02546 | 5.85642 | 9.95423 | 5.35491 | 1.32564 |
| 5 | 7.85214 | 0.32541 | 6.65482 | 3.02587 | 3.65821 | 9.78523 |
| 6 | 1.12597 | 2.32587 | 5.95421 | 0.65478 | 1.32587 | 4.58241 |
| 7 | 8.65874 | 2.32541 | 6.96325 | 4.74185 | 3.00254 | 1.21504 |
| 8 | 1.25846 | 3.24680 | 5.25813 | 7.89240 | 9.11005 | 1.90412 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Khader, M.M. Numerical Simulation for the Treatment of Nonlinear Predator–Prey Equations by Using the Finite Element Optimization Method. Fractal Fract. 2021, 5, 56. https://doi.org/10.3390/fractalfract5020056
Srivastava HM, Khader MM. Numerical Simulation for the Treatment of Nonlinear Predator–Prey Equations by Using the Finite Element Optimization Method. Fractal and Fractional. 2021; 5(2):56. https://doi.org/10.3390/fractalfract5020056
Chicago/Turabian StyleSrivastava, H. M., and M. M. Khader. 2021. "Numerical Simulation for the Treatment of Nonlinear Predator–Prey Equations by Using the Finite Element Optimization Method" Fractal and Fractional 5, no. 2: 56. https://doi.org/10.3390/fractalfract5020056
APA StyleSrivastava, H. M., & Khader, M. M. (2021). Numerical Simulation for the Treatment of Nonlinear Predator–Prey Equations by Using the Finite Element Optimization Method. Fractal and Fractional, 5(2), 56. https://doi.org/10.3390/fractalfract5020056







