A q-Gradient Descent Algorithm with Quasi-Fejér Convergence for Unconstrained Optimization Problems

Abstract

We present an algorithm for solving unconstrained optimization problems based on the q-gradient vector. The main idea used in the algorithm construction is the approximation of the classical gradient by a q-gradient vector. For a convex objective function, the quasi-Fejér convergence of the algorithm is proved. The proposed method does not require the boundedness assumption on any level set. Further, numerical experiments are reported to show the performance of the proposed method.

1. Introduction

The descent direction plays a central role in the development of optimization algorithms. The classical gradient descent method was first proposed by Cauchy [1] in 1847. The optimization problem is a significant mathematical model in a wide class of disciplines [2]. In applications such as image processing [3], data analysis [4], and machine learning [5], in which one needs to quickly provide an approximate solution, several gradient-based algorithms [6,7,8,9] have been proposed based on the iterative technique of the gradient descent method [2,10]. Quantum calculus is the modern field for the investigation of calculus without limits. Quantum calculus, or q-calculus, began with the work of Jackson in the early twentieth century [11], but similar kinds of calculus had already been developed by Euler and Jacobi in the eighteenth and nineteenth centuries, respectively. Recently it has come under deep interest due to the high demand of mathematics that models quantum computing. Besides appearing as a connection between mathematics and physics, q-calculus has many applications in different mathematical areas such as operator theory [12], combinatorics [13], orthogonal polynomials [14], basic hyper-geometric functions [15], and other sciences like quantum theory [16,17], mechanics [18], and fractional calculus [19,20,21,22,23,24,25]. For more recent studies about fractional calculus analysis and applications, refer to [26,27,28,29,30,31].

The q-Taylor formula for functions of several variables with mean value theorems in q-calculus was first used to develop a new method for solving systems of equations [32]. The advantage of q-calculus is shown in the next example [32] where the a scheme involving q-derivatives finds the solution, but the classical Newton–Kantorovich method fails to do so

$$\left\{\begin{array}{c}|x_1^2-4|+e^{7x_2-36}=2,\hfill \\ {log}_{10}\left|\frac{12x_1^2}{x_2}-6\right|+x_1^4=9.\hfill \end{array}\right.$$

For $q=0.9$, the iterations converge to the exact solution as

$${(x_1,x_2)}^T={\left(\sqrt{3},\frac{36}{7}\right)}^T.$$

The concept of the q-analogy of the gradient was first introduced in [33] for solving systems of equations. It has some advantages with respect the classical method when the functions are not differentiable. Further, the same concept of q-gradient was introduced in the steepest descent method [34] to optimize single objective functions [35]. The parameter q was generated by a Gaussian distribution with standard deviation $\sigma$ that decreases by an iterative process as

$${\sigma }^{(k+1)}=\beta {\sigma }^{\left(k\right)},$$

with a starting standard deviation ${\sigma }^0$ and the reduction factor $\beta$. The step length was generated using the golden section search method [34]. However, the convergence properties of the steepest descent method with inexact line searches have been studied under several strategies for the choice of the step length ${\alpha }_k$ [36,37,38]. Recently, several modified unconstrained optimization algorithms using the q-gradient have been proposed to solve unconstrained optimization problems [10,19,39,40,41].

In this paper, we propose a q-gradient line search scheme that provides a q-descent direction at every kth iteration. For this, a sequence $\left\{q^{\left(k\right)}\right\}$ [39] is taken to generate the values of q, and the backtracking technique is utilized to find the step length without requiring the bounded level sets or Lipschitz condition on the gradient of the function. We also provide the convergence proof theoretically when step length is fixed without any hypothesis on the level sets of the objective function. The advantage of using q-gradient is shown by comparing our method with the method given in [36] based on the number of iterations and function evaluations.

The paper is organized as follows. In the next section, some notations and definitions for q-calculus and other prerequisites are provided, which are used throughout the paper. In Section 3, the q-gradient descent algorithm is given, and its convergence analysis is provided in Section 4. Numerical experiments are performed in Section 4, which is followed by a section of concluding remarks.

2. Essential Preliminaries

We assume that ${\mathbb{R}}_{+}$ stands for the nonnegative real line, $q\in (0,1)$ is a real number, and the q-integer ${\left[n\right]}_q$ is given as:

$${\left[n\right]}_q=\left\{\begin{array}{cc}{\displaystyle \frac{1-q^n}{1-q}},\hfill & q\ne 1,\hfill \\ n,\hfill & q=1,\hfill \end{array}\right.$$

(1)

for all $n\in \mathbb{N}$. The expansion of ${(1+x)}_q^n$ is:

$${(1+x)}_q^n=\left\{\begin{array}{cc}1,\hfill & n=0,\hfill \\ (1+x)(1+qx)\dots (1+q^{n-1}x),\hfill & n\ge 1.\hfill \end{array}\right.$$

(2)

The q-derivative of $x^n$ with respect to x is:

$$D_q{x}^n={\left[n\right]}_q{x}^{n-1}.$$

The q-derivative of a function $\psi :\mathbb{R}\to \mathbb{R}$ is given by

$$D_q\psi \left(x\right)={\displaystyle \frac{\psi \left(qx\right)-\psi \left(x\right)}{qx-x}},(x\ne 0).$$

In the special case, $D_q\psi \left(0\right)=\frac{\mathrm{d}\psi \left(0\right)}{\mathrm{d}x}.$

If $\psi$ is differentiable, then

$$\underset{q\to 1}{lim}{D}_q\psi \left(x\right)=\underset{q\to 1}{lim}\frac{\psi \left(qx\right)-\psi \left(x\right)}{(q-1)x}=\frac{\mathrm{d}\psi \left(x\right)}{\mathrm{d}x}.$$

The higher order q-derivatives of $\psi$ are:

$$D_q^0\psi :=\psi ,D_q^n:=D_q\left(D_q^{n-1}\psi \right),(n=1,2,3,\dots ).$$

The q-derivative of a function is a linear operator [42] for any constants $c_1$ and $c_2$ as:

$$D_q\left\{c_1{\psi }_1\left(x\right)+c_2{\psi }_2\left(x\right)\right\}=c_1{D}_q{\psi }_1\left(x\right)+c_2{D}_q{\psi }_2\left(x\right).$$

Let $\psi \left(x\right)$ be a continuous function on $[a,b]$, where $a,b\in \mathbb{R}$. Then, there exists $\widehat{q}\in (0,1)$ and $x\in (a,b)$ [43] such that

$$\psi \left(b\right)-\psi \left(a\right)=D_q\psi \left(x\right)(b-a),$$

(3)

for all $q\in (\widehat{q},1)\cup (1,{\widehat{q}}^{-1})$. The q-partial derivative of function $\psi :{\mathbb{R}}^n\to \mathbb{R}$ at $x\in {\mathbb{R}}^n$ with respect to $x_i$ is defined as (see ([35]):

$$D_{q_i,x_i}\psi \left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{(1-q_i)x_i}}[\psi \left(x_1,x_2,\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_n\right)\hfill & \\ -\psi \left(x_1,x_2,\dots ,x_{i-1},q_i{x}_i,x_{i+1},\dots ,x_n\right)],\hfill & x_i\ne 0,q_i\ne 1,\hfill \\ {\displaystyle \frac{\partial }{\partial x_i}}\psi \left(x_1,x_2,\dots ,x_{i-1},0,x_{i+1},\dots ,x_n\right),\hfill & x_i=0,\hfill \\ {\displaystyle \frac{\partial }{\partial x_i}}\psi \left(x_1,x_2,\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_n\right),\hfill & q_i=1.\hfill \end{array}\right.$$

A function is called q-differentiable at a point if its q-partial derivatives are continuous. A continuously q-differentiable function $\psi$ is a function whose q-derivative function is also continuous at the point. We now choose the parameter q as a vector; that is,

$$q={(q_1,\dots ,q_i,\dots ,q_n)}^T\in {\mathbb{R}}^n.$$

Then, the q-gradient vector [35] of $\psi :{\mathbb{R}}^n\to \mathbb{R}$ is:

$${\nabla }_q\psi {\left(x\right)}^T=\left[\begin{array}{ccccc}{D}_{q_1,x_1}\psi \left(x\right)& \dots & D_{q_i,x_i}\psi \left(x\right)& \dots & D_{q_n,x_n}\psi \left(x\right)\end{array}\right].$$

(4)

Let $\left\{q_i^{\left(k\right)}\right\}$ [10,41] be a real sequence defined by

$$q_i^{(k+1)}=1-\frac{q_i^{\left(k\right)}}{{(k+1)}^2},$$

(5)

for each $i=1,\dots ,n$, where $k=0,1,2\dots$ and $0<q_i^{\left(0\right)}<1$. Of course, the sequence $\left\{q_i^{\left(k\right)}\right\}$ converges to ${(1,\dots ,1)}^T$ as $k\to \infty$, so that the q-gradient reduces to the classic gradient vector.

Proposition 1.

If $\psi \left(x\right)=a_0+x^{T}a$, where $a_0\in \mathbb{R}$ and $a\in {\mathbb{R}}^n,$ then for any x, $q\in {\mathbb{R}}^n$,

$${\nabla }_{q^{\left(k\right)}}\psi \left(x\right)=\nabla \psi \left(x\right)=a.$$

Example 1.

Consider a function $\psi :{\mathbb{R}}^2\to \mathbb{R}$ such that $\psi \left(x\right)=\frac{1}{x_1{x}_2}$. Then, the q-gradient is given as

$${\nabla }_{q^{\left(k\right)}}\psi \left(x\right)=-\frac{1}{x_1{x}_2}\left[\begin{array}{c}{\displaystyle \frac{1}{q_1^{\left(k\right)}{x}_1}}\\ {\displaystyle \frac{1}{q_2^{\left(k\right)}{x}_2}}\end{array}\right].$$

Definition 1

(q–Integral [42]). The q-analog of the integral is given by

$${\int }_0^b\psi \left(x\right){\mathrm{d}}_{q}x=b(1-q)\sum _{k=0}^{\infty }\psi \left(b{q}^k\right)q^k.$$

(6)

In the special case, it reduces to the classical integral ${\int }_0^b\psi \left(x\right)dx$, when $q\to 1$. It is right only in the case [44]

$${\int }_0^{1}x{d}_{q}x=(1-q)\sum _{k=0}^{\infty }{q}^k·q^k=\frac{1}{1+q}.$$

Definition 2

(q-Newton–Leibniz formula [42]). The q-anti-derivative of $\psi \left(x\right)$ is

$$F_q\left(x\right)={\int }_0^x\psi \left(t\right){\mathrm{d}}_{q}t.$$

(7)

In that manner, the q-Newton–Leibnitz formula is

$${\int }_a^b\psi \left(t\right){\mathrm{d}}_{q}t=F_q\left(b\right)-F_q\left(a\right).$$

(8)

Definition 3

(Quasi-Fejér Convergence [36]). A sequence $\left\{x^{\left(k\right)}\right\}$ is quasi-Fejèr convergent to a set $\mathcal{U}\subseteq {\mathbb{R}}^n$ if for every $u\in \mathcal{U}$, there exists a non-negative, summable sequence $\left\{{ϵ}_k\right\}\subseteq \mathbb{R}$ such that ${ϵ}_k\ge 0,$${\sum }_{k=0}^{\infty }{ϵ}_k<\infty$ and

$${∥x^{(k+1)}-u∥}^2\le {∥x^{\left(k\right)}-u∥}^2+{ϵ}_k,$$

for all k.

In the next section, the q-gradient descent algorithm is presented for solving unconstrained optimization problems.

3. A $\mathit{q}$–Gradient Descent Algorithm

We consider the unconstrained optimization problem:

$$min\psi \left(x\right),x\in {\mathbb{R}}^n,$$

(9)

where $\psi :{\mathbb{R}}^n\to \mathbb{R}$ is a continuously q-differentiable convex function. Note that min is same as the max of $-\psi \left(x\right)$. We choose a starting point $x^{\left(0\right)}\in {\mathbb{R}}^n$. The general iterative scheme to solve (9) using the q-gradient is of the following form:

$$x^{(k+1)}=x^{\left(k\right)}+{\alpha }_k{d}_{q^{\left(k\right)}}^{\left(k\right)},$$

(10)

where $x^{(k+1)}$ is a new iterative point, $x^{\left(k\right)}$ is the previous iterative point, and $d_{q^{\left(k\right)}}^{\left(k\right)}$ is a q-descent direction given as:

$$d_{q^{\left(k\right)}}^{\left(k\right)}=-{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right),$$

and ${\alpha }_k\in \mathbb{R}$ is called the step length can be computed by two main line search strategies: exact line search and inexact line search. The exact optimal step length theoretically cannot be found for practical computation, and it is expensive to generate the value of ${\alpha }_k$. Therefore, the most frequently used technique in practice is inexact line searching for finding the descent direction. When inexact line searches are performed then ${\alpha }_k$ is assigned a given predetermined value or through some finite iterative method. Note that existence of a solution to the minimization problem (9) is implicitly assumed. The condition for the existence of a solution [2] in the context of q-calculus is:

$$x^{\left(k\right)}\to x^{*}\in \mathsf{\Omega }:=\left\{x:{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)=0\right\}.$$

The following result presents the first-order necessary condition in the light of q-calculus.

Theorem 1.

Let Ω be a subset of ${\mathbb{R}}^n$ and ψ be a first-order q-differentiable real valued function on Ω. If $x^{*}$ is a local minimizer of ψ over Ω, then for any feasible q-direction $d_{q^{\left(k\right)}}^{\left(k\right)}$ at $x^{*}$, we have

$${\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)\ge 0.$$

Proof. 

We consider $x\left(\alpha \right):=x^{*}+\alpha d_{q^{\left(k\right)}}^{\left(k\right)}\in \mathsf{\Omega }$. For $\alpha =0$, we obtain $x\left(0\right)=x^{*}$. Define the composite function $f\left(\alpha \right)=\psi \left(x\right(\alpha \left)\right).$ Applying q-Taylor’s theorem to $\psi \left(\alpha \right)$ and taking $\alpha =0,$ we obtain

$$\psi \left(\alpha \right)=\psi \left(0\right)+\alpha {\psi }^{\prime }\left(0\right)+O\left(\alpha \right).$$

We can write this as

$$\begin{array}{cc}\hfill \psi \left(\alpha \right)-\psi \left(0\right)& =\alpha {\psi }^{\prime }\left(0\right)+O\left(\alpha \right)\hfill \\ \hfill \psi (x^{*}+\alpha d)-\psi \left(x^{*}\right)& =\alpha {\psi }^{\prime }\left(0\right)+O\left(\alpha \right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\psi }^{\prime }\left(\alpha \right)=\frac{{\mathrm{d}}_q}{{\mathrm{d}}_q\alpha }\psi \left(x\left(\alpha \right)\right)& =\frac{{\mathrm{d}}_q}{{\mathrm{d}}_q\alpha }\psi \left(x^{*}+\alpha d_{q^{\left(k\right)}}^{\left(k\right)}\right)\hfill \\ \hfill & ={\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}+\alpha d_{q^{\left(k\right)}}^{\left(k\right)}\right).\hfill \end{array}$$

At $\alpha =0$ and when we have $x^{*}=x\left(0\right)$, then

$${\psi }^{\prime }\left(0\right)={\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x\left(0\right)\right).$$

Therefore,

$$\begin{array}{c}\hfill \psi \left(x^{*}+\alpha d_{q^{\left(k\right)}}^{\left(k\right)}\right)-\psi \left(x^{*}\right)=\alpha {\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x\left(0\right)\right)+O\left(\alpha \right),\end{array}$$

(11)

where $\alpha \ge 0.$ Since $x^{*}$ is a local minimizer of $\psi$ over $\mathsf{\Omega }$, for $\alpha$ sufficiently small $\alpha >0$, we can write

$$\psi \left(x^{*}\right)\le \psi \left(x^{*}+\alpha d_{q^{\left(k\right)}}^{\left(k\right)}\right).$$

(12)

From (11) and (12),

$$\alpha {\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x\left(0\right)\right)=\psi \left(x^{*}+\alpha d_{q^{\left(k\right)}}^{\left(k\right)}\right)-\psi \left(x^{*}\right)\ge 0,$$

that is,

$$\alpha {\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x\left(0\right)\right)\ge 0.$$

Since $\alpha >0$, then

$${\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T\nabla \psi \left(x\left(0\right)\right)\ge 0.$$

Since $x\left(0\right)=x^{*}$, then

$${\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)\ge 0.$$

This completes the proof. □

We present the following result for the interior case in the context of q-calculus.

Corollary 1.

Let Ω be a subset of ${\mathbb{R}}^n$ and ψ be a first-order q-differentiable real valued function on Ω. If $x^{*}$ is a local minimizer of ψ over Ω and if $x^{*}$ is an interior point of Ω, then ${\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)=0$.

Proof. 

Since $x^{*}$ is a local minimizer of $\psi$ over $\mathsf{\Omega }$, then for any feasible q-direction, we have

$${\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)\ge 0.$$

(13)

Since $x^{*}$ is an interior point of $\mathsf{\Omega }$, then every q-direction is a feasible direction, therefore

$$-{\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}f\left(x^{*}\right)\ge 0.$$

(14)

From (13) and (14), we obtain

$${\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)=0.$$

For all $d_{q^{\left(k\right)}}^{\left(k\right)}\in {\mathbb{R}}^n$, we obtain ${\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)=0$. This completes the proof. □

Before writing an algorithm for the q-gradient descent method, we need the following assumptions.

Assumption 1.

We consider the two following assumptions:

1.

Let $\psi :{\mathbb{R}}^n\to \mathbb{R}$ be convex and continuously q-differentiable.

2.

The q-gradient of ψ with constant $\mathcal{L}>0$ satisfies the following condition:

$$∥{\nabla }_q\psi \left(x\right)-{\nabla }_q\psi \left(y\right)∥\le \mathcal{L}\parallel x-y\parallel ,$$

(15)

for all $x,y\in {\mathbb{R}}^n$.

Assumption 2.

Let $\varphi :{\mathbb{R}}_{+}\to \mathbb{R}$ be such that:

1.

ϕ is convex and continuously q-differentiable on $[0,\infty )$,

2.

$\varphi \left(0\right)=0$ and ${\varphi }^{\prime }\left(0\right)<1$,

3.

${lim}_{v\to 0^{+}}\frac{\varphi \left(v\right)}{v^2}>0$.

Note that (3) implies that ${\varphi }^{\prime }\left(0\right)\ge 0$, thus from (2), we obtain $0\le {\varphi }^{\prime }\left(0\right)<1$ and from (1), $\varphi$ is convex and continuously q-differentiable. Therefore, $\varphi$ is non-decreasing. The statement of the theorem given in [45] can be presented in the light of q-calculus as given below.

Theorem 2.

Let $\mathcal{F}:{\mathbb{R}}^n\times \mathbb{R}\to \mathbb{R}$ such that

1.

There exists $(x^{\circ },u^{\circ })\in {\mathbb{R}}^n\times \mathbb{R}$ such that $\mathcal{F}\left(x^{\circ },u^{\circ }\right)=0$,

2.

$\mathcal{F}$ is continuous in a neighborhood of $\left(x^{\circ },u^{\circ }\right)$,

3.

$\mathcal{F}$ is q-differentiable with respect to the variable u in $\left(x^{\circ },u^{\circ }\right)$ and

$$\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}\left(x^{\circ },u^{\circ }\right)\ne 0.$$

Then, there exists a neighborhood $\mathcal{U}\left(x^{\circ }\right)$ of $x^{\circ }$ and at least one function $\varrho :\mathcal{U}\left(x^{\circ }\right)\to \mathbb{R}$ such that $\varrho \left(x^{\circ }\right)=u^{\circ }$ and

$$\mathcal{F}(x,\varrho (x\left)\right)=0,$$

(16)

for any $x\in \mathcal{U}\left(x^{\circ }\right)$.

4.

If $\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}(.,.)$ is continuous at $(x^{\circ },u^{\circ }),$ then the function ϱ is the only one that satisfies (16) and is continuous at $(x^{\circ },u^{\circ })$.

Note that the proof q-analogue of the above implicit function theorem is out of the scope of the present research. For developing the algorithm, we need the following proposition whose proof is given in the light of [36].

Proposition 2.

Let

$$\mathcal{G}=\left\{x\in {\mathbb{R}}^n|{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)\ne 0\right\},$$

and ϕ satisfy Assumption 2. Then,

1.

For all $x\in \mathcal{G}$, there exists a unique $\varrho \left(x\right)>0$ such that

$$\psi \left(x\right)-\psi \left(x-\varrho \left(x\right){\nabla }_{q^{\left(k\right)}}\psi \left(x\right)\right)=\varphi \left(\varrho \left(x\right)\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)∥}^2,$$

(17)

and

$$\psi \left(x-u{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)\right)+\varphi \left(u\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)∥}^2\le \psi \left(x\right),$$

(18)

if and only if $0\le u\le \varrho \left(x\right)$.

2.

$\varrho :\mathcal{G}\to {\mathbb{R}}_{+}$ is continuous in $\mathcal{G}$.

Proof. 

• We first prove (1). Fix $x\in \mathcal{G}$, $u\in {\mathbb{R}}_{+}$ and define the function in the context of q-calculus as:

  $$\mathcal{F}(x,u)=\psi \left(x-u{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)\right)-\psi \left(x\right)+\varphi \left(u\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)∥}^2.$$

  (19)
  From (1) of Assumption 2, $\mathcal{F}(x,.)$ is convex and continuously q-differentiable, and when substituting $u=0$ in (19), then we obtain

  $$\mathcal{F}(x,0)=\varphi \left(0\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)∥}^2.$$
  From (2) of Assumption 2, we have $\varphi \left(0\right)=0$, thus

  $$\mathcal{F}(x,0)=0.$$

  (20)
  Applying q-derivative with respect to u to (19), then

  $$\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}={\nabla }_q\psi (x-u{\nabla }_q\psi \left(x\right))\left(-{\nabla }_q\psi \left(x\right)\right)+{\varphi }^{\prime }\left(0\right){\parallel {\nabla }_q\psi \left(x\right)\parallel }^2,$$

  (21)
  Substituting $u=0$ in the right hand side of above equation, we obtain

  $$\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}={∥{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)∥}^2\left(-1+{\varphi }^{\prime }\left(0\right)\right),$$

  (22)
  Since ${\varphi }^{\prime }\left(0\right)<1$, then

  $$\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}<0.$$

  (23)
  In addition,

  $$\mathcal{F}(x,u)\ge {\psi }^{*}-\psi \left(x\right)+\varphi \left(u\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x\right)∥}^2,$$

  (24)

  where ${\psi }^{*}$ is the minimum function value of $\psi$. From (20) and (23), we conclude that $\mathcal{F}(x,.)$ is negative in some interval to the right of zero, and from (24), (1) and (2) of Assumption 2, we obtain

  $$\underset{u\to \infty }{lim}\mathcal{F}(x,u)\ge +\infty .$$

  (25)
  From Theorem 2 it follows that there exists $\varrho \left(x\right)>0$ such that $\mathcal{F}(x,\varrho (x\left)\right)=0$. Using the above value in (19), we obtain (17). Since $\mathcal{F}(x,.)$ is convex, therefore there exists a uniqueness of $\varrho \left(x\right)$. Note that a convex function of a real variable can take a given value different from its minimum point at most two different points while

  $$\mathcal{F}(x,.)=\mathcal{F}(x,\varrho (x\left)\right)=0,$$

  and from (20) and (23), the minimum point of $\mathcal{F}(x,.)$ is not zero. Thus, (1) of this proposition is proved.
• Let $u^{\left(0\right)}=\varrho \left(x^{\left(0\right)}\right)$ given by (1), for a given $x^{\left(0\right)}\in \mathcal{G}$. Then, we have that

  $$\mathcal{F}(x^{\left(0\right)},u^{\left(0\right)})=0,$$
  $F(.,.)$ is continuous in a neighborhood of $(x^{\left(0\right)},u^{\left(0\right)})$ and from (21)

  $$\begin{array}{cc}\hfill \frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}\left(x^{\left(0\right)},u^{\left(0\right)}\right)& =-{\nabla }_{q^{\left(k\right)}}\psi {\left(x^{\left(0\right)}-u^{\left(0\right)}{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(0\right)}\right)\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(0\right)}\right)\hfill \\ \hfill & +{\varphi }^{\prime }\left(u^{\left(0\right)}\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(0\right)}\right)∥}^2.\hfill \end{array}$$

  (26)
  As $\mathcal{F}\left(x^{\left(0\right)},.\right)$ is strictly increasing at $u^{\left(0\right)}$, we have that

  $$\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}\left(x^{\left(0\right)},u^{\left(0\right)}\right)>0.$$
  From (26) we observe that $\frac{{\partial }_q\mathcal{F}}{{\partial }_{q}u}(.,.)$, is continuous at $\left(x^{\left(0\right)},u^{\left(0\right)}\right)$ and all the hypotheses of Theorem 2 hold. Thus u is continuous at $x^{\left(0\right)}$.

□

We present the following Algorithm 1.

Algorithm 1:q-Gradient Descent (q-GD) Algorithm

Remark 1

([36]). Two important facts about computing ${\alpha }_k$ are presented below:

1.

In Algorithm 1, the modified backtracking technique finds ${\alpha }_k$ using only one inequality instead of two inequalities required in [46]

2.

We can find ${\alpha }_k$ by another technique; we take positive numbers ${\delta }_1$ and ${\delta }_2$ such that

$${\displaystyle \frac{\mathcal{L}}{1+{\widehat{M}}_k}}{\delta }_1<1-{\delta }_2,$$

(27)

where

$${\widehat{M}}_k=\underset{1\le i\le n}{max}\left\{q_i^{\left(k\right)}\right\},$$

so that step length ${\alpha }_k$ can be computed using

$${\delta }_1\le {\alpha }_k\le \frac{1}{\mathcal{L}}\left(1+{\widehat{M}}_k\right)(1-{\delta }_2),$$

(28)

here $\mathcal{L}>0$.

Note that we start our Algorithm 1 by taking $s_0$ such that

$${\delta }_1<s_0<{\delta }_2,$$

(29)

where ${\delta }_1$ and ${\delta }_2$ are two positive numbers. This proposed algorithm is well defined, then it must be established that the following inequality used in Algorithm 1,

$$\psi \left(x^{\left(k\right)}-s_k{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\right)\le \psi \left(x^{\left(k\right)}\right)-\varphi \left(s_k\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2,$$

(30)

is satisfied after some finite number of steps. Note that every accumulation point of $\left\{x^{\left(k\right)}\right\}$ is a minimizer of $\psi$. Since $\left\{\psi \left(x^{\left(k\right)}\right)\right\}$ is non-increasing we have

$$\psi \left(x^{*}\right)\le \psi \left(x^{\left(k\right)}\right),$$

for all k with fixed $x^{*}$. The content of Theorem 5 will be argued later. The analysis of backtracking used in Algorithm 1 to compute ${\alpha }_k$ is shown below due to [36].

Proposition 3.

The backtracking method of Algorithm 1 defined by Equations (29) and (30) stops after a finite number of iterations with

$$min\left\{{\delta }_1,\frac{\varrho \left(x^{\left(k\right)}\right)}{1+{\widehat{M}}_k}\right\}\le {\alpha }_k\le min\left\{{\delta }_2,\varrho \left(x^{\left(k\right)}\right)\right\}.$$

(31)

Proof. 

We present two cases for the value of $s_0$:

• $s_0\in \left(0,\varrho \left(x^{\left(k\right)}\right)\right)$,
• $s_0\ge \varrho \left(x^{\left(k\right)}\right)$.

• From Equations (29) and (30), and (1) of Proposition 2, ${\alpha }_k=s_0$ and iteration stops at $j=0$. Since $s_0<{\delta }_2$, and $s_0<\varrho \left(x^{\left(k\right)}\right)$, then

  $${\alpha }_k=s_0<min\left\{{\delta }_2,\varrho \left(x^{\left(k\right)}\right)\right\},$$

  and since $s_0>{\delta }_1$, then

  $$s_0={\alpha }_k\ge min\left\{{\delta }_1,\frac{\varrho \left(x^{\left(k\right)}\right)}{1+{\widehat{M}}_k}\right\}.$$
• There exists a unique $t\in \mathbb{N}$, where $t\ge 1$ such that

  $${\left(1+{\widehat{M}}_k\right)}^{t-1}\varrho \left(x^{\left(k\right)}\right)<s_0\le {\left(1+{\widehat{M}}_k\right)}^t\varrho \left(x^{\left(k\right)}\right).$$

  (32)
  Then,

  $${\displaystyle \frac{\varrho \left(x^{\left(k\right)}\right)}{1+{\widehat{M}}_k}}<{\displaystyle \frac{s_0}{{\left(1+{\widehat{M}}_k\right)}^t}}\le \varrho \left(x^{\left(k\right)}\right).$$

  (33)
  From Equations (29) and (30), we have

  $$s_j=s_0{\left(1+{\widehat{M}}_k\right)}^{-j},$$

  used in Algorithm 1 so the above inequality establishes that

  $${\displaystyle \frac{\varrho \left(x^{\left(k\right)}\right)}{1+{\widehat{M}}_k}}<s_t\le \varrho \left(x^{\left(k\right)}\right).$$

  (34)
  We now claim that ${\alpha }_k=s_t$. From Equation (34), we obtain $s_t\le \varrho \left(x^{\left(k\right)}\right)$, and if we assume

  $$s_{t-1}>\varrho \left(x^{\left(k\right)}\right),$$

  then for $t=1$, we obtain Case 2, so this assumption is true. Using Proposition 2, and ${\alpha }_k=s_t$, the inequality (30) is satisfied, but this does not satisfy if ${\alpha }_k=s_{t-1}$. Note that (31) follows from (34) and in fact, we have that $s_t\le s_0<{\delta }_2$.

The proof is complete. □

The following proposition states that the q-gradient descent method moves in orthogonal steps whose proof is very similar to the proof of [2] (Proposition 6.1).

Proposition 4.

If ${\left\{x^{\left(k\right)}\right\}}_{k=0}^{\infty }$ is a q-gradient descent sequence for a given function $\psi :{\mathbb{R}}^n\to \mathbb{R}$, then for every k, the vector

$$x^{(k+1)}-x^{\left(k\right)},$$

is orthogonal to the vector $x^{(k+2)}-x^{(k+1)}$.

Proof. 

The iterative formula of the q-gradient descent is:

$$x^{(k+1)}-x^{\left(k\right)}=-{\alpha }_k{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right),$$

(35)

For $k=k+1,$ we obtain

$$x^{(k+2)}-x^{(k+1)}=-{\alpha }_{k+1}{\nabla }_{q^{\left(k\right)}}\psi \left(x^{(k+1)}\right).$$

(36)

From (35) and (36), we obtain

$$〈x^{(k+1)}-x^{\left(k\right)},x^{(k+2)}-x^{(k+1)}〉=〈-{\alpha }_k{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right),-{\alpha }_{k+1}{\nabla }_{q^{\left(k\right)}}\psi \left(x^{(k+1)}\right)〉.$$

(37)

We need to show that

$$〈{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right),{\nabla }_{q^{\left(k\right)}}\psi \left(x^{(k+1)}\right)〉=0.$$

Since ${\alpha }_k\ge 0$ is a minimizer of

$${\varphi }_k\left(\alpha \right)=\psi \left(x^{\left(k\right)}+{\alpha }_k{d}_{q^{\left(k\right)}}^{\left(k\right)}\right)-\psi \left(x^{\left(k\right)}\right)-\varphi \left(s_k\right){\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{g}_{q^{\left(k\right)}}^{\left(k\right)},$$

used in Algorithm 1, then from the first-order necessary condition, we have

$$\frac{{\mathrm{d}}_q{\varphi }_k\left(\alpha \right)}{{\mathrm{d}}_q\alpha }=0,$$

that is,

$$-{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}-\alpha {\nabla }_q\psi \left(x^{\left(k\right)}\right)\right){\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)=0,$$

that is,

$$-{\nabla }_{q^{\left(k\right)}}\psi \left(x^{(k+1)}\right){\left({\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\right)}^T=0,$$

We obtain the desired result after putting the value of the above equation in (37). □

The above theorem implies that ${\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)$ is parallel to the tangent plane to the level set

$$\left\{\psi \left(x\right)=\psi \left(x^{(k+1)}\right)\right\},$$

at $x^{(k+1)}$ when $q^{\left(k\right)}\to {(1,\dots ,1)}^T$ as $k\to \infty$. Note that each approximate point generated by the q-gradient descent algorithm decreases the corresponding objective function $\psi$.

Proposition 5.

If ${\left\{x^{\left(k\right)}\right\}}_{k=0}^{\infty }$ is the q-gradient descent sequence for $\psi :{\mathbb{R}}^n\to \mathbb{R}$ and

$${\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\ne 0,$$

then

$$\psi \left(x^{(k+1)}\right)<\psi \left(x^{\left(k\right)}\right).$$

Proof. 

We know that

$$x^{(k+1)}=x^{\left(k\right)}-{\alpha }_k{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right),$$

where ${\alpha }_k\ge 0$ is the minimizer of

$${\varphi }_k\left(\alpha \right)=\psi \left(x^{\left(k\right)}+{\alpha }_k{d}_{q^{\left(k\right)}}^{\left(k\right)}\right)-\psi \left(x^{\left(k\right)}\right)-\varphi \left(s_k\right){\left(d_{q^{\left(k\right)}}^{\left(k\right)}\right)}^T{g}_{q^{\left(k\right)}}^{\left(k\right)}.$$

Therefore, for $\alpha \ge 0,$ we have ${\varphi }_k\left({\alpha }_k\right)\le {\varphi }_k\left(\alpha \right)$ for all $\alpha$. For $\alpha =0$, we have

$$\frac{d_q{\varphi }_k}{d_q\alpha }=-{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2.$$

Since ${\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\ne 0,$ then $-{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2<0.$ Thus,

$$\frac{{\mathrm{d}}_q{\varphi }_k}{{\mathrm{d}}_q\alpha }<0.$$

There exists an $\overline{\alpha }>0$ such that ${\varphi }_k\left(0\right)>{\varphi }_k\left(\alpha \right)$, for each $\alpha \in (0,\overline{\alpha }]$. That is,

$$\psi \left(x^{(k+1)}\right)={\varphi }_k\left({\alpha }_k\right)\le {\varphi }_k\left(\alpha \right)<{\varphi }_k\left(0\right)=\psi \left(x^{\left(k\right)}\right).$$

Thus,

$$\psi \left(x^{(k+1)}\right)<\psi \left(x^{\left(k\right)}\right).$$

This completes the proof. □

4. Convergence Analysis

In this section, we present the convergence analysis of the proposed method with the inexact line searches and the concept of quasi Fejér convergence.

Theorem 3.

[36] If $\left\{x^{\left(k\right)}\right\}$ is quasi-Fejér convergence to a nonempty set $\mathcal{U}\subseteq {\mathbb{R}}^n$, then $\left\{x^{\left(k\right)}\right\}$ is bounded. Furthermore, if an accumulation point x of $\left\{x^{\left(k\right)}\right\}$ belongs to $\mathcal{U}$ then $\underset{k\to \infty }{lim}{x}^{\left(k\right)}=x$.

Proof. 

The proof of the above theorem can be seen in [36]. □

Theorem 4.

For Algorithm 1 it holds that

1.

There exists $\gamma >0$ such that

$$\psi \left(x^{(k+1)}\right)\le \psi \left(x^{\left(k\right)}\right)-\gamma {∥x^{(k+1)}-x^{\left(k\right)}∥}^2,$$

for all $k\in \mathbb{N}$,

2.

The $\left\{\psi \left(x^{\left(k\right)}\right)\right\}$ is nonincreasing and convergent,

3.

${\displaystyle \sum _{k=0}^{\infty }{∥x^{(k+1)}-x^{\left(k\right)}∥}^2<\infty }$.

Proof. 

• For Algorithm 1, we compute ${\alpha }_k$ using inequalities (27) and (29). Note that

  $${∥x^{(k+1)}-x^{\left(k\right)}∥}^2={\alpha }_k^2{∥{\nabla }_q\psi \left(x^{\left(k\right)}\right)∥}^2.$$
  Since ${\alpha }_k>0$, we also have

  $$\frac{\varphi \left({\alpha }_k\right)}{{\alpha }_k^2}{∥x^{(k+1)}-x^{\left(k\right)}∥}^2=\varphi \left({\alpha }_k\right){∥{\nabla }_q\psi \left(x^{\left(k\right)}\right)∥}^2.$$
  Since

  $$\varphi \left({\alpha }_k\right){∥{\nabla }_q\psi \left(x^{\left(k\right)}\right)∥}^2\le \psi \left(x^{\left(k\right)}\right)-\psi \left(x^{(k+1)}\right),$$

  thus

  $$\frac{\varphi \left({\alpha }_k\right)}{{\alpha }_k^2}{∥x^{(k+1)}-x^{\left(k\right)}∥}^2\le \psi \left(x^{\left(k\right)}\right)-\psi \left(x^{(k+1)}\right).$$

  (38)
  We take

  $$0<\xi <\underset{v\to 0^{+}}{lim}\frac{inf\varphi \left(u\right)}{u^2}.$$
  By definition of $\xi$, there exists $\theta >0$ such that if for a general case, the value of step length $\alpha \in (0,\theta )$, then

  $$\xi <\frac{\varphi \left(\alpha \right)}{{\alpha }^2}.$$

  (39)
  However, for every k, we take the following two cases for choosing the step length as:

  (i)

  If ${\alpha }_k\in (0,\theta )$, then from (39), we have $\frac{\varphi \left({\alpha }_k\right)}{{\alpha }_k^2}$.

  (ii)

  If ${\alpha }_k\ge \theta$. In this case, by Proposition 3, we have that

  $${\alpha }_k\le min\left\{{\delta }_2,\varrho \left(x^{\left(k\right)}\right)\right\}\le {\delta }_2,$$

  and it follows from (1) and (2) of Assumption A2 that $\varphi$ is increasing, implying $\varphi \left(\theta \right)\le \varphi \left({\alpha }_k\right)$. Thus, we have

  $$\frac{\varphi \left(\theta \right)}{{\delta }_2^2}\le \frac{\varphi \left({\alpha }_k\right)}{{\alpha }_k^2}.$$

  (40)

  From (38), we have

  $$\psi \left(x^{(k+1)}\right)\le \psi \left(x^{\left(k\right)}\right)-\frac{\varphi \left({\alpha }_k\right)}{{\alpha }_k^2}{∥x^{(k+1)}-x^{\left(k\right)}∥}^2.$$
  From Equations (39) and (40) and using above inequality, we obtain

  $$\psi \left(x^{(k+1)}\right)\le \psi \left(x^{\left(k\right)}\right)-\gamma {∥x^{(k+1)}-x^{\left(k\right)}∥}^2,$$

  where

  $$\gamma =min\left\{\xi ,\frac{\varphi \left(\theta \right)}{{\delta }_2^2}\right\}.$$
  Thus, (1) of this theorem is proved. If we use Equations (29) and (30) to compute the step length then from q-Newton–Leibniz formula [42]

  $$\begin{array}{cc}\hfill \psi \left(x^{(k+1)}\right)& =\psi \left(x^{\left(k\right)}\right)-{\alpha }_k{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2\hfill \\ \hfill & -{\alpha }_k{\int }_0^1\left[{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}-u{\alpha }_k{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\right)\right.\hfill \\ \hfill & {\left.-{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\right]}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right){\mathrm{d}}_{q}u.\hfill \end{array}$$
  From (2) of Assumption 1, we obtain

  $$\begin{array}{cc}\hfill \psi \left(x^{(k+1)}\right)& \le \psi \left(x^{\left(k\right)}\right)-{\alpha }_k{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2\hfill \\ \hfill & +\mathcal{L}{\alpha }_k^2{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2{\int }_0^{1}u{\mathrm{d}}_{q}u.\hfill \end{array}$$
  Using a special case of the q-integral [44], we obtain

  $$\psi \left(x^{(k+1)}\right)\le \psi \left(x^{\left(k\right)}\right)-{\alpha }_k\left(1-{\displaystyle \frac{\mathcal{L}{\alpha }_k}{1+{\widehat{M}}_k}}\right){∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2,$$

  where we assume

  $${\widehat{M}}_k=\underset{1\le i\le n}{max}\left\{q_i^{\left(k\right)}\right\}.$$
  Since

  $${∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2=\frac{1}{{\alpha }_k^2}{∥x^{(k+1)}-x^{\left(k\right)}∥}^2,$$

  then

  $$\psi \left(x^{(k+1)}\right)\le \psi \left(x^{\left(k\right)}\right)-\frac{1}{{\alpha }_k}\left(1-{\displaystyle \frac{\mathcal{L}{\alpha }_k}{1+{\widehat{M}}_k}}\right){∥x^{(k+1)}-x^{\left(k\right)}∥}^2.$$

  (41)
  From (28), we have

  $${\delta }_1\le {\alpha }_k\le {\displaystyle \frac{1+{\widehat{M}}_k}{\mathcal{L}}}(1-{\delta }_2),$$

  then we obtain

  $$\frac{1}{{\alpha }_k}\left(1-{\displaystyle \frac{\mathcal{L}{\alpha }_k}{1+{\widehat{M}}_k}}\right)\ge {\delta }_2\frac{\mathcal{L}}{\left(1+{\widehat{M}}_k\right)(1-{\delta }_2)}.$$
  From (41), we obtain

  $$\psi \left(x^{(k+1)}\right)\le \psi \left(x^{\left(k\right)}\right)-{\delta }_2\frac{\mathcal{L}}{\left(1+{\widehat{M}}_k\right)(1-{\delta }_2)}{∥x^{(k+1)}-x^{\left(k\right)}∥}^2.$$

  where

  $${\delta }_2\frac{\mathcal{L}}{\left(1+{\widehat{M}}_k\right)(1-{\delta }_2)}=\gamma .$$
  Thus, (1) is proved.
• It follows from (1) using $\gamma >0$.
• By (1), there exist $\gamma >0$ such that

  $$\sum _{k=0}^r{∥x^{(k+1)}-x^{\left(k\right)}∥}^2\le \frac{1}{\gamma }\left(\psi \left(x^{\left(0\right)}\right)-\psi \left(x^{\left(r\right)}\right)\right)\le \frac{1}{\delta }\left(\psi \left(x^{\left(0\right)}\right)-\psi \left(x^{*}\right)\right).$$
  Suppose that $r\to \infty$, we obtain

  $$\sum _{k=0}^{\infty }{∥x^{(k+1)}-x^{\left(k\right)}∥}^2<\infty .$$

This completes the proof. □

We also need to present the following proposition to prove the convergence of Algorithm 1.

Proposition 6.

Let

$$\mathcal{T}=\left\{\mathfrak{z}\in {\mathbb{R}}^n:\psi \left(\mathfrak{z}\right) \le \underset{k\to \infty }{lim}inf\psi \left(x^{\left(k\right)}\right)\right\}.$$

(42)

Every point generated by Algorithm 1 is placed in T, making T nonempty. For any $\mathfrak{z}\in \mathcal{T}$, we have

$${∥x^{(k+1)}-\mathfrak{z}∥}^2\le {∥x^{\left(k\right)}-\mathfrak{z}∥}^2+{∥x^{(k+1)}-x^{\left(k\right)}∥}^2,$$

then the sequence $\left\{x^{\left(k\right)}\right\}$ generated by Algorithm 1 is a quasi-Fejér convergence to a point $x^{*}\in \mathcal{T}$ with any ${\alpha }_k>0$.

Proof. 

Given that $\mathfrak{z}\in \mathcal{T}$, then

$$\begin{array}{cc}\hfill {∥x^{(k+1)}-\mathfrak{z}∥}^2-{∥x^{\left(k\right)}-\mathfrak{z}∥}^2& -{∥x^{(k+1)}-x^{\left(k\right)}∥}^2\hfill \\ \hfill & =-2{\left(\mathfrak{z}-x^{\left(k\right)}\right)}^T\left(x^{(k+1)}-x^{\left(k\right)}\right).\hfill \end{array}$$

Since $x^{(k+1)}-x^{\left(k\right)}=-{\alpha }_k{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)$, then

$$\begin{array}{cc}\hfill {∥x^{(k+1)}-\mathfrak{z}∥}^2-{∥x^{\left(k\right)}-\mathfrak{z}∥}^2& -{∥x^{(k+1)}-x^{\left(k\right)}∥}^2\hfill \\ \hfill & =2{\alpha }_k{\left(\mathfrak{z}-x^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right).\hfill \end{array}$$

A function will be called a q-convex function if $\psi$ satisfies the following inequality in the light of q-calculus:

$$\psi \left(\mathfrak{z}\right)-\psi \left(x^{\left(k\right)}\right)\ge {\left(\mathfrak{z}-x^{\left(k\right)}\right)}^T{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right).$$

With the above inequality and (42), we obtain

$$\begin{array}{cc}\hfill {∥x^{(k+1)}-\mathfrak{z}∥}^2-{∥x^{\left(k\right)}-\mathfrak{z}∥}^2& -{∥x^{(k+1)}-x^{\left(k\right)}∥}^2\hfill \\ \hfill & \le 2{\alpha }_k\left(\psi \left(\mathfrak{z}\right)-\psi \left(x^{\left(k\right)}\right)\right)\le 0,\hfill \end{array}$$

and from (3) of Theorem 2, we have

$$\sum _{k=0}^{\infty }{∥x^{(k+1)}-x^{\left(k\right)}∥}^2<\infty ,$$

then we have that $\left\{x^{\left(k\right)}\right\}$ is a quasi-Fejér convergence to $\mathcal{T}\subseteq {\mathbb{R}}^n$ with

$${∥x^{(k+1)}-x^{\left(k\right)}∥}^2={ϵ}_k,$$

and from Theorem 3, $\left\{x^{\left(k\right)}\right\}$ is bounded. Further, it has an accumulation point x of $\left\{x^{\left(k\right)}\right\}$, which is in $\mathcal{T}.$ Thus, ${lim}_{k\to \infty }{x}^{\left(k\right)}=x$. □

Theorem 5.

The sequence $\left\{x^{\left(k\right)}\right\}$ generated by Algorithm 1 converges in the sense of quasi-Fejér convergence to a minimizer of function $\psi :{\mathbb{R}}^n\to \mathbb{R}$.

Proof. 

From Proposition 6, ${lim}_{k\to \infty }{x}^{\left(k\right)}=x^{*}\in \mathcal{T}$, where T is a set of accumulation points that are responsible for decreasing the objective function in every iteration. However, we need to prove that $x^{*}\in {\mathcal{T}}^{*}$, where $T^{*}$ is a set of minimizers that minimize the objective function. From Algorithm 1, suppose that $x^{*}\notin {\mathcal{T}}^{*}$, then from the convexity of $\psi$, $x^{*}\in \mathcal{G}$ and

$$∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)∥>0.$$

From Proposition 2, $\varrho \left(x^{*}\right)>0$ and $\varrho \left(x^{\left(k\right)}\right)$ converges to $\varrho \left(x^{*}\right)$. Thus, there exists $k_0$ such that for all $k\ge k_0$, we have

$$v\left(x^{\left(k\right)}\right)\ge {\displaystyle \frac{\varrho \left(x^{*}\right)}{1+{\widehat{M}}_k}},$$

(43)

$${∥{\nabla }_q\psi \left(x^{\left(k\right)}\right)∥}^2\ge {\displaystyle \frac{1}{1+{\widehat{M}}_k}}{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)∥}^2.$$

(44)

Let

$$\sigma ={\left(min\left\{{\delta }_1,{\displaystyle \frac{\varrho \left(x^{*}\right)}{1+{\widehat{M}}_k}}\right\}\right)}^2\frac{{∥{\nabla }_q\psi \left(x^{*}\right)∥}^2}{1+{\widehat{M}}_k}.$$

Then, for any $k\ge k_0$,

$$\begin{array}{c}\hfill {∥x^{(k+1)}-x^{\left(k\right)}∥}^2={\alpha }_k^2{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2.\end{array}$$

Since

$${\alpha }_k^2\ge {\left(min\left\{{\delta }_1,{\displaystyle \frac{\varrho \left(x^{\left(k\right)}\right)}{1+{\widehat{M}}_k}}\right\}\right)}^2,$$

then

$$\begin{array}{c}\hfill {∥x^{(k+1)}-x^{\left(k\right)}∥}^2\ge {\left(min\left\{{\delta }_1,{\displaystyle \frac{\varrho \left(x^{\left(k\right)}\right)}{1+{\widehat{M}}_k}}\right\}\right)}^2{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2.\end{array}$$

(45)

From Equations (43) and (45), we obtain

$${∥x^{(k+1)}-x^{\left(k\right)}∥}^2\ge {\left(min\left\{{\delta }_1,{\displaystyle \frac{\varrho \left(x^{*}\right)}{{\left(1+{\widehat{M}}_k\right)}^2}}\right\}\right)}^2{\displaystyle \frac{{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{*}\right)∥}^2}{{\widehat{M}}_k}}=\sigma >0.$$

This contradicts (3) of Theorem 4. Thus it is proved that $x^{*}\in {\mathcal{T}}^{*}$. If we choose ${\alpha }_k$ using (27) and (28), then we have

$${∥x^{(k+1)}-x^{\left(k\right)}∥}^2={\alpha }_k^2{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2.$$

Since ${\alpha }_k^2\ge {\delta }_1^2$, then

$${∥x^{(k+1)}-x^{\left(k\right)}∥}^2\ge {\delta }_1^2{∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥}^2.$$

From (3) of Theorem 4, the continuity of ${\nabla }_{q^{\left(k\right)}}f(.)$, and ${\delta }_1>0$, used in the above inequality, we obtain ${\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)\to 0$ for $k\to \infty$. Moreover, as $q^{\left(k\right)}\to {(1,\dots ,1)}^T$, this implies that

$${\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right),$$

is a good approximation of $\nabla \psi \left(x^{\left(k\right)}\right)$ [2]. Further, see the proof of Proposition 2.2 in [47] for an affine function where the classical gradient and q-gradient of $\psi$ are the same. For other functions, Example 3.2 and Remark 3.3 can be seen again in [47]. Hence, the accumulation point $x^{*}=x^{\left(k\right)}$ is a minimizer of the function. □

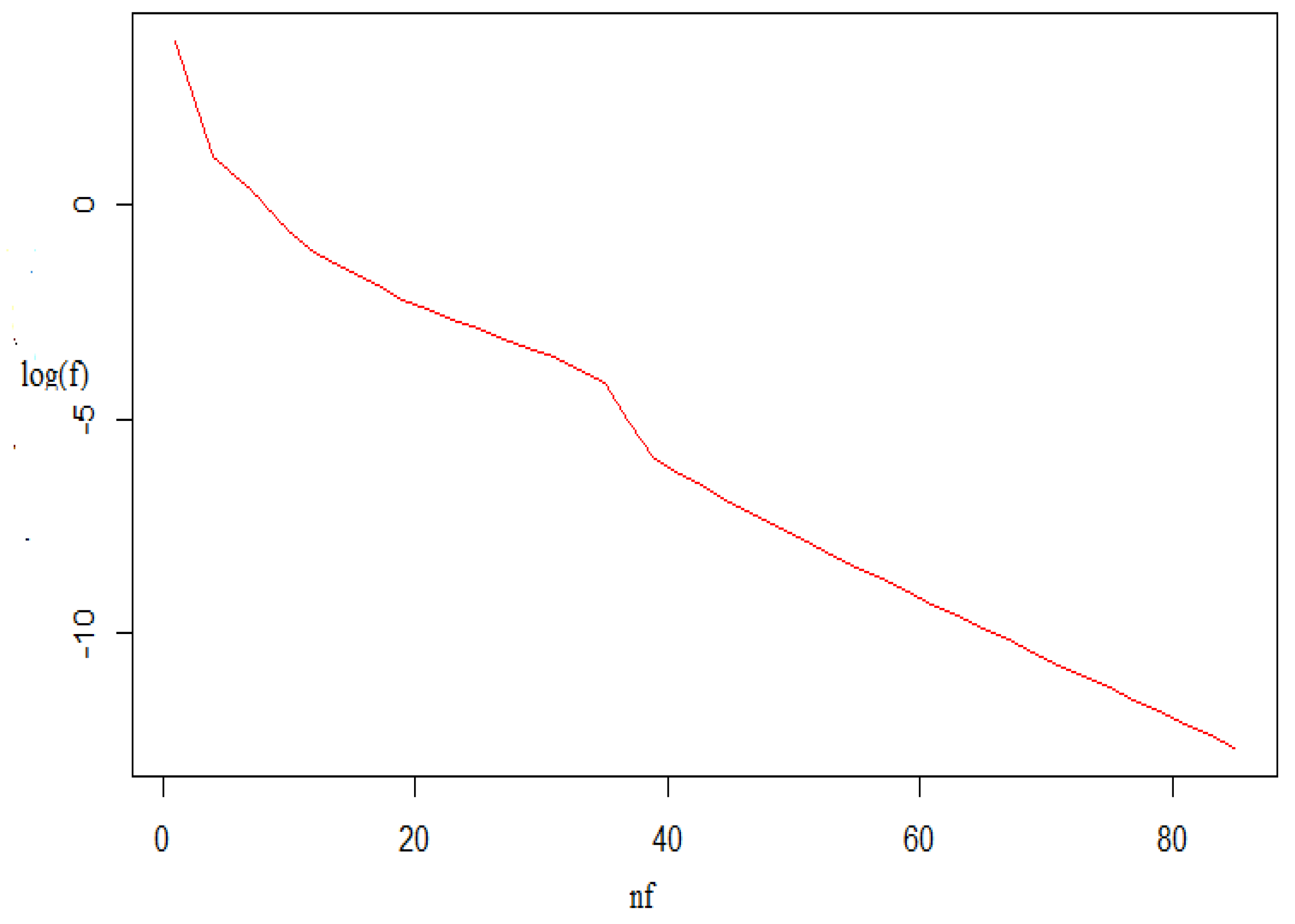
5. Experimental Results

We compared the numerical performance of our algorithm with the methodology used in [36]. The stopping criteria were set as

$$∥{\nabla }_{q^{\left(k\right)}}\psi \left(x^{\left(k\right)}\right)∥\le ϵ,$$

where $ϵ={10}^{-6}$ to terminate both the algorithms. Numerical results were compared based on the number of iterations and number of function evaluations. The iteration was stopped either when it satisfied the stopping criteria or when iteration counts were 500. All problems were taken from [48] and computer codes were written in R language.

The numerical experiments were performed on an Intel Core i5-3210M CPU with 2.5 GHz, 4 GB of RAM and a 64-bit XXX (Intel, Santa Clara, CA, USA) to solve the unconstrained minimization problems.

Example 2

([49]). Consider a function $\psi :{\mathbb{R}}^3\to \mathbb{R}$ is given by

$$\psi \left(x\right)=\frac{1}{2}{x}^{T}Qx-b^{T}x,$$

where

$$Q=\left[\begin{array}{ccc}1& 0& 0\\ 0& \tau & 0\\ 0& 0& \tau \end{array}\right],b=-\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right].$$

We apply a q-gradient descent algorithm with a starting point

$$x^{\left(0\right)}={(-3,-2,-1)}^T,$$

on different values of $\tau =2,5,10,20,50.$ We compared our method with the methodology used in [36] and the numerical results are described in

Table 1. Numerical results of Example 2.

$\mathit{\tau }$	$\overline{\mathit{x}}$	q-Gradient Descent
		$\mathit{\psi }\left(\overline{\mathit{x}}\right)$	$\mathbf{GN}$	$\mathbf{IT}$
2	${(-1.001E+00,-5.000E-01,-2.501E-01)}^T$	$-8.750E-01$	$3.683E-07$	16
5	${(-1.002E+00,-2.000E-01,-4.019E-02)}^T$	$-6.200E-01$	$8.270E-07$	56
10	${(-1.003E+00,-1.000E-01,-9.991E-03)}^T$	$-5.550E-01$	$8.859E-07$	97
20	${(-1.004E+00,-5.000E-02,-2.499E-03)}^T$	$-5.262E-01$	$9.984E-07$	139
50	${(-1.004E+00,-2.000E-02,-3.999E-04)}^T$	$-5.102E-01$	$9.913E-07$	353
		Classical Gradient Descent [36]
		$\mathbf{\psi }\left(\overline{\mathit{x}}\right)$	$\mathbf{GN}$	$\mathbf{IT}$
2	${(-1.001E+00,-5.000E-01,-2.498E-01)}^T$	$-8.750E-01$	$4.068E-07$	15
5	${(-1.003E+00,-2.000E-01,-3.993E-02)}^T$	$-6.200E-01$	$8.345E-07$	71
10	${(-1.004E+00,-1.000E-01,-1.012E-02)}^T$	$-5.550E-01$	$9.782E-07$	134
20	${(-1.006E+00,-5.000E-02,-2.497E-03)}^T$	$-5.262E-01$	$9.640E-07$	215
50	${(-1.010E+00,-2.000E-02,-4.272E-04)}^T$	$-5.101E-01$	$9.843E-07$	588

.

It is worth mentioning that the method given in this paper generates the least number of iterations, and minimizer $x^{*}$ and minimum function value $\psi \left(x^{*}\right)={\psi }^{*}$ are almost the same for both methods.

Example 3

([50]). Consider a function $\psi :{\mathbb{R}}^2\to \mathbb{R}$ such that

$$\psi \left(x\right)=x_1^4-2x_1^2{x}_2+x_1^2+x_2^2-2x_1+1.$$

With a starting point

$$x^{\left(0\right)}={(-2,-2)}^T,$$

Algorithm 1 shows improvement over the algorithm given in [36]. The numerical results are shown in the following Table 2 and Table 3, with abbreviations used in columns as ‘$gn$’ norm of gradient, ‘$nf$’ number of function evaluations, and step length computed using the backtracking technique. We observe that our proposed algorithm converges to the solution point in 28 iterations while the algorithm used in [36] converges to the same solution point in 40 iterations. The graphs for both methods in terms of $fe$ versus the logarithm of the function value are provided in Figure 1 and Figure 2. The three-dimensional pictorial representation of Example 3 is shown in Figure 3.

Table 2. Numerical output of Example 3 using Algorithm 1.

	q-Gradient Descent
It	$\mathit{\psi }$	$\mathit{g}2\mathit{n}$	$\mathit{nf}$
0	$4.50000E+01$	$5.53114E+01$	1
1	$3.05531E+00$	$3.83381E+00$	4
2	$1.44344E+00$	$2.45969E+00$	7
3	$5.37577E-01$	$1.48052E+00$	10
4	$3.32689E-01$	$8.22955E-01$	12
5	$2.09224E-01$	$7.95222E-01$	15
6	$1.50867E-01$	$5.00475E-01$	17
7	$1.10048E-01$	$5.35543E-01$	20
8	$8.48946E-02$	$3.57301E-01$	22
9	$6.60685E-02$	$3.64658E-01$	24
10	$5.33656E-02$	$2.90936E-01$	26
11	$4.33762E-02$	$2.65104E-01$	28
12	$3.57854E-02$	$2.51345E-01$	30
13	$2.96786E-02$	$1.99254E-01$	32
14	$2.45786E-02$	$2.26142E-01$	34
15	$2.04572E-02$	$1.51693E-01$	36
16	$1.66695E-02$	$2.10239E-01$	38
17	$1.36586E-02$	$1.14514E-01$	40
18	$1.05164E-02$	$2.01242E-01$	42
19	$8.15978E-03$	$8.24237E-02$	44
20	$5.09294E-03$	$2.12029E-01$	45
21	$2.88677E-03$	$4.64793E-02$	47
22	$4.05728E-04$	$8.80875E-02$	50
23	$6.74352E-05$	$7.16943E-03$	52
24	$1.98233E-05$	$1.75357E-02$	55
25	$5.78355E-06$	$2.33610E-03$	57
26	$3.56220E-06$	$6.21160E-03$	60
27	$1.61834E-06$	$1.41408E-03$	62
28	$1.32663E-06$	$3.28145E-03$	65

Table 2. Numerical output of Example 3 using Algorithm 1.

	q-Gradient Descent
It	$\mathit{\psi }$	$\mathit{g}2\mathit{n}$	$\mathit{nf}$
0	$4.50000E+01$	$5.53114E+01$	1
1	$3.05531E+00$	$3.83381E+00$	4
2	$1.44344E+00$	$2.45969E+00$	7
3	$5.37577E-01$	$1.48052E+00$	10
4	$3.32689E-01$	$8.22955E-01$	12
5	$2.09224E-01$	$7.95222E-01$	15
6	$1.50867E-01$	$5.00475E-01$	17
7	$1.10048E-01$	$5.35543E-01$	20
8	$8.48946E-02$	$3.57301E-01$	22
9	$6.60685E-02$	$3.64658E-01$	24
10	$5.33656E-02$	$2.90936E-01$	26
11	$4.33762E-02$	$2.65104E-01$	28
12	$3.57854E-02$	$2.51345E-01$	30
13	$2.96786E-02$	$1.99254E-01$	32
14	$2.45786E-02$	$2.26142E-01$	34
15	$2.04572E-02$	$1.51693E-01$	36
16	$1.66695E-02$	$2.10239E-01$	38
17	$1.36586E-02$	$1.14514E-01$	40
18	$1.05164E-02$	$2.01242E-01$	42
19	$8.15978E-03$	$8.24237E-02$	44
20	$5.09294E-03$	$2.12029E-01$	45
21	$2.88677E-03$	$4.64793E-02$	47
22	$4.05728E-04$	$8.80875E-02$	50
23	$6.74352E-05$	$7.16943E-03$	52
24	$1.98233E-05$	$1.75357E-02$	55
25	$5.78355E-06$	$2.33610E-03$	57
26	$3.56220E-06$	$6.21160E-03$	60
27	$1.61834E-06$	$1.41408E-03$	62
28	$1.32663E-06$	$3.28145E-03$	65

Figure 1. Number of function evaluations due to q-gradient descent algorithm for Example 3.

Figure 1. Number of function evaluations due to q-gradient descent algorithm for Example 3.

Table 3. Numerical results of Example 3 using Classical Gradient Descent [36].

	Classical Gradient Descent
It	$\mathit{\psi }$	$\mathit{g}2\mathit{n}$	$\mathit{nf}$
0	$4.50000E+01$	$5.53173E+01$	1
1	$3.05623E+00$	$3.83810E+00$	4
2	$1.44520E+00$	$2.46074E+00$	7
3	$5.38450E-01$	$1.48336E+00$	10
4	$3.33100E-01$	$8.23444E-01$	12
5	$2.09391E-01$	$7.95583E-01$	15
6	$1.51000E-01$	$5.00572E-01$	17
7	$1.10457E-01$	$4.84543E-01$	19
8	$8.61656E-02$	$3.86837E-01$	21
9	$6.78803E-02$	$3.30047E-01$	23
10	$5.44785E-02$	$3.30855E-01$	25
11	$4.40901E-02$	$2.35325E-01$	27
12	$3.51020E-02$	$3.02819E-01$	29
13	$2.81958E-02$	$1.68607E-01$	31
14	$2.07562E-02$	$2.94811E-01$	33
15	$1.54894E-02$	$1.13592E-01$	35
16	$6.31703E-03$	$2.74534E-01$	37
17	$2.67696E-03$	$4.64201E-02$	39
18	$1.88478E-03$	$1.04102E-01$	41
19	$1.35417E-03$	$3.27922E-02$	43
20	$9.76185E-04$	$7.34138E-02$	45
21	$7.13476E-04$	$2.36981E-02$	47
22	$5.22365E-04$	$5.29427E-02$	49
23	$3.86176E-04$	$1.73832E-02$	51
24	$2.85774E-04$	$3.87568E-02$	53
25	$2.12958E-04$	$1.28821E-02$	55
26	$1.58791E-04$	$2.86713E-02$	57
27	$1.19008E-04$	$9.61596E-03$	59
28	$8.92260E-05$	$2.13709E-02$	61
29	$6.71499E-05$	$7.21554E-03$	63
30	$5.05489E-05$	$1.60174E-02$	65
31	$3.81590E-05$	$5.43511E-03$	67
32	$2.88110E-05$	$1.20540E-02$	69
33	$2.17989E-05$	$4.10562E-03$	71
34	$1.64954E-05$	$9.09882E-03$	73
35	$1.25020E-05$	$3.10790E-03$	75
36	$9.47621E-06$	$6.88380E-03$	77
37	$7.19130E-06$	$2.35637E-03$	79
38	$5.45769E-06$	$5.21692E-03$	81
39	$4.14574E-06$	$1.78870E-03$	83
40	$3.14931E-06$	$3.95878E-03$	85

Table 3. Numerical results of Example 3 using Classical Gradient Descent [36].

	Classical Gradient Descent
It	$\mathit{\psi }$	$\mathit{g}2\mathit{n}$	$\mathit{nf}$
0	$4.50000E+01$	$5.53173E+01$	1
1	$3.05623E+00$	$3.83810E+00$	4
2	$1.44520E+00$	$2.46074E+00$	7
3	$5.38450E-01$	$1.48336E+00$	10
4	$3.33100E-01$	$8.23444E-01$	12
5	$2.09391E-01$	$7.95583E-01$	15
6	$1.51000E-01$	$5.00572E-01$	17
7	$1.10457E-01$	$4.84543E-01$	19
8	$8.61656E-02$	$3.86837E-01$	21
9	$6.78803E-02$	$3.30047E-01$	23
10	$5.44785E-02$	$3.30855E-01$	25
11	$4.40901E-02$	$2.35325E-01$	27
12	$3.51020E-02$	$3.02819E-01$	29
13	$2.81958E-02$	$1.68607E-01$	31
14	$2.07562E-02$	$2.94811E-01$	33
15	$1.54894E-02$	$1.13592E-01$	35
16	$6.31703E-03$	$2.74534E-01$	37
17	$2.67696E-03$	$4.64201E-02$	39
18	$1.88478E-03$	$1.04102E-01$	41
19	$1.35417E-03$	$3.27922E-02$	43
20	$9.76185E-04$	$7.34138E-02$	45
21	$7.13476E-04$	$2.36981E-02$	47
22	$5.22365E-04$	$5.29427E-02$	49
23	$3.86176E-04$	$1.73832E-02$	51
24	$2.85774E-04$	$3.87568E-02$	53
25	$2.12958E-04$	$1.28821E-02$	55
26	$1.58791E-04$	$2.86713E-02$	57
27	$1.19008E-04$	$9.61596E-03$	59
28	$8.92260E-05$	$2.13709E-02$	61
29	$6.71499E-05$	$7.21554E-03$	63
30	$5.05489E-05$	$1.60174E-02$	65
31	$3.81590E-05$	$5.43511E-03$	67
32	$2.88110E-05$	$1.20540E-02$	69
33	$2.17989E-05$	$4.10562E-03$	71
34	$1.64954E-05$	$9.09882E-03$	73
35	$1.25020E-05$	$3.10790E-03$	75
36	$9.47621E-06$	$6.88380E-03$	77
37	$7.19130E-06$	$2.35637E-03$	79
38	$5.45769E-06$	$5.21692E-03$	81
39	$4.14574E-06$	$1.78870E-03$	83
40	$3.14931E-06$	$3.95878E-03$	85

Dolan and Moré [51] presented an appropriate technique to demonstrate the performance profiles, which is a statistical process. The performance ratio is presented as:

$${\rho }_{p,s}={\displaystyle \frac{r_{(p,s)}}{min\left\{r_{(p,s)}:1\le r\le n_s\right\}}},$$

(46)

where $r_{(p,s)}$ refers to the iteration and function evaluations for solver s spent on problem p, and $n_s$ refers to the number of problems in the model test. The cumulative distribution function is given as:

$$P_s\left(\tau \right)=\frac{1}{n_p}\mathrm{size}\left\{p\in {\rho }_{(p,s)}\le \tau \right\},$$

(47)

where $P_s\left(\tau \right)$ is the probability that a performance ratio ${\rho }_{(p,s)}$ is within a factor of $\tau \in \mathbb{R}$. That is, for a subset of the methods being analyzed, we plot the fraction ${\rho }_s\left(\tau \right)$ of problems for which any given method is within a factor $\tau$ of the best. We use this tool to show the performance of Algorithm 1. First, we solved 28 test problems with different starting points and stored the number of iterations and number of function evaluation values in Table 4. In fact, Figure 4 and Figure 5 show that the q-Gradient Descent method solves about 86% and 79% of 28 test problems [48] with the least number of iterations and function evaluations, respectively. We can conclude that the proposed method is superior.

Figure 2. Number of function evaluations due to Classical Gradient Descent algorithm for Example 3.

Figure 2. Number of function evaluations due to Classical Gradient Descent algorithm for Example 3.

Figure 3. Performance profile for number of function evaluations based on Table 4.

Figure 3. Performance profile for number of function evaluations based on Table 4.

Figure 4. Performance profile for number of iterations based on Table 3.

Figure 4. Performance profile for number of iterations based on Table 3.

Figure 5. Graphics of Example 3.

Figure 5. Graphics of Example 3.

Table 4. Numerical results of 28 test problems.

Sl. No.	Problem Name	Starting Point	q-Gradient Descent (q-GD)		Classical Gradient Descent (CSD) [36]
			$\mathit{NI}$	$\mathit{FE}$	$\mathit{NI}$	$\mathit{FE}$
1	Booth	${(3.000E-01,6.000E+00)}^T$	7	16	7	15
2		Aluffi Pentini ${(-1.000E+00,7.000E-01)}^T$	3	8	4	9
3		Bohachevsky ${(8.000E-01,5.000E-01)}^T$	9	30	9	30
4		Branin ${(1.800E+00,1.500E+00)}^T$	19	43	20	52
5	Colville	${(1.000E+00,1.000E+00,1.000E+00,8.000E-01)}^T$	163	347	498	1012
6	Csendes	${(-1.300E+00,2.500E+00)}^T$	5	19	6	27
7	Ackley2	${(2.300E+00,1.600E+00)}^T$	2	26	2	36
8	Csendes	${(-1.600E+00,1.600E+00)}^T$	3	14	3	15
9	Cubic	${(1.300E+00,-1.300E+00)}^T$	61	197	251	645
10	Deckkers Aarts	${(2.000E+00,1.200E+00)}^T$	8	48	73	348
11	Dixon Price	${(-1.000E+00,-2.000E+00)}^T$	19	44	24	53
12	Himmelblau	${(1.000E+00,4.000E+00)}^T$	10	52	11	36
13	Leon	${(8.000E-01,1.400E+00)}^T$	64	153	284	595
14	diagonal4	${(-1.300E+00,-1.500E+00,1.300E+00,1.500E+00)}^T$	4	8	3	6
15	Zakharov	${(2.300E+00,-1.500E+00)}^T$	8	18	8	18
16	FH1	${(1.000E-02,1.000E-02)}^T$	19	51	33	76
17	Zakharov	${(-2.000E+00,2.500E+00)}^T$	8	18	8	18
18	Three Hump Camel	${(3.000E+00,5.000E+00)}^T$	18	45	19	45
19	Six Hump Camel	${(-1.000E+00,-3.000E+00)}^T$	9	24	9	24
20	Matyas	${(-1.000E+00,-3.000E+00)}^T$	3	7	2	6
21	FH2	${(1.010E+00,1.000E-02)}^T$	22	48	25	51
22	Raydan 1	${(1.000E+00,1.000E+00)}^T$	3	9	9	9
23	Raydan 2	${(1.000E+00,-1.000E+00)}^T$	4	7	4	7
24	Hager	${(1.000E+00,-1.000E+00)}^T$	5	11	6	12
25	Generalized Tridiagonal 1	${(1.200E+00,1.700E+00)}^T$	26	74	29	60
26	Extended Tridiagonal 1	${(1.200E+00,-2.700E+00)}^T$	28	63	34	73
27	BDEXP	${(1.000E+00,1.000E+00,1.000E+00,1.000E+00)}^T$	4	16	4	16
28	BDQRTIC	${(1.000E+00,1,1.2,1,1.3,1)}^T$	15	42	16	44

Table 4. Numerical results of 28 test problems.

Sl. No.	Problem Name	Starting Point	q-Gradient Descent (q-GD)		Classical Gradient Descent (CSD) [36]
			$\mathit{NI}$	$\mathit{FE}$	$\mathit{NI}$	$\mathit{FE}$
1	Booth	${(3.000E-01,6.000E+00)}^T$	7	16	7	15
2		Aluffi Pentini ${(-1.000E+00,7.000E-01)}^T$	3	8	4	9
3		Bohachevsky ${(8.000E-01,5.000E-01)}^T$	9	30	9	30
4		Branin ${(1.800E+00,1.500E+00)}^T$	19	43	20	52
5	Colville	${(1.000E+00,1.000E+00,1.000E+00,8.000E-01)}^T$	163	347	498	1012
6	Csendes	${(-1.300E+00,2.500E+00)}^T$	5	19	6	27
7	Ackley2	${(2.300E+00,1.600E+00)}^T$	2	26	2	36
8	Csendes	${(-1.600E+00,1.600E+00)}^T$	3	14	3	15
9	Cubic	${(1.300E+00,-1.300E+00)}^T$	61	197	251	645
10	Deckkers Aarts	${(2.000E+00,1.200E+00)}^T$	8	48	73	348
11	Dixon Price	${(-1.000E+00,-2.000E+00)}^T$	19	44	24	53
12	Himmelblau	${(1.000E+00,4.000E+00)}^T$	10	52	11	36
13	Leon	${(8.000E-01,1.400E+00)}^T$	64	153	284	595
14	diagonal4	${(-1.300E+00,-1.500E+00,1.300E+00,1.500E+00)}^T$	4	8	3	6
15	Zakharov	${(2.300E+00,-1.500E+00)}^T$	8	18	8	18
16	FH1	${(1.000E-02,1.000E-02)}^T$	19	51	33	76
17	Zakharov	${(-2.000E+00,2.500E+00)}^T$	8	18	8	18
18	Three Hump Camel	${(3.000E+00,5.000E+00)}^T$	18	45	19	45
19	Six Hump Camel	${(-1.000E+00,-3.000E+00)}^T$	9	24	9	24
20	Matyas	${(-1.000E+00,-3.000E+00)}^T$	3	7	2	6
21	FH2	${(1.010E+00,1.000E-02)}^T$	22	48	25	51
22	Raydan 1	${(1.000E+00,1.000E+00)}^T$	3	9	9	9
23	Raydan 2	${(1.000E+00,-1.000E+00)}^T$	4	7	4	7
24	Hager	${(1.000E+00,-1.000E+00)}^T$	5	11	6	12
25	Generalized Tridiagonal 1	${(1.200E+00,1.700E+00)}^T$	26	74	29	60
26	Extended Tridiagonal 1	${(1.200E+00,-2.700E+00)}^T$	28	63	34	73
27	BDEXP	${(1.000E+00,1.000E+00,1.000E+00,1.000E+00)}^T$	4	16	4	16
28	BDQRTIC	${(1.000E+00,1,1.2,1,1.3,1)}^T$	15	42	16	44

6. Conclusions

A q-gradient descent optimization algorithm was presented to solve unconstrained optimization problems. The approach was based on the q-gradient vector in place of the classical gradient to present the algorithm. The quasi-Fejér convergence of the algorithm was proved. The algorithm sometimes declares a fixed point that is not the solution, but it is very close to it because of using the q-derivative. Further, examples and numerical results demonstrate the improvement of the proposed method over the classical method. Our future work will include applying the q-gradient to the accelerated gradient descent method for unconstrained optimization.