A q-Gradient Descent Algorithm with Quasi-Fejér Convergence for Unconstrained Optimization Problems
Abstract
:1. Introduction
2. Essential Preliminaries
3. A –Gradient Descent Algorithm
- 1.
- Let be convex and continuously q-differentiable.
- 2.
- The q-gradient of ψ with constant satisfies the following condition:for all .
- 1.
- ϕ is convex and continuously q-differentiable on ,
- 2.
- and ,
- 3.
- .
- 1.
- There exists such that ,
- 2.
- is continuous in a neighborhood of ,
- 3.
- is q-differentiable with respect to the variable u in andThen, there exists a neighborhood of and at least one function such that andfor any .
- 4.
- If is continuous at then the function ϱ is the only one that satisfies (16) and is continuous at .
- 1.
- For all , there exists a unique such thatandif and only if .
- 2.
- is continuous in .
- We first prove (1). Fix , and define the function in the context of q-calculus as:From (1) of Assumption 2, is convex and continuously q-differentiable, and when substituting in (19), then we obtainFrom (2) of Assumption 2, we have , thusSubstituting in the right hand side of above equation, we obtainSince , thenIn addition,where is the minimum function value of . From (20) and (23), we conclude that is negative in some interval to the right of zero, and from (24), (1) and (2) of Assumption 2, we obtainFrom Theorem 2 it follows that there exists such that . Using the above value in (19), we obtain (17). Since is convex, therefore there exists a uniqueness of . Note that a convex function of a real variable can take a given value different from its minimum point at most two different points whileand from (20) and (23), the minimum point of is not zero. Thus, (1) of this proposition is proved.
- Let given by (1), for a given . Then, we have thatis continuous in a neighborhood of and from (21)As is strictly increasing at , we have thatFrom (26) we observe that , is continuous at and all the hypotheses of Theorem 2 hold. Thus u is continuous at .
| Algorithm 1:q-Gradient Descent (q-GD) Algorithm |
 |
- 1.
- In Algorithm 1, the modified backtracking technique finds using only one inequality instead of two inequalities required in [46]
- 2.
- We can find by another technique; we take positive numbers and such thatwhereso that step length can be computed usinghere .
- ,
- .
- There exists a unique , where such thatThen,
4. Convergence Analysis
- 1.
- There exists such thatfor all ,
- 2.
- The is nonincreasing and convergent,
- 3.
- .
- Since , we also haveSincethusWe takeBy definition of , there exists such that if for a general case, the value of step length , thenHowever, for every k, we take the following two cases for choosing the step length as:
- (i)
- If , then from (39), we have .
- (ii)
- If . In this case, by Proposition 3, we have thatand it follows from (1) and (2) of Assumption A2 that is increasing, implying . Thus, we have
From (38), we haveThus, (1) of this theorem is proved. If we use Equations (29) and (30) to compute the step length then from q-Newton–Leibniz formula [42]From (2) of Assumption 1, we obtainSincethenThus, (1) is proved. - It follows from (1) using .
- By (1), there exist such thatSuppose that , we obtain
5. Experimental Results
| q-Gradient Descent | |||
|---|---|---|---|
| It | |||
| 0 | 1 | ||
| 1 | 4 | ||
| 2 | 7 | ||
| 3 | 10 | ||
| 4 | 12 | ||
| 5 | 15 | ||
| 6 | 17 | ||
| 7 | 20 | ||
| 8 | 22 | ||
| 9 | 24 | ||
| 10 | 26 | ||
| 11 | 28 | ||
| 12 | 30 | ||
| 13 | 32 | ||
| 14 | 34 | ||
| 15 | 36 | ||
| 16 | 38 | ||
| 17 | 40 | ||
| 18 | 42 | ||
| 19 | 44 | ||
| 20 | 45 | ||
| 21 | 47 | ||
| 22 | 50 | ||
| 23 | 52 | ||
| 24 | 55 | ||
| 25 | 57 | ||
| 26 | 60 | ||
| 27 | 62 | ||
| 28 | 65 | ||

| Classical Gradient Descent | |||
|---|---|---|---|
| It | |||
| 0 | 1 | ||
| 1 | 4 | ||
| 2 | 7 | ||
| 3 | 10 | ||
| 4 | 12 | ||
| 5 | 15 | ||
| 6 | 17 | ||
| 7 | 19 | ||
| 8 | 21 | ||
| 9 | 23 | ||
| 10 | 25 | ||
| 11 | 27 | ||
| 12 | 29 | ||
| 13 | 31 | ||
| 14 | 33 | ||
| 15 | 35 | ||
| 16 | 37 | ||
| 17 | 39 | ||
| 18 | 41 | ||
| 19 | 43 | ||
| 20 | 45 | ||
| 21 | 47 | ||
| 22 | 49 | ||
| 23 | 51 | ||
| 24 | 53 | ||
| 25 | 55 | ||
| 26 | 57 | ||
| 27 | 59 | ||
| 28 | 61 | ||
| 29 | 63 | ||
| 30 | 65 | ||
| 31 | 67 | ||
| 32 | 69 | ||
| 33 | 71 | ||
| 34 | 73 | ||
| 35 | 75 | ||
| 36 | 77 | ||
| 37 | 79 | ||
| 38 | 81 | ||
| 39 | 83 | ||
| 40 | 85 | ||
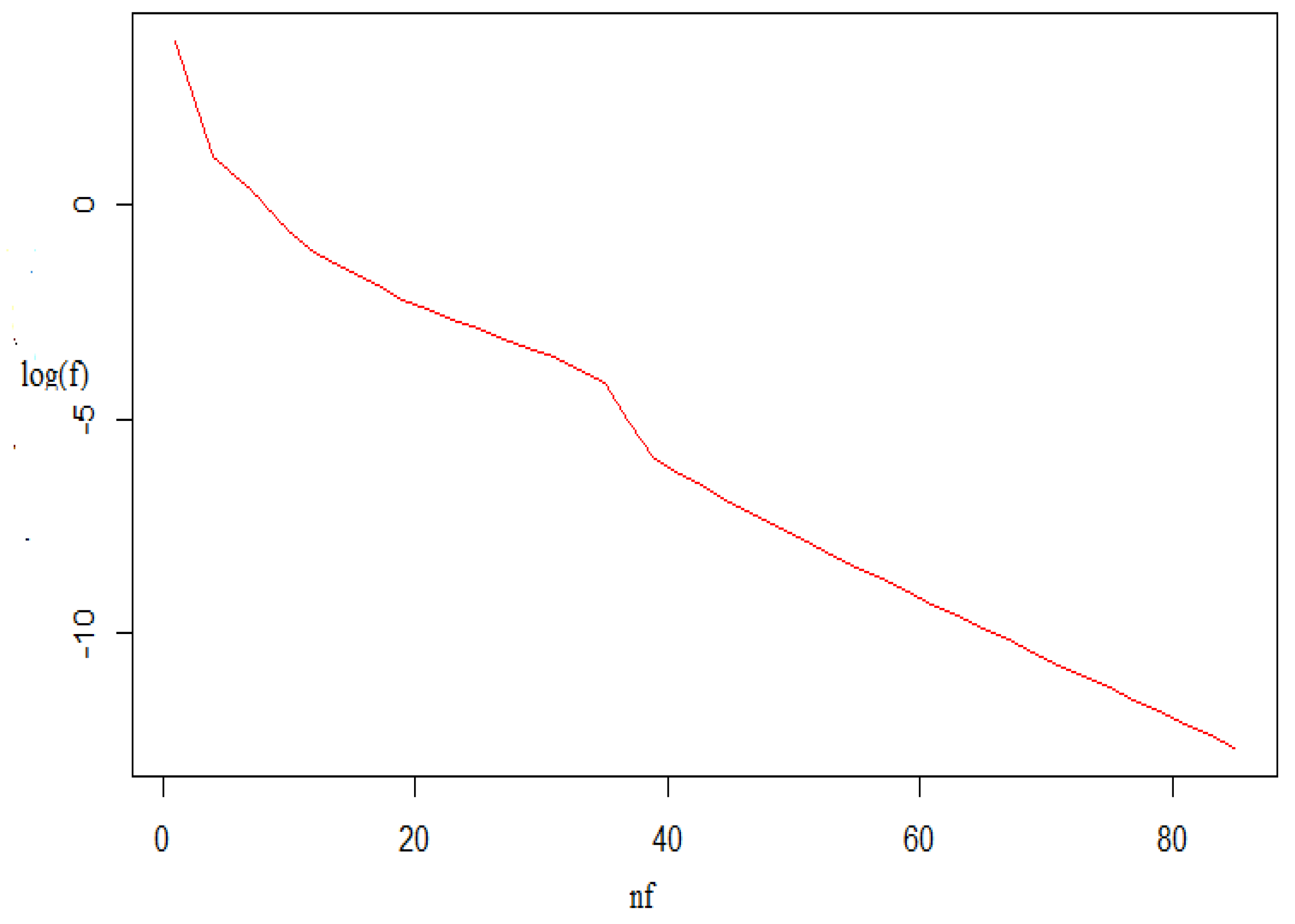



| Sl. No. | Problem Name | Starting Point | q-Gradient Descent (q-GD) | Classical Gradient Descent (CSD) [36] | ||
|---|---|---|---|---|---|---|
| 1 | Booth | 7 | 16 | 7 | 15 | |
| 2 | Aluffi Pentini | 3 | 8 | 4 | 9 | |
| 3 | Bohachevsky | 9 | 30 | 9 | 30 | |
| 4 | Branin | 19 | 43 | 20 | 52 | |
| 5 | Colville | 163 | 347 | 498 | 1012 | |
| 6 | Csendes | 5 | 19 | 6 | 27 | |
| 7 | Ackley2 | 2 | 26 | 2 | 36 | |
| 8 | Csendes | 3 | 14 | 3 | 15 | |
| 9 | Cubic | 61 | 197 | 251 | 645 | |
| 10 | Deckkers Aarts | 8 | 48 | 73 | 348 | |
| 11 | Dixon Price | 19 | 44 | 24 | 53 | |
| 12 | Himmelblau | 10 | 52 | 11 | 36 | |
| 13 | Leon | 64 | 153 | 284 | 595 | |
| 14 | diagonal4 | 4 | 8 | 3 | 6 | |
| 15 | Zakharov | 8 | 18 | 8 | 18 | |
| 16 | FH1 | 19 | 51 | 33 | 76 | |
| 17 | Zakharov | 8 | 18 | 8 | 18 | |
| 18 | Three Hump Camel | 18 | 45 | 19 | 45 | |
| 19 | Six Hump Camel | 9 | 24 | 9 | 24 | |
| 20 | Matyas | 3 | 7 | 2 | 6 | |
| 21 | FH2 | 22 | 48 | 25 | 51 | |
| 22 | Raydan 1 | 3 | 9 | 9 | 9 | |
| 23 | Raydan 2 | 4 | 7 | 4 | 7 | |
| 24 | Hager | 5 | 11 | 6 | 12 | |
| 25 | Generalized Tridiagonal 1 | 26 | 74 | 29 | 60 | |
| 26 | Extended Tridiagonal 1 | 28 | 63 | 34 | 73 | |
| 27 | BDEXP | 4 | 16 | 4 | 16 | |
| 28 | BDQRTIC | 15 | 42 | 16 | 44 | |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cauchy, A. Méthode générale pour la résolution des systemes d’équations simultanées. Comp. Rend. Sci. Paris 1847, 25, 536–538. [Google Scholar]
- Mishra, S.K.; Ram, B. Introduction to Unconstrained Optimization with R; Springer Nature: Gateway East, Singapore, 2019. [Google Scholar]
- El Mouatasim, A. Fast gradient descent algorithm for image classification with neural networks. Signal Image Video Process. 2020, 14, 1565–1572. [Google Scholar] [CrossRef]
- Chen, Y.; Miao, D. Granular regression with a gradient descent method. Inf. Sci. 2020, 537, 246–260. [Google Scholar] [CrossRef]
- Pan, H.; Niu, X.; Li, R.; Dou, Y.; Jiang, H. Annealed gradient descent for deep learning. Neurocomputing 2020, 380, 201–211. [Google Scholar] [CrossRef]
- Koshak, W.J.; Krider, E.P. A linear method for analyzing lightning field changes. J. Atmos. Sci. 1994, 51, 473–488. [Google Scholar] [CrossRef] [Green Version]
- Liao, L.Z.; Qi, L.; Tam, H.W. A gradient-based continuous method for large-scale optimization problems. J. Glob. Optim. 2005, 31, 271–286. [Google Scholar] [CrossRef]
- Nesterov, Y. Universal gradient methods for convex optimization problems. Math. Program. 2015, 152, 381–404. [Google Scholar] [CrossRef] [Green Version]
- Nezhadhosein, S. A Modified Descent Spectral Conjugate Gradient Method for Unconstrained Optimization. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 209–220. [Google Scholar] [CrossRef]
- MishraSamei Mishra, S.K.; Samei, M.E.; Chakraborty, S.K.; Ram, B. On q-variant of Dai–Yuan conjugate gradient algorithm for unconstrained optimization problems. Nonlinear Dyn. 2021, 104, 2471–2496. [Google Scholar] [CrossRef]
- Jackson, F.H. q-Difference equations. Am. J. Math. 1910, 32, 305–314. [Google Scholar] [CrossRef]
- Aral, A.; Gupta, V.; Agarwal, R.P. Applications of q-Calculus in Operator Theory; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ernst, T. The different tongues of q-calculus. Proc. Est. Acad. Sci. 2008, 57, 81–99. [Google Scholar] [CrossRef]
- Ernst, T. A method for q-calculus. J. Nonlinear Math. Phys. 2003, 10, 487–525. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Piejko, K.; Sokol, J.; Trkabka-Wikeclaw, K. On q-Calculus and Starlike Functions. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 2879–2883. [Google Scholar] [CrossRef] [Green Version]
- Mursaleen, M.; Ansari, K.J.; Nasiruzzaman, M. Approximation by q-analogue of Jakimovski–Leviatan operators involving q-Appell polynomials. Iran. J. Sci. Technol. Trans. A Sci. 2017, 41, 891–900. [Google Scholar] [CrossRef]
- Dimakis, A.; Müller-Hoissen, F. Quantum mechanics on a lattice and q-deformations. Phys. Lett. B 1992, 295, 242–248. [Google Scholar] [CrossRef]
- Lai, K.K.; Mishra, S.K.; Panda, G.; Chakraborty, S.K.; Samei, M.E.; Ram, B. A limited memory q-BFGS algorithm for unconstrained optimization problems. J. Appl. Math. Comput. 2020, 1–20. [Google Scholar] [CrossRef]
- Samei, M.E.; Hedayati, V.; Rezapour, S. Existence results for a fraction hybrid differential inclusion with Caputo-Hadamard type fractional derivative. Adv. Differ. Equ. 2019, 2019, 163. [Google Scholar] [CrossRef]
- Rezapour, S.; Imran, A.; Hussain, A.; Martínez, F.; Etemad, S.; Kaabar, M.K.A. Condensing Functions and Approximate Endpoint Criterion for the Existence Analysis of Quantum Integro-Difference FBVPs. Symmetry 2021, 13, 469. [Google Scholar] [CrossRef]
- Samei, M.E.; Ghaffari, R.; Yao, S.W.; Kaabar, M.K.A.; Martínez, F.; Inc, M. Existence of Solutions for a Singular Fractional q-Differential Equations under Riemann–Liouville Integral Boundary Condition. Symmetry 2021, 13, 1235. [Google Scholar] [CrossRef]
- Ntouyas, S.K.; Samei, M.E. Existence and uniqueness of solutions for multi-term fractional q-integro-differential equations via quantum calculus. Adv. Differ. Equ. 2019, 2019, 475. [Google Scholar] [CrossRef]
- Samei, M.E.; Hedayati, V.; Ranjbar, G.K. The existence of solution for k-dimensional system of Langevin Hadamard-type fractional differential inclusions with 2k different fractional orders. Mediterr. J. Math. 2020, 17, 37. [Google Scholar] [CrossRef]
- Etemad, S.; Rezapour, S.; Samei, M.E. On fractional hybrid and non-hybrid multi-term integro-differential inclusions with three-point integral hybrid boundary conditions. Adv. Differ. Equ. 2020, 2020, 161. [Google Scholar] [CrossRef]
- Kaabar, M.K.A.; Martínez, F.; Gómez-Aguilar, J.F.; Ghanbari, B.; Kaplan, M.; Günerhan, H. New approximate analytical solutions for the nonlinear fractional Schrödinger equation with second-order spatio-temporal dispersion via double Laplace transform method. Math. Methods Appl. Sci. 2021, 44, 11138–11156. [Google Scholar] [CrossRef]
- Alzabut, J.; Selvam, A.; Dhineshbabu, R.; Kaabar, M.K.A. The Existence, Uniqueness, and Stability Analysis of the Discrete Fractional Three-Point Boundary Value Problem for the Elastic Beam Equation. Symmetry 2021, 13, 789. [Google Scholar] [CrossRef]
- Etemad, S.; Souid, M.S.; Telli, B.; Kaabar, M.K.A.; Rezapour, S. Investigation of the neutral fractional differential inclusions of Katugampola-type involving both retarded and advanced arguments via Kuratowski MNC technique. Adv. Differ. Equ. 2021, 2021, 1–20. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kaabar, M.K.A.; Alzabut, J.; Selvam, A.G.M.; Rezapour, S. A Complete Model of Crimean-Congo Hemorrhagic Fever (CCHF) Transmission Cycle with Nonlocal Fractional Derivative. J. Funct. Spaces 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Matar, M.M.; Abbas, M.I.; Alzabut, J.; Kaabar, M.K.A.; Etemad, S.; Rezapour, S. Investigation of the p-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives. Adv. Differ. Equ. 2021, 2021, 1–18. [Google Scholar] [CrossRef]
- Alam, M.; Zada, A.; Popa, I.L.; Kheiryan, A.; Rezapour, S.; Kaabar, M.K.A. A fractional differential equation with multi-point strip boundary condition involving the Caputo fractional derivative and its Hyers–Ulam stability. Bound. Value Probl. 2021, 2021, 1–18. [Google Scholar] [CrossRef]
- Rajković, P.M.; Marinković, S.D.; Stanković, M.S. On q-Newton–Kantorovich method for solving systems of equations. Appl. Math. Comput. 2005, 168, 1432–1448. [Google Scholar] [CrossRef]
- Rajković, P.M.; Marinković, S.D.; Stanković, M. The q-gradient Method. In Proceedings of the International Symposium “Geometric Function Theory and Applications”, Sofia, Bulgaria, 27–31 August 2010; pp. 240–244. [Google Scholar]
- Kiefer, J. Sequential minimax search for a maximum. Proc. Am. Math. Soc. 1953, 4, 502–506. [Google Scholar] [CrossRef]
- Soterroni, A.C.; Galski, R.L.; Ramos, F.M. The q-gradient vector for unconstrained continuous optimization problems. In Operations Research Proceedings 2010; Springer: Berlin/Heidelberg, Germany, 2011; pp. 365–370. [Google Scholar]
- Burachik, R.; Graña Drummond, L.; Iusem, A.N.; Svaiter, B. Full convergence of the steepest descent method with inexact line searches. Optimization 1995, 32, 137–146. [Google Scholar] [CrossRef]
- Kiwiel, K.C.; Murty, K. Convergence of the steepest descent method for minimizing quasiconvex functions. J. Optim. Theory Appl. 1996, 89, 221–226. [Google Scholar] [CrossRef]
- Yuan, Y.X. A new stepsize for the steepest descent method. J. Comput. Math. 2006, 24, 149–156. [Google Scholar]
- Mishra, S.K.; Panda, G.; Ansary, M.A.T.; Ram, B. On q-Newton’s method for unconstrained multiobjective optimization problems. J. Appl. Math. Comput. 2020, 1–20. [Google Scholar] [CrossRef]
- Lai, K.K.; Mishra, S.K.; Ram, B. On q-Quasi-Newton’s Method for Unconstrained Multiobjective Optimization Problems. Mathematics 2020, 8, 616. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, S.K.; Panda, G. Newton like line search method using q-calculus. In International Conference on Mathematics and Computing; Springer: Singapore, 2017; pp. 196–208.q-calculus. In International Conference on Mathematics and Computing; Springer: Singapore, 2017; pp. 196–208. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus; Springer Science & Business Media: New York, NY, USA, 2001. [Google Scholar]
- Rajković, P.; Stanković, M.; Marinković, D.S. Mean value theorems in q-calculus. Mat. Vesn. 2002, 54, 171–178. [Google Scholar]
- Andrews, G.E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics and Computer Algebra: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra; Number 66; American Mathematical Soc.: Rhode Island, USA, 1986. [Google Scholar]
- Pastor, J.R.; Calleja, P.P.; Trejo, C.A. Análisis Matemático Volúmen: Cálculo Infinitesimal de Varias Variables Aplicaciones; McGraw-Hill: Madrid, Spain, 1963. [Google Scholar]
- Dennis, J.E., Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Lai, K.K.; Mishra, S.K.; Ram, B. A q-conjugate gradient algorithm for unconstrained optimization problems. Pac. J. Optim. 2021, 17, 57–76. [Google Scholar]
- Andrei, N. An unconstrained optimization test functions collection. Adv. Model. Optim. 2008, 10, 147–161. [Google Scholar]
- Meza, J.C. Steepest descent. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 719–722. [Google Scholar] [CrossRef]
- Snyman, J.; Hay, A. The spherical quadratic steepest descent (SQSD) method for unconstrained minimization with no explicit line searches. Comput. Math. Appl. 2001, 42, 169–178. [Google Scholar] [CrossRef] [Green Version]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
| q-Gradient Descent | ||||
|---|---|---|---|---|
| 2 | 16 | |||
| 5 | 56 | |||
| 10 | 97 | |||
| 20 | 139 | |||
| 50 | 353 | |||
| Classical Gradient Descent [36] | ||||
| 2 | 15 | |||
| 5 | 71 | |||
| 10 | 134 | |||
| 20 | 215 | |||
| 50 | 588 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, S.K.; Rajković, P.; Samei, M.E.; Chakraborty, S.K.; Ram, B.; Kaabar, M.K.A. A q-Gradient Descent Algorithm with Quasi-Fejér Convergence for Unconstrained Optimization Problems. Fractal Fract. 2021, 5, 110. https://doi.org/10.3390/fractalfract5030110
Mishra SK, Rajković P, Samei ME, Chakraborty SK, Ram B, Kaabar MKA. A q-Gradient Descent Algorithm with Quasi-Fejér Convergence for Unconstrained Optimization Problems. Fractal and Fractional. 2021; 5(3):110. https://doi.org/10.3390/fractalfract5030110
Chicago/Turabian StyleMishra, Shashi Kant, Predrag Rajković, Mohammad Esmael Samei, Suvra Kanti Chakraborty, Bhagwat Ram, and Mohammed K. A. Kaabar. 2021. "A q-Gradient Descent Algorithm with Quasi-Fejér Convergence for Unconstrained Optimization Problems" Fractal and Fractional 5, no. 3: 110. https://doi.org/10.3390/fractalfract5030110
APA StyleMishra, S. K., Rajković, P., Samei, M. E., Chakraborty, S. K., Ram, B., & Kaabar, M. K. A. (2021). A q-Gradient Descent Algorithm with Quasi-Fejér Convergence for Unconstrained Optimization Problems. Fractal and Fractional, 5(3), 110. https://doi.org/10.3390/fractalfract5030110







