Thermophysical Investigation of Oldroyd-B Fluid with Functional Effects of Permeability: Memory Effect Study Using Non-Singular Kernel Derivative Approach

Abstract

It is well established fact that the functional effects, such as relaxation and retardation of materials, can be measured for magnetized permeability based on relative increase or decrease during magnetization. In this context, a mathematical model is formulated based on slippage and non-slippage assumptions for Oldroyd-B fluid with magnetized permeability. An innovative definition of Caputo-Fabrizio time fractional derivative is implemented to hypothesize the constitutive energy and momentum equations. The exact solutions of presented problem, are determined by using mathematical techniques, namely Laplace transform with slipping boundary conditions have been invoked to tackle governing equations of velocity and temperature. The Nusselt number and limiting solutions have also been persuaded to estimate the heat emission rate through physical interpretation. In order to provide the validation of the problem, the absence of retardation time parameter led the investigated solutions with good agreement in literature. Additionally, comprehensively scrutinize the dynamics of the considered problem with parametric analysis is accomplished, the graphical illustration is depicted for slipping and non-slipping solutions for temperature and velocity. A comparative studies between fractional and non-fractional models describes that the fractional model elucidate the memory effects more efficiently.

1. Introduction

There is no denying fact that when heat extracts from a high temperature wall through a fluid having a certain movement; such a mechanism is termed as heat convection (advection). This mechanism is interacted by molecular diffusion and the motion of the fluid on the basis of natural, as well as forced convections. This is because of that convective heat transfer transpires when the surface temperature varies from that of encompassing fluid [1,2,3,4,5,6]. Solangi et al. [7] interrogated unique heat conduction properties for the enhancement of concentrations. The focus point in this work was to discuss the particle size control for heat exchange and mass concentration behavior on fluids. Soomro et al. [8] carried out the typical analysis of stretching surface to develop the heat transfer for flow of non-Newtonian nano-fluid. For the sake of physical aspects, numerical computation has been invoked to the governing equations based on the finite difference schemes to describe heat transfer phenomena. Shafiq et al. [9] explored an interesting study for the magnetohydrodynamic convective flow to explore the transfer rate of heat, motile microorganisms, and mass. They emphasized on the parametric study of the problem for Brownian motion, buoyancy forces, thermophoretic, magnetic field, and Newtonian heating for temperature and concentration. Kashif et al. [10] investigated dual thermal analysis for knowing the role of temperature dissimilarity versus the temperature or time by using the suspension of nanoparticles. The core objective of this study was to highlight the finding of the problem through fractional operators and special functions. Heat transmission over the stretching sheet based on the magnetohydrodynamic two-dimensional Casson fluid flow is observed by Hamid et al. [11]. They examined the linear convected heat effects on twofold solutions in which numerical stability was discussed for the dual results from governing equation of the problem. Abro et al. [12] suggested the fractional study for thermal radiation of Jeffery fluid and educed the sub-solutions from fluid motion of the second grade with and without magnetic fields. The thermal properties of the governing equations have been treated by integral transform approach. Sheikholeslami et al. [13] observed magnetizable hybrid fluid in the core of a circular cavity with two eaters in circular form subjected to the carbon nanotubes. Their focus point of this work was to have created the magnetic strengths by the wires through electrical current. Abdelmalek et al. [14] applied hybrid technique known as control volume finite element scheme to the curvy circular heater with nano sized particles on convective heat transmission. They suggested the finding and concluded that conformation of the curvy heater played an essential role to manage the heat transfer rate and controlling the convectional flow within the enclosure. Kashif [15] applied surface modification technology to analyze the thermo dissipation, effects on time dependent natural convectional flow of fluid. Finite Fourier sine transform, Laplace, and fractional techniques have been utilized to the governing equations for exhibiting typical and rheological properties of the problem. Although the studies on heat and transfer analysis can be continue yet the relevant studies can be observed therein in categorical format as heat transfer via analytical approaches [16,17,18,19,20,21,22,23], heat transfer via numerical approaches [24,25,26,27,28,29], heat transfer via fractional calculus approaches [30,31,32,33], and heat transfer via multi-dimensional approaches [34,35,36,37]. Motivating by the above consideration, the main theme of this manuscript is to have the significance of convective heating and variable heat source on Azimuthal oscillatory MHD convective flows developed in a cylindrical Darcy–Forchheimer porous medium filled by a radiating second-grade fluid.

Fractional order calculus has been rising these days vastly due to its useful and exclusive features. The integer order calculus, it is presumed that instant rate of change of the output, due to input level changes occur. Wherefore, it is unable to predict the earlier state of the process called memory effect which is absent in classical models, but fractional calculus famous for having memory effects. It is found in the literature, several fractional differential operators exists, for instance, Caputo with kernel (singular and local), Atangana–Baleanu with kernel (non-singular and non-local), Caputo–Fabrizio with kernel (non-singular and local), and few others are discussed [31,32,38,39]. For local and non-local kernel, convective flow with ramped conditions on temperature are studied by Riaz et al. [40]. Additionally, comparative study for MHD Maxwell fluid, the heat effect, with the application of local and non-local operators is highlighted by Riaz et al. [41]. Some other fractional associated references are investigated [42,43,44], dealing with non-integer differential operators, MHD Jeffrey fluid movement, heat transport, and second grade fluid.

Talha Anwar et al. [45] recently, discussed the same problem with different boundary conditions and executed the approximated result for the proposed problem by using the Laplace transformation technique and Durbin’s numerical algorithm. Based on aforesaid literature, the object of this exploration to develop the fractional model by using the modern interpretation of Caputo–Fabrizio, fractional time derivative operator, then derive the exact solution of the considered problem and accomplish the comparison with obtained results by Talha Anwar et al. [45]. The consequences of different related physical parameters, such as relaxation time parameter ${\lambda }_1$, retardation time parameter ${\lambda }_2$, grashof number Gr, magnetic field M, $\alpha ,\beta$ fractional parameters and Prandtl number Pr, on non-dimensional velocity and temperature. Results are discussed in detail and demonstrated graphically via Mathcad-15 software.

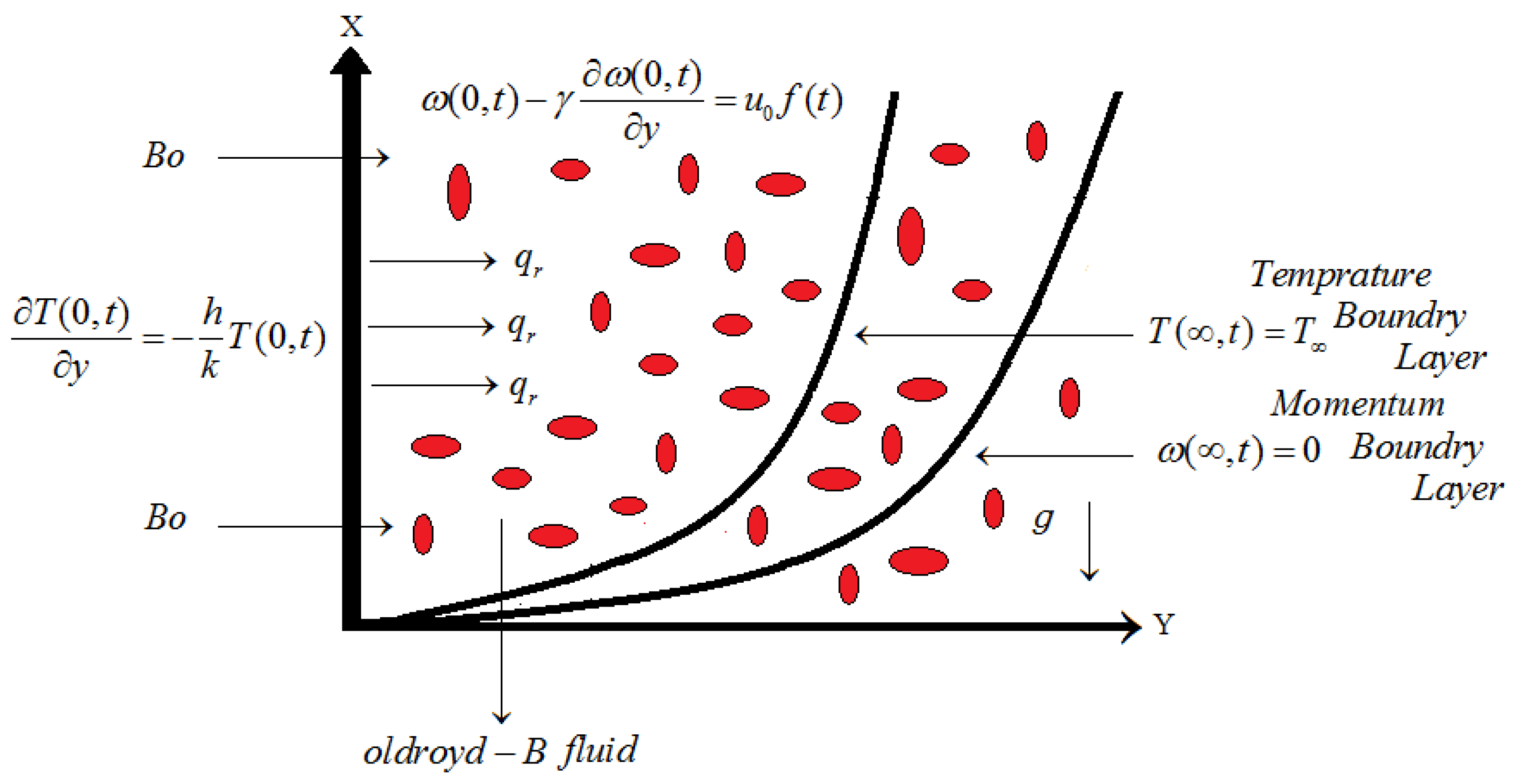
2. Mathematical Model

Consider the unsteady laminar slip flow of an Oldroyd-B fluid together with heat transfer near an infinite vertical plate subjected to Newtonian heating. It is assumed that fluid is electrically conducted and an external magnetic field is imposed in normal direction to the flow. The thermal radiation influence parallel to the plate is considered insignificant in contrast to that in the horizontal direction. Initially, it is assumed that system is in the state of rest. After a short time duration, due to mixed convection, fluid starts its motion along the plate, as configured in the Figure 1.

The constitutive flow equations for an Oldroyd-B fluid are given as [46,47]

$$\begin{array}{cc}\hfill \nabla ·\mathbb{V}& =0,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \nabla ·T+\rho g+\mathbb{J}& =\rho \left[(\nabla ·\mathbb{V})\mathbb{V}+\frac{\partial \mathbb{V}}{\partial t}\right],\mathbb{J}=J\times M,\hfill \end{array}$$

(2)

where $\mathbb{V}$, $\rho$, J, $\rho g$, t, T, and M are represented by velocity distribution, fluid density, electric density, body force, time, cauchy stress tensor, and total magnetic field (imposed and induced), respectively. The basic equations for Oldroyd-B fluid in which cauchy stress and extra stress tensor are represented by T and $\mathbb{S}$, respectively, is described as

$$\begin{array}{cc}\hfill T& =-pI+\mathbb{S},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \left(\mathbb{S}+{\lambda }_1\frac{\partial \mathbb{S}}{\partial t}\right)& =\mu \left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\mathbb{A},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathbb{A}& ={(\nabla \mathbb{V})}^T+(\nabla \mathbb{V})·\hfill \end{array}$$

(5)

In the above equations, ${\lambda }_1$, p, $\mu$, I, ${\lambda }_2$, $-pI$, and $\mathbb{A}$ are denoted by relaxation time, pressure, dynamic viscosity, identity tensor, retardation time, tensor’s indeterminate part, and Rivlin–Ericksen tensor, respectively. Additionally, the term $\frac{D}{Dt}$ is the convective time derivative. Furthermore, from Equation (1) we get the expression for classical viscous Newtonian fluid when ${\lambda }_1={\lambda }_2=0$. Additionally, Maxwell Equations for magnetic and electric field are defined in the following way

$$\begin{array}{c}\hfill \Delta ·M=0,\Delta \times M={\mu }_{m}J,\Delta \times E=-\frac{\partial M}{\partial t},J\times M=-\sigma M_0^2\mathbb{V},\end{array}$$

(6)

where J, M, $\sigma$ and ${\mu }_m$ are denoted by electric field, magnetic field, fluid electrical conductivity, and magnetic permeability, respectively. Furthermore, $M=M_0+M_1$ in which $M_0$ is denoted by imposed magnetic field and $M_1$ is induced magnetic field which is not considered in this situation. Assume that the fluid flow is one dimensional and unidirectional, $\mathbb{V}$ and $\mathbb{S}$ are velocity and shear stress in the shape of

$$\begin{array}{c}\hfill \mathbb{V}=w(y,t)\widehat{i}and\mathbb{S}=\mathbb{S}(y,t),\end{array}$$

(7)

where w is denoted by x-component of the velocity $\mathbb{V}$. After substituting Equations (3)–(7) in Equation (1) and using the Boussinesq’s approximation and Rosseland approximation. The principal governing equation of the considered problem for MHD oldroyd-B fluid with expropriate initial or boundary conditions are given as [48,49]:

$$\begin{array}{cc}\hfill \left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\partial w(y,t)}{\partial t}& =\upsilon \left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\frac{{\partial }^{2}w(y,t)}{\partial y^2}+g\beta \left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\left(T(y,t)-T_{\infty }\right)\hfill \\ \hfill & -\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\sigma {\beta }_0^2}{\rho }w(y,t),\hfill \end{array}$$

(8)

$$\begin{array}{c}\hfill \frac{\partial T(y,t)}{\partial t}=\frac{k}{\rho C_p}\frac{{\partial }^{2}T(y,t)}{\partial y^2},\end{array}$$

(9)

$$\begin{array}{c}\hfill \left(1+{\lambda }_1\frac{\partial }{\partial t}\right)S=\mu \frac{\partial w(y,t)}{\partial y},\end{array}$$

(10)

with corresponding conditions

$$\begin{array}{cc}\hfill w(y,{\pi }_0)=0,T(y,{\pi }_0)=T_{\infty },\frac{\partial w(y,{\pi }_0)}{\partial y}=0,\frac{\partial w(y,{\pi }_0)}{\partial t}& =0,y\ge 0,\hfill \end{array}$$

(11)

$$\begin{array}{c}\hfill w({\pi }_0,t)-\gamma \frac{\partial w({\pi }_0,t)}{\partial y}=u_{0}f\left(t\right),\frac{\partial T({\pi }_0,t)}{\partial y}=-\frac{h}{k}T({\pi }_0,t),\end{array}$$

(12)

$$\begin{array}{c}\hfill t\ge 0:{\pi }_0=0,w(y,t)\to 0,T(y,t)\to \infty asy\to \infty ·\end{array}$$

(13)

To non-dimentionalize the following new variables are introduced:

$$\begin{array}{c}\hfill y^{*}=\frac{h}{k}y,t^{*}=\frac{\upsilon h^2}{k^2}t,w^{*}=\frac{w}{u_0},\theta =\frac{T-T_{\infty }}{T_{\infty }},u_0^2=\frac{{\upsilon }^2{h}^2}{k^2},G_r=\frac{g\beta \upsilon T_{\infty }}{u_0^3},\\ \hfill M=\frac{k^2\sigma {\beta }_0^2}{h^2\mu },{\lambda }_1^{*}=\frac{\upsilon h^2}{k^2}{\lambda }_1,{\lambda }_2^{*}=\frac{\upsilon h^2}{k^2}{\lambda }_2,P_r=\frac{\upsilon C_p}{k},{\gamma }^{*}=\frac{h}{k}\gamma ,S^{*}=\frac{k}{h}\frac{S}{u_0\mu }·\end{array}$$

(14)

After employing the dimensionless quantities, ignore the asterisk * notation, the following partial differential equations in dimensionless form are derived as:

$$\begin{array}{cc}\hfill \left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\partial w(y,t)}{\partial t}& =\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\frac{{\partial }^{2}w(y,t)}{\partial y^2}+\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)Gr\theta \hfill \\ & -\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)Mw(y,t),\hfill \end{array}$$

(15)

$$\begin{array}{c}\hfill \frac{\partial \theta (y,t)}{\partial t}=\frac{1}{Pr}\frac{{\partial }^2\theta (y,t)}{\partial y^2},\end{array}$$

(16)

$$\begin{array}{c}\hfill \left(1+{\lambda }_1\frac{\partial }{\partial t}\right)S=\frac{\partial w(y,t)}{\partial y},\end{array}$$

(17)

for above equations the set of conditions initially and boundary are stated as:

$$\begin{array}{c}\hfill w(y,{\pi }_0)=0,\theta (y,{\pi }_0)=0,w_t(y,{\pi }_0)=0,w_y(y,{\pi }_0)=0,\end{array}$$

(18)

$$\begin{array}{c}\hfill w({\pi }_0,t)-\gamma \frac{\partial w({\pi }_0,t)}{\partial y}=f\left(t\right),\frac{\partial \theta ({\pi }_0,t)}{\partial y}=-\left(1+\theta ({\pi }_0,t)\right),\end{array}$$

(19)

$$\begin{array}{c}\hfill w(y,t)\to 0,\theta (y,t)\to 0,asy\to \infty ,{\pi }_0=0andt\ge 0·\end{array}$$

(20)

3. Preliminaries

CF fractional operator having non-singularized and local kernel is described as:

$$\begin{array}{c}\hfill {}^{CF}{D}_{\eta }^{\wp }f\left(z,\eta \right)=\frac{1}{1-\wp }{\int }_0^{\eta }exp\left(-\frac{\wp (\eta -\wp )}{1-\wp }\right)\frac{\partial f(z,\tau )}{\partial \tau }d\tau ,0<\wp <1·\end{array}$$

(21)

and Laplace transformation of Equation (21) is obtained as:

$$\begin{array}{c}\hfill \mathcal{L}\left({}^{CF}{D}_{\eta }^{\wp }f\left(z,\eta \right)\right)=\frac{s\mathcal{L}\left(f(z,\eta )\right)-f(z,0)}{(1-\wp )s+\wp },\end{array}$$

(22)

where ℘ is named as fractional parameter.

4. Solution of the Problem

4.1. Exact Solution of Heat Profile

Employing the CF operator, provided in Equation (21) on Equation (16) and substituting Equations (18)–(20) yield.

$$\begin{array}{c}\hfill {}^{CF}{D}_{\tau }^{\alpha }\theta \left(y,t\right)=\frac{1}{Pr}\frac{{\partial }^2\theta \left(y,t\right)}{\partial y^2}·\end{array}$$

(23)

Applying Laplace transformation, above equation has the form

$$\begin{array}{c}\hfill \frac{{\partial }^2\overline{\theta }(y,s)}{\partial y^2}-P_r\overline{\theta }(y,s)\left(\frac{s}{\alpha +(1-\alpha )s}\right)=0,\end{array}$$

(24)

with

$$\begin{array}{c}\hfill \frac{\partial \overline{\theta }({\pi }_0,s)}{\partial y}+\overline{\theta }({\pi }_0,s)+\frac{1}{s}=0,\overline{\theta }(y,s)\to 0asy\to \infty and{\pi }_0=0·\end{array}$$

(25)

The required solution of Equation (24) by using Equation (25) is written as:

$$\begin{array}{cc}\hfill \overline{\theta }(y,s)& =-\frac{e^{-y\sqrt{\frac{b{P}_{r}s}{s+c}}}}{s(1-\sqrt{\frac{b{P}_{r}s}{s+c}})},\hfill \\ \hfill & =-\overline{{\theta }_1}(y,s)·\left[\frac{1}{a}+\left(\frac{\sqrt{bPr}}{a}\right)\overline{{\theta }_3}(y,s)+\frac{c}{a}(a-1)\overline{{\theta }_2}(y,s)\right],\hfill \end{array}$$

(26)

To get the required solution of Equation (26), using Laplace inverse transformation, written as:

$$\begin{array}{c}\hfill \theta (y,t)=-\frac{1}{a}{\theta }_1(y,t)+\left(\frac{c-ac}{a}\right)({\theta }_1\ast {\theta }_2)\left(t\right)-\left(\frac{\sqrt{bPr}}{a}\right)({\theta }_1\ast {\theta }_3)\left(t\right),\end{array}$$

(27)

where

$$\begin{array}{cc}\hfill {\mathcal{L}}^{-1}\left\{\overline{{\theta }_1}(y,s)\right\}=& {\theta }_1(y,t)={\mathcal{L}}^{-1}\left\{\frac{e^{-y\sqrt{\frac{P_{r}s}{(1-\alpha )s+\alpha }}}}{s}\right\},\hfill \\ \hfill =& 1-\frac{2P_r}{\pi }{\int }_0^{\infty }\frac{sin\left(\frac{y}{\sqrt{1-\alpha }}\chi \right)}{\chi \left(P_r+{\chi }^2\right)}{e}^{\left(\frac{-\alpha }{1-\alpha }t{\chi }^2\right)}d\chi ,\hfill \\ \hfill {\mathcal{L}}^{-1}\left\{\overline{{\theta }_2}(y,s)\right\}=& {\theta }_2(y,t)={\mathcal{L}}^{-1}\left\{\frac{1}{s+\frac{c}{a}}\right\}=e^{-\frac{c}{a}t},\hfill \\ \hfill {\mathcal{L}}^{-1}\left\{\overline{{\theta }_3}(y,s)\right\}=& {\theta }_3(y,t)=({\theta }_4\ast {\theta }_5)\left(t\right),\hfill \\ \hfill {\mathcal{L}}^{-1}\left\{\overline{{\theta }_4}(y,s)\right\}=& {\theta }_4(y,t)={\mathcal{L}}^{-1}\left\{\sqrt{s}\right\}=-\frac{1}{2\sqrt{\pi t^3}},\hfill \\ \hfill {\mathcal{L}}^{-1}\left\{\overline{{\theta }_5}(y,s)\right\}=& {\theta }_5(y,t)={\mathcal{L}}^{-1}\left\{\frac{\sqrt{s+c}}{s+\frac{c}{a}}\right\}=\frac{e^{-ct}}{\sqrt{\pi t}}+\sqrt{(c-\frac{c}{a})}{e}^{-\frac{c}{a}t}erf\left(\sqrt{(c-\frac{c}{a})t}\right),\hfill \\ \hfill b=& \frac{1}{1-\alpha },c=b\alpha anda=1-b{P}_r·\hfill \end{array}$$

Nusselt Number

To estimate heat transfer rate, Nusselt number is used, which is calculated as:

$$\begin{array}{c}\hfill N_u=-\frac{\partial \theta (y,t)}{\partial y}{|}_{y=0}\end{array}$$

(28)

4.2. Exact Solution of Velocity Profile

Employing the CF derivative operator, mentioned in Equation (21) on Equation (15) and substituting Equations (18)–(20) yield:

$$\begin{array}{cc}\hfill s\overline{w}(y,s)\left(1+{\lambda }_1\frac{s}{\alpha +(1-\alpha )s}\right)=& \left(1+{\lambda }_2\frac{s}{(1-\beta )s+\beta }\right)\frac{{\partial }^2\overline{w}(y,s)}{\partial y^2}+\left(1+{\lambda }_1\frac{s}{\alpha +(1-\alpha )s}\right)G_r\overline{\theta }\left(y,s\right)\hfill \\ \hfill & -\left(1+{\lambda }_1\frac{s}{(1-\alpha )s+\alpha }\right)M\overline{w}(y,s),\hfill \\ \hfill \left(1+\frac{{\lambda }_{1}bs}{s+c}\right)\left(s+M\right)\overline{w}(y,s)=& \left(1+\frac{{\lambda }_2{b}_{1}s}{s+c_1}\right)\frac{{\partial }^2\overline{w}(y,s)}{\partial y^2}+\left(1+\frac{{\lambda }_{1}bs}{s+c}\right)G_r\overline{\theta }\left(y,s\right),\hfill \\ \hfill \left(\frac{b_{2}s+c}{s+c}\right)\left(s+M\right)\overline{w}(y,s)=& \left(\frac{b_{3}s+c_1}{s+c_1}\right)\frac{{\partial }^2\overline{w}(y,s)}{\partial y^2}+\left(\frac{b_{2}s+c}{s+c}\right)G_r\overline{\theta }\left(y,s\right),\hfill \end{array}$$

(29)

from Equation (26) substituting the value of $\overline{\theta }\left(y,s\right)$, the obtained solution of Equation (29) is written as

$$\begin{array}{cc}\hfill \overline{w}(y,s)=& A{e}^{y\sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}+B{e}^{-y\sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}\hfill \\ \hfill & +\frac{G_r(b_{2}s+c)(s+c_1)e^{-y\sqrt{\frac{b{P}_{r}s}{s+c}}}}{s(1-\sqrt{\frac{b{P}_{r}s}{s+c}})\left[(b_{3}s+c_1)b{P}_{r}s-(b_{2}s+c)(s+M)(s+c_1)\right]}·\hfill \end{array}$$

(30)

To determine the involving constants A and B in Equation (30), boundary conditions for velocity are applied, we have

$$\begin{array}{cc}\hfill \overline{w}(y,s)& =\frac{F\left(s\right)e^{-y\sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}}{1+\gamma \sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}\hfill \\ \hfill & -\frac{G_r(b_{2}s+c)(s+c_1)\left(e^{-y\sqrt{\frac{b{P}_{r}s}{s+c}}}-\left\{\frac{1+\gamma \sqrt{\frac{b{P}_{r}s}{s+c}}}{1+\gamma \sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}\right\}{e}^{-y\sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}\right)}{s(1-\sqrt{\frac{b{P}_{r}s}{s+c}})\left[(b_{3}s+c_1)b{P}_{r}s-(b_{2}s+c)(s+M)(s+c_1)\right]}·\hfill \end{array}$$

(31)

Equation (31) having complex combinations of multi-valued Laplace parameter s, in the equation of velocity field and it is difficult to derive solution analytically, the inverse Laplace transformation. Therefore, it is more adequate to find the exact solution of the present problem in series representation, for this, write the Equation (31) in series form, simplify it in more efficient way, then to get the exact velocity expression, applying inverse Laplace integral transformation.

Equation (31) can be written as in more suitable form:

$$\begin{array}{cc}\hfill \overline{w}(y,s)& =F\left(s\right)\overline{\Psi }(y,s)-G_r\overline{\Phi }(y,s)\left[\overline{\theta }(y,s)-\overline{\Pi }(y,s)\overline{\Psi }(y,s)\right],\hfill \\ \hfill & =F\left(s\right)\overline{\Psi }(y,s)-G_r\overline{\Phi }(y,s)\left[\overline{\theta }(y,s)-\overline{\Omega }(y,s)\right],\hfill \\ \hfill & =F\left(s\right)\overline{\Psi }(y,s)-G_r\overline{\Phi }(y,s)\overline{\theta }(y,s)+G_r\overline{\Phi }(y,s)\overline{\Omega }(y,s)·\hfill \end{array}$$

(32)

After employing Laplace inverse transformation with the application of convolution product on Equation (32), we get the solution in the final form as:

$$\begin{array}{c}\hfill w(y,t)=(f\ast \Psi )\left(t\right)+G_r\left[(\Phi \ast \Omega )\left(t\right)-(\Phi \ast \theta )\left(t\right)\right],\end{array}$$

(33)

where

$$\begin{array}{cc}\hfill \overline{\Psi }(y,s)=& e^{-y\sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}·\frac{1}{1+\gamma \sqrt{\frac{(b_{2}s+c)(s+M)(s+c_1)}{(s+c)(b_{3}s+c)}}}\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill =& \left[\sum _{\mu =0}^{\infty }\frac{{(-y)}^{\mu }}{\mu !}{\left(\frac{b_2{s}^3+b_4{s}^2+b_{5}s+c_2}{b_3{s}^2+b_{6}s+c_3}\right)}^{\frac{\mu }{2}}\right]\left[\sum _{\eta =0}^{\infty }{(-1)}^{\eta }{\left(\gamma \right)}^{\eta }{\left(\frac{b_2{s}^3+b_4{s}^2+b_{5}s+c_2}{b_3{s}^2+b_{6}s+c_3}\right)}^{\frac{\eta }{2}}\right]·\hfill \end{array}$$

(35)

Implementation of Cauchy product, discrete convolution, with two truncated series, both having m terms yields:

$$\begin{array}{cc}\hfill \overline{\Psi }(y,s)=& \sum _{\mu =0}^m\sum _{\eta =0}^m\frac{{(-y)}^{\mu }{(-1)}^{m-\eta }{\left(\gamma \right)}^{m-\eta }}{\mu !}{\left(\frac{b_2{s}^3+b_4{s}^2+b_{5}s+c_2}{b_3{s}^2+b_{6}s+c_3}\right)}^{m+\frac{\mu }{2}-\frac{\eta }{2}},\hfill \\ \hfill =& \sum _{\mu =0}^m\sum _{\eta =0}^m\sum _{d=0}^{\infty }\sum _{l=0}^{\infty }\sum _{p=0}^{\infty }\sum _{q=0}^{\infty }\sum _{k=0}^{\infty }\frac{{(-y)}^{\mu }{(-1)}^{m+p+k-\eta }{\left(\gamma \right)}^{m-\eta }{\left(c_5\right)}^{m+\frac{\mu }{2}-\frac{\eta }{2}}{\left(b_{1}1\right)}^{d-l}{\left(c_6\right)}^l{\left(c_{12}\right)}^q\Gamma (l+p)}{{\left(c_{10}\right)}^{l+p-q}{\left(c_7\right)}^{q+k}(\mu !)(l!)(q!)\Gamma \left(l\right)\Gamma (\eta -l+1)}·\hfill \\ \hfill & \frac{\Gamma (q+k)\Gamma (m+\frac{\mu }{2}-\frac{\eta }{2}+1)}{\Gamma (m+\frac{\mu }{2}-\frac{\eta }{2}-d+1)\Gamma \left(l\right)\Gamma \left(q\right)}·\frac{1}{s^{l+q-d-p-k}},\hfill \\ \hfill \Psi (y,t)=& \sum _{\mu =0}^m\sum _{\eta =0}^m\sum _{d=0}^{\infty }\sum _{l=0}^{\infty }\sum _{p=0}^{\infty }\sum _{q=0}^{\infty }\sum _{k=0}^{\infty }\frac{{(-y)}^{\mu }{(-1)}^{m+p+k-\eta }{\left(\gamma \right)}^{m-\eta }{\left(c_5\right)}^{m+\frac{\mu }{2}-\frac{\eta }{2}}{\left(b_{1}1\right)}^{d-l}{\left(c_6\right)}^l{\left(c_{12}\right)}^q\Gamma (l+p)}{{\left(c_{10}\right)}^{l+p-q}{\left(c_7\right)}^{q+k}(\mu !)(l!)(q!)\Gamma \left(l\right)\Gamma (\eta -l+1)}·\hfill \\ \hfill & \frac{\Gamma (q+k)\Gamma (m+\frac{\mu }{2}-\frac{\eta }{2}+1)}{\Gamma (m+\frac{\mu }{2}-\frac{\eta }{2}-d+1)\Gamma \left(l\right)\Gamma \left(q\right)}·\frac{t^{l+q-d-p-k-1}}{\Gamma (l+q-d-p-k)},\hfill \\ \hfill \overline{\Phi }(y,s)=& \frac{s^2+b_{14}s+c_{14}}{s^3+b_{12}{s}^2+b_{13}s+c_{13}},\hfill \\ \hfill =& \sum _{{\eta }_1=0}^{\infty }\sum _{l_1=0}^{\infty }\sum _{d_1=0}^{\infty }\frac{{(-1)}^{{\eta }_1}\left({\eta }_1\right)!{\left(b_{13}\right)}^{d_1}{\left(b_{12}\right)}^{l_1}}{\left(d_1\right)!({\eta }_1-l_1)!(l_1-d_1)!{\left(b_{12}\right)}^{d_1}{\left(c_{13}\right)}^{{\eta }_1+1}}·\frac{1}{s^{l_1+d_1-3{\eta }_1-2}}+\hfill \\ \hfill & \sum _{{\eta }_1=0}^{\infty }\sum _{l_1=0}^{\infty }\sum _{d_1=0}^{\infty }\frac{{(-1)}^{{\eta }_1}\left({\eta }_1\right)!{\left(b_{13}\right)}^{d_1}{\left(b_{12}\right)}^{l_1}{b}_{14}}{\left(d_1\right)!({\eta }_1-l_1)!(l_1-d_1)!{\left(b_{12}\right)}^{d_1}{\left(c_{13}\right)}^{{\eta }_1+1}}·\frac{1}{s^{l_1+d_1-3{\eta }_1-1}}+\hfill \\ \hfill & \sum _{{\eta }_1=0}^{\infty }\sum _{l_1=0}^{\infty }\sum _{d_1=0}^{\infty }\frac{{(-1)}^{{\eta }_1}\left({\eta }_1\right)!{\left(b_{13}\right)}^{d_1}{\left(b_{12}\right)}^{l_1}{c}_{14}}{\left(d_1\right)!({\eta }_1-l_1)!(l_1-d_1)!{\left(b_{12}\right)}^{d_1}{\left(c_{13}\right)}^{{\eta }_1+1}}·\frac{1}{s^{l_1+d_1-3{\eta }_1}},\hfill \\ \hfill \Phi (y,t)=& \sum _{{\eta }_1=0}^{\infty }\sum _{l_1=0}^{\infty }\sum _{d_1=0}^{\infty }\frac{{(-1)}^{{\eta }_1}\left({\eta }_1\right)!{\left(b_{13}\right)}^{d_1}{\left(b_{12}\right)}^{l_1}}{\left(d_1\right)!({\eta }_1-l_1)!(l_1-d_1)!{\left(b_{12}\right)}^{d_1}{\left(c_{13}\right)}^{{\eta }_1+1}}·\frac{t^{l_1+d_1-3{\eta }_1-3}}{\Gamma (l_1+d_1-3{\eta }_1-2)}+\hfill \\ \hfill & \sum _{{\eta }_1=0}^{\infty }\sum _{l_1=0}^{\infty }\sum _{d_1=0}^{\infty }\frac{{(-1)}^{{\eta }_1}\left({\eta }_1\right)!{\left(b_{13}\right)}^{d_1}{\left(b_{12}\right)}^{l_1}{b}_{14}}{\left(d_1\right)!({\eta }_1-l_1)!(l_1-d_1)!{\left(b_{12}\right)}^{d_1}{\left(c_{13}\right)}^{{\eta }_1+1}}·\frac{t^{l_1+d_1-3{\eta }_1-2}}{\Gamma (l_1+d_1-3{\eta }_1-1)}+\hfill \\ \hfill & \sum _{{\eta }_1=0}^{\infty }\sum _{l_1=0}^{\infty }\sum _{d_1=0}^{\infty }\frac{{(-1)}^{{\eta }_1}\left({\eta }_1\right)!{\left(b_{13}\right)}^{d_1}{\left(b_{12}\right)}^{l_1}{c}_{14}}{\left(d_1\right)!({\eta }_1-l_1)!(l_1-d_1)!{\left(b_{12}\right)}^{d_1}{\left(c_{13}\right)}^{{\eta }_1+1}}·\frac{t^{l_1+d_1-3{\eta }_1-1}}{\Gamma (l_1+d_1-3{\eta }_1)},\hfill \\ \hfill \overline{\Pi }(y,s)=& \frac{1}{s}\left(1+\gamma \sqrt{\frac{b{P}_{r}s}{s+c}}\right)\frac{1}{1-\sqrt{\frac{b{P}_{r}s}{s+c}}},\hfill \\ \hfill =& \sum _{ϵ=0}^{\infty }\sum _{\delta =0}^{\infty }{\left(b{P}_r\right)}^{\frac{ϵ}{2}}{(-1)}^{\delta }{\left(c\right)}^{\delta }\frac{\Gamma (\frac{ϵ}{2}+\delta )}{\Gamma \left(\frac{ϵ}{2}\right)}\frac{1}{s^{\delta +1}}+\gamma \sum _{ϵ=0}^{\infty }\sum _{n=0}^{\infty }{\left(b{P}_r\right)}^{\frac{ϵ+1}{2}}{(-1)}^{\frac{ϵ+1}{2}}{\left(c\right)}^n\frac{\Gamma (\frac{ϵ+1}{2}+n)}{\Gamma \left(\frac{ϵ+1}{2}\right)}\frac{1}{s^{n+1}}\hfill \\ \hfill \Pi (y,t)=& \sum _{ϵ=0}^{\infty }\sum _{\delta =0}^{\infty }{\left(b{P}_r\right)}^{\frac{ϵ}{2}}{(-1)}^{\delta }{\left(c\right)}^{\delta }\frac{\Gamma (\frac{ϵ}{2}+\delta )}{\Gamma \left(\frac{ϵ}{2}\right)}\frac{t^{\delta }}{\Gamma (\delta +1)}+\gamma \sum _{ϵ=0}^{\infty }\sum _{n=0}^{\infty }{\left(b{P}_r\right)}^{\frac{ϵ+1}{2}}{(-1)}^{\frac{ϵ+1}{2}}{\left(c\right)}^n\frac{\Gamma (\frac{ϵ+1}{2}+n)}{\Gamma \left(\frac{ϵ+1}{2}\right)}\frac{t^n}{\Gamma (n+1)}\hfill \\ \hfill \Omega (y,t)=& {\mathcal{L}}^{-1}\left\{\overline{\Omega }(y,s)\right\}={\mathcal{L}}^{-1}\left\{\overline{\Pi }(y,s)\overline{\Psi }(y,s)\right\}=(\Pi \ast \Psi )\left(t\right),\hfill \\ \hfill & b=\frac{1}{1-\alpha },b_1=\frac{1}{1-beta},c=b\alpha ,c_1=b_1\beta ,b_2=1+{\lambda }_{1}b,b_3=1+{\lambda }_2{b}_1,\hfill \\ \hfill & b_4=b_2(M+c_1)+c,b_5=b_{2}M{c}_1+c(M+c_1),c_2=Mc{c}_1,c_3=c^2,b_6=(b_3+1)c,\hfill \\ \hfill & c_4=c_2-\frac{b_7{c}_3}{b_3},c_5=\frac{b_7}{b_3},b_7=b_4-\frac{b_2{b}_6}{b_3},b_8=b_5-\frac{b_2{c}_3}{b_3},b_9=b_8-\frac{b_6{b}_7}{b_3},b_{10}=\frac{b_2}{b_3},\hfill \\ \hfill & b_{11}=\frac{b_{10}}{c_5},c_6=\frac{b_9}{b_3{c}_5},c_7=\frac{c_4}{b_9},c_8=\frac{b_6}{b_3},c_9=\frac{c_3}{b_3},c_{10}=c_8-c_7,c_{11}=c_9-c_7{c}_{10},\hfill \\ \hfill & c_{12}=\frac{c_{11}}{c_{10}},c_{13}=\frac{c_2}{b_2},c_{14}=\frac{c{c}_1}{b_2},b_{12}=\frac{b_4-b_{3}bPr}{b_2},b_{13}=\frac{b_5-c_{1}bPr}{b_2},b_{14}=\frac{b_2{c}_1+c}{b_2}·\hfill \end{array}$$

(36)

5. Limiting Cases

We recover the same expression for fractionalize velocity equation of Maxwell model by considering ${\lambda }_2=0$ as obtained by M M Ghalib et al. [49]. The velocity field in this case is written as:

$$\begin{array}{cc}\hfill \overline{u}(y,s)& =\frac{F\left(s\right)\sqrt{C}}{\sqrt{C}+\gamma \left(\sqrt{(s+b\alpha +\lambda bs)(s+M)}\right)}{e}^{-y\sqrt{\frac{C+\lambda bs}{C}(s+M)}}\hfill \\ \hfill & +\frac{G_r\sqrt{C}(C+\lambda bs)}{s(sb{P}_r-(C+\lambda bs)(s+M))(\sqrt{sb{P}_r}-\sqrt{C})}\hfill \\ \hfill & \times \left(\frac{\sqrt{C}}{\sqrt{C}+\gamma \left(\sqrt{(C+\lambda bs)(s+M)}\right)}{e}^{-y\sqrt{\frac{C+\lambda bs}{C}(s+M)}}-e^{-y\sqrt{\frac{sb{P}_r}{C}}}\right)\hfill \\ \hfill & +\frac{\gamma \sqrt{sb{P}_r}}{s(sb{P}_r-(C+\lambda bs)(s+M))(\sqrt{sb{P}_r}-\sqrt{C})}\hfill \\ \hfill & \times \left(\frac{G_r\sqrt{C}(C+\lambda bs)}{\sqrt{C}+\gamma \left(\sqrt{(C+\lambda bs)(s+M)}\right)}{e}^{-y\sqrt{\frac{C+\lambda bs}{C}(s+M)}}\right)\hfill \end{array}$$

where $b=\frac{1}{1-\alpha }$ and $C=s+b\alpha$.

The velocity distribution for Maxwell fluid can be deduced by implementing ${\lambda }_2\to 0$ and assigning the value of $F\left(s\right)=\frac{1}{s-a}$ in Equation (31) the same expression for velocity field is recovered as derived by Imran et al. [29].

Furthermore, for $\alpha ,\beta \to 1$, the temperature and momentum distributions are obtained as

$$\begin{array}{c}\hfill \theta (y,t)=-\left[e^{-ck}{e}^{c^{2}t}erfc\left(c\sqrt{t}+\frac{k}{2\sqrt{t}}\right)+erfc\left(\frac{k}{2\sqrt{t}}\right)\right],\end{array}$$

(37)

where $c=-\frac{1}{\sqrt{Pr}}$ and $k=y\sqrt{Pr}$.

$$\begin{array}{cc}\hfill \overline{w}(y,s)& =\frac{F\left(s\right)e^{-y\sqrt{\frac{{\lambda }_1{s}^2+as+M}{1+{\lambda }_{2}s}}}}{1+\gamma \sqrt{\frac{{\lambda }_1{s}^2+as+M}{1+{\lambda }_{2}s}}}-\left(\frac{G_r\left(1+{\lambda }_{1}s\right)e^{-y\sqrt{Prs}}}{s(\sqrt{Prs}-1)(Prs(1+{\lambda }_{2}s)-({\lambda }_1{s}^2+as+M))}\right)\hfill \\ \hfill & \times \left(\frac{(1+\gamma \sqrt{Prs})e^{-y\sqrt{\frac{{\lambda }_1{s}^2+as+M}{1+{\lambda }_{2}s}}}}{1+\gamma \sqrt{\frac{{\lambda }_1{s}^2+as+M}{1+{\lambda }_{2}s}}}-e^{-y\sqrt{Prs}}\right),\hfill \end{array}$$

(38)

where $a=1+{\lambda }_{1}M$.

Finally, we get the same solution for velocity and temperature expressions as investigated by Talha et al. [45], when $f\left(t\right)=0$.

This shows the validity of our current results with the publications.

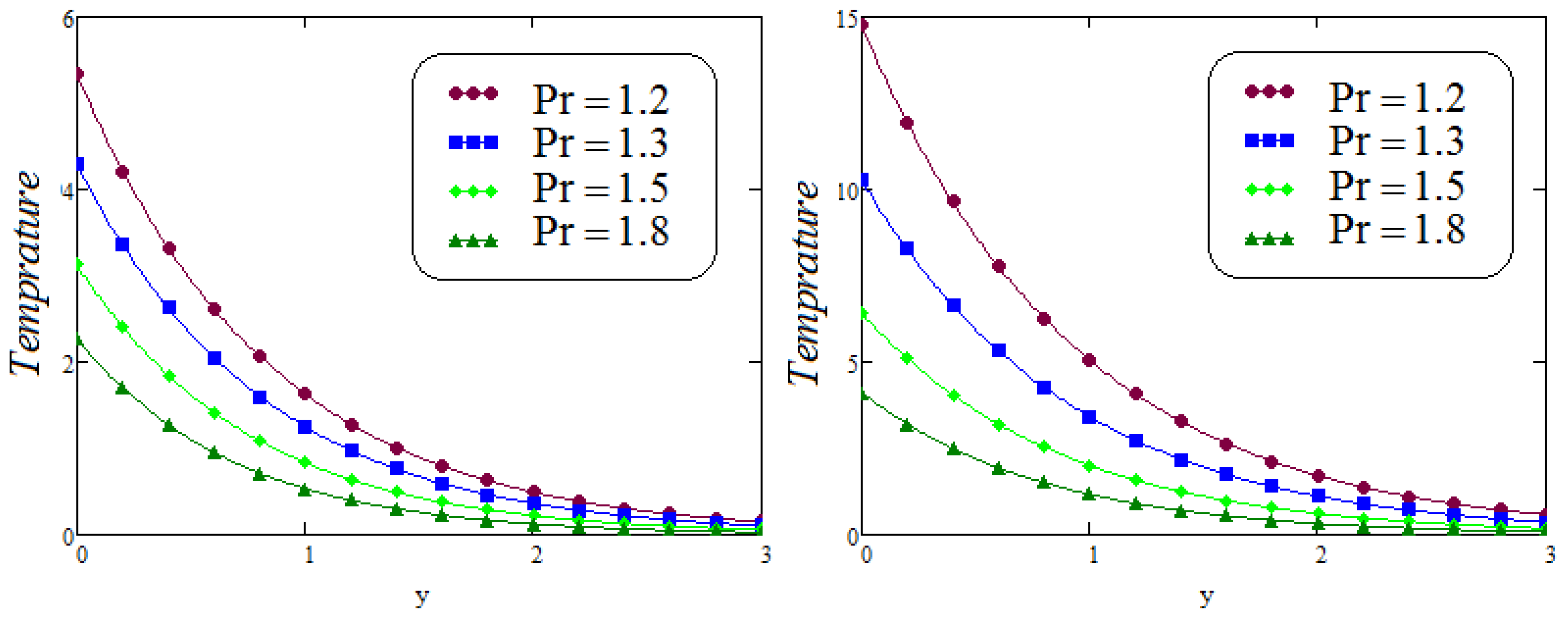
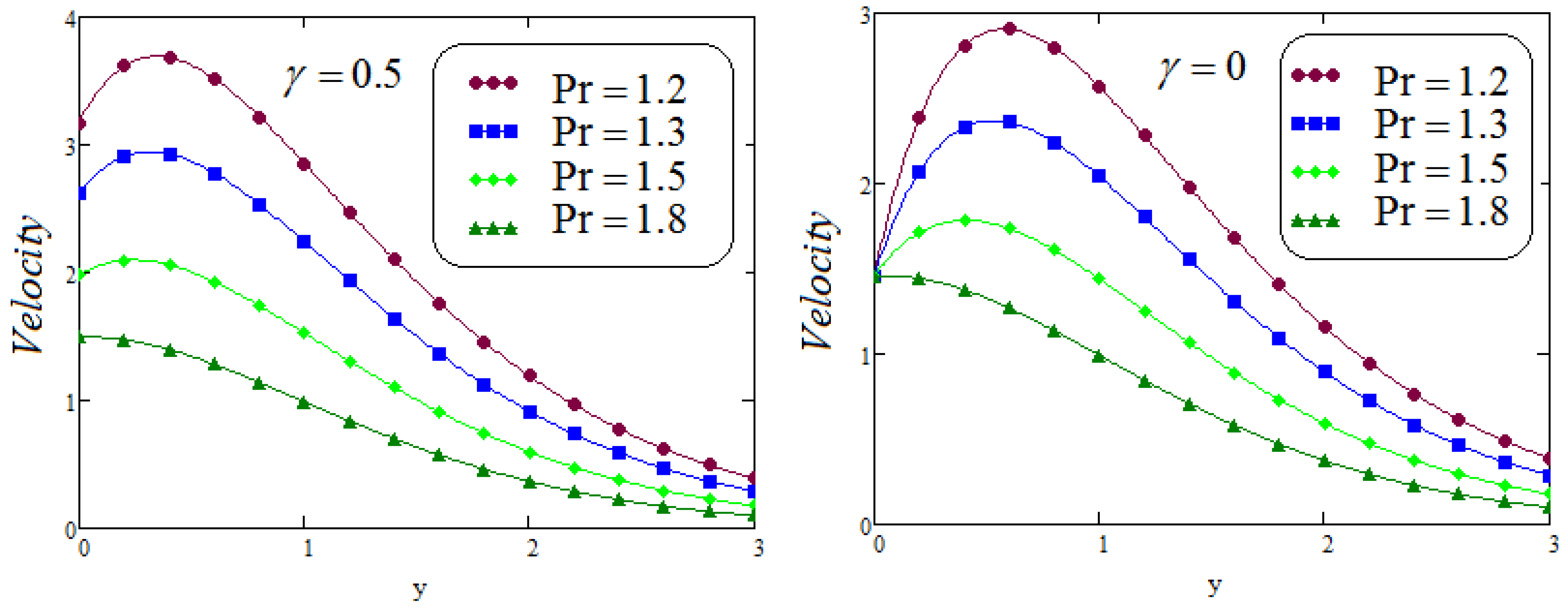
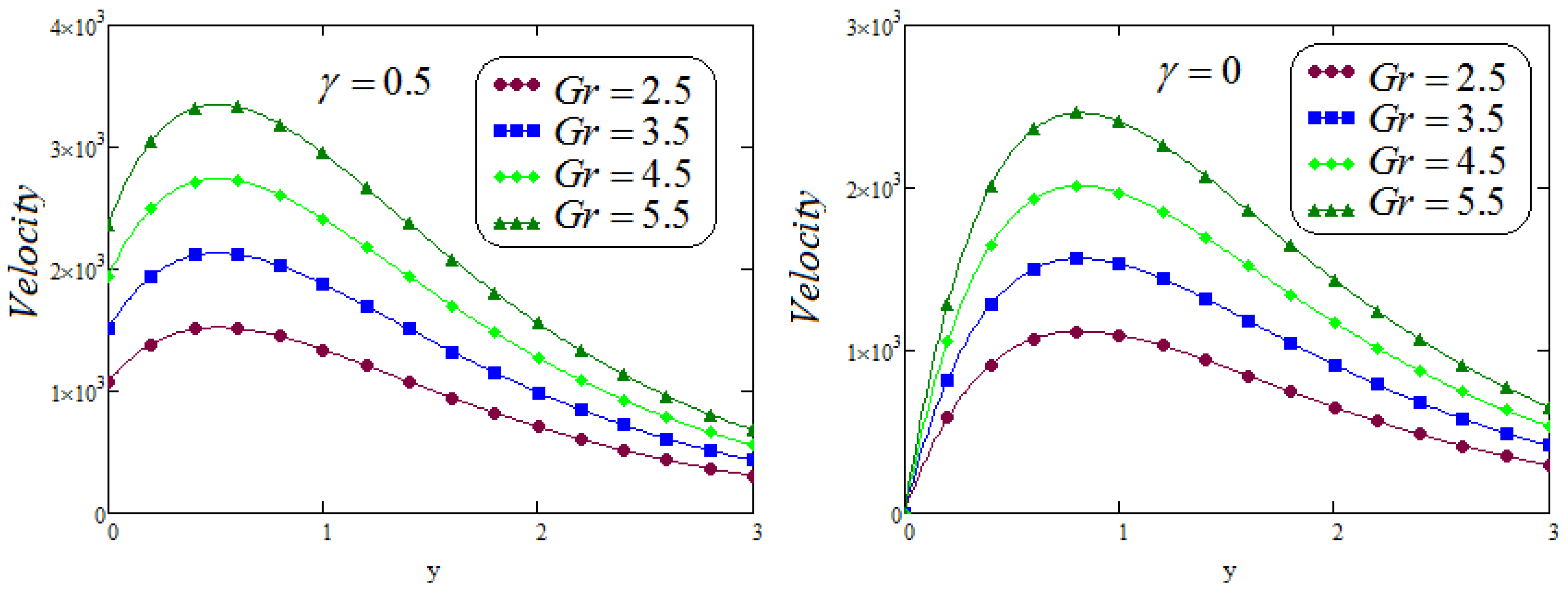
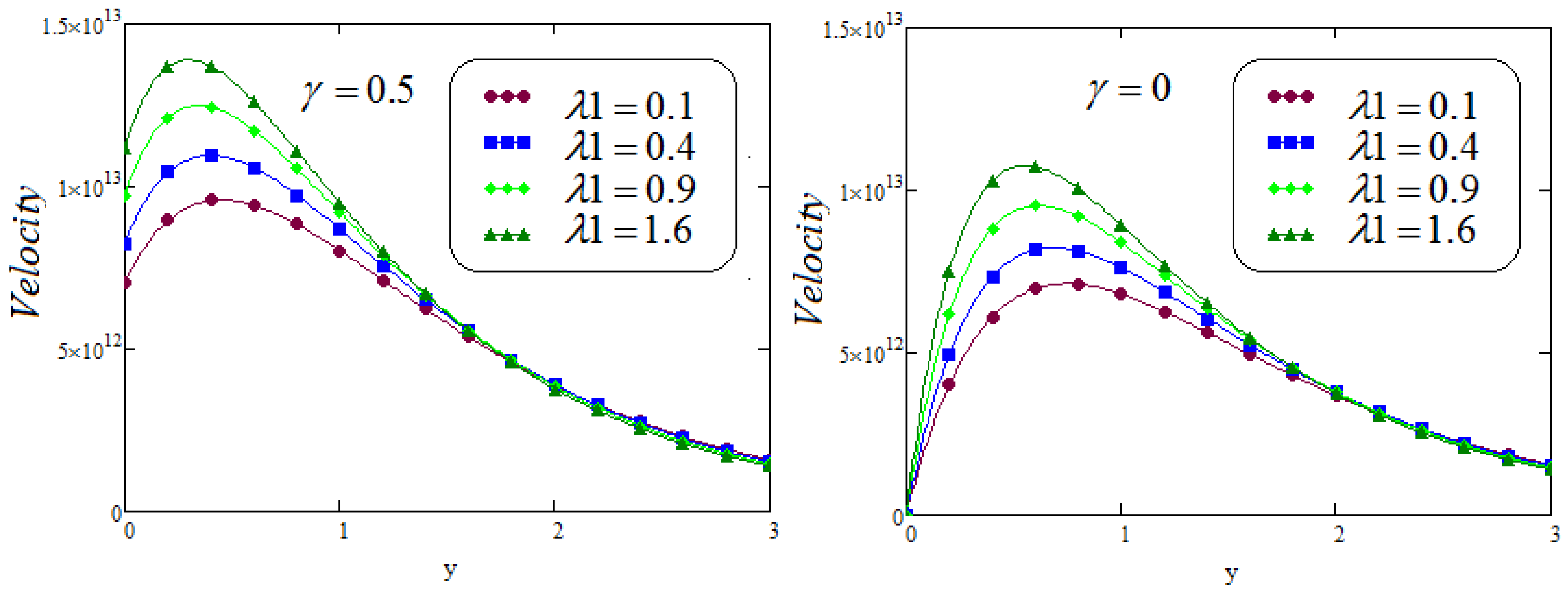
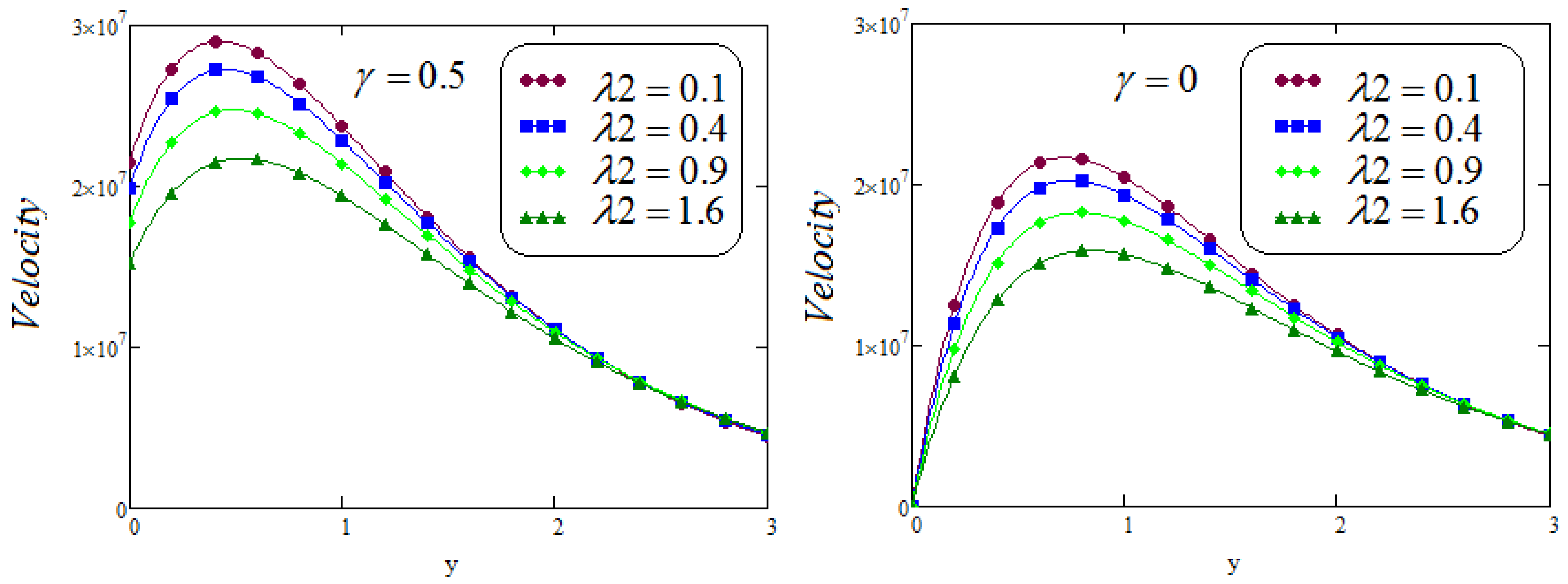
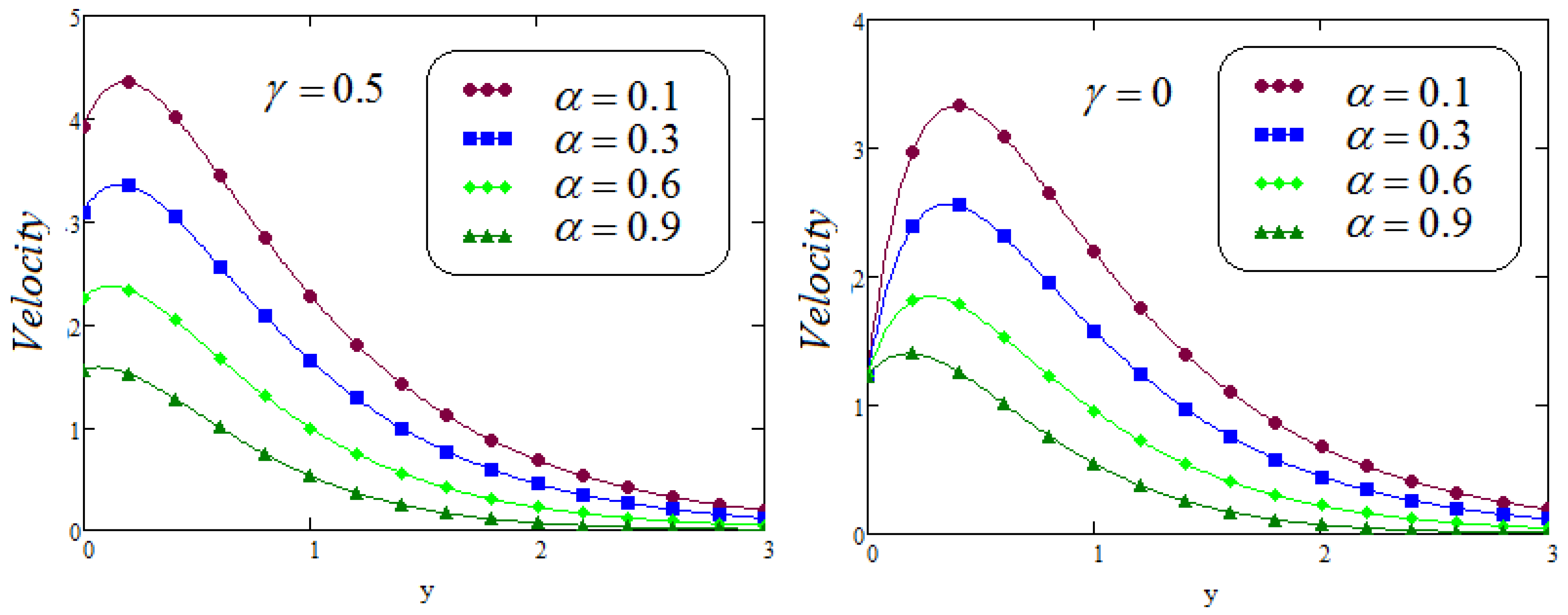
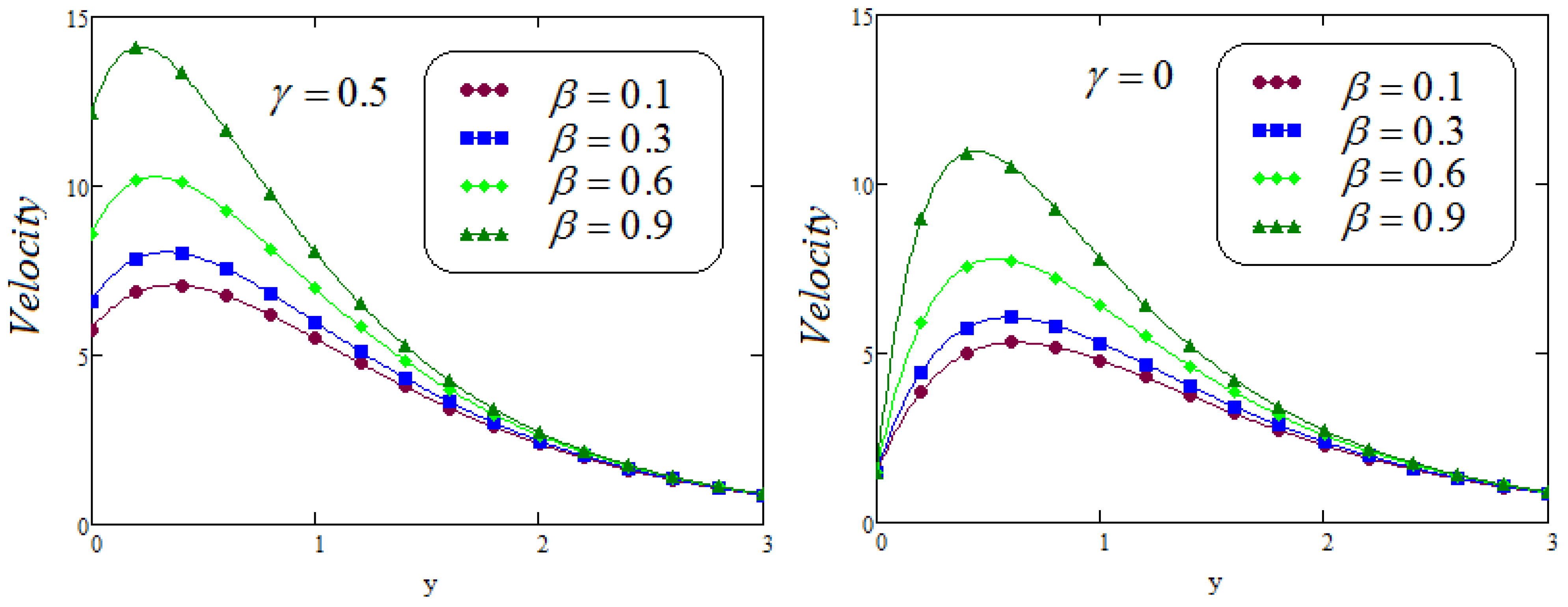
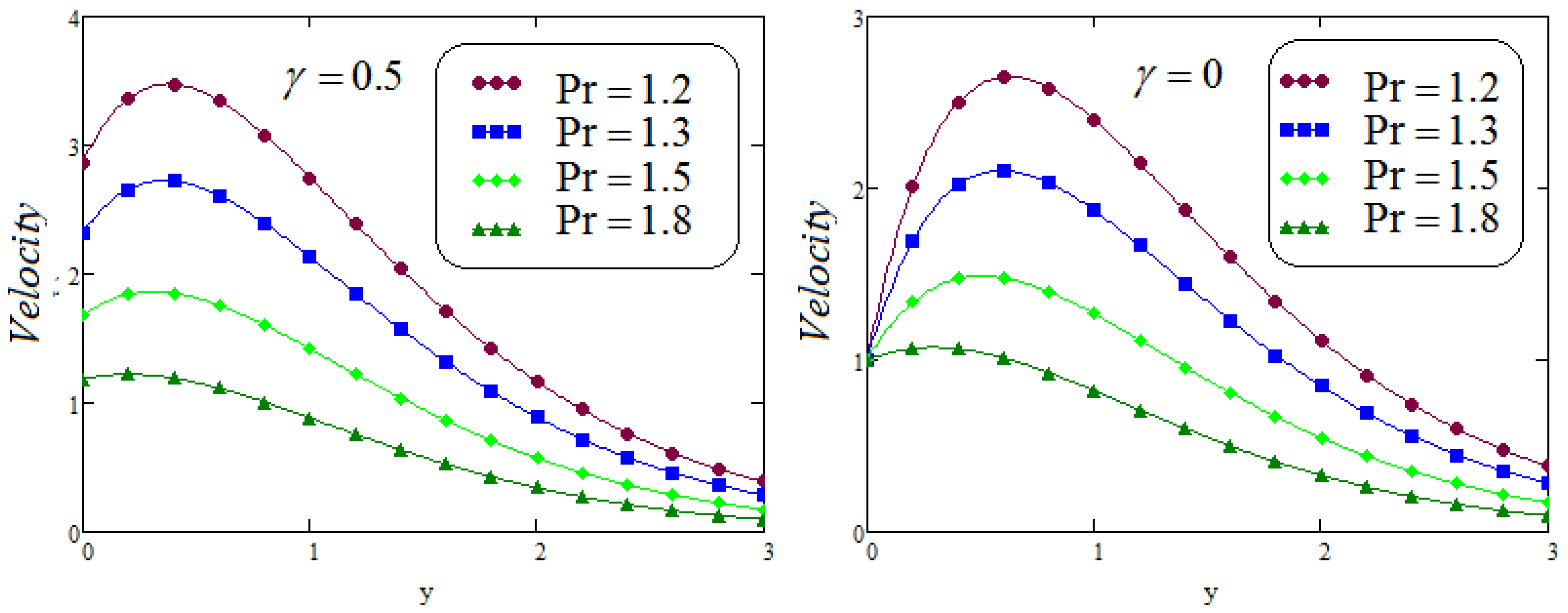
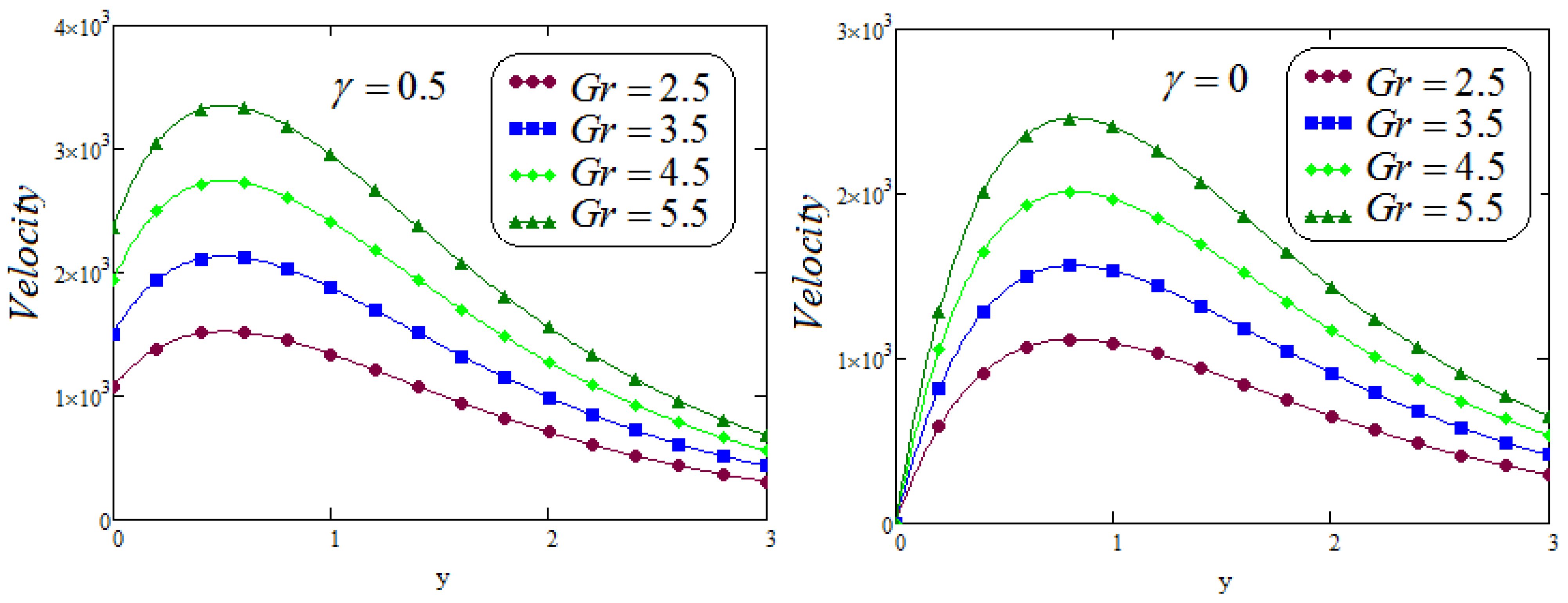
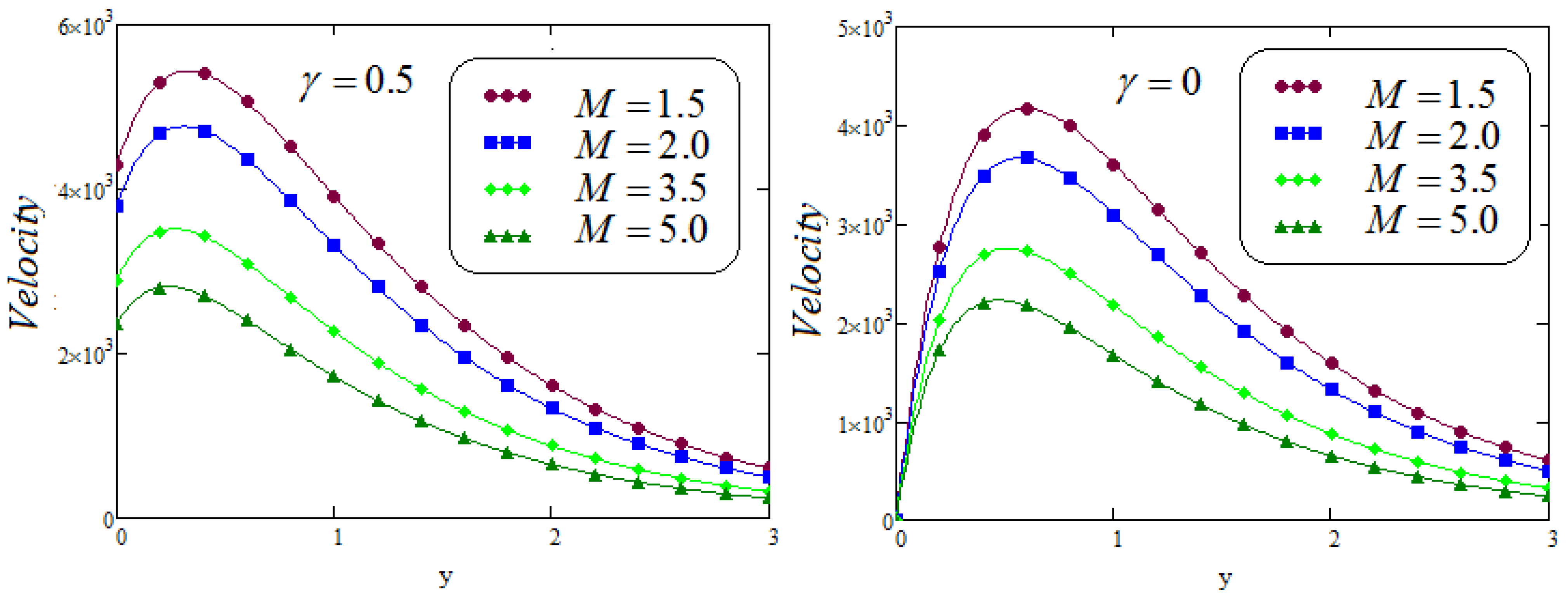
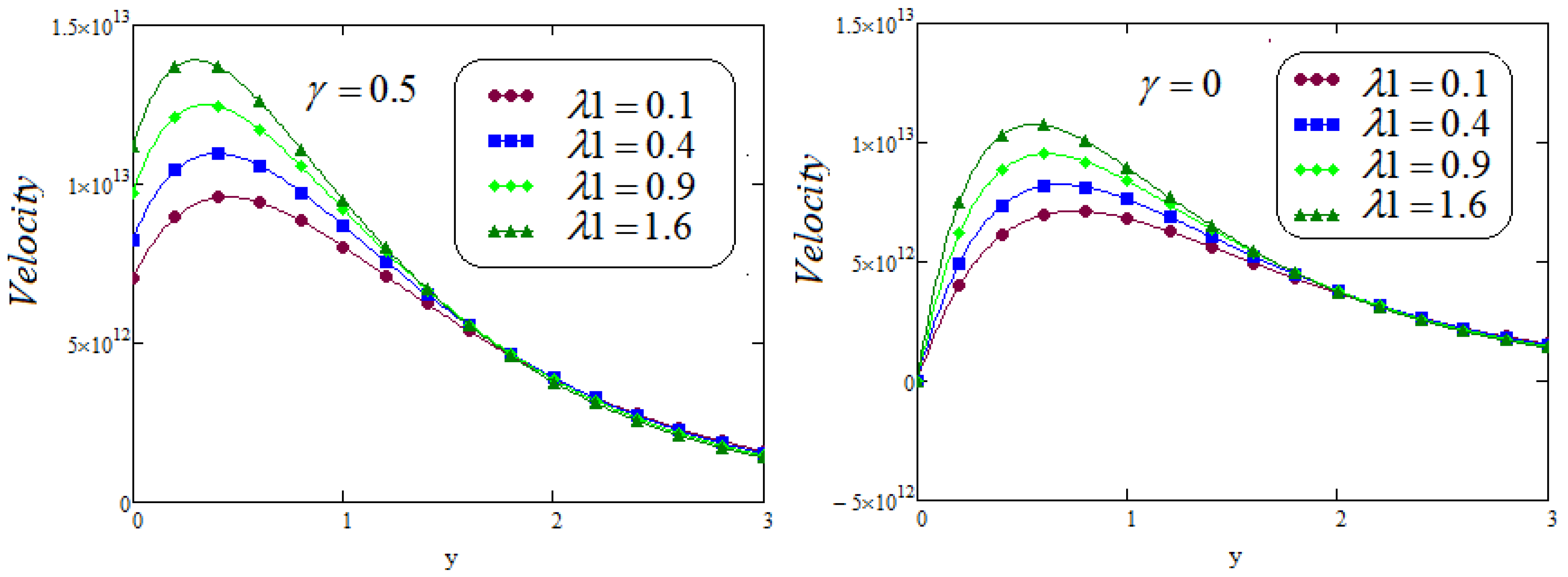
6. Results and Discussion

This section is determined to present the physical clarification of the obtained exact results via Laplace transformation and assayed the impacts of pertinent parameters on temperature and velocity expressions of oldroyd-B fluid. These exact solutions are very helpful for researchers to compare the results which are explored by different numerical techniques, and have great importance in different fields of engineering and scientific applied. Graphs demonstrate the velocity and thermal profiles to examined the behavior of these solutions. The influence of the relevant dimensionless several connected parameters ${\lambda }_1$, $P_r$, ${\lambda }_2$, $G_r$, M, $\alpha$, and $\beta$ are examined, and portrayed graphically, also deliberated their physical aspects. The relevant graphical representations to analyzed the impacts of concerned parameters will be included here to avoid recurrence.

Figure 2 portrays the impact of $P_r$, Prandtl number, over the thermal profile for dissimilar values of $P_r$. It is depicted that decay in the thermal outline layer due to increase in $P_r$. Generally, thermal outline layer thickness decreases rapidly, corresponding to high values of $P_r$. So that, increasing the values of $P_r$ improves the boundary thickness, which causes energy profile slowdown linearly.

In Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, velocity is plotted for the function $f\left(t\right)=e^{at}$ with and without slip effect $\gamma$ for several values of dimensionless parameters $M,Pr,Gr,{\lambda }_1$ and ${\lambda }_2$, by considering $t=1.5$ and $a=0.25$.

Figure 3 represent the influence of $P_r$ on momentum equation. It is noted that advances in Prandtl number declines the velocity of the moving fluid. The outline layer of velocity profile gets thicker due to the fact that the small rate of thermal diffusion, $P_r$ dominance the relative thickness of boundary layers of momentum in heat transfer problems.

Figure 4, exemplify the momentum field to analyzed the effect of $G_r$. A rise in velocity profile have appeared for boosting the value of grashof number. Physically, the result of the increase in $G_r$ which is the result of more induced fluid flows is due to a rise in buoyancy effects. Therefore, these forces can impact on enhancing the velocity.

Figure 5 discuss the control of magnetic number M. It is eminent that the velocity decline for boosting the values of magnetic parameter. Physically, the Lorentz force is the reason behind this because it is highly effected by the electromagnetic force, which opposes the movement of the fluid.

Figure 6 and Figure 7 portray the influence of ${\lambda }_1$, time relaxation parameter, and ${\lambda }_2$, time retardation parameter, over the velocity contour. It is clear that the rise in velocity for increasing the values of the time relaxation parameter ${\lambda }_1$ but reduction in velocity have appeared for boosting the values of the time retardation parameter ${\lambda }_2$. Physically, increase in ${\lambda }_1$, reduced the fluid viscosity, so that it will accelerate the fluid flow and hence velocity rises. Further, the increase the values of ${\lambda }_2$ which leads to boosted the outline layer thickness and decreased the fluid velocity. It is depicted that the effect of ${\lambda }_1$ and ${\lambda }_2$ on velocity profile are quite opposite.

It is depicted that for several values, of fractional parameters $\alpha$ and $\beta$, the behavior of fluid velocity in Figure 8, Figure 9 and Figure 10 are discussed, also compare the fractional and non-fractional model. Decay in velocity profile is noticed corresponding to large values of fractional parameter $\alpha$ but velocity profile enhanced by increasing the value of $\beta$.

Moreover, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 illustrated the behavior of velocity for the function $f\left(t\right)=sint$ with and without slip effect $\gamma$ for different values of parameters $M,Pr,Gr,{\lambda }_1$, ${\lambda }_2$, $\alpha$, and $\beta$ for dimensionless time $t=1.5$.

Figure 11 represent the influence of $P_r$ on momentum equation. It is noted that advances in Prandtl number declines the velocity of the moving fluid. The outline layer of velocity profile gets thicker due to the fact that the small rate of thermal diffusion, $P_r$ dominance the relative thickness of boundary layers of momentum in heat transfer problems. For both functions $f\left(t\right)=e^{at}$ and $f\left(t\right)=sint$ velocity behavior is nearly same.

Figure 12, exemplify the momentum field to analyzed the effect of $G_r$. A rise in velocity profile have appeared for boosting the value of grashof number. Physically, the result of the increase in $G_r$ which is the result of more induced fluid flows is due to a rise in buoyancy effects. Therefore, these forces can impact on enhancing the velocity.

Figure 13 discuss the control of magnetic number M. It is eminent that the velocity decline for boosting the values of magnetic parameter. Physically, the Lorentz force is the reason behind this because it is highly effected by the electromagnetic force, which opposes the movement of the fluid.

Figure 14 and Figure 15 portray the influence of ${\lambda }_1$, time relaxation parameter, and ${\lambda }_2$, time retardation parameter, over the velocity contour. It is clear that the rise in velocity for increasing the values of the time relaxation parameter ${\lambda }_1$ but reduction in velocity have appeared for boosting the values of the time retardation parameter ${\lambda }_2$. Physically, increase in ${\lambda }_1$, reduced the fluid viscosity, so that it will accelerate the fluid flow and, hence, velocity rises. Further, the increase the values of ${\lambda }_2$ which leads to boosted the outline layer thickness and decreased the fluid velocity. It is depicted that the effect of ${\lambda }_1$ and ${\lambda }_2$ on velocity profile are quite opposite.

It is analyzed that velocity profile shows same behavior for both functions $f\left(t\right)=e^{at}$ and $f\left(t\right)=sint$. It is depicted that for several values, of fractional parameters $\alpha$ and $\beta$, the behavior of fluid velocity in Figure 16, Figure 17 and Figure 18 are discussed, also compare the fractional and non-fractional model. Decay in velocity profile is noticed corresponding to large values of fractional parameter $\alpha$ but velocity profile enhanced by increasing the value of $\beta$. Additionally, it is seen that when $\alpha ,\beta \to 1$, then CF non-integer model turns into a classical model.

7. Conclusions

A thorough investigation of MHD convective flow of Oldroyd-B model has been analyzed in this research under the effects of different non-dimensional parameters. The model is generalized, in view of Caputo–Fabrizio fractional derivative, and exact solutions for dimensionless momentum and energy equations are evaluated by the technique of Laplace integral transformation. Graphs illustrate the velocity and thermal profiles for considering both zero and non-zero slip conditions to examined the pertinent feature of these solutions. The influence of the relevant dimensionless several involving system parameters time relaxation parameter ${\lambda }_1$, Prandtl number $P_r$, time retardation parameter ${\lambda }_2$, grashof number $G_r$, fractional parameters $\alpha ,\beta$ and magnetic parameter M are examined and portrayed graphically, also deliberated their physical aspects. The obtained outcomes are pointed out as:

• The temperature field decline with the larger values of $P_r$;
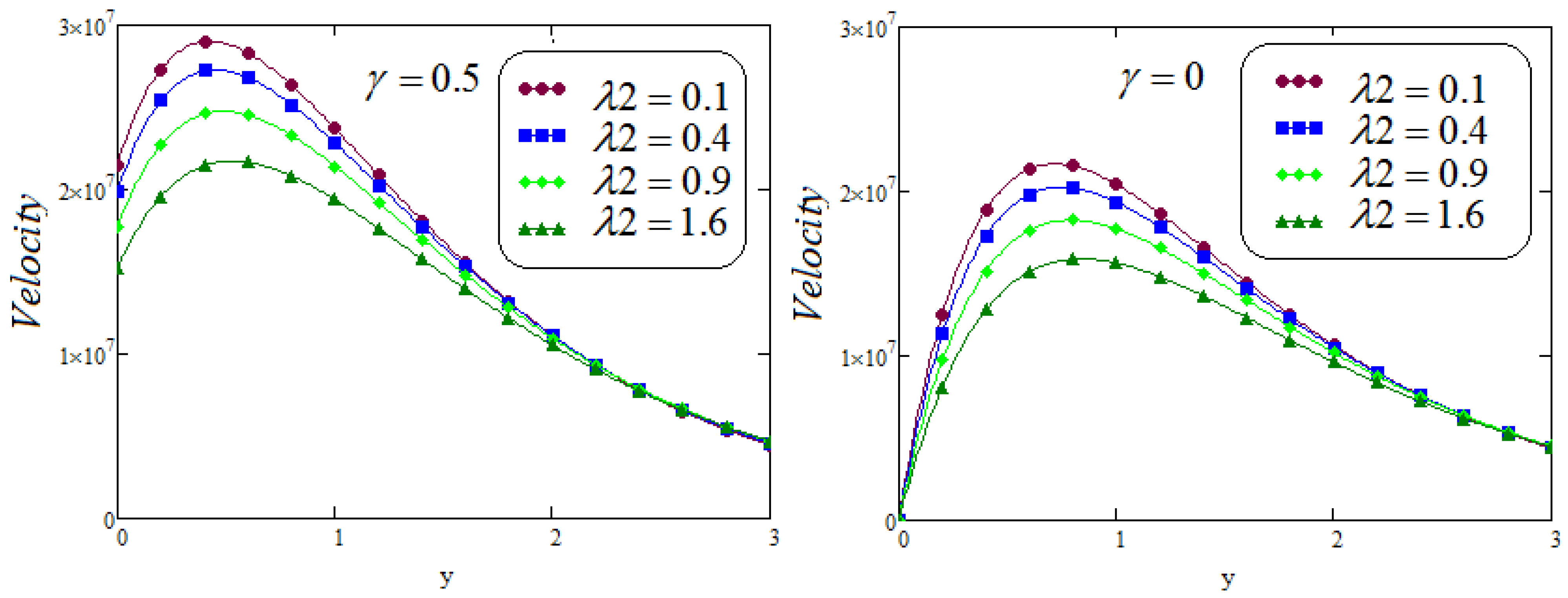
• It is examined that the impacts of ${\lambda }_1$ and ${\lambda }_2$ on velocity profile are quite opposite;
• The accumulative values of the parameters M and $P_r$ decrease in the velocity distribution noticed;
• The increasing values of the grashof number $G_r$ stimulates the velocity distribution;
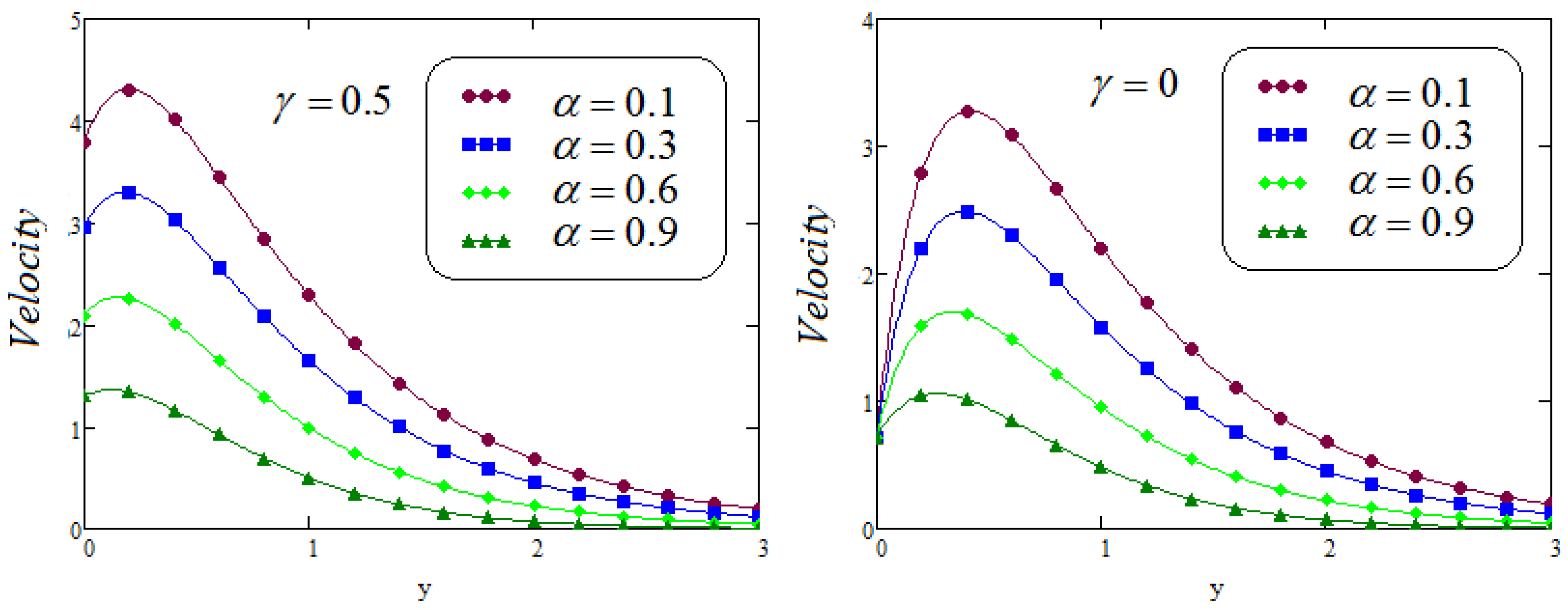
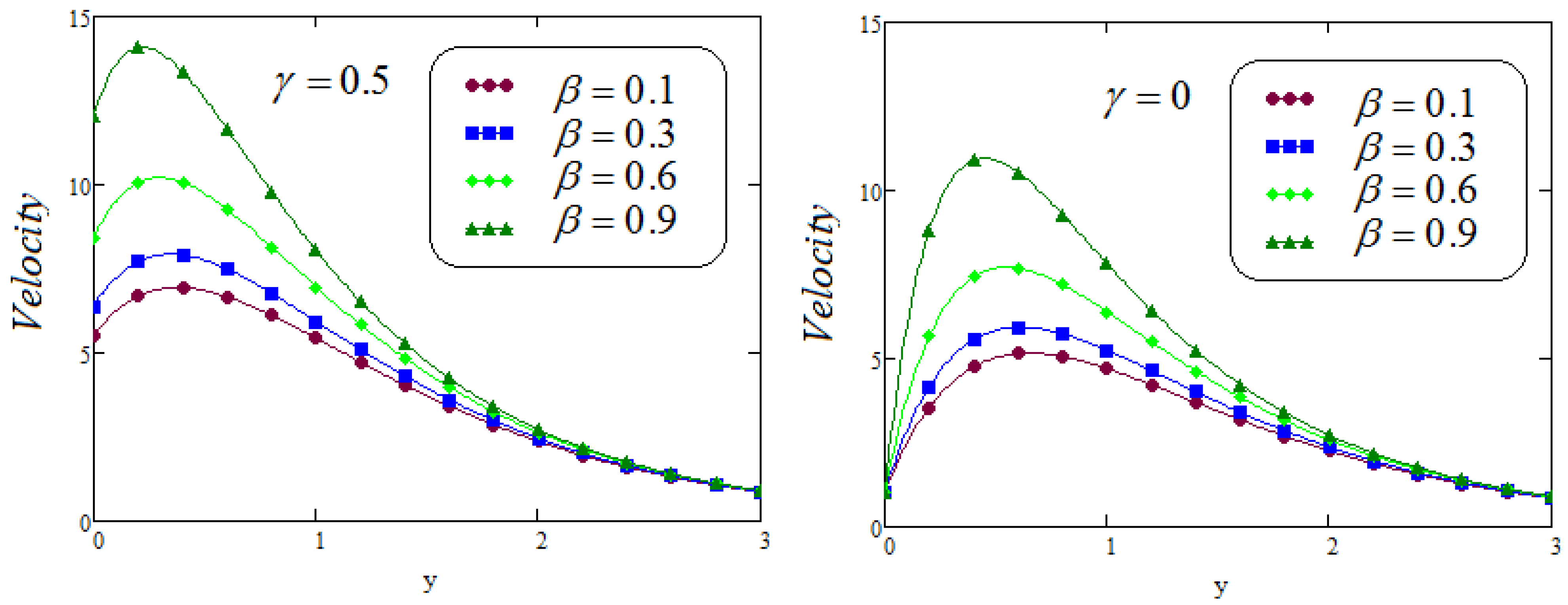
• It is analyzed that the effect of fractional parameters $\alpha$ and $\beta$ on velocity contour are quite converse;
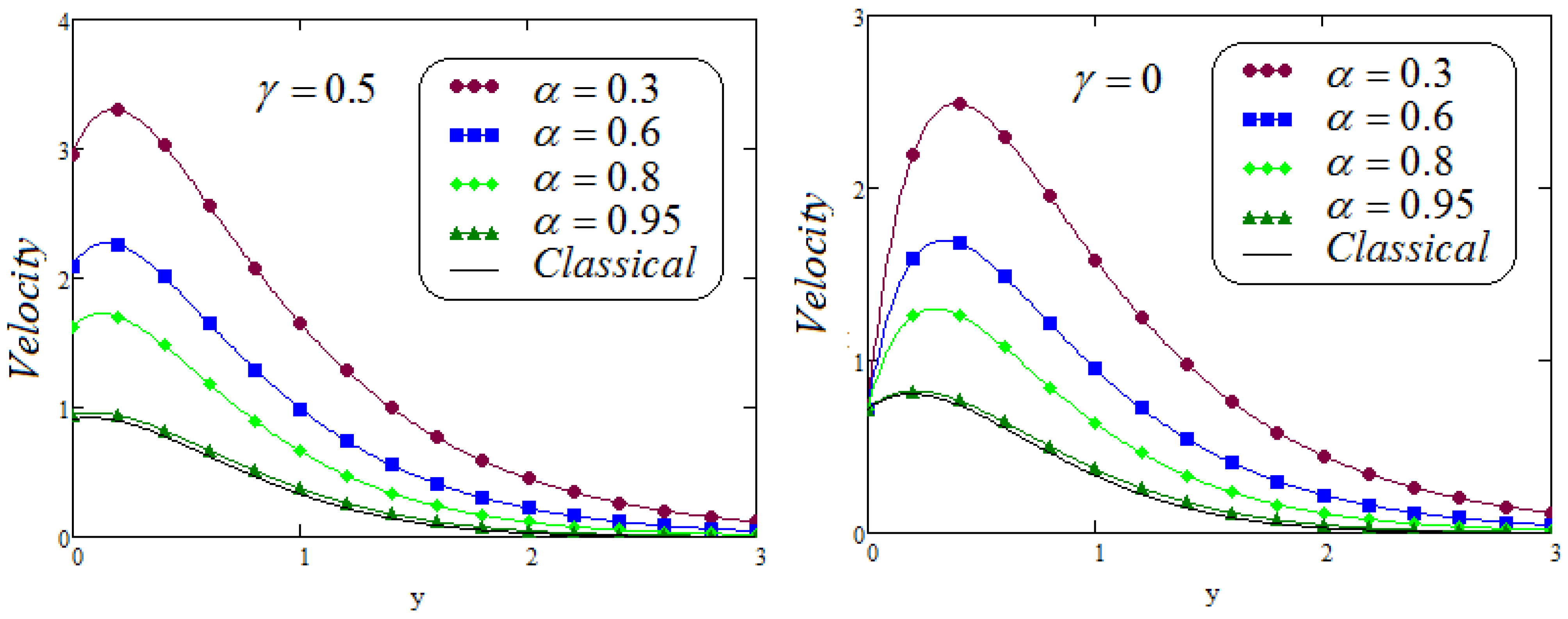
• Caputo Fabrizio fractional model approaches to classical model when $\alpha ,\beta \to 1$;
• It is noted that for two different functions $f\left(t\right)=e^{at}$ and $f\left(t\right)=sint$, velocity profile shows same behavior.