A Grey System Approach for Estimating the Hölderian Regularity with an Application to Algerian Well Log Data
Abstract
:1. Introduction
2. Background
2.1. Local Hölderian Regularity
2.2. Multifractional Brownian Motion
2.3. Local Estimation of the Hölderian Regularity
2.4. Grey System Theory (GST)
- (1)
- Data standardization
- (2)
- Modeling of the GM (1,1) is as follows:
- (a)
- Selecting a subsequence denoted by
The GM (1,1) requires a sequence with a length .- (b)
- Constructing an accumulation generation for the subsequence
where andThen, the GM (1,1) is built using Sequence (5):where and are fitting parameters. The column is determined by the least squares method:whereand is the transposed matrix of .- (c)
- Replacing in Equation (6), the grey model can be expressed by
where the function is fitted to the signal accumulated series .- (d)
- Differentiating to reduce
or simply computing by the subtraction- (e)
- Calculating the deviation (grey model error) between the accumulated sequence and the fitting function
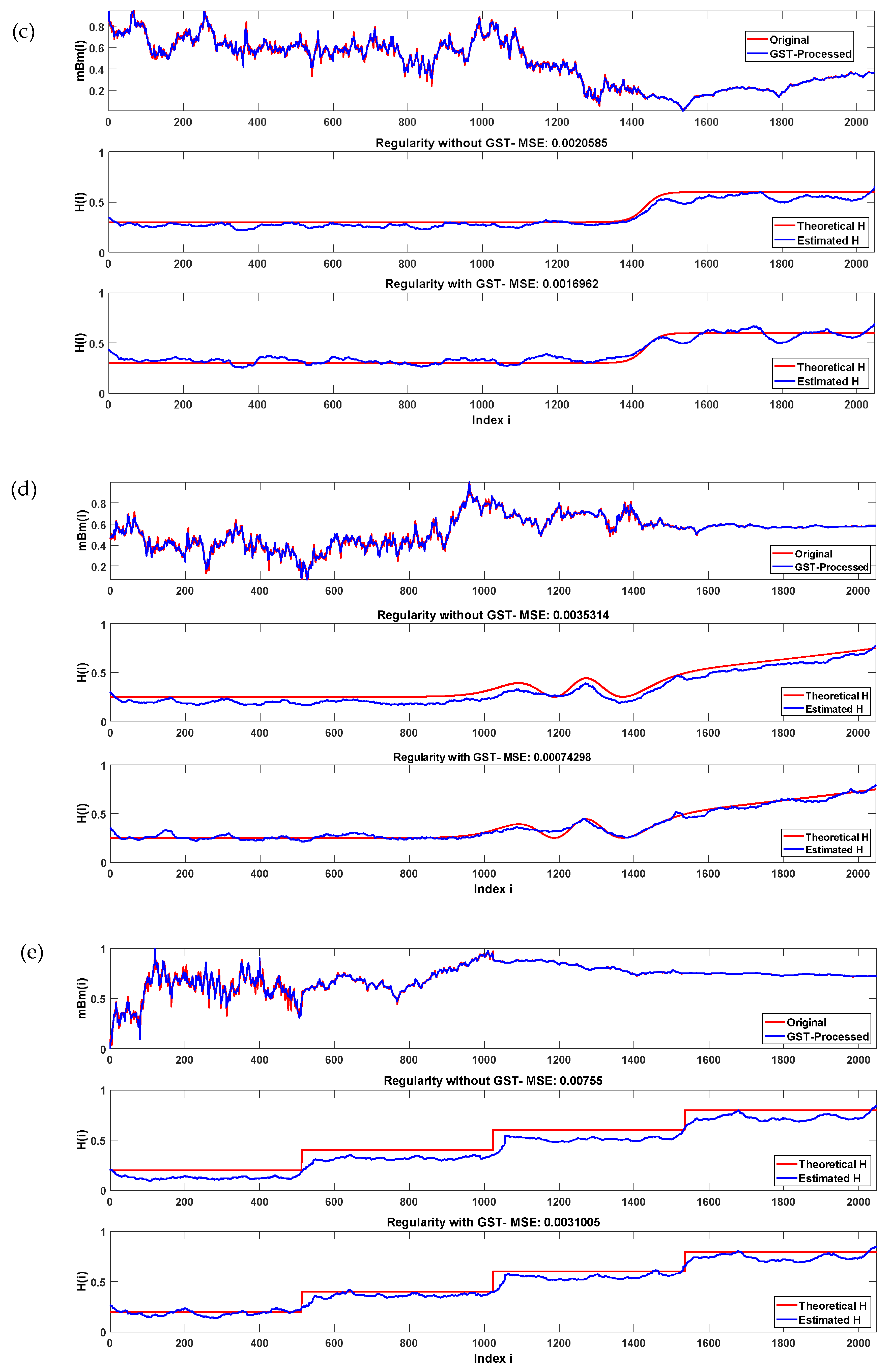
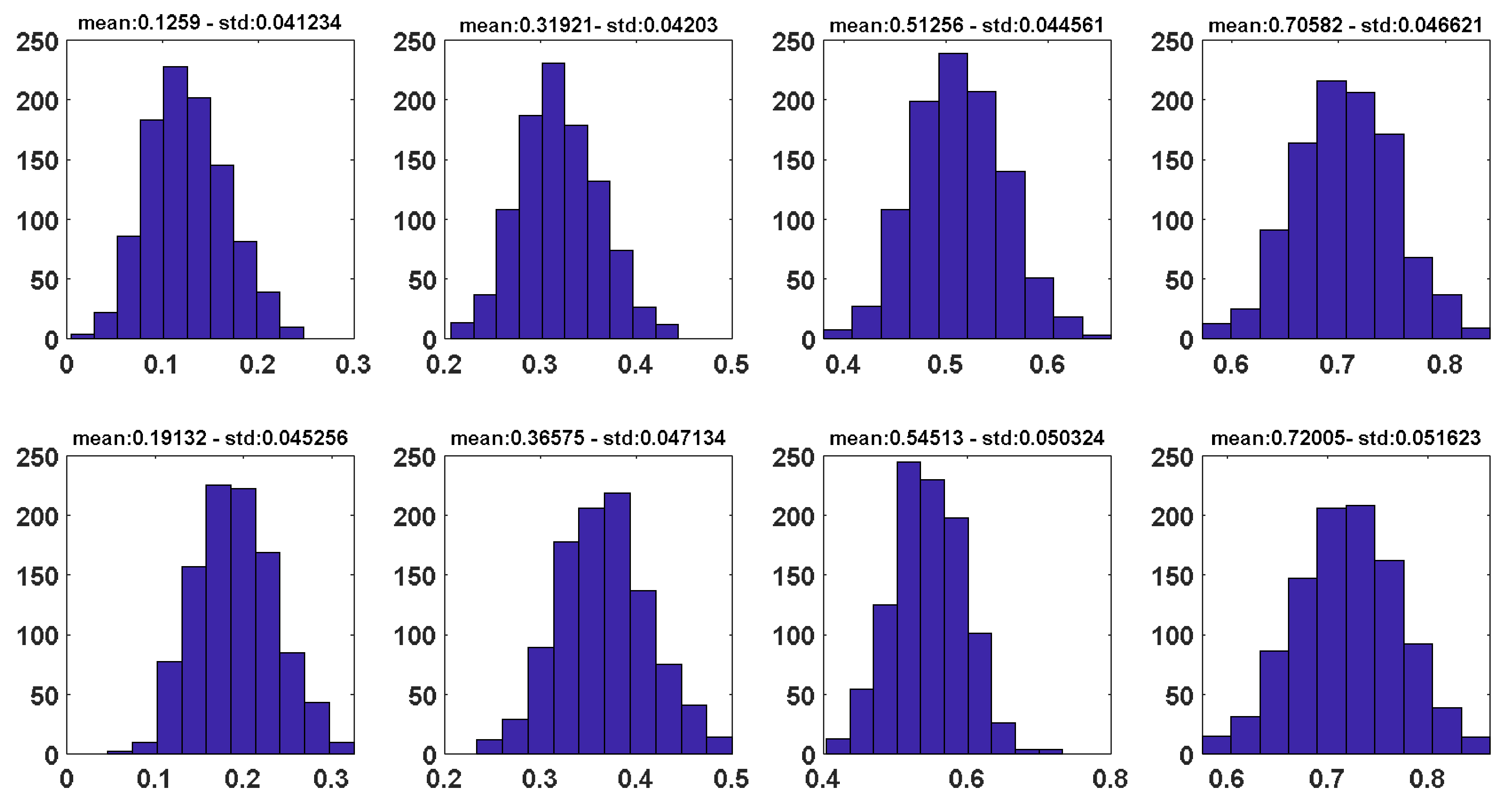
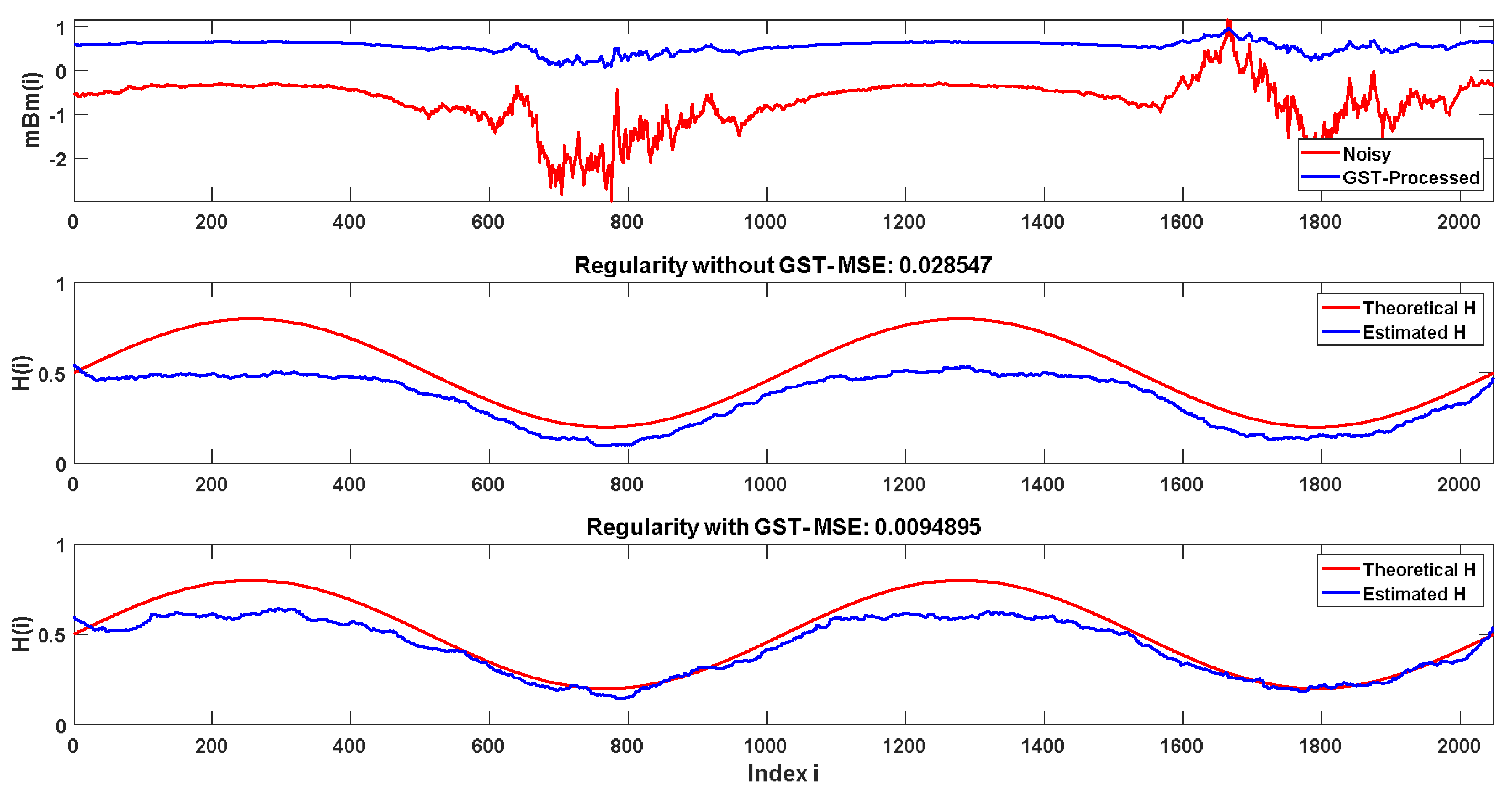
3. Application to Simulated Data
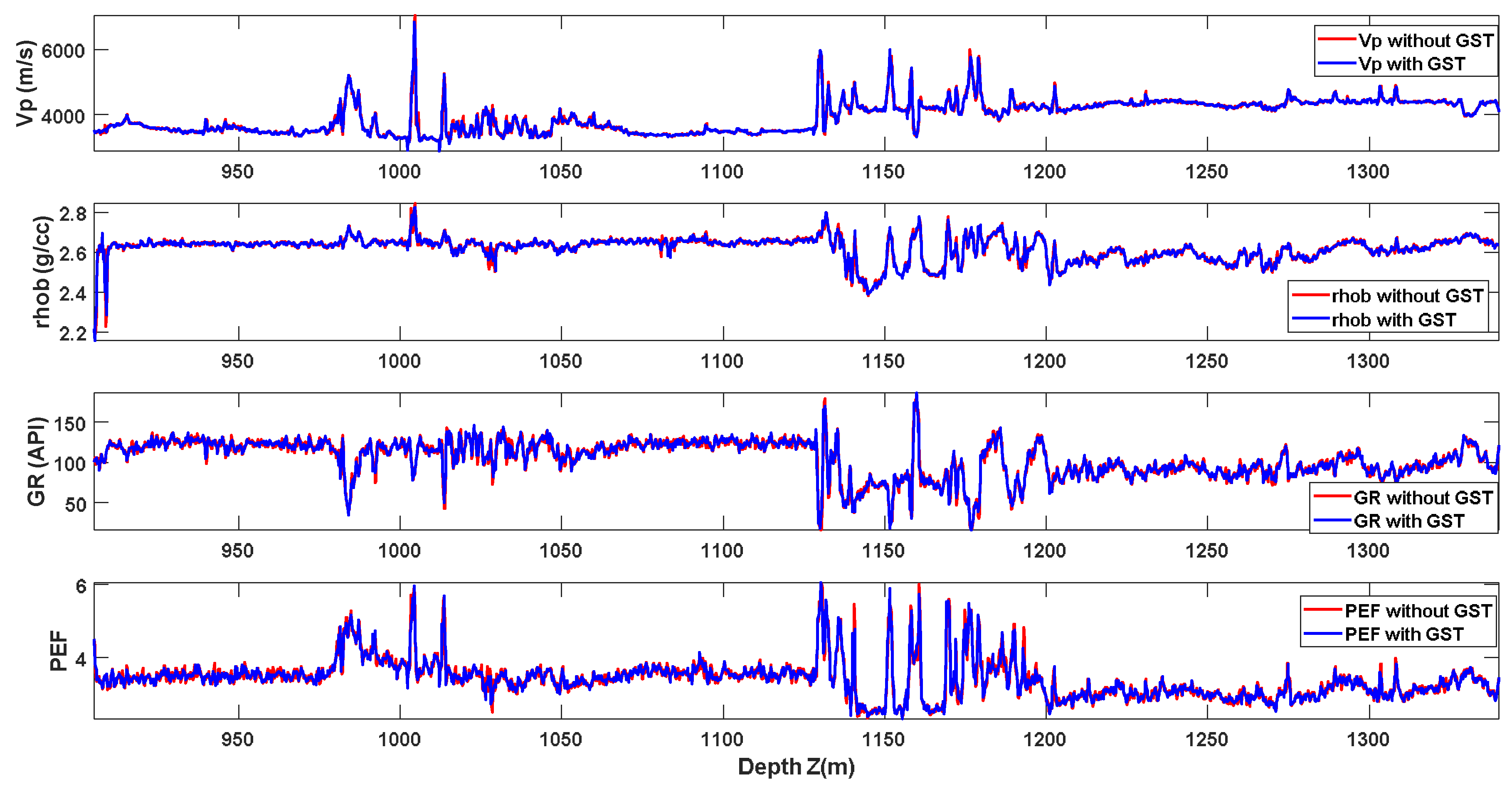
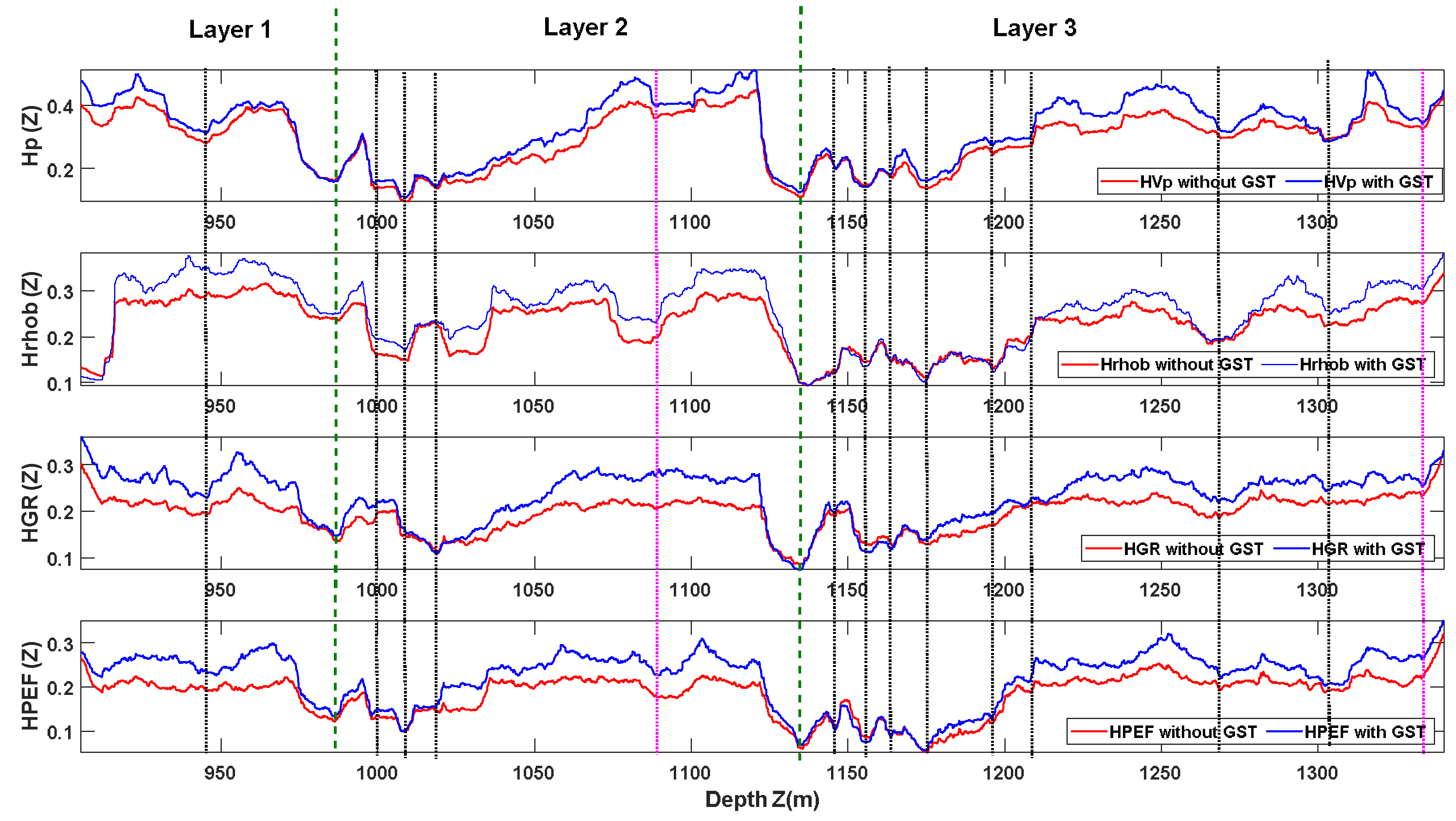
4. Application to Algerian Well Log Data
- Layer L1 (905–981 m): shale.
- Layer L2 (981–1133 m): alternation of sandstone and shale, with limestone layers.
- Layer L3 (1133–1340 m): sandstone.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peltier, R.F.; Lévy-Véhel, J. Multifractional Brownian Motion: Definition and preliminary results. Tech. Rep. INRIA RR 1995, 1, 2645. [Google Scholar]
- Bicego, M.; Trudda, A. 2D shape classification using multifractional brownian motion. Lect. Notes Comput. Sci. 2010, 5342, 906–916. [Google Scholar]
- Li, M.; Lim, S.C.; Hu, B.-J.; Feng, H. Towards describing multi-fractality of traffic using local Hurst function. Lect. Notes Comput. Sci. 2007, 4488, 1012–1020. [Google Scholar]
- Silva, M.; Rocha, F.G. Traffic modeling for communications networks: A multifractal approach based on few parameters. J. Frankl. Inst. 2021, 358, 2161–2177. [Google Scholar] [CrossRef]
- Wanliss, J. Fractal properties of SYM-H during quiet and active times. J. Geophys. Res. 2005, 110, 12. [Google Scholar] [CrossRef]
- Wanliss, J.A.; Cersosimo, D.O. Scaling properties of high latitude magnetic field data during different magnetospheric conditions. Int. Conf. Substorms 2006, 8, 325–329. [Google Scholar]
- Cersosimo, D.O.; Wanliss, J.A. Initial studies of high latitude magnetic field data during different magnetospheric conditions. Earth Planets Space 2007, 59, 39–43. [Google Scholar] [CrossRef] [Green Version]
- Gaci, S.; Zaourar, N. A new approach for the investigation of the local regularity of borehole wire-line logs. J. Hydrocarb. Mines Environ. Res. 2010, 1, 6–13. [Google Scholar]
- Gaci, S.; Zaourar, N.; Hamoudi, M.; Holschneider, M. Local regularity analysis of strata heterogeneities from sonic logs. Nonlin. Process. Geophys. 2010, 17, 455–466. [Google Scholar] [CrossRef] [Green Version]
- Gaci, S.; Zaourar, N. Heterogeneities characterization from velocity logs using multifractional Brownian motion. Arab. J. Geosci. 2011, 4, 535–541. [Google Scholar] [CrossRef]
- Gaci, S.; Zaourar, N. Two-Dimensional Multifractional Brownian Motion—Based Investigation of Heterogeneities from a Core Image. In Advances in Data, Methods, Models and Their Applications in Geoscience; InTech Ed.: London, UK, 2011. [Google Scholar]
- Gaci, S.; Zaourar, N.; Briqueu, L.; Hamoudi, M. Regularity Analysis of Airborne Natural Gamma Ray Data Measured in the Hoggar Area (Algeria). In Advances in Data, Methods, Models and Their Applications in Geoscience; InTech Ed.: London, UK, 2011. [Google Scholar]
- Gaci, S.; Zaourar, N.; Briqueu, L.; Holschneider, M. Regularity analysis applied to sonic logs data: A case study from KTB borehole site. Arab. J. Geosci. 2011, 4, 221–227. [Google Scholar] [CrossRef]
- Deng, J. Control problems of grey system. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Deng, J.L. The Primary Methods of Grey System Theory; Huazhong Institute of Technology Press: Wuhan, China, 1987; pp. 1–20. [Google Scholar]
- Deng, J.L. Grey Theory; Huangzhong University of Science and Technology Press: Wuhan, China, 2002; pp. 1–15. [Google Scholar]
- Liu, S.F.; Lin, Y. Grey Systems: Theory and Application; Springer: London, UK, 2006; pp. 1–78. [Google Scholar]
- Wu, H.; Dong, Y.; Shi, W.; Clarke, K.C.; Miao, Z.; Zhang, J.; Chen, X. An improved fractal prediction model for forecasting mine slope deformation using GM (1, 1). Struct. Health Monit. 2015, 14, 502–512. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Geng, J.; Guo, T. New seismic attribute: Fractal scaling exponent based on gray detrended fluctuation analysis. Appl. Geophys. 2015, 12, 343–352. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Han, H.; Ying, Y. Improving the signal subtle feature extraction performance based on dual improved fractal box dimension eigenvectors. R. Soc. Open Sci. 2018, 5, 180087. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Li, Y.; Qi, L. Research on multifractal dimension and improved gray relation theory for intelligent satellite signal recognition. Wirel. Netw. 2019, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Honório, B.; Drummond, R.; Vidal, A.; Sanchetta, A.; Leite, E. Well log denoising and geological enhancement based on discrete wavelet transform and hybrid thresholding. Energy Explor. Exploit. 2012, 30, 417–433. [Google Scholar] [CrossRef] [Green Version]
- Fedi, M.; Fiore, D.; La Manna, M. Regularity Analysis Applied to Well Log Data. In Fractal Behaviour of the Earth System; Springer: Berlin/Heidelberg, Germany, 2005; pp. 63–82. [Google Scholar]
- Khan, M.M.; Ahmad Fadzil, M.H. Singularity spectrum analysis of windowed seismograms. In Proceedings of the 8th International Conference on Frontiers of Information Technology—FIT ’10, Islamabad, Pakistan, 21–23 December 2010. [Google Scholar] [CrossRef]
- Subhakar, D.; Chandrasekhar, E. Reservoir characterization using multifractal detrended fluctuation analysis of geophysical well-log data. Phys. A Stat. Mech. Its Appl. 2016, 445, 57–65. [Google Scholar] [CrossRef]
- Partovi, S.M.A.; Sadeghnejad, S. Fractal parameters and well-logs investigation using automated well-to-well correlation. Comput. Geosci. 2017, 103, 59–69. [Google Scholar] [CrossRef]
- Amoura, S.; Gaci, S.; Bounif, M.; Boussa, L. On characterizing heterogeneities from velocity logs using Hölderian regularity analysis: A case study from Algerian tight Devonian reservoirs. J. Appl. Geophys. 2019, 170. [Google Scholar] [CrossRef]
- Prajapati, R.; Singh, U.K. Delineation of stratigraphic pattern using combined application of wavelet-Fourier transform and fractal dimension: A case study over Cambay Basin, India. Mar. Pet. Geol. 2020, 120, 104562. [Google Scholar] [CrossRef]
- Boulassel, A.; Zaourar, N.; Gaci, S.; Boudella, A. A new multifractal analysis-based for identifying the reservoir fluid nature. J. Appl. Geophys. 2021, 185, 104185. [Google Scholar] [CrossRef]
- Benassi, A.; Jaffard, S.; Roux, D. Gaussian processes and pseudodifferential elliptic operators. Rev. Mat. Iberoam. 1997, 13, 19–81. [Google Scholar] [CrossRef] [Green Version]
- Ayache, A.; Taqqu, M.S. Multifractional process with random exponent. Publ. Mat. 2005, 49, 459–486. [Google Scholar] [CrossRef] [Green Version]
- Ayache, A.; Jaffard, S.; Taqqu, M.S. Wavelet construction of generalized multifractional processes. Rev. Mat. Iberoam. 2007, 23, 327–370. [Google Scholar] [CrossRef] [Green Version]
- Peltier, R.F.; Lévy-Véhel, J. A new method for estimating the parameter of fractional brownian motion. Tech. Rep. INRIA 1994, 1, 2396. [Google Scholar]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press: Cambridge, UK, 1997; p. 398. [Google Scholar]
- Sonatrach. Internal Technical Report of Southwestern Algeria Exploration Assets; Internal Publisher: Boumerdes, Algeria, 2007; p. 100. [Google Scholar]


| HVp | HGR | Hrhob | HPEF | |
|---|---|---|---|---|
| HVp | 1.00|1.00 | 0.84|0.88 | 0.61|0.65 | 0.80|0.84 |
| HGR | 1.00|1.00 | 0.57|0.62 | 0.73|0.76 | |
| Hrhob | 1.00|1.00 | 0.83|0.84 | ||
| HPEF | 1.00|1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaci, S.; Nicolis, O. A Grey System Approach for Estimating the Hölderian Regularity with an Application to Algerian Well Log Data. Fractal Fract. 2021, 5, 86. https://doi.org/10.3390/fractalfract5030086
Gaci S, Nicolis O. A Grey System Approach for Estimating the Hölderian Regularity with an Application to Algerian Well Log Data. Fractal and Fractional. 2021; 5(3):86. https://doi.org/10.3390/fractalfract5030086
Chicago/Turabian StyleGaci, Said, and Orietta Nicolis. 2021. "A Grey System Approach for Estimating the Hölderian Regularity with an Application to Algerian Well Log Data" Fractal and Fractional 5, no. 3: 86. https://doi.org/10.3390/fractalfract5030086
APA StyleGaci, S., & Nicolis, O. (2021). A Grey System Approach for Estimating the Hölderian Regularity with an Application to Algerian Well Log Data. Fractal and Fractional, 5(3), 86. https://doi.org/10.3390/fractalfract5030086






