Quarter-Sweep Preconditioned Relaxation Method, Algorithm and Efficiency Analysis for Fractional Mathematical Equation
Abstract
:1. Introduction
2. Preliminary
3. Mixed Caputo Fractional Operator and Quarter-Sweep Discretization Scheme
4. Stability of Caputo’s Fractional Approximation with a Quarter-Sweep Scheme
5. Convergence of Caputo’s Fractional Approximation with a Quarter-Sweep Scheme
6. Concept and Formulation of Quarter-Sweep Preconditioned Relaxation Method
7. Implementation and Application of C++ for Numerical Experiment
8. Conclusions
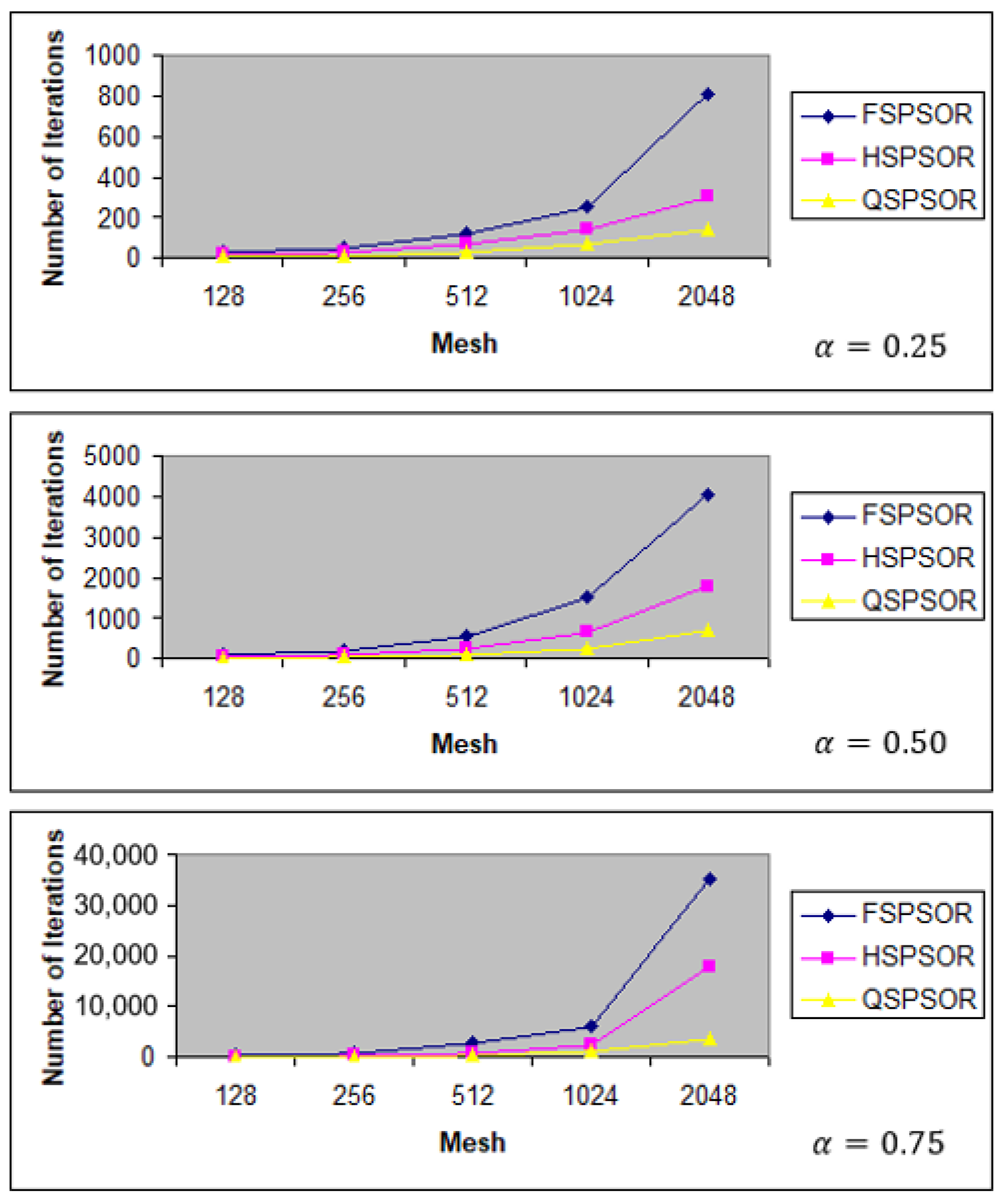
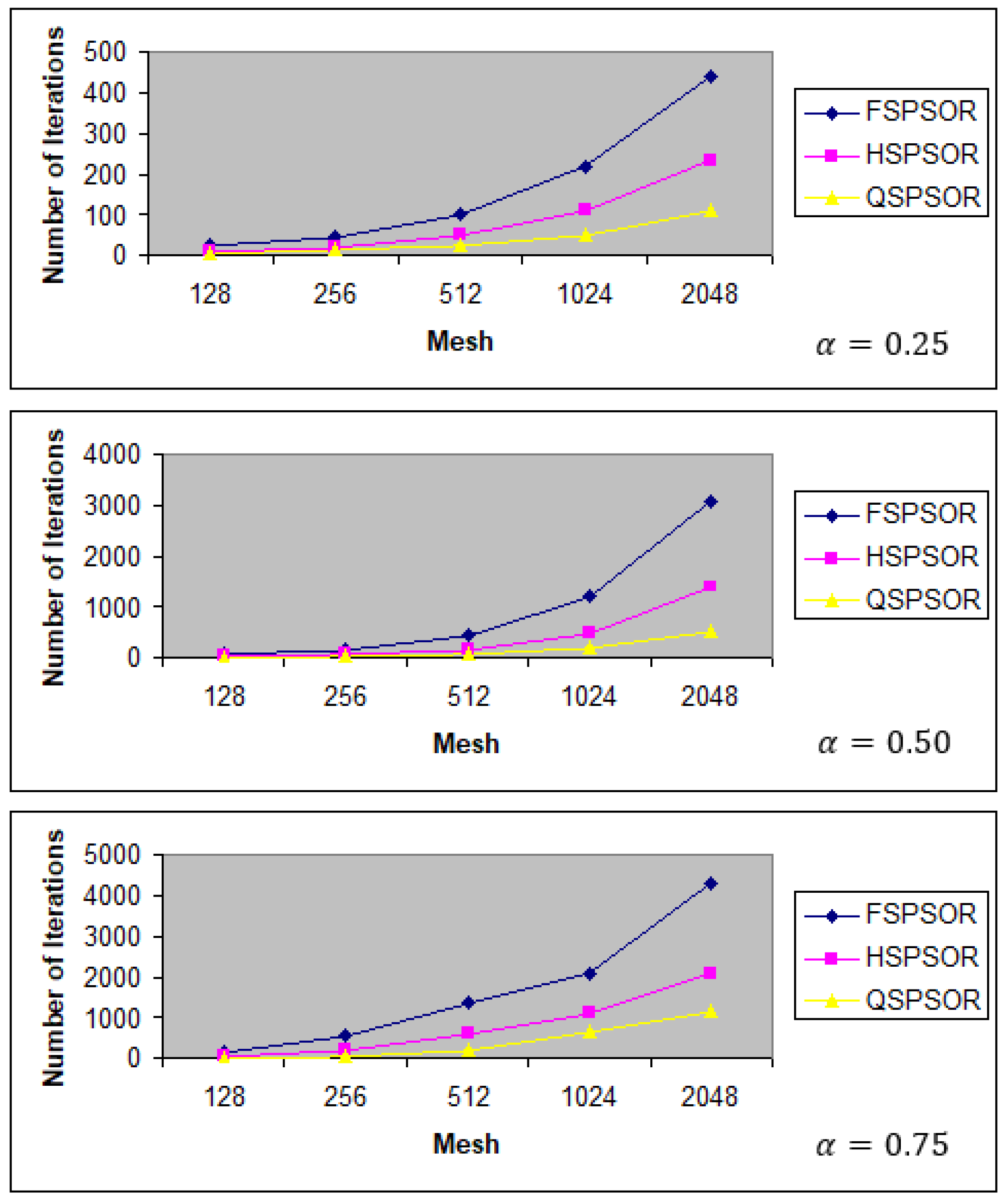
- The QSPSOR method significantly reduced the number of iterations and execution time compared to the existing FSPSOR and HSPSOR methods. On average, QSPSOR reduced the number of iterations and execution time by 81.19% and 84.06%, respectively, compared to FSPSOR. Moreover, QSPSOR reduced the number of iterations and execution time compared to HSPSOR by 59.94% and 66.00%, respectively. The result also showed that using the quarter-sweep scheme and PSOR iteration can reduce the computational complexity for solving the time FDE with a large matrix size.
- Observations regarding the accuracy of all of the implemented numerical methods indicated that their numerical solutions were in good agreement. Furthermore, the accuracy of the solutions of the time-FDE problems obtained by each of the three numerical methods was greater at , followed by and . The combination of the quarter-sweep implicit finite difference scheme and Caputo’s time-fractional derivative enabled an accurate solution for the time FDE to be computed.
- However, a disadvantage of the quarter-sweep difference scheme is that the magnitude of the absolute errors is slightly larger than that of the two previous methods. The accuracy of the quarter-sweep scheme can be improved by applying a suitable treatment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sweilam, N.; Kareem, W.A.; Al-Mekhlafi, S.; Nabih, Z. Numerical treatments for a complex order fractional HIV infection model with drug resistance during therapy. Prog. Fract. Differ. Appl. 2021, 7, 163–176. [Google Scholar] [CrossRef]
- Alrabaiah, H.; Zeb, A.; Alzahrani, E.; Shah, K. Dynamical analysis of fractional-order tobacco smoking model containing snuffing class. Alex. Eng. J. 2021, 60, 3669–3678. [Google Scholar] [CrossRef]
- Wang, X.; Qi, H.; Yang, X.; Xu, H. Analysis of the time-space fractional bioheat transfer equation for biological tissues during laser irradiation. Int. J. Heat Mass Transf. 2021, 177, 121555. [Google Scholar] [CrossRef]
- Moosavi, R.; Moltafet, R.; Shekari, Y. Analysis of viscoelastic non-Newtonian fluid over a vertical forward-facing step using the Maxwell fractional model. Appl. Math. Comput. 2021, 401, 126119. [Google Scholar] [CrossRef]
- Gu, X.-M.; Sun, H.-W.; Zhao, Y.-L.; Zheng, X. An implicit difference scheme for time-fractional diffusion equations with a time-invariant type variable order. Appl. Math. Lett. 2021, 120, 107270. [Google Scholar] [CrossRef]
- Davis, W.; Noren, R.; Shi, K. A Cα finite difference method for the Caputo time-fractional diffusion equation. Numer. Methods Part. Differ. Equ. 2021, 37, 2261–2277. [Google Scholar] [CrossRef]
- Hosseininia, M.; Heydari, M.H.; Maalek Ghaini, F.M. A numerical method for variable-order fractional version of the coupled 2D Burgers equations by the 2D Chelyshkov polynomials. Math. Methods Appl. Sci. 2021, 44, 6482–6499. [Google Scholar] [CrossRef]
- Mirzaee, F.; Sayevand, K.; Rezaei, S.; Samadyar, N. Finite difference and spline approximation for solving fractional stochastic advection-diffusion equation. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 607–617. [Google Scholar] [CrossRef]
- González-Olvera, M.A.; Torres, L.; Hernández-Fontes, J.V.; Mendoza, E. Time fractional diffusion equation for shipping water events simulation. Chaos Solitons Fractals 2021, 143, 110538. [Google Scholar] [CrossRef]
- Liao, X.; Feng, M. Time-fractional diffusion equation-based image denoising model. Nonlinear Dyn. 2021, 103, 1999–2017. [Google Scholar] [CrossRef]
- Maldon, B.; Thamwattana, N. A fractional diffusion model for dye-sensitized solar cells. Molecules 2020, 25, 2966. [Google Scholar] [CrossRef] [PubMed]
- Bohaienko, V.; Bulavatsky, V. Simplified mathematical model for the description of anomalous migration of soluble substances in vertical filtration flow. Fractal Fract. 2020, 4, 20. [Google Scholar] [CrossRef]
- Li, L.; Jiang, Z.; Yin, Z. Compact finite-difference method for 2D time-fractional convection–diffusion equation of groundwater pollution problems. Comput. Appl. Math. 2020, 39, 142. [Google Scholar] [CrossRef]
- Aguilar, J.-P.; Korbel, J.; Luchko, Y. Applications of the fractional diffusion equation to option pricing and risk calculations. Mathematics 2019, 7, 796. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, F.; Turner, I.W.; Li, T. Time-fractional diffusion equation for signal smoothing. Appl. Math. Comput. 2018, 326, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Sunarto, A.; Sulaiman, J. Preconditioned SOR method to solve time-fractional diffusion equations. J. Phys. Conf. Ser. 2019, 1179, 012020. [Google Scholar] [CrossRef]
- Sunarto, A.; Sulaiman, J. Application half-sweep preconditioned SOR method for solving time-fractional diffusion equations. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Detroit, MI, USA, 10–14 August 2020; pp. 3414–3420. [Google Scholar]
- Lung, J.C.V.; Sulaiman, J. On quarter-sweep finite difference scheme for one-dimensional porous medium equations. Int. J. Appl. Math. 2020, 33, 439–450. [Google Scholar] [CrossRef]
- Muhiddin, F.A.; Sulaiman, J.; Sunarto, A. Numerical evaluation of quarter-sweep KSOR method to solve time-fractional parabolic equations. Int. J. Eng. Trends Technol. 2020, 2020, 63–69. [Google Scholar] [CrossRef]
- Suardi, M.N.; Radzuan, N.Z.F.M.; Sulaiman, J. Performance analysis of quarter-sweep Gauss-Seidel iteration with cubic B-spline approach to solve two-point boundary value problems. Adv. Sci. Lett. 2018, 24, 1732–1735. [Google Scholar] [CrossRef]
- Atangana, A. Fractional Operators and Their Applications. In Fractional Operators with Constant and Variable Order with Application to Geo-Hydrology; Atangana, A., Ed.; Academic Press: Cambridge, MA, USA, 2018; Chapter 5; pp. 79–112. [Google Scholar]
- Demir, A.; Erman, S.; Özgür, B.; Korkmaz, E. Analysis of fractional partial differential equations by Taylor series expansion. Bound. Value Probl. 2013, 2013, 68. [Google Scholar] [CrossRef] [Green Version]


| and the Tolerance Error | |
|---|---|
| (i) | and for , iterate the formula shown in Equation (43), |
| (ii) | |
| (iii) | |
| (iv) | If the criterion is achieved, display approximate solutions. |
| Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 128 | FSPSOR | 28 | 0.84 | 2.36 × 102 | 80 | 1.90 | 6.20 × 104 | 246 | 5.76 | 3.99 × 102 |
| HSPSOR | 16 | 0.18 | 2.36 × 102 | 37 | 0.54 | 6.99 × 104 | 94 | 2.36 | 3.99 × 102 | |
| QSPSOR | 8 | 0.05 | 2.37 × 102 | 14 | 0.29 | 6.19 × 104 | 32 | 0.09 | 4.21 × 102 | |
| 256 | FSPSOR | 53 | 5.33 | 2.43 × 102 | 211 | 17.84 | 5.69 × 104 | 806 | 67.75 | 3.97 × 102 |
| HSPSOR | 34 | 2.20 | 2.43 × 102 | 94 | 6.90 | 6.21 × 104 | 303 | 34.65 | 3.97 × 102 | |
| QSPSOR | 15 | 0.27 | 2.44 × 102 | 39 | 2.37 | 6.99 × 104 | 101 | 12.84 | 4.03 × 102 | |
| 512 | FSPSOR | 120 | 41.43 | 2.46 × 102 | 566 | 182.83 | 5.36 × 104 | 2635 | 843.91 | 3.96 × 102 |
| HSPSOR | 67 | 21.65 | 2.46 × 102 | 246 | 86.09 | 5.36 × 104 | 988 | 421.58 | 3.96 × 102 | |
| QSPSOR | 31 | 5.04 | 2.47 × 102 | 100 | 40.61 | 6.21 × 104 | 337 | 198.20 | 3.96 × 102 | |
| 1024 | FSPSOR | 250 | 372.35 | 2.48 × 102 | 1514 | 726.29 | 5.13 × 104 | 6012 | 1699.87 | 3.95 × 102 |
| HSPSOR | 141 | 189.58 | 2.48 × 102 | 655 | 434.72 | 5.13 × 104 | 2413 | 1003.78 | 3.95 × 102 | |
| QSPSOR | 66 | 47.29 | 2.49 × 102 | 266 | 214.51 | 5.69 × 104 | 1095 | 501.76 | 3.95 × 102 | |
| 2048 | FSPSOR | 808 | 901.76 | 2.49 × 102 | 4052 | 3469.73 | 5.13 × 104 | 35,289 | 7052.28 | 3.93 × 102 |
| HSPSOR | 305 | 308.80 | 2.49 × 102 | 1788 | 1956.43 | 5.13 × 104 | 18,143 | 4025.90 | 3.93 × 102 | |
| QSPSOR | 143 | 95.25 | 2.50 × 102 | 709 | 365.43 | 5.35 × 104 | 3574 | 2000.83 | 3.93 × 102 | |
| Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 128 | FSPSOR | 28 | 0.84 | 2.36 × 102 | 80 | 1.90 | 6.20 × 104 | 246 | 5.76 | 3.99 × 102 |
| HSPSOR | 16 | 0.18 | 2.36 × 102 | 37 | 0.54 | 6.99 × 104 | 94 | 2.36 | 3.99 × 102 | |
| QSPSOR | 8 | 0.05 | 2.37 × 102 | 14 | 0.29 | 6.19 × 104 | 32 | 0.09 | 4.21 × 102 | |
| 256 | FSPSOR | 53 | 5.33 | 2.43 × 102 | 211 | 17.84 | 5.69 × 104 | 806 | 67.75 | 3.97 × 102 |
| HSPSOR | 34 | 2.20 | 2.43 × 102 | 94 | 6.90 | 6.21 × 104 | 303 | 34.65 | 3.97 × 102 | |
| QSPSOR | 15 | 0.27 | 2.44 × 102 | 39 | 2.37 | 6.99 × 104 | 101 | 12.84 | 4.03 × 102 | |
| 512 | FSPSOR | 120 | 41.43 | 2.46 × 102 | 566 | 182.83 | 5.36 × 104 | 2635 | 843.91 | 3.96 × 102 |
| HSPSOR | 67 | 21.65 | 2.46 × 102 | 246 | 86.09 | 5.36 × 104 | 988 | 421.58 | 3.96 × 102 | |
| QSPSOR | 31 | 5.04 | 2.47 × 102 | 100 | 40.61 | 6.21 × 104 | 337 | 198.20 | 3.96 × 102 | |
| 1024 | FSPSOR | 250 | 372.35 | 2.48 × 102 | 1514 | 726.29 | 5.13 × 104 | 6012 | 1699.87 | 3.95 × 102 |
| HSPSOR | 141 | 189.58 | 2.48 × 102 | 655 | 434.72 | 5.13 × 104 | 2413 | 1003.78 | 3.95 × 102 | |
| QSPSOR | 66 | 47.29 | 2.49 × 102 | 266 | 214.51 | 5.69 × 104 | 1095 | 501.76 | 3.95 × 102 | |
| 2048 | FSPSOR | 808 | 901.76 | 2.49 × 102 | 4052 | 3469.73 | 5.13 × 104 | 35,289 | 7052.28 | 3.93 × 102 |
| HSPSOR | 305 | 308.80 | 2.49 × 102 | 1788 | 1956.43 | 5.13 × 104 | 18,143 | 4025.90 | 3.93 × 102 | |
| QSPSOR | 143 | 95.25 | 2.50 × 102 | 709 | 365.43 | 5.35 × 104 | 3574 | 2000.83 | 3.93 × 102 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunarto, A.; Agarwal, P.; Sulaiman, J.; Chew, J.V.L.; Momani, S. Quarter-Sweep Preconditioned Relaxation Method, Algorithm and Efficiency Analysis for Fractional Mathematical Equation. Fractal Fract. 2021, 5, 98. https://doi.org/10.3390/fractalfract5030098
Sunarto A, Agarwal P, Sulaiman J, Chew JVL, Momani S. Quarter-Sweep Preconditioned Relaxation Method, Algorithm and Efficiency Analysis for Fractional Mathematical Equation. Fractal and Fractional. 2021; 5(3):98. https://doi.org/10.3390/fractalfract5030098
Chicago/Turabian StyleSunarto, Andang, Praveen Agarwal, Jumat Sulaiman, Jackel Vui Lung Chew, and Shaher Momani. 2021. "Quarter-Sweep Preconditioned Relaxation Method, Algorithm and Efficiency Analysis for Fractional Mathematical Equation" Fractal and Fractional 5, no. 3: 98. https://doi.org/10.3390/fractalfract5030098
APA StyleSunarto, A., Agarwal, P., Sulaiman, J., Chew, J. V. L., & Momani, S. (2021). Quarter-Sweep Preconditioned Relaxation Method, Algorithm and Efficiency Analysis for Fractional Mathematical Equation. Fractal and Fractional, 5(3), 98. https://doi.org/10.3390/fractalfract5030098










