A Special Study of the Mixed Weighted Fractional Brownian Motion

Abstract

In this work, we present the analysis of a mixed weighted fractional Brownian motion, defined by ${\eta }_t:=B_t+{\xi }_t$, where B is a Brownian motion and $\xi$ is an independent weighted fractional Brownian motion. We also consider the parameter estimation problem for the drift parameter $\theta >0$ in the mixed weighted fractional Ornstein–Uhlenbeck model of the form $X_0=0;X_t=\theta X_{t}dt+d{\eta }_t$. Moreover, a simulation is given of sample paths of the mixed weighted fractional Ornstein–Uhlenbeck process.

1. Introduction

Over the course of the last two decades, the investigation of a system of particles moving in ${\mathbb{R}}^d$ under the influence of a symmetric $\alpha$-stable Lèvy noise, $0<\alpha ⩽2$, has attracted many scholars’ attention (e.g., [1,2,3,4,5]). Research on certain particle systems and their occupational time-fluctuation limits has revealed new types of centered Gaussian processes that are self-similar and have long-range dependences [6]. The particle systems determine the values of the parameters in these stochastic processes. One of the most important of these stochastic processes is the weighted fractional Brownian motion (wfBm). Bojdecki et al. [6] were the first to bring it up in 2007, and called it “a weighted fractional Brownian motion” because of the weight function $u^a$ that appears in its covariance function

$$\begin{array}{c}\hfill k(s,t)={\int }_0^{s\wedge t}{u}^a[{(t-u)}^b+{(s-u)}^b]du,t⩾0,\end{array}$$

(1)

where $a,b$ satisfy

$$\begin{array}{c}\hfill -1<a,1>\left|b\right|,1+a>\left|b\right|.\end{array}$$

(2)

For $a=0,-1<b<1$, wfBm corresponds to the celebrated fractional Brownian motion (fBm) with Hurst index $\frac{b+1}{2}$, as well as to the well-known Brownian motion (Bm) when $a=0,b=0$. Many studies have been devoted to the weighted fractional Brownian motion and the related Ornstein–Uhlenbeck process, for instance [7,8,9].

Parameter estimation for dynamical models is the most essential component of the subject for engineers and applied scientists [10]. In recent years, the problem of statistical estimation for Gaussian Ornstein–Uhlenbeck processes has piqued the interest of various scholars. In the ergodic case where $\theta <0$, several works, such as [11,12] and the references therein, have focused on the statistical estimation of the parameter $\theta$. Furthermore, in the non-ergodic scenario corresponding to $\theta >0$, the estimation of parameter $\theta$ has been explored using the least squares method, as can be seen in [8,13,14,15,16,17] and its references.

Recently, the mixed Gaussian noise has become of interest because of its applications in many different fields, such as engineering [18], mathematical finance [19,20] and so on. These mixtures can solve problems in mathematical finance and option pricing. Cheridito [19] has pointed out that the mixed fractional Brownian motion (mfBm) is equivalent to Bm for $\frac{3}{4}<H⩽1$, which was applied by Cheridito to obtain a new type of Samuelson model, which is arbitrage-free and complete. Moreover, in [20], the pricing of Bermuda options on zero-coupons bound for the mixed fractional Vasicek process has been considered, for $H\in (\frac{3}{4},1)$. The authors applied the Akaike information criterion (AIC) on US interest rates from January 2015 to May 2019 to show that the Vasicek model driven by mfBm is more appropriate than the standard model with fBm.

Our motivation behind introducing the mixed-weighted fractional Brownian motion (mwfBm) comes from the fact that the filtration of wfBm does not satisfy the usual assumptions, which means that this cannot be a semimartingale; however this mixture, together with the asymptotic stationary properties for wfBm, opens up the possibility of mwfBm being martingale or equivalent to Bm, as it is the same as mfBm (see Remark 1).

Inspired by the aforementioned monographs and facts, in this work, we begin by introducing a new stochastic process named as the mixed weighted fractional Brownian motion and establish the stochastic integral and the canonical representation for such process. In addition, we apply this process to one of the most interesting problem in mathematical statistics which is parameter estimation problem, such that we investigate the problem of parameter estimation for Ornstein–Uhlenbek process in which the dynamics follows mwfBm. Consequently, new results have been established for the proposed estimator of parameter $\theta$ that are different from those that have previously been obtained for both fBm and wfBm (see Section 3). On the other hand, we used the most recent results for the numerical simulation (such as in [21,22,23,24]) to discuss the simulation of the sample paths of the mixed weighted fractional Ornstein–Uhlenbeck process.

The remainder of this paper is organised in the following manner. In the second section, some notions and basic facts related to the mwfBm and its stochastic calculus are presented. Section 3 focuses on the problem of estimating the drift parameter for the non-ergodic mixed weighted fractional Ornstein–Uhlenbeck process (mwfOUP). We provide a numerical simulation for the solution of the weighted fractional Ornstein–Uhlenbeck model in Section 5. The results of numerical simulations are summarised and discussed in Section 6. Finally, the last section highlights the results of this paper.

2. Notions and Auxiliary Results

This section introduces some fundamental concepts and facts about the mixed weighted fractional Brownian motion and its stochastic calculus.

First, we provide a definition for mwfBm.

Definition 1.

The stochastic process $\eta ={\left({\eta }_t\right)}_{t⩾0}$ will be called a mixed-weighted fractional Brownian motion (mwfBm) if it is described by the linear combination of a weighted fractional Brownian motion and an independent standard Brownian motion, namely

$$\begin{array}{c}\hfill {\eta }_t:=B_t+{\xi }_t,\end{array}$$

(3)

where B is Bm and ξ is the independent wfBm and the parameters $a,b$ of the wfBm satisfy condition (2).

In the following, we consider $(\mathsf{\Omega },\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t⩾0},P)$ to be a complete-probability space equipped with a natural filtration ${\left\{{\mathcal{F}}_t\right\}}_{t⩾0}$, where ${\mathcal{F}}_t$ stands for the $\sigma$-algebra generated by $\eta$ and ${\mathcal{F}}_0$ indicates the set of all P-null sets.

A Canonical Innovation Representation for mwfBm

Let $M={\left(M_t\right)}_{0⩽t⩽T}$ be a fundamental martingale and ${⟨M⟩}_t$ be its quadratic variance, such that, for $t⩾0$,

$$\begin{array}{c}\hfill M_t={\int }_0^{t}g(s,t)d{\eta }_s,{⟨M⟩}_t={\int }_0^{t}g(s,t)ds={\int }_0^t{g}^2(s,s)ds,\end{array}$$

(4)

where $g(s,t)$ can solve the following equation:

$$\begin{array}{c}\hfill g(s,t)=1-{\int }_0^{t}g(u,t)K(u,s)du,\end{array}$$

(5)

where $K(u,s):=b{(t\wedge s)}^a{(t\vee s-t\wedge s)}^{b-1};t\in [0,T]$. Then, by using the same strategy of Theorem 2.4 in [25], we have

$$\begin{array}{c}\hfill {\eta }_t:={\int }_0^{t}G(s,t)d{M}_s;t\in [0,T],\end{array}$$

with

$$\begin{array}{cc}\hfill G(s,t):=& 1-\frac{1}{g(s,s)}{\int }_0^{t}R(t_0,s)d_{t_0};s⩽t\in [0,T]\hfill \\ \hfill R(s,t):=& \frac{\partial g(s,t)}{\partial t}\times \frac{1}{g(t,t)};s\ne t.\hfill \end{array}$$

(6)

We introduce the function $\phi :[0,T]\times [0,T]⟶[0,T]$, which is defined as

$$\begin{array}{c}\hfill \phi (t,s)=\frac{{\partial }^{2}k(t,s)}{\partial t\partial s}={(t\wedge s)}^a{(t\vee s-t\wedge s)}^{b-1},t\in [0,T].\end{array}$$

Let $f:[0,T]⟶[0,T]$ be “a Borel measurable function” and define the space

$$\begin{array}{c}\hfill L_{\phi }^2\left([0,T]\right)={\{f:\parallel f\parallel }_{L_{\phi }^2\left([0,T]\right)}^2={\int }_0^T{\int }_0^{T}f\left(t\right)f\left(s\right)\phi (t,s)dsdt+{\int }_0^T{f}^2\left(t\right)dt<\infty \},\end{array}$$

which, under the following inner product formula, becomes a “separable Hilbert space”

$$\begin{array}{c}\hfill {⟨f,g⟩}_{L_{\phi }^2\left([0,T]\right)}={\int }_0^T{\int }_0^{T}f\left(t\right)g\left(s\right)\phi (t,s)dsdt+{\int }_0^{T}f\left(t\right)g\left(t\right)dt,f,g\in L_{\phi }^2\left([0,T]\right):=\mathcal{H}.\end{array}$$

Let $\psi \in \mathcal{H}$; then, from [26,27] and following the same technique as used in Section 2 of [25] and Section 2.2 of [28], we obtain

$$\begin{array}{c}\hfill {\int }_0^T\psi \left(t\right)d{\eta }_t={\int }_0^T[{\int }_{t_0}^T\psi \left(t\right)\frac{\partial G}{\partial t}(t_0,t)dt+\psi \left(t_0\right)G(t_0,t_0)]d{M}_{t_0},\end{array}$$

where M and G are given by Equations (4) and (6), respectively.

Moreover, there exists a Brownian motion $B={\left\{B_t\right\}}_{t⩾0}$ with the same filtration of $\eta$; hence,

$$\begin{array}{c}\hfill {\int }_0^T\psi \left(t\right)d{\eta }_t={\int }_0^T[{\int }_{t_0}^{T}g(t_0,t_0)\frac{\partial G}{\partial t}(t_0,t)\psi \left(t\right)dt+\psi \left(t_0\right)]d{B}_{t_0},\end{array}$$

where g is as defined below in (5).

Consider the operator ${\mathcal{G}}^{*}:\mathcal{H}⟶L^2[0,T]$ given by

$$\begin{array}{c}\hfill \left({\mathcal{G}}^{*}\psi \right)\left(t_0\right)={\int }_{t_0}^{T}g(t_0,t_0)\frac{\partial G}{\partial t}(t_0,t)\psi \left(t\right)dt+\psi \left(t_0\right).\end{array}$$

We will now define “the divergence integral” with respect to mwfBm.

Definition 2.

Let $u=u\left(\omega \right):[0,T]⟶\mathcal{H}$ be a random variable and ${\mathcal{G}}^{*}u$ be Skorohod–integral in terms of Bm B. Then, the Wiener integral of u in terms of η is given via

$$\begin{array}{c}\hfill \eta \left(u\right):={\int }_0^T\left({\mathcal{G}}^{*}u\right)\left(t_0\right)\delta B_{t_0}={\int }_0^{T}u\left(t\right)d{\eta }_t.\end{array}$$

in the following, we look at the set $\mathcal{E}$ of smooth random variables, which is described as

$$\begin{array}{c}\hfill F\left(\omega \right)=g\left({\int }_0^T{\psi }_1\left(t\right)d\eta \left(t\right),\dots ,{\int }_0^T{\psi }_n\left(t\right)d\eta \left(t\right)\right),\end{array}$$

where $g\in {\mathcal{C}}_b^{\infty }\left([0,T]\right)$ and ${\psi }_i\in \mathcal{H},i⩾1$. The following definition provides a representation of a Malliavin derivative related to the process $\eta$.

Definition 3.

The Malliavin derivative $D_t^{\eta }F$ of a smooth random variable F is a $\mathcal{H}$-valued random variable, such that

$$\begin{array}{c}\hfill D_t^{\eta }F=\sum _{i=1}^n\frac{\partial g}{\partial x_i}\left({\int }_0^T{\psi }_1\left(t\right)d\eta \left(t\right),...,{\int }_0^T{\psi }_n\left(t\right)d\eta \left(t\right)\right){\psi }_i\left(t\right),t⩾0.\end{array}$$

the operator $D_t^{\eta }$ is a closable operator in $L^p\left(\mathsf{\Omega }\right)$, so that $D_t^{\eta }:L^p\left(\mathsf{\Omega }\right)\mapsto L^p(\mathsf{\Omega },\mathcal{H})$. In addition, the iteration of the Malliavin derivative $D^{\eta }$ is indicated by $D_t^{\eta ,k},1⩽k$. For $1⩽p$, the Sobolev space ${\mathbb{D}}^{k,p}$ indicates the closure of the set $\mathcal{E}$ in terms of the following norm

$$\begin{array}{c}\hfill {\parallel F\parallel }_{k,p}^p={E\left|F\right|}^p+E\sum _{i=1}^k{\parallel D_t^{\eta ,i}F\parallel }_{{\mathcal{H}}^{⨂i}}^p,\end{array}$$

where “⨂” denotes the tensor product.

Definition 4.

Let ${\delta }^{\eta }$ be the adjoint operator of $D^{\eta }$. We call ${\delta }^{\eta }$ the Skorohod integral operator w.r.t η, ${\delta }^{\eta }$ is an unbounded operator on the space $L^2(\mathsf{\Omega };\mathcal{H})$, and the domain of ${\delta }^{\eta }$, which is indicated by $Dom\left({\delta }^{\eta }\right)$, represents a class of $\mathcal{H}$-valued square integrable random variables. If $u\in Dom\left({\delta }^{\eta }\right)$, then the Skorohod integral w.r.t η is denoted by

$$\begin{array}{c}\hfill {\delta }^{\eta }\left(u\right):={\int }_0^{T}u\left(t\right)\delta {\eta }_t.\end{array}$$

Definition 5.

Consider v to be a stochastic process with integrable trajectories and the below limits exist in terms of probability. Then

• The symmetric integral of v w.r.t η, is given by

  $$\begin{array}{c}\hfill {\int }_0^{T}v\left(t\right)d^{\circ }{\eta }_t:=\underset{ϵ\to 0}{lim}\frac{1}{2ϵ}{\int }_0^{T}v\left(t\right)\left[\eta \right(t+ϵ)-\eta (t-ϵ\left)\right]dt.\end{array}$$
• The forward integral of v in terms of η, is defined by

  $$\begin{array}{c}\hfill {\int }_0^{T}v\left(t\right)d^{-}{\eta }_t:=\underset{ϵ\to 0}{lim}\frac{1}{ϵ}{\int }_0^{T}v\left(t\right)\left[\frac{\eta (t+ϵ)-\eta \left(t\right)}{ϵ}\right]dt,\end{array}$$
• The backward integral of v in terms of η, can be expressed as

  $$\begin{array}{c}\hfill {\int }_0^{T}v\left(t\right)d^{+}{\eta }_t:=\underset{ϵ\to 0}{lim}\frac{1}{ϵ}{\int }_0^{T}v\left(t\right)\left[\frac{\eta (t-ϵ)-\eta \left(t\right)}{ϵ}\right]dt,\end{array}$$

Lemma 1.

Assume that the process ${\left(v_t\right)}_{0⩽t⩽T}$ is living in the space ${\mathbb{D}}^{1,2}$, and the following assertions hold true:

• ${\int }_0^T{\int }_0^T\left|D_s^{\eta }v\left(t\right)\right|\phi (t,s)dsdt<\infty$, a.s,
• ${\int }_0^T\left|D_t^{\eta }v\left(t\right)\right|dt<\infty$, a.s, $D_s^{\eta }v\left(t\right)=0$ if $t<s$,

here $D_t^{\eta }v\left(t\right)$ means $D_s^{\eta }v\left(t\right)$ when $s=t$. Then

$$\begin{array}{c}\hfill {\int }_0^{T}v\left(t\right)d^{\circ }{\eta }_t:={\delta }^{\eta }\left(v\right)+{\int }_0^T{\int }_0^T{D}_s^{\eta }v\left(t\right)\phi (s,t)dsdt+\frac{1}{2}{\int }_0^T{D}_t^{\eta }v\left(t\right)dt.\end{array}$$

Proof. 

We use the same arguments that are used to prove Lemma 2.7 in [28]. □

Remark 1.

Recently, Cai et al. [28] pointed out that the mixed fractional Brownian motion has an explicit form of its fundamental martingale in the case of $H<\frac{1}{2}$. This was also preceded by the monograph [19], which revealed using Theorem 1 of [29] that, for $H\in (\frac{3}{4},1]$, the mfBm is the same as Bm. These facts open a new problem regarding the possibility of the mixed Gaussian noises being martingales or equivalent to Bm. For wfBm, as its filtration does not satisfy the usual assumptions, ξ cannot be a semimartingale (see Theorem 2.4 of [6]). Meanwhile, wfBm has the property of asymptotic stationary increments for long time intervals, that is to say

$$\begin{array}{c}\hfill \underset{T⟶\infty }{lim}{T}^{-(1+a+b)}E{({\xi }_{t+T}-{\xi }_t)}^2=2{\int }_0^1{u}^a{(1-u)}^{b}du,\end{array}$$

and we know that (see Theorem 1.7 in [19]) mfBm has been shown to be equivalent to Bm based on the property of stationary increments. This opens up the possibility of mwfBm being equivalent to Bm. For the sake of brevity, we will not pursue further details here, but leave this problem open for future research.

3. Least Square Estimator for the mwfOU Process

This section deals with the problem of estimating drift parameter for the non-ergodic mwfOU process based on continuous observation $\{X_t,0⩽t⩽T\}$. The dynamic of this process is

$$\begin{array}{c}\hfill X_0=0;d{X}_t=\theta X_{t}dt+d{\eta }_t,t⩾0,\end{array}$$

(7)

where $0<\theta$ is considered to be an unknown parameter. Moreover, the explicit solution for (7) can be written as

$$\begin{array}{c}\hfill X_t=e^{\theta t}{\int }_0^t{e}^{-\theta s}d{\eta }_s,t⩾0.\end{array}$$

(8)

Consider the least square type estimator for (7), which is defined as follows:

$$\begin{array}{c}\hfill {\widehat{\theta }}_T=\frac{{\int }_0^T{X}_{t}d{X}_t}{{\int }_0^T{X}_t^{2}dt},t⩾0,\end{array}$$

(9)

from (7) and (8) and using Lemma 2.6, we obtain

$$\begin{array}{c}\hfill {\int }_0^T{X}_t\delta {\eta }_t={\int }_0^T{X}_t{d}^{\circ }{\eta }_t-b{\int }_0^T{\int }_0^{t}exp\left(\theta (t-s)\right){(t\wedge s)}^a{(t\vee s-t\wedge s)}^{b-1}dsdt-\frac{T}{2},\end{array}$$

Thus, we obtain the following expression for the LSE

$$\begin{array}{c}\hfill {\widehat{\theta }}_T=\frac{X_t^2}{2{\int }_0^T{X}_t^{2}dt}-\frac{b{\int }_0^T{\int }_0^{t}exp\left(\theta (t-s)\right){(t\wedge s)}^a{(t\vee s-t\wedge s)}^{b-1}dsdt}{{\int }_0^T{X}_t^{2}dt}-\frac{T}{{\int }_0^T{X}_t^{2}dt}.\end{array}$$

(10)

It is clear that the quadratic variation in the mwfOU process is not zero, which is the essential push for us to consider the mixed case.

Now, it is obvious, as $T⟶\infty$,

$$\begin{array}{c}\hfill e^{-2\theta T}\frac{b{\int }_0^T{\int }_0^{t}exp\left(\theta (t-s)\right){(t\wedge s)}^a{(t\vee s-t\wedge s)}^{b-1}dsdt}{{\int }_0^T{X}_t^{2}dt}⟶0,\end{array}$$

and

$$\begin{array}{c}\hfill e^{-2\theta T}\frac{T}{{\int }_0^T{X}_t^{2}dt}⟶0,\end{array}$$

hence, it follows that (10) can be written as

$$\begin{array}{c}\hfill {\check{\theta }}_T=\frac{X_t^2}{2{\int }_0^T{X}_t^{2}dt}.\end{array}$$

(11)

The Behavior of LSE ${\check{\theta }}_T$

The last square estimator’s strong consistency and asymptotic distribution for a class of Gaussian Ornstein–Uhlenbeck processes has recently been established by [13]. In our case, due the fact that the combination of two Gaussian processes is also Gaussian, the methodology used by [13] can be applied for the mwfOU process.

According to Theorem 3.1 in [7] and the properties of Bm, we have

$$\begin{array}{cc}\hfill E\left[{\eta }_t^2\right]⩽& E\left[{(B_t+{\xi }_t)}^2\right]\hfill \\ \hfill =& E\left[B_t^2\right]+E\left[{\xi }_t^2\right]\hfill \\ \hfill =& t+2\beta (1+a,1+b)t^{(a+b+1)}\hfill \\ \hfill ⩽& c^{\gamma }+t.\hfill \end{array}$$

where c is a positive constant, $\gamma :=a+b+1$ and $\beta (m,n)={\int }_0^1{x}^{m-1}{(1-x)}^{n-1}dx$ represents the usual Beta function.

In addition, we have

$$\begin{array}{cc}\hfill E{[{\eta }_t-{\eta }_s]}^2⩽& E\left[{\eta }_t^2\right]+E\left[{\eta }_s^2\right]\hfill \\ \hfill =& E\left[B_t^2\right]+E\left[{\xi }_t^2\right]+E\left[B_s^2\right]+E\left[{\xi }_s^2\right]\hfill \\ \hfill =& t+2\beta (1+a,1+b)t^{(a+b+1)}+s+2\beta (1+a,1+b)s^{(a+b+1)}\hfill \\ \hfill =& t+s+2\beta (1+a,1+b)(t^{(a+b+1)}+s^{(a+b+1)})\hfill \\ \hfill ⩽& c{t}^{\gamma }+|t-s|.\hfill \end{array}$$

Here the the last inequity stems from the fact that $(t+s)⩽|t-s|,0<s⩽t$, and $\gamma :=a+b+1$.

Next, we let $X_t$ to be

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & X_t=X_t^{\left(1\right)}+X_t^{\left(2\right)};\hfill \\ \hfill & d{X}_t^{\left(1\right)}:=\theta X_t^{\left(1\right)}dt+d{B}_t;0⩽t⩽T,\hfill \\ \hfill & d{X}_t^{\left(2\right)}:=\theta X_t^{\left(2\right)}dt+d{\xi }_t;0⩽t⩽T,\hfill \end{array}\right.\end{array}$$

(12)

Define the process $Z_t:={\int }_0^t{e}^{-\theta s}{\eta }_{s}ds;t⩾0$. Then, using the decomposition of X in (12) together with Lemma 2.1 of [13] and Theorem 3.1 of [7], we obtain

$$X_T^2⟶{\theta }^2{Z}_{\infty }^2,$$

and

$$e^{-2\theta T}{\int }_0^t{X}_t^{2}dt⟶\frac{\theta }{2}{Z}_{\infty }^2,$$

as $T⟶\infty$. From this discussion, and by virtue of Lemma 2.1 of [13] and Theorem 3.1 of [7], we deduce that the estimator ${\check{\theta }}_T$ is almost consistent with the parameter $\theta$, as $T⟶\infty$ and it is asymptotically Cauchy, as $T⟶\infty$. This is the message conveyed by the next theorem.

Theorem 1.

Let ${\check{\theta }}_T$ be the estimator given by (11), if $a,b$ satisfies the condition (2). Then, $T⟶\infty$

${\check{\theta }}_T⟶\theta$. Moreover, $e^{\theta T}({\check{\theta }}_T-\theta )\underrightarrow{law}-\frac{2}{\theta }\mathcal{C}\left(1\right)$, as $T⟶\infty$, here $\mathcal{C}\left(1\right)$ is a standard Cauchy distribution with a probability density function given by $\frac{1}{\pi (1+x^2)}$ with $x\in \mathbb{R}$.

4. Numerical Simulations

This section focuses on the simulation of the sample paths of the mixed-weighted fractional Brownian motion and related Ornstein–Uhlenbeck process. To date, different algorithms have been used to simulate correlated Gaussian random variables (see, for instance, [21,22,30]). However, few works have studied the simulation of wfBm (see, for example, [8]). In our algorithm, we rely on the initial push outlined in Remark 2.3 of [6], in which the authors claimed that, in the case of $b=1$, the process $\xi$ can be represented through Bm B, as follows:

$$\begin{array}{c}\hfill {\xi }_t={\int }_0^t{B}_{r^a}dr\end{array}$$

(13)

where $a⩾0$. Moreover, we provide an algorithm for the simulation solution of the mwfOU process. Our simulation procedures are given below:

1.

Set the sample size $N\in \mathbb{N}$ and the time span T.

2.

Consider the uniform mesh with step-size $h=\frac{T}{N}$ and let $0=t_0<t_1<\dots <t_N=T$.

3.

Choose two values for each of the parameters $\theta ,a$.

4.

Compute the sample paths of $\xi$ by

$$\begin{array}{c}\hfill \xi \left(t_{i+1}\right)=\xi \left(t_i\right)+h\sum _{i=0}^{N-1}B{\left(t_i\right)}^a.\end{array}$$

5.

Approximate the mwfOU process through

$$\begin{array}{c}\hfill X\left(t_{i+1}\right)=X\left(t_i\right)+\theta X\left(t_i\right)h+▵\xi \left(t_i\right)+▵B\left(t_i\right);i=0,\dots ,N.\end{array}$$

where $▵\xi \left(t_i\right)=\xi \left(t_{i+1}\right)-\xi \left(t_i\right)$ and

$$\begin{array}{c}\hfill ▵B\left(t_i\right):=B\left(t_{i+1}\right)-B\left(t_i\right)=\sqrt{t_{i+1}-t_i}\times N(0,1).\end{array}$$

In the following, for different values of $\theta ,a$, we generate the sample paths of the mwfOU process.

5. Discussion

In this section, we discuss the previous numerical results. For different values of $\theta ,a$, we generate the sample paths of the mwfOU process that is shown in Figure 1 and Figure 2. From these simulations, we can observe that the characterisation of the sample paths of mwfOU process can be determined by the values of $\theta ,a$. In other words, we get smooth sample paths of X in the case of large values of $\theta ,a$. However, small values of $\theta$ and a make the sample paths of mwfOU process fluctuate more wildly. In Figure 1, we generate the sample paths of mwfOU process with $\theta =2.5,a=2.5$, while we take $\theta =0.5,a=0.2$ in Figure 2.

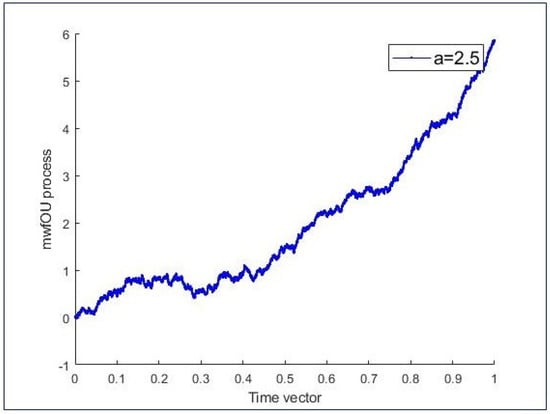
Figure 1. Simulation of sample paths of mwfOU process for large parameter values.

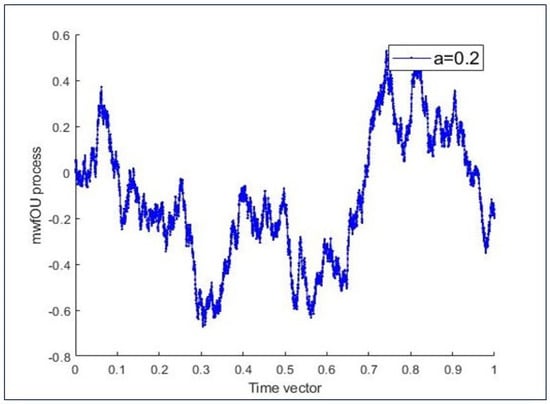
Figure 2. Simulation of sample paths of mwfOU process for small parameter values.

6. Conclusions

We first introduced the mixed weighted fractional Brownian motion; then, the stochastic integral and canonical representation were established for the mixed weighted fractional Brownian motion. Moreover, we considered the parameter estimation problem for the drift parameter of the mixed weighted fractional Ornstein–Uhlenbeck model, and proved that the proposed estimator ${\check{\theta }}_T$ is almost certainly consistent with the parameter $\theta$, as $T⟶\infty$ and is asymptotically Cauchy when T tends towards infinity. Finally, the simulation of the sample paths of the mixed-weighted fractional Ornstein–Uhlenbeck process is provided for different cases.