A Novel Treatment of Fuzzy Fractional Swift–Hohenberg Equation for a Hybrid Transform within the Fractional Derivative Operator

Abstract

This article investigates the semi-analytical method coupled with a new hybrid fuzzy integral transform and the Adomian decomposition method via the notion of fuzziness known as the Elzaki Adomian decomposition method (briefly, EADM). In addition, we apply this method to the time-fractional Swift–Hohenberg equation (SHe) with various initial conditions (IC) under gH-differentiability. Some aspects of the fuzzy Caputo fractional derivative (CFD) with the Elzaki transform are presented. Moreover, we established the general formulation and approximate findings by testing examples in series form of the models under investigation with success. With the aid of the projected method, we establish the approximate analytical results of SHe with graphical representations of initial value problems by inserting the uncertainty parameter $0\le \wp \le 1$ with different fractional orders. It is expected that fuzzy EADM will be powerful and accurate in configuring numerical solutions to nonlinear fuzzy fractional partial differential equations arising in physical and complex structures.

1. Introduction

Fractional calculus (FC) is now widely regarded as an essential method for characterizing real-world scenarios. Whereas mathematicians consider FC to be an essential resource in scientific research, the subject of fractional operators’ existence is invariably addressed in several domains. Specialists have created fractional differential equations (FDEs) to analyse and comprehend scientific developments in a multitude of disciplines. FC research includes a number of modifications in consideration of fractional operator nonlocal qualities, increased level of autonomy, and optimum informational implementation, and these characteristics exclusively manifest in fractional order procedures, not integer-order processes. Various studies have extensively explored a variety of novel theoretical formulations that incorporate the use of different singular and nonsingular fractional derivative operators, see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15].

In recent years, the concept of partial differential equations (PDEs) has become increasingly important in modelling scientific and mechanical challenges including thermodynamics, electrostatistics, solid state physics, and biological sciences. However, in practise, the indices, coefficients, and initial values in PDEs may be undetermined, or a hazy estimate of them may be discovered in particular by monitoring, experimentation, expertise, or reliability failure. As a result, instead of using crisp values, parameters, and predictor variables, one can employ uncertainty contexts to combat ambiguity and subtlety. Thus, generic PDES become fuzzy PDEs as a result of this uncertainty. Because acquiring the mathematical results for fuzzy PDEs in configuration scenarios is exceedingly problematic, a robust and sustainable numerical methodology for solving fuzzy PDEs may be required. In the review of research, there are numerous studies addressing FPDEs and their implementations in pattern formation theory, bifurcation, chaos, image encryption, industrial automation, stochastic processes, artificial intelligence/expert systems, and optimization. For a broader knowledge of the existing evaluation, a few studies are evaluated and referenced here [16,17]. The notion of fuzzy differentiability was first developed by Chang and Zadeh [18], then reinforced by Dubois and Prade [19], who articulated and employed the expansion theory in this strategy.

Nevertheless, according to this significance in a variety of research domains, fuzzy set theory has a striking relatedness to FC. In [20], authors proposed the concept of FDEs in 1978, and Agarwal et al. [21] were the pioneers in exploring Riemann–Liouville differentiability under the Hukuhara differentiability framework. Fuzzy set theory and FC integrate a number of mathematical techniques that permit a better understanding of intricate phenomena while still minimizing the processing complexity of addressing problems. Determining appropriate mathematical results in the context of FPDEs is a challenging task. Numerous computational techniques have been applied to achieve the governing equations of PDES and ODEs, including the Adomian decomposition method (ADM) [22], reproducing the kernel Hilbert space method [23], the residue power series method [24], Laguerre wavelets collocation method [25], the variation iteration method [26], and so on. Because of their wide usefulness and effectiveness in monitoring the perception of complicated structures, fuzzy FPDEs have gained popularity throughout the decades. The $gH$-differentiability have been contemplated on fuzzy FDEs via the Katugampola fractional derivative in the Caputo form by Hoa et al. [27,28]. Further, the author of [29] propounded the H-differentiability incorporating Laplace transform to find the solution of the FDEs. Arqub et al. [30] employed the reproducing kernel algorithm for the solution of two-point fuzzy boundary value problems. The fuzzy Fredholm–Volterra integrodifferential equations have been solved by the adaptation of the reproducing kernel algorithm by [31]. Ahmad et al. [32] investigated the dispersive PDEs in the singular and nonsingular kernels via the fuzzy frameworks. Researchers [33] demonstrated the solution of fuzzy FPDEs via the Laplace transform. To the best of our knowledge, the authors of [34,35] developed a novel extended approach and new numerical solutions for fuzzy conformable fractional differential equations and have constructed the numerical solutions for fuzzy differential equations using the reproducing kernel Hilbert space method.

PDEs have been frequently deployed as a framework for assessing several specific patterns of obstacles to accessing their impact from an extrinsic perspective. The impact of noise on bifurcations, pattern choice, spatiotemporal chaos, and defect dynamics are among them. The Swift–Hohenberg equation has been used to produce patterns in both simplistic (e.g., Rayleig–Bénard convection) and complicated liquids and biological substances (e.g., brain tissues). The general form of the SH equation was first investigated by Jack Swift and Pierre Hohenberg [36], as follows:

$$\begin{array}{c}\hfill {\mathcal{D}}_{\xi }\tilde{\mathcal{Q}}=\overline{s}\tilde{\mathcal{Q}}-{(1+{\Delta }^2)}^2\tilde{\mathcal{Q}}+\overline{N}\left(\tilde{\mathcal{Q}}\right),\end{array}$$

(1)

where $\tilde{\mathcal{Q}}$ is scalar, $\overline{s}$ is a real constant while $\overline{N}\left(\tilde{\mathcal{Q}}\right)$ represents a nonlinear factor. The proposed model has utilities in multiple scientific eras such as optics for lasers, magneto-convection, biological, chemical, and the liquid-crystal light-valve experiment, see [37,38,39].

In the present research, we aim to investigate the three different SH models via fuzzy CFD operator by implementing the EADM is represented as follows:

$$\begin{array}{c}\hfill {}^c{\mathcal{D}}_{\xi }^{\alpha }\tilde{\mathcal{Q}}(\eta ,\xi )+\frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi )+2\frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi )+(1-\theta )\tilde{\mathcal{Q}}(\eta ,xi)+{\tilde{\mathcal{Q}}}^3(\eta ,\xi )=0,0<\alpha \le 1,\theta \in \mathbb{R},\xi >0.\end{array}$$

(2)

The SHe having a dispersive term [40] is represented as

$$\begin{array}{c}\hfill {}^c{\mathcal{D}}_{\xi }^{\alpha }\tilde{\mathcal{Q}}(\eta ,\xi )+\frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi )+2\frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi )-\sigma \frac{{\partial }^3}{\partial {\eta }^3}\tilde{\mathcal{Q}}(\eta ,\xi )-\lambda \tilde{\mathcal{Q}}(\eta ,\xi )-2{\tilde{\mathcal{Q}}}^2(\eta ,\xi )+{\tilde{\mathcal{Q}}}^3(\eta ,\xi )=0,\end{array}$$

(3)

where $\sigma$ and $\lambda$ are dispersive and bifurcation real parameters, respectively.

The alternate form of the SH model is stated as follows:

$$\begin{array}{c}\hfill {}^c{\mathcal{D}}_{\xi }^{\alpha }\tilde{\mathcal{Q}}(\eta ,\xi )+\frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi )+2\frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi )+(1-\theta )\tilde{\mathcal{Q}}(\eta ,\xi )={\tilde{\mathcal{Q}}}^p(\eta ,\xi )-{\left(\frac{\partial \tilde{\mathcal{Q}}(\eta ,\xi )}{\partial \eta }\right)}^p,p\ge 0.\end{array}$$

(4)

Recently, Khan et al. [41] derived the approximate analytical solution of the SH model. In [42], Vishal et al. established the numerical findings respecting IC, $\tilde{\mathcal{Q}}(\eta ,0)=\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right).$ Further, the fractional order SHe has dispersion has been investigated by [43]. Lately, in [44], Merdan implemented the variational iteration method to find the exact-approximate solution to a similar condition as discussed above. In [45], Das and Vishal applied the HAM to find the approximate results for the SH model.

In 2001, Tarig Elzaki [46] expounded a revolutionary transformation, termed ET, in order to facilitate the process of solving ODEs and PDEs in the time domain. This new transform is a refinement of previous ones that can contribute in an analogous way to the Laplace and Sumudu transformations to determine the analytical solutions of the PDEs.

The ADM, first proposed by Adomian [47], is an analytical method to address linear–nonlinear functional equations arising in applied sciences. The solution is interpreted as the sum of an infinite series, which tends to precise solutions quickly. This methodology is precise and efficient, and it does not require the use of an unconditioned matrix, intricate integrals, or infinite series representations. This approach does not entail any specified problem configurations. This strategy has already been employed by a number of researchers [48,49,50,51].

Determining the accurate numerical solutions of fuzzy fractional PDEs is a complicated challenge due to the aforementioned proclivity. The objective of the current study is to develop a reliable approach for obtaining approximated findings for fuzzy fractional SHe, the generic SHe containing diffraction components susceptible to ambiguity in initial conditions due to EADM, which simulates the evolution behaviour under consideration. The ADM is termed as the fuzzy Elzaki Adomian decomposition method since the EADM is coupled with the ET. The time-fractional SHe equations are investigated by applying such an different approach. The results of a specific study instance are assessed by means of demonstrating the viability of the suggested approach. Modern techniques and procedures are utilized to evaluate the findings with an ambiguity component. The characterization theorem was also addressed extensively. To create synthetic dynamics, the SHe model was practised. We demonstrate the usefulness and feasibility of the proposed analytical methodologies for generating approximate methods in a simulating study. The new framework can be used to solve a variety of fuzzy fractional orders of linear and nonlinear PDEs.

In accordance with the prelude, the following sections are summarised in order: Section 2: Resources and prerequisites are crucial instruments in fuzzy analysis. Section 3: Fuzzy Caputo fractional derivative, definitions, and fuzzy Elzaki transforms are presented. Section 4: The Fuzzy Elzaki decomposition method is formulated. Section 5: Convergence and error frameworks, ensuring the existence of fuzzy Caputo fractional derivative solutions. Further, the characterization theorem is debated with proof. Section 6: Configuration of the fuzzy Caputo fractional derivative operator formulation and series solutions of the SH model are presented with their physical interpretations, analysis, results, and discussions. Ultimately, Section 7 details some highlights and future research.

2. Prelude

This section perfectly demonstrates some essential facts concerning ET, and perhaps some important aspects associated with the significance of fuzzy set theory and FC. For more information, see [52].

Definition 1

([53,54]). A mapping $\nabla :\mathbb{R}\mapsto [0,1]$ is said to be fuzzy number, if the underlying hypotheses are hold:

1. 

∇ is normal (for some ${\eta }_0\in \mathbb{R};\nabla \left({\eta }_0\right)=1$);

2. 

∇ is upper semi continuous;

3. 

$\nabla ({\eta }_1\xi +(1-\xi ){\eta }_2)\ge \left(\nabla \left({\eta }_1\right)\wedge \nabla \left({\eta }_2\right)\right)\forall \xi \in [0,1],{\eta }_1,{\eta }_2\in \mathbb{R},$ i.e., ∇ is a convex fuzzy set;

4. 

$cl\left\{\eta \in \mathbb{R},\nabla \left(\eta \right)>0\right\}$ is compact.

Definition 2

([53]). A fuzzy number ∇ is known to be ℘-level set, defined as

$$\begin{array}{c}\hfill {[\nabla ]}^{\wp }=\left\{\mathcal{Q}\in \mathbb{R}:\nabla \left(\mathcal{Q}\right)\ge \wp \right\},\end{array}$$

(5)

where $\wp \in [0,1].$

Definition 3

([53]). A fuzzy number has the parametric formulation $\left[\underline{\nabla }(\wp ),\overline{\nabla }(\wp )\right]$ such that $\wp \in [0,1]$ fulfils the underlying conditions:

1. 

$\underline{\nabla }(\wp )$ is nondecreasing, left continuous, bounded over $(0,1]$ and right continuous at $0.$;

2. 

$\overline{\nabla }(\wp )$ is nonincreasing, left continuous, bounded over $(0,1]$ and right continuous at $0.$;

3. 

$\underline{\nabla }(\wp )\le \overline{\nabla }(\wp ).$

Further, ∇ is a crisp number (or singleton number) if $\underline{\nabla }(\wp )=\overline{\nabla }(\wp )$ for any $\wp \in [0,1].$

Definition 4

([52]). For $\wp \in [0,1]$ and χ be a scalar. Consider two fuzzy numbers $\tilde{\psi }=\left[\underline{\psi },\overline{\psi }\right]$, $\tilde{\varphi }=\left[\underline{\varphi },\overline{\varphi }\right],$ then the algebraic properties are described as

1. 

$\tilde{\psi }\oplus \tilde{\varphi }=\left[\underline{\psi }(\wp )\oplus \underline{\varphi }(\wp ),\overline{\psi }(\wp )\oplus \overline{\varphi }(\wp )\right],$

2. 

$\tilde{\psi }\ominus \tilde{\varphi }=\left[\underline{\psi }(\wp )\ominus \underline{\varphi }(\wp ),\overline{\psi }(\wp )\ominus \overline{\varphi }(\wp )\right],$

3. 

$\chi \odot \tilde{\psi }=\left\{\begin{array}{c}\left[\chi \odot \underline{\psi },\chi \odot \overline{\psi }\right]\chi \ge 0,\hfill \\ \left[\chi \odot \overline{\psi },\chi \odot \underline{\psi }\right]\chi <0.\hfill \end{array}\right.$

Definition 5

([29]). Consider two fuzzy numbers $\tilde{\psi }=\left[\underline{\psi },\overline{\psi }\right],\tilde{\varphi }=\left[\underline{\varphi },\overline{\varphi }\right],$ the Hausdorff distance d between fuzzy numbers is represented as

$$\begin{array}{c}\hfill d(\tilde{\psi },\tilde{\varphi })=\underset{\wp \in [0,1]}{sup}\left[max\left\{|\underline{\psi }(\wp )-\underline{\varphi }(\wp )|,|\overline{\psi }(\wp )-\overline{\varphi }(\wp )|\right\}\right].\end{array}$$

(6)

In particular, $(\tilde{E},d)$ is a metric space.

Definition 6

([29]). Consider a fuzzy real-valued mapping $\Lambda :\mathbb{R}\mapsto \tilde{E},$ if for any $ϵ>0\exists \beta >0$ and fixed value of ${\nu }_0\in \mathbb{R},$ we have

$$\begin{array}{c}\hfill d(\Lambda \left(\nu \right),\Lambda \left({\nu }_0\right))<ϵ;whenever|\nu -{\nu }_0|<\beta ,\end{array}$$

(7)

then Λ is known to be continuous.

Definition 7

([55]). Let ${\beta }_1,{\beta }_2\in \tilde{E}.$ The $\mathcal{H}$-difference of ${\beta }_1$ and ${\beta }_2$ is the fuzzy number ${\beta }_3={\beta }_1\ominus {}^{\mathcal{H}}{\beta }_2$ such that ${\beta }_1={\beta }_2\oplus {\beta }_3.$ Observe that ${\beta }_1\ominus {}^{\mathcal{H}}{\beta }_2\ne {\beta }_1\ominus {\beta }_2.$

The $g\mathcal{H}$-difference ${\beta }_3$ of two fuzzy numbers ${\beta }_1,{\beta }_2\in \mathbb{R}$ is defined as:

$$\begin{array}{c}\hfill {\beta }_1\ominus {}_{g\mathcal{H}}{\beta }_2={\beta }_3\iff \left\{\begin{array}{c}\left(i\right){\beta }_1={\beta }_2\oplus {\beta }_3\hfill \\ or\hfill \\ \left(ii\right){\beta }_2={\beta }_1\oplus (-1){\beta }_3,\hfill \end{array}\right.\end{array}$$

The relationship between two cases is defined as

$$\begin{array}{c}\hfill {({\beta }_1\ominus {}_{g\mathcal{H}}{\beta }_2)}_i[\wp ]:=0\ominus {}_{\mathcal{H}}(-1)\left({({\beta }_1\ominus {}_{g\mathcal{H}}{\beta }_2)}_{ii}[\wp ]\right).\end{array}$$

Definition 8

([55]). The generalised Hukuhara derivative of a fuzzy-valued function $\Lambda :(b_1,b_2)\to \tilde{E}$ at ${\zeta }_0$ is defined as

$$\begin{array}{c}\hfill {\Lambda }_{\left(i\right)-g\mathcal{H}}^{\prime }\left({\zeta }_0\right)=\underset{h\to 0}{lim}\frac{\Lambda ({\zeta }_0+h){\ominus }_{\mathcal{H}}\Lambda \left({\zeta }_0\right)}{h},\end{array}$$

if ${(\Lambda )}_{\left(i\right)-g\mathcal{H}}^{\prime }\left({\zeta }_0\right)\in \tilde{E},$ we say that Λ is generalised Hukuhara differentiable ($g\mathcal{H}$-differentiable) at ${\zeta }_0.$

Moreover, we say that Λ is $\left[\right(i)-g\mathcal{H}]$-differentiable at ${\zeta }_0$ if

$$\begin{array}{cc}\hfill {\left[{\Lambda }_{\left(i\right)-g\mathcal{H}}^{\prime }\left({\zeta }_0\right)\right]}^{\wp }& =\left[{\left[\underset{h\to 0}{lim}\frac{\underline{\Lambda }({\zeta }_0+h){\ominus }_{\mathcal{H}}\underline{\Lambda }\left({\zeta }_0\right)}{h}\right]}^{\wp },{\left[\underset{h\to 0}{lim}\frac{\overline{\Lambda }({\zeta }_0+h){\ominus }_{\mathcal{H}}\overline{\Lambda }\left({\zeta }_0\right)}{h}\right]}^{\wp }\right]\hfill \\ & =\left[{\left(\underline{\Lambda }\right)}^{\prime }({\zeta }_0,\wp ),{\left(\overline{\Lambda }\right)}^{\prime }({\zeta }_0,\wp )\right],\hfill \end{array}$$

(8)

and that Λ is $\left[\right(ii)-g\mathcal{H}]$-differentiable at ${\zeta }_0$ if

$$\begin{array}{c}\hfill {\Lambda }_{\left(ii\right)-g\mathcal{H}}^{\prime }\left({\zeta }_0\right)=\underset{h\to 0}{lim}\frac{{\ominus }_{\mathcal{H}}(-1)\Lambda ({\zeta }_0+h)\oplus (-1)\Lambda \left({\zeta }_0\right)}{h}.\end{array}$$

Further, we have

$$\begin{array}{cc}\hfill {\left[{\Lambda }_{\left(ii\right)-g\mathcal{H}}^{\prime }\left({\zeta }_0\right)\right]}^{\wp }& =\left[{\left[\underset{h\to 0}{lim}\frac{{\ominus }_{\mathcal{H}}(-1)\overline{\Lambda }({\zeta }_0+h)\oplus (-1)\overline{\Lambda }\left({\zeta }_0\right)}{h}\right]}^{\wp },{\left[\underset{h\to 0}{lim}\frac{{\ominus }_{\mathcal{H}}(-1)\underline{\Lambda }({\zeta }_0+h)\oplus (-1)\underline{\Lambda }\left({\zeta }_0\right)}{h}\right]}^{\wp }\right]\hfill \\ & =\left[{\left(\overline{\Lambda }\right)}^{\prime }({\zeta }_0,\wp ),{\left(\underline{\Lambda }\right)}^{\prime }({\zeta }_0,\wp )\right].\hfill \end{array}$$

(9)

Throughout this investigation, we use the notation Λ is (1)-differentiable and (2)-differentiable, respectively, if it is differentiable under (8) and (9) defined in the above definition.

Theorem 1

([52]). Consider a fuzzy-valued function $\Lambda :\mathbb{R}\mapsto \tilde{E}$ such that $\Lambda ({\zeta }_0;\wp )=\left[\underline{\Lambda }({\zeta }_0;\wp ),\overline{\Lambda }({\zeta }_0;\wp )\right]$ and $\wp \in [0,1].$ Then

I. 

$\underline{\Lambda }({\zeta }_0;\wp )$ and $\overline{\Lambda }({\zeta }_0;\wp )$ are differentiable, if Λ is a (1)-differentiable, and

$$\begin{array}{c}\hfill {\left[{\Lambda }^{\prime }\left({\zeta }_0\right)\right]}^{\wp }=\left[{\underline{\Lambda }}^{\prime }({\zeta }_0;\wp ),{\overline{\Lambda }}^{\prime }({\zeta }_0;\wp )\right].\end{array}$$

(10)

II. 

$\underline{\Lambda }({\zeta }_0;\wp )$ and $\overline{\Lambda }({\zeta }_0;\wp )$ are differentiable, if Λ is a (2)-differentiable, and

$$\begin{array}{c}\hfill {\left[{\Lambda }^{\prime }\left({\zeta }_0\right)\right]}^{\wp }=\left[{\overline{\Lambda }}^{\prime }({\zeta }_0;\wp ),{\underline{\Lambda }}^{\prime }({\zeta }_0;\wp )\right].\end{array}$$

(11)

Let ${\mathcal{C}}^F[a_1,b_1]$ be the space of all continuous fuzzy-valued function on the interval $[a_1,b_1]$ and let ${\mathcal{L}}^F[a_1,b_1]$ be the space of all Lebesgue integrable fuzzy-valued function on the interval $[a_1,b_1]\subset \mathbb{R},$ and then, we have the following definition.

Definition 9

([29]). We say that a $\mathbf{F}$ mapping $\mathcal{Q}\in {\mathcal{C}}^F[a_1,b_1]\bigcap {\mathcal{L}}^F[a_1,b_1]$ represented in parameterised versions $\tilde{\mathcal{Q}}=\left[{\underline{\mathcal{Q}}}_{\wp }\left(\xi \right),{\overline{\mathcal{Q}}}_{\wp }\left(\xi \right)\right],\wp \in [0,1]$ and ${\xi }_0\in (a_1,b_1),$ then CFD operator in fuzzy formulation is expressed as

$$\begin{array}{c}\hfill {\mathcal{D}}_{g\mathcal{H}\mathcal{Q}}^{\alpha }\left(\xi \right)=\left\{\begin{array}{c}\frac{1}{\Gamma (q-\alpha )}\odot {\displaystyle \underset{{\eta }_0}{\overset{\xi }{\int }}}{(\xi -\eta )}^{q-\alpha -1}\odot {\mathcal{Q}}_{g\mathcal{H}}^{\left(q\right)}\left(\eta \right)d\eta ,q-1<\alpha <q,\hfill \\ {\left(\frac{d^{\alpha }}{d{\xi }^{\alpha }}\right)}^{q-1}\mathcal{Q}\left(\xi \right),\alpha =q-1.\hfill \end{array}\right.\end{array}$$

(12)

where $q=\lceil \wp \rceil$ and

$$\begin{array}{c}\hfill {\mathcal{Q}}^{\left(q\right)}\left(\eta \right)=\underset{\hslash \mapsto 0}{lim}\frac{{\mathcal{Q}}^{(q-1)}(\eta +\hslash )\ominus {}_{g\mathcal{H}}{\mathcal{Q}}^{(q-1)}\left(\eta \right)}{\hslash }.\end{array}$$

The $g\mathcal{H}$-difference is stated in two ways:

• $\left(i\right)-g\mathcal{H}$ differentiable:

  $$\begin{array}{c}\hfill {\mathcal{Q}}_{\left(i\right)-g\mathcal{H}}^{\left(q\right)}\left(\eta \right)=\underset{\hslash \mapsto 0}{lim}\frac{{\mathcal{Q}}^{(q-1)}(\eta +\hslash )\ominus {}_{\mathcal{H}}{\mathcal{Q}}^{(q-1)}\left(\eta \right)}{\hslash }.\end{array}$$

  (13)

  $$\begin{array}{c}\hfill {\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\mathcal{Q}({\xi }_0;\wp )=\left[{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}({\xi }_0;\wp ),{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}({\xi }_0;\wp )\right].\end{array}$$
• $\left(ii\right)-g\mathcal{H}$ differentiable:

  $$\begin{array}{c}\hfill {\mathcal{Q}}_{\left(ii\right)-g\mathcal{H}}^{\left(q\right)}\left(\eta \right)=\underset{\hslash \mapsto 0}{lim}\frac{{\mathcal{Q}}^{(q-1)}\left(\eta \right)\ominus {}_{\mathcal{H}}{\mathcal{Q}}^{(q-1)}(\eta +\hslash )}{\hslash }.\end{array}$$

  (14)

  $$\begin{array}{c}\hfill {\mathcal{D}}_{\left(ii\right)-g\mathcal{H}}^{\alpha }\mathcal{Q}({\xi }_0;\wp )=\left[{\mathcal{D}}_{\left(ii\right)-g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}({\xi }_0;\wp ),{\mathcal{D}}_{\left(ii\right)-g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}({\xi }_0;\wp )\right].\end{array}$$

  which are defined as the subsequent form for $q-1<\alpha <q,$

  $$\begin{array}{ccc}\hfill \left[{\mathcal{D}}^{\alpha }\underline{\mathcal{Q}}\left({\xi }_0\right)\right]& & =\frac{1}{\Gamma (q-\alpha )}{\left[{\displaystyle \underset{0}{\overset{\xi }{\int }}}{(\xi -\eta )}^{q-\alpha -1}\frac{d^q}{d{\eta }^q}\underline{\mathcal{Q}}\left(\eta \right)d\eta \right]}_{\xi ={\xi }_0},\hfill \\ \hfill \left[{\mathcal{D}}^{\alpha }\overline{\mathcal{Q}}\left({\xi }_0\right)\right]& & =\frac{1}{\Gamma (q-\alpha )}{\left[{\displaystyle \underset{0}{\overset{\xi }{\int }}}{(\xi -\eta )}^{q-\alpha -1}\frac{d^q}{d{\eta }^q}\overline{\mathcal{Q}}\left(\eta \right)d\eta \right]}_{\xi ={\xi }_0}.\hfill \end{array}$$

  (15)

3. Analysis of CFD Operator in View of Elzaki Transform

Recently, T. M. Elzaki [56], introduced the Elzaki transform, which is a refinement of the well-known Laplace transform. Here, we propose the Elzaki transform in the fuzzy set theory as follows:

Definition 10.

Consider $\mathcal{Q}$ be a continuous fuzzy mapping and a set $\mathcal{M}$ containing exponential mapping is presented as

$$\begin{array}{c}\hfill \mathcal{M}=\left\{\mathcal{Q}\left(\xi \right):\exists z,p_1,p_2>0,|\mathcal{Q}\left(\xi \right)|<z{e}^{\frac{\left|\xi \right|}{p_i}},if\xi \in {(-1)}^i\times [0,\infty )|\right\}.\end{array}$$

(16)

where z assumed to be finite, but $p_1,p_2$ may be finite or infinite, then the FET is stated as

$$\begin{array}{c}\hfill \mathbb{E}\left\{\tilde{\mathcal{Q}}\left(\xi \right)\right\}\left(\omega \right)=\mathbf{Q}\left(\omega \right)=\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}\odot \tilde{\mathcal{Q}}\left(\xi \right)d\xi ,\xi \ge 0,\omega \in [p_1,p_2].\end{array}$$

(17)

The specified parametric formulation of $\tilde{\mathcal{Q}}\left(\xi \right)$ is stated as

$$\begin{array}{c}\hfill \omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}\tilde{\mathcal{Q}}\left(\xi \right)d\xi =\left[\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}\underline{\mathcal{Q}}\left(\xi \right)d\xi ,\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}\overline{\mathcal{Q}}\left(\xi \right)d\xi \right].\end{array}$$

(18)

Thus,

$$\begin{array}{c}\hfill \mathbb{E}\left[\mathcal{Q}(\xi ,\wp )\right]=\left[\underline{\mathbf{E}}(\xi ,\wp ),\overline{\mathbf{E}}(\xi ,\wp )\right].\end{array}$$

(19)

Sedeeg [57] contemplated the Caputo fractional derivative form of the Elzaki transform. Adopting this trend, we present the fuzzy form of the Caputo fractional derivative coupled with the ET as follows:

Definition 11.

For $\alpha \in (0,1]$ and consider $\mathcal{Q}\in {\mathcal{C}}^F[0,\overline{d_1}]\bigcap {\mathcal{L}}^F[0,\overline{d_1}]$ such that $\tilde{\mathcal{Q}}\left(\xi \right)=\left[\underline{\mathcal{Q}}(\xi ,\wp ),\overline{\mathcal{Q}}(\xi ,\wp )\right],\wp \in [0,1],$ then the ET of Caputo-$g\mathcal{H}$ derivative is expressed as

$$\begin{array}{c}\hfill \mathbb{E}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\tilde{\mathcal{Q}}\left(\xi \right)\right]=\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}\odot {\mathcal{D}}_{g\mathcal{H}}^{\alpha }\mathcal{Q}\left(\xi \right)d\xi \end{array}$$

and

$$\begin{array}{ccc}\hfill \mathbb{E}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\tilde{\mathcal{Q}}(\xi ;\wp )\right]& & =\left[\mathbb{E}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}(\xi ;\wp )\right],\mathbb{E}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}(\xi ;\wp )\right]\right]\hfill \\ & & =\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}(\xi ;\wp ),{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}(\xi ;\wp )\right]d\xi \hfill \\ & & =\left[\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}(\xi ;\wp )d\xi ,\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}(\xi ;\wp )d\xi \right].\hfill \end{array}$$

Thus, we have

$$\begin{array}{ccc}& & \mathbb{E}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}(\xi ;\wp )\right]=\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\underline{\mathcal{Q}}(\xi ;\wp )d\xi ,\hfill \\ & & \mathbb{E}\left[{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}(\xi ;\wp )\right]=\omega {\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\frac{\xi }{\omega }}{\mathcal{D}}_{g\mathcal{H}}^{\alpha }\overline{\mathcal{Q}}(\xi ;\wp )d\xi .\hfill \end{array}$$

(20)

• $\left(i\right)-g\mathcal{H}$ differentiability:

  $$\begin{array}{ccc}& & {\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\mathcal{Q}(\eta ;\wp )=\left[{\mathcal{D}}^{\alpha }\underline{Q}(\eta ;\wp ),{\mathcal{D}}^{\alpha }\overline{Q}(\eta ;\wp )\right],\hfill \\ & & \mathbb{E}\left({\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\mathcal{Q}(\eta ;\wp )\right)=\frac{1}{{\omega }^{\alpha }}\odot \mathbf{E}\left[\mathcal{Q}(\xi ,\wp )\right]\ominus {\displaystyle \sum _{\kappa =0}^{q-1}}{{}_{\mathcal{H}}\mathcal{Q}}_{\left(\kappa \right)}(\eta ;\wp )\odot {\omega }^{2-\alpha +\kappa },\alpha \in (q-1,q].\hfill \end{array}$$

  (21)
• $\left(ii\right)-g\mathcal{H}$ differentiability:

  $$\begin{array}{ccc}& & {\mathcal{D}}_{\left(ii\right)-g\mathcal{H}}^{\alpha }\mathcal{Q}(\eta ;\wp )=\left[{\mathcal{D}}^{\alpha }\overline{Q}(\eta ;\wp ),{\mathcal{D}}^{\alpha }\underline{Q}(\eta ;\wp )\right],\hfill \\ & & \mathbb{E}\left({\mathcal{D}}_{\left(ii\right)-g\mathcal{H}}^{\alpha }\mathcal{Q}(\eta ;\wp )\right)=(-1){\displaystyle \sum _{\kappa =0}^{q-1}}{{}_{\mathcal{H}}\mathcal{Q}}_{\left(\kappa \right)}(\eta ;\wp )\odot {\omega }^{2-\alpha +\kappa }\ominus {}_{\mathcal{H}}(-1)\frac{1}{{\omega }^{\alpha }}\odot \mathbf{E}\left[\mathcal{Q}(\xi ,\wp )\right],\alpha \in (q-1,q].\hfill \end{array}$$

  (22)

4. Analysis Description

This section examines the basic mechanism for obtaining approximate results of time-fractional SHe using the CFD operator in the FET.

Step 1. The parametric formulation of (1) is described as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ \underline{\mathcal{Q}}(\eta ,0)=\underline{g}(\eta ;\wp ),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\overline{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ \overline{\mathcal{Q}}(\eta ,0)=\overline{g}(\eta ;\wp ).\hfill \end{array}\right.\end{array}$$

(23)

Step 2. By implementing FET on the first subsequent case of (23), we have

$$\begin{array}{c}\hfill \mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]=\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right]\end{array}$$

subject to the IC $\underline{\mathcal{Q}}(\eta ,0)=\underline{g}\left(\eta \right),$ we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]-{\displaystyle \sum _{\kappa =0}^{q-1}}{\underline{\mathcal{Q}}}_{\left(\kappa \right)}(\eta ;\wp ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right],\hfill \end{array}$$

or accordingly, we have

$$\begin{array}{c}\hfill \mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]={\omega }^2\underline{g}(\eta ;\wp )+{\omega }^{\alpha }\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right].\end{array}$$

(24)

Step 3. The unknown series solution is expressed as

$$\begin{array}{c}\hfill \underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp ).\end{array}$$

(25)

As a result, the nonlinear components are eliminated as

$$\begin{array}{c}\hfill \underline{\mathcal{N}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp ),\end{array}$$

(26)

where ${\underline{\mathcal{A}}}_q$ is known to Adomian polynomial is presented as

$$\begin{array}{c}\hfill {\underline{\mathcal{A}}}_q=\frac{1}{q!}\frac{d^q}{d{\lambda }^q}{\left[\underline{\mathcal{N}}\left({\displaystyle \sum _{q=0}^{\infty }}{\lambda }^q{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )\right)\right]}_{\lambda =0}.\end{array}$$

(27)

Step 4. Now, (24) can be expressed as

$$\begin{array}{ccc}& & \mathbb{E}\left[{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]\hfill \\ & & ={\omega }^2\underline{g}(\eta ;\wp )+{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{A}}(\eta ,\xi ;\wp )\right].\hfill \end{array}$$

(28)

Step 5. So, incorporating the inverse FET and evaluating values on both sides, we can arrive at

$$\begin{array}{ccc}\hfill {\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^2\underline{g}(\eta ;\wp )\right],\hfill \\ \hfill {\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^2\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_0(\eta ,\xi ;\wp )\right]\right],\hfill \\ \hfill {\underline{\mathcal{Q}}}_2(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^2\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_1(\eta ,\xi ;\wp )\right]\right],\hfill \\ \hfill ⋮\\ \hfill {\underline{\mathcal{Q}}}_{q+1}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^2\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp )\right]\right].\hfill \end{array}$$

(29)

Step 6. As a consequence, the appropriate approximate solution is written as

$$\begin{array}{c}\hfill \underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+\dots .\end{array}$$

(30)

Thus, the upper case of (23) is treated in the same manner. Finally, we present the parametric formulation of the solution as described in the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+\dots ,\hfill \\ \overline{\mathcal{Q}}(\eta ,\xi ;\wp )={\overline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+\dots .\hfill \end{array}\right.\end{array}$$

(31)

5. Convergence Analysis of Fuzzy EADM

Definition 12

([34]). Let $\mathbb{H}$ be a Hilbert space of mappings defined on $\Omega ,$ then

$$\begin{array}{c}\hfill W(\Omega )=\left\{{\left[\mathcal{Q}\left(\xi \right)\right]}_0^{\mathbb{T}}:\tilde{\mathcal{Q}}\left(\xi \right)\in \left|\mathcal{C}\right|(\Omega ),{\tilde{\mathcal{Q}}}^{″}\left(\xi \right)\in L^2(\Omega )\tilde{\mathcal{Q}}\left({\xi }_0\right)=0\right\},\end{array}$$

(32)

where $\mathcal{C}$ is the absolutely continuous mappings on $\Omega .$

Definition 13

([34]). For an absolutely continuous real-valued mapping ${\mathcal{Q}}^{(n-1)}\left(\xi \right)$ on Ω and

$$\begin{array}{c}\hfill W_2^n\left([a_1,b_1]\right)=\left\{\mathcal{Q}\left(\xi \right)|{\mathcal{Q}}^n\left(\xi \right)\in L^2(\Omega ),\left(Q\right)\left(a_1\right)=\mathcal{Q}\left(b_1\right)=0\right\},\end{array}$$

(33)

where $L^2[a_1,b_1]=\left\{\mathcal{Q}|{\displaystyle \underset{a_1}{\overset{b^1}{\int }}}{\mathcal{Q}}^{2}d\xi <\infty \right\}.$

The inner product and norm of the mappings ${\mathcal{Q}}_1,{\mathcal{Q}}_2\in W_2^q[a_1,b_1]$ are presented, respectively, by

$$\begin{array}{c}\hfill \langle {\mathcal{Q}}_1\left(\xi \right),{\mathcal{Q}}_2\left(\xi \right)\rangle ={\displaystyle \sum _{j=0}^{n-1}}{\mathcal{Q}}_1^{\left(j\right)}\left(a_1\right){\mathcal{Q}}_2^{\left(j\right)}\left(a_1\right)+{\displaystyle \underset{a_1}{\overset{b_1}{\int }}}{\mathcal{Q}}_1^{\left(n\right)}\left(\xi \right){\mathcal{Q}}_2^{\left(n\right)}\left(\xi \right)d\xi \end{array}$$

(34)

and

$${\parallel \mathcal{Q}\left(\xi \right)\parallel }_{W_2^n[a_1,b_1]}={\sqrt{\langle \mathcal{Q},\mathcal{Q}\rangle }}_{W_2^n[a_1,b_1]}.$$

Adopting the technique implemented by [51], we illustrate the convergence analysis of fuzzy EADM for the generalised fuzzy operator equation is presented as

$$\begin{array}{c}\hfill {\mathcal{D}}_{g\mathcal{H}}^{\alpha }\mathcal{Q}(\eta ,\xi ;\wp )\oplus \mathcal{R}\left(\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\right)\oplus \mathcal{N}\left(\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\right)=\tilde{g}(\eta ,\xi ;\wp ),\wp \in [0,1],\end{array}$$

(35)

where $\tilde{g}(\eta ,\xi ;\wp )$ is defined in $\mathbb{H}.$ Suppose that there is an operator $\mathbb{T}$ defined by $\mathbb{T}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )=\ominus \mathcal{R}\tilde{\mathcal{Q}}(\eta ,\xi )\ominus \mathcal{N}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp ).$

Now we assume that the Hilbert space $\mathbb{H}=L^2\left(({\gamma }_1^{*},{\gamma }_2^{*})\otimes [0,\mathbb{T}]\right)$ presented by the following:

$$\tilde{\mathcal{Q}}(\eta ,\xi ;\wp ):({\gamma }_1^{*},{\gamma }_2^{*})\otimes [0,\mathbb{T}]\mapsto \mathbb{R}$$

along with

$$\underset{({\gamma }_1^{*},{\gamma }_2^{*})\times [0,\mathbb{T}]}{\int }\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )d\eta d\xi <+\infty ,$$

where $\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )=[\underline{\mathcal{Q}}(\eta ,\xi ;\wp ),\overline{\mathcal{Q}}(\eta ,\xi ;\wp )].$ The following consequence illustrates us how to employ the approximate analytical solution of fuzzy Caputo fractional derivative in general.

Theorem 2.

(Characterization theorem) Consider $\mathcal{Q}\in \mathcal{C}\left(\Omega \times \Omega \left(\mathbb{R}\right),\Omega \left(\mathbb{R}\right)\right)$ with $\wp \in [0,1].$ Assume that the following assumptions hold:

(i) 

The mappings $\tilde{\mathcal{Q}}$ are equicontinuous and uniformly bounded on any bounded set;

(ii) 

There exist $\mathcal{M}>0$ such that

$$\begin{array}{c}\hfill |\tilde{\mathcal{Q}}(\xi ,{\varphi }_1,{\varphi }_2)-\tilde{\mathcal{Q}}(\xi ,{\psi }_1,{\psi }_2)|\le \mathcal{M}max\left\{|{\varphi }_1-{\psi }_1|,|{\varphi }_2-{\psi }_2|\right\},\forall \xi \in [0,1],\end{array}$$

(36)

then the following are working:

(i) 

For $\left(i\right)-{}_{g\mathcal{H}}{\mathcal{D}}^{\alpha }\mathcal{Q}\left(\xi \right)$ of (35) and the fuzzy form of (23) are equivalent;

(ii) 

For $\left(ii\right)-{}_{g\mathcal{H}}{\mathcal{D}}^{\alpha }\mathcal{Q}\left(\xi \right)$ of (35) and the fuzzy form of (23) are equivalent.

Proof. 

Here, we suppose assertion (i) (analogous proof can be employed for other part.) Let $\varphi$ be a $\left(i\right)-{}_{g\mathcal{H}}{\mathcal{D}}^{\alpha }\mathcal{Q}\left(\xi \right).$ The equicontinuity of $\tilde{\mathcal{Q}}$ reveals the continuity of $\mathcal{Q}.$ The Lipschitz property of (ii) confirms that $\tilde{\mathcal{Q}}$ holds the Lipschitz property of fuzzy metric space “$d$” as

$$\begin{array}{ccc}& & d(\tilde{\mathcal{Q}}(\xi ,{\varphi }_1\left(\xi \right),{\varphi }_2\left(\xi \right)),\tilde{\mathcal{Q}}(\xi ,{\psi }_1\left(\xi \right),{\psi }_2\left(\xi \right))\hfill \\ & & =\underset{\xi \in [0,1]}{sup}max\left\{|\underline{\mathcal{Q}}(\xi ,{\varphi }_1\left(\xi \right),{\varphi }_2\left(\xi \right))-\overline{\mathcal{Q}}(\xi ,{\varphi }_1\left(\xi \right),{\varphi }_2\left(\xi \right))|,|\underline{\mathcal{Q}}(\xi ,{\psi }_1\left(\xi \right),{\psi }_2\left(\xi \right))-\overline{\mathcal{Q}}(\xi ,{\psi }_1\left(\xi \right),{\psi }_2\left(\xi \right))|\right\}\hfill \\ & & =\underset{\xi \in [0,1]}{sup}max\{\underline{\mathcal{Q}}\left((\xi ,{\underline{\varphi }}_1\left(\xi \right),{\underline{\varphi }}_2\left(\xi \right)),(\xi ,{\overline{\varphi }}_1\left(\xi \right),{\overline{\varphi }}_2\left(\xi \right))\right)-\underline{\mathcal{Q}}\left((\xi ,{\underline{\psi }}_1\left(\xi \right),{\underline{\psi }}_2\left(\xi \right)),(\xi ,{\overline{\psi }}_1\left(\xi \right),{\overline{\psi }}_2\left(\xi \right))\right),\hfill \\ & & \overline{\mathcal{Q}}\left((\xi ,{\underline{\varphi }}_1\left(\xi \right),{\underline{\varphi }}_2\left(\xi \right)),(\xi ,{\overline{\varphi }}_1\left(\xi \right),{\overline{\varphi }}_2\left(\xi \right))\right)-\overline{\mathcal{Q}}\left((\xi ,{\underline{\psi }}_1\left(\xi \right),{\underline{\psi }}_2\left(\xi \right)),(\xi ,{\overline{\psi }}_1\left(\xi \right),{\overline{\psi }}_2\left(\xi \right))\right)\}\hfill \\ & & =\mathcal{M}\underset{\xi \in [0,1]}{sup}max\left\{|\tilde{\varphi }\left(\xi \right)-\tilde{\psi }\left(\xi \right)|,|\tilde{\varphi }\left(\xi \right)-\tilde{\psi }\left(\xi \right)|\right\}\hfill \\ & & =\mathcal{M}d(\tilde{\varphi }\left(\xi \right),\tilde{\psi }\left(\xi \right)).\hfill \end{array}$$

(37)

By the continuity, Lipschitzian and boundedness of $\tilde{\mathcal{Q}},$ it means that the fuzzy CFD of (35) has a unique solution on $\Omega .$ Meanwhile it is $\left(i\right)-{}_{g\mathcal{H}}{\mathcal{D}}^{\alpha }\mathcal{Q}\left(\xi \right)$, which proves that $\tilde{\varphi },\tilde{\psi }\in \mathcal{C}(\Omega \times \Omega \left(\mathbb{R}\right),\Omega \left(\mathbb{R}\right)).$ This shows that $(\tilde{\varphi },\tilde{\psi })$ is a solution of fuzzy form of (23).

Conversely, suppose that $(\tilde{\varphi },\tilde{\psi })$ is a solution of fuzzy form of (23) The Lipschitzian of (36) implies the existence and uniqueness of solution $\tilde{\mathcal{Q}}$ of (35). Because $\tilde{\mathcal{Q}}$ is $\left(i\right)-{}_{g\mathcal{H}}{\mathcal{D}}^{\alpha }\mathcal{Q}\left(\xi \right),$ then $\tilde{\mathcal{Q}}$ that are the extremities of $\left[\tilde{\mathcal{Q}}(\eta ;\wp )\right]$, which is a solution of (35). Furthermore, because the solution of generalized fuzzy operator Equation (35) is unique, we have that

$$\left[\tilde{\mathcal{Q}}(\eta ;\wp )\right]=[\underline{\mathcal{Q}}(\eta ;\wp ),\underline{\mathcal{Q}}(\eta ;\wp )]=[\underline{\mathcal{Q}}(\eta ;\wp ),\overline{\mathcal{Q}}(\eta ;\wp )]=\left[\tilde{\mathcal{Q}}(\eta ;\wp )\right],$$

As a result, the fuzzy forms of (23) and (35) are equivalent. □

6. Numerical Findings and Their Physical Evaluation

In what follows, we intend to find the analytical solutions of the SH model with the aid of EADM considering the Caputo fractional derivative operator concerning different initial conditions.

To begin, we use EADM to estimate the SH model (1).

Example 1.

Consider the time-fractional fuzzy SH model supplemented with fuzzy ICs

$$\begin{array}{ccc}\hfill & & \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\odot \tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus \frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus 2\odot \frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )-{\tilde{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ & & \tilde{\mathcal{Q}}(\eta ,0)=\tilde{\chi }(\wp )\odot exp\left(\eta \right),\hfill \end{array}$$

(38)

where $\tilde{\chi }(\wp )=[\underline{\chi }(\wp ),\overline{\chi }(\wp )]=[\wp -1,1-\wp ]$ for $\wp \in [0,1]$ is fuzzy number.

The parameterized version of the problem (38) is expressed as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ \underline{\mathcal{Q}}(\eta ,0)=\underline{\chi }(\wp )exp\left(\eta \right),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\overline{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ \overline{\mathcal{Q}}(\eta ,0)=\overline{\chi }(\wp )exp\left(\eta \right).\hfill \end{array}\right.\end{array}$$

(39)

In order to find the EADM solution, we analyse the first case of (39).

By virtue of the process stated in Section 4, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]-{\displaystyle \sum _{\kappa =0}^{q-1}}{\underline{\mathcal{Q}}}_{\left(\kappa \right)}(\eta ;\wp ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right].\hfill \end{array}$$

Simple computations result in

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ;\wp )& & =(\wp -1)exp\left(\eta \right)\hfill \\ & & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right]\right].\hfill \end{array}$$

(40)

Let us surmise the infinite sum $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )$ accompanying the by (27) and affirm the nonlinearity. Therefore, (40) takes the form

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )& & =(\wp -1)exp\left(\eta \right)+{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[(\theta -1){\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )\hfill \\ & & -\frac{{\partial }^4}{\partial {\eta }^4}{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp )\left]\right].\hfill \end{array}$$

(41)

Using the fact of (26), we have

$$\begin{array}{c}\hfill {\underline{\mathcal{A}}}_q\left({\underline{\mathcal{Q}}}^3\right)=\left\{\begin{array}{c}{\underline{\mathcal{Q}}}_0^3,q=0,\hfill \\ 3{\underline{\mathcal{Q}}}_0^2{\underline{\mathcal{Q}}}_1,q=1,\hfill \\ 3{\underline{\mathcal{Q}}}_0^2{\underline{\mathcal{Q}}}_1^2+3{\underline{\mathcal{Q}}}_0^2{\underline{\mathcal{Q}}}_2,q=2,\hfill \\ {\underline{\mathcal{Q}}}_1^3+4{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_2+2{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_1{\underline{\mathcal{Q}}}_2+3{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_{3}q=3.\hfill \end{array}\right.\end{array}$$

(42)

then (41) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathcal{Q}}_0}(\eta ,\xi ;\wp )& & =(\wp -1)exp\left(\eta \right),\hfill \\ \hfill \underline{{\mathcal{Q}}_1}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_0(\eta ,\xi ;\wp )\right]\right]\hfill \\ & & =\left[(\wp -1)(\theta -4)exp\left(\eta \right)-{(\wp -1)}^{3}exp\left(3\eta \right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathcal{Q}}_2}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_1(\eta ,\xi ;\wp )\right]\right]\hfill \\ & & =\left[(\wp -1){(\theta -4)}^{2}exp\left(\eta \right)-(112-4\theta ){(\wp -1)}^{3}exp\left(3\eta \right)+30{(\wp -1)}^{5}exp\left(5\eta \right)\right]\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)},\hfill \\ & & ⋮.\hfill \end{array}$$

The additional components of $\underline{\mathcal{Q}}q(q\ge 3)$ of the EADM solution may be conveniently discovered in an analogous manner. Additionally, as the recursive approach progresses, the reliability of the acquired result increases substantially, and the determined solution becomes increasingly relatively equal to the interpretive framework. Consequently, we have arrived at the accompanying responses, which are organised in a series form

$$\begin{array}{c}\hfill \tilde{\mathcal{Q}}(\eta ,\xi ,\wp )={\tilde{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\underline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\overline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots .\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}& & \underline{\mathcal{Q}}(\eta ,\xi ,\wp )\hfill \\ & & =(\wp -1)exp\left(\eta \right)+\left[(\wp -1)(\theta -4)exp\left(\eta \right)-{(\wp -1)}^{3}exp\left(3\eta \right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\left[(\wp -1){(\theta -4)}^{2}exp\left(\eta \right)-(112-4\theta ){(\wp -1)}^{3}exp\left(3\eta \right)+3{(\wp -1)}^{5}exp\left(5\eta \right)\right]\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}+...,\hfill \\ & & \overline{\mathcal{Q}}(\eta ,\xi ,\wp )\hfill \\ & & =(1-\wp )exp\left(\eta \right)+\left[(1-\wp )(\theta -4)exp\left(\eta \right)-{(1-\wp )}^{3}exp\left(3\eta \right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\left[(1-\wp ){(\theta -4)}^{2}exp\left(\eta \right)-(112-4\theta ){(1-\wp )}^{3}exp\left(3\eta \right)+3{(1-\wp )}^{5}exp\left(5\eta \right)\right]\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}+....\hfill \end{array}$$

In this analysis, Figure 1a,b demonstrate the comprehension of the impact of two-layer and multiple-layer 3D representations for Example 1 associated with the CFD and Elzaki transform via fuzzification. Interestingly, it is noted that the description reveals the fluctuation in $\mathcal{Q}(\eta ,\xi ;\wp )$ on space co-ordinate $\eta$ with respect to $\xi$ and uncertainty parameter $\wp \in [0,1]$.

The analysis demonstrates that even as time penetrates, the visualization of $\mathcal{Q}(\eta ,\xi ;\wp )$ will become more complex.

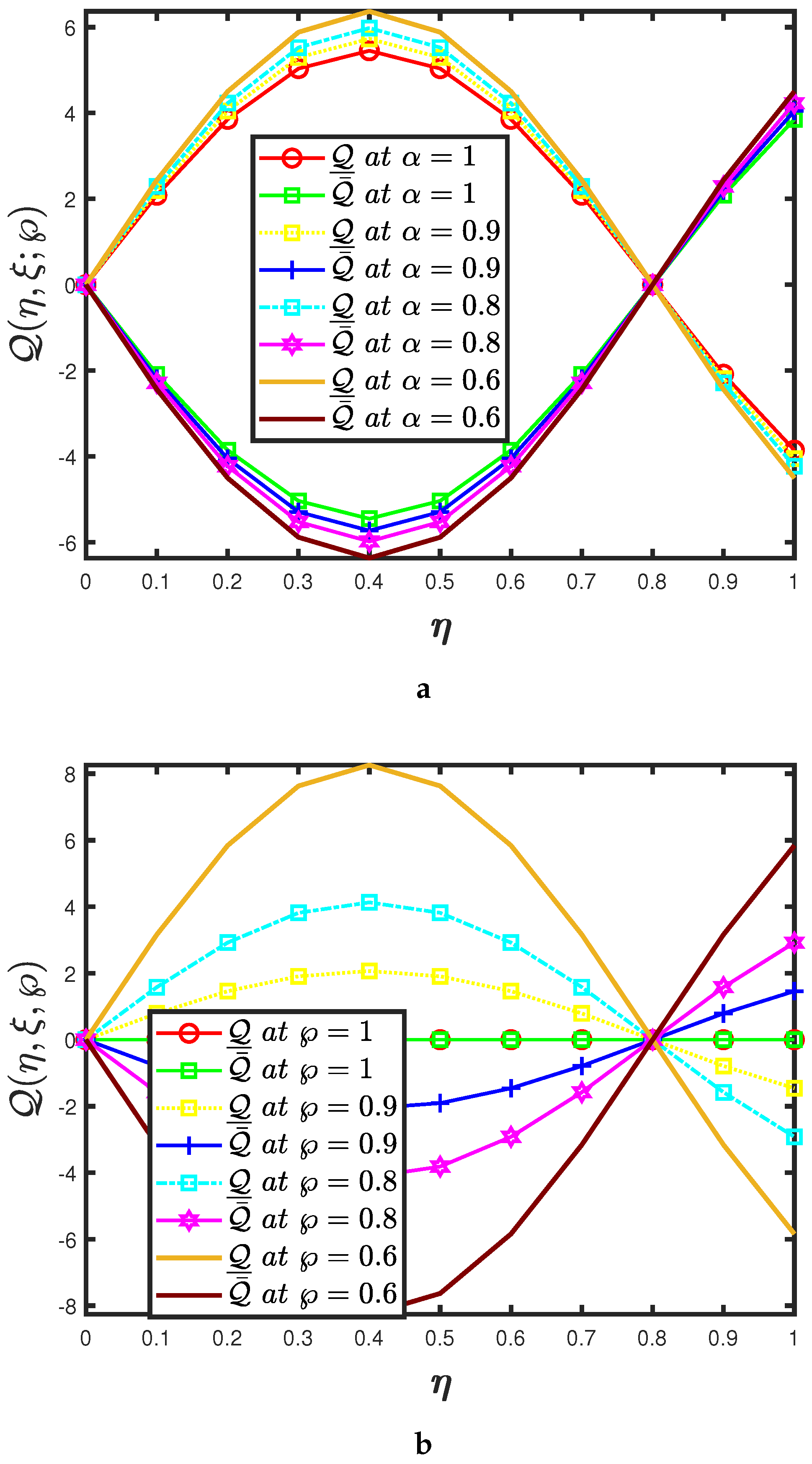
• The mapping effectiveness of the suggested algorithm, $\mathcal{Q}(\eta ,\xi ;\wp )$ is displayed in Figure 2a for the constant parameter $\theta =5.$ The analysis demonstrates a minor improvement in $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ with the decrease in $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$;
• The uncertainty parameter of the mappings $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ and $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$ are presented in Figure 2a,b and it elaborates the behaviour of the specified fractional order of the mapping at various uncertainty parameters;
• The aforementioned graphs presented in Figure 1 and Figure 2 assist us in comprehending the statistical behaviour of time and space variation. Furthermore, the offered approach will aid scientists working in pattern formation theory, optical design, and statistical dynamics in evaluating performance through analysis of variance testing. As a result, the uncertainty parameter can strengthen the results after increasing the number of iterations.

Figure 2. (a) Two-dimensional representation of Example 1 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.5,$ $\theta =5$ and $\xi =0.5$. (b) Two-dimensional representation of example 1 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.7$ and $\xi =0.5$.

Figure 2. (a) Two-dimensional representation of Example 1 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.5,$ $\theta =5$ and $\xi =0.5$. (b) Two-dimensional representation of example 1 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.7$ and $\xi =0.5$.

Remark 1.

When $\underline{\chi }(\wp )=\overline{\chi }(\wp )=\wp ,$ then both solutions of Example 1 leads to the classical solution of Alrabaiah et al. [58].

Example 2.

Consider the time-fractional fuzzy SH model supplemented with fuzzy ICs

$$\begin{array}{ccc}\hfill & & \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\odot \tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus \frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus 2\odot \frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus {\tilde{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ & & \tilde{\mathcal{Q}}(\eta ,0)=\tilde{\chi }(\wp )\odot sin\eta ,\hfill \end{array}$$

(43)

where $\tilde{\chi }(\wp )=[\underline{\chi }(\wp ),\overline{\chi }(\wp )]=[\wp -1,1-\wp ]$ for $\wp \in [0,1]$ is fuzzy number.

The parameterized version of the problem (43) is expressed as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ \underline{\mathcal{Q}}(\eta ,0)=\underline{\chi }(\wp )sin\eta ,\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\overline{\mathcal{Q}}}^3(\eta ,\xi ;\wp ),\hfill \\ \overline{\mathcal{Q}}(\eta ,0)=\overline{\chi }(\wp )sin\eta .\hfill \end{array}\right.\end{array}$$

(44)

In order to find the EADM solution, we analyse the first case of (44).

By virtue of the process stated in Section 4, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]-{\displaystyle \sum _{\kappa =0}^{q-1}}{\underline{\mathcal{Q}}}_{\left(\kappa \right)}(\eta ;\wp ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right],\hfill \end{array}$$

Simple computations yield

$$\begin{array}{ccc}\hfill & & \underline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\wp -1)sin\eta \hfill \\ & & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\right]\right].\hfill \end{array}$$

(45)

Let us surmise the infinite sum $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )$ accompanying the by (27) and affirm the nonlinearity. Therefore, (45) takes the form

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )& & =(\wp -1)exp\left(\eta \right)+{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[(\theta -1){\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )\hfill \\ & & -\frac{{\partial }^4}{\partial {\eta }^4}{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp )\left]\right].\hfill \end{array}$$

(46)

In view of (42), then (46) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathcal{Q}}_0}(\eta ,\xi ;\wp )& & =(\wp -1)sin\eta ,\hfill \\ \hfill \underline{{\mathcal{Q}}_1}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_0(\eta ,\xi ;\wp )\right]\right]\hfill \\ & & =\left[\theta (\wp -1)sin\eta -{(\wp -1)}^3{sin}^3\eta \right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathcal{Q}}_2}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_1(\eta ,\xi ;\wp )\right]\right]\hfill \\ & & =[{\theta }^2(\wp -1)sin\eta -2(2\theta +7){(\wp -1)}^3{sin}^3\eta \hfill \\ & & -48{(\wp -1)}^3{cos}^2\eta sin\eta +3{(\wp -1)}^5{sin}^5\eta ]\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)},\hfill \\ & & ⋮.\hfill \end{array}$$

The additional components of $\underline{\mathcal{Q}}q(q\ge 3)$ of the EADM solution may be conveniently discovered in an analogous manner. Additionally, as the recursive approach progresses, the reliability of the acquired result increases substantially, and the determined solution becomes increasingly relatively equal to the interpretive framework. Consequently, we have arrived at the accompanying responses, which are organised in a series form.

$$\begin{array}{c}\hfill \tilde{\mathcal{Q}}(\eta ,\xi ,\wp )={\tilde{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\underline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\overline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots .\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & =(\wp -1)sin\eta +\left[\theta (\wp -1)sin\eta -{(\wp -1)}^3{sin}^3\eta \right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +[{\theta }^2(\wp -1)sin\eta -2(2\theta +7){(\wp -1)}^3{sin}^3\eta \hfill \\ & & -48{(\wp -1)}^3{cos}^2\eta sin\eta +3{(\wp -1)}^5{sin}^5\eta ]\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}+...,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & =(1-\wp )sin\eta +\left[\theta (1-\wp )sin\eta -{(1-\wp )}^3{sin}^3\eta \right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +[{\theta }^2(1-\wp )sin\eta -2(2\theta +7){(1-\wp )}^3{sin}^3\eta \hfill \\ & & -48{(1-\wp )}^3{cos}^2\eta sin\eta +3{(1-\wp )}^5{sin}^5\eta ]\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}+\dots .\hfill \end{array}$$

In what follows, we measure the effects of changes in some parameters on the overall behaviour of the SH model (2).

Figure 3a,b dealt with the influence of the $gH$-differentiability using a fractional-order SHe model’s impact of two-layer and multiple-layer 3D representations for Example 2 associated with the Elzaki transform via fuzzification. The analysis, in particular, reveals the fluctuation in $\mathcal{Q}(\eta ,\xi ;\wp )$ on space co-ordinate $\eta$ with respect to $\xi$ and uncertainty parameter $\wp \in [0,1]$ is taken into account.

Ultimately, as time penetrates, the visualization of $\mathcal{Q}(\eta ,\xi ;\wp )$ will show more intricacies;

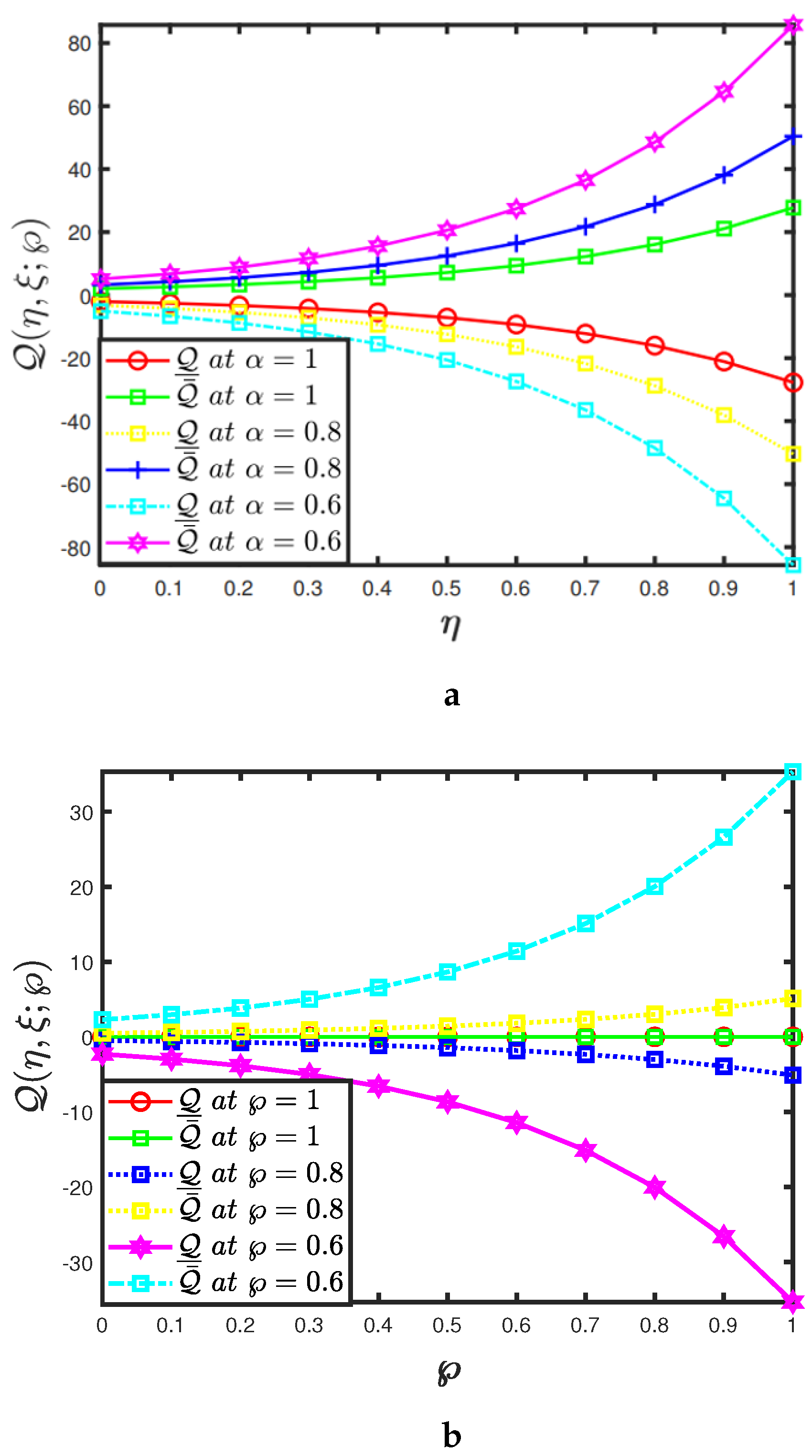
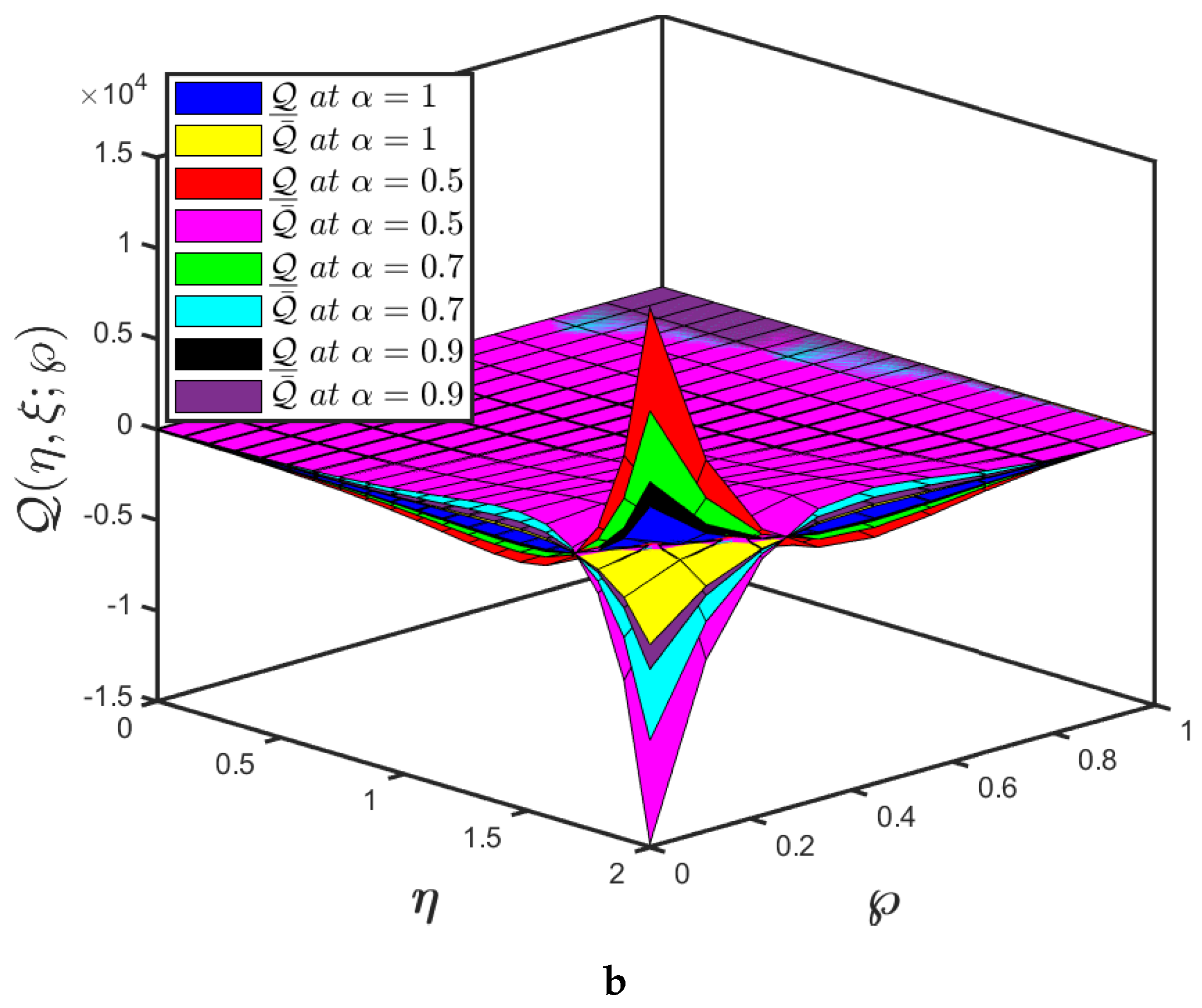
• The mapping effectiveness of the suggested algorithm, $\mathcal{Q}(\eta ,\xi ;\wp )$ is displayed in Figure 4a for the constant parameter $\theta =5.$ The analysis demonstrates a minor improvement in $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ with the decrease in $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$;
• The uncertainty parameter of the mappings $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ and $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$ are presented in Figure 4a,b and it elaborates the behaviour of specified fractional order of the mapping at various uncertainty parameters;
• The aforementioned graphs presented in Figure 3 and Figure 4 assist us in comprehending the statistical behaviour of time and space variation. The representations aid us in gaining a better understanding of the characteristics and interpretations of problem behaviour.

Figure 4. (a) Two-dimensional representation of Example 2 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.5,$ $\theta =5$ and $\xi =0.5$ (b) Two-dimensional representations of Example 2 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.9$ and $\xi =0.5$.

Figure 4. (a) Two-dimensional representation of Example 2 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.5,$ $\theta =5$ and $\xi =0.5$ (b) Two-dimensional representations of Example 2 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.9$ and $\xi =0.5$.

Remark 2.

When $\underline{\chi }(\wp )=\overline{\chi }(\wp )=\wp ,$ then both solutions of Example 2 leads to the classical solution of Alrabaiah et al. [58].

In the next result, we aim to find an approximate solution for SH model (2) having dispersion by means of Definition 11.

Example 3.

Consider the time-fractional fuzzy SH model supplemented with fuzzy ICs

$$\begin{array}{ccc}\hfill \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )& & =\varsigma \odot \tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\oplus 2{\tilde{\mathcal{Q}}}^2(\eta ,\xi ;\wp )\ominus {\tilde{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\ominus \frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ & & \ominus 2\odot \frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\oplus \sigma \odot \frac{{\partial }^3}{\partial {\eta }^3}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \hfill \tilde{\mathcal{Q}}(\eta ,0)& & =\tilde{\chi }(\wp )\odot exp\left(\eta \right),\hfill \end{array}$$

(47)

where $\tilde{\chi }(\wp )=[\underline{\chi }(\wp ),\overline{\chi }(\wp )]=[\wp -1,1-\wp ]$ for $\wp \in [0,1]$ is fuzzy number.

The parameterized version of the problem (47) is expressed as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )=\varsigma \underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\underline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\underline{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \underline{\mathcal{Q}}(\eta ,0)=\underline{\chi }(\wp )exp\left(\eta \right),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )=\varsigma \overline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\overline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\overline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\overline{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \overline{\mathcal{Q}}(\eta ,0)=\overline{\chi }(\wp )exp\left(\eta \right),\hfill \end{array}\right.\end{array}$$

In order to find the EADM solution, we analyse the first case of (48).

By virtue of the process stated in Section 4, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]-{\displaystyle \sum _{\kappa =0}^{q-1}}{\underline{\mathcal{Q}}}_{\left(\kappa \right)}(\eta ;\wp ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}\left[\varsigma \underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\underline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right],\hfill \end{array}$$

Simple computations yield

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ;\wp )& & =(\wp -1)exp\left(\eta \right)\hfill \\ & & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma \underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\underline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \end{array}\right.\right].\hfill \end{array}$$

(48)

Let us surmise the infinite sum $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )$ accompanying the by (27) and affirm the nonlinearity. Therefore, (48) takes the form

$$\begin{array}{cc}\hfill {\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )& =(\wp -1)exp\left(\eta \right)\hfill \\ & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma {\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q(\eta ,\xi ;\wp )-{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \end{array}\right.\right].\hfill \end{array}$$

The aforementioned equation has two nonlinear terms such as ${\underline{\mathcal{Q}}}^3={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q$ and ${\underline{\mathcal{Q}}}^2={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q$ that can be calculated with the aid of Adomian polynomial (26). Therefore, taking into consideration (42) and first few Adomian polynomials for ${\underline{\mathcal{Q}}}^2={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q$ are computed as

$$\begin{array}{c}\hfill {\underline{\mathcal{B}}}_q\left({\underline{\mathcal{Q}}}^2\right)=\left\{\begin{array}{c}{\underline{\mathcal{Q}}}_0^2,q=0,\hfill \\ 2{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_1,q=1,\hfill \\ 2{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_2+{\underline{\mathcal{Q}}}_1^2,q=2,\hfill \end{array}\right.\end{array}$$

(49)

then (49) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathcal{Q}}_0}(\eta ,\xi ;\wp )& & =(\wp -1)exp\left(\eta \right),\hfill \\ \hfill \underline{{\mathcal{Q}}_1}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma {\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+2{\underline{\mathcal{B}}}_0(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_0(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )\hfill \end{array}\right.\right]\hfill \\ & & =\left[(\wp -1)(\varsigma +\sigma -3)exp\left(\eta \right)+2{(\wp -1)}^{2}exp\left(2\eta \right)-{(\wp -1)}^{3}exp\left(3\eta \right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathcal{Q}}_2}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma {\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+2{\underline{\mathcal{B}}}_1(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_1(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )\hfill \end{array}\right.\right]\hfill \\ & & =\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}\left({\varsigma }^2+{\sigma }^2-6(\varsigma +\sigma )+2\varsigma \sigma +9\right)(\wp -1)exp\left(\eta \right)+{(\wp -1)}^{2}exp\left(2\eta \right)\left(20\sigma +6\varsigma -60\right)\hfill \\ +{(\wp -1)}^{3}exp\left(3\eta \right)\left(116-4\varsigma -30\sigma \right)-10{(\wp -1)}^{4}exp\left(4\eta \right)+3{(\wp -1)}^{5}exp\left(5\eta \right),\hfill \end{array}\right.\hfill \\ & & ⋮.\hfill \end{array}$$

The additional components of $\underline{\mathcal{Q}}q(q\ge 3)$ of the EADM solution may be conveniently discovered in an analogous manner. Additionally, as the recursive approach progresses, the reliability of the acquired result increases substantially, and the determined solution becomes increasingly relatively equal to the interpretive framework. Consequently, we have arrived at the accompanying responses, which are organised in a series form.

$$\begin{array}{c}\hfill \tilde{\mathcal{Q}}(\eta ,\xi ,\wp )={\tilde{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\underline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\overline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots .\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}& & \underline{\mathcal{Q}}(\eta ,\xi ,\wp )=(\wp -1)exp\left(\eta \right)\hfill \\ & & +\left[(\wp -1)(\varsigma +\sigma -3)exp\left(\eta \right)+2{(\wp -1)}^{2}exp\left(2\eta \right)-{(\wp -1)}^{3}exp\left(3\eta \right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}\left({\varsigma }^2+{\sigma }^2-6(\varsigma +\sigma )+2\varsigma \sigma +9\right)(\wp -1)exp\left(\eta \right)+{(\wp -1)}^{2}exp\left(2\eta \right)\left(20\sigma +6\varsigma -60\right)\hfill \\ +{(\wp -1)}^{3}exp\left(3\eta \right)\left(116-4\varsigma -30\sigma \right)-10{(\wp -1)}^{4}exp\left(4\eta \right)+3{(\wp -1)}^{5}exp\left(5\eta \right)\hfill \end{array}\right.\hfill \\ & & +\dots ,\hfill \\ & & \overline{\mathcal{Q}}(\eta ,\xi ,\wp )=(1-\wp )exp\left(\eta \right)\hfill \\ & & +\left[(1-\wp )(\varsigma +\sigma -3)exp\left(\eta \right)+2{(1-\wp )}^{2}exp\left(2\eta \right)-{(1-\wp )}^{3}exp\left(3\eta \right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}\left({\varsigma }^2+{\sigma }^2-6(\varsigma +\sigma )+2\varsigma \sigma +9\right)(1-\wp )exp\left(\eta \right)+{(1-\wp )}^{2}exp\left(2\eta \right)\left(20\sigma +6\varsigma -60\right)\hfill \\ +{(1-\wp )}^{3}exp\left(3\eta \right)\left(116-4\varsigma -30\sigma \right)-10{(1-\wp )}^{4}exp\left(4\eta \right)+3{(1-\wp )}^{5}exp\left(5\eta \right)\hfill \end{array}\right.\hfill \\ & & +\dots .\hfill \end{array}$$

Now, the trajectories describe the sensitivity of the model with respect to some of the parameters in the formulation presented in the SH model (3).

Figure 5a,b show that as the fractional order increases, the two-layer system behaves more vibrantly. However, for smaller values of fractional order in multiple-layer 3D, the system is stable and tends towards a certain equilibrium point.

Interestingly, the finding demonstrates that a variation in the values for the $\mathcal{Q}(\eta ,\xi ;\wp )$ on space co-ordinate $\eta$ with respect to the type of uncertainty parameter $\wp \in [0,1].$ The analysis shows that even as time penetrates, the visualisation of $\mathcal{Q}(\eta ,\xi ;\wp )$ will become closer to the integer-order solution.

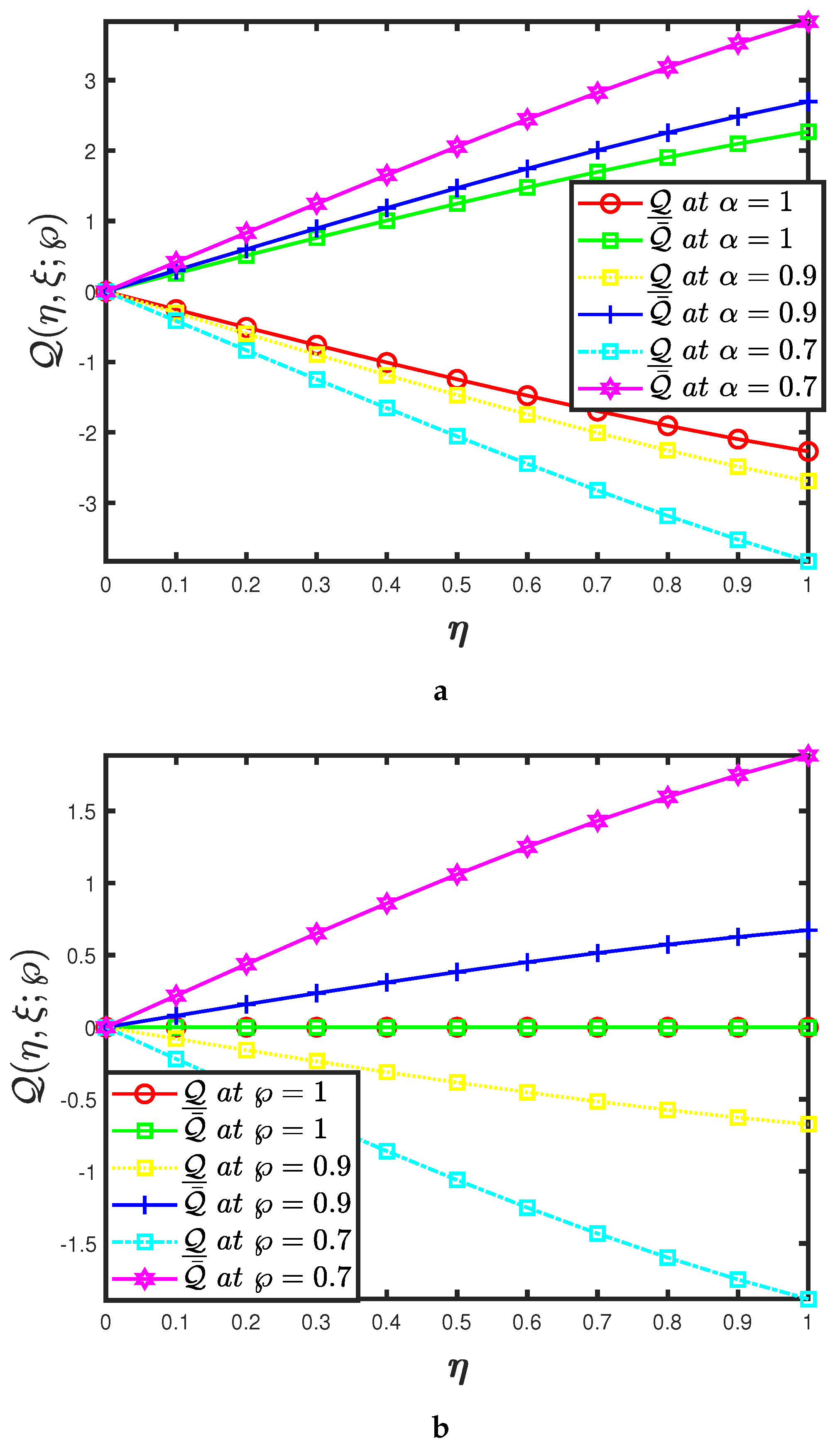
• The mapping effectiveness of the suggested algorithm, $\mathcal{Q}(\eta ,\xi ;\wp )$ is displayed in Figure 6a for the constant parameter $\sigma =10$ and $\varsigma =5.$ The analysis demonstrates a minor improvement in $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ with the decrease in $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$;
• The uncertainty parameter of the mappings $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ and $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$ are presented in Figure 6a,b and it elaborates the behaviour of specified fractional order of the mapping at various uncertainty parameters.

Figure 6. (a) Two-dimensional representation of Example 3 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.9,$ $\varsigma =10=5$ and $\sigma =3$ with $\xi =0.2$ (b) Two-dimensional representation of Example 3 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.9$ and $\xi =0.2$.

Figure 6. (a) Two-dimensional representation of Example 3 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.9,$ $\varsigma =10=5$ and $\sigma =3$ with $\xi =0.2$ (b) Two-dimensional representation of Example 3 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.9$ and $\xi =0.2$.

The representations obtained show that the graphs are strikingly similar, have analogous characteristics, and are in good agreement with one another, especially when examining the crisp integer-order derivative. Consequently, the fuzzy Caputo fractional orders have considerable influence on model characteristics, leading to pretty weird behaviours when a significant deviation from the crisp integer value of $\alpha =1$ and $\wp \in [0,1]$ occurs.

Remark 3.

When $\underline{\chi }(\wp )=\overline{\chi }(\wp )=\wp ,$ then both solutions of Example 3 leads to the classical solution of Alrabaiah et al. [58].

Example 4.

Consider the time-fractional fuzzy SH model supplemented with fuzzy ICs

$$\begin{array}{ccc}\hfill \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )& & =\varsigma \odot \tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\oplus 2\odot {\tilde{\mathcal{Q}}}^2(\eta ,\xi ;\wp )\ominus {\tilde{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\ominus \frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ & & \ominus 2\odot \frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\oplus \sigma \odot \frac{{\partial }^3}{\partial {\eta }^3}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ & & \tilde{\mathcal{Q}}(\eta ,0)=\tilde{\chi }(\wp )\odot cos\eta ,\hfill \end{array}$$

(50)

where $\tilde{\chi }(\wp )=[\underline{\chi }(\wp ),\overline{\chi }(\wp )]=[\wp -1,1-\wp ]$ for $\wp \in [0,1]$ is $\mathbf{F}$ number.

The parameterized version of the problem (50) is expressed as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )=\varsigma \underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\underline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\underline{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \underline{\mathcal{Q}}(\eta ,0)=\underline{\chi }(\wp )cos\eta ,\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )=\varsigma \overline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\overline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\overline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\overline{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \overline{\mathcal{Q}}(\eta ,0)=\overline{\chi }(\wp )cos\eta .\hfill \end{array}\right.\end{array}$$

In order to find the EADM solution, we analyse the first case of (51).

By virtue of the process stated in Section 4, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]-{\displaystyle \sum _{\kappa =0}^{q-1}}{\underline{\mathcal{Q}}}_{\left(\kappa \right)}(\eta ;\wp ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}\left[\varsigma \underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\underline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right],\hfill \end{array}$$

Simple computations yield

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ;\wp )& & =(\wp -1)cos\eta \hfill \\ & & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma \underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\underline{\mathcal{Q}}}^2(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \end{array}\right.\right].\hfill \end{array}$$

(51)

Let us surmise the infinite sum $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )$ accompanying the by (27) and affirm the nonlinearity. Therefore, (51) takes the form

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )& & =(\wp -1)cos\eta \hfill \\ & & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma {\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+2{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q(\eta ,\xi ;\wp )-{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}{\displaystyle \sum _{q=0}^{\infty }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\hfill \end{array}\right.\right].\hfill \end{array}$$

The aforementioned equation has two nonlinear terms such as ${\underline{\mathcal{Q}}}^3={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q$ and ${\underline{\mathcal{Q}}}^2={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q$ that can be calculated with the aid of Adomian polynomial (26). Therefore, taking into consideration (42) and first few Adomian polynomials for ${\underline{\mathcal{Q}}}^2={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q$ are computed as

$$\begin{array}{c}\hfill {\underline{\mathcal{B}}}_q\left({\underline{\mathcal{Q}}}^2\right)=\left\{\begin{array}{c}{\underline{\mathcal{Q}}}_0^2,q=0,\hfill \\ 2{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_1,q=1,\hfill \\ 2{\underline{\mathcal{Q}}}_0{\underline{\mathcal{Q}}}_2+{\underline{\mathcal{Q}}}_1^2,q=2,\hfill \end{array}\right.\end{array}$$

(52)

then (52) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathcal{Q}}_0}(\eta ,\xi ;\wp )& & =(\wp -1)cos\eta ,\hfill \\ \hfill \underline{{\mathcal{Q}}_1}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma {\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+2{\underline{\mathcal{B}}}_0(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_0(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )\hfill \end{array}\right.\right]\hfill \\ & & =\left[(\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathcal{Q}}_2}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left\{\begin{array}{c}\varsigma {\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+2{\underline{\mathcal{B}}}_1(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_1(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )\hfill \\ -2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )+\sigma \frac{{\partial }^3}{\partial {\eta }^3}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )\hfill \end{array}\right.\right]\hfill \\ & & =\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}\varsigma \left((\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right)\hfill \\ +4(\wp -1)cos\eta \left((\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right)\hfill \\ -3(\wp -1){cos}^2\eta \left((\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right)\hfill \\ -(\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+24{(\wp -1)}^2({cos}^2\eta -{sin}^2\eta )\hfill \\ +3{(\wp -1)}^3(20cos\eta {sin}^2\eta -7{cos}^3\eta )+2(\wp -1)((\varsigma +1)cos\eta +\sigma sin\eta )\hfill \\ -6{(\wp -1)}^3({cos}^3\eta -2cos\eta {sin}^2\eta )+\sigma (\wp -1)((\varsigma +1)sin\eta -\sigma cos\eta )\hfill \\ +16{(\wp -1)}^{2}cos\eta sin\eta +3{(\wp -1)}^3(2{sin}^3\eta -7{cos}^2\eta sin\eta )\hfill \end{array}\right.\hfill \\ & & ⋮.\hfill \end{array}$$

The additional components of $\underline{\mathcal{Q}}q(q\ge 3)$ of the EADM solution may be conveniently discovered in an analogous manner. Additionally, as the recursive approach progresses, the reliability of the acquired result increases substantially, and the determined solution becomes increasingly relatively equal to the interpretive framework. Consequently, we have arrived at the accompanying responses, which are organised in a series form.

$$\begin{array}{c}\hfill \tilde{\mathcal{Q}}(\eta ,\xi ,\wp )={\tilde{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\underline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\overline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots .\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & =(\wp -1)cos\eta +\left[(\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}\varsigma \left((\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right)\hfill \\ +4(\wp -1)cos\eta \left((\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right)\hfill \\ -3(\wp -1){cos}^2\eta \left((\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(\wp -1)}^2{cos}^2\eta -{(\wp -1)}^3{cos}^3\eta \right)\hfill \\ -(\wp -1)\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+24{(\wp -1)}^2({cos}^2\eta -{sin}^2\eta )\hfill \\ +3{(\wp -1)}^3(20cos\eta {sin}^2\eta -7{cos}^3\eta )+2(\wp -1)((\varsigma +1)cos\eta +\sigma sin\eta )\hfill \\ -6{(\wp -1)}^3({cos}^3\eta -2cos\eta {sin}^2\eta )+\sigma (\wp -1)((\varsigma +1)sin\eta -\sigma cos\eta )\hfill \\ +16{(\wp -1)}^{2}cos\eta sin\eta +3{(\wp -1)}^3(2{sin}^3\eta -7{cos}^2\eta sin\eta )\hfill \end{array}\right.\hfill \\ & & +\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & =(1-\wp )cos\eta +\left[(1-\wp )\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(1-\wp )}^2{cos}^2\eta -{(1-\wp )}^3{cos}^3\eta \right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}\varsigma \left((1-\wp )\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(1-\wp )}^2{cos}^2\eta -{(1-\wp )}^3{cos}^3\eta \right)\hfill \\ +4(1-\wp )cos\eta \left((1-\wp )\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(1-\wp )}^2{cos}^2\eta -{(1-\wp )}^3{cos}^3\eta \right)\hfill \\ -3(1-\wp ){cos}^2\eta \left((1-\wp )\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+2{(1-\wp )}^2{cos}^2\eta -{(1-\wp )}^3{cos}^3\eta \right)\hfill \\ -(1-\wp )\left((\varsigma +1)cos\eta +\sigma sin\eta \right)+24{(1-\wp )}^2({cos}^2\eta -{sin}^2\eta )\hfill \\ +3{(1-\wp )}^3(20cos\eta {sin}^2\eta -7{cos}^3\eta )+2(1-\wp )((\varsigma +1)cos\eta +\sigma sin\eta )\hfill \\ -6{(1-\wp )}^3({cos}^3\eta -2cos\eta {sin}^2\eta )+\sigma (1-\wp )((\varsigma +1)sin\eta -\sigma cos\eta )\hfill \\ +16{(1-\wp )}^{2}cos\eta sin\eta +3{(1-\wp )}^3(2{sin}^3\eta -7{cos}^2\eta sin\eta )\hfill \end{array}\right.\hfill \\ & & +\dots .\hfill \end{array}$$

The modal validation is conducted by comparing the fractional-order and uncertainty parameters for the fuzzy fractional SH model 4 predicted by the fuzzy fractional Caputo derivative and EADM.

Figure 7a,b show an understanding of the impact of two-layer and multiple-layer 3D representations for Example 4. Observe that the time resolution is also small enough to see the onset of the instability, considering that this time step was the maximum possible to achieve numerical stability incorporating the uncertainty parameter $\wp \in [0,1]$.

The analysis demonstrates that even as time penetrates, the visualization of $\mathcal{Q}(\eta ,\xi ;\wp )$ will arise in cross patterns.

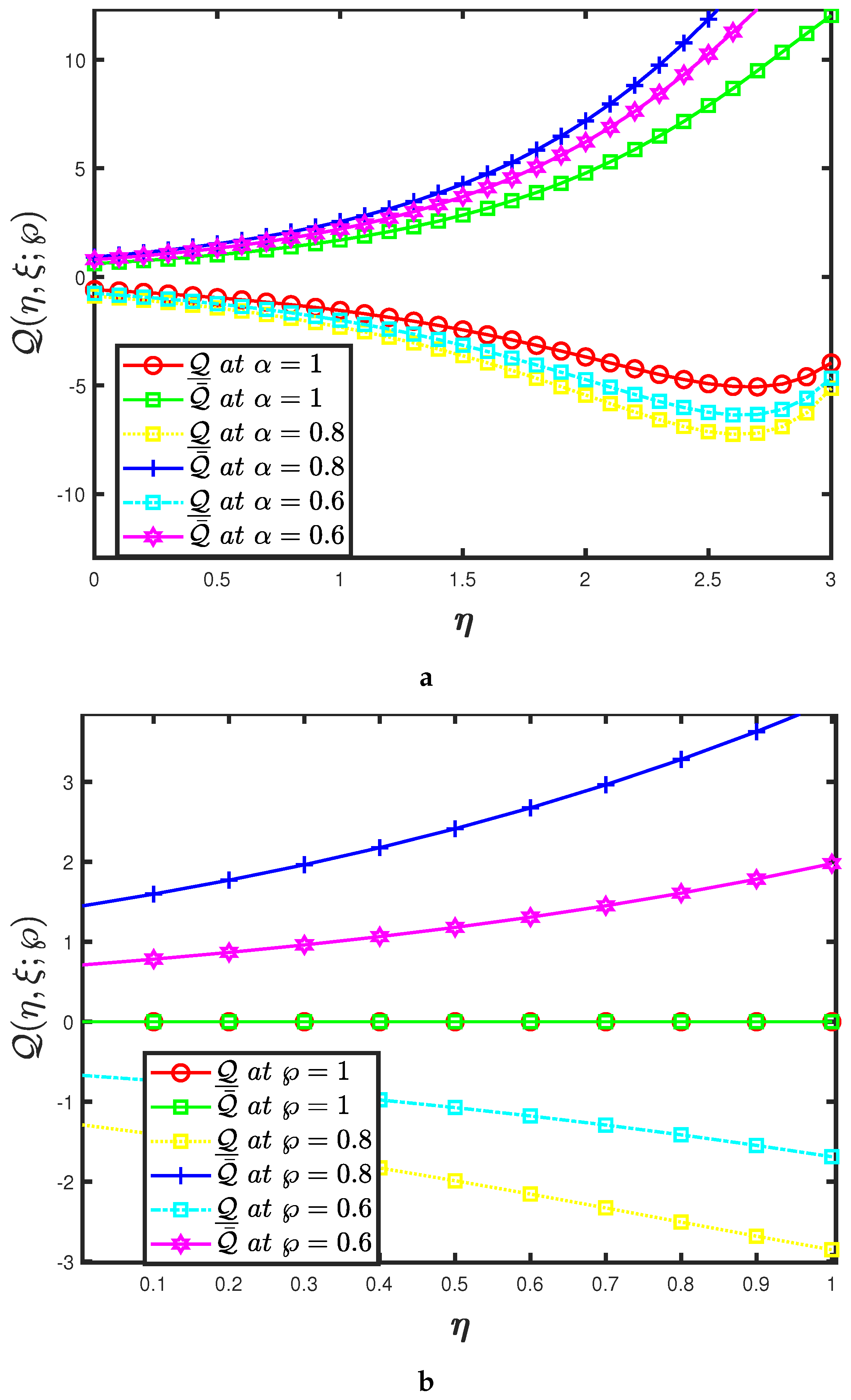
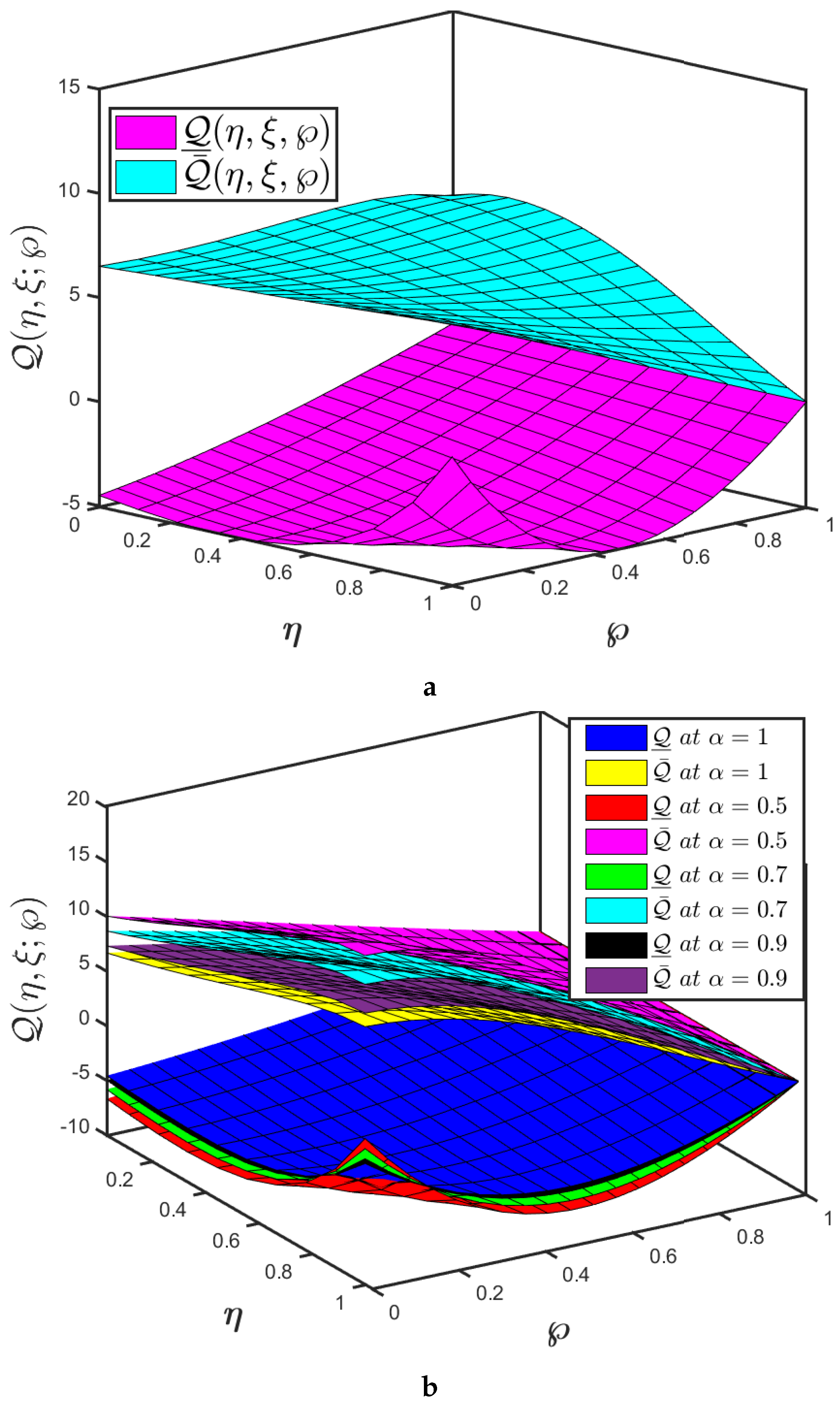
• The mapping effectiveness of the suggested algorithm, $\mathcal{Q}(\eta ,\xi ;\wp )$ is displayed in Figure 8a for the constant parameter $\sigma =100$ and $\varsigma =10.$ The analysis demonstrates a minor improvement in $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ with the decrease in $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$.
• The uncertainty parameter of the mappings $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ and $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$ are presented in Figure 8a,b and it elaborates the behaviour of specified fractional order of the mapping at various uncertainty parameters.
• With these findings, the qualitative resemblance of the cross patterns created to those occurring in nature, such as Rayleigh–Bénard convection, may be confirmed. Despite the various factors that initiate and enhance the instability, pattern development is the consequence of self-organization systems, and all of these are good instances of this phenomena.

Figure 8. (a) Two-dimensional representation of Example 4 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.7,$ $\sigma =\varsigma =100$ and $\xi =0.9$ (b) Two-dimensional representation of Example 4 established by the different uncertainty parameters and fractional-order considered to be $\alpha =0.7$ and $\xi =0.9$.

Figure 8. (a) Two-dimensional representation of Example 4 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.7,$ $\sigma =\varsigma =100$ and $\xi =0.9$ (b) Two-dimensional representation of Example 4 established by the different uncertainty parameters and fractional-order considered to be $\alpha =0.7$ and $\xi =0.9$.

Remark 4.

When $\underline{\chi }(\wp )=\overline{\chi }(\wp )=\wp ,$ then both solutions of Example 4 leads to the classical solution of Alrabaiah et al. [58].

Example 5.

Consider the time-fractional fuzzy SH model supplemented with fuzzy ICs

$$\begin{array}{ccc}\hfill & & \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\odot \tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus {\tilde{\mathcal{Q}}}^3(\eta ,\xi ;\wp )\ominus \frac{{\partial }^4}{\partial {\eta }^4}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp )\ominus 2\odot \frac{{\partial }^2}{\partial {\eta }^2}\tilde{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ & & \tilde{\mathcal{Q}}(\eta ,0)=\tilde{\chi }(\wp )\odot \frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right),\hfill \end{array}$$

(53)

where $\tilde{\chi }(\wp )=[\underline{\chi }(\wp ),\overline{\chi }(\wp )]=[\wp -1,1-\wp ]$ for $\wp \in [0,1]$ is fuzzy number.

The parameterized version of the problem (53) is expressed as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \underline{\mathcal{Q}}(\eta ,0)=\left(\underline{\chi }(\wp )\right)\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )=(\theta -1)\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\overline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\overline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\overline{\mathcal{Q}}(\eta ,\xi ;\wp ),\hfill \\ \overline{\mathcal{Q}}(\eta ,0)=\overline{\chi }(\wp )\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right),\hfill \end{array}\right.\end{array}$$

(54)

In order to find the EADM solution, we analyse the first case of (54).

By virtue of the process stated in Section 4, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]-{\displaystyle \sum _{\kappa =0}^{q-1}}{\underline{\mathcal{Q}}}_{\left(\kappa \right)}(\eta ;\wp ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right].\hfill \end{array}$$

Simple computations yield

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ;\wp )& & =(\wp -1)\frac{1}{10}sin\left(\frac{\pi \eta }{\omega }\right)\hfill \\ & & +{\mathbb{E}}^{-1}\left[{\varrho }^{\alpha }\mathbb{E}\left[(\theta -1)\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-{\underline{\mathcal{Q}}}^3(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}\underline{\mathcal{Q}}(\eta ,\xi ;\wp )\right]\right].\hfill \end{array}$$

(55)

Let us surmise the infinite sum $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )$ accompanying the by (27) and affirm the nonlinearity. Therefore, (55) takes the form

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )& & =(\wp -1)\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ & & +{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{Q}}}_q(\eta ,\xi ;\wp )\right]\right].\hfill \end{array}$$

(56)

The aforementioned equation has two nonlinear terms such as ${\underline{\mathcal{Q}}}^3={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{A}}}_q$ and ${\underline{\mathcal{Q}}}^2={\displaystyle \sum _{q=0}^{\infty }}{\underline{\mathcal{B}}}_q$ that can be calculated with the aid of Adomian polynomial (26), then (56) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathcal{Q}}_0}(\eta ,\xi ;\wp )& & =(\wp -1)\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right),\hfill \\ \hfill \underline{{\mathcal{Q}}_1}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_0(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_0(\eta ,\xi ;\wp )\right]\right]\hfill \\ & & =\frac{1}{1000{\varrho }^4}\left[(\wp -1)sin\left(\frac{\pi \eta }{\varrho }\right)\left(100{\varrho }^4(\theta -1)-100{\pi }^4+200{\pi }^2{\varrho }^2\right)-{\varrho }^4{(\wp -1)}^3{sin}^3\left(\frac{\pi \eta }{\varrho }\right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathcal{Q}}_2}(\eta ,\xi ;\wp )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[(\theta -1){\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-\frac{{\partial }^4}{\partial {\eta }^4}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-2\frac{{\partial }^2}{\partial {\eta }^2}{\underline{\mathcal{Q}}}_1(\eta ,\xi ;\wp )-{\underline{\mathcal{A}}}_1(\eta ,\xi ;\wp )\right]\right]\hfill \\ & & =\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}(100{\varrho }^4(\theta -1)-100{\pi }^4+2000{\pi }^2{\varrho }^2)[\frac{(\theta -1)(\wp -1)\pi }{1000{\varrho }^5}cos\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ -\frac{{\pi }^4}{1000{\varrho }^8}(\wp -1)sin\left(\frac{\pi \eta }{\varrho }\right)+\frac{2{\pi }^2}{1000{\varrho }^6}(\wp -1)sin\left(\frac{\pi \eta }{\varrho }\right)-\frac{3}{100000{\varrho }^4}{(\wp -1)}^3{sin}^4\left(\frac{\pi \eta }{\varrho }\right)]\hfill \\ -{sin}^2\left(\frac{\pi \eta }{\varrho }\right)cos\left(\frac{\pi \eta }{\varrho }\right)\left(\frac{3\pi (\theta -1)}{1000\varrho }{(\wp -1)}^3+\frac{42{\pi }^3}{1000{\varrho }^3}{(\wp -1)}^3\right)\hfill \\ -\frac{60{\pi }^4}{1000{\varrho }^4}{(\wp -1)}^{3}sin\left(\frac{\pi \eta }{\varrho }\right){cos}^2\left(\frac{\pi \eta }{\varrho }\right)+\frac{21{\pi }^4}{1000{\varrho }^4}{(\wp -1)}^{3}si{n}^3\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ +\frac{12{\pi }^3}{1000{\varrho }^3}{(\wp -1)}^3{cos}^3\left(\frac{\pi \eta }{\varrho }\right)+\frac{3}{100000}{(\wp -1)}^5{sin}^6\left(\frac{\pi \eta }{\varrho }\right)\hfill \end{array}\right.,\hfill \\ \hfill ⋮.\end{array}$$

The additional components of $\underline{\mathcal{Q}}q(q\ge 3)$ of the EADM solution may be conveniently discovered in an analogous manner. Additionally, as the recursive approach progresses, the reliability of the acquired result increases substantially, and the determined solution becomes increasingly relatively equal to the interpretive framework. Consequently, we have arrived at the accompanying responses, which are organised in a series form.

$$\begin{array}{c}\hfill \tilde{\mathcal{Q}}(\eta ,\xi ,\wp )={\tilde{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\tilde{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\underline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\underline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & ={\overline{\mathcal{Q}}}_0(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+{\overline{\mathcal{Q}}}_1(\eta ,\xi ,\wp )+\dots .\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathcal{Q}}(\eta ,\xi ,\wp )& & =(\wp -1)\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ & & +\frac{1}{1000{\varrho }^4}\left[(\wp -1)sin\left(\frac{\pi \eta }{\varrho }\right)\left(100{\varrho }^4(\theta -1)-100{\pi }^4+200{\pi }^2{\varrho }^2\right)-{\varrho }^4{(\wp -1)}^3{sin}^3\left(\frac{\pi \eta }{\varrho }\right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}(100{\varrho }^4(\theta -1)-100{\pi }^4+2000{\pi }^2{\varrho }^2)[\frac{(\theta -1)(\wp -1)\pi }{1000{\varrho }^5}cos\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ -\frac{{\pi }^4}{1000{\varrho }^8}(\wp -1)sin\left(\frac{\pi \eta }{\varrho }\right)+\frac{2{\pi }^2}{1000{\varrho }^6}(\wp -1)sin\left(\frac{\pi \eta }{\varrho }\right)-\frac{3}{100000{\varrho }^4}{(\wp -1)}^3{sin}^4\left(\frac{\pi \eta }{\varrho }\right)]\hfill \\ -{sin}^2\left(\frac{\pi \eta }{\varrho }\right)cos\left(\frac{\pi \eta }{\varrho }\right)\left(\frac{3\pi (\theta -1)}{1000\varrho }{(\wp -1)}^3+\frac{42{\pi }^3}{1000{\varrho }^3}{(\wp -1)}^3\right)\hfill \\ -\frac{60{\pi }^4}{1000{\varrho }^4}{(\wp -1)}^{3}sin\left(\frac{\pi \eta }{\varrho }\right){cos}^2\left(\frac{\pi \eta }{\varrho }\right)+\frac{21{\pi }^4}{1000{\varrho }^4}{(\wp -1)}^{3}si{n}^3\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ +\frac{12{\pi }^3}{1000{\varrho }^3}{(\wp -1)}^3{cos}^3\left(\frac{\pi \eta }{\varrho }\right)+\frac{3}{100000}{(\wp -1)}^5{sin}^6\left(\frac{\pi \eta }{\varrho }\right)\hfill \end{array}\right.\hfill \\ & & +\dots ,\hfill \\ \hfill \overline{\mathcal{Q}}(\eta ,\xi ,\wp )& & =(1-\wp )\frac{1}{10}sin\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ & & +\frac{1}{1000{\varrho }^4}\left[(1-\wp )sin\left(\frac{\pi \eta }{\varrho }\right)\left(100{\varrho }^4(\theta -1)-100{\pi }^4+200{\pi }^2{\varrho }^2\right)-{\varrho }^4{(1-\wp )}^3{sin}^3\left(\frac{\pi \eta }{\varrho }\right)\right]\frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}\left\{\begin{array}{c}(100{\varrho }^4(\theta -1)-100{\pi }^4+2000{\pi }^2{\varrho }^2)[\frac{(\theta -1)(1-\wp )\pi }{1000{\varrho }^5}cos\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ -\frac{{\pi }^4}{1000{\varrho }^8}(1-\wp )sin\left(\frac{\pi \eta }{\varrho }\right)+\frac{2{\pi }^2}{1000{\varrho }^6}(1-\wp )sin\left(\frac{\pi \eta }{\varrho }\right)-\frac{3}{100000{\varrho }^4}{(1-\wp )}^3{sin}^4\left(\frac{\pi \eta }{\varrho }\right)]\hfill \\ -{sin}^2\left(\frac{\pi \eta }{\varrho }\right)cos\left(\frac{\pi \eta }{\varrho }\right)\left(\frac{3\pi (\theta -1)}{1000\varrho }{(1-\wp )}^3+\frac{42{\pi }^3}{1000{\varrho }^3}{(1-\wp )}^3\right)\hfill \\ -\frac{60{\pi }^4}{1000{\varrho }^4}{(1-\wp )}^{3}sin\left(\frac{\pi \eta }{\varrho }\right){cos}^2\left(\frac{\pi \eta }{\varrho }\right)+\frac{21{\pi }^4}{1000{\varrho }^4}{(1-\wp )}^{3}si{n}^3\left(\frac{\pi \eta }{\varrho }\right)\hfill \\ +\frac{12{\pi }^3}{1000{\varrho }^3}{(1-\wp )}^3{cos}^3\left(\frac{\pi \eta }{\varrho }\right)+\frac{3}{100000}{(1-\wp )}^5{sin}^6\left(\frac{\pi \eta }{\varrho }\right)\hfill \end{array}\right.\hfill \\ & & +\dots .\hfill \end{array}$$

Given the above constraints and our computational resources, Figure 9a,b depicts the comprehension of the impact of two-layer and multiple-layer 3D representations for Example 5. These plots help us to understand the behaviour of probability density function with changing space and time-scale variables via fuzzifications.

The analysis demonstrates that even as time penetrates, the visualization of $\mathcal{Q}(\eta ,\xi ;\wp )$ will show oscillatory behaviour.

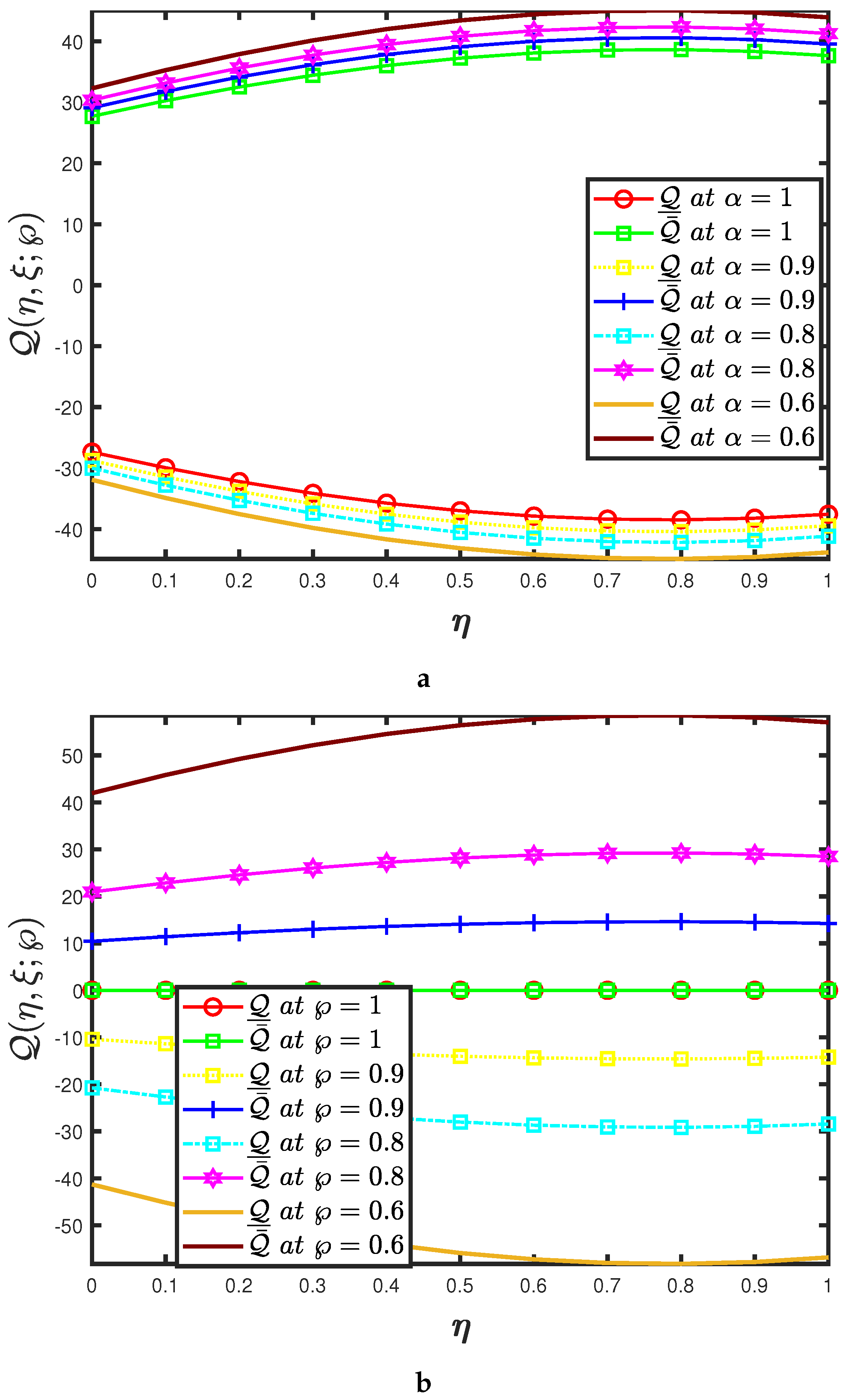
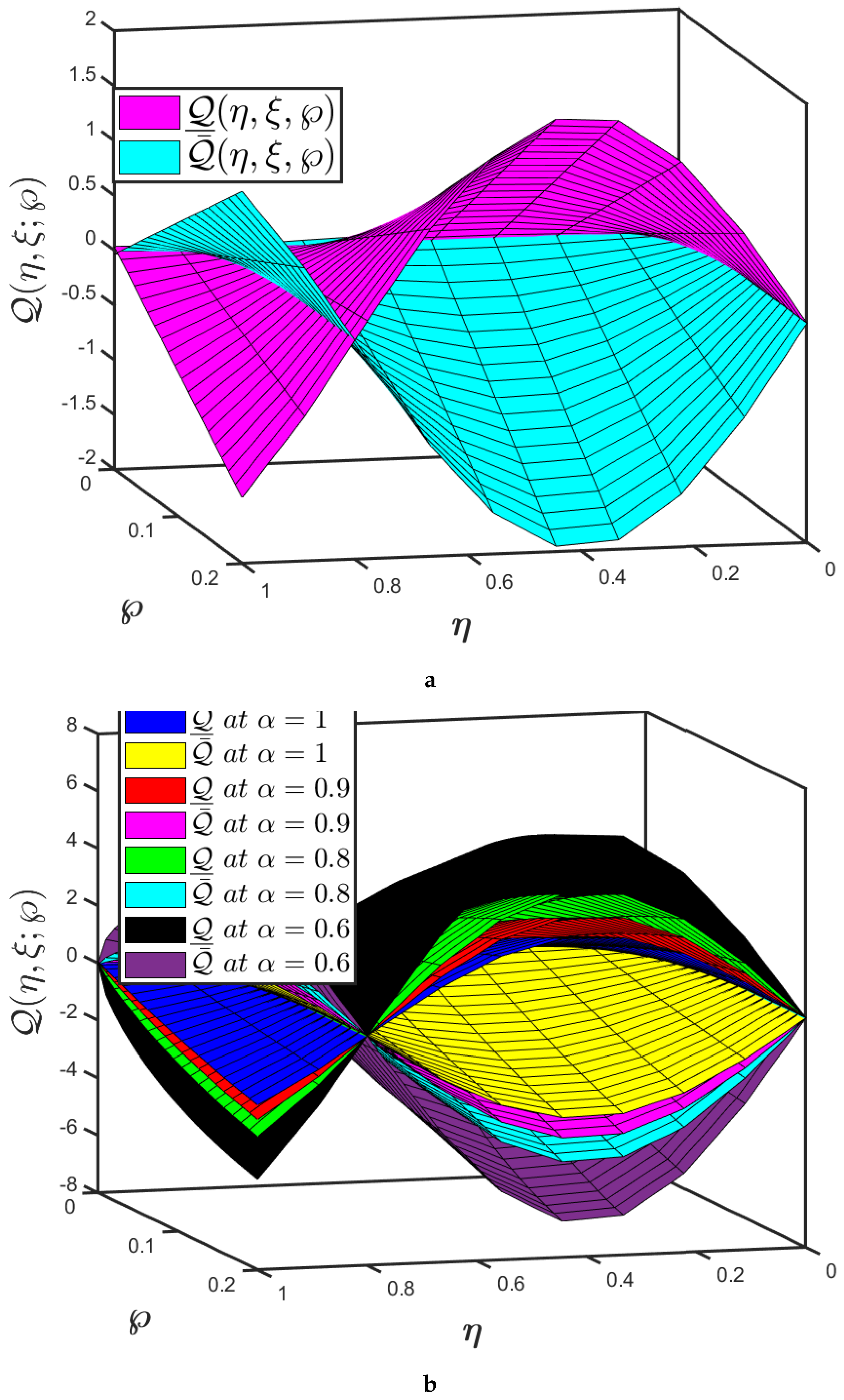
• The mapping effectiveness of the suggested algorithm, $\mathcal{Q}(\eta ,\xi ;\wp )$ is displayed in Figure 10a for the constant parameter $\theta =5$ and $\varrho =5$. The analysis demonstrates a minor improvement in $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ with the decrease in $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$;
• The uncertainty parameter of the mappings $\underline{\mathcal{Q}}(\eta ,\xi ;\wp )$ and $\overline{\mathcal{Q}}(\eta ,\xi ;\wp )$ are presented in Figure 10a,b and it elaborates the behaviour of specified fractional order of the mapping at various uncertainty parameters;
• The nature of the probability density function is controlled by dispersion, fractional order and uncertainty parameters, according to these findings. The behaviour of hydrodynamic stability is defined by the oscillatory wave patterns of the bifurcation parameter. Further, (5) describes the convective describes the convective heat current in a Rayleigh–Bénard cell and the nature of hydrodynamic stability.

Figure 10. (a) Two-dimensional representation of Example 5 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.7,$ $\varrho =0.8,\theta =0.5$ and $\xi =0.9$ (b) Two-dimensional representation of Example 5 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.7$ and $\xi =0.9$.

Figure 10. (a) Two-dimensional representation of Example 5 established by the different fractional-order with uncertainty parameters assumed to be $\wp =0.7,$ $\varrho =0.8,\theta =0.5$ and $\xi =0.9$ (b) Two-dimensional representation of Example 5 established by the different uncertainty parameters and fractional-order assumed to be $\alpha =0.7$ and $\xi =0.9$.

Remark 5.

When $\underline{\chi }(\wp )=\overline{\chi }(\wp )=\wp ,$ then both solutions of Example 5 leads to the classical solution of Alrabaiah et al. [58].

7. Conclusions

The Swift–Hohenberg model deals with pattern-forming behaviour. This involves the relationship between noise in bifurcations, pattern selection, spatiotemporal chaos, and the dynamics of defects. The governing equation is utilized as a nonlinear PDE. In contrast, in an uncertain context, the crisp operators are incapable of representing any mechanical structure. As a result, uncertain functions offer a better way to represent the scientific process in this case. We explored the SH equation in a fuzzy approach, taking into account the uncertainty in the IC. We have generalized the fractional SHe to the fuzzy fractional SH model in the CFD system in this research. To obtain the approximate expression of the suggested problem in its parametric form, we then used EADM. We identified numerous illustrations to support the intended methodology and achieved a parametric solution for each case. We also presented simulations for two dimensional and surface plots with varying fractional-order and uncertainty levels. We could observe in the illustrations that the outcome profiles indicate the fuzzy consequences since they fulfil the fuzzy number requirements. The suggested scheme’s convergence and error analysis have been addressed. Based on simulations, we have identified that fractional-order solution contours resemble integer-order ones. In a nutshell, the imprecise logic associated with FC enables a methodology for conducting efficiently in an ambiguous environment. We shall look into an analogous topic in the upcoming studies, incorporating various fuzzy fractional operators and solution methodologies.